Exploring the potential energy surface of small lead clusters using the gradient embedded genetic algorithm and an adequate treatment of relativistic effects

Abstract

It is a well-known fact that theoretical methodologies play a crucial role to assure an adequate structural assignment of gas-phase clusters. Particularly, in heavy-element containing clusters the inclusion of relativistic effects (scalar and spin–orbit coupling) can significantly affect their chemistry. Therefore, these effects become the keystone on their structural determination. In our work, the way in which relativistic effects were treated, as well as their influence in the process of an adequate identification of lowest-energy isomer (the global minima – “GM” – energy structure), were evaluated in small lead clusters. The potential energy surfaces of small Pb_n (n = 3–10) clusters was explored by means of the gradient embedded genetic algorithm program (GEGA). Subsequently, the most stable isomers were re-optimized incorporating relativistic effects through two different approximations: (i) using relativistic effective core potentials (RECPs) or pseudopotentials, which mimics the scalar and spin–orbit coupling relativistic effects (SR and SO) of the core electrons; and (ii) using relativistic Hamiltonians (with proper all-electron basis sets), like, the zeroth-order regular approximation (ZORA) to the Dirac equation, in which the scalar (SR) and spin–orbit coupling (SOC) relativistic effects were also included. The results evidence that methodologies including SOC effect allow to identify the GM energy structure correctly in all the studied cases. Besides, the GEGA algorithm, using a modest RECP, provides good initial structures that become GM after re-optimization at the SOC level.

---

Introduction

Atomic clusters are fascinating systems that have increasingly attracted the attention of the world of science and technology. This is due to their unique electronic structures and resulting unusual physical and chemical properties. In the cluster research field, structural characterization is essential to rationalize their unique composition and size-dependent properties (ranging from a diatomic molecule to a maximum size before becoming the bulk).^1,2

Nowadays, the identification of the global minimum energy (GM) structure is an indispensable task in predictive theoretical studies of atomic clusters.^3–10 In gas-phase experiments, it is possible to adjust the conditions to obtain the energetically preferred isomer as a major product, thus obtaining the GM energy structure. However, the GM prediction is a great challenge that has motivated the proposal of several computational strategies to explore the potential energy surface (PES) looking for the GM.^3–10

The most well-known advances evaluate many candidate structures, which are discriminated according to their relative stability (minimum energy). This process is commonly performed in two or more steps. Initially, a large population is evaluated using computationally cheaper methodologies and finally, a more accurate level of theory is used in the calculation of the geometric and electronic structures of the most promising individuals. The success in identifying the GM depends on many factors, such as: the PES complexity of the clusters to be studied, the number of evaluated candidates, the way they have been obtained and the methods used for both energy calculations and geometry optimizations. Each of these factors may be particularly important depending on the nature of the system under study.

In this work, we are interested in evaluating how the treatment of relativistic effects influences the identification of the GM energy structure of small lead clusters (Pb_n, n = 3–10). For this purpose, a genetic algorithm (GA) inspired by the Darwinian evolution theory, was used.^11,12 This GA mimics the natural selection and evolution processes in nature, meaning that only the fittest candidates can survive. Specifically, the gradient embedded genetic algorithm (GEGA) developed by Alexandrova et al.,^13,14 in combination with DFT calculations, was employed.

Our interest in these systems is due to the abundant experimental and theoretical studies concerning their structural elucidation when compared with our results.^15–23 From an experimental view, small lead clusters have been obtained via laser vaporization and determined by ion mobility,^16,24–28 gas phase ion electron diffraction,^27–29 and photoionization mass spectrometry.^21,30–32 In these studies, “magic” numbers were observed in size distributions under a variety of ionization conditions.^{16,21,24–32}

Moving on to a theoretical view, some studies have been carried out using different approximations for the inclusion of relativistic effects. For instance, B. Wang et al.,¹⁷ performed ab initio total-energy pseudopotential calculations on neutral and negatively charged Sn_n and Pb_n (n = 3–10) clusters. They discovered a poor agreement between the computed density of states and the main features of the experimental photoelectron spectra, in contrast to what happens with the lighter Si_n clusters. They attributed it to large spin–orbit splitting effects, which had been neglected in their calculations. More recently, DFT in conjunction with projector augmented wave (PAW) pseudopotential and plane wave basis set calculations were carried out.^18,22 In these studies, PAW pseudopotential was generated taking scalar relativistic corrections into account, correcting the stability trends based on binding energy calculations, but still exhibiting a poor description of the spin–orbit splitting energies.

Particularly, since the Pb is a 6p-block element, the importance of scalar and spin–orbit coupling effects (which can be included through relativistic Hamiltonians or relativistic-corrected pseudopotentials) lies into the “s”- and “p”-orbital energetics as has been firstly described in 1979 by Pitzer and Pyykkö–Desclaux, on independently works.^33,34 These topics were later extensively studied by M. Klobukowski et al.,³⁵ L. Visscher et al.³⁶ for atoms and dimers, and, P. Schwerdtfeger et al.,³⁷ T. Enevoldsen et al.,³⁸ S. Komorovsky et al.,³⁹ for group-14 halides and hydrides. In all those contributions, the authors point out the relevance of including spin–orbit coupling corrections in the description and quantification of bond lengths and bonding energies, mainly; as well as in other derived electronic properties like ionization potentials, electron affinities and valency changes. The latter, has been extensively study by K. A. Peterson et al., particularly from the side of the pseudopotentials and/or ECP.^40,41 In these works, it has been put on evidence the difficulties for pseudopotentials and/or RECP to reproduce experimental geometrical parameters (bond distances) when oxidation states of heavy-elements were change drastically.

As can be seen, until this point the evaluated structures were built according to chemical intuition or based on experimental data of analogous systems. However, there are a few studies that use GA methods to identify the lead cluster GM structures.^15,19 In these works, spin–orbit coupling was either not considered during the search or included at a later step for energetic corrections only.^16,19,22,23 Based on these studies, both scalar and spin–orbit effects are important for a proper structural determination and electronic structure description of lead clusters. Consequently, structural search via GA methods and including relativistic effects (scalar and spin–orbit coupling) emerges as an adequate alternative.

Lead clusters are also attractive for their potential use as assembly blocks of new materials that can store hydrogen reversibly, with high gravimetric and volumetric densities.⁴² Considering this, metal organic frameworks (MOFs) containing a lead dimer have been recently proposed as promising hydrogen storage systems due to their large superficial area, their energetically favourable adsorption sites, and their high adsorption energies per site.⁴³ Another interesting application of lead clusters and their derivatives is on the design of photovoltaic solar cells, being lead perovskites one of the most suitable materials to produce renewable energy.^44–46 Finally, the wealth of cluster chemistry in the main group elements highly requires to clarify the cautions which should be taken to avoid the risks of erroneous interpretations in clusters of heavier elements.

Computational details

The exploration of the Pb_n (n = 3–10) PES was performed using the GEGA program (for a detailed description of GEGA see the ref. 11 and 12) at PBE0 (ref. 47 and 48)/LANL2DZ⁴⁹ level of theory. The geometries of the most stable isomers found by GEGA, in a range of 30 kcal mol⁻¹, were further re-optimized, in both singlet and triplet multiplicities, with two different approaches: (a) through relativistic effective core potentials (RECPs)^50,51 PBE0/Def2-TZVP-SR⁵² and PBE0/CRENBL-SO,⁵³ which incorporates the scalar and spin–orbit relativistic effects, respectively; and (b) using the relativistic Hamiltonian ZORA at PBE0/TZ2P level,⁵⁴ which includes scalar and spin–orbit coupling relativistic effects (SR and SO), respectively. All structures were verified as true minima on the PES by the absence of imaginary frequencies in their computed harmonic frequencies. All the calculations were carried out in gas phase considering lead atoms with oxidation state zero (Pb⁰) as units of assembling in the clusters. In this way, the methodology overcome the deficiencies of pseudopotentials, ECPs and RECPS on describe geometrical parameters when oxidation states vary as was explained by K. A. Peterson in ref. 40 and 41.

To compute the electronic structure as accurately as possible, single point energy calculations, through different Hamiltonians (the four-component Dirac-Coulomb (DC)^55–57 and the exact two-component (X2C),^58–64 both at PBE0/DYALL.V3Z⁶⁵ level), were performed on the GM identified by ZORA-SO calculations.

Cluster stability was further analysed according to their binding energies, second order difference in total energies and HOMO–LUMO gaps. Finally, the generalized gradient approximation, PBE methodology, was employed under the same procedure as the PBE0. All mentioned calculations were performed with the following set of computational codes: GAUSSIAN 09,⁶⁶ NWCHEM-6.5,^66,67 ADF2013,⁶⁸ and DIRAC14.⁶⁹

Results and discussions

Global and local minima analysis

Initially, the GEGA program was used in combination with PBE0 hybrid functional and the basis set LANL2DZ (to geometry optimization) to search the best structures of the Pb_n (n = 3–10) clusters according to their stability. The lowest energy isomers, in a range of 30 kcal mol⁻¹, were selected for a subsequent re-optimization, using different approximations to include relativistic effects. These results were divided into two groups, those that include relativistic effects at the scalar relativistic (SR) level, and those that additionally incorporate spin–orbit coupling relativistic (SOC) effects (Fig. ESI-1 and Table ESI-1†).

At the SR level, which also includes the results delivered by GEGA, the GM of nearly the whole set of clusters was identified as a singlet multiplicity isomer, with the most stable triplet lying at approximately 10 kcal mol⁻¹ above it. Only one exception was observed: for the Pb₃, the triplet structure proved to be more stable than the singlet one by approximately 6.6 kcal mol⁻¹. These results agree with the investigations reported by Wang et al.,¹⁵ and Rajesh et al.²² Interestingly, when the SOC effect was included, the GM of Pb₃, Pb₅, Pb₆, Pb₈ and Pb₁₀ changed with respect to those identified by SR calculations (see Fig. 1 and Table 1). It is important to note that different approximations into each scheme, SR or SOC effects, provided the same lowest energy isomer. This point will be further discussed in the next paragraphs. Because the incorporation of relativistic effects could lead to significant changes in their energetics and geometries, a comparative study of the relative energies for the different local minima found by GEGA (and the re-optimized structures at different methodologies for the inclusion of relativistic effects) was carried out. The results shown in Table 1 evidence a common feature: relativistic effects, through RECPs and ZORA Hamiltonian, provided similar trends regarding low-lying isomers prediction, when SR and SOC versions were compared.

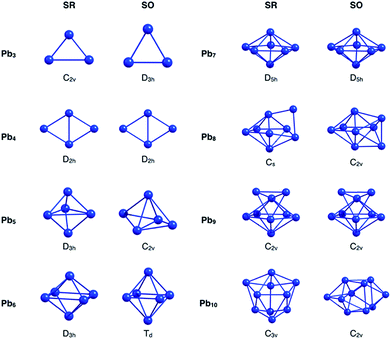Fig. 1 Singlet state global minima geometries for Pb_n systems, optimized at PBE0/Def2-TZVP-SR, PBE0/CRENBL-SO, PBE0/TZ2P-SR and PBE0/TZ2P-SO levels of theory.

Table 1 Isomer relative energies in kcal mol⁻¹ respect to global minima in singlet state^a

System	Isomers	LANL2DZ (SR)	Def2-TZVP (SR)	ZORA (SR)	CRENBL (SO)	ZORA (SO)
a Results in parenthesis correspond to PBE calculations. *These structures do not converge at this level of theory.
Pb3	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)
	Isomer 02	9.4	12.1 (7.9)	12.2 (8.2)	0.0 (0.0)	0.0 (0.0)
	Isomer 01-t	−4.2	−6.7 (−3.2)	−6.7 (−3.1)
Pb4	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)
	Isomer 02	27.7	21.8 (19.2)	21.5 (18.7)	6.6 (7.2)	8.7 (9.6)
Pb5	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	10.9 (7.5)	11.2 (8.6)
	Isomer 02	7.8	9.5 (9.0)	9.3 (9.1)	1.0 (0.9)	0.0 (0.1)
	Isomer 03	15.4	13.9 (14.3)	13.7 (14.0)	0.0 (0.0)	0.2 (0.0)
	Isomer 04	7.8	31.2 (29.9)	9.3 (9.1)	8.9 (8.3)	9.2 (8.6)
Pb6	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)
	Isomer 02	11.7	14.8 (13.3)	14.8 (13.6)	0.0 (0.0)	0.0 (0.0)
	Isomer 03	32.3	39.0 (36.6)	38.8 (36.7)	0.0 (0.0)	0.0 (0.0)
	Isomer 04	33.7	41.1 (37.0)	41.1 (38.1)	0.0 (0.0)	0.0 (0.0)
Pb7	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)
	Isomer 02	24.3	25.4 (22.2)	24.4 (22.5)	0.0 (0.0)	0.0 (0.0)
	Isomer 03	24.4	26.2 (24.0)	25.8 (24.5)	22.3 (20.2)	22.8 (21.5)
	Isomer 04	22.1	26.9 (23.7)	25.6 (24.4)	0.0 (0.0)	0.0 (0.0)
Pb8	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)	0.0 (0.0)
	Isomer 02	9.9	9.3 (7.2)	9.9 (7.5)	11.6 (8.9)	12.9 (10.5)
	Isomer 03	9.0	11.3 (10.6)	11.4 (10.8)	21.4 (7.8)	11.7 (11.1)
	Isomer 04	13.3	14.0 (10.7)	13.8 (12.6)	0.0 (0.0)	0.0 (0.0)
	Isomer 05	14.1	15.6 (12.0)	15.8 (14.1)	17.8 (0.0)	0.0 (0.0)
	Isomer 06	18.4	21.5 (18.0)	21.9 (20.4)	0.0 (0.0)	0.0 (0.0)
	Isomer 07	17.5	22.2 (19.4)	22.4 (21.6)	19.8 (16.4)	18.8 (18.4)
	Isomer 08	26.5	29.0 (23.8)	29.1 (26.2)	*(8.8)	8.5 (8.1)
Pb9	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	(0.0)	0.0 (0.0)
	Isomer 02	12.0	16.1 (15.3)	16.3 (15.9)	(15.2)	14.9 (15.4)
	Isomer 03	18.6	20.0 (18.7)	19.4 (19.0)	(17.1)	(17.4)
	Isomer 04	20.1	21.7 (19.7)	20.8 (20.0)	(18.8)	(18.8)
	Isomer 05	19.7	22.4 (20.4)	21.8 (20.7)	(16.6)	(16.2)
	Isomer 06	22.6	24.6 (22.9)	24.1 (23.2)	(18.8)	(19.2)
	Isomer 07	23.5	28.1 (26.7)	28.3 (27.6)	(23.5)	(23.6)
	Isomer 08	30.9	35.5 (31.7)	35.3 (32.4)	(29.8)	(30.3)
	Isomer 09	31.5	35.7 (31.3)	35.5 (32.2)	(31.3)	(29.9)
	Isomer 10	31.9	38.4 (36.2)	0.0 (0.0)	(32.9)	(31.7)
Pb10	Isomer 01	0.0	0.0 (0.0)	0.0 (0.0)	(1.9)	(0.5)
	Isomer 02	1.0	0.7 (0.9)	1.0 (0.9)	(4.2)	(0.5)
	Isomer 03	3.6	1.1 (0.4)	0.3 (0.3)	(0.0)	(0.0)
	Isomer 04	18.1	13.9 (13.2)	13.7 (12.8)	(12.4)	(11.5)

---

This suggests that the relative energies are quite similar when the scalar relativistic or spin–orbit coupling effects are included. These results are significant from the viewpoint of the computational cost, since the SO-ECP calculations were found to be significantly less expensive than SO-ZORA.

Another interesting aspect corresponds to a reduction in the number of isomers, when structures were optimized by various methods including spin–orbit coupling effects. The most dramatic situation, among the studied cases, was the one of the Pb₆ cluster. For this cluster, Table 1 shows four isomers identified by SR-calculations, which converged to just one isomer after SO-optimizations. Similar results were found for the Pb₇ and Pb₈ clusters (Fig. ESI-2†).

Going back to Fig. 1, we will focus our attention now on the GM structural changes after including spin–orbit coupling effects in the optimizations. The small analysed cluster, Pb₃, changes from an isosceles C_2v (SR-singlet) to an equilateral D_3h (SOC) triangle. The same resulting D_3h symmetry was obtained when the calculation was performed in triplet multiplicity, but without the inclusion of the SOC relativistic effects. Pb₅ and Pb₁₀ clusters deserve special attention. These systems change with the inclusion of the SOC effect from a D_3h to a less symmetric C_2v structure and from a C_3v to a less symmetric C_2v structure for the Pb₅ and Pb₁₀, respectively. However, it is important to mention that these SOC-GM (GM including SR + SOC effects) did not come from their respective SR-GM (GM just including SR effect). Instead, these GM structures were obtained from a third SR-isomer for both Pb₅ and Pb₁₀ systems. Furthermore, the Pb₅ and Pb₁₀ SR-GM became the fourth- and the second-isomer with the inclusion of the SOC effect. Additionally, since the energy difference among structural isomers for the Pb₅ and the Pb₁₀ systems is respectively small under a SOC scheme, it can be concluded that these systems can coexist.

In the case of Pb₆, an increase of the axial-atoms distance (∼0.9 Å) produce a change from D_4h to T_d symmetry after optimizing the SR-GM with SOC effects. Similar results were obtained by M. Kühn et al.⁷⁰ and M. K. Armbruster et al.⁷¹ using two-component calculations.

The greatest distortion was observed in the Pb₈ system, changing from an edge-capped pentagonal bipyramid (C_s) to a face-bi-capped octahedron (C_2v) structure. Finally, in the case of isomers, which are not the global minimum, small geometrical variations were found by incorporating the SOC effects in the calculation (Table ESI-1†). These findings evidence that the SOC effect needs to be considered to identify the correct GM structures of small lead clusters. Furthermore, on the studied cases, the set of low-lying isomers identified by GEGA, in conjunction with the economical ECP (LANL2DZ), provide the GM isomers after re-optimization with SOC methods. This validates the use of RECP in the GEGA procedure, which has been routinely used in the past.

From these previous results, it can be stated that inclusion of spin–orbit coupling relativistic effects could lead to important changes in the geometrical parameters of small lead clusters. Now, we are interested in evaluating the influence of SOC effects on the electronic structure of these clusters. To achieve this, the electronic structure of the GM structures was analysed by means of the X2C and 4C-DC Hamiltonians.

Electronic structure analysis

A starting point is to analyse the cause of the deformation of the Pb₃ cluster, when only SR effects and SR + SOC effects are included. The SR calculations showed that the global minimum in singlet multiplicity (C_2v – isosceles triangle) was less stable than the corresponding triplet multiplicity (D_3h – equilateral triangle) by 6.6 kcal mol⁻¹. This difference could be rationalized in terms of the composition of the highest occupied molecular orbital (HOMO) for each isomer: firstly, in the D_3h triplet structure, the HOMO is a four-fold degenerate molecular orbital with symmetry E′, in which each α electron could occupy one single molecular orbital, thus obtaining a stable electronic conformation. Secondly, in the singlet structure, the HOMO showed partial occupations, two electrons sharing one of the two E′ molecular orbitals. Subsequently, the degeneration of this molecular orbital was broken by the Jahn–Teller phenomenon distorting towards an isosceles triangle (C_2v symmetry), where now the HOMO orbital with B₁ symmetry has two electrons in the same molecular orbital.

Moving on to the relativistic framework, the HOMO was split in two different Kramer's spinors, E_3/2 ⊕ E_5/2, by the SOC effect, thus conserving its D_3h symmetry and solving the problem of partial occupation (see Fig. 2). A similar situation was presented for the hexamer system, where the SOC calculations symmetrize this molecule to a T_d symmetry point group. When a SR calculation was used for the Pb₆ system under this symmetry constraint, the HOMO showed partial electron occupation due to the presence of a six-fold degenerate molecular orbital with T_d symmetry. To solve this, the hexamer systems should reduce its symmetry to a D_4h, decreasing the length between the axial lead atoms by 0.9 Å, because of the Jahn–Teller distortion.

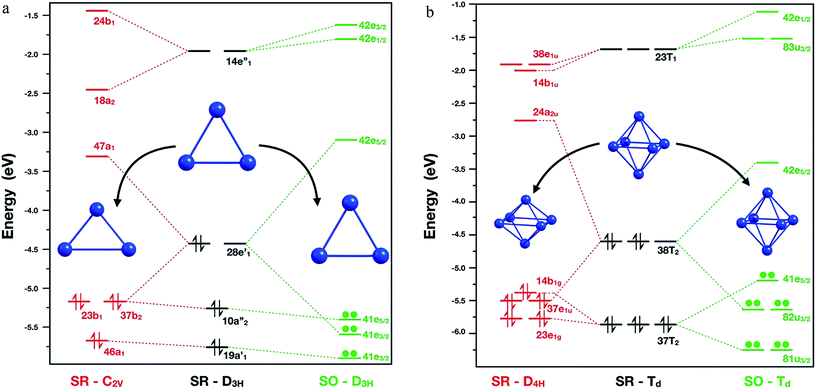Fig. 2 Molecular orbital diagram for Pb₃ (left) and Pb₆ (right) systems calculated at PBE0/TZ2P/ZORA-SR and PBE0/TZ2P/ZORA-SO levels of theory, respectively.

Interestingly, as can be seen in Fig. 2, the SOC calculations solve this problem by splitting the HOMO in U_3/2 ⊕ E_5/2 Kramer's spinors. Similar results for Pb₃ and Pb₆ systems were found by Balasubramanian et al.^72,73 using multiconfigurational calculations. In the case of Pb₈ system, the structural changes can be attributed to the decoupling and stabilization–destabilization of the frontier molecular orbitals, which provides more flexibility to the system (Fig. ESI-3†). Finally, the Pb₅ and Pb₁₀ cluster global minimum changes will be discussed later in terms of the HOMO–LUMO gap stability criterion. These results show that the inclusion of the SOC effect is fundamental for an adequate description of the electronic structure and for the structure prediction of the studied clusters.

Cluster stability analysis

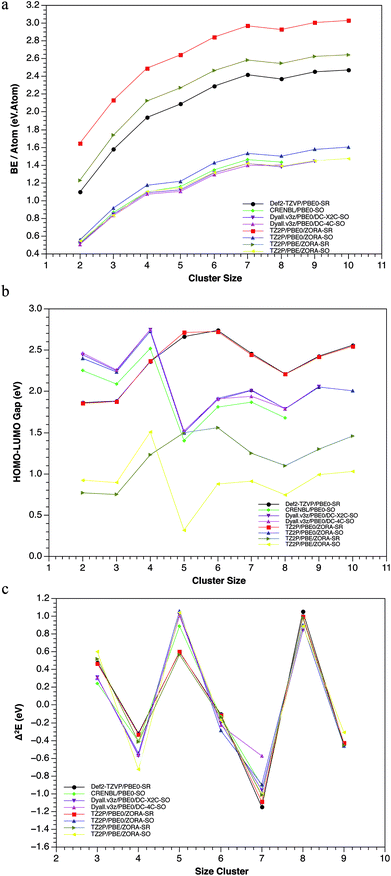
Several experimental studies have shown that the Pb_n clusters, with n = 4, 7, 10 and 13 exhibit the highest stability and, therefore, the greatest abundance.^18,19,21,74 From a theoretical point of view, it is well-known that some electronic properties as the Binding Energy (BE), HOMO–LUMO gap (H–L) and the second order difference in total energy (Δ²E), can be useful to predict the thermodynamic and chemical stability of clusters. Most computational works have used these three criteria to determine the stability of lead clusters.

Nevertheless, a discrepancy has frequently been found between the BE and H–L, especially for the heptamer system.^15,20,22 Generally, the use of different schemes (SR and SR + SOC) can provide various results for the same properties. For instance: (1) the experimental bulk binding energy per atom of 2.03 eV per atom, is overestimated in the case of SR-calculations and underestimated for SR + SOC-calculations. However, a good agreement between the experimental binding energies^72,75,76 (0.42, 0.77, 1.06 eV per atom) and the calculated ones, including SR + SOC effect (0.48, 0.83, 1.07 eV per atom), was found for the dimmer, trimer and tetramer cluster, respectively.

In addition, some lead clusters showed similar trend compared with other previous works,^15,19,22 showing peaks at n = 4, 7 and 10, indicating its high stability (see Fig. 3). (2) The HOMO–LUMO gap (which is a chemical reactivity descriptor where a high value indicates high stability) also showed significant differences for both methodologies: while in the SR scheme, the Pb₅ and Pb₆ systems have the highest values; in the SOC scheme, the Pb₄ and Pb₇ are the highest, evidencing a conflictive prediction of the most stable compounds (according to this descriptor).

Fig. 3 Binding energy (top), HOMO–LUMO gap (middle) and second order difference in total energy (bottom) behaviours, calculated at Def2-TZVP-SR/PBE0, TZ2P-SR/PBE0, CRENBL-SO/PBE0, TZ2P-SO/PBE0, DYALL.3VZ-X2C-SO/PBE0 and DYALL.2VZ-DC-SO/PBE0 levels of theory.

These differences can be attributed to structural and energetic changes on the isomers when SR + SOC effects were included in the calculations. Another important aspect to be highlighted is the fact that the GM-structures were almost the ones that exhibited the largest H–L gap (Table ESI-2†). There is only one exception, the Pb₇ system. In the Pb₇, the third isomer showed a larger H–L gap value at SR methodology. However, when the SOC was incorporated, this third SR-isomer became the SOC-GM. This allows us to point out that there are other stabilizing factors with significant implications. Examples of this are the structural changes in the GM of Pb₅ and Pb₁₀ clusters when SR + SOC effects were incorporated. In both clusters, the SR-GM showed an appreciable decrease in the H–L gap of the global minimum, while for the other isomers this value remains almost unchanged, i.e., the stabilization-destabilization of the frontier molecular orbitals due to SOC was more important for the GM than for the other isomers. Finally, the second order difference in total energy, showed that the tetramer and heptamer systems are the most stable in agreement with previous results and with the ones reported in literature.^15,18,19,22 In conclusion, it can be observed how these three criteria, at the SR + SOC scheme, indicates that the Pb₄, Pb₇ and Pb₁₀ clusters are the most stable, which agrees with the experimental evidence.

Conclusions

The main conclusion is that both scalar and spin–orbit coupling relativistic effects are fundamental to describe the geometrical parameters and electronic structure properties of small lead clusters. Particularly, in some systems, the use of the SR + SOC effects allows us to provide a rational explanation for the preference of certain geometries (Pb₅ and Pb₁₀), distortions (Pb₃ and Pb₆) and stabilities (Pb₄, Pb₇ and Pb₁₀), which are mainly due to the close relationship among these parameters with the electronic structure. Particularly, the molecular p-orbital (spinor in the relativistic framework) splitting of the valence region, which is a directly consequence of the SOC (as was explained time ago by Pitzer, Pyykkö and Desclaux), show that many of the anomalous departures from periodic table trends for heavy atoms can be attributed to these relativistic effects. For that reason, a deeply understanding of the interaction between relativistic shell-structure effects and their corresponding spatial conformations will form the impact of relativity on chemistry, and specifically on the structural elucidation of heavy-element clusters.

From the methodological viewpoint, it was found that the inclusion of the SR + SOC effects by means of RECPs or self-consistent Hamiltonians showed similar results and trends, with the advantage of requiring less computational cost when using pseudopotentials or RECPs. From this, the use of pseudopotentials or RECPs arise as a low-cost computational alternative to accurately describe geometrical parameters, as well as some electronic and energetic trends. Nevertheless, the lack of inclusion of relativistic corrections on pseudopotentials or ECPs (like LANL2DZ or Def2-TZVP) provide the same results that SR-ZORA Hamiltonian (which only includes SR effects). This pinpoint that SOC is essential for the structural elucidation of the global minima and the relative energies of stable isomers. In addition, the properties derived from fine or hyperfine electronic structures and splitting energetics deserve more rigorous approximations and methodologies, like the ones based on the resolution of the Dirac's equation in conjunction of 4C-wavefunctions.

Finally, the use of PBE xc-functional (GGA) showed very good results with less computational cost in comparison with those obtained from the calculations with the hybrid PBE0 xc-functional.

Conflicts of interest

The authors state that there are no conflicts to declare.

Acknowledgements

F. F. and E. O. are grateful for the financial support of Colciencias “El Patrimonio Autónomo Fondo Nacional de Financiamiento para la Ciencia, la Tecnología y la Innovación Francisco José de Caldas” (Grant No. 211665842965)”. W. T. acknowledges UNAB regular grant No. DI-1365-16/RG. W. R. acknowledges CONICYT for his postdoctoral Project FONDECYT/Postdoctorado-2016 No. 3160388. Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02).

Notes and references

1. A. W. Castleman and S. N. Khanna, J. Phys. Chem. C, 2009, 113, 2664.
2. S. A. Claridge, A. W. Castleman, S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, ACS Nano, 2009, 3, 244.
3. D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B, 1995, 51, 12947.
4. P. Bobadova-Parvanova, K. A. Jackson, S. Srinivas, M. Horoi, C. Köhler and G. Seifert, J. Chem. Phys., 2002, 116, 3576.
5. I. Rata, A. A. Shvartsburg, M. Horoi, T. Frauenheim, K. W. M. Siu and K. A. Jackson, Phys. Rev. Lett., 2000, 85, 546.
6. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671.
7. R. O. Jones, Angew. Chem., Int. Ed., 1991, 30, 630.
8. J. F. Pérez, C. Z. Hadad and A. Restrepo, Int. J. Quantum Chem., 2008, 108, 1653.
9. B. Hartke, J. Phys. Chem., 1993, 97, 9973.
10. M. Bertolus, V. Brenner, P. Millie and J.-B. Maillet, ZPhys-e.D: At., Mol. Clusters, 1997, 39, 239.
11. S. K. Gregurick, M. H. Alexander and B. Hartke, J. Chem. Phys., 1996, 104, 2684.
12. D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288.
13. A. N. Alexandrova and A. I. Boldyrev, J. Chem. Theory Comput., 2005, 1, 566.
14. A. N. Alexandrova, J. Phys. Chem. A, 2010, 114, 12591.
15. B. Wang, J. Zhao, X. Chen, D. Shi and G. Wang, Phys. Rev. A, 2005, 71, 33201.
16. R. Kelting, R. Otterstätter, P. Weis, N. Drebov, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2011, 134, 24311.
17. B. Wang, L. M. Molina, M. J. López, A. Rubio, J. A. Alonso and M. J. Stott, Ann. Phys., 1998, 510, 107.
18. C. Rajesh, C. Majumder, M. G. R. Rajan and S. K. Kulshreshtha, Phys. Rev. B, 2005, 72, 235411.
19. X.-P. Li, W.-C. Lu, Q.-J. Zang, G.-J. Chen, C. Z. Wang and K. M. Ho, J. Phys. Chem. A, 2009, 113, 6217.
20. L. Xiao-ping, Z. Wei, L. Wen-cai, W. Cai-zhuang and H. Kai-ming, Chem. Res. Chin. Univ., 2010, 6, 996–1001.
21. K. LaiHing, R. G. Wheeler, W. L. Wilson and M. A. Duncan, J. Chem. Phys., 1987, 87, 3401.
22. C. Rajesh and C. Majumder, J. Chem. Phys., 2007, 126, 244704.
23. D. A. Götz, A. Shayeghi, R. L. Johnston, P. Schwerdtfeger and R. Schäfer, J. Chem. Phys., 2014, 140, 164313.
24. K.-M. Ho, A. A. Shvartsburg, B. Pan, Z.-Y. Lu, C.-Z. Wang, J. G. Wacker, J. L. Fye and M. F. Jarrold, Nature, 1998, 392, 582.
25. M. F. Jarrold and J. E. Bower, J. Chem. Phys., 1992, 96, 9180.
26. R. R. Hudgins, M. Imai, M. F. Jarrold and P. Dugourd, J. Chem. Phys., 1999, 111, 7865.
27. E. Oger, R. Kelting, P. Weis, A. Lechtken, D. Schooss, N. R. M. Crawford, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2009, 130, 124305.
28. N. Drebov, E. Oger, T. Rapps, R. Kelting, D. Schooss, P. Weis, M. M. Kappes and R. Ahlrichs, J. Chem. Phys., 2010, 133, 224302.
29. A. Lechtken, N. Drebov, R. Ahlrichs, M. M. Kappes and D. Schooss, J. Chem. Phys., 2010, 132, 211102.
30. M. F. Jarrold and J. E. Bower, J. Phys. Chem., 1988, 92, 5702.
31. Y. Tai, J. Murakami, C. Majumder, V. Kumar, H. Mizuseki and Y. Kawazoe, Eur. Phys. J. D, 2003, 24, 295.
32. Y. Tai and J. Murakami, Chem. Phys. Lett., 2001, 339, 9.
33. K. Pitzer, Acc. Chem. Res., 1979, 12(8), 271.
34. P. Pyykkö and J. Desclaux, Acc. Chem. Res., 1979, 12(8), 276.
35. T. Zeng, D. G. Fedorov, M. W. Schmidt and M. Klobukowski, J. Chem. Phys., 2011, 134, 214107.
36. S. Höfener, R. Ahlrichs, S. Knecht and L. Visscher, ChemPhysChem, 2012, 13, 3952.
37. P. Schwerdtfeger, G. A. Heath, M. Dolg and M. A. Bennett, J. Am. Chem. Soc., 1992, 114, 7518.
38. T. Enevoldsen, L. Visscher, T. Saue, H. J. A. Jensen and J. Oddershede, J. Chem. Phys., 2000, 112, 3493.
39. S. Komorovsky, M. Repisky, E. Malkin, T. B. Demissie and K. Ruud, J. Chem. Theory Comput., 2015, 11, 3729.
40. K. A. Peterson, J. Chem. Phys., 2015, 142, 074105.
41. R. Feng and K. A. Peterson, J. Chem. Phys., 2017, 147, 084108.
42. C. Giraldo, F. Ferraro, C. Z. Hadad, L. Ruiz, W. Tiznado and E. Osorio, RSC Adv., 2017, 7, 16069.
43. S. Rahali, M. Seydou, Y. Belhocine, F. Maurel and B. Tangour, Int. J. Hydrogen Energy, 2016, 41, 2711.
44. J.-Y. Yang and M. Hu, J. Phys. Chem. Lett., 2017, 8, 3720.
45. I. A. Shkrob and T. W. Marin, J. Phys. Chem. Lett., 2014, 5, 1066.
46. A. R. b. M. Yusoff and M. K. Nazeeruddin, J. Phys. Chem. Lett., 2016, 7, 851.
47. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284.
48. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
49. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029.
50. M. Dolg, Handbook of Relativistic Quantum Chemistry, 2002, vol. 11, p. 793.
51. Y. S. Lee, W. C. Ermler and K. S. Pitzer, J. Chem. Phys., 1977, 67, 5861.
52. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
53. R. B. Ross, J. M. Powers, T. Atashroo, W. C. Ermler, L. A. LaJohn and P. A. Christiansen, J. Chem. Phys., 1990, 93, 6654.
54. S. Faas, J. G. Snijders, J. H. van Lenthe, E. van Lenthe and E. J. Baerends, Chem. Phys. Lett., 1995, 246, 632.
55. L. Vischer, Theor. Chem. Acc., 1997, 98, 68.
56. T. Saue and T. Helgaker, J. Comput. Chem., 2002, 23, 814.
57. T. Saue, ChemPhysChem, 2011, 12, 3077.
58. K. G. Dyall, J. Chem. Phys., 1997, 106, 9618.
59. K. G. Dyall, J. Chem. Phys., 1998, 109, 4201.
60. K. G. Dyall, J. Chem. Phys., 1999, 111, 10000.
61. K. G. Dyall, J. Chem. Phys., 2001, 115, 9136.
62. M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102.
63. W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 031104.
64. D. Peng and M. Reiher, J. Chem. Phys., 2012, 136, 243108.
65. K. G. Dyall, Theor. Chem. Acc., 2002, 108, 335.
66. M. J. Frisch, Gaussian 09, Revis. C.01, Gaussian, Inc., Wallingford, CT, 2009.
67. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477.
68. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
69. L. Visscher, H. J. A. Jensen, R. Bast and T. Saue, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, T. Helgaker, J. K. Lærdahl, Y. S. Lee, J. Henriksson, M. Iliaš, C. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, C. V. Larsen, H. S. Nataraj, P. Norman, G. Olejniczak, J. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, K. Ruud, P. Sałek, B. Schimmelpfennig, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther and S. Yamamoto, DIRAC, a relativistic ab initio electronic structure program, Release DIRAC13 (2013), (see http://www.diracprogram.org.
70. M. Kühn, J. Chem. Theory Comput., 2014, 10, 623.
71. M. K. Armbruster, F. Weigend, C. van Wullen and W. Klopper, Phys. Chem. Chem. Phys., 2008, 10, 1748.
72. K. Balasubramanian and D. Majumdar, J. Chem. Phys., 2001, 115, 8795.
73. C. Zhao and K. Balasubramanian, J. Chem. Phys., 2002, 116, 10287.
74. J. Mühlbach, K. Sattler, P. Pfau and E. Recknagel, Phys. Lett. A, 1982, 87, 415.
75. K. A. Gingerich, D. L. Cocke and F. Miller, J. Chem. Phys., 1976, 64, 4027.
76. R. W. Farley, P. Ziemann and A. W. Castleman, ZPhys-e.D: At., Mol. Clusters, 1989, 14, 353.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. ESI-1: the lowest energy isomers of Pb_n (n = 3–10) clusters at scalar (SR) and spin–orbit (SO) schemes. Fig. ESI-2: convergence of SR-isomers towards to SO-isomer for Pb₃, Pb₆, Pb₇ and Pb₈. Fig. ESI-3: molecular orbital diagram for Pb₈ system calculated at PBE0/TZ2P-SR and PBE0/TZ2P-SO levels of theory. Fig. ESI-4: binding energy (BE), HOMO–LUMO gap and second order difference in total energy behaviors calculated using the GGA-PBE/Def2-TZVP methodology. Table ESI-1: cartesians coordinates and relative energies for Pb_n (n = 3–10) isomers. Table ESI-2: HOMO–LUMO gap for Pb_n (n = 3–10) isomers. Energy in eV. See DOI: 10.1039/c7ra11449d

---