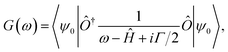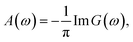Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Many-body effects and non-local charge fluctuations in the double perovskite Sr2FeMoO6
Henrique P. Martins *a,
Eduardo B. Guedesa,
Rodrigo J. O. Mossaneka,
Fernando D. Pradob,
Alberto Caneiroc and
Miguel Abbatea
*a,
Eduardo B. Guedesa,
Rodrigo J. O. Mossaneka,
Fernando D. Pradob,
Alberto Caneiroc and
Miguel Abbatea
aDepartamento de Física, Universidade Federal do Paraná, Caixa Postal 19044, 81531-990 Curitiba, PR, Brazil. E-mail: hpmartins@gmail.com
bDepartamento de Física, Universidad Nacional del Sur, Av. Leandro N. Alem 1253, 8000 Bahía Blanca, Argentina
cCentro Atómico Bariloche, Comisión Nacional de Energía Atómica, Av. Ezequiel Bustillo 9500, 8400 Bariloche, Argentina
First published on 22nd January 2018
Abstract
We studied the electronic structure of Sr2FeMoO6 using core level and valence band photoemission. The spectra were obtained using high energy X-rays of 1840 eV, which provide bulk sensitive information on the electronic structure. The experimental data were analyzed using the spectral weight from cluster model calculations. The ground state reveals a large Fe–O and Mo–O hybridization, as well as the importance of non-local Fe–O–Mo charge fluctuations. The latter is crucial to explain the half-metallic character attributed to the Sr2FeMoO6 compound. The core level and valence band photoemission spectra show charge transfer satellites. These satellites are related to many-body effects and are larger for the Fe levels than for the Mo states.
1 Introduction
The Sr2FeMoO6 (SFMO) double perovskite presents very interesting physical properties.1,2 The crystal structure of this compound is tetragonal with a = 5.557 Å and c = 7.887 Å. This material is a half-metallic ferrimagnet with an ordering temperature of TC = 420 K. The magnetic moment, up to μ = 3.7 μB, depends on the degree of Fe/Mo cationic disorder.3 The SFMO oxide exhibits a considerable magneto-resistance (MR) at room temperature. The accepted MR mechanism involves tunneling across grain boundaries. For these reasons, this compound is being considered for applications in spintronic devices. More details on the SFMO double perovskite can be found in recent reviews.4–6The electronic structure of SFMO was studied using a variety of spectroscopic techniques, which aimed at understanding the microscopic origin of its physical properties.7 The optical conductivity confirmed the half-metallic character of the SFMO compound.2 The core-level X-ray photoelectron spectra (XPS) determined the chemical shifts of the Fe/Mo ions.8,9 The valence band X-ray photoemission spectra (PES) elucidated the electronic states at the Fermi level.10–12 The X-ray absorption spectra (XAS) was utilized to investigate the Fe/Mo valencies.9,11,13 The X-ray emission spectra (XES) provided site selected information on the electronic structure.14 Finally, the magnetic circular dichroism spectra (MCD) was used to study the Fe/Mo magnetic moments.13,15
In an ionic approximation, the electronic structure of SFMO can be viewed as a combination of Fe3+ (3d5) and Mo5+ (4d1).1,2 However, the Fe 3d and Mo 4d electrons present a covalent hybridization with the O 2p states.12 Further, the majority Fe3+ (3d5) electrons are localized, whereas the minority Mo5+ (4d1) electron is itinerant, which is consistent with both the half-metallic conductivity and the ferrimagnetic ordering of SFMO. In fact, the conducting electron is delocalized along Mo–O–Fe–O–Mo chains in this material, indicating the importance of the Fe 3d–O 2p and Mo 4d–O 2p covalent mixing, as well as the non-local Mo–O–Fe charge fluctuations.
The valence band spectra of SFMO were compared to diverse density functional theory (DFT) methods. The agreement with the experiment improves if one includes in the calculation the Mott–Hubbard U.10,11 The values of U used in the LDA + U approach at the Fe sites are relatively large, about U = 2–4 eV. Based on these values, Kuepper et al. concluded that the electronic structure of SFMO was highly correlated.14 In particular, the valence band spectra of this oxide might present distinct many-body effects beyond the DFT description.
We studied the electronic structure of SFMO using a cluster model approach,16–19 which consists of two FeO6 and MoO6 octahedra which are either connected (double cluster model) or not (single cluster model) by one corner O atom. This method includes both the Fe 3d–O 2p and Mo 4d–O 2p hybridization, as well as the Mo–O–Fe charge fluctuations in the FeO6–MoO6 double cluster. The electronic structure is calculated using the configuration interaction approach,17 which includes many relevant correlation effects within the double cluster. The calculations are compared to the core level and valence band spectra of SFMO. Finally, the experimental spectra were obtained using bulk sensitive high-energy X-rays.
2 Experimental details
The ceramic Sr2FeMoO6 sample was prepared using the solid-state reaction method. The corresponding reagents were mixed and calcined in air at 950 °C for 24 h. The resulting powder was pulverized, mixed and fired again several times. The reduction of the powder was carried out in a flowing mixture of 1% H2–Ar gas at 1050 °C for 1 h. Finally, the substance was ground, pressed into pellets, and sintered in a vacuum for 12 h at 1200 °C. The powder XRD analysis confirmed that the sample was a single-phase material. The Rietveld refinement showed a tetragonal I4/mmm structure with the aforementioned parameters. The relative intensity of the (101) reflection indicated a highly ordered sample with less than 3% cationic disorder.3The photoemission measurements were performed at the SXS beamline at the Laboratório Nacional de Luz Síncrotron (LNLS) in Campinas (Brazil).20 The photon energy scale of the monochromator was calibrated using the Si K absorption edges. The photoemission spectra was taken using a SPECS Phoibos 150 electron energy analyzer; the energy scale of the analyzer was calibrated using a clean gold foil. All the spectra presented here were taken at room temperature with a photon energy of 1840 eV. The base pressure in the UHV experimental chamber was in the low 10−9 mbar range. The pellets were thoroughly scraped with a diamond file to remove the surface contamination. The core level Fe 2p and Mo 3p spectra presented here are new, whereas the valence band spectrum was already presented in a previous study.21
3 Calculation details
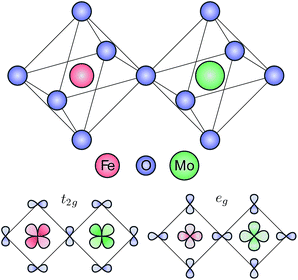
The electronic structure of Sr2FeMoO6 was calculated using a double cluster model, composed by an FeO6 and a MoO6 octahedra sharing a corner O atom. The double octahedra considered here is represented schematically in the top panel of Fig. 1. The double cluster model was solved using a symmetry-adapted configuration interaction method.16,18 The Fe 3d and Mo 4d orbitals are split by crystal field effects into t2g and eg symmetries. The symmetry-adapted combination of orbitals with a local t2g and eg character are depicted in the bottom panel of Fig. 1. The t2g combination is crucial to describe the minority Fe–O–Mo delocalized electron, which is related to both the half-metallic and ferrimagnetic character of Sr2FeMoO6.In a first ionic approximation, the transition metals ions in Sr2FeMoO6 are in a 3d54d1 state.22 The ground state is expanded in terms of 3d5+n![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) n+m4d1+m covalently mixed configurations, where
n+m4d1+m covalently mixed configurations, where ![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) denotes a symmetry-adapted O 2p ligand hole. All the possible charge transfer configurations are included explicitly in the ground state expansion. Non-local charge fluctuations such as 3d54d1 → 3d44d2 and 3d54d1 → 3d64d0 are also contemplated. They can be achieved by an indirect second-order process via the O 2p orbitals, for instance: 3d54d1 → 3d6
denotes a symmetry-adapted O 2p ligand hole. All the possible charge transfer configurations are included explicitly in the ground state expansion. Non-local charge fluctuations such as 3d54d1 → 3d44d2 and 3d54d1 → 3d64d0 are also contemplated. They can be achieved by an indirect second-order process via the O 2p orbitals, for instance: 3d54d1 → 3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d1 → 3d64d0.
4d1 → 3d64d0.
There are two complete sets of model parameters for each transition metal octahedron: the Coulomb repulsion U, the p–d charge transfer energy Δ, the core-hole potential Q (Q = U/0.83), and the pdσ charge transfer integral Tσ (Tπ = −Tσ/2).17 These parameters are given with respect to the average of the multiplet of each configuration. The multiplet splittings of each 3d5+n![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) n+m4d1+m charge transfer configuration are given in terms of the crystal field parameter 10Dq, the set of Kanamori parameters u, u′, and j, as well as the p–p hybridization ppσ–ppπ.17 The main model parameters and the multiplet parameters for the FeO6 and MoO6 octahedra are given in Table 1. These parameters follow the expected chemical trend,17,18 and are consistent with those in related compounds.22–24
n+m4d1+m charge transfer configuration are given in terms of the crystal field parameter 10Dq, the set of Kanamori parameters u, u′, and j, as well as the p–p hybridization ppσ–ppπ.17 The main model parameters and the multiplet parameters for the FeO6 and MoO6 octahedra are given in Table 1. These parameters follow the expected chemical trend,17,18 and are consistent with those in related compounds.22–24
| Parameter | Fe3+ | Mo5+ |
|---|---|---|
| U | 7.5 | 2.6 |
| Δ | 3.0 | 6.1 |
| Tσ | 2.1 | 3.9 |
| 10Dq | 1.3 | 3.3 |
| j | 0.8 | 0.6 |
| ppσ–ppπ | 1.0 | 1.0 |
The calculation of the different spectral weights is performed in three steps. First, the Hamiltonian matrix Ĥ is diagonalized to obtain the ground state |ψ0〉. Then, the corresponding Green function G(ω) is calculated using the following expression:
The entire calculation procedure is implemented using the built in facilities of the Quanty package.25–27 The single cluster model calculations of the FeO6 and MoO6 octahedra were performed in the same way and using the same set of parameters.
4 Results and discussion
4.1 Ground state properties
The occupancy of the different configuration in the ground state of Sr2FeMoO6 are listed in Table 2. The dominant contribution is given by the charge transfer configurations 3d5![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d2 and 3d6
4d2 and 3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d1, which are followed by the base ionic configuration 3d54d1. The relatively large occupancy of the charge transfer configurations indicates a great degree of covalent bonding. The calculated occupation of the Fe 3d orbitals in the ground state is 5.5 electrons, whereas the calculated occupation of the Mo 4d levels is 1.6 electrons. These occupations are larger than the expected Fe3+ (3d5) and Mo5+ (4d1) ionic values, which signals the importance of the Fe 3d–O 2p and Mo 4d–O 2p hybridization. The relevance of hybridization is also revealed by the relatively large occupancy of the double charge transfer configuration 3d6
4d1, which are followed by the base ionic configuration 3d54d1. The relatively large occupancy of the charge transfer configurations indicates a great degree of covalent bonding. The calculated occupation of the Fe 3d orbitals in the ground state is 5.5 electrons, whereas the calculated occupation of the Mo 4d levels is 1.6 electrons. These occupations are larger than the expected Fe3+ (3d5) and Mo5+ (4d1) ionic values, which signals the importance of the Fe 3d–O 2p and Mo 4d–O 2p hybridization. The relevance of hybridization is also revealed by the relatively large occupancy of the double charge transfer configuration 3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 24d2.
24d2.
| Configuration | Occupancy |
|---|---|
3d5![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d2 4d2 |
20.9% |
3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d1 4d1 |
20.0% |
| 3d54d1 | 19.6% |
3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 24d2 24d2 |
15.2% |
3d5![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 24d3 24d3 |
7.7% |
| 3d64d0 | 7.3% |
3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 34d3 34d3 |
4.8% |
3d5![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 34d4 34d4 |
1.3% |
3d7![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 24d1 24d1 |
1.2% |
3d7![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 34d2 34d2 |
0.7% |
3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 44d4 44d4 |
0.7% |
3d7![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d0 4d0 |
0.5% |
| 3d44d2 | 0.1% |
The relatively large percentage of the 3d64d0 configuration indicates the importance of non-local Mo–O–Fe charge fluctuations. This configuration is not achieved by the direct 3d54d1 → 3d64d0 process, but rather by the indirect 3d54d1 → 3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d1 → 3d64d0 process. On the other hand, the opposite non-local Fe–O–Mo charge transfer 3d4d2 configuration shows a relatively small occupation. This charge fluctuation is strongly suppressed due to the relatively large exchange stabilization of the Fe 3d5 electrons. It is worth noting that the relatively strong 3d54d1 → 3d64d0 process corresponds to the minority Mo 4d1 electron, whereas the 3d54d1 → 3d44d2 transition involves the majority Fe 3d5 electrons and is greatly diminished. The opposite behavior of the minority vs. majority charge fluctuations is in agreement with the half-metallic character of Sr2FeMoO6.
4d1 → 3d64d0 process. On the other hand, the opposite non-local Fe–O–Mo charge transfer 3d4d2 configuration shows a relatively small occupation. This charge fluctuation is strongly suppressed due to the relatively large exchange stabilization of the Fe 3d5 electrons. It is worth noting that the relatively strong 3d54d1 → 3d64d0 process corresponds to the minority Mo 4d1 electron, whereas the 3d54d1 → 3d44d2 transition involves the majority Fe 3d5 electrons and is greatly diminished. The opposite behavior of the minority vs. majority charge fluctuations is in agreement with the half-metallic character of Sr2FeMoO6.
4.2 Fe 2p core level spectroscopy
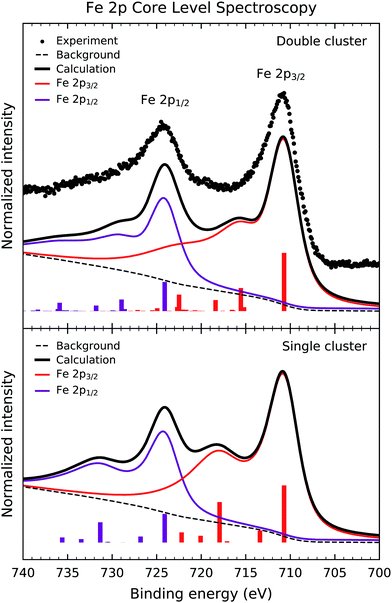
Fig. 2 shows the experimental Fe 2p core level photoemission spectrum of Sr2FeMoO6 (dots). The Fe 2p peak is split by spin–orbit interaction into the Fe 2p3/2 and Fe 2p1/2 contributions about 711 and 724 eV, respectively. In turn, these peaks are followed by broad charge transfer satellites at around 718 eV and 731 eV.Fig. 2 also compares the experimental result to the calculated core level spectral weight (solid line). The top panel displays the results of the double cluster calculation, whereas the bottom panel compares to the single cluster model results. The discrete contributions were broadened with Gaussian and Lorentzian broadenings to account for the experimental resolution and the core hole lifetime. Finally, an integral background was added to the calculated curve to take into account inelastic processes.
The calculated spectral weight of the double cluster model reproduces satisfactorily the experimental data. The main peaks are due to the well screened Fe 2p53d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) states, whereas the satellite structures are composed of Fe 2p53d7
states, whereas the satellite structures are composed of Fe 2p53d7![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 2 states. These charge transfer satellites in the core level spectrum represent a many-body effect, which reflects the highly correlated nature of the Fe3+ (3d5) ion in Sr2FeMoO6 (U > Tσ). The energy position and relative intensity of the satellites are sensitive to the U, Δ and Tσ parameters. On the other hand, the single cluster calculation overestimates the intensity of the charge transfer satellites, mainly because it does not include the non-local screening contribution which comes from the MoO6 octahedra.
2 states. These charge transfer satellites in the core level spectrum represent a many-body effect, which reflects the highly correlated nature of the Fe3+ (3d5) ion in Sr2FeMoO6 (U > Tσ). The energy position and relative intensity of the satellites are sensitive to the U, Δ and Tσ parameters. On the other hand, the single cluster calculation overestimates the intensity of the charge transfer satellites, mainly because it does not include the non-local screening contribution which comes from the MoO6 octahedra.
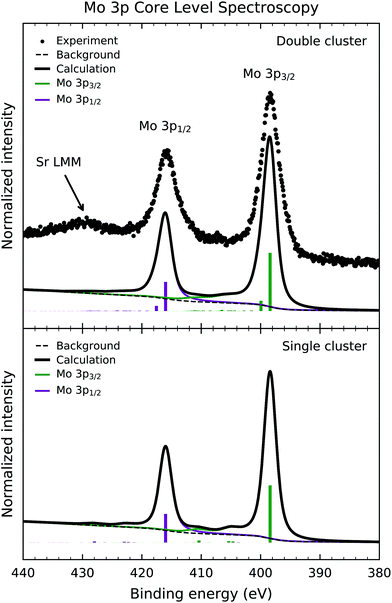
4.3 Mo 3p core level spectroscopy
Fig. 3 shows the experimental Mo 3p core level photoemission spectrum of Sr2FeMoO6 (dots). The Mo 3p peaks are split by spin–orbit interaction into the Mo 3p3/2 and Mo 3p1/2 contributions around 398 and 416 eV, respectively. In this case, the core level spectrum does not exhibit a prominent satellite structure. Finally, the experimental data presents an accidental superposition with the Sr LMM Auger electron decay around 430 eV.Fig. 3 also compares the experimental data to the calculated core-level spectral weight (solid line) of the double and single cluster models. Likewise, the discrete contributions were also broadened to account for the experimental resolution and the core hole lifetime. In the same way, the integral background was calculated and added to the final calculated curve.
The calculated spectral weight of the double cluster calculation successfully reproduces the peaks in the experimental result. The leading structure at 398 eV arises from mixed Mo 3p54d2![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) and 3p54d1 final states, while the smaller contribution at 400 eV has mainly Mo 3p54d1 character. The smaller satellite structure, in this case, is attributed to the less correlated character of the Mo5+ (4d1) ion in Sr2FeMoO6 (U < Tσ). For this reason, the calculated results are less sensitive to the values of the model parameters. In this case, the single cluster calculation reproduces reasonably well the experimental spectrum, mainly because the charge transfer processes are less important than in the Fe 2p core level spectrum.
and 3p54d1 final states, while the smaller contribution at 400 eV has mainly Mo 3p54d1 character. The smaller satellite structure, in this case, is attributed to the less correlated character of the Mo5+ (4d1) ion in Sr2FeMoO6 (U < Tσ). For this reason, the calculated results are less sensitive to the values of the model parameters. In this case, the single cluster calculation reproduces reasonably well the experimental spectrum, mainly because the charge transfer processes are less important than in the Fe 2p core level spectrum.
4.4 Valence band spectroscopy
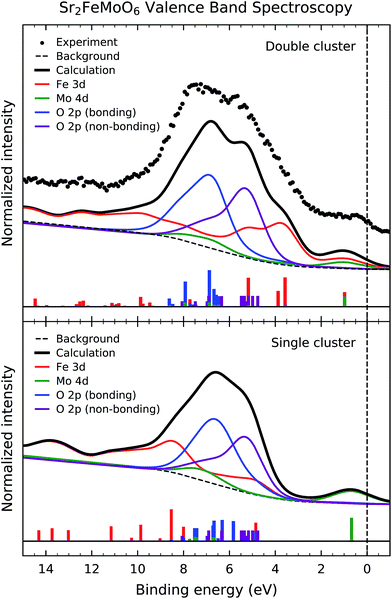
Fig. 4 presents the experimental valence band photoemission spectrum of Sr2FeMoO6 (dots). The dashed line denotes the Fermi level energy EF. The spectrum is composed of three main regions: the Fe 3d–O 2p–Mo 4d mixed states close to the Fermi level, the non-bonding and bonding O 2p band from 9 to 4 eV, and the Fe 3d charge transfer satellites from 15 to 9 eV.Fig. 4 also compares the experimental data to the calculated spectral weight (solid line) using double and single cluster model calculations. The individual contributions of the Fe 3d, Mo 4d and O 2p states are presented below. The intensity of the peaks were weighted with the appropriate photoelectron cross-sections for a photon energy of 1840 eV. The discrete peaks were convoluted with a Gaussian function to account for the experimental resolution. Finally, an integral background was added to take into account inelastic scattering effects. The single cluster result was calculated using a linear combination of the FeO6 and MoO6 single clusters.
The calculated spectral weight of the double cluster model is in good agreement with the experimental valence band photoemission data. The first feature around 1.0 eV is attributed to Fe 3d–O 2p–Mo 4d mixed states; these are related to the non-local charge fluctuations which give rise to the conducting behavior of Sr2FeMoO6. The Fe 3d states are split by crystal field effects into the Fe t2g and Fe eg contributions, and appear about 5.5 and 4.0 eV, respectively. The non-bonding O 2p band corresponds to O 2p states which are not hybridized with Fe 3d and Mo 4d states, and shows up between 4.0 and 8.0 eV (purple line). On the other hand, the bonding O 2p band corresponds to O 2p states which are hybridized with Fe 3d and Mo 4d states, and arises from 6.0 and 10.0 eV (blue line). Finally, the charge transfer satellites, mostly related to the Fe 3d states, emerge above 9.0 eV. We note that the Fe 3d–O 2p and Mo 4d–O 2p hybridization are crucial to describe the features in the valence band spectrum. Further, the correlation effects of the Fe 3d states is essential to explain the charge transfer satellites at high binding energies.
The Mo 4d spectral weight (green line) presents a peak around 1.0 eV as well as structure about 8.0 eV. The former is related to the Fe 3d–O 2p–Mo 4d mixed states, whereas the later is attributed to Mo 4d–O 2p hybridization. The energy position and relative intensity of these Mo 4d structures are in agreement with those observed in a recent Mo L3 resonant photoemission experiment.21
Although the single cluster model results reproduce the overall shape of the valence band, they fail to explain the magnetic order and the electrical conductivity of the compound. The double cluster model gives an anti-parallel ordering of the Fe 3d5 and Mo 4d1 magnetic moments, which is in agreement with the observed ferrimagnetic ordering in Sr2FeMoO6, whereas the single cluster model produces an independent alignment of the magnetic moments yielding a paramagnetic state. Further, the double cluster model indicates the importance of the non-local Fe 3d–O 2p–Mo 4d fluctuations, which are related to the half-metallic character of this oxide, whereas the single cluster model only consider the local Fe 3d–O 2p and Mo 4d–O 2p fluctuations and gives rise to an insulating state.
The non-local charge fluctuations are reflected not only in the composition of the ground state, but also contribute to the individual transitions in the experimental spectra. In fact, the first removal state in the valence band spectra, around 1 eV, is a non-local Fe 3d–O 2p–Mo 4d mixed state, according to the double cluster, but it is a local Mo 4d–O 2p state in the single cluster calculation. Therefore, the double cluster calculation is crucial to explain not only the physical properties of Sr2FeMoO6, but also the character of the spectral features present in the valence band spectrum.
5 Summary and conclusions
In summary, we studied the electronic structure of Sr2FeMoO6 using bulk sensitive photoemission spectroscopy. The experimental data were analyzed using configuration interaction cluster model calculations. The charge transfer 3d5![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d2 and 3d6
4d2 and 3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d1 configurations dominate the ground state; this indicates a large degree of Fe–O and Mo–O hybridization in this compound. The occupancy of the 3d64d0 configuration shows the importance of non-local Fe–O–Mo charge fluctuations; this configuration is achieved through the indirect 3d54d1 → 3d6
4d1 configurations dominate the ground state; this indicates a large degree of Fe–O and Mo–O hybridization in this compound. The occupancy of the 3d64d0 configuration shows the importance of non-local Fe–O–Mo charge fluctuations; this configuration is achieved through the indirect 3d54d1 → 3d6![[L with combining low line]](https://www.rsc.org/images/entities/char_004c_0332.gif) 4d1 → 3d64d0 process. This non-local charge fluctuation occurs in the minority spin channel, whereas the transitions in the majority spin sector are strongly suppressed; which is in accordance with the half-metallic character attributed to the Sr2FeMoO6 compound. The Fe 2p core level photoemission spectrum shows rather large charge transfer satellites. These satellites are related to many-body effects caused by the highly correlated nature of the Fe 3d levels. On the other hand, these effects are smaller in the Mo 3p core level spectrum due to the less correlated character of the Mo 4d states. Charge transfer satellites are also observed in the valence band spectrum and are again associated to the Fe 3d electrons. Although the single cluster model calculations are able to reproduce the experimental spectra, they fail to explain the physical properties of the Sr2FeMoO6 compound. In this context, the double cluster model calculations are crucial to explain both the ferrimagnetic ordering and the half-metallic character of this compound. To conclude, the metal–oxygen hybridization, non-local Fe–O–Mo charge fluctuations, and many-body effects are all relevant topics in the electronic structure of Sr2FeMoO6.
4d1 → 3d64d0 process. This non-local charge fluctuation occurs in the minority spin channel, whereas the transitions in the majority spin sector are strongly suppressed; which is in accordance with the half-metallic character attributed to the Sr2FeMoO6 compound. The Fe 2p core level photoemission spectrum shows rather large charge transfer satellites. These satellites are related to many-body effects caused by the highly correlated nature of the Fe 3d levels. On the other hand, these effects are smaller in the Mo 3p core level spectrum due to the less correlated character of the Mo 4d states. Charge transfer satellites are also observed in the valence band spectrum and are again associated to the Fe 3d electrons. Although the single cluster model calculations are able to reproduce the experimental spectra, they fail to explain the physical properties of the Sr2FeMoO6 compound. In this context, the double cluster model calculations are crucial to explain both the ferrimagnetic ordering and the half-metallic character of this compound. To conclude, the metal–oxygen hybridization, non-local Fe–O–Mo charge fluctuations, and many-body effects are all relevant topics in the electronic structure of Sr2FeMoO6.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) and Fundação Araucária do Paraná for their financial support.References
- K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680 CrossRef CAS.
- Y. Tomioka, T. Okuda, Y. Okimoto, R. Kumai, K.-I. Kobayashi and Y. Tokura, Phys. Rev. B, 2000, 61, 422–427 CrossRef CAS.
- L. Balcells, J. Navarro, M. Bibes, A. Roig, B. Martínez and J. Fontcuberta, Appl. Phys. Lett., 2001, 78, 781–783 CrossRef CAS.
- A. Gupta and J. Z. Sun, J. Magn. Magn. Mater., 1999, 200, 24–43 CrossRef CAS.
- M. Ziese, Rep. Prog. Phys., 2002, 65, 143 CrossRef CAS.
- D. Serrate, J. M. De Teresa, P. A. Algarabel, C. Marquina, J. Blasco, M. R. Ibarra and J. Galibert, J. Phys.: Condens. Matter, 2007, 19, 436226 CrossRef.
- D. D. Sarma, P. Mahadevan, T. Saha-Dasgupta, S. Ray and A. Kumar, Phys. Rev. Lett., 2000, 85, 2549–2552 CrossRef CAS PubMed.
- M. S. Moreno, J. E. Gayone, M. Abbate, A. Caneiro, D. Niebieskikwiat, R. D. Sánchez, A. de Siervo, R. Landers and G. Zampieri, Solid State Commun., 2001, 120, 161–164 CrossRef CAS.
- K. Kuepper, I. Balasz, H. Hesse, A. Winiarski, K. C. Prince, M. Matteucci, D. Wett, R. Szargan, E. Burzo and M. Neumann, Phys. Status Solidi A, 2004, 201, 3252–3256 CrossRef CAS.
- T. Saitoh, M. Nakatake, A. Kakizaki, H. Nakajima, O. Morimoto, S. Xu, Y. Moritomo, N. Hamada and Y. Aiura, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035112 CrossRef.
- J.-S. Kang, J. H. Kim, A. Sekiyama, S. Kasai, S. Suga, S. W. Han, K. H. Kim, T. Muro, Y. Saitoh, C. Hwang, C. G. Olson, B. J. Park, B. W. Lee, J. H. Shim, J. H. Park and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 113105 CrossRef.
- J. Navarro, J. Fontcuberta, M. Izquierdo, J. Avila and M. C. Asensio, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 115101 CrossRef.
- S. Ray, A. Kumar, D. D. Sarma, R. Cimino, S. Turchini, S. Zennaro and N. Zema, Phys. Rev. Lett., 2001, 87, 097204 CrossRef CAS PubMed.
- K. Kuepper, M. Kadiroglu, A. V. Postnikov, K. C. Prince, M. Matteucci, V. R. Galakhov, H. Hesse, G. Borstel and M. Neumann, J. Phys.: Condens. Matter, 2005, 17, 4309–4317 CrossRef CAS.
- M. Besse, V. Cros, A. Barthélémy, H. Jaffrès, J. Vogel, F. Petroff, A. Mirone, A. Tagliaferri, P. Bencok, P. Decorse, P. Berthet, Z. Szotek, W. M. Temmerman, S. S. Dhesi, N. B. Brookes, A. Rogalev and A. Fert, Europhys. Lett., 2002, 60, 608–614 CrossRef CAS.
- G. van der Laan, C. Westra, C. Haas and G. A. Sawatzky, Phys. Rev. B, 1981, 23, 4369–4380 CrossRef CAS.
- A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1561–1570 CrossRef CAS.
- M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039–1263 CrossRef CAS.
- E. B. Guedes, M. Abbate, K. Ishigami, A. Fujimori, K. Yoshimatsu, H. Kumigashira, M. Oshima, F. C. Vicentin, P. T. Fonseca and R. J. O. Mossanek, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235127 CrossRef.
- M. Abbate, F. C. Vicentin, V. Compagnon-Cailhol, M. C. Rocha and H. Tolentino, J. Synchrotron Radiat., 1999, 6, 964–972 CrossRef CAS.
- H. P. Martins, F. Prado, A. Caneiro, F. C. Vicentin, R. J. O. Mossanek and M. Abbate, Europhys. Lett., 2017, 118, 37002 CrossRef.
- H. P. Martins, F. Prado, A. Caneiro, F. C. Vicentin, D. S. Chaves, R. J. O. Mossanek and M. Abbate, J. Alloys Compd., 2015, 640, 511–516 CrossRef CAS.
- M. Abbate, G. Zampieri, J. Okamoto, A. Fujimori, S. Kawasaki and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165120 CrossRef.
- V. Stoeberl, M. Abbate, L. M. S. Alves, C. A. M. dos Santos and R. J. O. Mossanek, J. Alloys Compd., 2017, 691, 138–143 CrossRef CAS.
- M. W. Haverkort, M. Zwierzycki and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165113 CrossRef.
- M. W. Haverkort, G. Sangiovanni, P. Hansmann, A. Toschi, Y. Lu and S. Macke, Europhys. Lett., 2014, 108, 57004 CrossRef.
- Y. Lu, M. Höppner, O. Gunnarsson and M. W. Haverkort, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085102 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |