Open Access Article
Open Access ArticleDouble-exponential refractive index sensitivity of metal–semiconductor core–shell nanoparticles: the effects of dual-plasmon resonances and red-shift†
Hailong Zhanga,
Pengfei Cao *ab,
Jie Doua,
Lin Chenga,
Tiaoming Niua and
Guanmao Zhanga
*ab,
Jie Doua,
Lin Chenga,
Tiaoming Niua and
Guanmao Zhanga
aSchool of Information Science and Engineering, Lanzhou University, Lanzhou 730000, China. E-mail: caopf@lzu.edu.cn
bKirchhoff-Institute for Physics, Im Neuenheimer Feld 227, 69120 Heidelberg, Germany
First published on 5th January 2018
Abstract
In order to improve the refractive index sensitivity of a localized surface plasmon resonance (LSPR) sensor, we present a new type of LSPR sensor whose refractive index sensitivity can be improved by greatly increasing the plasmon wavelength red-shift of metal–semiconductor core–shell nanoparticles (CSNs). Using extended Mie theory and Au@Cu2−xS CSNs, we theoretically investigate the optical properties of metal–semiconductor CSNs in the entire near-infrared band. Compared with dielectric–metal and metal–metal CSNs under the same conditions, the metal–semiconductor CSNs have a higher double-exponential sensitivity curve because their core and shell respectively support two LSPRs that greatly increase the LSPR red-shift to the entire near-infrared range. It is worth noting that the sensitivity can be improved effectively by increasing the ratio of the shell-thickness to core-radius, instead of decreasing it in the case of the dielectric–metal CSNs. The underlying reason for the enhancement of sensitivity is the increase of repulsive force with the enlargement of shell thickness, which is different from the dielectric–metal CSNs. This design method not only paves the way for utilizing metal–semiconductor CSNs in biology and chemistry, but also proposes new ideas for the design of sensors with high sensitivity.
1. Introduction
In recent years, many researchers have demonstrated that metal nanoparticles,1 semiconductor nanoparticles2 and dielectric–metal core–shell nanoparticles (CSNs)3 have unique and tunable localized surface plasmon resonance (LSPR).4–8 In particular, the LSPR peaks exhibit red-shift or blue-shift behavior as the structure of the nanoparticle and the refractive index (RI) of the surrounding medium change. The LSPR shifts caused by the RI changes have proven useful to detect a variety of chemical changes taking place at the molecular scale, including protein interactions,9 antigen–antibody binding,10 inorganic ion sensing,11 as well as Alzheimer's biomarker recognition.12The RI sensitivity of the surface plasmon resonance (SPR) plays a significant role for determining the reliability of LSPR sensors. There are two ways to increase RI sensitivity of metal nanoparticle LSPR sensors. One is to elongate the nanoparticle and sharpen its apexes.13–16 The other way is to change the constituent materials of the nanoparticles, which also plays an important role in the sensor's RI sensitivity.17,18 Although the RI sensitivity can be greatly improved to 665 nm/RIU through the two methods mentioned above, the sensors cannot work in a broader band because the absorption peaks of metal nanoparticles shift in the visible range.19
To broaden resonance band, the CSNs with dielectric cores and metal shells (e.g. SiO2@Au) or metal cores and metal shells (e.g. Au@Ag) structures are designed to construct a LSPR-based sensor. Its plasmon resonance wavelength can be tuned from the visible range to the near-infrared range through varying its geometrical parameters.20 Simultaneously, it has been discovered that the RI sensitivity of CSNs sensors, increases near-exponentially as the reduction of the ratio of the shell-thickness to core-radius21,22 and can be larger than that of mental nanoparticles.17,23 The underlying reason for the enhancement of sensitivity is that the resonance wavelength of CSNs is longer than that of mental nanoparticles, which results in the reduction of the restoring force from the negative electrons and the positive metal cations.24 Many studies25,26 have found that the RI sensitivity of CSNs has been generally increased with longer plasmon wavelengths, higher curvatures, and larger polarizabilities. In addition, plasmon wavelengths can become longer (red-shift) with the increment of relative refractivity. In other words, the utilization of longer plasmon wavelengths cannot only enhance RI sensitivity, but also widen CSNs sensors' applications. However, the resonance frequency of these CSNs still cannot cover the entire near-infrared region because the resonance wavelength of the metal shell is concentrated in visible light, which plays a more important role in influencing the optical properties of CSNs.27 It means that the resonance frequency of these CSNs not only have limited sensitivity, but also restricted its applications. For example, the present LSPR sensors concentrate on detecting the conventional materials whose refractive indices are below 1.6.28,29 In addition, in most studies,30,31 the plasmon wavelengths of CSNs have been compared in experiments, but the studies are incomplete due to they didn't pay enough attention to study the reason for plasmon wavelength red-shift of the CSNs in theory.
To further improve RI sensitivity, we present a new type of LSPR sensor based on metal–semiconductor CSNs that show a wide resonance frequency band by controlling the semiconductor with appreciable free carrier concentrations. The metal–semiconductor CSNs are designed for two reasons. On the one hand, the optical properties of the semiconductor can be tuned by controlling the carrier concentration,32–35 which can effectively extend the resonance frequency band to entirely near-infrared region. On the other hand, due to the optical properties of metal core and semiconductor shell, there are two LSPRs in different light regions supported by the metal core and semiconductor shell, respectively, which are different from dielectric–metal23 and metal–dielectric36 CSNs. The result is the greatly increased red-shift of LSPR peak, the broadened resonance wavelength, which could greatly improve sensitivity. Taking Au@Cu2−xS CSNs as an example, by varying their geometrical parameters, we can tune the resonance wavelengths of CSNs to cover the entire near-infrared band. Compared with other CSNs, the Au@Cu2−xS CSNs can not only increase the red-shift of LSPR peak and broaden the resonance wavelength,35,37 but also improve the RI sensitivity and widen LSPR sensors' applications. Furthermore, by studying the charge distribution of Au@Cu2−xS CSNs, we obtained a new phenomenon: the high sensitivity can be obtained by increasing the ratio of the shell-thickness to core-radius instead of decreasing it.21,22
2. Results and discussion
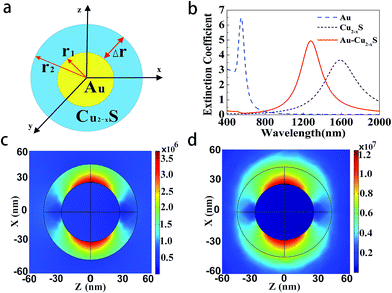
The schematic diagram of cross-section of the proposed Au@Cu2−xS CSNs is shown in Fig. 1a; the golden part indicates the Au core, while the blue is the Cu2−xS shell. The radius meets the requirements of the Rayleigh approximation. Its extinction spectra are calculated by using extended Mie theory. The optical constants of Au in the light region of interest are obtained through a “pchip” interpolation method based of the experimental data,38 and the optical constants of Cu2−xS are calculated with Drude's model.35The extinction spectra of the Au@Cu2−xS CSNs, Au and Cu2−xS nanoparticle are calculated, as shown in Fig. 1b. The refractive index of the surrounding medium is 1.33. The resonance peak of the Au nanoparticle is at 550 nm, while the resonance peak of the Cu2−xS nanoparticle is at 1588 nm. In the extinction spectrum of the Au@Cu2−xS CSNs, two resonant peaks at 500 and 1280 nm, respectively, are observed. The two resonant peaks can be explained by plasmon hybridization theory,39 which interprets how the plasmon resonances of the elementary parts interact with each other to generate the hybridized plasmon modes of the composite nanostructure. We assume that both the metal core and semiconductor shell are lossless, and the permittivities agree with Drude's model with the form ε1 = ε∞1 − wp12/w2, ε2 = ε∞2 − wp22/w2 and that where ε∞1(ε∞2) and wp1(wp2) are high-frequency permittivities and bulk plasma frequencies of the core (shell), respectively. Then we obtain40 the following expressions:
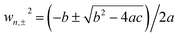 | (1) |
| a = [ε∞2 + n(ε∞1 + ε∞2)][ε3 + n(ε∞2 + ε3)] + (n2 + n)(ε∞1 − ε∞2)(ε∞2 − ε3)xn | (2) |
| b = −n[ε3 + n(ε∞2 + ε3)]wp12 − [ε3 + 2n(ε∞2 + ε3) + n2(ε∞1 + 2ε∞2 + ε3)]wp22 − (n2 + n)[(ε∞2 − ε3)wp12 + (ε∞1 − 2ε∞2 + ε3)wp22]xn | (3) |
| c = n2wp12wp22 + (n2 + n)wp22[wp22 + (wp12 − wp22)xn] | (4) |
| xn = (r1/r2)1 + 2n | (5) |
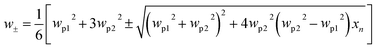 | (6) |
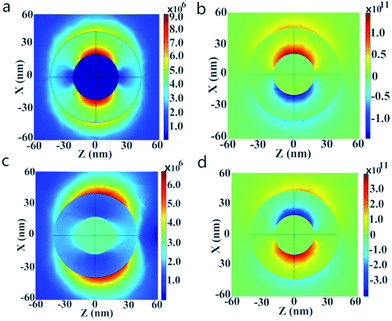
Here, the plasmon resonance of the Au@Cu2−xS CSNs can be considered as the interaction between the essentially fixed-frequency plasmon response of the Au nanosphere and the Cu2−xS nanocavity. The interaction results in the splitting of the plasmon resonances into two new resonances: lower energy (1280 nm) and higher energy (500 nm). To study this interaction of the plasmonic coupling more thoroughly, we calculate the local electric field distribution of the Au@Cu2−xS CSNs with different hybridization modes. As shown in Fig. 1c, the enhanced local field concentrates in the Au-core outer surface and polarizes parallel to the incident polarization. This is caused by the interaction of the different types of charges concentrated on the inner and outer surfaces of the Cu2−xS shell along the incident polarization. This demonstrates that the peak at 500 nm along the visible band presents ω+ mode. On the contrary, for the resonant wavelength at 1280 nm, a strong local field appears on both the inner and outer surfaces of the Cu2−xS shell (see Fig. 1d), which is similar to what happens with the Ag@Au CSNs.41 This demonstrates that at peak 1280 nm, a near-infrared band presents ω− mode. Our interest is to research the RI sensitivity of Au@Cu2−xS at a near-infrared band; therefore, we will focus on ω− mode of Au@Cu2−xS CSNs.
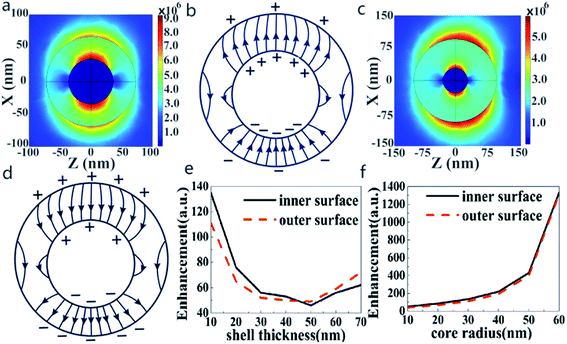
The change of shell thickness leads to a variation in the electric field. As shown in Fig. 2a, when the core radius and shell thickness are 30 nm, the electric field intensity on the shell inner surface of Au@Cu2−xS CSNs is stronger than that on the shell outer surface. A similar result has also been found in Ag@Au CSNs suspended in water.41 Thus, the electric field lines in the shell strongly repel each other and are highly compressed at the poles along the polarization direction,41 as shown in Fig. 2b. But, as the shell thickness increases with the constant core radius, the electric field intensity on the shell outer surface of Au@Cu2−xS CSNs grows larger than that on the shell inner surface, as shown in Fig. 2c. In this case, the electric field lines inside the shell repel each other at the poles along the incident polarization and compress at the poles against the polarization direction, as shown in Fig. 2d. The precise variation of the enhancements on the outer and inner surfaces of Au@Cu2−xS CSNs shell can be seen in Fig. 2e. The enhancement of the electric field on the shell inner surface is larger than that on the shell outer surface when the shell thickness is less than 45 nm. Nevertheless, when the shell thickness is larger than 45 nm, the induced electrons on the shell outer surface are more than those on the shell inner surface, which is due to the contribution of the Cu2−xS shell. The reason for this is that the number of conduction electrons on the outer surface increases with the larger Cu2−xS shell thickness.42 Moreover, the increase in core radius leads to an increase of the enhancements on the outer and inner surfaces, as shown in Fig. 2f. This shows that the increase in the core radius has almost no effect on the electric field distribution of core and shell surface.
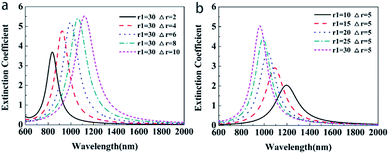
To study the effect of the geometrical parameters (core radius and shell thickness) on the LSPR property of Au@Cu2−xS CSNs, we calculate the extinction spectra of Au@Cu2−xS CSNs with varied shell thicknesses and core radii. As shown in Fig. 3a with Cu2−xS shell thickness variation from 2 to 10 nm, ω− mode shows a red-shift trend from 837 nm to 1121 nm (the variation of ω+ mode in ESI Fig. S1a†), which indicates that its resonance wavelength can be shifted to entirely near-infrared by increasing the shell thickness with a constant core radius. In Fig. 3b, however, with Au core radius variation ranging from 10 to 30 nm, ω− mode presents a blue-shift trend from 1195 nm to 962 nm, respectively (the variation of ω+ mode in ESI Fig. S1b†). This implies that its resonance wavelength can also be shifted to entirely near-infrared by decreasing the core radius with a constant shell thickness. Eqn (6) provides precise explanations for this situation. Here, the wp1 is larger than wp2, and the xn will become smaller with an increase in shell thickness, leading to the decrease of the ω−; therefore, ω− mode shows a tendency to red-shift.
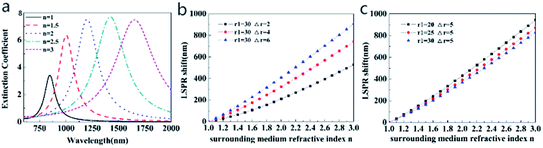
To study the LSPR properties of core–shell structures with different refractive indices of the surrounding medium, the extinction spectra of the Au@Cu2−xS CSNs are investigated, as shown in Fig. 4a. The LSPR peak of ω− mode red-shifts from 847 nm to 1652 nm when the refractive index of the surrounding medium changes from 1.0 to 3.0, respectively (the variation of ω+ mode in ESI Fig. S2†), which is sufficient to meet the conditions for the detection of most analytes. Simultaneously, peak intensity increases gradually, which provides potential for biosensing based on SPR. The reason for this is that the restoring force for the electron oscillation decreases with an increase in polarizability of the dielectric media, which damps the plasmon oscillations.43 Therefore, the tunability of the resonance peak induced by the media provides an application for sensors detecting the refractive indices of the surrounding medium.
To find the shift property of ω− mode (the lower-energy LSPR peak), Fig. 4b and c show the LSPR shift as a function of surrounding medium refractive index with different shell thicknesses and core radii (the extinction spectra in ESI Fig. S3 and S4†). The curves in Fig. 4b and c present clear evidence of the nearly linear shift with a change in the surrounding refractive index. In Fig. 4b, for Au@Cu2−xS CSNs with a thickness of 6 nm, the LSPR shift may reach 900 nm with an increasing surrounding medium refractive index that ranges from 1.0 to 3.0. As we systematically diminish the shell thickness from 6 nm to 2 nm while keeping the core radius at a constant 30 nm, it is observed that the LSPR shift is reduced from 900 nm to 530 nm when the refractive index is 3.0. In Fig. 4c, however, as we systematically enlarge the core radius from 20 nm to 30 nm while keeping the shell thickness at a constant 5 nm, we observe that the LSPR shift reduces from 944 nm to 828 nm when the refractive index is 3.0. Therefore, the resonance wavelength shift with a change of shell thickness is larger than that with the variation in core radius, which is more evident at a large refractive index.
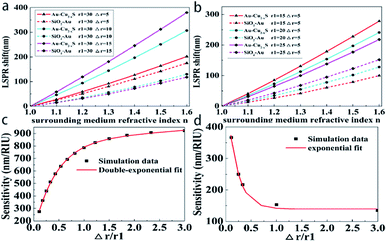
Refractive index sensitivity is defined as a change in LSPR wavelength per unit refractive index (RIU).23 In Fig. 4, it is observed that the resonance wavelength of Au@Cu2−xS CSNs shows a strong tunability with a change in RI between 1.0 and 3.0. To compare the sensitivity of Au@Cu2−xS CSNs with SiO2@Au CSNs under the same conditions, we set the refractive indices of the Au@Cu2−xS CSNs to 1.0 and 1.6, which is the same as the SiO2@Au CSNs.23 Fig. 5a and b show the LSPR shift of Au@Cu2−xS and SiO2@Au CSNs with the change of geometrical parameters (core radius and shell thickness) and surrounding refractive index. Obviously, under the same core radius, shell thickness and surrounding refractive index, Au@Cu2−xS CSNs show the larger LSPR shifts than that of SiO2@Au CSNs, which is more evident with the increase of surrounding refractive index. It demonstrates that Au@Cu2−xS CSNs have larger LSPR shift. Meanwhile, the changes of core radius and shell thickness also have effect on LSPR shift. Therefore, it is necessary to investigate the sensitivity of SiO2@Au and Au@Cu2−xS CSNs with different geometrical parameters. Fig. 5c and d show the sensitivity of Au@Cu2−xS and SiO2@Au CSNs with different shell thicknesses but the same total radius of 40 nm. Our calculations show that plasmon sensitivity changes nonlinearly with enlarging shell thickness. As shown in Fig. 5c, sensitivity reaches 925 nm per RIU in the case of the shell thickness equaling 30 nm. The sensitivity rises double-exponentially as the ratio of shell-thickness to core-radius increases because of the double LSPR originating core (Au) and shell (Cu2−xS). A similar phenomenon can also be found in Au@Ag CSNs (ESI Fig. S6†). However, in the SiO2@Au CSNs, only the shell (Au) supports the LSPR and shows different situations in which the plasmon sensitivity of CSNs increases near-exponentially as the ratio of the shell-thickness to core-radius decreases (Fig. 5d). This demonstrates that the RI sensitivity of Au@Cu2−xS CSNs is not only larger than that of SiO2@Au CSNs but also shows a stronger tunability with regard to improving sensitivity than SiO2@Au CSNs.
Our next goal is to find the cause of the tunable sensitivity in a core–shell nanostructure. As is well known, LSPR becomes attractive due to collective motion of free electrons on the surface of nanoparticles. Hence, we calculated the local electric field pattern and electric charge distribution of Au@Cu2−xS and SiO2@Au CSNs when the surrounding refractive index is 1.6. As shown in Fig. 6a and b, the plasmon of Au@Cu2−xS CSNs is caused by the oscillations of the same type of charge on the outer and inner shell surfaces. The free electrons at the outer surface of Au@Cu2−xS CSNs will be exposed to a repulsive force from the electrons on the inner surface, leading to the reduction of restoring force and increase of sensitivity24 determined by the ease of polarization of the electrons.21 It indicated that the repulsive force plays an important role in improving the sensitivity of metal–semiconductor CSNs. Therefore, with the increasing shell thickness, the oscillation electrons on both inner and outer shell surface becomes intense due to the conduction electrons increased by a thicker shell,41 which leads to enhance in repulsive force. This will result in to improve the ease of polarization of the electrons, increase plasmon wavelength red-shift and enhance sensitivity. However, different types of charges are concentrated on the inner and outer Au shell surfaces in SiO2@Au CSNs (see Fig. 6c and d). An attraction from the charges of the outer and inner surfaces leads to an increase in the restoring force and a reduction of sensitivity. It shows that the attraction could determinate the sensitivity of dielectric–metal CSNs, which is different from the metal–semiconductor CSNs. Therefore, with decreasing shell thickness, the oscillation of both inner and outer surface electrons becomes weak because of the decreasing conduction electrons in the thinner shell, which leads to decrease attraction. It results in improving the ease of polarization of the electrons and enhancement in sensitivity. The most essential difference for sensitivity between metal–semiconductor CSNs sensor and dielectric–metal CSNs sensor is different electric charge distributions.
3. Conclusion
In summary, taking Au@Cu2−xS CSNs as an example and using extended Mie theory, we improve the refractive index sensitivity by increasing red-shift plasmon wavelengths based on metal–semiconductor CSNs. The Au@Cu2−xS CSNs show a tunable resonance wavelength across the entire near-infrared band and high sensitivity in the surrounding medium possessing a large refractive index. The bulk sensitivity of the Au@Cu2−xS CSNs shows an increasing trend that meets a double-exponential curve with increasing shell thickness, which is due to the double LSPR supported by core and shell that greatly increase the LSPR red-shift to entire near-infrared area. The reason for the improvement of sensitivity of metal–semiconductor CSNs is the increase of the repulsive force caused by the thicker shell, which is different from the dielectric–metal CSNs. Taking advantages of this benefit, the present work is significant in broadening the sensing applications of metal–semiconductor CSNs in biochemistry and provides new ideas for sensor designs with high sensitivity.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 61205204 and 61701207), the China Scholarship Council Foundation (No. 201406185011), the Natural Science Foundation of Gansu Province (No. 1606RJZA068), State Key Laboratory of Millimeter Waves of Southeast University (No. K201717), the Fundamental Research Funds for the Central Universities of China and the Scientific Research Foundation for the Returned Overseas Chinese Scholars.References
- K. M. A. El-Nour, E. T. A. Salam, H. M. Soliman and A. S. Orabi, Nanoscale Res. Lett., 2017, 12, 231 CrossRef CAS PubMed.
- A. Boltasseva and H. A. Atwater, Science, 2011, 331, 290 CrossRef CAS PubMed.
- M. Wan, Y. Li, J. Chen, W. Wu, Z. Chen, Z. Wang and H. Wang, Sci. Rep., 2017, 7, 32 CrossRef PubMed.
- Y. Xie, W. Chen, G. Bertoni, I. Kriegel, M. Xiong, N. Li, M. Prato, A. Riedinger, A. Sathya and L. Manna, Chem. Mater., 2017, 29, 1716–1723 CrossRef CAS PubMed.
- H. Mu, J. Lv, Z. Liu, S. Zheng, L. Yang, T. Sun, Q. Liu and C. Liu, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 419 CrossRef.
- J. Jana, M. Ganguly and T. Pal, RSC Adv., 2016, 6, 86174–86211 RSC.
- H. Mu, J. Lv, C. Liu, T. Sun, P. K. Chu and J. Zhang, Opt. Commun., 2017, 402, 216–220 CrossRef CAS.
- Y. Tao, Z. Guo, A. Zhang, J. Zhang, B. Wang and S. Qu, Opt. Commun., 2015, 349, 193–197 CrossRef CAS.
- A. J. Haes and R. P. Van Duyne, J. Am. Chem. Soc., 2002, 124, 10596–10604 CrossRef CAS PubMed.
- J. Wang, H. Z. Zhang, R. S. Li and C. Z. Huang, TrAC, Trends Anal. Chem., 2016, 80, 429–443 CrossRef CAS.
- E. A. Terenteva, V. V. Arkhipova, V. V. Apyari, P. A. Volkov and S. G. Dmitrienko, Sens. Actuators, B, 2017, 241, 390–397 CrossRef CAS.
- X. R. Cheng, B. Y. H. Hau, T. Endo and K. Kerman, Biosens. Bioelectron., 2014, 53, 513–518 CrossRef CAS PubMed.
- H. Chen, X. Kou, Z. Yang, W. Ni and J. Wang, Langmuir, 2008, 24, 5233–5237 CrossRef CAS PubMed.
- T. Kawawaki, N. Shinjo and T. Tatsuma, Anal. Sci., 2016, 32, 271–274 CrossRef CAS PubMed.
- J. Pai, C. Yang, H. Hsu, A. B. Wedding and B. Thierry, Anal. Chim. Acta, 2017, 974, 87–92 CrossRef CAS PubMed.
- C. L. Nehl, H. W. Liao and J. H. Hafner, Nano Lett., 2006, 6, 683–688 CrossRef CAS PubMed.
- Y. Sun and Y. Xia, Anal. Chem., 2002, 74, 5297–5305 CrossRef CAS PubMed.
- J. Singh Sekhon and S. S. Verma, Plasmonics, 2011, 6, 311–317 CrossRef.
- J. Cao, T. Sun and K. T. V. Grattan, Sens. Actuators, B, 2014, 195, 332–351 CrossRef CAS.
- P. K. Jain, K. S. Lee, I. H. El-Sayed and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 7238–7248 CrossRef CAS PubMed.
- P. K. Jain and M. A. El-Sayed, J. Phys. Chem. C, 2007, 111, 17451–17454 CAS.
- M. Cao, M. Wang and N. Gu, J. Phys. Chem. C, 2009, 113, 1217–1221 CAS.
- J. Zhu, F. Zhang, J. Li and J. Zhao, Sens. Actuators, B, 2013, 183, 556–564 CrossRef CAS.
- J. Zhu and X. Deng, Sens. Actuators, B, 2011, 155, 843–847 CrossRef CAS.
- D. E. Charles, D. Aherne, M. Gara, D. M. Ledwith, Y. K. Gun Ko, J. M. Kelly, W. J. Blau and M. E. Brennan-Fournet, ACS Nano, 2010, 4, 55–64 CrossRef CAS PubMed.
- H. Chen, L. Shao, K. C. Woo, T. Ming, H. Lin and J. Wang, J. Phys. Chem. C, 2009, 113, 17691–17697 CAS.
- J. Zhu, Phys. E, 2005, 27, 296–301 CrossRef CAS.
- M. Morsin, M. M. Salleh, A. A. Umar and M. Z. Sandan, Sensors, 2017, 17, 947 CrossRef PubMed.
- A. Steinbrueck, O. Stranik, A. Csaki and W. Fritzsche, Anal. Bioanal. Chem., 2011, 401, 1241–1249 CrossRef CAS PubMed.
- Y. H. Lee, H. Chen, Q. Xu and J. Wang, J. Phys. Chem. C, 2011, 115, 7997–8004 CAS.
- C. Chen, S. Cheng, L. Chau and C. R. C. Wang, Biosens. Bioelectron., 2007, 22, 926–932 CrossRef CAS PubMed.
- G. Garcia, R. Buonsanti, E. L. Runnerstrom, R. J. Mendelsberg, A. Llordes, A. Anders, T. J. Richardson and D. J. Milliron, Nano Lett., 2011, 11, 4415–4420 CrossRef CAS PubMed.
- S. Hsu, W. Bryks and A. R. Tao, Chem. Mater., 2012, 24, 3765–3771 CrossRef CAS.
- H. Matsui, S. Furuta and H. Tabata, Appl. Phys. Lett., 2014, 104, 211903 CrossRef.
- J. M. Luther, P. K. Jain, T. Ewers and A. P. Alivisatos, Nat. Mater., 2011, 10, 361–366 CrossRef CAS PubMed.
- L. J. Mendoza Herrera, L. B. Scaffardi and D. C. Schinca, RSC Adv., 2016, 6, 110471–110481 RSC.
- E. A. Chaffin, S. Bhana, R. T. O. Connor, X. Huang and Y. Wang, J. Phys. Chem. B, 2014, 118, 14076–14084 CrossRef CAS PubMed.
- R. W. Christy and P. B. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 4370–4379 CrossRef.
- E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419 CrossRef CAS PubMed.
- H. Zhou, D. Gao and L. Gao, Plasmonics, 2017, 1–8 Search PubMed.
- D. Wu, X. Xu and X. Liu, Solid State Commun., 2008, 148, 163–167 CrossRef CAS.
- D. D. Evanoff and G. Chumanov, J. Phys. Chem. B, 2004, 108, 13957–13962 CrossRef CAS.
- E. Prodan, A. Lee and P. Nordlander, Chem. Phys. Lett., 2002, 360, 325–332 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra11981j |
| This journal is © The Royal Society of Chemistry 2018 |