Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis, magnetic and transport properties of HTP-Ni3Sn2 single crystals obtained by the chemical vapor transport method
Cong Xian *ab and
Jian Wanga
*ab and
Jian Wanga
aThe Anhui Key Laboratory of Condensed Matter Physics at Extreme Conditions, High Magnetic Field Laboratory, Chinese Academy of Sciences, Hefei 230031, China. E-mail: xiancong@hmfl.ac.cn
bUniversity of Science and Technology of China, Hefei 230026, China
First published on 2nd January 2018
Abstract
Here, we report the synthesis, magnetic properties and transport properties of HTP-Ni3Sn2 single crystals. The magnetic measurements reveal that HTP-Ni3Sn2 has a paramagnetic temperature dependence and the c axis has a stronger magnetic interaction. Despite the existence of strong antiferromagnetic interactions, the long range magnetic order is not observed due to the geometrical frustration. Moreover, the sublinear temperature dependence of the resistivity is presented, which is attributed to short-range correlations among the geometrical frustration. Our study suggests that the geometrical frustration has an important influence on the physical properties of HTP-Ni3Sn2.
1. Introduction
Frustrated materials are interesting because their physical properties are difficult to predict. And frustration can lead to qualitatively new states of matter and novel physical properties, such as quantum criticality,1–3 quantum or topological anomalous Hall effect,4–8 spin liquid9–14 and spin ice.15–17 Magnetic materials with frustrated lattice structures are good platforms to investigate those novel properties induced by geometrical frustration, where the interaction between spins cannot be simultaneously satisfied. Although a lot of work has been reported about those novel properties, the underlying mechanism needs to be further studied on more geometrically frustrated materials.Ni3Sn2 is a transition metal compound, with two different phases at different temperature ranges.18–20 The low temperature phase (LTP) Ni3Sn2 has a Ni3Sn2-type orthorhombic structure with the space group oP12/Pnma. Above ∼780 K the compound transforms to a high temperature phase (HTP) Ni3Sn2, which has a Ni2In-type hexagonal structure with the space group P63/mmc. In HTP-Ni3Sn2, Ni atoms with different coordination form the triangular lattices, which is one of the key ingredients for spin frustration that may induce quantum phenomena with exotic physical properties. Though crystal structure and phase diagram for Ni3Sn2 have been reported in the previous studies,18–20 less work has been done to study the magnetic and transport properties.
In this work, we first report magnetic and transport properties of HTP-Ni3Sn2 single crystal. The magnetic measurements show that HTP-Ni3Sn2 is a paramagnetic compound with an obvious magnetic anisotropy. Due to the existence geometrical frustration arising from the triangular nickel lattices, the long range magnetic order is not observed. The temperature dependence of the resistivity and MR also reveal a strong contribution from the short range magnetic order. Our results suggest that the long-range magnetic order may be suppressed by the geometrical frustration in HTP-Ni3Sn2.
2. Experimental
Single crystals of HTP-Ni3Sn2 were first grown by the chemical vapor transport method by using iodine as a transport agent. The detailed process can be described as follows. The polycrystalline Ni3Sn2 was obtained by reacting Ni powder with Sn powder with Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sn = 3
Sn = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 at 800 °C for 3 days. The polycrystalline powder together with iodine was sealed in a long quartz tube under vacuum. The quartz tube was then kept in a gradient furnace for 7 days with the cooler end at 1000 °C, while the hot end with the mixed powder at 1070 °C. The quartz tube naturally cooled to 800 °C in furnace, and then quenching. Single crystals of HTP-Ni3Sn2 were obtained at the cooler end. Single crystal X-ray diffraction (XRD) was used to determine crystal growth orientation (Rigaku-TTR3). The transport measurements were investigated on the Oxford Instrument TeslatronPT cryogenic system by four probe technique. The magnetic measurements were carried out using the Quantum Design 7 T Magnetic Property Measurement System.
2 at 800 °C for 3 days. The polycrystalline powder together with iodine was sealed in a long quartz tube under vacuum. The quartz tube was then kept in a gradient furnace for 7 days with the cooler end at 1000 °C, while the hot end with the mixed powder at 1070 °C. The quartz tube naturally cooled to 800 °C in furnace, and then quenching. Single crystals of HTP-Ni3Sn2 were obtained at the cooler end. Single crystal X-ray diffraction (XRD) was used to determine crystal growth orientation (Rigaku-TTR3). The transport measurements were investigated on the Oxford Instrument TeslatronPT cryogenic system by four probe technique. The magnetic measurements were carried out using the Quantum Design 7 T Magnetic Property Measurement System.
3. Results and discussion
The HTP-Ni3Sn2 has a Ni2In-type hexagonal structure with the P63/mmc space group, as shown in Fig. 1(a). Ni atoms occupy two positions and form triangular lattices, which is presented in Fig. 1(a) and (b). Two Ni2 atoms and a Ni1 atom form the triangular lattices with distorted configuration, indicating the existence of frustrated structures. The single crystal and powder XRD of HTP-Ni3Sn2 are presented in Fig. 1(c). Only (00m) reflections are present in the single crystal XRD, indicating the large surface of HTP-Ni3Sn2 crystal is ab plane. The c axis lattice parameter is estimated to be 5.208 Å from the (002) peak position by using Bragg's law. In order to verify whether the sample is a single phase compound, we studied the XRD of the powder sample ground from single crystals, which is consistent with the data of the HTP-Ni3Sn2.18 The results also indicate that the sample has a pure phase.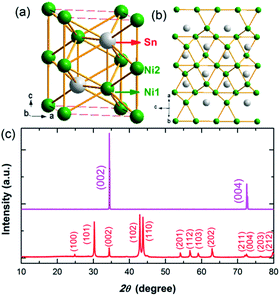 | ||
| Fig. 1 (a) The crystal structure of HTP-Ni3Sn2. (b) The triangular lattices of Ni atoms. (c) The single-crystal and powder XRD patterns of HTP-Ni3Sn2. | ||
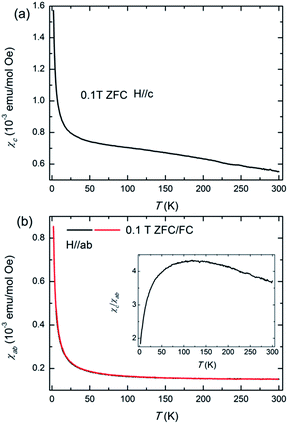
To investigate the magnetic properties of HTP-Ni3Sn2, magnetic susceptibility (χ = M/H) measurements on a single-crystalline HTP-Ni3Sn2 was performed. Fig. 2 shows the temperature dependence of susceptibility χ at 0.1 T and the T range 2 K ≤ T ≤ 300 K for both magnetic field directions. It's obvious that the paramagnetic behaviour is presented for both directions. And the value of χ for c axis is larger than that of ab plane, indicating that the c axis has stronger magnetic correlations. The anisotropy ratio γ = χc/χab as a function of temperature is shown in the inset of Fig. 2(b). With decreasing the temperature, the γ slowly increases at the temperature of 120–300 K and then decreases down to 2 K. In general, χ slowly increases due to the thermal fluctuation at high temperature, leading to a little change for the value of γ. Upon further decreasing temperature, χ increases sharply with the decrease of thermal fluctuation. The anisotropic magnetic structure results in the obvious difference of slope of χ for both directions. It is obvious that the slope of χ for ab plane is more than that for c axis at low temperature. Therefore, the value of γ decreases. In the paramagnetic regime, the χ(T) curves follow the Curie–Weiss law χ(T) = χ0 + C/(T − θp), where χ0 is a T-independent contribution term of the susceptibility, C is the Curie constant and θp is the Weiss temperature. The derived effective moments are 1.96 μB/Ni for H∥c and 0.07 μB/Ni for H∥ab, indicating that the c axis is the easy axis and has a stronger magnetic correlation. The effective moments for the c axis is close to the theoretical value of 1.73 μB/Ni for S = 1/2 Ni3+ ions and less than the theoretical value of 2.83 μB/Ni for high spin S = 1 Ni2+ ions.21 In addition, the obtained Curie–Weiss temperatures θp are −1102 K and 23 K for H∥c and H∥ab. The large negative Weiss temperature indicates strong antiferromagnetic correlations along c axis. In spite of the observed large negative Weiss temperature, the long range magnetic order is absent in χ(T) because the geometrical frustration suppress the long-range magnetic order. As we known, this situation often is observed in frustrated materials. For example, despite existence of antiferromagnetic interaction, Pr2Ir2O7 has no long range magnetic order due to strong geometrical frustration.22 For HTP-Ni3Sn2, the geometrical frustration in the triangular nickel lattice shown in Fig. 1 is likely a possibility to result in the absence of long range magnetic order.
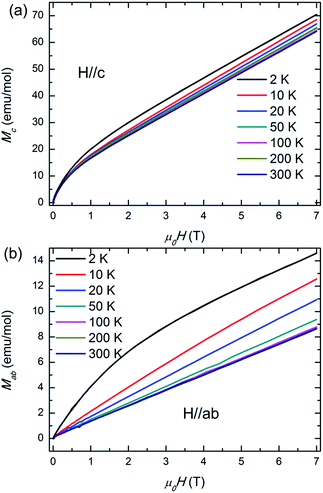
Magnetization M of HTP-Ni3Sn2 single crystal as a function of applied magnetic field H measured at different temperatures between 2 K and 300 K for H applied along the c axis and perpendicular to the ab axis are shown in Fig. 3(a) and (b), respectively. For the c axis, the M increases sharply upon the increase of field at low field (<1 T), then the M increases linearly and shows no saturation at all temperatures. But for the ab plane, only the behaviour of M at 2 K is similar with that for c axis due to the magnetic correlation is weak and suppressed with increasing the temperature. At other indicated temperatures, the M increases linearly and shows no saturation. This also indicates that HTP-Ni3Sn2 has an anisotropic magnetic structure.
The temperature dependence of the electrical resistivity ρ(T) down to 2 K for HTP-Ni3Sn2 single crystals is shown in Fig. 4(a). The ρ(T) at zero field exhibits a metallic behaviour. At low temperature, a kondo-like increase of resistivity was observed, which is due to the scattering of conducting carriers from the magnetic atoms. But above ∼80 K, the resistivity ρ temperature dependence is different with the ordinary metals. For the ordinary metals, the temperature dependence of the total resistivity at high temperature is T-linear mainly due to electron–phonon scattering.23,24 But for HTP-Ni3Sn2, the sublinear temperature dependence was presented at high temperature. The red sublinear lines shows the fitting results by using the formula ρ = A + BTn, obtaining n = 0.07 at the temperature of 80–200 K (n < 1), which is unusual. This abnormal behaviour for resistivity is attributable to the short-range order correlations arising from the geometrical frustration, indicating the geometrical frustration is existed in this material. The similar behaviour was also observed in the frustrated compound PdCrO2.25
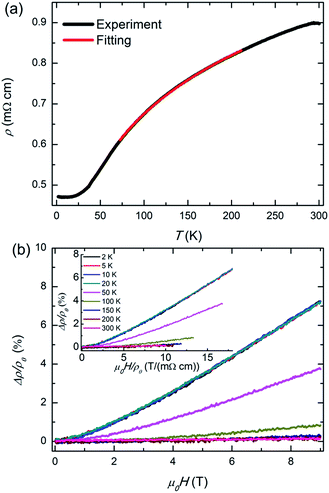 | ||
| Fig. 4 (a) Temperature dependence of resistivity ρ at temperature ranging from 2 K to 300 K. (b) Magnetoresistance for HTP-Ni3Sn2 at various temperatures. Inset: corresponding Δρ/ρ(0) vs. H/ρ(0). | ||
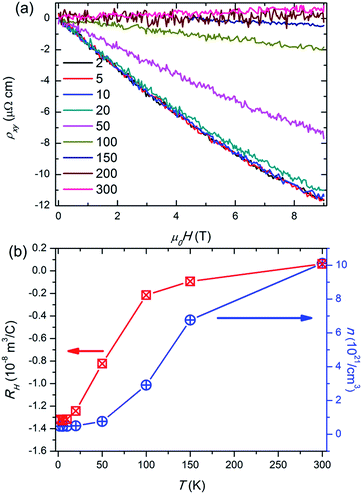
Magnetic field dependence of in-plane magnetoresistance (MR) at indicated temperatures are showed in Fig. 4(b). The MR is calculated by Δρ/ρ = [ρ(H) − ρ(0)]/ρ(0). The positive MR is presented under the magnetic field up to 9 T at different temperatures. At 2 K and 9 T, the value of MR reaches the maximum value, which is ∼7%. With increasing temperature, the MR decreases and then tends to the zero. According to the Kohler's Rule,26 the MR versus H/ρ(0) have a universal function Δρ/ρ(0) = f(H/ρ(0)) for the metals at all temperatures and fields. Here, we also analysed the data of MR by the Kohler's Rule, as shown in the inset of Fig. 4(b). It's obvious that the MR deviates from the Kohler's law at T > 50 K. This may be due to the change of contribution from magnetic scattering upon the change of temperature. Based on the above results of transport, we would conclude that the magnetic correlations have an important influence on the transport properties of HTP-Ni3Sn2.
To quantify the electrical transport properties under applied magnetic field, the field dependence of Hall resistivity ρxy of HTP-Ni3Sn2 is investigated under H∥c at different temperatures, as shown in Fig. 5(a). The ρxy shows nearly linear dependence to the applied field in the whole temperature range, indicating that ρxy is derived from the ordinary Hall effect. And the ρxy decreases with the increase of H. This suggests that the electron-type carrier in HTP-Ni3Sn2 is dominant. The Hall coefficient (RH) and carrier concentrations (n = −1/(eRH)) were presented in Fig. 5(b). The normal Hall coefficient RH reaches the maximum of ∼−1.3 × 10−8 m3 C−1 at 2 K. which is an order of magnitude less than that in Fe3Sn2.27 The carrier concentrations n varies from the minimal value 0.5 × 1021 cm−3 at 2 K to 1.0 × 1022 cm−3 at 300 K, which is in the range of typical metal.
4. Conclusions
In summary, we synthesized single crystals of HTP-Ni3Sn2 by using chemical vapor transport method and characterized their magnetic and transport properties. The anisotropic magnetic properties were presented on HTP-Ni3Sn2. Due to the geometrical frustration arising from the triangular nickel lattice, the long range magnetic order is absent. In addition, the sublinear temperature dependence of the resistivity was presented and the MR deviates from the Kohler's law. The detailed analysis proposes that the magnetic correlations play an important role on the transport properties of HTP-Ni3Sn2.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Ministry of Science and Technology of China (National Key Research and Development Program No. 2016YFA0300404), and the National Natural Science Foundation of China (Grant No. U1432138, 11474288, 11604344, 11574322, 21503233, 11574317).References
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed.
- V. Fritsch, J. Hemberger and N. Büttgen, et al., Phys. Rev. Lett., 2004, 92, 116401 CrossRef CAS PubMed.
- G. Chen, L. Balents and A. P. Schnyder, Phys. Rev. Lett., 2009, 102, 096406 CrossRef PubMed.
- R. Moessner and A. P. Ramirez, Phys. Today, 2006, 59, 24 CrossRef CAS.
- Y. Taguchi, Y. Oohara, H. Yoshizawa, N. Nagaosa and Y. Tokura, Science, 2001, 291, 2573–2576 CrossRef CAS PubMed.
- Y. Taguchi, T. Sasaki and S. Awaji, et al., Phys. Rev. Lett., 2003, 90, 257202 CrossRef CAS PubMed.
- C. Sürgers, G. Fischer, P. Winkel and H. V. Löhneysen, Nat. Commun., 2014, 5, 3400 Search PubMed.
- S. Nakatsuji, N. Kiyohara and T. Higo, Nature, 2015, 527, 212–215 CrossRef CAS PubMed.
- R. Moessner and J. T. Chalker, Phys. Rev. Lett., 1998, 80, 2929–2932 CrossRef CAS.
- R. Moessner and A. P. Ramirez, Phys. Today, 2006, 59, 24 CrossRef CAS.
- B. G. Levi, Phys. Today, 2007, 60, 16 CrossRef.
- T. Imai and Y. S. Lee, Phys. Today, 2016, 69, 30 CrossRef.
- M. R. Norman, Rev. Mod. Phys., 2016, 88, 041002 CrossRef.
- L. Savary and L. Balents, Rep. Prog. Phys., 2017, 80, 016502 CrossRef PubMed.
- C. Castelnovo, R. Moessner and S. L. Sondhi, Nature, 2008, 451, 42–45 CrossRef CAS PubMed.
- S. T. Bramwell, S. R. Giblin, S. Calder, R. Aldus, D. Prabhakaran and T. Fennell, Nature, 2009, 461, 956–959 CrossRef CAS PubMed.
- H. R. Molavian, M. J. P. Gingras and B. Canals, Phys. Rev. Lett., 2007, 98, 157204 CrossRef PubMed.
- G. F. Zhou, L. M. Di and H. Bakker, J. Appl. Phys., 1993, 73, 1521–1527 CrossRef CAS.
- C. Schmetterer, H. Flandorfer and K. W.Richter, et al., Intermetallics, 2007, 15, 869–884 CrossRef CAS.
- A. Leineweber, E. J. Mittemeijer and M. Knapp, et al., Philos. Mag., 2007, 87, 1821–1844 CrossRef CAS.
- N. W. Ashcroft and N. D. Mermin, Solid state physics, 1976, ch. 31, p. 658 Search PubMed.
- Y. Machida, S. Nakatsuji, Y. Maeno, T. Tayama, T. Sakakibara and S. Onoda, Phys. Rev. Lett., 2007, 98, 057203 CrossRef CAS PubMed.
- T. Kasuya, Prog. Theor. Phys., 1956, 16, 58 CrossRef.
- K. Mori and K. Sato, J. Phys. Soc. Jpn., 1980, 49, 246 CrossRef CAS.
- H. Takatsu, H. Yoshizawa, S. Yonezawa and Y. Maeno, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104424 CrossRef.
- L. Forr, K. Biljakovi, J. R. Cooper and K. Bechgaard, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 2839–2842 CrossRef.
- Q. Wang, S. Sun, X. Zhang, F. Pang and H. Lei, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 075135 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |