Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural and impedance spectroscopy characteristics of BaCO3/BaSnO3/SnO2 nanocomposite: observation of a non-monotonic relaxation behavior
S. A. Salehizadeha,
Hossein Mahmoudi Chenarib,
Mehdi Shabanicd,
Hossein Abbastabar Ahangare,
Reza Zamiri *fg,
Avito Rebeloc,
J. Suresh Kumara,
M. P. F. Graçaa and
J. M. F. Ferreira
*fg,
Avito Rebeloc,
J. Suresh Kumara,
M. P. F. Graçaa and
J. M. F. Ferreira c
c
aPhysics Department (I3N), University of Aveiro, Campus Universitario de Santiago, Aveiro, Portugal
bDepartment of Physics, Faculty of Science, University of Guilan, Namjoo Ave, Po Box 41335-1914, Rasht, Iran
cDepartment of Materials and Ceramic Engineering (DEMaC), University of Aveiro, Campus Santiago, Aveiro, 3810-193 Portugal
dSustainable Developments in Civil Engineering Research Group (SDCE), Faculty of Civil Engineering (FCE), Ton Duc Thang University, Ho Chi Minh City, Vietnam
eDepartment of Chemistry, Islamic Azad University, Najafabad Branch, Najafabad, Iran
fLaser Applications Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: reza.zamiri@tdt.edu.vn
gFaculty of Applied Sciences, Ton Duc Thang University, Ho Chi Minh City, Vietnam
First published on 9th January 2018
Abstract
A BaCO3/BaSnO3/SnO2 nanocomposite has been prepared using a co-precipitation method without adding any additives. The prepared sample was characterized by using X-ray diffraction (XRD), high-resolution transmission electron microscopy (HRTEM), scanning electron microscopy (SEM), Fourier-transform infrared (FT-IR) spectroscopy, energy dispersive X-ray spectroscopy (EDS) and Raman spectroscopy. Detailed studies on the dielectric and electrical behavior (dielectric constant, complex impedance Z*, ac conductivity, and relaxation mechanisms) of the nanocomposite have been performed using the nondestructive complex impedance spectroscopy technique within the temperature range 150–400 K. The dielectric constant of the sample as a function of temperature showed the typical characteristics of a relaxor. The maximum dielectric constant value was observed to depend on frequency. The non-monotonic relaxation behavior of the prepared nanocomposite was evidenced from the spectra of loss tan, tan(δ). The relaxation kinetics was modeled using a non-Arrhenius model.
1. Introduction
Over the last two decades barium stannate, BaSnO3, from the perovskite family with the general formula of ABO3 (A = mono/di, B = tri/tetra/penta) has received increasing attention for humidity sensors, computer memories, pyroelectric detectors and electro-optic modulators, due to its superior optical and electrical nature.1–4Barium stannate is also an important n-type semiconductor resulting from the formation of oxygen vacancies or by suitably doping at the Ba and/or Sn sites.5,6 However, this perovskite-like material is also interesting for other applications like ceramic capacitors due to the characteristics of its dielectric constant.7,8
It is complicated to synthesize pure single phase of BaSnO3. It was shown that the highly crystalline barium stannate could be conventionally obtained by a solid-state calcination process at T > 1200 °C.9,10 Recent studies on the kinetics and mechanism of solid state reaction clearly showed that the particle size reduction of the raw materials (BaCO3 and SnO2) to the submicrometer or even the nanometer scales results in a significant decrease of the synthesis temperature of the perovskite material. Therefore, some wet chemistry routes, such as alkoxide hydrolysis, sol–gel,6,11,12 hydrothermal,13,14 and co-precipitation15 methods were proposed as effective ways to shorten the reactions paths. In these methods, the main solid reactants (e.g. BaCO3 and SnO2) could be mixed at the nanoscale, which led to the formation of BaSnO3 nanopowders at a much lower temperatures of 500–900 °C.6,11–15 However, the large amounts of organic solvents or reacting agents required for these routes could be hardly removed from the systems. This is likely to change the electrical performance due to contrasting properties depending upon the type of forming system and the mixed solid solution.16 It includes phase transition (ferro–paraelectric), dielectric and alternates (increase/decrease) in resistance with temperature and frequency.17 The obtained modification makes this material suitable and useful for many industrial applications.
In ferroelectric materials with perovskite structure (ABO3) the inherent anisotropy arised from high degree of microstress and structural defects, including the random distribution of oxygen defects and dopant, make these ceramics promising for possible applications in various technologies like memory storage devices, microelectro mechanical systems, multilayer ceramic capacitors, and recently in the area of opto-electronic devices.18
Relaxor ferroelectrics (“relaxors” for short) have attracted significant interest due to their superior dielectric and electro mechanical properties.19 The most typical feature of relaxors is a strongly broadened frequency-dependent peak of the dielectric permittivity versus temperature, whose position shifts to lower temperatures when the frequency decreases.19 Several models have been proposed to explain the relaxation behavior in relaxors.18,20,21 A commonly proposed explanation is that it arises from the motion of polar nanoregions due to the local distortion of the structure coming from chemical inhomogeneity.20–22 The existence of the local nanometric clusters can be confirmed experimentally using several measurements including optic index of refraction,23 synchrotron-ray scattering,24 diffuse neutron scattering,25 and transmission electron microscopy.26 Moreover, dielectric spectroscopy measurements in broad temperature and frequency ranges are fruitful to investigate the relaxational behavior of the clusters in a relaxor.19–21 However, the origin of this dipolar relaxation is still open for discussion.
In the present work, the structure and morphology of the BaCO3/BaSnO3/SnO2 nanocomposite synthesized by precipitation method has been studied using X-ray diffraction, FT-IR, Raman spectroscopy, SEM, and TEM techniques. These studies indeed prove the predominance of the reactants BaCO3 and SnO2 in the sample, and the formation of nanoscale particles of BaSnO3. To have a better understanding of the electric and dielectric behaviors of the material, these properties were studied within wide ranges of frequency and temperature. The observation of the relaxational behavior is modeled and discussed using the proper theoretical model.
2. Experimental procedure
In a typical experiment, appropriate amounts of SnCl4·5H2O (0.01 mol) and BaCl2·2H2O (0.01 mol) were separately dissolved in deionized water under continuous stirring for 30 minutes at room temperature. A quantitative volume of aqueous NaOH solution was slowly added into the mixture solution under vigorous stirring to promote the precipitation. The precipitate was filtered and washed with deionized water for several times, and then dried at 100 °C. The white precipitate was calcined at 500 °C for 5 h to obtain BaCO3/BaSnO3/SnO2 nanocomposites.The precipitate formation can be summarized by the following reactions:27
The synthesized nanoparticles were then used for experimental characterization studies. Phase identification was performed using X-ray diffractometer (XRD; X'Pert Philips Materials Research System) with Cu-Kα radiation (λ = 1.5406 Å) under accelerating voltage of 45 kV and current of 40 mA in the 2θ range from 20–80°. Powder pellets were molded into disks (thickness ≈ 2.0 mm; diameter = 7 mm). The bulk sensitive X-ray diffraction (XRD) patterns were acquired with a Philips X'Pert MPD equipment with Cu Kα, λ = 1.5406 Å (40 kV). The Raman spectroscopy of the pellets was carried out in a T64000 JobinYvon SPEX spectrometer, using an Ar laser (λ = 532 nm) as excitation font. The spectra were obtained between 100 and 1200 cm−1 in a back scattering geometry.
For the electrical measurements the opposite sides of the pellet were painted with silver paste. Impedance spectroscopy measurements were performed in temperature range of 150 to 400 K, between 102 Hz and 106 Hz using an Agilent 4294A network analyzer in the Cp–Rp configuration.28
3. Results and discussion
The X-ray diffraction pattern of the nanocomposite powder sample calcined at 500 °C shown in Fig. 1 reveals the existence of a mixture of BaCO3/BaSnO3/SnO2 phases. The Bragg's peaks for the predominant SnO2 phase correspond to the tetragonal symmetry, consistent with the JCPDS No. 41-1455. The XRD peaks of BaCO3 are in agreement with the orthorhombic structure and space group of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (JCPDS card 44-1487). In addition, the reaction between BaCO3 and SnO2 led to the formation of small amounts of an intermediate phase, cubic BaSnO3 as indicated by the XRD line (110). The small content of cubic BaSnO3 can be attributed to the relatively low calcination temperature. Additionally, Reference Intensity Ratio (RIR) method was employed to quantitatively determine the proportion of each component within the nanocomposite. The analysis revealed that the prepared composite consists of 71% SnO2, 17% BaSnO3, with only 12% of BaCO3. This was further supported by an exclusive Raman study on the composition, as will be discussed below. The reflection peaks corresponding to the main phases are indicated in Fig. 1.
m (JCPDS card 44-1487). In addition, the reaction between BaCO3 and SnO2 led to the formation of small amounts of an intermediate phase, cubic BaSnO3 as indicated by the XRD line (110). The small content of cubic BaSnO3 can be attributed to the relatively low calcination temperature. Additionally, Reference Intensity Ratio (RIR) method was employed to quantitatively determine the proportion of each component within the nanocomposite. The analysis revealed that the prepared composite consists of 71% SnO2, 17% BaSnO3, with only 12% of BaCO3. This was further supported by an exclusive Raman study on the composition, as will be discussed below. The reflection peaks corresponding to the main phases are indicated in Fig. 1.
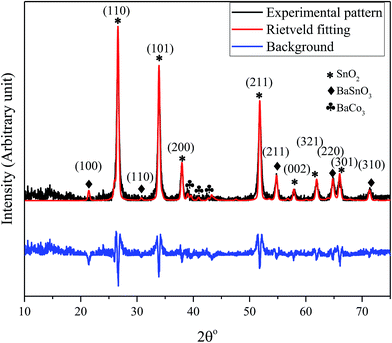 | ||
| Fig. 1 XRD pattern and the Rietveld refinement of BaCO3/BaSnO3/SnO2 nanocomposite powder along with the crystal plan indexation for the main phases. | ||
3.1. SEM/EDS and TEM analyses
The EDS analysis spectrum, and SEM image, of the prepared BaCO3/BaSnO3/SnO2 nanocomposite are shown in Fig. 2a and b, respectively.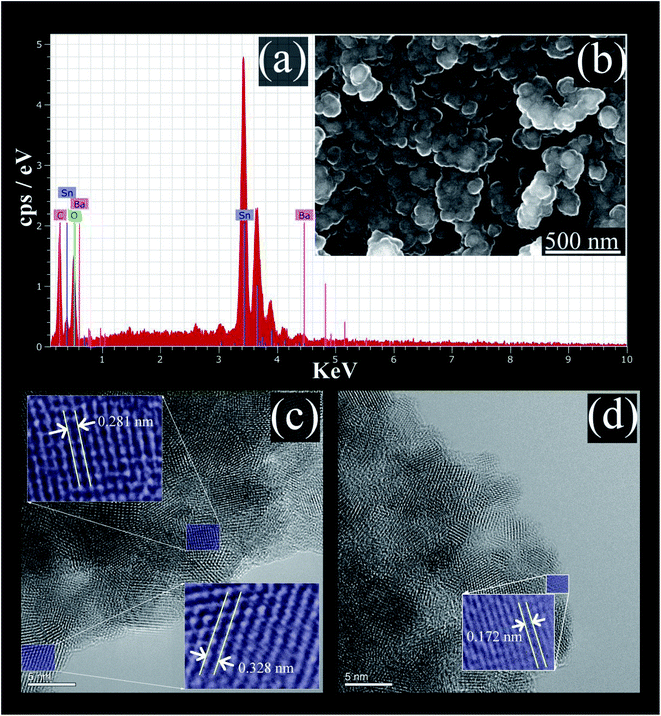 | ||
| Fig. 2 (a) The EDS spectrum; (b) SEM micrograph; (c) and (d) HRTEM images of BaCO3/BaSnO3/SnO2 nanocomposite. | ||
The EDS analysis confirms that the product contains Ba, Sn, C and O without the presence of any impurity. The SEM image reveals that spherical shaped nanoparticles were initially formed and then tended to merge partially into agglomerates. In addition, the lattice plane fringes from HRTEM images were used to calculate the d-spacing values (Fig. 2c and d). The d-spacing's equal to 0.328 nm, 0.172 nm, and 0.281 nm correspond to the (110), (113), and (110) crystal planes of SnO2, BaCO3, and BaSnO3, respectively.29
3.2. FT-IR spectroscopy
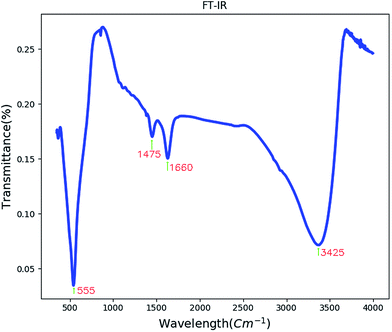
Fig. 3 shows the FT-IR spectrum of BaCO3/BaSnO3/SnO2 nanocomposite. The peak appearing at 550 cm−1 corresponds to the Sn–O stretching vibration.13The band centered at 1660 cm−1 is related to the C–O stretching vibrations and C–C stretching vibration of the BaCO3. Absorption peak at 1475 cm−1 may correspond to carbonate group in BaCO3. The band centered at 3425 cm−1 corresponds to the ν(OH) stretching vibration of the surface adsorbed water molecules.30,31
3.3. Raman spectroscopy
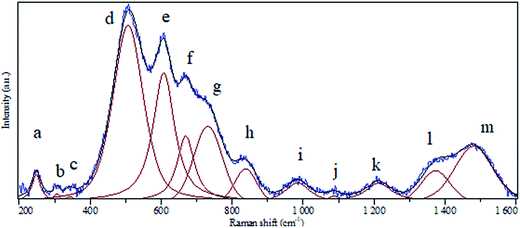
A clear batch of Raman active modes was detected for the case of BaCO3/BaSnO3/SnO3 nanocomposite. The deconvolution of Raman spectrum for this composition was carried out using Gaussian fitting as described in ref. 32 and 33 to identify and assign all possible vibrational modes. The peak positions labeled in alphabetic order, and the assignments of the modes could be precisely obtained, being presented in Fig. 4 and reported in Table 1, respectively. For the case of BaCO3, the free ion CO32− with D3h symmetry exhibits four normal vibrational modes: a symmetric stretching vibration (1); an autoquantitative analysis of the of-plane bend (2); a doubly degenerate asymmetric stretch (3); and a doubly degenerate bending mode (4). The symmetries of these modes are A1′(R) + A2′′ (IR) + E′(R, IR) + E′(R, IR) occur at 1064, 879, 1415 and 680 cm−1, respectively. The symmetric stretching vibration is very intense in the Raman spectrum, while the asymmetric stretching is weak. The asymmetric bending, although Raman-allowed, is very weak.3,34,35| Peak notation | Position (cm−1) | Assignment | |
|---|---|---|---|
| a | 247 | Corresponds to defect or oxygen vacancy in BaSnO3 | |
| b | 306 | Corresponds to defect or oxygen vacancy in BaSnO3 | |
| c | 342 | Corresponds to defect or oxygen vacancy in BaSnO3 | |
| d | 507 | Sn–O–Sn vibration mode (B1u symmetry) | |
| e | 607 | Sn–O vibration mode (A1g symmetry) in SnO2 | |
| f | 669 | Sn–O vibration mode (A2u symmetry) in SnO2 | |
| g | 731 | Sn–O vibration mode (LO symmetry) in SnO2 | |
| h | 838 | Bending in-plane vibration in BaCO3 | |
| i | 984 | Corresponds to defect or oxygen vacancy in BaSnO3 | |
| j | 1087 | Bending in-plane vibration in BaCO3 | |
| k | 1212 | Corresponds to defect or oxygen vacancy in BaSnO3 | |
| l | 1373 | Corresponds to defect or oxygen vacancy in BaSnO3 | |
| m | 1480 | Asymmetric stretching vibration in BaCO3 |
Rutile tetragonal SnO2, containing two Sn and four O atoms in a single unit cell, belongs to the space group D144h. According to the group theory, the representation of normal vibration modes at the center of the Brillouin zone is Γ = A1g + A2g + 2A2u + B1g + B2g + 2B1u + Eg + 4Eu.36 However, we could not find all the modes regarding to SnO2 and BaCO3. In sufficient intensity arising from small polarizability of several modes could be the reason for the less number of modes observed relatively to that predicted by group theoretical calculation.37
It should be pointed out that there are no Raman-active modes in the ideal perovskite crystal of the centrosymmetric BaSnO3 with ideal cubic structure belonging to the space group Pn3m because of inversion symmetry of all-atom occupying site.3 Although some of modes could be assigned, there are no assignments in literature corresponding to the detected a, b, c, i, k and l modes. It is likely that these modes are induced by defects such as oxygen vacancies, which destroy the translational periodicity of the lattice BaSnO3.3 To confirm the result of RIR analysis we have calculated the relative area of the bands pertaining to each phase to qualitatively determine the abundance of each component in the composite using the following relation:
| Rphase(i) (in %) = (area of bands assigned to phase(i)/total area of the spectrum) × 100 | (1) |
According to eqn (1), RSnO2, RBaSnO3 and RBaCO3 were found to be 67%, 18% and 15%. These values are very consistent with the ones obtained from RIR analysis.
3.4. Impedance spectroscopy
Fig. 5 represents the variation of imaginary part of impedance (Z′) with frequency (Hz). The variation pattern is characterized by: (a) the appearance of peaks at a particular frequency at each temperature; (b) a decrease in the height of the peaks with rise in temperature; (c) significant broadening of the peaks with rise in temperature; (d) marked asymmetry in the peak pattern; and (e) merging of the spectra at higher frequencies irrespective of temperature. Broadening of the peaks with the rise in temperature suggests the presence of temperature-dependent relaxation process in the material. The asymmetric broadening of the peaks suggests the presence of electrical processes in the material with the spread of relaxation time (indicated by peak width) with two equilibrium portions. The relaxation species may possibly be electrons/immobile species at lower temperatures, and defects at a higher temperatures that may be responsible for electrical conduction in the material by hopping of electrons/oxygen ion vacancy among the available localized sites.38,39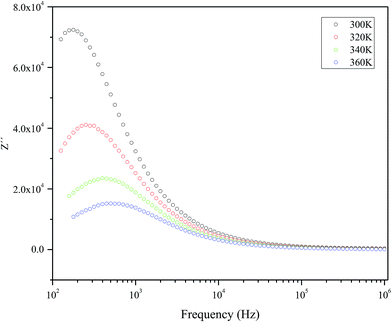 | ||
| Fig. 5 The frequency dependency of imaginary part of impedance (Z′) measured at selected temperatures. | ||
The complex impedance spectrum is a powerful method to study the relaxation polarization mechanism of the grain and grain boundaries in ceramics.40 Fig. 6 shows the variation of the real part of impedance (Z′) with the imaginary part of impedance (Z′) (Nyquist plots) for sample at different temperatures (from 280 to 360 K).
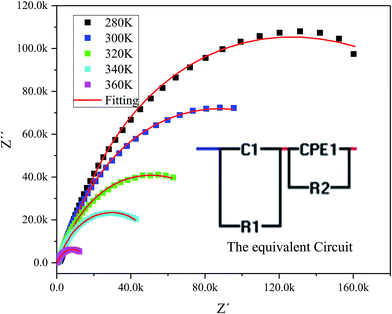 | ||
| Fig. 6 The experimental complex impedance spectra combined with the fitting curves modeled by the equivalent circuit (inset). | ||
The Nyquist plots feature single semicircles with radii of curvatures decreasing with temperature increasing. In order to model the physical interpretation of the distributed elements, the experimental data were fitted to an equivalent circuit combining a parallel grain resistance (R–C1) and constant phase element impedance (CPE) (R–CPE circuit) (inset of Fig. 6) by means of ZView Software. Through this equivalent circuit we could obtain the best fit to the data measured at different temperatures. The experimental spectra of the sample along with the fitting curve are shown in Fig. 6b. The CPE impedance (CPE) is given by the following relation:41
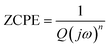 | (2) |
| Temperature (K) | Rg | Cg | Rgb | CPEgb | ngb | nIII |
|---|---|---|---|---|---|---|
| a Both Rgb and Rg values are decreasing as temperature increases indicating a negative temperature coefficient of resistance (NTCR) behavior which can be explained by the increment of the mobility of charge carriers.42 | ||||||
| 280 | 1.45 × 105 | 6.18 × 10−9 | 2.55 × 105 | 4.08 × 10−7 | 0.53 | 0.31 |
| 300 | 8.89 × 104 | 8.36 × 10−9 | 1.35 × 105 | 2.45 × 10−7 | 0.60 | 0.33 |
| 320 | 4.92 × 104 | 1.01 × 10−8 | 6.65 × 104 | 2.31 × 10−7 | 0.63 | 0.35 |
| 340 | 2.82 × 104 | 1.06 × 10−8 | 4.80 × 104 | 5.25 × 10−7 | 0.57 | 0.4 |
| 360 | 6.97 × 103 | 1.30 × 10−8 | 1.24 × 104 | 6.99 × 10−7 | 0.58 | 0.5 |
| 400 | — | — | — | — | — | 0.37 |
Furthermore, the obtained values can be used to calculate the activation energies for grain-interior and grain boundary conductivity. The grain and grain boundary conductivity can be defined as a function of temperature following the Arrhenius law:43
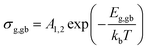 | (3) |
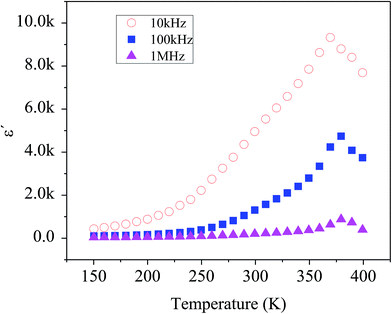
Fig. 7 shows the temperature dependency of dielectric constant for the composite at several frequencies. Variation of dielectric constant as a function of temperature indicates the appearance of a peak at a particular temperature (Tmax) ranging from 370–380 K with increasing in frequency from 1 kHz to 1 MHz, attributed to the ferroelectric–paraelectric phase transition. This observation is in good agreement with the previous reports on the presence of phase transition corresponding to the ferroelectric–paraelectric in compounds with perovskite (ABO3) structure8–10 and also with ABO4 structure.11–14 This Tmax value is much lower than 800 K for Te modified BaSnO3 and larger than 200 K for highly doped Pb–BaSnO3.45 Considering the inhomogeneity within the nanocomposite (see Raman, XRD and TEM data), it is obvious that atoms undergo a notable displacement with respect to their high-symmetry locations. Hence, there is a local dipole moment in both Ba–O and Sn–O planes which gives rise to spontaneous polarization. Moreover, compressive strain due to the heterogeneity of the structure leads to the emergence of out of phase oxygen octahedral rotation along the [110] axis resulting in an out of plane polarization along the [110] direction. Thus, the zone-center polar lattice distortion completely accounting for the symmetry lost and also oxygen octahedral rotation and tilting along [110] direction is responsible for the paraelectric–ferroelectric transition.46,47
The variation of ac conductivity (σac) of the composition as a function of frequency at different temperatures is shown in Fig. 8a and b. It is observed that at lower temperatures three distinct regions are visible in the conductivity spectra of the sample: in region I, conductivity curve is nearly frequency independent; in region II, conductivity increases almost proportionally with increasing frequency; whereas in region III the increasing trend of conductivity continues but at gradually slower rates due to a different type of response of bound charge carriers at higher frequencies in comparison with region II. The levels of low-frequency conductivity plateau increase with increasing temperature. These results indicate the thermally activated process of electrical conduction in close agreement with the observations from impedance spectrum results. Dispersion with different slope in the intermediate region can be due to multiwell potential barriers coming from non-homogeneity and random distribution of defects.
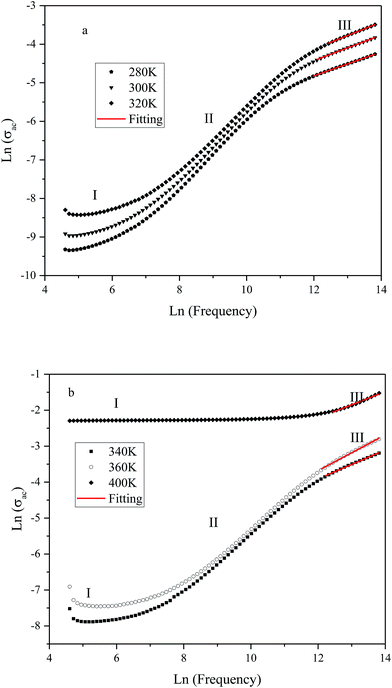 | ||
| Fig. 8 Variation of ac conductivity (σac) as function of frequency at different temperatures (K): (a) 280, 300 and 320; (b): 340, 360 and 400. | ||
These results suggest that electrical conduction in the material takes place via hopping mechanism governed by the Jonscher's universal power law:1
| σac = σdc + Aωn | (4) |
Fig. 9 shows the variation of tangent loss as a function of frequency at selected temperature (below and above the phase transition). It can be seen that tan(δ) increases gradually when the frequency values rise, reaching a maximum, and then decreasing, indicating the presence of a relaxation phenomenon. The tan(δ) peak shifts towards higher frequencies as temperature increases in the ferroelectric region (the temperatures below the phase transition). Inversely, for the paraelectric region, above the phase transitions, the peak shifts backwardly to the lower frequencies. It is worth noting that no relaxation was observed in temperature range of 310–370 K. The temperature dependency of the tan(δ) relaxation time is presented in Fig. 10. Quantitative examination of the relaxation time revealed that it follows a non-Arrhenius behavior in the ferroelectric region. The nonmonotonic behavior of relaxation kinetics for our nanocomposite can be discussed as a complex phenomenon, having its origin in two different processes.50 The first process is the tilt of oxygen octahedron, which changes the orientation of the elementary dipole moments, associated with the perovskite unit cell, and can be presented by an Arrhenius term with activation energy of Ea. The second process is the jump of Ba and Sn ions between the several local minima positions created due to the heterogeneity of the composition. For the latter process, the heterogeneous structure creates “defects” with multiwall potentials in the unit cell structure and hinder tilting of the oxygen octahedrons. Hence, the increasing number of such “defects” with an increase in temperature slows down the relaxation process and can be described by the exponential term with the activation energy of Eb. This argument is in good similarity with that for evaluation of the non-monotonic relaxation kinetics observed in the copper-doped KTa1−xNbxO3 ferroelectric perovskite.50 Thus, were present a non-monotonic temperature dependence of the relaxation time since it is related to two processes of a different nature, in the form of:51
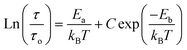 | (5) |
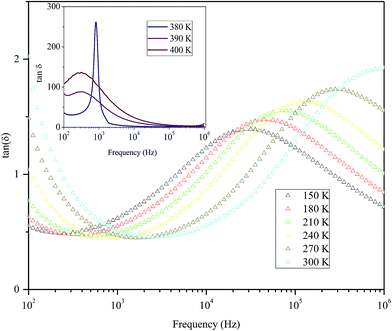 | ||
| Fig. 9 Variation of tangent loss as a function of frequency at selected temperatures below and above phase transition of the nanocomposite. | ||
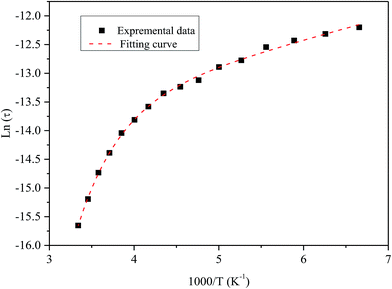 | ||
| Fig. 10 Temperature dependence of the tan(δ) relaxation time of the nanocomposite. Symbol (black) represents experimental data. The dashed line (red) corresponds to the best fit according to the eqn (5). | ||
4. Conclusion
A BaCO3/BaSnO3/SnO2 heterogeneous nanocomposite was prepared via precipitation–calcination method. The phase identification, structural and morphological evolutions, was extensively investigated using XRD, FT-IR, Raman, SEM and TEM analyses.The complex impedance plots revealed the existence of grain and grain boundary contributions. Z′ showed distributed relaxation phenomena at higher temperatures, and was found to be temperature dependent. The temperature dependence of and tangent loss is characterized by the appearance of a peak ranging from 370–380 K, depending on the frequency. This phenomenon is related to the ferroelectric–paraelectric phase transition, due to the tiling of the oxygen octahedral and the zone-center polar lattice distortion. The larger contribution of the grain boundary for conduction was evaluated considering the high concentration of oxygen vacancies and other compositional heterogeneities.
In the paraelectric state, electrical conduction was again associated with the oxygen vacancies. The non-monotonic dependence of the relaxation time of tan(δ) on temperature was explained using a non-Arrhenius model.
Conflicts of interest
There are no conflicts to declare.References
- A. Kumar, B. P. Singh, R. N. P. Choudhary and A. K. Thakur, J. Alloys Compd., 2005, 394, 292–302 CrossRef CAS.
- S. V. Manorama, C. V. Gopal Reddy and V. J. Rao, Appl. Surf. Sci., 2001, 174, 91–105 CrossRef.
- J. Cerda, J. Arbiol, G. Dezanneau, R. Diaz and J. R. Morante, Mater. Lett., 2002, 56, 131–136 CrossRef CAS.
- N. Horchidan, A. C. Ianculescu, C. A. Vasilescu, M. Deluca, V. Musteata, H. Ursic, R. Frunza, B. Malic and L. Mitoseriu, J. Eur. Ceram. Soc., 2014, 34, 3661–3674 CrossRef CAS.
- P. Singh, B. J. Brandenburg, C. P. Sebastian, P. Singh, S. Singh, D. Kumar and O. Prakash, J. Appl. Phys., 2008, 47(5), 3540–3545 CrossRef CAS.
- R. M. Katiliute, P. Seibutas, M. Ivanov, R. Grigalaitis, A. Stanulis, J. Banys and A. Kareiva, Ferroelectrics, 2014, 464, 49–58 CrossRef CAS.
- A. Kumar, B. P. Singh, R. N. P. Choudhary and A. K. Thakur, Mater. Chem. Phys., 2006, 99, 150–159 CrossRef CAS.
- A. Kumar and R. N. P. Choudhary, J. Mater. Sci., 2007, 42, 2476–2485 CrossRef CAS.
- S. Upadhyay, O. Parkash and D. Kumar, J. Mater. Sci. Lett., 1997, 16(16), 1330–1332 CrossRef CAS.
- I. A. Alagdaland and A. R. West, J. Mater. Chem. C, 2016, 4, 4770–4777 RSC.
- Y. H. Ochoa, F. Schipani, C. M. Aldao, J. E. Rodriguez-Paez and M. A. Ponce, J. Mater. Res., 2015, 30(22), 3423–3430 CrossRef CAS.
- M. Yasukawa, T. Kono, K. Ueda, H. Yanagi, S. Wang Kimand and H. Hosono, Solid State Commun., 2013, 172, 49–53 CrossRef CAS.
- C. P. Udawatte and M. Yoshimura, Mater. Lett., 2001, 47, 7–10 CrossRef CAS.
- W. Lu and H. Schmidt, Ceram. Int., 2008, 34, 645–649 CrossRef CAS.
- S. Tao, F. Gao, X. Liu and O. T. Sorensen, Sens. Actuators, B, 2000, 71, 223–227 CrossRef CAS.
- C. Huang, X. Wang, X. Wang, X. Liu, Q. Shi, X. Pana and X. Li, RSC Adv., 2016, 6, 25379–25387 RSC.
- X. Xianran, J. Chen, G. Wei, J. Deng and G. Liu, J. Am. Ceram. Soc., 2004, 87(7), 1371–1373 CrossRef.
- S. Mahajan, O. P. Thakur, D. K. Bhattacharya and K. Sreenivas, J. Phys. D: Appl. Phys., 2009, 42, 065413 CrossRef.
- A. A. Bokov, M. Maglione and Z. G. Ye, J. Phys.: Condens. Matter, 2007, 19, 092001 CrossRef.
- C. Lei, A. A. Bokov and Z.-G. Ye, J. Appl. Phys., 2007, 101, 084105 CrossRef.
- D. Wang, A. A. Bokov, Z.-G. Ye, J. Hlinka and L. Bellaiche, Nat. Commun., 2016, 7, 11014 CrossRef CAS PubMed.
- P. Yadav, S. Sharma and N. P. Lalla, J. Appl. Phys., 2017, 121, 184101 CrossRef.
- G. Burns and F. H. Dacol, Solid State Commun., 1983, 48(10), 853–856 CrossRef CAS.
- K. Hirota, Z.-G. Ye, S. Wakimoto, P. M. Gehring and G. Shirane, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104015 Search PubMed.
- S. Vakhrushev, A. Nabereznov, S. K. Sinha, Y. P. Feng and T. Egami, J. Phys. Chem. Solids, 1996, 57, 1517–1523 CrossRef CAS.
- M. Yoshida, S. Mori, N. Yamamoto, Y. Uesu and J. M. Kiat, Ferroelectrics, 1998, 217, 327–333 CrossRef CAS.
- C. Huang, X. Wang, X. Liu, M. Tian and T. Zhang, J. Eur. Ceram. Soc., 2015, 36(3), 583–592 CrossRef.
- S. A. Salehizadeh, M. P. F. Graça and M. A. Valente, Phys. Status Solidi C, 2014, 11(9–10), 1455–1458 CrossRef CAS.
- C. Huang, X. Wang, X. Wang, X. Liu, Q. Shi, X. Pan and X. Li, RSC Adv., 2016, 6, 25379–25387 RSC.
- B. Sreedhar, C. Satya Vani, D. Keerthi Devi, V. Sreeram and M. V. Basaveswara Rao, Am. J. Mater. Sci., 2012, 2(4), 105–109 CrossRef.
- U. SujanaKumari, P. Sureshand and A. V. Prasada Rao, Int. Res. J. Pure Appl. Chem., 2013, 3(4), 347–356 CrossRef CAS.
- S. A. Salehizadeh, B. M. G. Melo, F. N. A. Freire, M. A. Valente and M. P. F. Graça, J. Non-Cryst. Solids, 2016, 443(1), 65–74 CrossRef CAS.
- R. Zamiri, S. A. Salehizadeh, H. AbbastabarAhangar, M. Shabani, A. Rebelo, J. Suresh Kumar, M. J. Soares, M. A. Valente and J. M. F. Ferreira, Mater. Chem. Phys., 2017, 192(1), 330–338 CrossRef CAS.
- W. Kaabar, S. Botta and R. Devonshire, Spectrochim. Acta, Part A, 2011, 78, 136–141 CrossRef CAS PubMed.
- X. Cao, T. Hong, R. Yang, J. Tian, C.-R. Xia, J.-C. Dong and J. Li, J. Phys. Chem. C, 2016, 120(40), 22895–22902 CAS.
- V. Bonu, A. Das, A. K. Sivadasan, A. K. Tyagi and S. Dhara, J. Raman Spectrosc., 2015, 46(11), 1037–1040 CrossRef CAS.
- S. N. Tripathy, K. K. Mishra, S. Sen and D. K. Pradhan, J. Am. Ceram. Soc., 2014, 97(6), 1846–1854 CrossRef CAS.
- A. Kumar, R. N. P. Choudhary, B. P. Singh and A. K. Thakur, Ceram. Int., 2006, 32, 73–83 CrossRef CAS.
- O. Prakash, D. Kumar, K. K. Shrivastava and R. K. Dwivedi, J. Mater. Sci., 2001, 36(24), 5805–5810 CrossRef.
- T. Wu, Y. Pu and K. Ch, Ceram. Int., 2013, 39, 6787–6793 CrossRef CAS.
- E. Barsoukov and J. Ross Macdonald, Impedance Spectroscopy Theory, Experiment and Applications, Wiley Interscience, 2nd edn, 2005, p. 14 Search PubMed.
- T. Acharya and R. N. P. Choudhary, Appl. Phys. A, 2015, 121, 707–714 CrossRef CAS.
- K. P. Padmasree, D. K. Kanchan and A. R. Kulkami, Solid State Ionics, 2006, 177, 475 CrossRef CAS.
- A. Kumar, B. P. Singh, R. N. P. Choudhary and A. K. Thakur, Mater. Lett., 2005, 59, 1880–1888 CrossRef CAS.
- S. Markovic, C. Jovalekic, L. Veselinovic, S. Mentus and D. Uskokovic, J. Eur. Ceram. Soc., 2010, 30, 1427–1435 CrossRef CAS.
- Y. Zhang, J. Wang, M. P. K. Sahoo, X. Wang, T. Shimada and T. Kitamura, Phys. Chem. Chem. Phys., 2016, 18, 24024–24032 RSC.
- H. Sim, S. W. Cheong and B. G. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014101 CrossRef.
- B. K. Barick, K. K. Mishra, A. K. Arora, R. N. P. Choudhary and D. K. Pradhan, J. Phys. D: Appl. Phys., 2011, 44, 355402 CrossRef.
- V. Thakur, A. Singh, A. M. Awasthi and L. Singh, AIP Adv., 2015, 5, 087110 CrossRef.
- Y. E. Ryabov, A. Puzenko and Y. Feldman, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 014204 CrossRef.
- Y. Ryabov, A. Gutina, V. Arkhipov and Y. Feldman, J. Phys. Chem. B, 2001, 105, 1845–1850 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |