Open Access Article
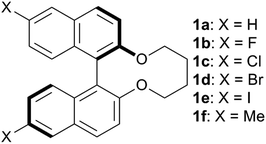
Open Access ArticleSubstituent effects of bridged binaphthyl-type chiral dopants on the helical twisting power in dopant-induced chiral liquid crystals†
Yu Narazaki a,
Hiroya Nishikawab,
Hiroki Higuchib,
Yasushi Okumurab and
Hirotsugu Kikuchi
a,
Hiroya Nishikawab,
Hiroki Higuchib,
Yasushi Okumurab and
Hirotsugu Kikuchi *b
*b
aInterdisciplinary Graduate School of Engineering Sciences, Kyushu University, 6-1, Kasuga-koen, Kasuga, Fukuoka 816-8580, Japan
bInstitute for Materials Chemistry and Engineering, Kyushu University, 6-1, Kasuga-koen, Kasuga, Fukuoka 816-8580, Japan. E-mail: kikuchi@cm.kyushu-u.ac.jp
First published on 3rd January 2018
Abstract
A new series of chiral dopants, (R)-6,6′-halogenated (1b–1e, X = F, Cl, Br and I) and -methylated (1f) binaphthyl compounds, were designed and synthesized to create chiral liquid crystals by doping them into an achiral nematic liquid crystal (NLC). The influence of halogen (X = F, Cl, Br and I) and methyl substituent factors, such as steric, polar, and polarizability properties, on the helical twisting power (HTP) and their temperature dependences on the chiral dopants were investigated in two host NLCs with different characteristics, fluorinated JC-1041XX and N-(4-methoxybenzylidene)-4-butylaniline (MBBA). The chiral dopants possessing less steric and larger polarizability factors increased the HTP values. The structural similarity and electrostatic arene–arene interactions between the chiral dopants and the NLC molecules also exerted important influences on these values. The temperature dependence of the HTP (HTPt.d.) values also correlated well with the steric and polarizability substituents factors in the two host NLCs. Their correlation coefficients (R2) depended on the molecular structural similarity between the chiral dopant and the NLC.
Introduction
Chirality is a geometric property of chemical structures that indicates a lack of mirror symmetry, and it often induces intriguing physical properties in materials.1 For example, chiral liquid crystals (CLCs), especially chiral nematic liquid crystals (N*LCs)2 and blue phase liquid crystals (BPLCs)3 including polymer-stabilized cholesteric BPLCs,4 exhibit unusual physical properties, such as periodic helical structures, selective reflections of circularly polarized light based on Bragg's law,5,6 and a fast electric response.4,7–9 These CLCs have potential applications in low energy consumption displays10,11 and tunable optical or laser devices12–14 because of their unique properties. The development of CLCs or chiral dopants that enable the formation of a N*LC from a nematic liquid crystal (NLC), therefore, has attracted considerable attention. Chiral dopants are asymmetric molecules, and their molecular structures can be classified into four types: central, axial, planar, and helical chirality. The ability of a chiral dopant to generate a helical structure in a given host NLC is evaluated using helical twisting power (HTP), as expressed below:| HTP = (Pcw)−1 | (1) |
To date, significant efforts have been devoted to revealing an interrelation between the molecular structure of chiral dopants and the HTP value. For example, studies have been conducted using chiral aryl alkyl carbinol,15 trans-stilbene oxide,16 binapthyl,17–19 biphenyl,20,21 1-(1-naphthyl)ethylamine,22 TADDOL (α,α,α,α-tetraaryl-1,3-dioxolane-4,5-dimethanol),23 1,2-diphenylethane-1,2-diol,24 helicene,25 tartaric imide derivatives26 and ruthenium complexes possessing octahedral molecular geometry.27,28 Among them, for several decades, binapthyl-type chiral dopants bridged by an alkyl chain in the 2,2′-position have attracted a great deal of attention both experimentally17–19 and theoretically29 since they exhibit a relatively large HTP value in several host NLCs. This means their effective chirality makes them act as solutes to nematic solvent. However, the mechanism of chirality transfer from chiral dopants to host nematics remains unclear. If the mechanism was to be understood on a molecular level, the field of LC science and technology would greatly advance in chemical structure modeling and material design to produce high performance LCs.
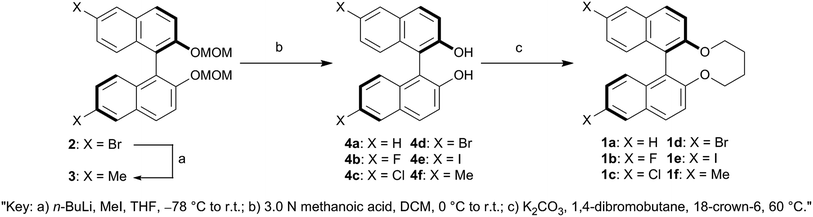
In our previous research, the 6,6′-fluorinated binaphthyl-type chiral dopant (1b) exhibited a large HTP value, high solubility,30 and availability of slightly wider blue phase (BP) temperature range31 in the fluorinated NLC. The effects of fluorine substituents on the HTP value in the induced N*LC phase and the BP temperature range have not yet been well understood. Herein, non-substituted (1a), 6,6′-halogenated (1b–1e, X = F, Cl, Br and I) and -methylated (1f) binaphthyl-type chiral dopants were synthesized to examine dominant molecular factors like the steric hindrance, polarity, and polarizability of their substituents that affect the chirality transfer between the chiral dopant and the host nematic (Fig. 1 and Scheme 1). The effects on the induced HTP due to the substituents in the 6,6′ positions of the binaphthyl-type chiral dopants in two different host NLCs are presented. The binaphthyl-type dopants possessing smaller volumes, larger polarizabilities, and good molecular structural similarities to that of the host NLC exhibited excellent HTP values. Moreover, the electronic states of the aromatic rings of the dopants and the host nematics have a great impact on the HTP values.
Results and discussion
Effect of substituents on dihedral angle of a synthesized binaphthyl-type chiral dopant
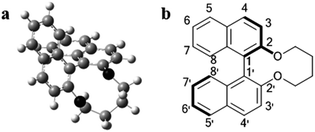
The dihedral angle of all of the synthesized chiral dopants was calculated by means of density functional theory (DFT) under the conditions described in Experimental section, and the optimized structure of 1a is represented in Fig. 2a. According to the DFT calculations, the calculated dihedral angle, θ (C8–C1–C1′–C8′, see Fig. 2b), of 1a, 1b, 1c, 1d, 1e, and 1f were −67.7°, −67.6°, −67.6°, −67.7°, −67.4°, and −67.3°, respectively. The variation in the dihedral angle caused by the different substituents was small even though the sizes of the substituents were different. Additionally, using the contact method, the helical sense of the N*LC induced by the chiral dopant was confirmed to be left-handed for all of the synthesized 1a–1f compounds in the two host NLCs, JC-1041XX and MBBA, whose dielectric anisotropies were positive and negative, respectively (see the ESI, Fig. S1†).It is known that the cisoid (0° < θ < 90°) and transoid (90° < θ < 180°) conformations of (R)-binaphthyl-type chiral dopants induce the left-handed and the right-handed senses, respectively.16,17 Therefore, the results of the contact method indicate that the conformations of 1a–1f adopt a cisoid conformation in the host NLCs. These experimental results agree well with the DFT calculations (θ = 67–68°).
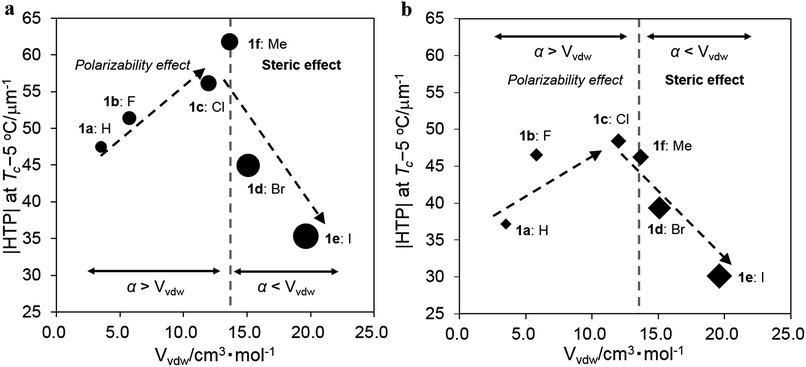
Effects of the substituents on the induced |HTP| value
The absolute HTP values, |HTP|, obtained at the clearing point (Tc) below 5 °C, termed Tc −5 °C, in JC-1041XX and MBBA and three types of substituent parameters that are expected to affect the intermolecular interaction between the chiral dopants and the LC molecules are shown in Table 1. The van der Waals volume parameter (Vvdw) corresponds to the steric size of the substituent group.32 The Hammett constant at the para position (σp) indicates an electron-withdrawing or -donating inductive effect of the substituent group.33 The polarizability (α) is a relative tendency of electric charge distribution of the substituent group, which is calculated as per an equation given in ref. 20. The |HTP| values of 1a–f in JC-1041XX and MBBA are plotted for substituents of Vvdw in Fig. 3a and b to indicate a relationship between the steric effect of their substituents and their |HTP| values. Three trends were found to stand out in the Fig. 3a and b. First, as the substituents volume Vvdw increased from 3.5 cm3 mol−1 (X = H) to 12.0 cm3 mol−1 (X = Cl), the |HTP| values tended to increase; however, upon a further increase in the substituents volume to 15.1 cm3 mol−1 (X = Br) and 19.6 cm3 mol−1 (X = I), the |HTP| values decreased. Second, the overall values of 1a–f in JC-1041XX were larger than those in the MBBA. Third, comparing the |HTP| values of the two host nematics, it was found that the maximum values were for 1f in JC-1041XX in Fig. 3a and for 1c in MBBA in Fig. 3b, meaning that the substituents with the highest value was swapped in these two NLCs. In order to understand the causes of those three tendencies, the material parameters affecting the HTPs had to be taken into account.| Entry | X | |HTP|/μm−1 | Substituent parameters | |||
|---|---|---|---|---|---|---|
| JC-1041XX | MBBA | Vvdw/cm mol−1 | σp | α/10−23 cm3 | ||
| 1a | H | 49.9 | 37.1 | 3.5 | 0 | 1.04 |
| 1b | F | 51.7 | 46.5 | 5.8 | 0.06 | 1.03 |
| 1c | Cl | 56.1 | 48.4 | 12.0 | 0.24 | 1.24 |
| 1d | Br | 44.9 | 39.3 | 15.1 | 0.27 | 1.35 |
| 1e | I | 35.3 | 30.1 | 19.6 | 0.30 | 1.55 |
| 1f | Me | 61.7 | 46.2 | 13.7 | −0.13 | 1.23 |
 | ||
| Fig. 3 Plots of the |HTP| values of 1a–f in (a) JC-1041XX and (b) MBBA vs. the Vvdw of their substituents. | ||
According to ref. 29, the theoretical HTP equation is expressed as follows:
| HTP = RTεQ/2πK22νm | (2) |
| Entry | X | |HTP|K22/10−9 μm−1 N | |
|---|---|---|---|
| JC-1041XX | MBBA | ||
| 1a | H | 4.1 | 1.6 |
| 1b | F | 4.3 | 2.0 |
| 1c | Cl | 4.7 | 2.0 |
| 1d | Br | 3.7 | 1.7 |
| 1e | I | 2.9 | 1.3 |
| 1f | Me | 5.1 | 1.9 |
The possible intermolecular interactions for the three tendencies observed in Fig. 3a and b should be discussed. First, the substituents volume, Vvdw, dependences of the |HTP| values showed a maximum of around 13–14 cm3 mol−1 in both JC-1041XX and MBBA. We assume that the steric volume and polarizability effects of the substituents are involved in this phenomenon.
Since both the chiral solute and the host LC solvent have phenyl or naphthyl groups, the arene–arene interaction38 should be a dominant intermolecular interaction that could regulate the alignment of the molecular axes, by which the twisted molecular alignment of the LC molecules is induced. The intermolecular interactions are mainly governed by a van der Waals interaction in which the polarizability and/or a dipole moment is involved. This means that the interaction should be stronger if a molecule possesses a larger polarizability and/or dipole moment. If the 6,6′ positions of 1a are replaced by the small-sized halogens, F and Cl, the polarizability and/or the dipole moment of the chiral dopant would be increased. This was seen in the data, where the induced |HTP| values of the chiral dopants possessing smaller substituents increased from non-substituents (X = H) to chlorine (X = Cl) groups. The substituents steric hindrance should have an influence on the intermolecular interaction between the chiral dopants and the host NLC molecules since the arene–arene interactions between them are short-range. Hence, it is reasonable that the weakened intermolecular interactions lead to decrease in the |HTP| values for chiral dopants with large substituents. Furthermore, similar results were already reported with biphenyl20 and 1,2-diphenylethane-1,2-diol.24 These studies suggested that lower steric hindrance in the substituents on the phenyl ring plays an important role in inducing a larger HTP value because of the presence of arene–arene interactions between the chiral dopants and the host NLC molecules.
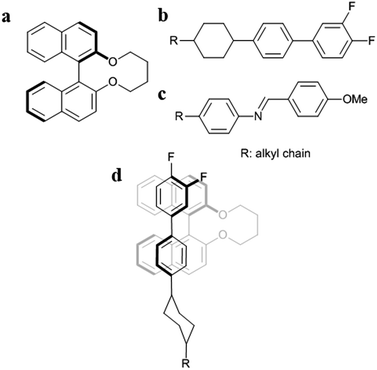
Second, it is important to discuss that the |HTP| values of 1a–f are larger in the JC-1041XX (Fig. 3a) than in the MBBA (Fig. 3b). The mesogen core of JC-1041XX is biphenyl cyclohexane (Fig. 4b); in contrast, the mesogen core of MBBA is azomethine (Fig. 4c). The length of the aromatic unit at the core of JC-1041XX corresponds to the surface of a bridged binaphthyl-type chiral dopant (Fig. 4a), particularly in comparison with the core of the MBBA. JC-1041XX, which has a higher structural similarity to its dopant than MBBA, should interact well with the chiral dopants. This is seen in the larger |HTP| values for 1a–f in JC-1041XX than that for in the MBBA. Gottarelli et al. (1983) proposed the model for the solute–solvent interaction between the bridged binaphthyl-type chiral solute and the host NLC solvent (Fig. 4d). The model indicates that the structural similarity between the chiral solutes and the host NLC solvents leads to a larger HTP value. The HTP values for bridged binaphthyl-type chiral dopants tend to be larger in the biphenyl-type NLC, such as 5CB and E7, than that in the MBBA17,19 because both the dopant and the NLC have a biphenyl core. Therefore, it is reasonable that such a strong intermolecular interaction between chiral dopants and host NLC molecules contribute to chiral transfer.
Third, the relationship between the |HTP| values for 1c (X = Cl) and 1f (X = Me) was reversed between JC-1041XX (Fig. 3a) and MBBA (Fig. 3b). The steric and polarizability parameters (Vvdw and α) are almost similar between 1c and 1f. Conversely, the signs of the Hammett constant at the para position, σp, of 1c and 1f are the opposite, i.e., positive for 1c and negative for 1f. JC-1041XX and MBBA bear one part of an electron withdrawing and donating aromatic ring, respectively. The electronic states of the aromatic rings of 1f and JC-1041XX are electron rich and electron deficient, respectively. In contrast, those of 1c and MBBA are electron deficient and electron rich, respectively. The combination of the electron-rich and -deficient aromatic rings can lead to favorable arene–arene interactions.39 Additionally, the strong solute–solvent molecular interaction between the chiral dopants and the nematic solvents is known to enhance the HTP value.40 This explains why the |HTP| values were maximized for 1f in JC-1041XX (Fig. 3a) and 1c in MBBA (Fig. 3b).
Substituent effect on the temperature dependence of the HTP value
Unlike pure cholesterol materials, the pitch of induced N* doped with 1a–f increases as a function of temperature, i.e., the |HTP| values decrease with increase in the temperature. An HTP temperature dependence value (HTPt.d.) was defined as below:
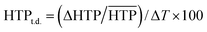 | (3) |
 is the arithmetic mean of the |HTP| values in the temperature range from T–Tc = −5 to 25 °C.30,41 The index indicates the percentage change in the |HTP| values per 1 °C.30,41 The HTPt.d. values for 1a–1f and their substituents parameters are shown in Table 3. The HTPt.d. values for 1a–f in (a) JC-1041XX and (b) MBBA are plotted against their steric (Vvdw) and polarizability (α) substituents parameters in Fig. 5a and b to evaluate the effect of the substituents on their subsequent HTPt.d. values.
is the arithmetic mean of the |HTP| values in the temperature range from T–Tc = −5 to 25 °C.30,41 The index indicates the percentage change in the |HTP| values per 1 °C.30,41 The HTPt.d. values for 1a–1f and their substituents parameters are shown in Table 3. The HTPt.d. values for 1a–f in (a) JC-1041XX and (b) MBBA are plotted against their steric (Vvdw) and polarizability (α) substituents parameters in Fig. 5a and b to evaluate the effect of the substituents on their subsequent HTPt.d. values.
| Entry | X | HTPt.d./% T−1 | Substituent parameters | |||
|---|---|---|---|---|---|---|
| JC-1041XX | MBBA | Vvdw/cm mol−1 | σp | α/10−23 cm3 | ||
| 1a | H | 0.46 | 0.49 | 3.5 | 0 | 1.04 |
| 1b | F | 0.43 | 0.73 | 5.8 | 0.06 | 1.03 |
| 1c | Cl | 0.59 | 0.85 | 12.0 | 0.24 | 1.24 |
| 1d | Br | 0.60 | 0.87 | 15.1 | 0.27 | 1.35 |
| 1e | I | 0.69 | 0.87 | 19.6 | 0.30 | 1.55 |
| 1f | Me | 0.64 | 0.82 | 13.7 | −0.13 | 1.23 |
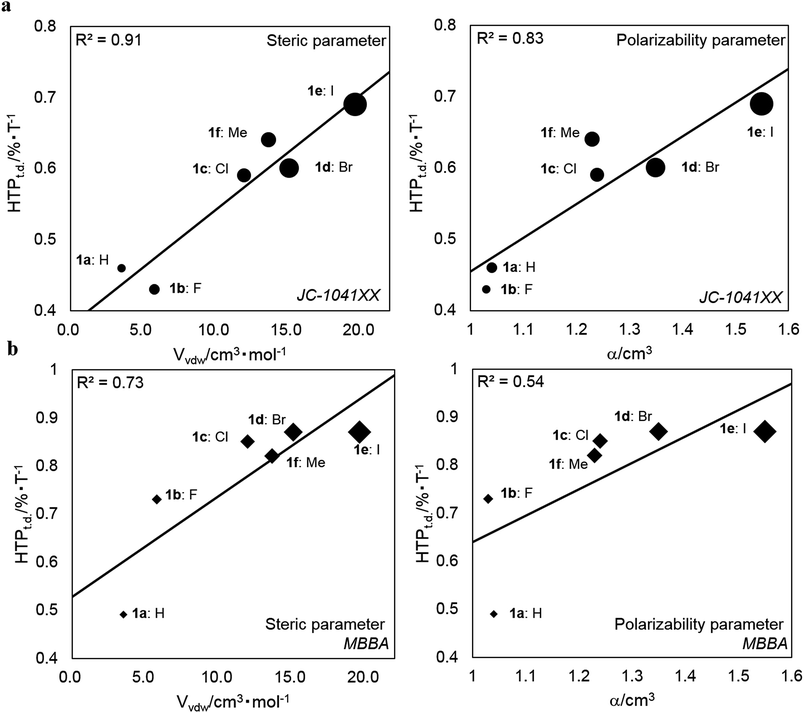 | ||
| Fig. 5 Plots of the HTPt.d. values for 1a–1f against the Vvdw and α of their substituents in (a) JC-1041XX and (b) MBBA. R2 denotes the correlation coefficient. | ||
As shown in Fig. 5a and b, the HTPt.d. values increased with increasing Vvdw and α. This trend was especially clear in JC-1041XX, more so than in MBBA. In addition, the HTPt.d. values in MBBA were larger than those in JC-1041XX. When the host NLC was JC-1041XX, the correlation coefficients (R2) for the steric and polarizability parameters were 0.91 and 0.83, respectively. Those same in parameters had correlations of 0.73 and 0.54, respectively, in MBBA. From these results, it is clear that the HTPt.d. values and R2 values in JC-1041XX were better than those in MBBA. It is appropriate that molecular structural similarity of a solute–solvent interaction between a bridged chiral solute and host nematic solvent can affect the HTPt.d. and R2 values. It is assumed that the structural similarity between the chiral solutes and MBBA might cause the resultant LCs to thermally disintegrate faster than in JC-1041XX.
In comparison with the HTPt.d. values in the two host nematics with their steric and polarizability substituents parameters, it became clear that the HTPt.d. values correlated well with their substituents parameters. Our understanding is that a van der Waals interaction involving polarizability can impact the HTPt.d. values of the smaller substituents of synthesized chiral dopants, such as 1a–c and 1f, because these HTPt.d. values gradually increase as their polarizability increased. Moreover, the steric substituents effects of the relevant chiral dopants on HTPt.d. values were observed; chiral dopants possessing larger substituents, such as the bromo and iodo groups, promoted a disaggregation of the arene–arene interactions between these chiral dopants and the host NLC molecules. This could be because the steric hindrance between them should affect their short-range interactions. This effect should be reflected the HTPt.d. values of 1d–e, since these values were comparatively larger than those of 1a–c and 1f in the two host NLCs. Therefore, the 6,6′ substituents of synthesized chiral dopants also affect their HTPt.d. values.
Conclusions
Our systematic studies of the 6,6′-substituted bridged, binaphthyl-type chiral dopants suggested that the induced |HTP| and HTPt.d. values were significantly dependent on the arene–arene interactions between the chiral dopants and the host nematic NLCs. Furthermore, their interactions were affected by the steric hindrance, aromatic ring polarity, and polarizability of the substituents. The bridged binaphthyl-type chiral dopant with the least steric hindrance and a largest substituents polarizability, the 6,6′-chlorinated chiral dopant, exhibited large |HTP| values in both host NLCs since the chlorine group has an adequate substituents volume and large polarizability that contribute to a strong arene–arene interaction between the dopants and the host NLC molecules. Moreover, the aromatic polarity of the chiral dopants and host NLCs exerted a beneficial impact on the induced |HTP| values to give a strong electrostatic arene–arene interaction between them. In HTPt.d. investigations, the HTPt.d. values depended upon the structural similarity of a solute–solvent interaction between the chiral solutes and host nematic solvents. Structural similarity between the synthesized chiral dopants and biphenyl cyclohexane type NLC, JC-1041XX, lead to smaller HTPt.d. values, indicating a better thermal property for a chiral dopant. By contrast, the values between the chiral dopants and azomethine-type NLC, MBBA, exhibited larger HTPt.d. values, meaning they displayed a lesser stability toward heat. Furthermore, the HTPt.d. values were affected by the steric and polarizability substituents parameters since the HTPt.d. values in the two host NLCs had a good correlation with their substituents parameters. Our understanding is that when substituents polarizability are larger, which is relevant for a van der Waals interaction between the chiral dopants and the NLC molecules, the HTPt.d. values for the smaller substituents increase. In the case of larger substituents, such as bromo and iodo groups, the HTPt.d. values are considerably larger because of a disaggregation of the arene–arene interactions between these chiral dopants and the host NLCs via steric hindrance. We believe that our results presented herein significantly advance the design of novel binaphthyl-type chiral dopants with larger HTP values.Experimental
General
(R)-6,6′-Dibromo-2,2′-bis(methoxymethoxy)-1,1′-binaphthalene (2), (R)-6,6′-difluoro-2,2′-dihydroxy-1,1′-binaphthalene (4b), (R)-6,6′-dichloro-2,2′-dihydroxy-1,1′-binaphthalene (4c), (R)-6,6′-dibromo-2,2′-dihydroxy-1,1′-binaphthalene (4d) and (R)-6,6′-diiodo-2,2′-dihydroxy-1,1′-binaphthalene (4e) were prepared as reported previously.42,43 All of reagents and solvents were purchased from Aldrich Chemical Co., Kanto Chemical Co., Inc., Tokyo Chemical Industry Co., Ltd. and Wako Pure Chemical Industries, Ltd. and used without further purification. Analytical thin layer chromatography (TLC) was performed on silica gel layer glass plate Merck 60 F254 and visualized by UV irradiation (254 nm). Column chromatography was undertaken on Wako Pure Chemical Industries, Ltd. Wakogel 60N 63–212 μm or Wakogel C-400HG 20–40 μm. 1H- and 13C-NMR spectra were recorded on JEOL JNM-LA 400 and JNM-ECA 600 with the TMS (trimethylsilane) as an internal standard for 1H and the deuterated solvent for 13C. 19F-NMR spectra were recorded on JEOL ECZ 400 with the benzotrifluoride as an internal standard. Chemical shift (δ) was expressed in parts-per million (ppm) to relative internal standards. Signal multiplicities were abbreviated by s (singlet), d (doublet), t (triplet), q (quartet), dd (double–doublet), br (broad) and m (multiplet), respectively. High resolution mass spectra were performed on JEOL JNM-700. Elemental analyses were made on YANACO CHN-recorder MT-5 or YANACO CHN-recorder MT-6. Polarized optical microscopy was performed on Nikon ECLIPSE E600 POL equipped with Zeiss AxioCam HRc as a high-resolution camera. The temperature of the samples was controlled using the heating stage Linkam LTS420E with Linkam 10084L controller. The geometry optimizations of all synthesized chiral dopants were calculated using B3LYP/6-31G(d) for 1a, 1b, 1c, 1d and 1f and B3LYP/Gen basis set for the iodo atom of 1e level of density function theory (DFT) via the Gaussian 09 program.44Synthesis
General procedure of (R)-closed binaphthyl type chiral dopants
A solution of 4a–b (1 equiv.), 18-crown-6 (catalytical quantity), and K2CO3 (2.2 equiv.) in acetone (100 mL per 1 mmol of (R)-6,6′-substituted-2,2′-dihydroxy-1,1′-binaphthalene) was refluxed under argon atmosphere at 60 °C. After refluxing for 2 h at 60 °C, a solution of 1,4-dibromobutane (1.1 equiv.) in acetone (15.5 mL per 1 mmol of 1,4-dibromobutane) was slowly added to the refluxing solution for over 8 h by using syringe pump and then the resulting mixture was refluxed for 120 h at 60 °C. After cooling, the reaction mixture was filtered out and evaporated. The residue was diluted with water and extracted with Et2O (2 × 50 mL). The ethereal extracts were washed with water (50 mL) and brine (50 mL), dried over MgSO4 and evaporated. The crude product was purified by silica-gel chromatography (DCM/hexanes) and then recrystallization from EtOH or DCM/hexanes to afford the titled compounds.Measurement of synthesized chiral dopants' HTP
Synthesized chiral dopants were dissolved in host NLCs. JC-1041XX, which is a fluorinated nematic mixture supplied by JNC Co., and N-(4-methoxybenzylidene)-4-butylaniline (MBBA) were used as 0.5 wt% sample solutions. Prepared solutions were stirred at their isotropic phase temperature for three hours and were injected in a Grandjean–Cano wedge-shaped cell (E. H. C. Co., KCRK-03, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0.0079 ± 10%). After cooling to a N* phase, the interval distances of the striped defect lines that appeared in the cell were measured at temperatures well below the clearing point (Tc), Tc −5 °C, −10 °C, −15 °C, −20 °C, and −25 °C, in JC-1041XX and MBBA by means of a polarizing optical microscope. Measurements were repeated three times, and their given HTP values were averaged.
θ = 0.0079 ± 10%). After cooling to a N* phase, the interval distances of the striped defect lines that appeared in the cell were measured at temperatures well below the clearing point (Tc), Tc −5 °C, −10 °C, −15 °C, −20 °C, and −25 °C, in JC-1041XX and MBBA by means of a polarizing optical microscope. Measurements were repeated three times, and their given HTP values were averaged.
Identification of the helical sense of the synthesized chiral dopants
The helical sense of the synthesized chiral dopants was determined by a contact method using cholesteryl oleyl carbonate (COC) as a reference material. The 0.5 wt% samples doped with chiral dopants were injected from one side of the Grandjean–Cano wedge-shaped cell, and the COC was injected from the other side of its cell. After being in static for several hours, the helical sense was determined by polarizing optical microscopy.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed under the Advanced Graduate Program in Global Strategy for Green Asia, Kyushu University. The authors thank to K. Ideta (Kyushu University, Institute for Materials Chemistry and Engineering) for valuable discussion on 13C-NMR spectroscopy. This work was partially supported by a Grant-in-Aid for Scientific Research (A) JSPS KAKENHI Grant Number JP25248021 from the Japan Society for the Promotion of Science, Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials from the Ministry of Education, Culture, Sports, Science and Technology, Japan (MEXT), the Cooperative Research Program of “Network Joint Research Center for Materials and Devices.” and CREST, JST (JPMJCR1424).Notes and references
- I. Dierking, Symmetry, 2014, 6, 444–472 CrossRef.
- G. Solladié and R. G. Zimmermann, Angew. Chem., Int. Ed. Engl., 1984, 23, 348–362 CrossRef.
- D. C. Wright and N. D. Mermin, Rev. Mod. Phys., 1989, 61, 385–432 CrossRef CAS.
- H. Kikuchi, M. Yokota, Y. Hisakado, H. Yang and T. Kajiyama, Nat. Mater., 2002, 1, 64–68 CrossRef CAS PubMed.
- S. Shibayama, H. Higuchi, Y. Okumura and H. Kikuchi, Adv. Funct. Mater., 2013, 23, 2387–2396 CrossRef CAS.
- H. K. Bisoyi and Q. Li, Acc. Chem. Res., 2014, 47, 3184–3195 CrossRef CAS PubMed.
- Y. Hisakado, H. Kikuchi, T. Nagamura and T. Kajiyama, Adv. Mater., 2005, 17, 96–98 CrossRef CAS.
- S. Yabu, H. Yoshida, G. Lim, K. Kaneko, Y. Okumura, N. Uehara, H. Kikuchi and M. Ozaki, Opt. Mater. Express, 2011, 1, 1577–1584 CrossRef CAS.
- H. Choi, H. Higuchi and H. Kikuchi, Soft Matter, 2011, 7, 4252–4256 RSC.
- Y. Hirakata, D. Kubota, A. Yamashita, H. Miyake, M. Hayakawa, J. Koyama, S. Yamazaki, K. Okazaki, R. Sato, T. Cho, K. Tochibayashi and M. Sakakura, SID'11 Digest, 2011, vol. 42, pp. 32–35 Search PubMed.
- J. Chen and C. T. Liu, IEEE Access, 2013, 1, 150–158 CrossRef.
- M. Ozaki, Y. Matsuhisa, H. Yoshida, R. Ozaki and A. Fujii, Phys. Status Solidi A, 2007, 204, 3777–3789 CrossRef CAS.
- W. Cao, A. Muñoz, P. Palffy-Muhoray and B. Taheri, Nat. Mater., 2002, 1, 111–113 CrossRef CAS PubMed.
- S. Yokoyama, S. Mashiko, H. Higuchi, K. Uchida and T. Nagamura, Adv. Mater., 2006, 18, 48–51 CrossRef CAS.
- G. Gottarelli, B. Samori, C. Stremmenos and G. Torre, Tetrahedron, 1981, 37, 395–399 CrossRef CAS.
- G. Gottarelli, P. Mariani, G. P. Spada, B. Samori, A. Forni, G. Solladie and M. Hobert, Tetrahedron, 1983, 39, 1337–1344 CrossRef CAS.
- G. Gottarelli, M. Hobert, B. Samori, G. Solladié, G. P. Spada and R. Zimmermann, J. Am. Chem. Soc., 1983, 105, 7318–7321 CrossRef CAS.
- H.-J. Deuβen, P. V. Shibaev, R. Vinokur, T. Bjørnholm, K. Schaumburg, K. Bechgaard and V. P. Shibaev, Liq. Cryst., 1996, 21, 327–340 CrossRef.
- G. Proni and G. P. Spada, J. Org. Chem., 2000, 65, 5522–5527 CrossRef CAS PubMed.
- V. E. Williams and R. P. Lemieux, Chem. Commun., 1996, 2259–2260 RSC.
- A. di Matteo, S. M. Todd, G. Gottarelli, G. Solladié, V. E. Williams, R. P. Lemieux, A. Ferrarini and G. P. Spada, J. Am. Chem. Soc., 2001, 123, 7842–7851 CrossRef CAS PubMed.
- K. Fukuda, H. Suzuki, J. Ni, M. Tokita and J. Watanabe, Jpn. J. Appl. Phys., 2007, 46, 5208–5212 CrossRef CAS.
- H. G. Kuball, B. Weiß, A. K. Beck and D. Seebach, Helv. Chim. Acta, 1997, 80, 2507–2514 CrossRef CAS.
- S. Superchi, M. I. Donnoli, G. Proni, G. P. Spada and C. Rosini, J. Org. Chem., 1999, 64, 4762–4767 CrossRef CAS PubMed.
- G. Gottarelli, G. Proni, G. P. Spada, D. Fabbri, S. Gladiali and C. Rosini, J. Org. Chem., 1996, 61, 2013–2019 CrossRef CAS.
- K. Kishikawa, Y. Furukawa, T. Watanabe, M. Kohri, T. Taniguchi and S. Kohmoto, Liq. Cryst., 2017, 44, 969–988 CrossRef.
- Y. Matsuoka, H. Sato, A. Yamagishi, K. Okamoto and N. Hoshino, Chem. Mater., 2005, 17, 4910–4917 CrossRef CAS.
- J. Yoshida, G. Watanabe, K. Kakizawa, Y. Kawabata and H. Yuge, Inorg. Chem., 2013, 52, 11042–11050 CrossRef CAS PubMed.
- A. Ferrarini, P. L. Nordio, P. V. Shibaev and V. P. Shibaev, Liq. Cryst., 1998, 24, 219–227 CrossRef CAS.
- K. Kakisaka, H. Higuchi, Y. Okumura and H. Kikuchi, Chem. Lett., 2014, 43, 624–625 CrossRef CAS.
- K. Kakisaka, H. Higuchi, Y. Okumura and H. Kikuchi, J. Mater. Chem. C, 2014, 2, 6467–6470 RSC.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- P. R. Wells, Chem. Rev., 1963, 63, 171–219 CrossRef CAS.
- A. Ferrarini, G. J. Moro and P. L. Nordio, Mol. Phys., 1996, 87, 485–499 CrossRef CAS.
- A. Ferrarini, G. J. Moro and P. L. Nordio, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 681–688 CrossRef CAS.
- The K22 of JC-1041XX was provided by JNC Co.
- A. Krekhov and W. Pesch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 051706-1–051706-13 CrossRef PubMed.
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 651–669 RSC.
- F. Cozzi, M. Cinquini, R. Annunziata, T. Dwyer and J. S. Siegel, J. Am. Chem. Soc., 1992, 144, 5729–5733 CrossRef.
- S. Pieraccini, A. Ferrarini, K. Fuji and G. P. Spada, Chirality, 2008, 20, 749–759 CrossRef CAS PubMed.
- H. Nishikawa, D. Mochizuki, H. Higuchi, Y. Okumura and H. Kikuchi, ChemistryOpen, 2017, 6, 710–720 CrossRef CAS PubMed.
- H. Ishitani, M. Ueno and S. Kobayashi, J. Am. Chem. Soc., 2000, 122, 8180–8186 CrossRef CAS.
- M. Jahjah, M. Alame, S. P. Rostaing and M. Lemaire, Tetrahedron: Asymmetry, 2007, 18, 2305–2312 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The polarizing optical microscopic images of the contact method of the synthesized chiral dopants, 1H-, 13C, 19F-NMR and high resolution mass spectra of the synthesized chiral dopants. See DOI: 10.1039/c7ra12465a |
| This journal is © The Royal Society of Chemistry 2018 |