Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding viscosity reduction of a long-tail sulfobetaine viscoelastic surfactant by organic compounds†
Lionel T. Foganga,
Abdullah S. Sultan *ab and
Muhammad S. Kamal
*ab and
Muhammad S. Kamal b
b
aDepartment of Petroleum Engineering, King Fahd University of Petroleum & Minerals, 31261 Dhahran, Saudi Arabia. E-mail: sultanas@kfupm.edu.sa
bCenter for Integrative Petroleum Research, King Fahd University of Petroleum & Minerals, 31261 Dhahran, Saudi Arabia
First published on 24th January 2018
Abstract
Though the transition from cylindrical micelles to spherical micelles of the anionic surfactant potassium oleate in the presence of oils has been studied, these changes have not been studied for long-tail zwitterionic surfactants. The effects of n-decane, crude oil (CO), extra virgin olive oil (EVOO) and polyglycolic acid (PGA) on the zero-shear viscosity of an aqueous solution of a sulfobetaine surfactant system were investigated at 30 °C and 60 °C. The main surfactant in the system was erucamidopropyl hydroxypropyl sulfobetaine. The methods employed were rheology and cryo-TEM. The solution with 3.96 wt% surfactant system and 6.2 wt% CaCl2 was viscoelastic at both test temperatures due to the formation of entangled cylindrical micelle networks. n-Decane induced the following regimes of zero-shear viscosity change at both temperatures: (i) the high viscosity regime (HVR), (ii) the transition regime (TR), and (iii) the low viscosity regime (LVR). The HVR was characterized by high zero-shear viscosities. The TR was characterized by a sharp drop in zero-shear viscosity due to the formation of untangled micelles. The LVR was due to the formation of microemulsions. The formation of these regimes depended on the balance between micellization and oil solubilization. We reveal for the first time that the number of regimes depends on the type of oil: both CO and EVOO induced only one and two regimes at 30 °C and 60 °C, respectively. PGA did not significantly affect the solution at either temperature with increasing concentration, meaning the solution was resistant to decreasing pH even at higher temperatures.
Introduction
Surfactants are composed of unimers that aggregate to form micelles at the critical micelle concentration.1 Viscoelastic surfactants (VES) are a class of surfactants that have both viscous and elastic behavior.2 Micelles can take different shapes depending on the type of surfactant, temperature, salinity and surfactant concentration.3,4 Micelles change from a spherical to a cylindrical shape with an increase in surfactant concentration, accounting for the increase in the viscosity of surfactant solutions.5–8 Cylindrical micelles in surfactant solutions are modeled as “living polymers” because they are able to break and reform.9,10VES have important uses in oilfield operations such as drilling, well stimulation and enhanced oil recovery.11–13 They are used in well stimulation because of their ease of preparation and their stability at high temperatures.11,14 VES are used in well stimulation to improve oil and gas well productivity because they form high viscous gels which are desirable for well stimulation.14–16 After well stimulation, the gels need to be removed from the reservoir in order to resume oil and gas production. VES gels are easily removed from oil reservoirs when compared to polymer gels14 because reservoir oils reduce their viscosities easily.11 This makes reservoir oil referred to as an external breaker of these gels.17 But the reduction of the viscosity by reservoir oil is inefficient.18,19 Moreover, the gels are detrimental to natural gas production if left in the reservoir.18 These factors led to the development of internal breakers: chemical compounds which are mixed with the VES solution to reduce the viscosity of the VES gel in the reservoir after well stimulation.20–27
Experimental studies have determined how some organic compounds, especially hydrocarbons, reduce the viscosity of surfactant solutions with cylindrical micelles. These organic compounds reduce the viscosity of the surfactant solutions by solubilizing in the core of cylindrical micelles.5,6,8,28–30 Solubilization disrupts the cylindrical micelle structure, changing longer cylindrical micelles into shorter cylindrical micelles,8 short rod micelles,29 spherical micelles or microemulsions.5,8,30
Kralchvesky and coworkers31,32 determined the solubilization kinetics of non-polar oils in mixed cylindrical micelles of a nonionic surfactant and a triblock copolymer. The micelles adsorb on the oil-aqueous solution interface before solubilization takes place.31,32 Shibaev and co-workers30 showed there are three regimes of micelle change in viscoelastic solutions of potassium oleate at 20 °C: (i) the micellar network regime (ii) the transition regime, and (iii) the microemulsion regime. The existence of micellar network regime was attributed to the reduction in length of the cylindrical micelles, disrupting the micelle network. This occurs when the oil solubilizes in the cylindrical micelles, preferably at the semispherical endcaps. The existence of the transitional regime was attributed to the simultaneous reduction in length of cylindrical micelles and the formation of microemulsions.
Long-tail surfactants have been of interest of research due to their various applications as viscosifying agents.5 Moreover, long-tail sulfobetaine surfactants have been reported to be a good candidate for especially high-temperature applications such as well stimulation.33 Despite this interest, micellar changes of long-tail sulfobetaine surfactants induced by organic compounds have not been published. Moreover, previous studies revealing the kinetics of transition from cylindrical micelles to spherical micelles has been on potassium oleate surfactant solutions at low temperatures and with only alkanes. There is no clear mechanism on the effect of different oils and temperature on such a transition. The mechanism of viscosity reduction of long-tail sulfobetaine surfactant solutions after the addition of an organic compound is especially important for any application that requires the viscosity reduction of such solutions. Furthermore, it is not known if a surfactant system with a different functional group and headgroup charge will follow the same behavior as potassium oleate when in contact with viscosity-reducing organic compounds.
Thus, the objective of this work was to investigate the mechanism of micellar changes that leads to a decrease in viscosity of a long-tail sulfobetaine surfactant solution. This was achieved by conducting rheological and cryo-TEM studies at two temperatures, and using four organic compounds at different concentrations.
Theoretical considerations
Viscoelastic fluid behavior can be modeled using the Maxwellian fluid model, which have the following relations| η0 = G0τR | (1) |
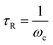 | (2) |
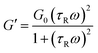 | (3) |
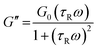 | (4) |
VES solutions have cylindrical micelles at high concentrations. The ends of a cylindrical micelle are semispherical in shape. According to Cates and Candau,9 the average contour length of a cylindrical micelle, L, is related to surfactant volume fraction, c, by the following equation
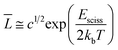 | (5) |
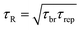 | (6) |
VES deviate from Maxwellian fluid behavior at high angular frequencies. At this point, breaking time greatly exceeds reptation time. This leads to the existence of a local minimum of G′′, 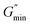 .10 Cates and coworkers9,10 derived the following relationship between micelle mesh size, ξ, and plateau modulus
.10 Cates and coworkers9,10 derived the following relationship between micelle mesh size, ξ, and plateau modulus
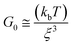 | (7) |
Experimental section
Materials
A surfactant system composed of 40–45 wt% of erucamidopropyl hydroxypropyl sulfobetaine surfactant was obtained from AkzoNobel. The general structure of the surfactant33 is shown in Fig. 1, where: (i) R1 is a saturated or unsaturated hydrocarbon chain with 17–29 carbon atoms (ii) R2 and R3 are each independently selected from a straight chain or branched, alkyl or hydroxyalkyl group with 1–6 carbon atoms (iii) R4 is either H, hydroxyl, alkyl or hydroxyalkyl group with 1–4 carbon atoms (iv) k, m and n are integers from 2–20, 1–20, and 0–20, respectively. The system also contained sodium gluconate, ethanol, propylene glycol, water, and sodium chloride. The organic compounds used were n-decane (99% purity), crude oil, extra virgin olive oil (EVOO), and polyglycolic acid (PGA). Hydrated calcium chloride, n-decane, CaCl2·2H2O, and PGA were purchased from Panreac, Acros Organics, and DuPont, respectively. EVOO with a specific gravity of 0.907 was purchased from a local supermarket. The crude oil had a specific gravity of 0.897.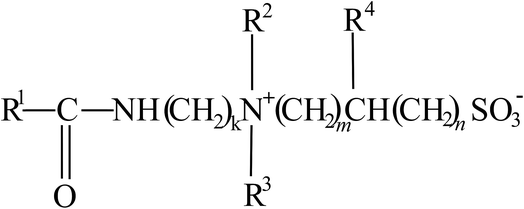 | ||
| Fig. 1 Structure of erucamidopropyl hydroxypropyl sulfobetaine.33 | ||
Samples preparation
The surfactant system (3.96 wt%) was dispersed in deionized water (Barnstead™ Nanopure™, Thermo Scientific) with 6.2 wt% CaCl2 using a disperser (T 25 digital ULTRA-TURRAX®, IKA) at 5200 rpm for at most 5 minutes. The surfactant is insoluble in deionized water, which necessitated the use of salt.For surface tension measurements, a batch solution of surfactant was prepared and left for a day. For rheological measurements, the surfactant solutions were mixed with the organic compounds and equilibrated for one week at 30 °C and 60 °C. In case there was phase separation in the solution, the surfactant solution phase was tested.
Surface tension
Surface tension measurements were done using the Sigma 702 tensiometer (Biolin Scientific) with a platinum Du Noüy ring at 30 °C and 60 °C. A Julabo water bath was used to set up the temperatures at the test temperatures. The initial batch was left to equilibrate for 30 minutes at the required temperature before the first measurement. The sample was then diluted with CaCl2 solution, stirred, and then left for five minutes before taking the next measurements. The sample was fully covered during temperature equilibration at 60 °C to minimize evaporation. During the measurement at 60 °C, the samples were covered enough to allow the ring to pass through the covering.Rheology
Steady and dynamic rheological measurements were performed using the Discovery Hybrid Rheometer 3 (DHR-3) from TA Instruments. Both rheological measurements were carried out at 30 °C and 60 °C in a DIN concentric cylinder geometry (cup diameter of 30.43 mm, and bob diameter and length of 28 mm and 41.92 mm respectively). A solvent trap was used to minimize water evaporation. The shear rate range used for steady shear viscosity measurements was 0.001–1000 s−1. The zero-shear viscosity was estimated using the best-fit correlation option in the rheometer software, or by extrapolation at low shear rate regions. Dynamic shear measurements were conducted within an angular frequency range of 0.1–100 rad s−1 in the linear viscoelastic region of each solution.Cryo-TEM
Gel samples with olive oil were further diluted with ethyl acetate in order to obtain a proper concentration for the TEM observation. Meanwhile, gel samples without olive oil were further diluted in milli-Q water. A 50 μl droplet of the suspension was placed on a TEM copper holey carbon grid (AGAR SCIENTIFIC), and the solvent was left to dry out overnight. Finally, a droplet of phosphotungstic acid was added as a negative stain to enhance the contrast of the organic material in the TEM images. The TEM grids were analyzed in a Tecnai F30 microscope (FEI company), operated at 300 kV, coupled with a Gatan CCD camera. Images were obtained and analyzed with the software Digital Micrograph (Gatan) in Bright Field TEM mode.Results and discussion
The discussion is divided into three parts. The first two parts discuss the surface tension and rheological properties of the pure surfactant solution. The last part discusses the effect of the organic compounds on the rheological properties of the surfactant solution.Surface tension of the pure surfactant solution
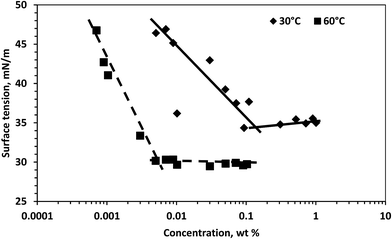
The surface tension of the surfactant solution decreased with temperature. The critical micelle concentrations (CMCs) were approximately 1.3 × 10−1 wt% and 5.0 × 10−3 wt% at 30 °C and 60 °C, respectively. This is determined from the break point in the variation of surface tension as shown in Fig. 2. The CMC at both temperatures differ by a factor of around 26. This is due to the fact that the surfactant monomers had more kinetic energy to aggregate at 60 °C.Rheology of the pure surfactant solution
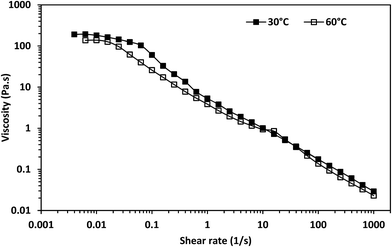
The rheology of 3.96 wt% surfactant aqueous solution was investigated at 30 °C and 60 °C. The zero-shear viscosity of the solution increased during the equilibration period at both temperatures (see Fig. S1†). This is probably due to the fact that the tail length makes the monomers require more time to reach equilibrium.34The viscosity of the surfactant solution as a function of shear rate at both temperatures measured after the equilibration period is shown in Fig. 3. There was a transition from the Newtonian to the shear-thinning region with increasing shear rate at both temperatures. The transitions at both temperatures were evidence that the surfactant solution had cylindrical micelles that aligned themselves along the direction of flow at both temperatures.34,35 Cryo-TEM confirmed the presence of micelles in the surfactant solution equilibrated at 30 °C (Fig. 4), even after dilution with ethyl acetate (see Fig. S2 and S3†).
 | ||
| Fig. 4 Cryo-TEM image of 3.96 wt% surfactant solution at 30 °C. The black lines represent the micelle edges. | ||
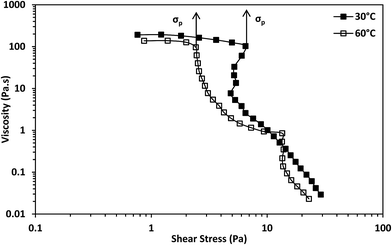
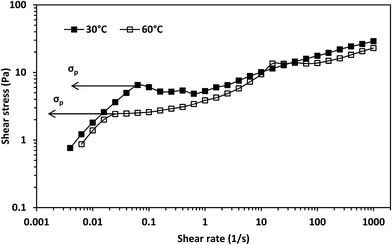
There was a sharp drop in viscosity during the transition from the Newtonian to the shear-thinning region from the viscosity against shear stress plot at both temperatures (Fig. 5). This is considered a characteristic of shear-banding during the transition from the Newtonian to the shear-thinning region; the separation of a fluid into macroscopic sections with different shear rates.36 This implies micelle networks were present at both temperatures. Moreover, there was an inflection point during this transition from the shear stress versus shear rate plot at 30 °C (Fig. 6) and an apparent yield stress at 30 °C as seen from the viscosity versus shear stress graph (Fig. 5). An inflection point and apparent yield stress have been reported in another erucyl-tailed sulfobetaine surfactant, 3-(N-erucamidopropyl-N,N-dimethyl ammonium)propane sulfonate (EDAS). This was explained to be as a result of shear banding.34,37 Given the presence of shear-banding at both temperatures, the presence of the inflection point at 30 °C shows shear banding was more prominent at the lower temperature than at the higher temperature. This was most likely due to the greater closeness of the cylindrical micelles to each other at 30 °C than at 60 °C. The closeness of the cylindrical micelles might also explain why the zero-shear viscosity of the surfactant solution was higher at 30 °C than at 60 °C (Fig. 3, see estimates in Table S1†). This will be elaborated when considering the dynamic shear rheology of the surfactant solution.
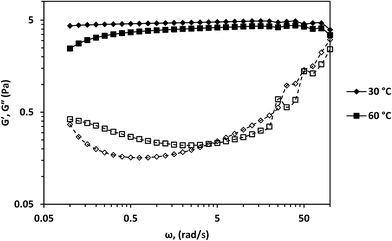
The dynamic rheology of the surfactant solution at 30 °C and 60 °C is shown in Fig. 7. G′ dominated G′′ within the tested frequency range at both temperatures. Moreover, the crossover frequency was absent within the measured frequency range. Erucyl-tailed amphoteric surfactants such as erucyl dimethyl amidopropyl betaine (EDAB),5 EDAS34 and erucyldimethyl amidopropyl amine oxide (EMAO)38 have such behavior within a frequency range of 0.01–100 rad s−1 at high concentrations and low temperatures. Viscoelastic fluids typically show a region where G′′ dominates G′ at lower angular frequencies and a crossover frequency. The complete dominance of G′ over G′′ in the angular frequency range of 0.01–100 rad s−1 is attributed to gels.5 But the existence of the Newtonian region at low shear rates (Fig. 3) and G0 (Fig. 7) is evidence that the surfactant solution followed the Maxwellian fluid model at low angular frequencies at both temperatures. Chu and Feng showed that a solution with 100 mM and 250 mM of EDAS followed Maxwellian fluid behavior even with the total dominance of G′ over G′′ within an angular frequency range of 0.01–100 rad s−1.37 This implies the surfactant solution had a crossover frequency at both temperatures. The crossover frequencies and relaxation times of the surfactant solution at both temperatures are estimated from eqn (1) and (2) (Table S1†). The estimated crossover frequencies at both temperatures were below 0.1 rad s−1. Thus, the absence of the crossover frequency was because the angular frequencies used for measurement were not able to detect the crossover frequency.
According to Granek and Cates,10 another evidence for the presence of entangled wormlike micelles is the presence of 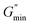 on the dynamic rheology profile. The presence of
on the dynamic rheology profile. The presence of 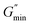 shows the deviation of the fluid from Maxwellian behavior at high angular frequencies.10
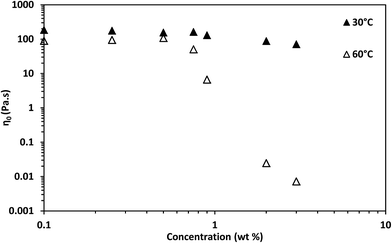
shows the deviation of the fluid from Maxwellian behavior at high angular frequencies.10 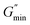 was present at both temperatures. This means ξ can be estimated from eqn (6). The estimated value of ξ at 30 °C was lower than that 60 °C (see Table S1†), signifying that the micelles were highly entangled at 30 °C than at 60 °C. This explains why the viscosity of the surfactant solution at 30 °C was higher than at 60 °C, and why shear-banding was more pronounced at the lower temperature than at the higher temperature. Micelles close to each other will offer more resistance to shear than micelles far apart. Also, the more the micelles are close together, the more the micelles will experience shear banding transitions.36
was present at both temperatures. This means ξ can be estimated from eqn (6). The estimated value of ξ at 30 °C was lower than that 60 °C (see Table S1†), signifying that the micelles were highly entangled at 30 °C than at 60 °C. This explains why the viscosity of the surfactant solution at 30 °C was higher than at 60 °C, and why shear-banding was more pronounced at the lower temperature than at the higher temperature. Micelles close to each other will offer more resistance to shear than micelles far apart. Also, the more the micelles are close together, the more the micelles will experience shear banding transitions.36
Such rheological behaviors have been attributed to the fact that the tail lengths are very long, thus high hydrophobic. This disfavors the exchange of monomers from one micelle to another through water whenever a micelle breaks and reforms.5
Rheology of surfactant solution with organic compounds
The effects of four organic compounds on 3.96 wt% of the surfactant system with 6.2 wt% CaCl2 solutions were investigated. These organic compounds were crude oil, n-decane, EVOO, and PGA. The effect of the oils and PGA at both temperatures will be presented and discussed separately.Effect of the oils
The estimated zero-shear viscosities of the surfactant solutions with 0.1–3 wt% of n-decane and crude oil are shown in Fig. 8 and Fig. 9, respectively. Zero-shear viscosities were higher at 30 °C than at 60 °C. The response of the surfactant solution to increasing EVOO and crude oil concentrations were similar at both temperatures (see Fig. S4†). n-Decane induced drastic drops in zero-shear viscosity at both temperatures. Meanwhile, crude oil and EVOO induced drastic drops only at 60 °C.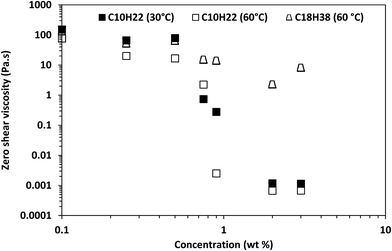 | ||
| Fig. 8 Estimated zero-shear viscosity of 3.96 wt% surfactant solution with different n-decane and octadecane concentrations. | ||
 | ||
| Fig. 9 Estimated zero-shear viscosity of 3.96 wt% surfactant solution with different crude oil concentrations. | ||
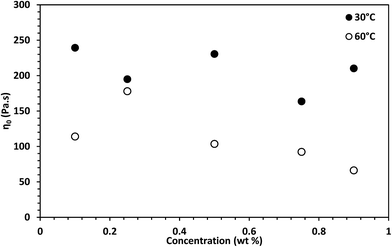
The estimated difference in zero-shear viscosities between the surfactant solutions with the oils and the pure surfactant solutions at the test temperatures are in Table S2.† At 30 °C, 0.9 wt% n-decane induced a difference of approximately two orders of magnitude, whereas 0.9 wt% EVOO and crude oil induced a difference of approximately one fold. The steady state rheology of the surfactant solutions with 2 wt% and 3 wt% of crude oil and EVOO were measured to check if the effect of 0.9 wt% of these oils were due to low oil concentrations. The differences induced by 3 wt% crude oil and EVOO were less than ten folds. Meanwhile, the viscosities of the surfactant solutions with 2 wt% and 3 wt% n-decane were approximately 0.001 Pa s (Fig. 8); an approximate difference of five orders of magnitude. At 60 °C, 0.9 wt% of the oils induced drastic differences, with n-decane inducing the greatest difference. This was also the same with 2 wt% and 3 wt% of the oils at 60 °C. Hence, n-decane was the most efficient breaker among the oils at both temperatures. Furthermore, temperature enhanced the breaking effect of crude oil and EVOO on the surfactant solution.
Zero-shear viscosity reduction by non-polar oils is linked to the solubilization of oil molecules in the micelle core.7,8,29,30 The solubilization of the oil molecules in the micelle core disrupts the micelle structure, leading to structural changes and reducing the zero-shear viscosity of a surfactant solution. Because crude oil and EVOO did not induce drastic viscosity differences like n-decane at 30 °C, these oils faced a barrier to solubilization in the micelle core.
The solubilization mechanism of non-polar oils by cylindrical micelles proposed by Kralchevsky and co-workers31 will be used to interpret the results, as this mechanism has been experimentally verified.32 Moreover, the formation of cylindrical micelles as soon as the surfactant system was dissolved in the aqueous solution will be taken into account. The effect of temperature explained as follows: temperature increased the average number of transient adsorptions of cylindrical micelles on the oil-aqueous solution interface. Temperature also increased the kinetic energy of the oil molecules, permitting oil molecules to migrate from the oil phase into the cylindrical micelle core. It is only in the cylindrical micelle core that oils can solubilize as they are insoluble in a salt solution. The increase in temperature provided the kinetic energy necessary for crude oil and EVOO oil molecules to overcome the barrier to solubilization. To confirm that competition between the different components in EVOO and crude oil did not affect their solubilization in the micelles, the effect of octadecane at 60 °C was tested. The viscosity of the surfactant solution with octadecane was also higher than that of the surfactant solution with n-decane (see Fig. 8 and Table S2†). This confirms oil molecular weight is a significant factor for oil solubilization in micelles.
Zero-shear viscosity dropped with increasing n-decane, crude oil, and EVOO concentration (Fig. 8, Fig. 9 and Fig. S4,† respectively). The oils induced several regimes of viscosity change, similar to Shibaev and co-workers.30 n-Decane induced three regimes at both temperatures in the following order: (i) the high viscosity regime (HVR), (ii) the transition regime (TR), and (iii) the low viscosity regime (LVR). Each regime existed within a concentration range. The other oils induced only the HVR at 30 °C, and the HVR and TR at 60 °C.
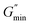 were present from the dynamic shear rheology at these concentrations (Fig. S19–S24†). These features support the existence of dense micelle networks in this regime.
were present from the dynamic shear rheology at these concentrations (Fig. S19–S24†). These features support the existence of dense micelle networks in this regime.The reason for the existence of this regime depended on the nature of the oil. This is because the concentration range for which the HVR existed for n-decane was lower than that of crude oil and EVOO. It is suspected that the existence of the HVR in the case of n-decane was mainly due to the concentrations not being enough to prevent the formation of a micelle network. In the case of crude oil and EVOO, it is suspected that there were few molecules in these oils that had enough kinetic energy to penetrate the micelles at 30 °C, even at high concentrations. These oils have molecules of high molecular weight and complex structure, which might be a reason for the solubilization barrier. The HVR did not exist at high concentrations of crude oil and EVOO at 60 °C. Thus, the reason for the existence of HVR at 60 °C was possibly mainly due to the low oil concentrations.
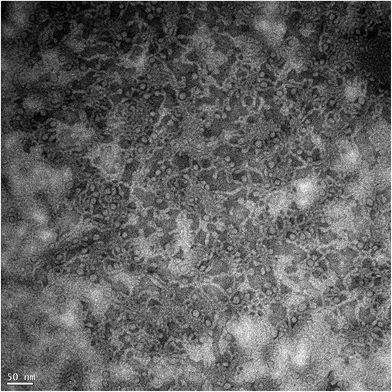 | ||
| Fig. 11 Cryo-TEM image of 3.96 wt% surfactant solution with 3 wt% n-decane at 60 °C. The white sections are the micelles. | ||
Thus, the formation of each regime depended on the balance between the formation of a dense micelle network and the solubilization of the oils by cylindrical micelles. Furthermore, we show for the first time that the formation of each region also depends on the type of oil which is solubilized by the micelle.
Effect of PGA
The steady shear rheology of the surfactant solutions with 0.1–0.9 wt% PGA at 30 °C and 60 °C was similar in some aspects to that of surfactant solutions with crude oil at 30 °C. There were no significant differences in zero-shear viscosity at both temperatures (Fig. 12). There were also transitions from the Newtonian to the shear-thinning region (Fig. S26 and S27†) and shear banding transitions (Fig. S28 and S29†) at all concentrations at both temperatures, implying that cylindrical micelles were present in the solutions.The dynamic shear rheology of the surfactant solutions with 0.1–0.9 wt% PGA at 30 °C and 60 °C was similar in some respects to that of the surfactant solutions with 0.1–0.9 wt% crude oil at 30 °C (Fig. S30 and S31†). The region where G′′ dominates G′ at lower angular frequencies and the crossover frequency were absent at both temperatures, except with the surfactant solution with 0.9 wt% PGA at 60 °C. The reason for this absence is the same for the pure surfactant solution at both temperatures.
The effect of PGA on these surfactant solutions can be understood by comparing its effect on the amphoteric carboxylic betaine surfactant, EDAB.26 Amphoteric carboxylic betaine surfactants become cationic or anionic at low and high pH respectively,39,40 unlike sulfobetaine surfactants which remain zwitterionic at all pH.40 Increasing the PGA concentration reduces the pH, changing EDAB into a cationic surfactant. This change increases the headgroup charge, thus increasing the effective headgroup area of the surfactant. The increase in the headgroup area reduces the packing parameter, changing EDAB from cylindrical to spherical micelles, which reduces the viscosity of EDAB solution. This mechanism was also proposed for the changes induced by sodium salicylate (NaSal) and sodium hydroxynaphthalene carboxylate (NaHNC) on EDAB.5 Because the surfactant was a sulfobetaine, it resisted a change in charge with reducing pH. Therefore, the micelles were insignificantly affected.
Conclusions
In this work, we studied the effect of several organic compounds on a long-tailed sulfobetaine surfactant solution at 30 °C and 60 °C. Such a study has been conducted only with potassium oleate solution at 20 °C. We show that there are at most three regimes of viscosity reduction as with viscous oleate surfactant solutions. But in contrast to oleate surfactant solutions, the number of regimes of viscosity reduction of the sulfobetaine surfactant solution depends greatly on the type and size of the organic compound being solubilized and the temperature. Both EVOO and crude oil, which have higher molecular components, produced one and two regimes at 30 °C and 60 °C, respectively in contrast to n-decane which produced the three regimes. PGA does not significantly affect the surfactant solution even at high temperatures, meaning the surfactant is resistant to pH reductions even at high temperature. Viscosity reduction of such a system is also affected by a balance between micellization and solubilization.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Abbreviations
| VES | Viscoelastic surfactant |
| EVOO | Extra virgin olive oil |
| PGA | Polyglycolic acid |
| HVR | High viscosity regime |
| TR | Transition regime |
| LVR | Low viscosity regime |
| DHR-3 | Discovery Hybrid Rheometer 3 |
| EDAS | 3-(N-erucamidopropyl-N,N-dimethyl ammonium)propane sulfonate |
| EDAB | Erucyl dimethyl amidopropyl betaine |
| EMAO | Erucyldimethyl amidopropyl amine oxide |
Acknowledgements
The authors would like to thank King Abdulaziz City for Science and Technology (KACST) for funding this research under project no. 10-OIL1378-04. L. T. F. thanks King Fahd University of Petroleum & Minerals for a scholarship. We acknowledge (i) Akzo Nobel for providing the surfactant for the study (ii) The Laboratory for Advanced Microscopy of the Nanoscience Institute of Aragon (LMA-INA) for their support with the Transmission Electron Microscopy images (iii) Mr Ahmad Mahboob, Mr Mobeen Murtaza, and Mr Abdulsamad Idrissu for helping with the surface tension measurements.References
- Dynamics of Surfactant Self-Assemblies: Micelles, Microemulsions, Vesicles and Lyotropic Phases, ed. R. Zana, CRC Press, 2005, vol. 125 Search PubMed.
- H. Rehage and H. Hoffmann, J. Phys. Chem., 1988, 92, 4712 CrossRef CAS.
- D. Danino, A. Bernheim-Groswasser and Y. Talmon, Colloids Surf., A, 2001, 183, 113 CrossRef.
- C. O. Rangel-Yagui, A. Pessoa Jr and L. C. Tavares, J. Pharm. Pharm. Sci., 2005, 8, 147 CAS.
- R. Kumar, G. C. Kalur, L. Ziserman, D. Danino and S. R. Raghavan, Langmuir, 2007, 23, 12849 CrossRef CAS PubMed.
- Z. Lin and C. D. Eads, Langmuir, 1997, 13, 2647 CrossRef CAS.
- V. S. Molchanov, O. E. Philippova, A. R. Khokhlov, Y. A. Kovalev and A. I. Kuklin, Langmuir, 2007, 23, 105 CrossRef CAS PubMed.
- S. C. Sharma, R. G. Shrestha, L. K. Shrestha and K. Aramaki, J. Phys. Chem. B, 2009, 113, 1615 CrossRef CAS PubMed.
- M. E. Cates and S. J. Candau, J. Phys.: Condens. Matter, 1990, 2, 6869 CrossRef CAS.
- R. Granek and M. E. Cates, J. Chem. Phys., 1992, 96, 4758 CrossRef CAS.
- S. Kefi, J. Lee, T. Pope, P. Sullivan, E. Nelson, A. Hernandez, T. Olsen, M. Parlar, B. Powers and A. Roy, Oilfield Rev., 2004, 16, 10 CAS.
- R. Ravitz, L. Moore and C. Svoboda, VES: An Alternative to Biopolymers in Reservoir Drill-In Fluids, Society of Petroleum Engineers, Scheveningen, The Netherlands, 2009 Search PubMed.
- L. L. Schramm, E. N. Stasiuk and D. G. Marangoni, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2003, 99, 3 RSC.
- M. Samuel, R. Card, E. Nelson, J. Brown, P. S. Vinod, H. Temple, Q. Qu and D. Fu, Polymer-Free Fluid for Hydraulic Fracturing, Society of Petroleum Engineers, San Antonio, Texas, 1997 Search PubMed.
- F. Chang, Q. Qu and M. Miller, US Pat., US6399546 B1, 2002.
- H. Nasr-El-Din, S. Al-Driweesh, K. Bartko, H. Al-Ghadhban, V. Ramanathan, S. Kelkar and M. Samuel, Acid Fracturing of Deep Gas Wells Using a Surfactant-Based Acid: Long-Term Effects on Gas Production Rate, Society of Petroleum Engineers, San Antonio, Texas, 2006 Search PubMed.
- J. Crews and T. Huang, Internal Breakers for Viscoelastic-Surfactant Fracturing Fluids, Society of Petroleum Engineers, Houston, Texas, 2007 Search PubMed.
- T. Huang and J. Crews, Do Viscoelastic-Surfactant Diverting Fluids for Acid Treatments Need Internal Breakers?, Society of Petroleum Engineers, Lafayette, Louisana, 2008 Search PubMed.
- M. Yu, M. Mahmoud and H. Nasr-El-Din, Propagation and Retention of Viscoelastic Surfactants Following Matrix Acidizing Treatments in Carbonate Cores, Society of Petroleum Engineers, Lafayette, Louisana, 2010 Search PubMed.
- J. B. Crews, US Pat., US8236864 B2, 2012.
- J. B. Crews and T. Huang, US Pat., US8101557 B2, 2012.
- L. Li, L. Lin, C. Abad and T. Bui, US Pat., US7635028 B2, 2009.
- L. Lin, L. Li and C. Abad, US Pat., US7879770 B2, 2011.
- L. Lin, L. Li and C. Abad, US Pat., US8067342 B2, 2011.
- P. F. Sullivan, B. Baser, C. Abad, Y. Chen, M. Parlar and G. Kubala, US Pat., US7431087 B2, 2008.
- P. F. Sullivan, J. E. Brown, J. C. Lee and G. Salamat, US Pat., US7219731 B2, 2007.
- C. Abad, J. C. Lee, P. F. Sullivan, E. Nelson, Y. Chen, B. Baser and L. Lin, US Pat., US7857051 B2, 2010.
- H. Hoffmann and W. Ulbricht, J. Colloid Interface Sci., 1989, 129, 388 CrossRef CAS.
- T. Sato, D. P. Acharya, M. Kaneko, K. Aramaki, Y. Singh, M. Ishitobi and H. Kunieda, J. Dispersion Sci. Technol., 2006, 27, 611 CrossRef CAS.
- A. V. Shibaev, M. V. Tamm, V. S. Molchanov, A. V. Rogachev, A. I. Kuklin, E. E. Dormidontova and O. E. Philippova, Langmuir, 2014, 30, 3705 CrossRef CAS PubMed.
- P. A. Kralchevsky, N. D. Denkov, P. D. Todorov, G. S. Marinov, G. Broze and A. Mehreteab, Langmuir, 2002, 18, 7887 CrossRef CAS.
- P. D. Todorov, G. S. Marinov, P. A. Kralchevsky, N. D. Denkov, P. Durbut, G. Broze and A. Mehreteab, Langmuir, 2002, 18, 7896 CrossRef CAS.
- M. J. Engel, J. F. Gadberry, J. D. Nowak, X. Wang and J. Zhou, World Intellectual Property Organization, WO2012160008 A1, 2012.
- Z. Chu, Y. Feng, X. Su and Y. Han, Langmuir, 2010, 26, 7783 CrossRef CAS PubMed.
- V. Croce, T. Cosgrove, C. A. Dreiss, S. King, G. Maitland and T. Hughes, Langmuir, 2005, 21, 6762 CrossRef CAS PubMed.
- J.-F. Berret, in Molecular Gels, ed. R. G. Weiss and P. Terech, Springer, Netherlands, 2006, p. 667 Search PubMed.
- Z. Chu and Y. Feng, Soft Matter, 2010, 6, 6065 RSC.
- Y. Zhang, P. An and X. Liu, RSC Adv., 2015, 5, 19135 RSC.
- K. Kato, H. Kondo, A. Morita, K. Esumi and K. Meguro, Colloid Polym. Sci., 1986, 264, 737 CAS.
- T. Yoshimura, T. Ichinokawa, M. Kaji and K. Esumi, Colloids Surf., A, 2006, 273, 208 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Steady shear viscosity plots of the surfactant solution with the oils and cryo-TEM pictures. See DOI: 10.1039/c7ra12538k |
| This journal is © The Royal Society of Chemistry 2018 |