Mechanism and thermal rate constants for complete series reactions of bromochlorophenols with H

Abstract

Bromochlorophenoxy radicals (BCPRs) are the principal precursors for the formation of mixed polybrominated and chlorinated dibenzo-p-dioxins and dibenzofurans (PBCDD/Fs). In this study, the formation of BCPRs from a complete series of reactions of 96 bromochlorophenol (BCP) congeners with H atoms was analyzed using quantum chemical methods at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level. The rate constants of each reaction were obtained using canonical variational transition-state (CVT) theory along with a small-curvature tunneling (SCT) contribution over a wide temperature range of 600–1200 K. In addition, abstraction reactions of bromophenols (BPs) and chlorophenols (CPs) by H are compared with reactions of BCPs with H. The computational results indicate that the relative reactivity of the O–H bonds in the BCPs appears to be assisted and dominated by the total degree and pattern of halogenation, but it does not appear to be determined by the distribution of the bromine and chlorine atoms. In addition, halogen substitution at the ortho position increases the stability of the BCPs and reduces the reactivity of the O–H bonds. This work is beneficial in that it provides reference data for future experimental research into the formation of PBCDD/Fs.

---

1. Introduction

Mixed polybrominated and chlorinated dibenzo-p-dioxins and dibenzofurans (PBCDD/Fs) are halogenated derivatives of polychlorinated dibenzo-p-dioxin and dibenzofurans (PCDD/Fs) or polybrominated dibenzo-p-dioxins and dibenzofurans (PBDD/Fs), in which all halogen atoms are substituted by both bromine and chlorine atoms. These three groups of compounds are all classed as polyhalogenated dibenzo-p-dioxins and furans (PHDD/Fs) and have similar structures, toxicity levels, physicochemical properties, and biological activity.^1–3 PBCDD/Fs have been detected in several environment matrices such as air, soil, and sediments, as well as in the tissues of aquatic animals, and they have been particularly detected in fly ash and flue gas from municipal waste incinerators and industrial waste incinerators.^4–8 Moreover, PBCDD/Fs are unintentionally produced persistent organic pollutants, and the dominant sources are combustion of waste materials and many other high-temperature industrial processes.^9–12 In addition, electronic waste recycling and pyrolysis or combustion of waste-containing brominated flame retardants constitute a new source of PBCDD/Fs, because they contain both brominated and chlorinated materials.^13–15 Studies on PBCDD/F formation are necessary because they can serve as a basis for minimizing PBCDD/F emissions and harm. The formation of PBCDD/Fs is likely to occur from the same analogy mechanisms as PBDD/F or PCDD/F formation, but the processes involved are much less understood than those involved in PBDD/F and PCDD/F formation. Further research on PBCDD/F formation in thermal processes is required.

Bromochlorophenols (BCPs) are bromophenols (BP) and chlorophenol (CP) analogues in which some of the hydrogen atoms in phenol are substituted by both the bromine and chlorine atoms. Due to the different substitution pattern of phenol, BCPs have 96 isomers. BCPs have properties typical of persistent organic pollutants (POPs). Additionally, BCPs have been widely used as feedstock and intermediates for many chemical products such as dyes, pulp, fungicides, wood preservatives, herbicides, and flame retardants.^16–19 Typically, the main sources of BCPs are high-temperature processes such as typical combustion processes, accidental fires, and municipal waste incineration.^20,21 BCPs have also been frequently detected in various environmental media including marine ecosystems, blood plasma, and human, wildlife, and industrial effluents.^22–27 The oxidation and reaction pathways of CPs and BPs are attracting increasing attention; however, little research has been conducted on the chemical and physical features of BCPs.

Dioxins are formed via two general pathways: de novo synthesis and precursor pathways. Diversify precursors have been demonstrated, such as catechol,²⁸ captan pesticide,²⁹ polycyclic aromatic hydrocarbons (PAHs),³⁰ cypermethrin,³¹ and polybrominated biphenyls.³² Among various precursors, halogenated phenols are generally considered as the predominant precursors of dioxins and implicated as key intermediates in the de novo synthesis. Dioxins are formed from halogenated phenols via two general mechanisms: homogeneous gas-phase mechanism and heterogeneous metal mediated mechanism. Although over 70% of all dioxins are formed through surface-mediated reactions over catalytic surfaces in the post-flame, cool zone of combustion systems at the temperature range of 200−600 °C,^33–37 the homogeneous gas-phase mechanism also make a significant contribution to the dioxin formations at high temperatures (>600 °C).^38,39 Studies have shown that the radical–radical coupling of halogenated phenoxy radicals plays a considerable role in the homogeneous gas-phase formation of dioxins and furans.^40–45 Halogenated phenoxy radicals have been considered crucial intermediates in the formation of halogenated dioxins and furans.^42–46 Under combustion or pyrolysis conditions, halogenated phenoxy radicals can be formed from BPs or CPs through the loss of the phenoxyl-hydrogen via unimolecular, bimolecular, or possibly other low-energy pathways (including heterogenous reactions). The unimolecular reaction includes the decomposition of bromophenoxy radicals (BPRs) and chlorophenoxy radicals (CPRs) with the cleavage of the O–H bond. The bimolecular reactions include attack by H, OH, O (³P), Cl, and Br, which are abundant in the combustion environment. The gas-phase formation of PBCDD/Fs is likely to have similar mechanisms to those responsible for PBDD/F and PCDD/F productions. On the one hand, PBCDD/Fs can be formed from the combustion or high-temperature pyrolysis of the BP and CP mixture;^45–49 on the other hand, BCPs are also structurally similar to PBCDD/Fs and have been demonstrated to be the predominant precursors for or key intermediates in the formation of PBCDD/Fs. The dimerization of bromochlorophenoxy radicals (BCPRs) is the major pathway for the gas-phase formation of PBCDD/Fs from BCP precursors. Thus, the formation of BCPRs from BCPs is expected to play the most central role in the formation of PBCDD/Fs. Thus far, little is known about these reactions under pyrolysis or combustion conditions.

Nowadays, quantum chemistry calculation and multiple rate constants calculation methods, as a supplement to experimental evaluation, has been successfully employed to elucidate the reaction mechanism and kinetics of organic pollutants in the environment.^{32,38,42–45,50,51} In recent research conducted from this laboratory, we have performed quantum chemistry to investigate the formation of BPRs and CPRs from BPs and CPs with a H atom.^52,53 In the current study, we complemented and expanded on our previous work in this field to continue mechanistic and kinetic studies into the formation of BCPRs from the reaction of BCPs with H. We performed a direct density functional theory kinetic study on the complete series reactions of BCP congeners with H atom. The effect of the bromine and chlorine substitution pattern on the structural parameters, thermochemical property, rate constants and reactivity of the O–H bonds in BCPs was examined. The formation potential of BCPRs from BCPs with H was compared with that of BPs from CPs with H. The results can be input into environmental PBCDD/F control and prediction models as important parameters, which can in turn be used to predict potential PBCDD/F outcomes, confirm PBCDD/F risk analyses, reduce PBCDD/F emissions, and establish PBCDD/F control strategies.

2. Computational method

The Gaussian 09 program suite⁵⁴ was used to perform all the calculations on the chemical structures, energies, and frequencies for reactants, transition states, and products, along with the hybrid meta functional MPWB1K.⁵⁵ This computational approach was chosen for its effective performance in quantum calculations of thermochemistry, thermochemical kinetics, hydrogen bonding, and weak interactions. The geometry and vibrational frequency calculations were performed at the MPWB1K/6-31+G(d,p) level. Vibrational frequency analysis was performed for each stationary point to verify that the minima had no imaginary frequency and that transition states had a single imaginary frequency. Additionally, the zero-point energy (ZPE) and the thermal contributions to the free energy of activation can be derived from frequency calculations. The complete reactions discussed in this paper were verified using intrinsic reaction coordinate (IRC) calculations and the minimum energy path (MEP) analysis of all transition states. The last structures of the IRC in both directions were further optimized, to confirm the two desired minima to which each transition state is linked.⁵⁶ To obtain more reliable potential barriers and reaction heat, a more flexible basis set, 6-311+G(3df,2p), was used to determine the single-point energies of the various species, based on the optimized geometries. All the energies quoted and discussed in this paper include ZPE corrections.

Rate constants of key elementary steps involved in this study were calculated over a wide temperature range (600–1200 K) using canonical variational transition-state (CVT) theory with small-curvature tunneling (SCT) correction.^57–60 The rate constant calculations were performed using the POLYRATE 9.7 program.⁶¹ To calculate the rate constants, 40 nonstationary points near the transition state along the MEP (20 points on the reactant side and 20 points on the product side) were selected for frequency calculations at the MPWB1K/6-31+G(d,p) level. The SSTEP, a variable keyword in the POLYRATE 9.7 program that specifies the step size along the mass-scaled MEP, was confirmed as 0.05 bohr. The SRANGE, which is required to specify the limits on the reaction coordinate, was selected from −1.5 bohr to 1.5 bohr. Parameters such as energy data, force constant matrices, hessian matrices, stationary point coordinates, and unstationary points were obtained from the Gaussian 09 program output files and were input into the POLYRATE input files automatically by our self-compiled program.

3. Results and discussion

It is crucial to confirm the reliability of the theoretical calculations, especially for a continuous work. Owing to the absence of the experimental values of structural, thermal and kinetic data of BCPs, we have to verify the accuracy of our calculation methods by comparing the BCP data in this study with the experimental data of phenol, 2-BP and 2-CP or the theoretical values of BCPs in the literatures. The optimized geometries and the calculated vibrational frequencies of phenol, 2-BP and 2-CP at the MPWB1K/6-31+G(d,p) level are in good agreement with the available experimental values, and the relative error remains within 2%.⁶² In order to verify the reliability of the energies, we calculated the reaction enthalpies for the reactions of C₆H₅OH + H → C₆H₅O + H₂ at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level. The calculated values of −17.77 kcal mol⁻¹ at 298.15 K and 1.0 atm show great consistency with the corresponding experimental values of −16.13 kcal mol⁻¹ obtained from the measured standard formation enthalpies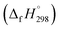 of C₆H₅OH (−23.02 kcal mol⁻¹), C₆H₅O (12.90 kcal mol⁻¹), H (52.08 kcal mol⁻¹), and H₂ (0.03 kcal mol⁻¹).^63–65 For the clarify the accuracy of the rate constants, the CVT/SCT rate constants of C₆H₅OH + H → C₆H₅O + H₂ are in good agreement with the available experimental values with the maximum relative deviation less than 3 times.⁶⁶ For example, at 1000 K, the calculated CVT/SCT rate constant, 1.68 × 10⁻¹³ cm³ per molecule per s, agrees well with experimental value of 3.72 × 10⁻¹³ cm³ per molecule per s. In addition, the kinetic properties of 2-CP + H → 2-CPR + H₂ were also studied by Altarawneh.⁶⁷ The potential barrier calculated by Altarawneh at the BB1K/6-311+G(3df,2p)//BB1K/6-31+G(d,p) level is 0.7 kcal mol⁻¹ lower than that obtained in our study at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level. The CVT/SCT rate constants calculated by Altarawneh matches well with our CVT/SCT ones. For example, at 1000 K, the CVT/SCT rate constant calculated by Altarawneh is 7.66 × 10⁻¹⁴ cm³ per molecule per s, while the CVT/SCT value in our study is 1.76 × 10⁻¹⁴ cm³ per molecule per s. This good agreement confirms that our CVT/SCT results may provide a good estimate for the formation of BCPRs from the reactions of BCPs with H. Moreover, Saeed also calculated the structures and thermodynamic parameters of a large number of BCPs and their radicals.⁶⁸ We compared the C–O and O–H bond lengths, the O–H bond dissociation enthalpies (BDH) and standard enthalpies 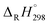of reaction BCP + OH → BCPR + H₂O calculated at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level with values of Saeed at the M062X/6-311+G(3df,2p)//M062X/6-311+G(d,p) level involving in Table S1 (ESI†), and relative error remains within 0.02 Å for the geometrical parameters (except for the C–O of 2B-4CP and 2,3,5,6TeB-4CP, its relative error is about 0.09 Å), 1.2 kcal mol⁻¹ for D₀(O–H) and 1.5 kcal mol⁻¹ for the .

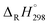Due to the different substitution pattern of phenol, BCPs have 96 congeners, comprising 10 dibromochlorophenols, 32 tribromochlorophenols, 36 tetrabromochlorophenols, and 18 pentabromochlorophenols. For a given BCP, the compound name m-bromo-n-chlorophenol is abbreviated to mB-nCP. For example, 2,3-dibromo-4,6-dichlorophenol is abbreviated to 2,3DB-4,6DCP. All the BCPs can be divided into three molds: BCPs with both two ortho carbon atoms connected with halogen atom (short for BCP^X–X), BCPs with both two ortho carbon atoms connected with hydrogen atom (short for BCP^H–H) and BCPs with one ortho carbon atom connected with halogen atom and the other with hydrogen atom (short for BCP^H–X). The asymmetric halogen substitution of all these three BCP molds result in the existence of syn- and anti-conformers (Scheme 1). Fig. S1 (ESI†) shows the syn- and anti-conformers of BCPs and energy differences at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level. By analogy with BCP^Br–Cl, if the H atom of the OH group points toward a C (Br) atom (syn) rather than toward a C (Cl) site (anti), slightly more stable isomers (within 1 kcal mol⁻¹) may be produced. In addition, by analogy with BCP^H–H, the energy differences of syn- and anti-conformers are even smaller (within 0.1 kcal mol⁻¹). However, by analogy with BCP^H–X, if the H atom of the OH group points toward a C (halogen) atom (syn), the stabiliproduced is approximately 3.0 kcal mol⁻¹ greater than that produced with the H atom of the OH group pointing toward a C (H) atom (anti). The energy differences of syn- and anti-conformers of BCPs^H–X are larger than those of BCPs^X–X and BCPs^H–H. Therefore, throughout this paper, BCPs denote the syn-conformers. The 38 selected anti-conformers of BCPs^H–X are also discussed to compare with the relative syn-conformers.

Scheme 1 Syn- and anti-conformers of BCPs.

3.1 Structural analysis

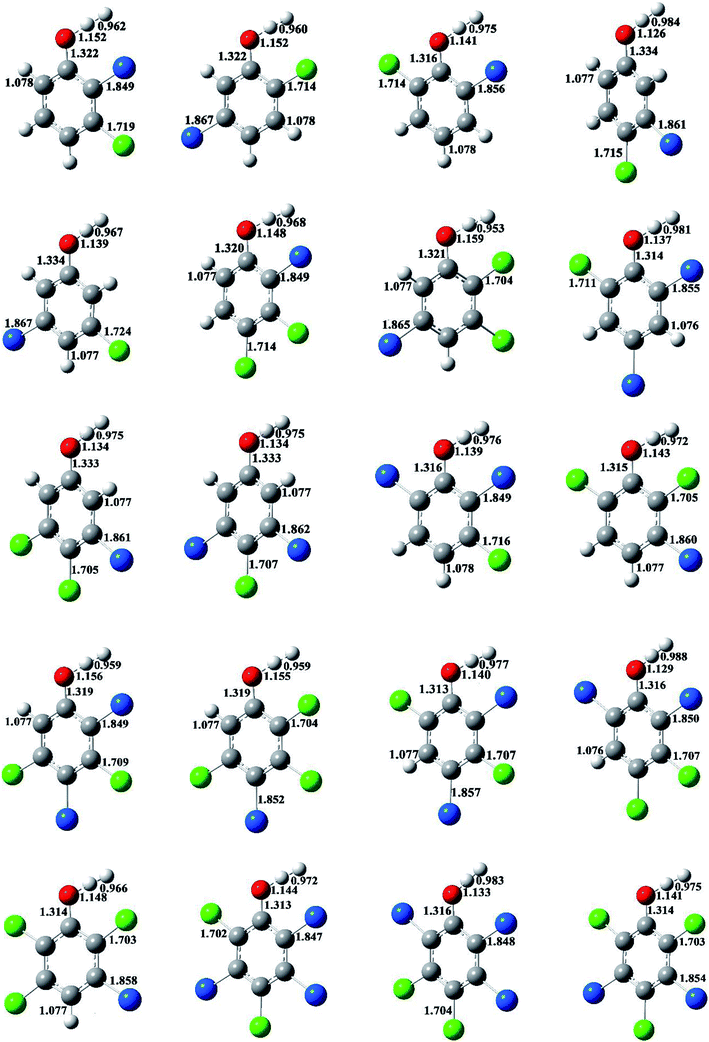
The optimized structures of selected congeners of BCPs, transition states, and BCPRs were determined to be located at the MPWB1K/6-31+G(d,p) level and are shown in Fig. 1–3, respectively. The structures of the 96 congeners of the BCPs, transition states, and BCPRs are depicted in Fig. S2–S4 (ESI†), respectively. Fig. 1 and S2† show that the O–H bonds in ortho-halogen-substituted phenols are longer than those without ortho halogen substitution. The O–H bond lengths in BCPs with ortho halogen substitution are 0.958–0.961 Å, whereas the value is 0.955 Å for BCPs without ortho halogen substitution. In Fig. 1 and S2,† there exists weak intramolecular hydrogen bonding in the ortho-halogen-substituted phenols. The lengths of the Br–H hydrogen bonds in the BCPs with ortho bromine substitution are from 2.391 to 2.466 Å, which are longer than those of Cl–H hydrogen bonds in the BCPs with ortho chlorine substitution (2.329 to 2.403 Å). The O–H bond lengths in BCPs with Br–H intramolecular hydrogen bonding (0.960 or 0.961 Å) are slightly longer than those in BCPs with Cl–H intramolecular hydrogen bonding (0.959 or 0.960 Å).

Fig. 1 MPWB1K/6-31+G(d,p) optimized geometries for selected bromochlorophenols (BCPs). Distances are in angstroms. Gray sphere, C; white sphere, H; red sphere, O; blue sphere, Br; green sphere, Cl.

Fig. 2 MPWB1K/6-31+G(d,p) optimized geometries for selected transition states of bromochlorophenols with H. Distances are in angstroms. Gray sphere, C; white sphere, H; red sphere, O; blue sphere, Br; green sphere, Cl.

Fig. 3 MPWB1K/6-31+G(d,p) optimized geometries for selected bromochlorophenoxy radicals (BCPRs). Distances are in angstroms. Gray sphere, C; white sphere, H; red sphere, O; blue sphere, Br; green sphere, Cl.

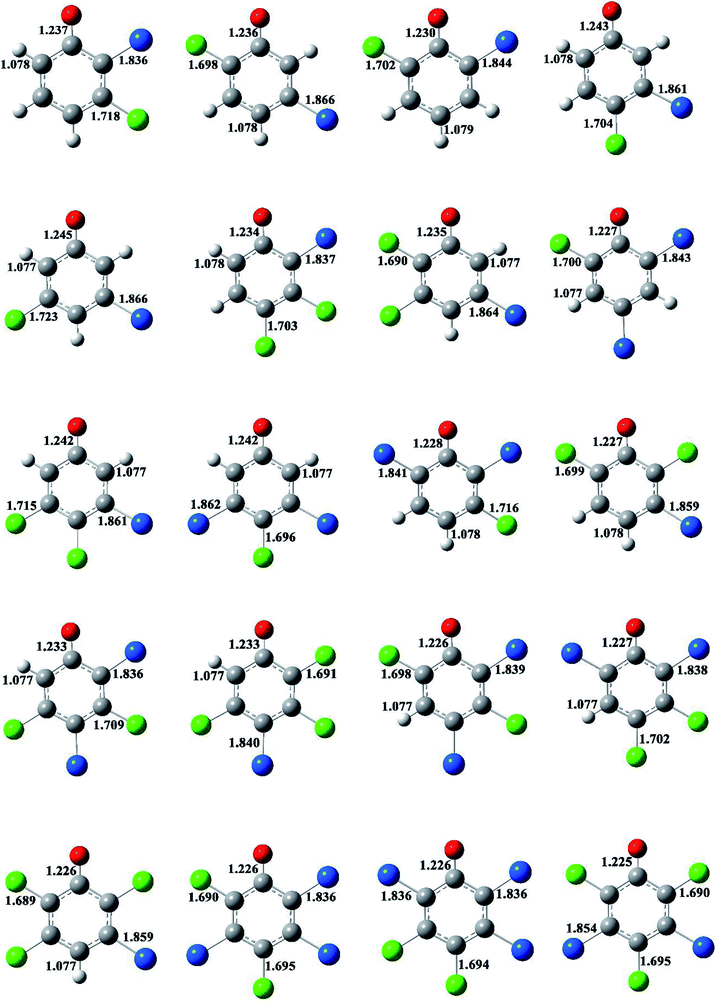
The formation of BCPRs from the reactions of the BCPs with H proceeds through a direct hydrogen abstraction mechanism. In the transition states in Fig. 2 and S3 (ESI†), the O–H bonds are broken, the C–O bonds are shortened, and the H–H bonds are formed. The lengths of the O–H bonds in the transition states are from 1.125 to 1.162 Å, which are stretched by 17% to 21% compared with the corresponding equilibrium value in the BCPs. The lengths of the C–O bonds in the transition states are from 1.313 to 1.334 Å, which are 1% shorter than the corresponding equilibrium value in the BCPs. The lengths of the H–H bonds in the transition states are from 0.952 to 0.993 Å, which are elongated by 29% to 35% compared with the bond value in a H₂ molecule.

The structures of the BCPRs are displayed in Fig. 3 and S4 (ESI†). The BCPR is delocalized, which is a hybrid of one oxygen-centered and three carbon-centered radicals (two ortho and one para carbon sites). In Fig. 3 and S4,† the C–O bond lengths in the BCPRs also vary with the degree and pattern of halogen substitutions, and they decrease with an increase in the number of the ortho halogen substitutions, regardless of whether they are ortho bromine or ortho chlorine substitutions. The C–O bond lengths are 1.242–1.245 Å, 1.232–1.237 Å, and 1.225–1.230 Å in BCPRs with zero, one, and two halogen substitutions, respectively. This may be caused by the effect of the induction of bromine or chlorine at the ortho position in the phenolic ring.

3.2 Energy analysis

The formation of BCPRs from the reactions of the BCPs with H proceeds through a direct hydrogen abstraction mechanism. All of the transition states have only one imaginary frequency, as shown in Table S2 (ESI†). The values of the imaginary frequencies are high, which means that the quantum tunneling contribution may play a crucial role in the rate constant calculation. The potential barriers and reaction heats calculated at the MPWB1K/6-31+G(d,p)//MPWB1K/6-311+G(3df,2p) level in this study are listed in Table 1. The potential barrier is the relative energy of the transition state with respect to the total energy of the separated reactants (the corresponding BCP and H). The reaction heat is the relative energy of the total energy of the products (the corresponding BCPRs and H₂) with respect to the total energy of the reactants. The formation of BCPRs from the reactions of BCPs with H is strongly exothermic. To be displayed more intuitively, the values in Table 1 are fitted in to histograms in Fig. 4 and 5, respectively. The maximum and minimum of potential barriers for reactions of given BCPs with the same degree and position of halogen substitution with H can be obtained from the histograms. To compare the effect of anti-conformers, the potential barriers and reaction heats for the reactions of the selected 38 anti-BCPs with H are listed in Table S3 (ESI†). Typically, transition states of anti-BCPs with H are difficult to optimize. Although the H–H group was pointed toward the C (hydrogen) atom in the input file, this would reverse to the C (halogen) atom after optimization. Thus, all the transition states of syn- and anti-conformers are performed using the same syn-structures. Tables 1, S2,† Fig. 4 and 5 also present our previous data calculated at the same level for reactions of BPs with H and CPs with H.^52,53

Table 1 Potential barrier ΔE₀ (in kcal mol⁻¹, 0 K, including ZPE correction) and reaction heat ΔH₀ (in kcal mol⁻¹, 0 K, including ZPE correction) for reactions of bromochlorophenols (BCPs) with H. For comparison, ΔE₀ and ΔH₀ of reactions of bromophenols (BPs)^a and chlorophenols (CPs)^b with H are also provided (^aReproduced with permission from R. Gao et al.⁵³ Copyright 2013, Elsevier. ^bReproduced with permission from Q. Z. Zhang et al.⁵² Copyright 2009, American Chemical Society)^a

BCP	ΔE0	ΔH0	BP	ΔE0^a	ΔH0^a	CP	ΔE0^b	ΔH0^b
a ΔE0, potential barrier (in kcal mol^−1, 0 K, including ZPE correction), the relative energy of the transition state with respect to the total energy of the separated reactants. Calculated at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level of theory. ΔH0, reaction heat (in kcal mol^−1, 0 K, including ZPE correction), the relative energy of total energy of the separated products with respect to the total energy of the separated reactants. Calculated at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level of theory.
2B-3CP	14.18	−11.11	2,3-DBP	14.49	−11.22	2,3-DCP	14.25	−11.22
3B-2CP	14.36	−11.31
2B-4CP	13.54	−13.04	2,4-DBP	13.58	−13.35	2,4-DCP	13.71	−12.81
4B-2CP	13.70	−12.99
2B-5CP	14.49	−11.04	2,5-DBP	14.44	−11.16	2,5-DCP	14.44	−11.01
3B-6CP	14.36	−11.15
2B-6CP	13.40	−13.10	2,6-DBP	13.33	−13.26	2,6-DCP	13.56	−12.99
3B-4CP	11.90	−14.17	3,4-DBP	12.01	−14.04	3,4-DCP	12.02	−13.89
4B-3CP	12.06	−13.91
3B-5CP	12.92	−11.85	3,5-DBP	12.99	−11.76	3,5-DCP	12.85	−11.90
2B-3,4DCP	13.99	−12.37	2,3,4-TBP	14.17	−12.56	2,3,4-TCP	13.88	−12.22
3B-2,4DCP	14.05	−12.70
4B-2,3DCP	14.02	−12.26
2,3DB-4CP	13.80	−12.50
2,4DB-3CP	14.03	−12.11
3,4DB-2CP	13.92	−12.38
2B-3,5DCP	14.84	−10.22	2,3,5-TBP	14.92	−10.43	2,3,5-TCP	14.59	−10.44
3B-2,5DCP	14.92	−10.52
3B-5,6DCP	14.87	−10.57
2,3DB-5CP	14.76	−10.34
2,5DB-3CP	14.77	−10.34
3,5DB-2CP	14.72	−10.56
2B-3,6DCP	14.01	−12.61	2,3,6-TBP	13.88	−12.82	2,3,6-TCP	13.89	−12.63
2B-5,6DCP	13.88	−12.67
3B-2,6DCP	13.90	−12.85
2,3DB-6CP	13.73	−12.79
2,5DB-6CP	13.73	−12.79
2,6DB-3CP	13.98	−12.44
2B-4,5DCP	13.81	−12.37	2,4,5-TBP	13.96	−12.56	2,4,5-TCP	13.88	−12.07
3B-4,6DCP	13.75	−12.63
4B-2,5DCP	14.00	−12.22
2,4DB-5CP	14.02	−12.09
2,5DB-4CP	13.77	−12.33
3,4DB-6CP	13.87	−12.28
2B-4,6DCP	13.07	−14.51	2,4,6-TBP	12.81	−14.64	2,4,6-TCP	13.17	−14.17
4B-2,6DCP	13.27	−14.40
2,4DB-6CP	13.07	−14.25
2,6DB-4CP	13.01	−14.45
3B-4,5DCP	12.35	−13.27	3,4,5-TBP	12.42	−13.14	3,4,5-TCP	12.45	−12.82
4B-3,5DCP	12.54	−12.81
3,4DB-5CP	12.49	−12.86
3,5DB-4CP	12.33	−13.21
2B-3,4,5TCP	14.41	−11.61	2,3,4,5-TeBP	14.21	−11.79	2,3,4,5-TeCP	14.23	−10.56
3B-2,4,5TCP	14.31	−11.77
3B-4,5,6TCP	14.44	−11.96
4B-2,3,5TCP	14.40	−11.45
2,3DB-4,5DCP	14.38	−11.50
2,4DB-3,5DCP	14.44	−11.14
2,5DB-3,4DCP	14.35	−10.90
3,4DB-2,5DCP	14.36	−11.46
3,4DB-5,6DCP	14.26	−11.52
3,5DB-2,4DCP	14.20	−11.79
2,3,4TB-5CP	14.33	−10.90
2,3,5TB-4CP	14.30	−11.09
2,4,5TB-3CP	14.34	−11.13
3,4,5TB-2CP	14.42	−11.43
2B-3,4,6TCP	13.36	−13.94	2,3,4,6-TeBP	13.60	−14.00	2,3,4,6-TeCP	13.60	−13.57
2B-4,5,6TCP	13.34	−14.08
3B-2,4,6TCP	13.48	−14.06
4B-2,3,6TCP	13.57	−13.74
2,3DB-4,6DCP	13.27	−14.03
2,4DB-3,6DCP	13.48	−13.55
2,4DB-5,6DCP	13.39	−13.89
2,5DB-4,6DCP	13.25	−14.18
2,6DB-3,4DCP	13.55	−13.87
3,4DB-2,6DCP	13.53	−13.76
2,3,4TB-6CP	13.51	−13.67
2,3,6TB-4CP	13.43	−13.96
2,4,5TB-6CP	13.29	−13.99
2,4,6TB-3CP	13.75	−13.43
2B-3,5,6TCP	14.28	−12.10	2,3,5,6-TeBP	14.11	−12.32	2,3,5,6-TeCP	14.15	−12.00
3B-2,5,6TCP	14.21	−12.39
2,3DB-5,6DCP	14.16	−12.22
2,5DB-3,6DCP	14.19	−12.27
2,6DB-3,5DCP	14.31	−12.17
3,5DB-2,6DCP	14.24	−12.35
2,3,5TB-6CP	14.22	−12.04
2,3,6TB-5CP	14.28	−11.89
2B-3,4,5,6TeCP	13.82	−13.41	PBP	13.68	−13.55	PCP	13.84	−13.17
3B-2,4,5,6TeCP	13.89	−13.53
4B-2,3,5,6TeCP	13.96	−13.22
2,3DB-4,5,6TCP	13.72	−13.43
2,4DB-3,5,6TCP	13.75	−13.12
2,5DB-3,4,6TCP	13.51	−13.50
2,6DB-3,4,5TCP	13.81	−13.37
3,4DB-2,5,6TCP	13.84	−13.42
3,5DB-2,4,6TCP	13.76	−13.62
2,3,4TB-5,6DCP	13.76	−13.14
2,3,5TB-4,6DCP	13.70	−13.51
2,3,6TB-4,5DCP	13.74	−13.48
2,4,5TB-3,6DCP	13.90	−13.30
2,4,6TB-3,5DCP	13.88	−12.96
3,4,5TB-2,6DCP	13.78	−13.46
2,3,4,5TeB-6CP	13.69	−13.22
2,3,4,6TeB-5CP	13.91	−13.07
2,3,5,6TeB-4CP	13.61	−13.54

---

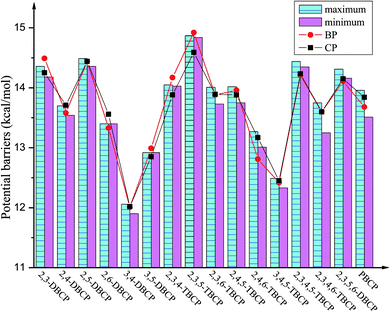Fig. 4 Histograms of maximum and minimum of potential barriers ΔE₀ (in kcal mol⁻¹, 0 K, including ZPE correction) for given bromochlorophenols (BCPs) with the same degree and position of halogen substitution abstracted by H. For comparison, ΔE₀ of reactions of bromophenols (BPs)^a and chlorophenols (CPs)^b with H are also provided (^aReproduced with permission from R. Gao et al.⁵³ Copyright 2013, Elsevier. ^bReproduced with permission from Q. Z. Zhang et al.⁵² Copyright 2009, American Chemical Society).

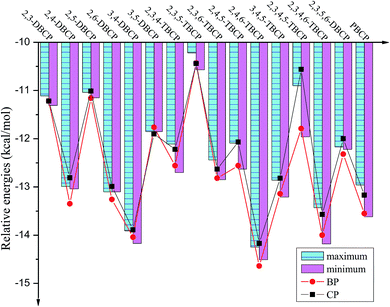Fig. 5 Histograms of maximum and minimum of reaction heats ΔH₀ (in kcal mol⁻¹, 0 K, including ZPE correction) for given bromochlorophenols (BCPs) with the same degree and position of halogen substitution abstracted by H. For comparison, ΔH₀ of reactions of bromophenols (BPs)^a and chlorophenols (CPs)^b with H are also provided (^aReproduced with permission from R. Gao et al.⁵³ Copyright 2013, Elsevier. ^bReproduced with permission from Q. Z. Zhang et al.⁵² Copyright 2009, American Chemical Society).

As presented in Table 1, Fig. 4 and 5, the potential barriers are significantly correlated with the halogen substitution at the ortho position in the BCPs. The potential barriers for phenoxyl-hydrogen abstraction from the ortho-halogen-substituted BCPs are consistently higher than those from the BCPs without ortho halogen substitution. Therefore, phenoxyl-hydrogen abstraction from the BCPs with intramolecular hydrogen bonding is more difficult than that from the BCPs without intramolecular hydrogen bonding. For example, the potential barriers of phenoxyl-hydrogen abstraction from 3B-4CP, 4B-3CP, 3B-5CP, 3B-4,5DCP, 4B-3,5DCP, 3,4DB-5CP, and 3,5DB-4CP are within the range of 11.90–12.91 kcal mol⁻¹, whereas the values for abstraction from other structural conformer BCPs are within the range of 13.01–14.92 kcal mol⁻¹. The halogen substitution at the ortho position reduces the reactivity of the O–H bonds in the BCPs. This may be caused by the formation of intramolecular hydrogen bonding, which appears to stabilize the BCPs with ortho halogen substitution and increases the potential barriers. A similar result has also been observed in our previous studies of BC and CPs with H.^52,53

As clearly demonstrated in Table 1, for a given BCP with the same degree and position of halogen substitution, the values for the potential barriers and reaction heat are close, regardless of the specific position or number of bromine and chlorine atoms. The different Br and Cl arrangements in BCPs with a given halogen substitution induce a slight variation. Fig. 4 and 5 demonstrate that the range between maximum and minimum of potential barriers and reaction heats for given bromochlorophenols (BCPs) with the same degree and position of halogen substitution abstracted by H is within 1.0 kcal mol⁻¹, even mostly within 0.6 kcal mol⁻¹. For example, the potential barriers of 2B-4,5DCP, 3B-4,6DCP, 4B-2,5DCP, 2,4DB-5CP, 2,5DB-4CP, and 3,4DB-6CP are within the range of 13.75–14.02 kcal mol⁻¹, whereas the corresponding reaction heat values are within the range of −12.63 to −12.09 kcal mol⁻¹. Similar result can be obtained by analyzing the 38 selected anti-conformers in Table S3 of ESI.† For example, the potential barriers of 2B-4,5DCP^anti, 3B-4,6DCP^anti, 4B-2,5DCP^anti, 2,4DB-5CP^anti, 2,5DB-4CP^anti, and 3,4DB-6CP^anti are within the range of 10.43–10.84 kcal mol⁻¹, whereas the corresponding reaction heat values are within the range of −15.75 to −15.37 kcal mol⁻¹. This indicates that the relative reactivity of the O–H bonds in BCPs appears to be assisted and dominated by the total degree and pattern of halogenation, but it does not appear to be determined by the distribution of the bromine and chlorine atoms. When substituted by Br or Cl in the same position of the phenolic ring, the Br or Cl steric repulsion effect and the inductive effect on the relative strength of the O–H bonds are similar. Comparison of syn- and anti-conformer values shows that although the syn-BCPs are more stable than the anti-BCPs, the reactions of anti-BCPs with H can occur via lower potential barriers and more exothermic than those of syn-BCPs with H. So, the anti-conformers also make a significant contribution to the formation of BCPRs.

Comparing the values derived for reactions of the BCPs with H with those derived for reactions of the corresponding BPs and CPs with H is necessary.^52,53 As indicated in Tables 1 and S3 (ESI†), for given BCPs with the same halogen substitution, the values of the potential barriers and reaction heats derived for the reactions of the BCPs with H are close to the values derived for the reactions of completely Br-substituted BPs with H or the reactions of completely Cl-substituted CPs with H, which have the same degree and position of Br or Cl substitution.^52,53 This conclusion can be vividly displayed in Fig. 4 and 5 by the trend consistency between histogram of BCPs and line graph of BPs and CPs. For example, the potential barriers and reaction heats for phenoxyl-hydrogen abstraction from 2B-3,5DCP, 3B-2,5DCP, 2,3DB-5CP, 2,5DB-3CP, 3,5DB-2CP, and 3B-5,6DCP by H are within the range of 14.72 to 14.92 and −10.57 to −10.22 kcal mol⁻¹, whereas the values for abstraction from 2,3,5-TBP by H are 14.92 and −10.43 kcal mol⁻¹ and those for abstraction from 2,3,5-TCP by H are 14.59 and −10.44 kcal mol⁻¹.^52,53 Similarly, by analyzing the anti-conformers, the potential barriers and reaction heats for phenoxyl-hydrogen abstraction from 2B-3,5DCP^anti, 3B-2,5DCP^anti, 2,3DB-5CP^anti, 2,5DB-3CP^anti, 3,5DB-2CP^anti, and 3B-5,6DCP^anti by H are within the range of 11.08 to 11.49 and −14.02 to −13.87 kcal mol⁻¹, whereas the values for abstraction from 2,3,5-TBP^anti by H are 11.27 and −14.08 kcal mol⁻¹ and those for abstraction from 2,3,5-TCP^anti by H are 11.16 and −13.87 kcal mol⁻¹.^52,53 This indicates that the mixture of bromine and chlorine substitutions of the BCPs would not greatly change the strength of the O–H bonds, and the reactions of the BCPs with H can occur analogously to those of BPs and CPs with H.

The O–H bonds in BCPs can signify a direct fission. The O–H bond dissociation energies, D₀(O–H), at the MPWB1K/6-311+G(3df,2p)//and MPWB1K/6-31+G(d,p) level were calculated to further study the relative strength of the O–H bonds in the BCPs. The values of the 96 BCPs are listed in Table S2 (ESI†) and compared with the BP and CP data derived in our previous studies.^52,53 As presented in Table S2 (ESI†), several conclusions could be obtained that agree with the preceding energy analysis. First, the halogen substitution at the ortho position appears to increase the strength of the O–H bonds in the BCPs. For example, the D₀(O–H) values of 2B-3CP, 3B-2CP, 2B-4CP, 4B-2CP, 2B-5CP, 3B-6CP, and 2B-6CP are higher than those of 3B-4CP and 4B-3CP. However, the O–H bond dissociation energies in the BCPs with ortho substitutions are not consistently higher than those in the BCPs without ortho substitution. For example, the D₀(O–H) values of 3B-2,6DCP, 2B-4,6DCP, 4B-2,6DCP, 2,4DB-6CP, and 2,6DB-4CP are lower than that of 4B-3,5DCP. The intramolecular hydrogen bonding in the ortho-substituted BCPs, as well as the steric effect and inductive effect, may influence the relative strength of the O–H bonds in the BCPs. Second, BCPs with the same degree and position of halogen substitution have similar D₀(O–H) values, with the deviation being within 0.05–1.06 kcal mol⁻¹. For example, the D₀(O–H) values of 2B-3,5DCP, 3B-2,5DCP, 3B-5,6DCP, 2,3DB-5CP, 2,5DB-3CP, and 3,5DB-2CP are within the range of 87.36–87.71 kcal mol⁻¹. Third, comparing the values of the BCPs with those of the corresponding BPs and CPs with the same halogenation degree and pattern reveals that the D₀(O–H) values of the BCPs are close to those of the corresponding BPs and CPs with complete Br and Cl substitution, respectively. For example, the D₀(O–H) values of 2B-3,4DCP, 3B-2,4DCP, 4B-2,3DCP, 2,3DB-4CP, 2,4DB-3CP, and 3,4DB-2CP are within the range of 85.23–85.82 kcal mol⁻¹, whereas the D₀(O–H) values of 2,3,4-TBP and 2,3,4-TCP are 85.71 and 85.37 kcal mol⁻¹, respectively.

3.3 Rate constant calculation

The rate constants for the abstraction reactions of BCPs with H were calculated using CVT/SCT method over a wide temperature range of 600–1200 K on the basis of the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level; the results are shown in Table S5 (ESI†). The values of 38 selected anti-conformers are listed in Table S6 (ESI†). The temperature range covers the possible formation temperature of PBCDD/Fs under pyrolysis or combustion conditions. The CVT/SCT method has been successfully performed for abstraction reactions of BPs and CPs with H atom,^52,53 as well as for the elementary reactions involved in PBCDD/F formation from radical–radical cross-condensation of BPRs with CPRs.⁴⁵

The halogen substitution pattern of phenol strongly affects the CVT/SCT rate constants. Generally, at a given temperature, the CVT/SCT rate constants derived for phenoxyl-hydrogen abstraction from the ortho halogen-substituted BCPs are smaller than those derived for abstraction from the BCPs without ortho halogen substitution, for a given number of halogen substitutions. For example, at 1000 K, the CVT/SCT rate constants are 3.2 × 10⁻¹⁴, 1.2 × 10⁻¹⁴, 3.8 × 10⁻¹⁴, 1.6 × 10⁻¹⁴, 2.1 × 10⁻¹⁴, 2.1 × 10⁻¹⁵, and 1.8 × 10⁻¹⁴ cm³ per molecule per s for reactions of 2B-3CP, 3B-2CP, 2B-4CP, 4B-2CP, 2B-5CP, 3B-6CP, and 2B-6CP with H, respectively; the rate constants are 5.7 × 10⁻¹⁴, 1.4 × 10⁻¹³, and 3.8 × 10⁻¹⁴ cm³ per molecule per s for reactions of 3B-4CP, 4B-3CP, and 3B-5CP with H, respectively. Similarly, at 800 K, the CVT/SCT rate constants are 1.7 × 10⁻¹⁵, 2.4 × 10⁻¹⁵, 6.6 × 10⁻¹⁶, 1.7 × 10⁻¹⁵, and 8.8 × 10⁻¹⁶ per molecule per s for reactions of 2,3,4-TCP, 2,3,5-TCP, 2,3,6-TCP, 2,4,5-TCP, and 2,4,6-TCP with H, respectively; the rate constant is 4.0 × 10⁻¹⁵ cm³ per molecule per s for the reaction of 3,4,5-TCP with H. This finding perfectly matches the finding of the preceding structural and thermodynamic analysis that the halogen substitution at the ortho position of the BCPs increases the strength of the O–H bonds and its reactivity.

For the given halogen-substituted BCPs, regardless of the specific distribution of bromine and chlorine atoms, the CVT/SCT rate constants for bromochlorophenoxyl-hydrogen abstraction by H are similar throughout studied temperature range. For example, at 1000 K, the CVT/SCT rate constants are 1.9 × 10⁻¹⁴, 1.6 × 10⁻¹⁴, 7.3 × 10⁻¹⁵, 2.9 × 10⁻¹⁴, 1.7 × 10⁻¹⁴, and 2.2 × 10⁻¹⁴ cm³ per molecule per s for reactions of 2B-3,5DCP, 3B-2,5DCP, 2,3DB-5CP, 2,5DB-3CP, 3,5DB-2CP, and 3B-5,6DCP with H, respectively. Similarly, at 800 K, the CVT/SCT rate constants are 2.0 × 10⁻¹⁴, 2.1 × 10⁻¹⁴, 1.8 × 10⁻¹⁴, and 1.5 × 10⁻¹⁴ cm³ per molecule per s for reactions of 3B-4,5DCP, 4B-3,5DCP, 3,4DB-5CP, and 3,5DB-4CP with H, respectively. For the anti-conformers of Table S6 (ESI†), at 1000 K, the CVT/SCT rate constants are within the range of 1.9 × 10⁻¹⁴ to 1.5 × 10⁻¹³ cm³ per molecule per s for reactions of 2B-3,5DCP^anti, 3B-2,5DCP^anti, 2,3DB-5CP^anti, 2,5DB-3CP^anti, 3,5DB-2CP^anti, and 3B-5,6DCP^anti with H. This is consistent with thermodynamic analysis: the different Br and Cl arrangements in BCPs with a given halogen substitution affect the strength of the O–H bonds to a small extent.

Comparing the rate constants for the reactions of the BCPs with H with the rate constants for phenoxyl-hydrogen abstraction from the corresponding BPs and CPs with the same halogenation degree and pattern reveals that the compared constants are close at a given temperature.^52,53 For example, at 1000 K, the CVT/SCT rate constants are 3.8 × 10⁻¹⁴, 2.7 × 10⁻¹⁴, 5.7 × 10⁻¹⁴, 3.8 × 10⁻¹⁴, 4.1 × 10⁻¹⁴, and 5.8 × 10⁻¹⁴ cm³ per molecule per s for reactions of 2B-3,4DCP, 3B-2,4DCP, 4B-2,3DCP, 2,3DB-4CP, 2,4DB-3CP, and 3,4DB-2CP with H, respectively; the rate constants are 5.5 × 10⁻¹⁴ and 1.1 × 10⁻¹⁴ cm³ per molecule per s for reactions of 2,3,4-TBP and 2,3,4-TCP with H. Similarly, at 800 K, the CVT/SCT rate constants are 2.0 × 10⁻¹⁴, 2.1 × 10⁻¹⁴, 1.8 × 10⁻¹⁴, and 1.5 × 10⁻¹⁴ cm³ per molecule per s for reactions of 3B-4,5DCP, 4B-3,5DCP, 3,4DB-5CP, and 3,5DB-4CP with H, respectively; the rate constants are 4.0 × 10⁻¹⁵ and 3.4 × 10⁻¹⁶ cm³ per molecule per s for reactions of 3,4,5-TCP and 3,4,5-TBP with H, respectively. This reconfirms the finding of the thermodynamic analysis that the reactivity of the mixed bromine- and chlorine-substituted BCPs with H are similar to those of completely bromine- and chlorine-substituted BPs and CPs with H.

To be applied more effectively, the CVT/SCT rate constants were fitted, and Arrhenius formulas are presented in Tables 2 and S4 (ESI†) for BCPRs formation from the abstraction reactions of the BCPs abstracted by H atom. The pre-exponential factors and activation energies can be obtained from these Arrhenius formulas.

Table 2 Arrhenius formulas for reaction of the bromochlorophenols (BCPs) with H over the temperature range of 600–1200 K (cm³ per molecule per s)

Reactions	Arrhenius formulas
2B-3CP + H → 2B-3CPR + H2	k(T) = (7.1 × 10^−12)exp(−4272.6/T)
3B-2CP + H → 3B-2CPR + H2	k(T) = (2.4 × 10^−12)exp(−4203.7/T)
2B-4CP + H → 2B-4CPR + H2	k(T) = (5.6 × 10^−12)exp(−3948.4/T)
4B-2CP + H → 4B-2CPR + H2	k(T) = (2.7 × 10^−12)exp(−4052.7/T)
2B-5CP + H → 2B-5CPR + H2	k(T) = (5.7 × 10^−12)exp(−4431.6/T)
3B-6CP + H → 3B-6CPR + H2	k(T) = (3.2 × 10^−13)exp(−3969.9/T)
2B-6CP + H → 2B-6CPR + H2	k(T) = (2.1 × 10^−12)exp(−3764.8/T)
3B-4CP + H → 3B-4CPR + H2	k(T) = (1.6 × 10^−11)exp(−4134.6/T)
4B-3CP + H → 4B-3CPR + H2	k(T) = (1.2 × 10^−11)exp(−3488.7/T)
3B-5CP + H → 3B-5CPR + H2	k(T) = (3.1 × 10^−12)exp(−3476.0/T)
2B-3,4DCP + H → 2B-3,4DCPR + H2	k(T) = (6.6 × 10^−12)exp(−4079.2/T)
3B-2,4DCP + H → 3B-2,4DCPR + H2	k(T) = (3.8 × 10^−12)exp(−3929.6/T)
4B-2,3DCP + H → 4B-2,3DCPR + H2	k(T) = (6.4 × 10^−12)exp(−3739.4/T)
2,3DB-4CP + H → 2,3DB-4CPR + H2	k(T) = (5.3 × 10^−12)exp(−3889.4/T)
2,4DB-3CP + H → 2,4DB-3CPR + H2	k(T) = (7.3 × 10^−12)exp(−4088.9/T)
3,4DB-2CP + H → 3,4DB-2CPR + H2	k(T) = (8.3 × 10^−12)exp(−3919.9/T)
2B-3,5DCP + H → 2B-3,5DCPR + H2	k(T) = (5.5 × 10^−12)exp(−4495.7/T)
3B-2,5DCP + H → 3B-2,5DCPR + H2	k(T) = (4.9 × 10^−12)exp(−4522.7/T)
3B-5,6DCP + H → 3B-5,6DCPR + H2	k(T) = (4.3 × 10^−12)exp(−4165.0/T)
2,3DB-5CP + H → 2,3DB-5CPR + H2	k(T) = (1.1 × 10^−12)exp(−3953.8/T)
2,5DB-3CP + H → 2,5DB-3CPR + H2	k(T) = (5.6 × 10^−12)exp(−4179.6/T)
3,5DB-2CP + H → 3,5DB-2CPR + H2	k(T) = (4.8 × 10^−12)exp(−4481.2/T)
2B-3,6DCP + H → 2B-3,6DCPR + H2	k(T) = (6.4 × 10^−12)exp(−3903.5/T)
2B-5,6DCP + H → 2B-5,6DCPR + H2	k(T) = (7.4 × 10^−12)exp(−3979.8/T)
3B-2,6DCP + H → 3B-2,6DCPR + H2	k(T) = (8.4 × 10^−12)exp(−3920.6/T)
2,3DB-6CP + H → 2,3DB-6CPR + H2	k(T) = (9.2 × 10^−12)exp(−3953.7/T)
2,5DB-6CP + H → 2,5DB-6CPR + H2	k(T) = (1.1 × 10^−11)exp(−3942.6/T)
2,6DB-3CP + H → 2,6DB-3CPR + H2	k(T) = (6.9 × 10^−12)exp(−3950.7/T)
2B-4,5DCP + H → 2B-4,5DCPR + H2	k(T) = (2.8 × 10^−12)exp(−3903.2/T)
3B-4,6DCP + H → 3B-4,6DCPR + H2	k(T) = (5.7 × 10^−12)exp(−3924.5/T)
4B-2,5DCP + H → 4B-2,5DCPR + H2	k(T) = (5.6 × 10^−12)exp(−3852.9/T)
2,4DB-5CP + H → 2,4DB-5CPR + H2	k(T) = (7.7 × 10^−13)exp(−3554.6/T)
2,5DB-4CP + H → 2,5DB-4CPR + H2	k(T) = (2.1 × 10^−13)exp(−3993.6/T)
3,4DB-6CP + H → 3,4DB-6CPR + H2	k(T) = (8.4 × 10^−12)exp(−4153.5/T)
2B-4,6DCP + H → 2B-4,6DCPR + H2	k(T) = (6.2 × 10^−12)exp(−3685.0/T)
4B-2,6DCP + H → 4B-2,6DCPR + H2	k(T) = (6.9 × 10^−12)exp(−3696.2/T)
2,4DB-6CP + H → 2,4DB-6CPR + H2	k(T) = (3.3 × 10^−13)exp(−3700.0/T)
2,6DB-4CP + H → 2,6DB-4CPR + H2	k(T) = (5.6 × 10^−13)exp(−3985.6/T)
3B-4,5DCP + H → 3B-4,5DCPR + H2	k(T) = (1.4 × 10^−11)exp(−3798.8/T)
4B-3,5DCP + H → 4B-3,5DCPR + H2	k(T) = (1.2 × 10^−11)exp(−3638.0/T)
3,4DB-5CP + H → 3,4DB-5CPR + H2	k(T) = (1.4 × 10^−11)exp(−3840.0/T)
3,5DB-4CP + H → 3,5DB-4CPR + H2	k(T) = (8.0 × 10^−12)exp(−3623.0/T)
2B-3,4,5TCP + H → 2B-3,4,5TCPR + H2	k(T) = (6.7 × 10^−12)exp(−4192.2/T)
3B-2,4,5TCP + H → 3B-2,4,5TCPR + H2	k(T) = (5.6 × 10^−12)exp(−3766.5/T)
3B-4,5,6TCP + H → 3B-4,5,6TCPR + H2	k(T) = (4.3 × 10^−12)exp(−4008.1/T)
4B-2,3,5TCP + H → 4B-2,3,5TCPR + H2	k(T) = (6.6 × 10^−12)exp(−4098.6/T)
2,3DB-4,5DCP + H → 2,3DB-4,5DCPR + H2	k(T) = (6.4 × 10^−12)exp(−4068.0/T)
2,4DB-3,5DCP + H → 2,4DB-3,5DCPR + H2	k(T) = (6.5 × 10^−12)exp(−4084.2/T)
2,5DB-3,4DCP + H → 2,5DB-3,4DCPR + H2	k(T) = (6.5 × 10^−12)exp(−4090.5/T)
3,4DB-2,5DCP + H → 3,4DB-2,5DCPR + H2	k(T) = (6.8 × 10^−12)exp(−4378.6/T)
3,4DB-5,6DCP + H → 3,4DB-5,6DCPR + H2	k(T) = (7.4 × 10^−12)exp(−4164.9/T)
3,5DB-2,4DCP + H → 3,5DB-2,4DCPR + H2	k(T) = (1.2 × 10^−12)exp(−3712.2/T)
2,3,4TB-5CP + H → 2,3,4TB-5CPR + H2	k(T) = (8.0 × 10^−12)exp(−4413.8/T)
2,3,5TB-4CP + H → 2,3,5TB-4CPR + H2	k(T) = (5.5 × 10^−12)exp(−4308.8/T)
2,4,5TB-3CP + H → 2,4,5TB-3CPR + H2	k(T) = (6.2 × 10^−12)exp(−3831.9/T)
3,4,5TB-2CP + H → 3,4,5TB-2CPR + H2	k(T) = (5.5 × 10^−12)exp(−4363.5/T)
2B-3,4,6TCP + H → 2B-3,4,6TCPR + H2	k(T) = (1.1 × 10^−11)exp(−3939.8/T)
2B-4,5,6TCP + H → 2B-4,5,6TCPR + H2	k(T) = (1.0 × 10^−11)exp(−4116.6/T)
3B-2,4,6TCP + H → 3B-2,4,6TCPR + H2	k(T) = (8.6 × 10^−12)exp(−3767.9/T)
4B-2,3,6TCP + H → 4B-2,3,6TCPR + H2	k(T) = (8.4 × 10^−12)exp(−3877.8/T)
2,3DB-4,6DCP + H → 2,3DB-4,6DCPR + H2	k(T) = (9.7 × 10^−12)exp(−3818.3/T)
2,4DB-3,6DCP + H → 2,4DB-3,6DCPR + H2	k(T) = (3.2 × 10^−12)exp(−3439.2/T)
2,4DB-5,6DCP + H → 2,4DB-5,6DCPR + H2	k(T) = (7.2 × 10^−13)exp(−3832.8/T)
2,5DB-4,6DCP + H → 2,5DB-4,6DCPR + H2	k(T) = (2.6 × 10^−12)exp(−3976.0/T)
2,6DB-3,4DCP + H → 2,6DB-3,4DCPR + H2	k(T) = (1.7 × 10^−11)exp(−4124.5/T)
3,4DB-2,6DCP + H → 3,4DB-2,6DCPR + H2	k(T) = (8.5 × 10^−12)exp(−3868.9/T)
2,3,4TB-6CP + H → 2,3,4TB-6CPR + H2	k(T) = (1.1 × 10^−11)exp(−4086.0/T)
2,3,6TB-4CP + H → 2,3,6TB-4CPR + H2	k(T) = (1.5 × 10^−12)exp(−3980.6/T)
2,4,5TB-6CP + H → 2,4,5TB-6CPR + H2	k(T) = (8.6 × 10^−12)exp(−3822.3/T)
2,4,6TB-3CP + H → 2,4,6TB-3CPR + H2	k(T) = (1.1 × 10^−11)exp(−4185.4/T)
2B-3,5,6TCP + H → 2B-3,5,6TCPR + H2	k(T) = (7.9 × 10^−12)exp(−4174.4/T)
3B-2,5,6TCP + H → 3B-2,5,6TCPR + H2	k(T) = (7.5 × 10^−13)exp(−4043.1/T)
2,3DB-5,6DCP + H → 2,3DB-5,6DCPR + H2	k(T) = (9.2 × 10^−12)exp(−4085.1/T)
2,5DB-3,6DCP + H → 2,5DB-3,6DCPR + H2	k(T) = (8.1 × 10^−12)exp(−4173.8/T)
2,6DB-3,5DCP + H → 2,6DB-3,5DCPR + H2	k(T) = (3.3 × 10^−11)exp(−4330.4/T)
3,5DB-2,6DCP + H → 3,5DB-2,6DCPR + H2	k(T) = (6.4 × 10^−12)exp(−3994.2/T)
2,3,5TB-6CP + H → 2,3,5TB-6CPR + H2	k(T) = (1.4 × 10^−12)exp(−4179.9/T)
2,3,6TB-5CP + H → 2,3,6TB-5CPR + H2	k(T) = (2.0 × 10^−11)exp(−4099.4/T)
2B-3,4,5,6TeCP + H → 2B-3,4,5,6TeCPR + H2	k(T) = (8.2 × 10^−13)exp(−4015.8/T)
3B-2,4,5,6TeCP + H → 3B-2,4,5,6TeCPR + H2	k(T) = (1.1 × 10^−12)exp(−4406.0/T)
4B-2,3,5,6TeCP + H → 4B-2,3,5,6TeCPR + H2	k(T) = (6.3 × 10^−12)exp(−3896.2/T)
2,3DB-4,5,6TCP + H → 2,3DB-4,5,6TCPR + H2	k(T) = (9.7 × 10^−12)exp(−3848.7/T)
2,4DB-3,5,6TCP + H → 2,4DB-3,5,6TCPR + H2	k(T) = (9.5 × 10^−12)exp(−3966.9/T)
2,5DB-3,4,6TCP + H → 2,5DB-3,4,6TCPR + H2	k(T) = (1.6 × 10^−12)exp(−3920.4/T)
2,6DB-3,4,5TCP + H → 2,6DB-3,4,5TCPR + H2	k(T) = (2.4 × 10^−11)exp(−4200.8/T)
3,4DB-2,5,6TCP + H → 3,4DB-2,5,6TCPR + H2	k(T) = (2.4 × 10^−12)exp(−4197.1/T)
3,5DB-2,4,6TCP + H → 3,5DB-2,4,6TCPR + H2	k(T) = (6.1 × 10^−12)exp(−3858.4/T)
2,3,4TB-5,6DCP + H → 2,3,4TB-5,6DCPR + H2	k(T) = (7.6 × 10^−12)exp(−3900.3/T)
2,3,5TB-4,6DCP + H → 2,3,5TB-4,6DCPR + H2	k(T) = (6.3 × 10^−12)exp(−3895.8/T)
2,3,6TB-4,5DCP + H → 2,3,6TB-4,5DCPR + H2	k(T) = (2.9 × 10^−12)exp(−4272.0/T)
2,4,5TB-3,6DCP + H → 2,4,5TB-3,6DCPR + H2	k(T) = (7.3 × 10^−12)exp(−3956.6/T)
2,4,6TB-3,5DCP + H → 2,4,6TB-3,5DCPR + H2	k(T) = (2.6 × 10^−12)exp(−4344.6/T)
3,4,5TB-2,6DCP + H → 3,4,5TB-2,6DCPR + H2	k(T) = (7.7 × 10^−12)exp(−4004.0/T)
2,3,4,5TeB-6CP + H → 2,3,4,5TeB-6CPR + H2	k(T) = (3.7 × 10^−12)exp(−4133.0/T)
2,3,4,6TeB-5CP + H → 2,3,4,6TeB-5CPR + H2	k(T) = (1.0 × 10^−11)exp(−4090.6/T)
2,3,5,6TeB-4CP + H → 2,3,5,6TeB-4CPR + H2	k(T) = (2.5 × 10^−11)exp(−4256.8/T)

---

4. Conclusion

This study conducted structural, frequency, and energy analyses for the formation of BCPRs from abstraction reactions of 96 mixed brominated and chlorinated phenol congeners with H at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level. Rate constants for each abstraction reaction were computed using CVT/SCT method contribution by employing the POLYRATE 9.7 program. The relevant values of the bond lengths, potential barriers, reaction heat, and reaction rate constants derived in this study were compared with those derived for reactions of BPs and CPs with H. Several conclusions can be drawn:

(1) Halogen substitution at the ortho position increases the stability of the BCPs and reduces the reactivity of O–H bonds.

(2) The different Br and Cl arrangements in BCPs with a given halogen substitution affect the strength of the O–H bond to a small extent.

(3) The reactivity levels of the mixed bromine- and chlorine-substituted BCPs with H are similar to those of completely bromine- and chlorine-substituted BPs and CPs with H.

In consideration of the importance of heterogeneous metal mediated mechanism of dioxin formation, further study would be focused on the adsorption of BCPs and subsequent reactions on transition metals, as well as their oxides and chlorides in the temperature range of 200−600 °C, which is expected to compare with the homogeneous gas-phase mechanism and support detailed parameters of the environmental dioxin controlling and prediction models.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (project No. 21407096, 21337001), the Fundamental Research Funds of Shandong University (project No. 2017JC033, 2016WLJH51), and the State Key Laboratory of Environmental Chemistry and Ecotoxicology, Research Center for Eco-Environmental Sciences, Chinese Academy of Sciences (project No. KF2014–16). The authors thank Professor Donald G. Truhlar for providing the POLYRATE 9.7 program.

References

1. L. W. Weber and H. Greim, J. Toxicol. Environ. Health, 1997, 50, 195–215.
2. A. Sepulveda, M. Schluep, F. G. Renaud, M. Streicher, R. Kuehr, C. Hageluken and A. C. Gerecke, Environ. Impact Assess. Rev., 2010, 30, 28–41.
3. F. Samara, B. Wyrzykowska, D. Tabor, D. Touati and B. K. Gullett, Environ. Int., 2010, 36, 247–253.
4. Z. W. Tang, Q. F. Huang and Y. F. Yang, Environ. Sci. Technol., 2013, 47, 5520–5521.
5. S. Watanabe and S. Sakai, Organohalogen Compd., 2001, 52, 529–549.
6. R. Weber and B. Kuch, Environ. Int., 2003, 29, 699–710.
7. L. Q. Huang, H. Y. Tong and J. R. Donnelly, Anal. Chem., 1992, 64, 1034–1040.
8. W. Chatkittikunwong and C. S. Creaser, Chemosphere, 1994, 29, 559–566.
9. B. Du, M. H. Zheng, Y. R. Huang, A. M. Liu, H. H. Tian, L. L. Li, N. Li, T. Ba, Y. W. Li, S. P. Dong, W. B. Liu and G. J. Su, Environ. Sci. Technol., 2010, 44, 5818–5823.
10. M. Zennegg, X. Yu, M. H. Wong and R. Weber, Ewasteguide Info., 2009, 71, 2263–2267.
11. S. Gunilla and M. Stellan, Environ. Sci. Technol., 2004, 38, 825–830.
12. K. Kawamoto, J. Hazard. Mater., 2009, 168, 641–648.
13. R. Weber, B. Kuch, T. Ohno and T. Sakurai, Organohalogen Compd., 2002, 56, 181–184.
14. G. Soderstrom and S. Marklund, Environ. Sci. Technol., 2002, 36, 1959–1964.
15. G. Soderstrom and S. Marklund, Environ. Sci. Technol., 2004, 38, 825–830.
16. N. Balasundram, K. Sundram and S. Samman, Food Chem., 2006, 99, 191–203.
17. L. C. Felton and C. B. McLaughlin, J. Org. Chem., 1947, 12, 298–302.
18. P. M. Armenante, D. Kafkewitz, G. A. Lewandowski and C. J. Jou, Water Res., 1999, 33, 681–692.
19. J. Swietoslawski, A. Silowiecki, A. Ratajczak, B. Nocon and B. Z. Less, US4112242A, 1987.
20. W. Schaefer and K. Ballschmiter, Chemosphere, 1986, 15, 755–763.
21. N. V. Heeb, I. S. Dolezal, T. Buhrer, P. Mattrel and M. Wolfensberger, Chemosphere, 1995, 31, 3033–3041.
22. W. J. Sim, S. H. Lee, I. S. Lee, S. D. Choi and J. E. Oh, Chemosphere, 2009, 77, 552–558.
23. C. Leuenberger, W. Giger, R. Coney, J. W. Graydon and E. K. Molnar, Water Res., 1985, 19, 885–894.
24. V. K. Gupta, I. Ali and V. K. Saini, Environ. Sci. Technol., 2004, 38, 4012–4018.
25. D. Schuler and J. Jager, Chemosphere, 2004, 54, 49–59.
26. M. Castillo, D. Puig and D. Barcelo, J. Chromatogr. A, 1997, 778, 301–311.
27. L. Hovander, T. Malmberg, M. Athanasiadou, I. Athanassiadis, S. Rahm, A. Bergman and E. K. Wehler, Arch. Environ. Contam. Toxicol., 2002, 42, 105–117.
28. M. Altarawneh, B. Z. Dlugogorski, E. M. Kennedy and J. C. Mackie, J. Phys. Chem. A, 2010, 114, 1060–1067.
29. K. Chen, D. Wojtalewicz, M. Altarawneh, J. C. Mackie, E. M. Kennedy and B. Z. Dlugogorski, Proc. Combust. Inst., 2011, 33, 701–708.
30. U. Cosentino and G. Moro, Theor. Chem. Acc., 2012, 131, 1–12.
31. S. L. Summoogum, D. Wojtalewicz, M. Altarawneh, J. C. Mackie, E. M. Kennedy and B. Z. Dlugogorski, Proc. Combust. Inst., 2013, 34, 3499–3507.
32. M. Altarawneh and B. Z. Dlugogorski, Chemosphere, 2015, 119, 1048–1053.
33. E. R. Altwicker, Chemosphere, 1996, 33, 1897–1904.
34. S. Nganai, S. Lomnicki and B. Dellinger, Environ. Sci. Technol., 2009, 43, 368–373.
35. S. Lomnicki and B. Dellinger, J. Phys. Chem. A, 2003, 107, 4387–4395.
36. M. Altarawneh, B. Z. Dlugogorski, E. M. Kennedy and J. C. Mackie, Prog. Energy Combust. Sci., 2009, 35, 245–274.
37. S. Mosallanejad, B. Z. Dlugogorski, E. M. Kennedy, M. Stockenhuber, S. M. Lomnicki, N. W. Assaf and M. Altarawneh, Environ. Sci. Technol., 2016, 50, 1412–1418.
38. R. Luijk, D. Akkerman, P. Slot, K. Olie and F. Kepteijn, Environ. Sci. Technol., 1994, 28, 312–321.
39. L. C. Dickson, D. Lenoir and O. Hutzinger, Environ. Sci. Technol., 1992, 26, 1822–1828.
40. R. Louw and S. I. Ahonkhai, Chemosphere, 2002, 46, 1273–1278.
41. M. Altarawneh, B. Z. Dlugogorski, E. M. Kennedy and J. C. Mackie, J. Phys. Chem. A, 2007, 111, 2563–2573.
42. Q. Z. Zhang, S. Q. Li, X. H. Qu, X. Y. Shi and W. X. Wang, Environ. Sci. Technol., 2008, 42, 7301–7308.
43. F. Xu, W. N. Yu, Q. Zhou, R. Gao, X. Y. Sun, Q. Z. Zhang and W. X. Wang, Environ. Sci. Technol., 2011, 45, 643–650.
44. W. N. Yu, J. T. Hu, F. Xu, X. Y. Sun, R. Gao, Q. Z. Zhang and W. X. Wang, Environ. Sci. Technol., 2011, 45, 1917–1925.
45. X. L. Shi, W. N. Yu, F. Xu, Q. Z. Zhang, J. T. Hu and W. X. Wang, J. Hazard. Mater., 2015, 295, 104–111.
46. A. Saeed, M. Altarawneh and B. Z. Dlugogorski, Chemosphere, 2015, 137, 149–156.
47. C. S. Evans and B. Dellinger, Environ. Sci. Technol., 2006, 40, 3036–3042.
48. C. S. Evans and B. Dellinger, Environ. Sci. Technol., 2005, 39, 7940–7948.
49. Y. C. Na, K. J. Kim, C. S. Park and J. Hong, J. Anal. Appl. Pyrolysis, 2007, 80, 254–261.
50. H. B. Xie, C. Li, N. He, C. Wang, S. W. Zhang and J. W. Chen, Environ. Sci. Technol., 2014, 48, 1700–1706.
51. J. Zheng and D. G. Truhlar, Faraday Discuss., 2012, 157, 59–88.
52. Q. Z. Zhang, X. H. Qu, F. Xu, X. Y. Shi and W. X. Wang, Environ. Sci. Technol., 2009, 43, 4105–4112.
53. R. Gao, F. Xu, S. Q. Li, J. T. Hu, Q. Z. Zhang and W. X. Wang, Chemosphere, 2013, 92, 382–390.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, revision A.02, Gaussian, Inc., Wallingford, CT, USA, 2009.
55. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918.
56. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
57. M. S. Baldridge, R. Gordon, R. Steckler and D. G. Truhlar, J. Phys. Chem., 1989, 93, 5107–5119.
58. A. Gonzalez-Lafont, T. N. Truong and D. G. Truhlar, J. Chem. Phys., 1991, 95, 8875–8894.
59. B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 1052–1079.
60. A. Fernandez-Ramos, B. A. Ellingson, B. C. Garret and D. G. Truhlar, in Reviews in Computational Chemistry, Wiley-VCH, Hoboken, NJ, USA, 2007.
61. J. C. Corchado, Y. Y. Chuang, P. L. Fast, J. Villa, W. P. Hu, Y. P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels and V. S. Melissas, POLYRATE version 9.7, University of Minnesota, Minneapolis, Minnesota, MN, USA, 2007.
62. K. H. Hellwege and A. M. Hellwege, Landolt-Bornstein: Group II: Atomic and Molecular Physics, Springer-Verlag, Berlin, 1976, vol. 7.
63. M. W. Chase, J. Phys. Chem., 1998, 1–1951.
64. J. D. Cox, Pure Appl. Chem., 1961, 2, 125–128.
65. W. Tsang, Energetics of Organic Free Radicals, Blackie Academic and Professional, London, 1996, pp. 22–58.
66. Y. Z. He, W. G. Mallard and W. Tsang, J. Phys. Chem., 1988, 92, 2196–2201.
67. M. Altarawneh, B. Z. Dlugogorski, E. M. Kennedy and J. C. Mackie, J. Phys. Chem. A, 2008, 112, 3680–3692.
68. A. Saeed, M. Altarawneh, G. Hefter and B. Z. Dlugogorski, J. Chem. Eng., 2016, 61, 160–172.

---

Footnote

† Electronic supplementary information (ESI) available: Imaginary frequencies v (in cm⁻¹), ZPEs, and total energies of the transition states involved in this study and the O–H bond dissociation energies D₀(O–H) (in kcal mol⁻¹) of the reactions of BCPs with H. CVT/SCT rate constants for the reactions of the BCPs with H over the temperature range of 600–1200 K (cm³ per molecule per s). MPWB1K/6-31+G(d,p) optimized geometries for 96 congeners of the BCPs, BCPRs, and transition states. Potential barrier ΔE₀, reaction heat ΔH₀, Arrhenius formulas, and CVT/SCT rate constants for reactions of anti-BCPs with H. Energy difference between syn- and anti-conformers of BCPs. See DOI: 10.1039/c7ra12781b

---