Open Access Article
Open Access ArticleA family of 3d metal clusters based on N–N single bonds bridged quasi-linear trinuclear cores: the Mn analogue displaying single-molecule magnet behavior†
Kai Wang a,
Shen Tanga,
Zhao-Bo Hub,
Hua-Hong Zoub,
Xiao-Lu Wangb,
Yan Lia,
Shu-Hua Zhang
a,
Shen Tanga,
Zhao-Bo Hub,
Hua-Hong Zoub,
Xiao-Lu Wangb,
Yan Lia,
Shu-Hua Zhang a,
Zi-Lu Chen
a,
Zi-Lu Chen b and
Fu-Pei Liang
b and
Fu-Pei Liang *ab
*ab
aGuangxi Key Laboratory of Electrochemical and Magnetochemical Functional Materials, College of Chemistry and Bioengineering, Guilin University of Technology, Guilin, 541004, China. E-mail: fliangoffice@yahoo.com
bState Key Laboratory for the Chemistry and Molecular Engineering of Medicinal Resources, School of Chemistry and Pharmacy, Guangxi Normal University, Guilin, 541004, China
First published on 7th February 2018
Abstract
The reactions of the diacylhydrazine ligands N,N′-bisalicyl-2,6-pyridine dicarbohydrazide (H6sphz) and N,N′-bis(3-methoxysalicyl)-2,6-pyridine dicarbohydrazide (H6msphz) with various 3d metal salts, afforded a series of coordination clusters, namely, [MnIII2MnII(sphz)(acac)2(CH3OH)4] (1, acac− = acetylacetone anions), [NiII3(msphz)(Py)4] (2, Py = pyridine), [CuII6(sphz)2(Py)4] (3) and [CuII6(msphz)2(Py)4]·2DMF·2H2O (4). Cluster 1 and 2 are single ligand assembled quasi-linear trinuclear structures. Both 3 and 4 consist a pair of quasi-linear {Cu3} cores, which are linked together by two crossed ligands. The adjacent 3d metal ions in all trinuclear cores of 1–4 are bridged by N–N single bonds of ligands, which convey ferromagnetic (FM) interactions between 3d metal centers of 1, and antiferromagnetic (AFM) interactions between those of 2–4. In particular, the FM interactions and linear arrangement of mixed-valence Mn centers in 1 result in a large spin ground states value (ST) of 13/2, as well as single-molecule magnet (SMM) behavior of slow relaxation and hysteresis of magnetization.
Introduction
In the last two decades, impressive growth in the studies of molecular magnetic materials has been initiated by the discovery of some polynuclear 3d clusters that was termed as SMMs.1 These SMMs exhibit slow magnetic relaxation and hysteresis as the macroscopic magnets below blocking temperature (Tb), affording potential applications in the fields of ultra-high density information storage, molecular spintronics and quantum computation.2 It is believed that the properties of 3d SMMs are determined by two essential required factors, high spin ground states and strong easy axis-type magnetic anisotropy,3 which are closely related to intramolecular magnetic interactions and the spatial arrangements of anisotropic 3d metal centers.4The continuous efforts in this field thus achieved many 3d SMMs with various structural topologies.5 Wherein those with linear or quasi-linear topologies (nuclearity ≥ 3) are one of species attracting particular concerns. Their relatively simple bridging structures are helpful for the deliberate tuning of magnetic interactions. They also facilitate co-linear alignments of anisotropy axes of 3d spins, which might bring significant global anisotropies for the whole systems. All these features are favour of promising SMM properties and special magnetic phenomenon. Typical representative includes a family of quasi-linear {MnIII2NiII3} SMMs showing pronounced quantum tunnelling steps in hysteresis loops,5c and a linear {CoII3} SMM displaying two magnetic relaxation processes at zero dc bias fields, etc.6 Nevertheless, this species is still rare until now, except above two cases. In Mn clusters family with so many SMM members, there were only three trinuclear and one tetranuclear linear cases reported to show SMM behavior so far as we know (list in Table S1†).7 Linear SMMs based on other anisotropic 3d centers, such as CoII, FeIII and NiII ions, were also seldom found in previous literature.8 Thus, the incorporation of 3d metal ions into linear or quasi-linear SMMs remains to be a meaningful research subject in this field.
On the other hand, to tune the magnetic interactions between 3d ions, the sensible choices of bridging ligands are crucial.9 The ligands containing N–N bridges are just one kind of versatile candidates. Under the premise of small M–N–N–M torsion angles, they could transmit FM interactions and may result in desirable SMM properties. But these expected results are more achievable for ligands bearing aromatic N–N bridges, such as various pyrazoles, triazoles, tetrazoles, etc.10 Those affording saturated N–N single bonds as magnetic exchange pathways, which represented by a variety of acylhydrazines and acylhydrazones, can only transmit AFM interactions between 3d ions in most cases.11 Up to now, only very limited 3d systems in which N–N single bonds convey FM coupling and/or result in SMM behavior were reported.8c,12
In recent years, our group is interested in the coordination chemistry of diacylhydrazine derivatives.13,14 On the basis of our previous work, we realized that two diacylhydrazine derivatives H6sphz and H6msphz, whose chelating pockets preferred by 3d ions arrange in a quasi-linear manner (Scheme 1), might be the right candidates to assemble quasi-linear 3d clusters. We thus started to explore their possibilities in this aspect. Various terminal ligands were also introduced by different ways, so as to block the formation of polymeric products and allow for successful achievement of discrete linear topologies. A family of 3d clusters 1–4 that contain N–N bonds bridged linear trinuclear cores were finally synthesized as we intended. The magnetic investigations revealed the N–N single bonds transmit FM and AFM interactions between the 3d ions of 1 and 2–4, respectively. Notably, cluster 1 is found to be the rare quasi-linear 3d SMM employing N–N single bonds as magnetic coupling pathways.
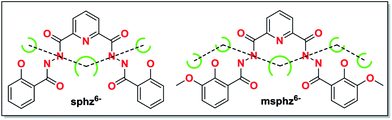 | ||
| Scheme 1 Potential chelating pockets arranging in quasi-linear fashion for H6sphz and H6msphz ligands. | ||
Results and discussion
Structural description
X-ray single crystal diffraction revealed that 1 belongs to orthorhombic Pbcn space group. As shown in Fig. 1, its centro-symmetric molecular structure contains a sphz6− ligand, three Mn centers, two acac− ions and four CH3OH molecules. Bond valence sum (BVS) calculations15 (3.40 for Mn1 and 1.90 for Mn2) and charge balance consideration established that terminal Mn1 and central Mn2 are trivalent and divalent, respectively. The Mn1 displays a six-coordinated octahedron geometry, whose four equatorial positions are occupied by a Nacylhydrazine (N1), an Ophenol (O1), an Oacylhydrazine (O3) and an Oacac (O4) atoms. As expected for high-spin Mn3+ ions in an octahedral geometry, an Oacac (O5) and an Omethanol (O6) atoms locate in two axial positions along a J–T elongation axis, forming two long Mn–O bonds whose lengths are 2.161(2) and 2.347(2) Å, respectively. The central Mn2 residing on an inversion center displays a seven-coordinated pentagonal bipyramid geometry. Its equatorial plane is composed of a NPy (N1), four Nacylhydrazine (N2, N3, N2a and N3a) and two Oacylhydrazine (O3 and O3a) atoms. The axial positions are held by two Omethanol (O7 and O7a) atoms with Mn–O bond length of 2.211(2) Å.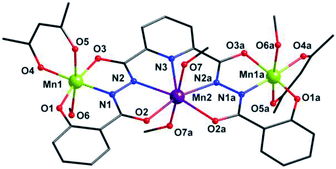 | ||
| Fig. 1 Molecular structure of 1. Symmetry codes: (a) −x, y, −z + 1/2. Color scheme: black for C, red for O, blue for N, purple for Mn2+ ion and grass-green for Mn3+ ions. | ||
Three Mn centers are linked together in a quasi-linear fashion by two N–N single bonds of ligand, which is completely deprotonated and displays an μ3-η11 mode (mode-I in Scheme 2). Two acac− ions and four CH3OH act as terminal groups, preventing the formation of infinite expand products. The torsion angle of Mn1–N–N–Mn2 and the Mn1⋯Mn2 distance are 172.5° and 4.935 Å respectively (Table S2†). The angle of Mn1⋯Mn2⋯Mn1a is 153.1°, indicating that three Mn centers are not arranged in a straight line, but remain have a considerable bent angle. However, if seen from c-axis direction, three Mn centers and all their donors in equatorial positions are nearly coplanar, with a least-square deviation of 0.092 (Fig. S1†). Note that the J–T axes of two Mn3+ ions are nearly co-parallel, and the angle between them is about 6.2°.
Additionally, hydrogen bonds (O6a–H6a⋯O5b: 2.172 Å; O7a–H7a⋯O1c: 1.993 Å) are found between the neighboring clusters, which extend the discrete {Mn3} clusters into a 2D supramolecular layer in the ac plane (Fig. 2). They may also help to stabilize axially elongated Mn1–O6 (2.347(2) Å) and Mn1–O5 (2.1612(2) Å) bonds, contributing to the formation of +3 oxidation states of Mn1 ions.16
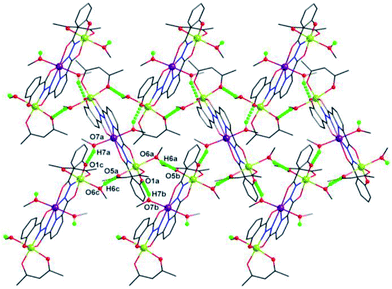 | ||
| Fig. 2 2D supramolecular layer in ac plane linked together by interclusters hydrogen bonds of 1. Symmetry codes: (a) x, −y, z − 1/2; (b) −x + 1/2, y − 1/2, z − 1; (c) −x + 1/2, y − 1/2, z − 2. | ||
Cluster 2 crystallizes in orthorhombic Pnma space group. Its msphz6− ligand adopts the same μ3-η11 mode (mode-II, Scheme 2) as sphz6− ligand in 1, leaving two Omethoxyl atoms uncoordinated. Thus 2 also displays a centro-symmetric linear trinuclear structure (Fig. 3). Central Ni2 has a pentagonal bipyramid geometry formed by four Nacylhydrazine (N1, N1a, N2 and N2a), a NPy (N4), two Oacylhydrazine (O3 and O3a) atoms in the equatorial plane, and two NPy (N5 and N6) atoms locating at axial positions. However, the peripheral two Ni2+ ions (Ni1 and Ni1a) adopt four-coordinated square geometry completed by a Nacylhydrazine (N1), a NPy (N3), an Ophenol (O2) and an Oacylhydrazine (O4) atoms. Three Ni2+ centers and all their donors are located in a plane, except two axial coordinated NPy (N5 and N6) atoms, giving a least-square deviation of 0.133 (Fig. S1†). The torsion angle of Ni1–N–N–Ni2, Ni1⋯Ni2 distance and Ni1⋯Ni2⋯Ni1a angle are 177.2°, 4.728 Å and 151.9°, respectively (Table S2†). The π–π interactions are found between the ligands (Table S3†), which further link the adjacent {Ni3} clusters to form supramolecular chains along b axis (Fig. S2†).
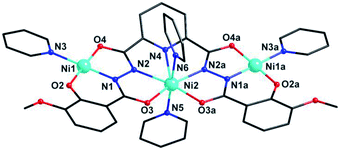 | ||
| Fig. 3 Molecular structure of 2. Symmetry codes: (a) x, 1.5 − y, z. Color scheme: black for C, red for O, blue for N, sky-blue for Ni. | ||
Clusters 3 and 4 show quite similar hexanuclear structures consisting of two N–N single bonds bridged quasi-linear {Cu3} cores (Fig. 4), though they were assembled by different ligands, respectively. The reason is that sphz6− in 3 and msphz6− in 4 display the same μ4-η11 mode (mode-III vs. IV, Scheme 2). Here only 3 is taken as the representative to discuss their structures in detail. Cluster 3 crystallizes in triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . It consists of two sphz6− ligands, six Cu2+ ions, four coordinative Py and one free DMF molecules (Fig. 4a). Among six Cu2+ ions, terminal Cu1, Cu3, Cu4 and Cu6 all display four-coordinated square geometries provided by a Nacylhydrazine (N1, N12, N8 or N5), a NPy (N6, N14, N13 or N7), an Ophenol (O1, O12, O7 or O6) and an Oacylhydrazine (O3, O10, O9 or O4) atoms. While the geometries of the two central Cu2+ ions (Cu2 and Cu5) are distorted square pyramidal ones, as established by the calculation of geometrical parameters τ (0.47 for Cu2 and 0.25 for Cu5). Their basal planes are formed by two Nacylhydrazine (N2 and N11 or N4 and N9), a NPy (N3 or N10) and an Oacylhydrazine (O2 or O8) atoms, and the apex are occupied by Oacylhydrazine (O11 or O5) atoms. The Cu2–N3 and Cu5–N10 bonds are 2.671(1) and 2.882(1) Å, respectively. Both of them are much longer than those of any other Cu–N bonds in 3, and close to the Cu–N van der Waals radii limit (2.95 Å).17
. It consists of two sphz6− ligands, six Cu2+ ions, four coordinative Py and one free DMF molecules (Fig. 4a). Among six Cu2+ ions, terminal Cu1, Cu3, Cu4 and Cu6 all display four-coordinated square geometries provided by a Nacylhydrazine (N1, N12, N8 or N5), a NPy (N6, N14, N13 or N7), an Ophenol (O1, O12, O7 or O6) and an Oacylhydrazine (O3, O10, O9 or O4) atoms. While the geometries of the two central Cu2+ ions (Cu2 and Cu5) are distorted square pyramidal ones, as established by the calculation of geometrical parameters τ (0.47 for Cu2 and 0.25 for Cu5). Their basal planes are formed by two Nacylhydrazine (N2 and N11 or N4 and N9), a NPy (N3 or N10) and an Oacylhydrazine (O2 or O8) atoms, and the apex are occupied by Oacylhydrazine (O11 or O5) atoms. The Cu2–N3 and Cu5–N10 bonds are 2.671(1) and 2.882(1) Å, respectively. Both of them are much longer than those of any other Cu–N bonds in 3, and close to the Cu–N van der Waals radii limit (2.95 Å).17
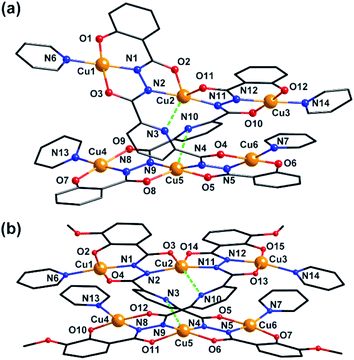 | ||
| Fig. 4 Molecular structure of 3 and 4. Color scheme: black for C, red for O, blue for N, yellow for Cu. | ||
In contrast to nearly planar configurations of sphz6− in 1, two acylhydrazine wings of each sphz6− in 3 twists with each other. Two such “V” shaped sphz6− ligands thus cross together with their notches face to face, and use their donors in notches to chelate two Cu2+ ions (Cu2 and Cu5) synergistically. In addition, each of four hydrozine groups also catch a Cu2+ ion (Cu1, Cu3, Cu4 and Cu6) with the help of Ophenol, with the Py as terminal ligands. In this way a hexanuclear structure that contains two discrete {Cu3} cores formed. Both {Cu3} cores show a N–N single bonds bridged quasi-linear topologies as {Mn3} in 1 and {Ni3} in 2. However, what's different is that the two N–N bridges in each {Cu3} core are belonging to different sphz6− ligands, respectively. This dissimilarity did not lead to obvious variations in the torsion angle of M–N–N–M, M⋯M distances and M–M–M angle for 1–3 (Table S2†). But it makes the Cu2+ ions and their donors in each {Cu3} core form two crossed meaning planes (Fig. S1†). The least-square deviations of four meaning planes in 3 are 0.048, 0.079, 0.047 and 0.078 Å, and the twist angles of two crossing meaning planes in each {Cu3} core are 62.376 and 39.867°, respectively. Furthermore, due to the intermolecular π–π interactions (Table S3†) between ligands, the {Cu6} clusters of 3 further form supramolecular chain along c-axis (Fig. S3†).
Magnetic properties
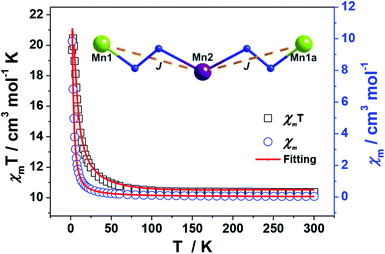
The magnetic susceptibilities of 1–4 have been studied in the range of 300–2 K with an applied direct current magnetic field of 1 kOe. The room temperature χmT value of 1 is 10.35 cm3 K mol−1, being close to the theoretical value of 10.375 cm3 K mol−1 for an uncoupled {MnIII2MnII} system with S(Mn3+) = 2 and S(Mn2+) = 5/2 assuming g = 2.00 (Fig. 5, Table S2†). Upon cooling, the χmT value increases gradually, reaching the maximum of 20.44 cm3 K mol−1 at 3 K, before dropping rapidly to a minimum of 19.69 cm3 K mol−1 at 2 K. The Curie–Weiss fitting for the χm−1–T data at the temperature range of 300–50 K gave C = 10.28 mol cm−3 and θ = 2.17 K (Fig. S4†). The overall profile of χmT–T curve and the positive θ are characteristic of FM coupling between Mn3+ and Mn2+ centers of 1. While for the faster decrease of χmT value in the low temperature region, it may be ascribed to the presence of magnetic anisotropy zero field splitting (mainly for Mn3+ centers) and/or the effect of interclusters interactions.18MAGPACK program19 was used to fit magnetic interactions of 1. On the basis of its centro-symmetric molecular structure, the magnetic interactions can be simplified as a linear trinuclear model (Fig. 5 inset) based on following Hamilton operator (eqn (1)):
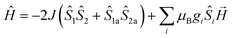 | (1) |
The J represents the interactions mediated by the N–N single bond pathways between the adjacent Mn centers, and the Si is the spin vector for each Mn ion. The fitting result agrees well with the experimental data in whole temperature range (red line in Fig. 5), and gave the best parameters of J = 5.1 cm−1, g = 1.99 and interclusters magnetic interactions zJ = −0.12 cm−1. Both experimental and fitting results suggest a ST = 13/2 spin ground state for 1 at T = 0 K.7b,20
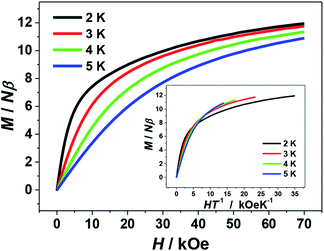
The isothermal magnetization data for 1 were collected in the fields of 0–70 kOe at 2–5 K. As shown by the plot of M–H in Fig. 6, the magnetization value (M) of 1 rises rapidly from at low fields and reaches a maximum value of 11.95 Nβ at the 70 kOe at 2 K. The lack of saturation for the curve implies the appreciable magnetic anisotropy arising from the two J–T elongated peripheral Mn3+ ions and/or the presence of low-lying excited states of the system. This could be also supported by the plot of M–HT−1 (Fig. 6, inset), in which the curves at different temperature are not superposed. In addition, these isothermal magnetization data were also fit to investigate the zero-field splitting D, a parameter that related to the magnetic anisotropy of the system. However, all attempts lead to unreasonable values and/or prevent the fits from converging, which can also be seen in some other Mn clusters reported previously.16,21
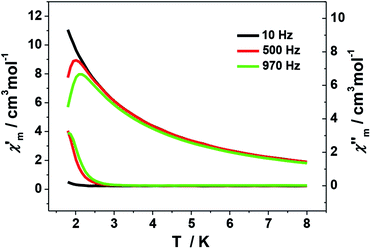
The ac magnetic measurements of 1 were performed under zero dc fields with an ac driving field of 2.5 Oe at different frequencies. As shown in Fig. 7, cluster 1 is observed to exhibit frequency-dependent out-of-phase (χ′′) ac signal at low temperature. This feature is characteristic of a superparamagnetic-like slow relaxation and thus of potential SMM behavior. Nevertheless, it is difficult to estimate the energy barrier of 1 due to the absence of full peaks with maxima in the out-of-phase χ′′ ac signal. This might be ascribed to the fast relaxation and/or small energy barrier of the system. Similar situation is commonly seen in previous Mn SMMs.7a,b,22 In addition, the dc magnetization measurement performed at 1.8 K shows hysteresis curve with coercive field of about 50 Oe and remnant magnetization of about 0.075 Nβ (Fig. S5†).
For 2–4, their χmT values at 300 K are 2.94, 2.57 and 2.29 cm3 mol−1 K, respectively, which are in agreement with the expected values of 3.0 cm3 mol−1 K for 2 (three uncoupled Ni2+ ions with S = 1 and g = 2.2) and 2.5 cm3 mol−1 K for 3 and 4 (six uncoupled Cu2+ ions with S = 1/2 and g = 2). As the temperature was lowered, the χmT–T values of 2–4 all show smoothly and sharply decrease in high and low temperature region successively (Fig. 8). The χmT values finally reach the minimum of 1.19, 0.78 and 0.59 cm3 mol−1 K at 2 K, respectively. Curie–Weiss fitting afford C = 3.15 mol cm−3 and θ = −26.20 K for 2, C = 2.76 mol cm−3 and θ = −23.58 K for 3 and C = 2.37 mol cm−3 and θ = −12.82 K for 4 (Fig. S4†).
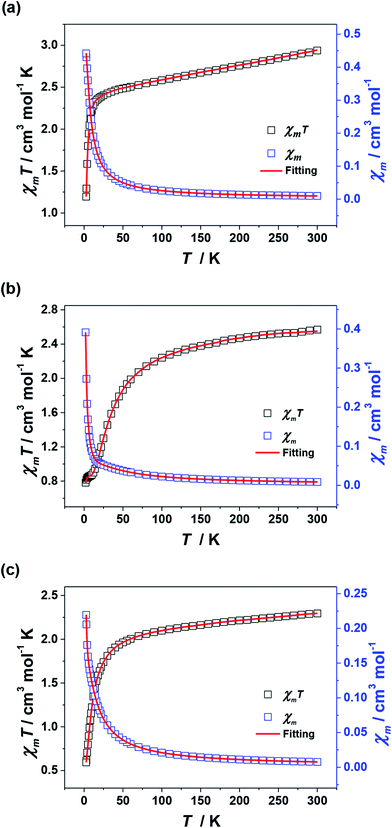 | ||
| Fig. 8 Plots of χmT–T and χm–T for 2 (a), 3 (b) and 4 (c). The red lines represent the best fitting. | ||
On account of the similar molecular structures and magnetic exchange pathways, the magnetic fitting of 2 is based on the same 2J model as that of 1 (eqn (1)). While those of 3 and 4 were modelled using following Hamiltonian (eqn (2)):
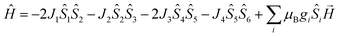 | (2) |
The J1, J2, J3 and J4 are the magnetic interactions between Cu1 and Cu2, Cu2 and Cu3, Cu4 and Cu5, and Cu5 and Cu6, respectively. All these fitting data by MAGPACK support experimental results well for every system (red line in Fig. 8). The best parameters of fitting are following: J = −12.6 cm−1, g = 2.2 and zJ = −0.18 cm−1 for 2, J1 = −5.2 cm−1, J2 = −3.9 cm−1, J3 = −4.7 cm−1, J4 = −3.5 cm−1, g = 2.1 and zJ = −0.27 cm−1 for 3 and J1 = −11.1 cm−1, J2 = −9.5 cm−1, J3 = −10.9 cm−1, J4 = −9.1 cm−1, g = 2.1 and zJ = −0.33 cm−1 for 4 (Table S2†). All above results indicate dominant AFM interactions between the metallic centers in each system of 2–4.
It can be seen from the above results that the N–N single bonds in 1–4 play different roles in magnetic interactions conveying, though the trinuclear cores of 1–4 have approximately the same M–N–N–M torsion angles, M⋯M distances and M–M–M angles (Table S2†). Only in 1, the N–N single bonds mediate FM interactions. This might be related to the special orbital overlaps of Mn3+···Mn2+ pairs, which are different from those between the adjacent 3d metal ions of 2–4. According to Hund's rule, the Mn3+ would transfer a fraction of unpaired electron from the z2 to the x2 − y2 orbital, in order to keep the spin of the other unpaired electrons parallel to that in z2 orbital.23 The overlap of the magnetic orbital of an empty orbital of Mn3+ ions with an Mn2+ ion results in FM coupling on the basis of the spin polarization mechanism,24 and thus led to a large spin ground state of 1. Combined with the nearly perfect alignment Jahn–Teller axes of Mn3+ centers in its linear topology, which bring significant global anisotropy, cluster 1 finally displays SMM behavior.
Conclusions
In summary, we have assembled a family of novel 3d metal clusters, employing two diacylhydrazine ligands containing linearly arranged chelating pockets. They feature acylhydrazine N–N single bonds bridged quasi-linear trinuclear cores. These N–N bonds transmit FM exchange between the Mn centers in 1, but common AFM exchanges between the adjacent 3d metal centers of 2–4. Furthermore, cluster 1 exhibits SMM behavior. This work thus affords rare case of quasi-linear 3d SMM using N–N single bonds as magnetic coupling pathways, and provides a new insight to the role of N–N bridges in the conveying of magnetic interactions.Experimental
General materials and methods
All reagents were used as received without further purification. The H4sphz and H6msphz ligands were synthesized according to the literature.14 IR spectra were recorded in the range of 4000–400 cm−1 on a Perkin-Elmer Spectrum One FT/IR spectrometer using a KBr pellet. Elemental analyses for C, H and N were carried out on a Model 2400 II, Perkin-Elmer elemental analyzer. The magnetic measurements were performed with a Quantum Design MPMS SQUIDXL-5 magnetometer equipped with a 7 T magnetic field using polycrystalline samples. Direct current (dc) magnetic susceptibility were measured in the temperature range of 300–2 K. Field-dependant magnetization plots were measured with the magnetic field varying from 0 to 7 T at the indicated temperatures. The ac susceptibility measurements were carried out with an oscillating ac field of 2.5 Oe at various frequencies at 0 Oe dc fields. The diamagnetic corrections for the complexes were estimated using Pascal's constants, and magnetic data were corrected for diamagnetic contributions of the sample holder.Syntheses
X-ray structure determination
All the data for 1–4 were collected with an Agilent Supernova diffractometer by using graphite monochromatic Mo-Kα radiation (λ = 0.71073 Å). The data were collected at 296.15 (for 1) and 150.15 K (for 2–4), respectively. Absorption effects were corrected by semi-empirical methods. The structures were solved by direct methods and were refined by full-matrix least-squares methods with a suite of SHELX programs25 via the Olex2 interface.26 The non-hydrogen atoms were refined anisotropically. The aromatic hydrogen atoms were placed in calculated positions and refined by using a riding model, while other hydrogen atoms were located in the last final difference Fourier map. The final cycle of full-matrix least-squares refinement was based on observed reflections and variable parameters. Several severely disordered DMF and H2O molecules in the unit cell of 4 were treated with SQUEEZE routine included in PLATON27 during the structural refinement. Their number was estimated on the basis of the electron counts calculated by PLATON software and elemental microanalysis. A summary of crystal data and relevant refinement parameters for 1–4 are given in Table S4.† Selected bond lengths and bond angles are given in Table S5–S8.† CCDC 1496802 (1), 1496805 (2), 1496806 (3) and 1496807 (4) contain the supplementary crystallographic data for this paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 51572050), the Guangxi Natural Science Foundation (Grant No. 2015GXNSFDA139007), and Scientific Research Staring Foundation of Guilin University of Technology (Grant No. GUTQDJJ20172016028). We thank the supported from the Program of the Collaborative Innovation Center for Exploration of Hidden Nonferrous Metal Deposits and Development of New Materials in Guangxi (No. GXYSXTZX2017-II-3).Notes and references
- (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (b) M. Murrie, Chem. Soc. Rev., 2010, 39, 1986 RSC; (c) K. Liu, X. J. Zhang, X. X. Meng, W. Shi, P. Cheng and A. K. Powell, Chem. Soc. Rev., 2016, 45, 2423 RSC.
- (a) P. Zhang, Y. N. Guo and J. K. Tang, Coord. Chem. Rev., 2013, 257, 1728 CrossRef CAS; (b) G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Chem. Soc. Rev., 2013, 42, 1796 RSC; (c) C. Papatriantafyllopoulou, E. E. Moushi, G. Christou and A. J. Tasiopoulos, Chem. Soc. Rev., 2016, 45, 1597 RSC.
- (a) G. E. Kostakis, A. M. Ako and A. K. Powell, Chem. Soc. Rev., 2010, 39, 2238 RSC; (b) A. Vinslava, A. J. Tasiopoulos, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2016, 55, 3419 CrossRef CAS PubMed.
- (a) S. L. Castro, Z. Sun, C. M. Grant, J. C. Bollinger, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 1998, 120, 2365 CrossRef CAS; (b) Y. Y. Zhu, T. T. Yin, S. D. Jiang, A. Barra, W. Wernsdorfer, P. Neugebauer, R. Marx, M. Dörfel, B. W. Wang, Z. Q. Wu, J. Slageren and S. Gao, Chem. Commun., 2014, 50, 15090 RSC; (c) J. D. Leng, S. K. Xing, R. Herchel, J. L. Liu and M. L. Tong, Inorg. Chem., 2014, 53, 5458 CrossRef CAS PubMed; (d) G. Aromí, S. Parsons, W. Wernsdorfer, E. K. Brechin and E. J. L. McInnes, Chem. Commun., 2005, 5038 RSC; (e) C. J. Milios, A. Vinslava, P. A. Wood, S. Parsons, W. Wernsdorfer, G. Christou, S. P. Perlepes and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 8 CrossRef CAS PubMed; (f) A. Tomsa, J. Martínez-Lillo, Y. L. Li, L. Chamoreau, K. Boubekeur, F. Farias, M. A. Novak, E. Cremades, E. Ruiz, A. Proust, M. Verdaguer and P. Gouzerh, Chem. Commun., 2010, 46, 5106 RSC.
- (a) G. Aromi and E. K. Brechin, Struct. Bonding, 2006, 122, 1 CrossRef CAS; (b) A. J. Tasiopoulos and S. P. Perlepes, Dalton Trans., 2008, 5537 RSC; (c) A. Das, K. Gieb, Y. Krupskaya, S. Demeshko, S. Dechert, R. Klingeler, V. Kataev, B. Büchner, P. Müller and F. Meyer, J. Am. Chem. Soc., 2011, 133, 3433 CrossRef CAS PubMed.
- K. Y. Monakhov, J. van Leusen, P. Kçgerler, E. L. Zins, M. E. Alikhani, M. Tromp, A. A. Danopoulos and P. Braunstein, Chem.–Eur. J., 2017, 23, 6504 CrossRef CAS PubMed.
- (a) A. Prescimone, J. Wolowska, G. Rajaraman, S. Parsons, W. Wernsdorfer, M. Murugesu, G. Christou, S. Piligkos, E. J. L. McInnes and E. K. Brechin, Dalton Trans., 2007, 5282 RSC; (b) P. H. Lin, S. Gorelsky, D. Savard, T. J. Burchell, W. Wernsdorfer, R. Clérac and M. Murugesu, Dalton Trans., 2010, 39, 7650 RSC; (c) C. L. Zhou, Z. M. Wang, B. W. Wang and S. Gao, Dalton Trans., 2012, 41, 13620 RSC; (d) D. C. Li, H. S. Wang, S. N. Wang, Y. P. Pan, C. J. Li, J. M. Dou and Y. Song, Inorg. Chem., 2010, 49, 3688 CrossRef CAS PubMed.
- (a) Y. Z. Zhang, A. J. Brown, Y. S. Meng, H. L. Sun and S. Gao, Dalton Trans., 2015, 44, 2865 RSC; (b) Y. Z. Zheng, M. Speldrich, H. Schilder, X. M. Chen and P. Kögerler, Dalton Trans., 2010, 39, 10827 RSC; (c) D. Y. Wu, X. X. Zhang, P. Huang, W. Huang, M. Y. Ruan and Z. W. Ouyang, Inorg. Chem., 2013, 52, 10976 CrossRef CAS PubMed.
- (a) C. Papatriantafyllopoulou, S. Zartilas, M. J. Manos, C. Pichon, R. Clérac and A. J. Tasiopoulos, Chem. Commun., 2014, 50, 14873 RSC; (b) Y. Z. Zhang, U. P. Mallik, N. P. Rath, R. Clérac and S. M. Holmes, Inorg. Chem., 2011, 50, 10537 CrossRef CAS PubMed; (c) T. N. Nguyen, W. Wernsdorfer, M. Shiddiq, K. A. Abboud, S. Hillc and G. Christou, Chem. Sci., 2016, 7, 1156 RSC; (d) Y. F. Zeng, X. Hu, F. C. Liu and X. H. Bu, Chem. Soc. Rev., 2009, 38, 469 RSC.
- (a) H. Yang, F. Cao, D. C. Li, S. Y. Zeng, Y. Song and J. M. Dou, Dalton Trans., 2015, 44, 6620 RSC; (b) E. C. Yang, Z. Y. Liu, L. Zhang, N. Yang and X. J. Zhao, Dalton Trans., 2016, 45, 8134 RSC; (c) X. B. Li, G. M. Zhuang, X. Wang, K. Wang and E. Q. Gao, Chem. Commun., 2013, 49, 1814 RSC.
- (a) S. T. Wu, H. L. Tang, S. M. Lu, Q. Y. Ye, X. H. Huang, C. C. Huang, X. L. Hu and S. T. Zheng, CrystEngComm, 2014, 16, 9792 RSC; (b) L. K. Thompsona and L. N. Dawe, Coord. Chem. Rev., 2015, 289–290, 13 CrossRef.
- Z. Q. Xu, L. K. Thompson, D. O. Miller, H. J. Clase, J. A. K. Howard and A. E. Goeta, Inorg. Chem., 1998, 37, 3620 CrossRef CAS PubMed.
- (a) K. Wang, Z. L. Chen, H. H. Zou, K. Hu, H. Y. Li, Z. Zhang, W. Y. Sun and F. P. Liang, Chem. Commun., 2016, 52, 8297 RSC; (b) Z. L. Chen, S. N. Qin, D. C. Liu, Y. L. Shen and F. P. Liang, Cryst. Growth Des., 2013, 13, 3389 CrossRef CAS; (c) Z. L. Chen, Y. L. Shen, L. L. Li, H. H. Zou, X. X. Fu, Z. Y. Liu, K. Wang and F. P. Liang, Dalton Trans., 2017, 46, 15032 RSC.
- (a) S. N. Qin, Z. L. Chen, D. C. Liu, W. Y. Huang and F. P. Liang, Inorg. Chem. Commun., 2011, 14, 784 CrossRef CAS; (b) K. Wang, X. K. Huang, L. Zhu, Z. L. Chen and F. P. Liang, Chin. J. Struct. Chem., 2016, 35, 1912 CAS.
- N. E. Brese and M. O'keeffe, Acta Crystallogr., 1991, B47, 192 CAS.
- F. Habib, G. Brunet, F. Loiseau, T. Pathmalingam, T. J. Burchell, A. M. Beauchemin, W. Wernsdorfer, R. Clerac and M. Murugesu, Inorg. Chem., 2013, 52, 1296 CrossRef CAS PubMed.
- P. M. Cheung, R. F. Berger, L. N. Zakharov and J. D. Gilbertson, Chem. Commun., 2016, 52, 4156 RSC.
- A. Jana, N. Aliaga-Alcalde, E. Ruiz and S. Mohanta, Inorg. Chem., 2013, 52, 7732 CrossRef CAS PubMed.
- (a) J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. J. Tsukerblat, Inorg. Chem., 1999, 38, 6081 CrossRef; (b) J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. J. Tsukerblat, Comput. Chem., 2001, 22, 985 CrossRef.
- A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clerac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 4926 CrossRef CAS PubMed.
- (a) C. J. Milios, R. Inglis, L. F. Jones, A. Prescimone, S. Parsons, W. Wernsdorfer and E. K. Brechin, Dalton Trans., 2009, 2812 RSC; (b) M. J. H. Ojea, M. A. Hay, G. Cioncoloni, G. A. Craig, C. Wilson, T. Shiga, H. Oshio, M. D. Symes and M. Murrie, Dalton Trans., 2017, 46, 11201 RSC.
- (a) T. N. Nguyen, M. Shiddiq, T. Ghosh, K. A. Abboud, S. Hill and G. Christou, J. Am. Chem. Soc., 2015, 137, 7160 CrossRef CAS PubMed; (b) T. N. Nguyen, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2011, 133, 20688 CrossRef CAS PubMed.
- T. Glaser, Chem. Commun., 2011, 47, 116 RSC , and references therein.
- H. Liu, J. L. Tian, Y. Y. Kou, J. Y. Zhang, L. Feng, D. D. Li, W. Gu, X. Liu, D. Z. Liao, P. Cheng, J. Ribas and S. P. Yan, Dalton Trans., 2009, 10511 RSC.
- (a) G. M. Sheldrick, Acta Crystallogr., 2008, A64, 112 CrossRef PubMed; (b) G. M. Sheldrick, Acta Crystallogr., 2015, C71, 3 Search PubMed.
- O. V. Dolomanov, L. J. Bourthis, R. L. Gildea, J. A. K. Howard and H. J. Puschmann, Appl. Crystallogr., 2009, 42, 339 CrossRef CAS.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional structural figures and magnetic data. Tables of selected bond lengths (Å) and angles (°). CCDC 1496802 and 1496805–1496807. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra12844d |
| This journal is © The Royal Society of Chemistry 2018 |