Open Access Article
Open Access ArticleProbing the surface structure of hydroxyapatite through its interaction with hydroxyl: a first-principles study†
Xian Wang,
Li Zhang*,
Zeyu Liu,
Qun Zeng ,
Gang Jiang and
Mingli Yang
,
Gang Jiang and
Mingli Yang *
*
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China. E-mail: lizhang@scu.edu.cn; myang@scu.edu.cn; Fax: +86-28-85405515; Tel: +86-28-85405515
First published on 18th January 2018
Abstract
Understanding the interaction of the hydroxyapatite (HAp) surface with hydroxyl originating from either the alkalescent physiological environment or HAp itself is crucial for the development of HAp-based biomaterials. Periodical density functional theory calculations were carried out in this study to explore the interaction of the HAp (100), (010) and (001) facets with hydroxyl. Based on a comparison study of Ca-rich, PO4-rich and Ca–PO4–OH mixed surfaces, the interaction pattern, interaction energy and effect of an additional water molecule on the Ca–OH interaction were comprehensively studied. The formation of CaOH on the Ca-rich surface was energetically favored on (100) and (001), while Ca(OH)2 was energetically favored on (010). The Ca–water interaction was competitive, but had lower interaction energy than Ca–OH. Furthermore, Ca–O bonding and its influence on the OH stretching vibration were analyzed. Our calculations suggest that the hydroxyl-coated surface structure is more appropriate than the commonly used Ca-terminated surface model for studying HAp surface activity in its service environments.
Introduction
Biomaterials such as hydroxyapatite (HAp) are used in biomedical devices that are implanted in vivo to substitute diseased or damaged organs and tissues.1,2 HAp has found wide applications in reconstructive surgery, drug carriers, and bone regeneration due to its specific biological activity such as biofunctionability, biocompatibility, and chemical stability.3–5Therefore, a thorough understanding of the surface structure of HAp is crucial for the design and development of novel biocompatible HAp-based materials. The surface-dependent protein adsorption, cellular adhesion and biomineralization of HAp have great impact on the bone growth and repair processes.6,7 Thus, many studies8–18 have been devoted to the HAp surface structure including its morphology, surface energy, charge, crystallinity and stoichiometry. Using nuclear magnetic resonance NMR spectroscopy, Jager et al.13 and Osman et al.14 explored the surface structure of HAp nanocrystals and found that neither composition nor structure in the surface layer is same as that in the bulk crystal. Lu et al.15 observed different Ca/P ratios in the HAp surface from that in crystal using X-ray photoelectron spectroscopy (XPS) and time-of-flight secondary ion mass spectrometry (TOF-SIMS). Ospina et al.,16 Sato et al.17 and Rivas et al.18 investigated the structure of the HAp (010) and (100) surfaces via X-ray diffraction (XRD), XPS and Fourier transform infrared (FTIR) spectroscopy, and addressed their strong interaction with biological media. A number of computer simulations19–31 have been conducted to investigate the HAp surface structure and its interaction with various biomolecules using stoichiometric or nonstoichiometric HAp as a model surface in the first-principles or force-fields level. Slepko et al.22 identified the low energy surface orientations and stoichiometry under diverse chemical environments using a slab model. Almora et al.,23 Filgueiras et al.24 and Rimola et al.25 studied the interaction of the HAp surface with citric, glycine, lysine, and proline, and demonstrated that the HAp surface substantially affects the interaction patterns, amino acid conformation, and interaction strength. Molecular dynamics simulations26–30 with various force field parameters indicated that surface Ca2+ and PO43− ions serve as effective adsorption sites binding with adsorbates, and the adsorption is facilitated by the ionic nature of the HAp surface. In most calculations, a Ca-exposed surface was used as the HAp model to explore its interaction with biomolecules. Evidently, studies on the HAp surface–adsorbate interaction shed light not only on its adsorption behaviors, but also on the details of the HAp surface structure.
Various studies have been devoted to the interaction of the HAp surface with hydroxyl originating from either HAp itself or the environment. The chemical adsorption of water molecules on the HAp surface generates and leaves hydroxyl ions on its surface.7,27,31,32 The existence of hydroxyl groups on the HAP surface significantly alters its activity. Hokkanen et al.33 characterized the electrostatic attraction between surface hydroxyl groups and other adsorbates. Chen et al.34 studied the adsorption mechanism of sulfate-doped hydroxyapatite and found that the hydroxyl groups on the surface cooperatively enhanced fluoride removal. The hydroxyl-terminated (010) surface was found7 to be stable and inactive for water decomposition. The treatment of NaOH or KOH on natural bone whose main component is HAp led to the growth of HAp crystallites35 and a shape variation from B-type to A-type. The enrichment of hydroxyl on the HAp surface significantly promoted collagen self-assembly, fibrous network formation and cell adhesion.36 The coating of hydroxyl groups on the HAp surface provides an effective way to functionalize the HAp surface since many other species may link directly with the hydroxyls.37,38
Since HAp-based biomaterials are usually applied in alkalescent physiological environment,39,40 hydroxyl groups play an important role in the determination of HAp surface activity; however, knowledge on the surface–hydroxyl interaction is still scarce. Calcium or phosphate-terminated exposed surfaces sliced from the HAp crystal are often used to represent the surface structure of HAp. However, this surface model is not supported by some experimental and computational results. Kolmas et al.41 identified structural hydroxyl groups and surface P–OH groups with near-infrared spectroscopy. Osman et al.14 and Bertinetti et al.42 found no Ca(OH)2 formation on the HAp surface with a developed NMR strategy. Wang et al.43 predicted at the force-field level the formation of CaOH and POH on the HAp surface, which exert considerable influence on the adsorption energy of proteins. In our previous studies,26,43 we noted via an annealed MD simulation that hydroxyl groups have a tendency to cap exposed surface calcium ions. In this study, we conduct a first-principles study on the HAp surface–hydroxyl interaction. As revealed below, a strong Ca–OH interaction is noted. The surface reorganization caused by CaOH or Ca(OH)2 formation is energetically favorable on the surface, but the formed species are different and dependent on the facet. Moreover, water molecules are competitive with hydroxyl and weaken to some extent the Ca–OH interaction. Based on our calculations, a hydroxyl-coated surface structure is suggested to replace the commonly used Ca-terminated surface model for HAp in its service environment.
Computational method
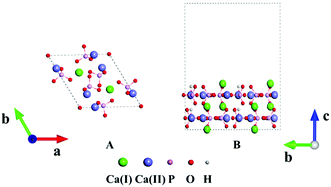
HAp has two phases, hexagonal and monoclinic, in crystal. These two phases exhibit parallel behaviors in many cases and the former is often selected in many studies.44 Fig. 1A displays the crystal structure of hexagonal HAp, where 44 atoms are in a unit cell. The crystal contains tetrahedral phosphate groups, hydroxyl groups, and calcium ions. There are two types of Ca ions, which are denoted as Ca(I) and Ca(II), in the cell. Ca(I) is arranged in single atomic columns parallel to the c axis and is surrounded by phosphate tetrahedra, whereas the Ca(II) ions form a hexagonal column, at the center of which are the hydroxyl groups.The (100), (010) and (001) facets were constructed by slicing the crystal structure. For each facet, three slab models with different exposed atoms were constructed. Thus, nine surface models in total were studied for HAp in this work. The chemical components were kept stoichiometric in all the slab models. A 1 × 2 × 1 supercell was chosen in the relaxation for the lattice constants, and the surface was modeled with 1 × 2 × 1 supercells separated with 15 Å thick vacuum layers, as depicted in Fig. 1B. The vacuum layers were stacked along the direction perpendicular to the slab. In the calculations for the HAp surfaces, atoms in the bottom unit were fixed to mimic the real inner crystalline HAp, while all the atoms in the upper unit were allowed to relax. Since both calcium and phosphate ions are highly charged, they might form a strong artificial dipolar electric field in the slab model. Thus, a dipolar correction45 along the normal direction of the slabs was introduced to remove the polarization effect caused by the slab and its periodic images.
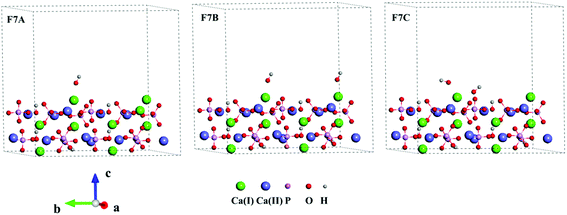
Three Ca-rich surfaces, one for each facet, among the nine surface models were selected to explore their interaction with hydroxyl and water. Two Ca ions were exposed for all three surfaces. Although the hydroxyl may attack several sites on the surface, we found it always prefers the Ca ions, which has also been addressed in other studies.26,43 The hydroxyl groups have several interaction patterns with the surface Ca ions. As shown in Fig. 2, three types of hydroxyl–Ca interaction patterns on the (001) surface were designed. In the first pattern (F7A), one hydroxyl binds to one Ca ion on the surface. In the second (F7B), two hydroxyls bind to two different Ca ions, while in the last (F7C) two hydroxyls bind to one Ca ion. Additionally, to examine the effect of water on the hydroxyl–Ca interaction, one water molecule was added to the model, as shown in Fig. 3, in which three patterns, W7, W7A and W7B are presented. Similar patterns were designed for the hydroxyl and water adsorption on the (010) and (100) facets, which are presented in Fig. S1 and S2 in the ESI.† In the systems with hydroxyl groups, protons were introduced to balance the system. To avoid their influence on hydroxyl adsorption, the protons were added to the phosphate groups at the lower surface.
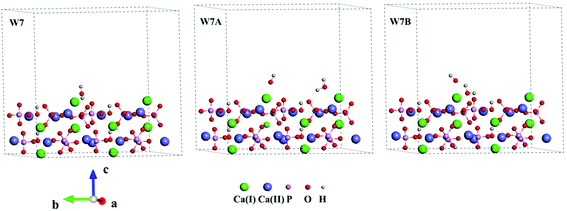 | ||
| Fig. 3 Interaction patterns of the water molecule (W7), hydroxyl and water (W7A and W7B) on the Ca-rich (001) surface of HAp. | ||
All calculations were carried out with the density functional theory (DFT) method in the Vienna ab initio simulation package (VASP) code.46 The generalized gradients approximation (GGA) of the Perdew–Wang 1991 (PW91) functional was employed with the projection augmented wave (PAW) type of pseudopotential.47 The energy cut-off was set to 550 eV in all calculations. A 2 × 2 × 2 Monkhorst–Pack k-point mesh was applied to the Brillouin zone sampling of the HAp single cell, while a 2 × 2 × 1 mesh was chosen for the slab models. The atomic configurations were relaxed with the conjugate-gradient (CG) approach.48 The force convergence was set to be 0.001 eV Å−1 for successive structures. Furthermore, harmonic vibrational frequency calculations were performed to ensure that the relaxed structures were local minima on the potential energy surface.
Results and discussion
The optimized lattice constants of the HAp crystal were given in Table 1, together with the results of some other computational and experimental studies.23,49–51 The deviations are less than 0.05 Å for a, b and c, compared to the measurement, and our calculations agree well with other computations.23,50,51 Generally, the hydroxyl and phosphate groups retain their orientations as in the measurement. The O–H and P–O bond lengths are 0.978 Å and 1.535 Å, which match well with the measurement (0.971 Å and 1.540 Å), respectively.10The nine constructed HAp surfaces (SF1–9) were optimized and presented in Fig. S3.† For the (100) facet, SF1, SF2 and SF3 are terminated with Ca-rich, PO4-rich and Ca–PO4–OH surfaces, respectively. Ca–PO4–OH denotes the situation where Ca, PO43− and OH are all on the surface. Similar surface characteristics are observed for SF4, SF5 and SF6 on the (010) facet, and SF7, SF8 and SF9 on the (001) facet. The stability of a surface is usually measured according to its surface energy, which corresponds to the energy required to cleave the bulk crystal and to expose its surface. Surface energy was evaluated computationally as follows:52
| γ = (Eslab − nEbulk)/2A | (1) |
| Patterna | Facet | Termination | This work | Other studies |
|---|---|---|---|---|
| a See Fig. S3 for the patterns.b With force-fields.c With B3LYP-D*.d With B3LYP.e With PBE.f With force-fields.g With PW91.h With force-fields. | ||||
| F1 | (100) | Ca-rich | 1.42 | 1.22b (ref. 24) |
| F2 | (100) | PO4-rich | 1.56 | 1.33b (ref. 24) |
| F3 | (100) | Ca–PO4–OH | 1.26 | — |
| F4 | (010) | Ca-rich | 1.35 | 1.14c (ref. 54), 1.41d (ref. 51), 1.76e (ref. 50) |
| F5 | (010) | PO4-rich | 1.18 | 0.99c (ref. 54), 1.28e (ref. 50), 1.16f (ref. 53) |
| F6 | (010) | Ca–PO4–OH | 1.27 | 1.68e (ref. 50) |
| F7 | (001) | Ca-rich | 1.24 | 1.12b (ref. 24), 1.44g (ref. 22), 1.29h (ref. 26) |
| F8 | (001) | PO4-rich | 1.37 | 1.60g (ref. 22) |
| F9 | (001) | Ca–PO4–OH | 1.09 | 1.12e (ref. 50) |
The surface energy depends on not only the crystal facet, but also the surface species. For (100) and (001), the Ca–PO4–OH surface is the most stable, followed by the PO4-rich and Ca-rich surfaces. The same order was reported by Slepko et al.22 for the HAp (100) and (001) surfaces. For (010), the PO4-rich surface is the most stable, followed by the Ca–PO4–OH and Ca-rich surfaces. Astala et al.50 also found that the Ca-rich (010) surface is more active than the PO4-rich surface. Therefore, surfaces with different species may have different stability, and also the same species on different facets. The Ca-rich surfaces generally have high activity toward other molecules with nucleophilic activity, such as hydroxyl and water. Therefore, we therefore focused on the interaction of hydroxyl groups on the Ca-rich surface (SF1, SF4 and SF7) in the subsequent calculations.
The interaction of hydroxyl with the HAp surface was analyzed in terms of interaction pattern and interaction energy. All three patterns, which are denoted as A, B and C, for each facet were relaxed and their interaction energy evaluated as:
| Eint = Esys − (Eslab + Eads) | (2) |
| Patterna | Facet | NCab | NOHc | Eint |
|---|---|---|---|---|
| a See Fig. 2, 3, S1 and S2 for the patterns.b Number of exposed Ca ions binding with hydroxyl.c Number of hydroxyls binding with exposed Ca ion. | ||||
| F1A | (100) | 1 | 1 | −1.37 |
| F1B | (100) | 2 | 2 | −2.10 |
| F1C | (100) | 1 | 2 | −1.94 |
| F4A | (010) | 1 | 1 | −1.48 |
| F4B | (010) | 2 | 2 | −2.60 |
| F4C | (010) | 1 | 2 | −2.78 |
| F7A | (001) | 1 | 1 | −1.44 |
| F7B | (001) | 2 | 2 | −2.43 |
| F7C | (001) | 1 | 2 | −2.23 |
The interaction of hydroxyl on the dry HAp surface was analyzed above. In most of its applications, HAp exists in an environment with water. Thus, we used a simple explicit model in which one water molecule was added on the surface to explore the effect of water on the hydroxyl–HAp interaction. The hydroxyl–HAp interaction did not show notable changes when the water molecule is far from hydroxyl. Thus, we focused on the model in which the water molecule binds directly with hydroxyl or its bonded Ca ion. In absence of hydroxyl, the water molecule adsorbs onto the surface by its O atom attacking the exposed Ca ion, as displayed in Fig. 3 (7W), S1 (1W) and S2 (4W).† The Ca–O distances are about 2.30 Å. Meanwhile, one or two H atoms form hydrogen bonds with the O atoms of a nearby phosphate. The hydrogen bonds are 1.50–2.10 Å in length. The interaction energies of the water molecule with the facets are given in Table 4. The (010) facet has the greatest Eint with the water molecule, while (100) has the smallest value, which corresponds well with the order of their surface energies. Our finding is in agreement with many other studies.7,50,54,57 The Eint values are 0.78–1.07 eV for the three facets, which are about 0.50 eV less than that of hydroxyl. It is understandable that the negatively charged hydroxyl has stronger interaction with the positively charged Ca ion than the neutral water molecule.
| Patterna | Facet | NOHb | NH2Oc | Eintd | E′inte |
|---|---|---|---|---|---|
| a See Fig. 2, 3, S1 and S2 for the patterns.b Number of hydroxyls binding with exposed Ca ion.c Number of water molecules binding with exposed Ca ion.d Eint = EHAp+H2O+OH − (EHAP + EH2O + EOH).e E′int = EHAp+H2O+OH − (EHAP + EH2O + EOH). | |||||
| W1 | (100) | 0 | 1 | −0.78 | — |
| W1A | (100) | 1 | 1 | −1.84 | −0.96 |
| W1B | (100) | 1 | 1 | −1.76 | −0.88 |
| W4 | (010) | 0 | 1 | −1.07 | — |
| W4A | (010) | 1 | 1 | −2.46 | −1.26 |
| W4B | (010) | 1 | 1 | −2.37 | −1.17 |
| W7 | (001) | 0 | 1 | −0.92 | — |
| W7A | (001) | 1 | 1 | −2.20 | −1.10 |
| W7B | (001) | 1 | 1 | −2.12 | −1.02 |
Fig. 2, 3, S1 and S2† show the optimized structures of the hydroxyl–HAp–water systems. The water molecule has two options on the surface, interacting with the Ca ion with or without a hydroxyl, which are denoted as A and B, respectively. In both cases, the co-addition of hydroxyl and one water molecule lowers the total energy and leads to a lower surface energy. The (010) facet has the greatest Eint, followed by (001) and (100), which is the same order as that of hydroxyl on the dry HAp surface. In the first case, the water molecule competes with hydroxyl. On (010), the Ca–OH distance changes from 2.12 Å to 2.20 Å after the addition of water. Meanwhile, the water molecule forms a hydrogen bond with the surface phosphate. The addition of a water molecule to some extent weakens the interaction between hydroxyl and surface Ca ion. Table 4 lists the interaction energies of the hydroxyl–HAp–water systems. On (010), the Eint of hydroxyl decreases from 1.48 eV to 1.17 eV. In the second case, water and hydroxyl are on different Ca ions. The water molecule almost retains its conformer in the absence of hydroxyl. The changes in the Ca–OH and Ca–OH2 distances are less than 0.1 Å, and the corresponding Eint of hydroxyl has a very small decrease of 0.22 eV. Therefore, the hydroxyl and water molecule may co-adsorb on the HAp surface, and have the option to locate at the Ca ion without a water molecule.
It has been found experimentally58,59 that HAp grows predominantly along the (001) direction, which means that (001) facet is unstable and has stronger interaction with adsorbates. However, in our work, hydroxyl and water molecules have weaker interaction with Ca ions on the (001) facet than on the (010) facet. It should be mentioned that the computed interaction energies reveal only the nucleophilic activity of surface Ca ions. The activity of other surface species such as phosphates is not considered. The computed interaction energy is therefore not an indicator of the preferred growth direction of HAp.
The interaction between hydroxyl and the Ca-rich HAp surface was further studied by computing the stretching vibrational frequencies of the Ca–O and O–H bonds. Table 5 lists the wavenumbers of the Ca–O and O–H bonds on the dry and hydrated (100), (010) and (001) facets. Although some studies56,57,60,61 have characterized the O–H vibrational frequency, the motion of the Ca–O bond has been seldom studied. The strong adsorption of hydroxyl and water and adsorption on the Ca-rich facets generates stretching vibrational motions for the Ca–O bonds with frequencies in the range of 360–450 cm−1 for Ca–OH2 and 380–550 cm−1 for Ca–OH. In general, the stretching vibrations of Ca–OH2 lie at lower frequencies than that of Ca–OH in the same surface structure, which corresponds well with the stronger interaction between HAp and hydroxyl. Moreover, for the same pattern, the formed Ca–O bonds on the (010) facet stretch at higher frequencies than that on (100) and (001). The frequencies for the F4 and W4 series are always higher than that of the F1, W1, F7 and W1 series, which is consistent with their interaction energy orders. On the same facet, the interaction pattern also has an effect on the vibrational frequency. The mono-adsorbed Ca–OH bonds in F1A, F4A and F7A have higher frequencies than the di-adsorbed Ca–OH bonds in the other patterns. Upon the water addition, the Ca–OH bonds exhibit red shifts of 3–35 cm−1. It is clear from the stretching frequencies and their changes that the surface Ca ions have strong interaction with hydroxyl, which is stronger than that between Ca–water, but slightly weakened on the hydrated surface.
| Pattern | Facet | Ca–OH | Ca–Ow | OH–H | Ow–H |
|---|---|---|---|---|---|
| F1A | (100) | 410 | — | 3783 | — |
| F1B | (100) | 407, 379 | — | 3746, 3723 | — |
| F1C | (100) | 401, 396 | — | 3765, 3751 | — |
| F4A | (010) | 548 | — | 3863 | — |
| F4B | (010) | 540, 509 | — | 3834, 3804 | — |
| F4C | (010) | 543, 530 | — | 3846, 3818 | — |
| F7A | (001) | 480 | — | 3809 | — |
| F7B | (001) | 474, 458 | — | 3801, 3785 | — |
| F7C | (001) | 451, 465 | — | 3799, 3804 | — |
| W1 | (100) | — | 360 | — | 3476 |
| W1A | (100) | 389 | 357 | 3743 | 3447 |
| W1B | (100) | 381 | 351 | 3732 | 3432 |
| W4 | (010) | — | 452 | — | 3672 |
| W4A | (010) | 537 | 449 | 3832 | 3631 |
| W4B | (010) | 507 | 442 | 3821 | 3579 |
| W7 | (001) | — | 415 | — | 3586 |
| W7A | (001) | 450 | 396 | 3795 | 3508 |
| W7B | (001) | 445 | 380 | 3786 | 3501 |
The O–H stretching vibrations of the hydroxyl groups on the HAp surfaces vary from 3723 cm−1 to 3863 cm−1. The corresponding frequency of the free hydroxyl is 3696 cm−1, which is in agreement with the previous computation of 3642 cm−1 (ref. 62) and measurement of 3738 cm−1 (ref. 62 and 63). Upon adsorption on the surface, the vibration moves to a lower wavenumber with a shift of 36–167 cm−1. The shifts are dependent on the interaction patterns and facets. The strong Ca–OH interaction usually leads to a large red shift. The addition of one water molecule leads to a blue shift in the Ca–OH vibration, which results from the weakening of the Ca–OH interaction. Experimentally, the band at 3570–3613 cm−1 (ref. 10, 60, 64 and 65) was assigned to column hydroxyl in bulk HAp. Some computational studies by the density function method predicted the OH stretching frequency at 3757 and 3774 cm−1 in crystal.66,67 A wide range of bands, including 3636, 3670, 3680, 3729, and 3734 cm−1, have been assigned for PO–H on the surface.60 The band at 3572 cm−1 was assigned to both column and surface hydroxyl56,60,61 when the measurement for surface hydroxyl was carried out upon CO2 adsorption on the HAp surface. Thus, the adsorbed CO2 made the band shift to a low wavenumber.
Conclusion
Density functional theory calculations with the PW91 functional and PAW pseudopotential were performed to study the bulk and surface structures of HAp, as well as their interaction with hydroxyl groups and water molecules. Our computed lattice parameters and surface structures of pure HAp agree well with previous computational and experimental studies. The interaction patterns of Ca-rich surfaces on the (100), (010) and (001) facets with one or two hydroxyl groups were constructed and optimized using a slab model. Strong bonding between the surface Ca ion and hydroxyl was noted. The interaction energies vary with the interaction pattern and facet. The (010) facet has the greatest interaction energy, followed by (001) and (100), which results from the different arrangements of Ca ions on the facets. Although the formation of CaOH or Ca(OH)2 is controversial in the literature, we found that both are energetically favorable on the HAp surface. The former is more favorable on the (001) and (100) facets, and the latter is more favorable on the (010) facet. The addition of a water molecule tends to weaken the Ca–OH interaction, but its interaction strength is weaker than that of Ca–OH. The interaction energy of Ca–OH is also dependent on the interaction pattern and facet. Calculations on the stretching vibration of surface Ca–O and O–H confirmed the bonding between the surface Ca ion and hydroxyl. Our calculations reveal a strong Ca–OH interaction on the Ca-rich HAp surface. Since HAp-based biomaterials are usually used in alkalescent physiological environment, the hydroxyl-coated surface structure is more appropriate than the Ca-terminated surface model for studying the surface activity of HAp toward biomolecules.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank financial support from National High Technology Research and Development Program of China (No. 2015AA034202) and National Natural Science Foundation of China (No. 21373140). Part of the calculations were carried out at High Performance Computing Center of Sichuan University.References
- J. Reyes-Gasga, R. Garcia and L. Vargas-Ulloa, Philos. Mag. A, 1997, 75, 1023–1040 CAS.
- L. A. Adams and E. R. Essien, J. Adv. Ceram., 2016, 5, 47–53 CrossRef CAS.
- P. Choudhury and D. C. Agrawal, Surf. Coat. Technol., 2011, 206, 360–365 CrossRef CAS.
- M. Wang, Biomaterials, 2003, 24, 2133–2151 CrossRef CAS PubMed.
- M.-H. Hong, D. S. Oh and Y.-K. Lee, Bone, 2011, 48, S186 CrossRef.
- R. M. Rajachar, A. Q. Truong and C. M. Giachelli, J. Mater. Sci.: Mater. Med., 2008, 19, 3279–3285 CrossRef CAS PubMed.
- J. Zeglinski, M. Nolan, D. Thompson and S. A. M. Tofail, Surf. Sci., 2014, 623, 55–63 CrossRef CAS.
- H. Kheimehsari, S. Izman and M. R. Shirdar, J. Mater. Eng. Perform., 2015, 24, 2294–2302 CrossRef CAS.
- N. Almora-Barrios and N. H. De Leeuw, Cryst. Growth Des., 2012, 12, 756–763 CAS.
- M. Yashima, Y. Yonehara and H. Fujimori, J. Phys. Chem. C, 2011, 115, 25077–25087 CAS.
- H. Chappell, M. Duer, N. Groom, C. Pickard and P. Bristowe, Phys. Chem. Chem. Phys., 2008, 10, 600–606 RSC.
- P. Rulis, H. Yao, L. Ouyang and W. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245410 CrossRef.
- C. Jager, T. Welzel, W. Meyer-Zaika and M. Epple, Magn. Reson. Chem., 2006, 44, 573–580 CrossRef PubMed.
- M. Ben Osman, S. Diallo-Garcia, V. Herledan, D. Brouri, T. Yoshioka, J. Kubo, Y. Millot and G. Costentin, J. Phys. Chem. C, 2015, 119, 23008–23020 CAS.
- H. B. Lu, C. T. Campbell, D. J. Graham and B. D. Ratner, Anal. Chem., 2000, 72, 2886–2894 CrossRef CAS PubMed.
- C. A. Ospina, J. Terra, A. J. Ramirez, M. Farina, D. E. Ellis and A. M. Rossi, Colloids Surf., B, 2012, 89, 15–22 CrossRef CAS PubMed.
- K. Sato, T. Kogure, T. Ikoma, Y. Kumagai and J. Tanaka, Key Eng. Mater., 2000, 192, 283–286 Search PubMed.
- M. Rivas, J. Casanovas, L. J. Del Valle, O. Bertran, G. Revilla-Lopez, P. Turon, J. Puiggalí and C. Alemán, Dalton Trans., 2015, 44, 9980–9991 RSC.
- Q. Wang, M. Wang, K. Wang, Y. Liu, H. Zhang, X. Lu and X. Zhang, Biomed. Mater., 2015, 10, 032001 CrossRef PubMed.
- W. Zhu and P. Wu, Chem. Phys. Lett., 2004, 396, 38–42 CrossRef CAS.
- L. J. Del Valle, O. Bertran, G. Chaves, G. Revilla-Lopez, M. Rivas, M. T. Casas, J. Casanovas, P. Turon, J. Puiggalí and C. Alemán, J. Mater. Chem. B, 2014, 2, 6953–6966 RSC.
- A. Slepko and A. A. Demkov, J. Chem. Phys., 2013, 139, 044714 CrossRef PubMed.
- N. Almora-Barrios, K. F. Austen and N. H. De Leeuw, Langmuir, 2009, 25, 5018–5025 CrossRef CAS PubMed.
- M. R. T. Filgueiras, D. Mkhonto and N. H. De Leeuw, J. Cryst. Growth, 2006, 294, 60–68 CrossRef CAS.
- A. Rimola, M. Corno, C. M. Zicovich-Wilson and P. Ugliengo, J. Am. Chem. Soc., 2008, 130, 16181–16183 CrossRef CAS PubMed.
- W. Zhao, Z. Xu, Y. Yang and N. Sahai, Langmuir, 2014, 44, 13283–13292 CrossRef PubMed.
- M. Prakash, T. Lemaire, D. Di Tommaso, N. H. De Leeuw, M. Lewerenz, M. Caruel and S. Naili, Appl. Surf. Sci., 2017, 418, 296–301 CrossRef CAS.
- D. Zahn and O. Hochrein, Phys. Chem. Chem. Phys., 2003, 5, 4004–4007 RSC.
- J. O'Young, Y. Liao, Y. Xiao, J. Jalkanen, G. Lajoie, M. Karttunen, H. A. Goldberg and G. K. Hunter, J. Am. Chem. Soc., 2011, 133, 18406–18412 CrossRef PubMed.
- J.-W. Shen, T. Wu, Q. Wang and H.-H. Pan, Biomaterials, 2008, 29, 513–532 CrossRef CAS PubMed.
- T. T. Pham, T. Lemaire, E. Capiez-Lernout, M. Lewerenz, Q. D. To, J. K. Christie, D. Di Tommaso, N. H. de Leeuw and S. Naili, Theor. Chem. Acc., 2015, 134, 59 CrossRef.
- S. E. Ruiz Hernandez, N. H. De Leeuw and I. Streeter, Phys. Chem. Chem. Phys., 2015, 17, 22377–22388 RSC.
- S. Hokkanen, A. Bhatnagar, E. Repo, S. Lou and M. Sillanpää, Chem. Eng. J., 2016, 283, 445–452 CrossRef CAS.
- L. Chen, K.-S. Zhang, J.-Y. He, W.-H. Xu, X.-J. Huang and J.-H. Liu, Chem. Eng. J., 2016, 285, 616–624 CrossRef CAS.
- J. Brzezińska-Miecznik, P. Jeleń, K. Haberko, W. Mozgawa and M. Sitarz, Ceram. Int., 2017, 43, 12540–12545 CrossRef.
- J. He, Y. Su, T. Huang, B. Jiang, F. Wu and Z. Gu, Colloids Surf., B, 2014, 116, 303–308 CrossRef CAS PubMed.
- A. Michelot, S. Sarda, C. Audin, E. Deydier, E. Manoury, R. Poli and C. Rey, J. Mater. Sci., 2015, 50, 5746–5757 CrossRef CAS.
- J. Zhang, X. Liu, T. Deng, P. Yao, H. Song, S. Zhou and W. Yan, J. Nanomater., 2015, 16, 145 Search PubMed.
- B. T. Mortensen, P. O. Jensen, N. Helledie, P. O. Iversen, E. Ralfkiaer, J. K. Larsen and M. T. Madsen, Br. J. Haematol., 1998, 102, 458–464 CrossRef CAS PubMed.
- D. H. Kohn, M. Sarmadi, J. I. Helman and P. H. Krebsbach, J. Biomed. Mater. Res., 2002, 60, 292–299 CrossRef CAS PubMed.
- J. Kolmas, D. Marek and W. Kolodziejski, Appl. Spectrosc., 2015, 69, 902–912 CrossRef CAS PubMed.
- L. Bertinetti, A. Tampieri, E. Landi, C. Ducati, P. A. Midgley, S. Coluccia and G. Martra, J. Phys. Chem. C, 2007, 111, 4027–4035 CAS.
- K. Wang, M. Wang, Q. Wang, X. Lu and X. Zhang, J. Eur. Ceram. Soc., 2017, 37, 2509–2520 CrossRef CAS.
- T. Biktagirov, M. Gafurov, K. Iskhakova, G. Mamin and S. Orlinskii, J. Low Temp. Phys., 2016, 185, 627–632 CrossRef CAS.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Renaudin, P. Laquerriere, Y. Fillinchuk, E. Jallot and J. M. Nedelec, J. Mater. Chem., 2008, 18, 3593–3600 RSC.
- R. Astala and M. J. Stott, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075427 CrossRef.
- G. Ulian, D. Moro and G. Valdre, J. Appl. Crystallogr., 2016, 49, 1893–1903 CAS.
- D. Mei, J. Phys. Chem. C, 2010, 114, 1867–1874 CAS.
- N. H. De Leeuw, J. Mater. Chem., 2010, 20, 5376–5389 RSC.
- F. Chiatti, M. Delle Piane, P. Ugliengo and M. Corno, Theor. Chem. Acc., 2016, 135, 54 CrossRef.
- J. C. Elliot, Structure and Chemistry of the Apatites and Other Calcium Orthophosphates, Elsevier, Amsterdam, 1994, pp. 1–404 Search PubMed.
- S. Diallo-Garcia, M. Ben Osman, J.-M. Krafft, S. Casale, C. Thomas, J. Kubo and G. Costentin, J. Phys. Chem. C, 2014, 118, 12744–12757 CAS.
- V. Bolis, C. Busco, G. Martra, L. Bertinetti, Y. Sakhno, P. Ugliengo, F. Chiatti, M. Corno and N. Roveri, Philos. Trans. R. Soc., A, 2012, 370, 1313–1336 CrossRef CAS PubMed.
- J. P. Simmer and A. G. Fincham, Crit. Rev. Oral Biol. Med., 1995, 6, 84 CAS.
- T. Kobayashi, S. Ono, S. Hirakura, Y. Oaki and H. Imai, CrystEngComm, 2012, 14, 1143–1149 RSC.
- S. Diallo-Garcia, M. Ben Osman, J.-M. Krafft, S. Boujday and C. Guylène, Catal. Today, 2014, 226, 81–88 CrossRef CAS.
- S. Nakamura, H. Takeda and K. Yamashita, J. Appl. Phys., 2001, 89, 5386–5392 CrossRef CAS.
- H.-T. Chen, Y. M. Man Choi, M. Liu and M. C. Lin, ChemPhysChem, 2007, 8, 849–855 CrossRef CAS PubMed.
- S. P. Walch, C. M. Rohlfing, C. F. Melius and C. W. Bauschlicher Jr, J. Chem. Phys., 1988, 88, 6273–6281 CrossRef CAS.
- E. Balan, S. Delattre, D. Roche, L. Ségalen, G. Morin, M. Guillaumet, M. Blanchard, M. Lazzeri, C. Brouder and E. K. H. Salje, Phys. Chem. Miner., 2011, 38, 111–122 CrossRef CAS.
- H. Tanaka, T. Watanabe and M. Chikazawa, J. Chem. Soc., Faraday Trans., 1997, 93, 4377–4381 RSC.
- M. Corno, C. Busco, B. Civalleri and P. Ugliengo, Phys. Chem. Chem. Phys., 2006, 8, 2464–2472 RSC.
- G. Ulian, G. Valdre, M. Corno and P. Ugliengo, Am. Mineral., 2013, 98, 752–759 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra13121f |
| This journal is © The Royal Society of Chemistry 2018 |