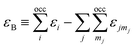Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Retracted Article: A highest stable cluster Au58 (C1) re-optimized via a density-functional tight-binding (DFTB) approach†
K. Vishwanathan * and
M. Springborg
* and
M. Springborg
Physical and Theoretical Chemistry, University of Saarland, 66123 Saarbrücken, Germany. E-mail: vishwa_nathan_7@yahoo.com; Tel: +49-0151-63119680
First published on 21st March 2018
Abstract
The vibrational spectrum ωi of a re-optimized neutral gold cluster Au58 has been calculated using a numerical finite-difference approach and the density-functional tight-binding (DFTB) method. We have exactly predicted the vibrational frequency ranging from 3.88 through to 304.49 cm−1 which depends on the size and the arrangement of the atoms in the nanoparticle morphology of the cluster at ΔE = 0. Our investigation has revealed that the vibrational spectrum is strongly influenced by size and structure. It is well known that gold atomic clusters can have planar or hollow cage-like structures due to their relativistic effect. However, in our study, by first principles calculations on a Au58 cluster we have proposed that gold clusters of medium size can form a shell-like structure (skeleton/helmet), this is demonstrated by the remarkable robustness of a double shell structure with a hollow inner shell of about ten atoms. Finally, the structure symmetry (C1) is confirmed through the cluster size, vibrational spectroscopy, and by studying the effect of temperature on a neutral gold cluster for the first time.
Introduction
The study of nanostructured materials exhibiting novel properties is one of the most fascinating fields in current research. Small nanomaterials are of particular interest because of their intriguing characteristics.1–4 Nanoparticles with smaller dimensions may exhibit different properties in comparison to bulk material. Nanoparticles possess unique physico-chemical, optical, and biological properties which can be suitably manipulated for a desired application.5The vibrational properties of clusters and small particles have been studied very thoroughly,6–13 and are vital for understanding and describing the atomic interactions within a cluster.14–19 Thermal properties like heat capacity and thermal conductivity, as well as many other material properties, are strongly influenced by the vibrational density of states (VDOS). For this reason, a better understanding of the rules governing the vibrational properties of nanostructured materials is of high technological importance and must be given a high priority. The vibrational properties play a major role in the structural stability.12,13,20,21
In addition to that, the size-dependent properties of metallic clusters are currently of considerable interest, both experimentally22 and theoretically.11,23 Although the size effect on specific heat capacity has recently received great attention,24 many publications only focus on low temperatures.25 Some of the theoretical studies on the thermodynamic properties of clusters are based on molecular-dynamic simulations26 from which the caloric curve, the heat capacity of clusters, and the phase transitions can be determined. Nanoclusters are interesting because their physical, optical and electronic characteristics are strongly size dependent. Often changing their size by only one atom can significantly alter the physical chemical properties of the system.27 Many new periodic tables can therefore be envisioned which classify different-sized clusters of the same material as new elements. The potential applications are enormous, ranging from devices in nano-electronics and nano-optics28 to applications in medicine and materials.
Very often, gold chemistry plays a very important role in nanoelectronics and bionanosciences.29 Gold clusters are of potential relevance in the nanoelectronics industry and hence remain the subject of many experimental as well as theoretical studies. Clusters differ from the bulk material because they contain edge atoms which have a low coordination3,4,19,30 and can adopt binding geometries which lead to a more reactive electronic structure.31 Gold in the nanoregime, especially gold nanocrystals, has been shown to have size-sensitive reactive properties and is considered to be a promising chemical catalyst.32–34 As one of the noble metals, gold has good corrosion resistance and an extremely high stability, and has been widely researched for biomedical applications.35
Most recently, a very few researchers reported that in gold clusters, from Au21 to Au35, the structure evolves from pyramidal to tubular, and then to a core–shell structure.36 The global minimum of Au40 has been predicted, by first principles basin hopping, to have a twisted pyramid structure with a tetrahedral Au4 core.37 One of the largest Au clusters explored by DFT is Au58 and the putative global minimum was found to have a double-shell structure of Au10@Au44 with C1/C4 symmetry which was calculated by Dong et al.,38 and Runhai et al.39 The main reason is that the core–shell structure can be considered as an intermediate phase between cage-like structures of smaller clusters and compact structures of the bulk material.
Generally speaking, the larger gold clusters pose major challenges because of their structural diversity.40–42 Nevertheless, it should be pointed out that these clusters are quite complex and computationally extremely challenging. Wei Huang et al.,43 focused on gold clusters with 55 to 64 atoms using photoelectron spectroscopy (PES) of size-selected anions, and first principles calculations. They found that Au58 exhibits a major electron-shell closing and is shown to possess low-symmetry, but a nearly spherical structure with a large energy gap. Clear spectroscopic and computational evidence has been observed, showing that Au58 is a highly robust cluster and additional atoms are simply added to its surface, from Au59 to Au64, without inducing significant structural changes.43 Above all, some more detailed information can be found in the recently reviewed article by Lei-Ming Wang and Lai-Sheng Wang.44
More significantly, it becomes increasingly difficult to perform global minimization for larger Au clusters (say, n > 50) using first principles methods such as density functional theory (DFT) due to the exponential increase of the local minima number with size45,46 and the nonlinear scaling of the computational cost (roughly n3 for DFT). In this context, alternative methods such as empirical potentials were often employed,39,47–50 such as the Rosato–Guillope–Legrand potentials for Au clusters up to 318 atoms,47 Sutton-Chen embedded atom potentials for Pt55 and Au55,48 and effective-medium-theory potentials for Au147 and Au309.51 Most empirical potentials, however, are not accurate enough and can sometimes lead to unreliable predictions.36,46,48
Subsequently, our newly developed numerical method for computational science and engineering has given a new deep insight into the vibrational spectra that can be obtained from gold clusters with up to 20 atoms.52–55 The structures were found through a so called genetic algorithm (GA) in combination with Density Functional Tight-Binding (DFTB) energy calculations and a steepest descent algorithm which permit a local total energy minimization studied by Dong and Springborg.56 However, upon knowing that there are great computational challenges for bigger clusters,45,46 for example Au58, through our model we have confirmed the symmetric structure of the cluster via the size and the temperature effect. Therefore, with this, we can confirm that the DFTB models and the calculations can now allow one to treat a broad range of systems (molecules, clusters and solids), and their computational efficiency enables one to consider systems with up to several hundreds of atoms with respect to a proper computational set up, this is the brilliance of our method of calculations.
In this study we have combined a numerical finite-difference approach along with density functional tight-binding (DFTB) method. At ΔE = 0 K, the vibrational frequency of the optimized neutral gold cluster Au58 (ref. 56) was extracted through a re-optimization process. The desired set of system eigenfrequencies (3N − 6) was obtained by a diagonalization of the symmetric positive semidefinite Hessian matrix. The effect of the range of interatomic forces has been studied.
Theoretical and computational procedure
The DFTB57–59 is based on the density functional theory of Hohenberg and Kohn in the formulation of Kohn and Sham. In addition, the Kohn–Sham orbitals ψi(r) of the system of interest are expanded in terms of atom-centered basis functions {ϕm(r)},
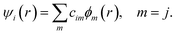 | (1) |
While so far the variational parameters have been the real-space grid representations of the pseudo wave functions, it will now be the set of coefficients cim. Index m describes the atom, where ϕm is centered and it is angular as well as radially dependant. The ϕm is determined by self-consistent DFT calculations on isolated atoms using large Slater-type basis sets.
In calculating the orbital energies, we need the Hamilton matrix elements and the overlap matrix elements. The above formula gives the secular equations
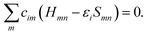 | (2) |
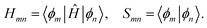 | (3) |
They depend on the atomic positions and on a well-guessed density ρ(r). By solving the Kohn–Sham equations in an effective one particle potential, the Hamiltonian Ĥ is defined as
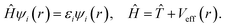 | (4) |
To calculate the Hamiltonian matrix, the effective potential Veff has to be approximated. Here, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) being the kinetic-energy operator
being the kinetic-energy operator 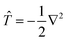 and Veff(r) being the effective Kohn–Sham potential, which is approximated as a simple superposition of the potentials of the neutral atoms,
and Veff(r) being the effective Kohn–Sham potential, which is approximated as a simple superposition of the potentials of the neutral atoms,
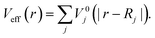 | (5) |
The short-range interactions can be approximated by simple pair potentials, and the total energy of the compound of interest relative to that of the isolated atoms is then written as,
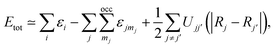 | (6) |
here, the majority of the binding energy (εB) is contained in the difference between the single-particle energies εi of the system of interest and the single-particle energies εjmj of the isolated atoms (atom index j, orbital index mj), Ujj′(|Rj − Rj′|) is determined as the difference between εB and εSCFB for diatomic molecules (with εSCFB being the total energy from parameter-free density-functional calculations). In the present study, only the 5d and 6s electrons of the gold atoms are explicitly included, whereas the rest are treated within a frozen-core approximation.57,59,60
Computational challenges: re-optimization process and numerical force constants (FCs)
In our study, we have calculated the numerical first-order derivatives of the forces (Fiα, Fjβ) instead of the numerical-second-order derivatives of the total energy (Etot). In principle, there is no difference, but numerically the approach of using the forces is more accurate,
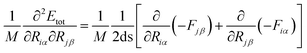 | (7) |
It is a reasonable value and allows us to discriminate between the translational motion, the rotational motion (zero-eigenvalues) and the vibrational motion (non-zero-eigenvalues).
Calculation of heat capacity of clusters
The specific heat capacity is a measurable physical quantity that characterizes the ability of a body to store heat when the sample temperature is changed. The effect of body size on the specific heat capacity has recently attracted a lot of attention.62–65 Now we proceed to calculate the specific heat contribution due to vibrational energy.The Helmholtz free energy
| F = U − TS. | (8) |
| Uvib = Fvib + TSvib | (9) |
For the moment, we only need to focus on the vibrational part of the free energy. We start with Fvib = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(z) and substitute in the eqn below,
ln(z) and substitute in the eqn below,
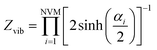 | (10) |
in which NVM is the number of normal vibrational modes of the cluster. The above calculations were used to examine the Helmholtz free energy of the clusters as a function of temperature.
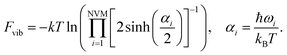 | (11) |
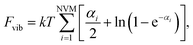 | (12) |
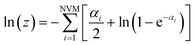 | (13) |
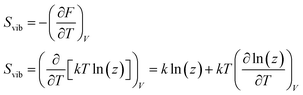 | (14) |
As we mentioned before, as the heat capacity of a material is directly related to the atomic structure, measurements of heat capacity as a function of temperature could provide information about the structural properties of nanostructured materials. The vibrational frequencies dependent upon the molecular structure.
The vibrational contribution to the heat capacity of a system of interest is the derivative of the vibrational energy with respect to the temperature. It can be calculated by
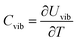 | (15) |
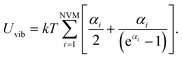 | (16) |
Combining eqn (15) and (16) eventually yields an equation linking together the cluster’s set of eigen-frequencies and its vibrational heat capacity:
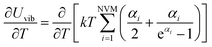 | (17) |
Finally, we can obtain the formula to investigate size, structure and temperature effects on the heat capacity of clusters
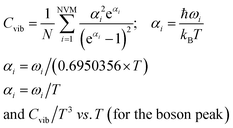 | (18) |
| 0.6950356 = [h(6.626 × 10−34 J s)c(2.9979 × 1010 cm s−1)/kB(1.380 × 10−23 J K−1)]−1. |
Zero vibrational modes are excluded from the summation in eqn (18). N is the size of the atomic clusters.
Results and discussion
In this article, we present an in-depth study on the behavior of vibrational frequency (at ΔE = 0) and heat capacity (at T = 300 K) of the re-optimized neutral gold cluster (AuN, N = 58). We have found that the vibrational frequencies depend upon the cluster size and structure.The vibrational frequency (ωi) range of Au58
Table 1 shows the low (at the least) and the high (at the most) frequency range of the Au58 cluster. The lowest and the highest frequency are in the range between 3.88 cm−1 and 304.49 cm−1.| Normal vibrational modes (NVM (3N − 6) = 1–168) and Vibrational frequency (ωi) in cm−1; N − is the total number of atoms (size) in a cluster | |||||||
|---|---|---|---|---|---|---|---|
| NVM | ωi | NVM | ωi (cm−1) | NVM | ωi (cm−1) | NVM | ωi (cm−1) |
| 1 | 3.88 | 43 | 34.98 | 85 | 85.72 | 127 | 170.40 |
| 2 | 4.46 | 44 | 35.37 | 86 | 86.39 | 128 | 171.18 |
| 3 | 4.77 | 45 | 36.29 | 87 | 87.54 | 129 | 172.29 |
| 4 | 5.44 | 46 | 37.07 | 88 | 89.86 | 130 | 176.02 |
| 5 | 5.74 | 47 | 38.23 | 89 | 90.56 | 131 | 178.66 |
| 6 | 7.36 | 48 | 38.99 | 90 | 93.60 | 132 | 181.60 |
| 7 | 7.76 | 49 | 39.44 | 91 | 96.19 | 133 | 184.48 |
| 8 | 8.45 | 50 | 41.34 | 92 | 97.26 | 134 | 186.36 |
| 9 | 8.64 | 51 | 41.65 | 93 | 97.46 | 135 | 188.21 |
| 10 | 9.68 | 52 | 42.36 | 94 | 100.32 | 136 | 190.92 |
| 11 | 10.06 | 53 | 43.27 | 95 | 102.74 | 137 | 194.11 |
| 12 | 10.70 | 54 | 44.12 | 96 | 105.09 | 138 | 197.16 |
| 13 | 12.04 | 55 | 45.86 | 97 | 107.14 | 139 | 199.79 |
| 14 | 12.41 | 56 | 47.03 | 98 | 108.92 | 140 | 200.56 |
| 15 | 12.71 | 57 | 47.49 | 99 | 111.30 | 141 | 201.90 |
| 16 | 13.64 | 58 | 48.27 | 100 | 112.12 | 142 | 202.66 |
| 17 | 14.07 | 59 | 49.01 | 101 | 115.72 | 143 | 208.03 |
| 18 | 14.35 | 60 | 50.90 | 102 | 115.94 | 144 | 209.58 |
| 19 | 15.66 | 61 | 52.00 | 103 | 119.80 | 145 | 211.21 |
| 20 | 16.44 | 62 | 52.52 | 104 | 121.62 | 146 | 213.83 |
| 21 | 17.62 | 63 | 52.97 | 105 | 123.39 | 147 | 214.63 |
| 22 | 18.10 | 64 | 54.99 | 106 | 124.18 | 148 | 220.05 |
| 23 | 18.99 | 65 | 57.44 | 107 | 128.27 | 149 | 223.46 |
| 24 | 19.11 | 66 | 57.84 | 108 | 129.54 | 150 | 224.87 |
| 25 | 20.02 | 67 | 59.19 | 109 | 133.18 | 151 | 228.62 |
| 26 | 21.12 | 68 | 60.96 | 110 | 134.01 | 152 | 230.99 |
| 27 | 21.60 | 69 | 62.11 | 111 | 135.11 | 153 | 236.98 |
| 28 | 22.34 | 70 | 62.57 | 112 | 136.70 | 154 | 238.10 |
| 29 | 23.28 | 71 | 64.75 | 113 | 139.08 | 155 | 241.91 |
| 30 | 23.67 | 72 | 65.90 | 114 | 141.77 | 156 | 244.29 |
| 31 | 24.14 | 73 | 66.86 | 115 | 145.20 | 157 | 247.75 |
| 32 | 24.93 | 74 | 68.07 | 116 | 146.83 | 158 | 249.31 |
| 33 | 25.65 | 75 | 69.18 | 117 | 150.08 | 159 | 253.31 |
| 34 | 26.37 | 76 | 72.58 | 118 | 151.83 | 160 | 255.06 |
| 35 | 26.80 | 77 | 73.84 | 119 | 152.23 | 161 | 258.95 |
| 36 | 29.09 | 78 | 75.03 | 120 | 154.27 | 162 | 269.92 |
| 37 | 29.46 | 79 | 77.34 | 121 | 157.71 | 163 | 272.17 |
| 38 | 30.10 | 80 | 78.98 | 122 | 160.14 | 164 | 282.61 |
| 39 | 31.61 | 81 | 79.43 | 123 | 161.87 | 165 | 283.31 |
| 40 | 31.86 | 82 | 80.87 | 124 | 163.58 | 166 | 287.11 |
| 41 | 32.99 | 83 | 82.98 | 125 | 166.98 | 167 | 298.72 |
| 42 | 33.59 | 84 | 83.58 | 126 | 167.08 | 168 | 304.49 |
Firstly, the cluster has some low frequency (ωmin) ranges between 3.88 and 9.68 cm−1, this is only for the first 10 normal vibrational modes (NVM), and are below the scale of Far Infrared FIR, IR-C 200–10 cm−1.
Secondly, the frequency ranges between 10.06 and 199.79 cm−1 for the 11–139 normal vibrational modes (NVM) are within the range of Far Infrared FIR, IR-C 200–10 cm−1.
Thirdly, for the rest of the normal vibrational modes (NVM) 140–168, the maximum high frequency (ωmax-200.56–304.49 cm−1) falls within the range of Mid Infrared MIR, IR-C 3330–200 cm−1.
The double and the triple state degeneracy of Au58 at ΔE = 0
The vibrational spectra of the eigenvalues were found within the range of 3.88 and 304.49 cm−1. We have observed that most of the 122 eigenvalues are non-degenerate (single state) vibrations.More significantly, due to the interactions between the repulsive and attractive forces of the excellent motions of the atoms, 40 of the normal modes released 20 pairs of double state degeneracies which are [(4.46, 4.77), (5.44, 5.74), (7.36, 7.76), (8.45, 8.64), (10.06, 10.70), (14.07,14.35), (18.10, 18.99), (21.12, 21.60), (23.28, 23.67), (24.14, 24.93), (26.37, 26.80), (29.09, 29.46), (31.61, 31.86), (38.23, 38.99), (41.34, 41.65), (47.03, 47.49), (57.44, 57.84), (62.11, 62.57), (97.26, 97.46), (115.72, 115.94), units in cm−1].
At the same time, 2 sets of the triple state degeneracy have been observed: [NVM 13, 14, 15 → (12.04, 12.41, 12.71) cm−1] and [NVM 61, 62, 63 → (52.00, 52.52, 52.97) cm−1] which are in the range of Far Infrared FIR, IR-C 200–10 cm−1.
The above information indicates that some of the atoms are vibrating with the same level of frequency, and release an equal amount of energy as well as absorbing the same amount of energy when the Au58 cluster is exposed to photon energy (see Table 1), where it can be stored up. This was strongly confirmed through the vibrational heat capacity (see Fig. 6). This is a very strong confirmation of the structural stability and can also give a deep insight into the surface morphology of the cluster.
Interestingly, it was noticed that the first 4 pairs of double state degeneracy occur below the scale of Far Infrared FIR, IR-C 200–10 cm−1 (see Table 1). It may not be possible to observe such kinds of frequency in experimental calculations or if they are observed, they will be very difficult to detect. The main reason could be that short and long range forces of attraction of atoms have played a major role within the cluster. This means that there is a minute energy gap between the outermost orbits or valence electrons which are due to atoms being more strongly bonded with more charge.
The unique low-symmetric structures of the gold clusters observed at this critical size may provide key insights into the catalytic effects of gold nanoparticles. The protruding surface atoms are expected to become the active sites for chemical reactions. Thus, we only focused on and discussed selectively relevant literature.38,43,44
Comparison to other investigations
First of all, we must remember that photoelectron spectroscopy (PES) on anionic clusters yields spectroscopic information on the corresponding neutral species, which are often of interest. The most stable cluster structure can be obtained through comparison of the well resolved PES spectrum with simulated densities of states (DOSs) for a pool of potential structures gathered from either known structural motifs or global minimum search algorithms. Although having low symmetries, starting from n = 56 and onward, the structures of Aun− clusters has a clear core-shell motifs, in contrast to the amorphous-like Au55−. Specifically, Au56− and Au57− both consist of a central atom core and a 10-atom first shell with a 45-atom and 46-atom second shell, respectively; Au58 possesses a central atom core, an 11-atom first shell, and a 46-atom outer shell with 6 surface “square-defects”. The Au58 cluster is nearly spherical, with the ratio between its three principal axes of 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0
1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0, and structurally very robust. The neutral Au58 is a major shell closing (1S21P61D102S21F142P61G18) optimized structure and PES spectra of Au58 indeed revealed a large HOMO–LUMO gap.36 Thus, the Au58 cluster is both a geometrically and electronically stable cluster. Nevertheless, most importantly for core–shell structures, the relative size of the inner core and the outer shell is a fundamental aspect of the structural property and would most probably dramatically influence the stability of the cluster.38
1.0, and structurally very robust. The neutral Au58 is a major shell closing (1S21P61D102S21F142P61G18) optimized structure and PES spectra of Au58 indeed revealed a large HOMO–LUMO gap.36 Thus, the Au58 cluster is both a geometrically and electronically stable cluster. Nevertheless, most importantly for core–shell structures, the relative size of the inner core and the outer shell is a fundamental aspect of the structural property and would most probably dramatically influence the stability of the cluster.38
Both anions and neutral clusters were calculated by Wei Huang et al.,43 and they were found to exhibit very similar structures, which is consistent with the sharp photoelectron spectra (PES) peaks. The PES spectra represent approximately the occupied electron density of states (DOS) of the negatively charged clusters. Moreover, as pointed out by Taylor et al.,66 the lower binding energy features, from about 3.5 to 5.5 eV, come primarily from the Au 6s states whereas the congested PES features beyond 5.6 eV are mainly derived from the Au 5d band.
Naturally, as the size increases the clusters will show more metallic behavior, in this case, the s-electrons become more delocalized, favoring more compact structures with higher coordination. When the cluster grows to a certain size range the compromise of RE-enhanced s–d hybridization and the s-electrons’ delocalization would give rise to structures in the core–shell configuration. In this configuration, the coordination is improved due to the existence of an inner core, while the outer shell may still be stabilized by the RE-induced s-d hybridization which causes surface contraction.40,43,67–69 Thus, the core–shell structure can be considered as an intermediate phase between the cage-like structure of smaller clusters and the compact structure of the bulk material. The existence of the core–shell structures has been proven by recent studies on Au34, Au58, and ligand-protected gold clusters.40,43,67–69
Our calculation is in excellent agreement with the symmetric structure (C1/C4) of Dong et al.,38 and Runhai Ouyang et al.,39 their isomer has (C1/C4) symmetry and is of a prolate spheroid shape with two squares at the top and bottom. It comprises a 48-atom outer shell and a 10-atom inner core. Remarkably, a major driving force in the cluster is the creation of a closer-packed surface layer because of the strong relativistic effects even at the expense of the inner core.43 Most significantly, we have also observed that many different kinds of shape exist in the Au58 cluster, for example; different sets of triangles, squares, zig-zags, and hexagonal and pentagonal (regular, irregular and cyclic) shapes, which are nothing but a combination of many varieties of symmetries. This has been strongly reflected in the vibrational frequencies (see Table 1). In particular, the outer shell of Au58 is composed of triangles like the Au(111) surface, with some local defects such as pentagons and squares.38
To study the dependence of stability on the core–shell size, the existing core–shell structures are important starting points. A spherical structure of Au58 was recently reported by Wei Huang et al.,43 it consists of a 46-atom outer shell and a 12-atom inner core. The inner core can be roughly considered as a centered icosahedron with one corner atom missing. The region around the missing atom just below the outer shell forms a small bubble. At the same time, by using the genetic algorithm, a structure with 11 inner atoms forming a centered pentagon prism was obtained by Dong and Gong.38 A structure with a smaller core might be more stable.
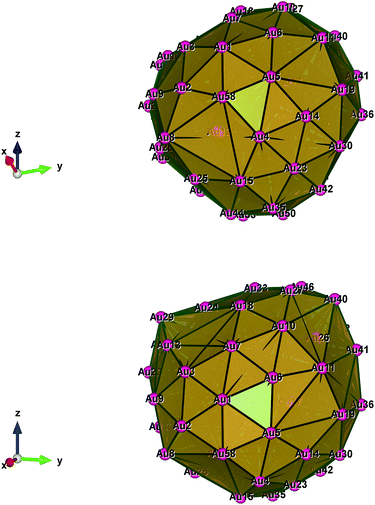
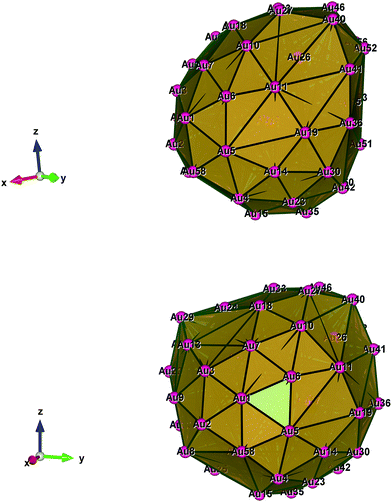
Fig. 1–5 show a diamond shape from the top view of a Au29 atom, and each atom forms bonds with four nearest neighbours (the enclosed angles are 109.47°). In our case, the total energy is −4.95 eV per atom for Au58, with the most stable structure having only one ground state isomer.56 Fig. 4 and 5, clearly show the pentagonal and hexagonal (as a benzene ring) shapes that can be seen along the a-axis, the view along the b-axis and the view along the c-axis (from top to bottom). In one case, we are looking down the direct space a, b, or c axis and in the other case we are looking down the reciprocal space a*, b*, and c* axes. Here, a*, b*, c* are directions of reciprocal lattice vectors. They do not make sense for a cluster which is not periodic. Anyway, the vectors a, b, c are somehow defined, and the a*, b*, c* are formally assigned. Since the coordinate system is orthogonal, a*‖a, b*‖b and c*‖c, logically, we don’t see any difference in the cartesian coordinates. Whatever is shown is the structure (in direct space) with the coordinate system (in direct space). If we select an orientation of our figure with respect to a*/b*/c* only the orientation may change, not the structure.
 | ||
| Fig. 1 Style (polyhedral), Au58 (C1/C4): rotate around the X-axis (top) and standard orientation of crystal shape (bottom). | ||
 | ||
| Fig. 2 Style (polyhedral), Au58 (C1/C4): rotate around the Y-axis (top) and standard orientation of crystal shape (bottom). | ||
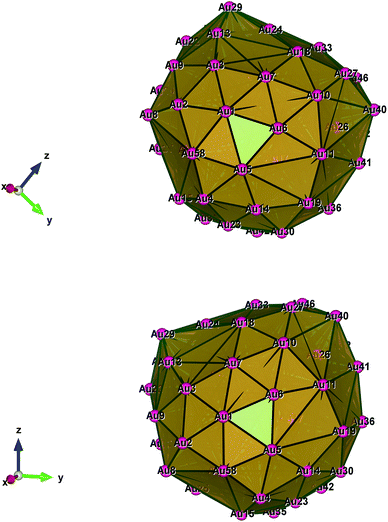 | ||
| Fig. 3 Style (polyhedral), Au58 (C1/C4): rotate around the Z-axis (top) and standard orientation of crystal shape (bottom). | ||
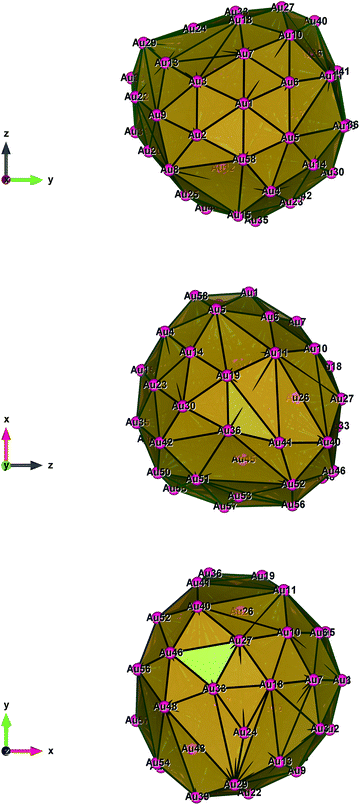 | ||
| Fig. 4 Style (polyhedral), Au58 (C1/C4): view along the a-axis, view along the b-axis and view along the c-axis (from top to bottom). | ||
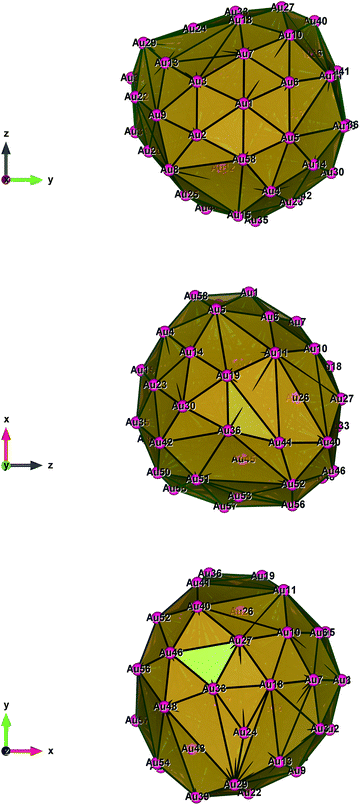 | ||
| Fig. 5 Style (polyhedral), Au58 (C1/C4): view along the a*-axis, view along the b*-axis and view along the c*-axis (from top to bottom). | ||
Apparently, the prominent minimum at ten inner atoms indicates that the Au58 cluster acquires the highest stability with an optimal relative core–shell size. The existence of an optimal relative core–shell size is easy to understand. Since the total number of atoms is fixed, a larger core shell must lead to a smaller surface shell. A structure with a too large inner core and a too small outer shell would be subject to large surface strain, whereas a small core and a large shell would sacrifice the core–shell binding due to the large difference between the radii of the surface shell and the inner shell. We can see that the surface bonds are generally shorter than other bonds and are particularly shorter than the bonds between inner atoms and outer ones. As the number of inner atoms increases, the average core–shell distance becomes shorter and the surface bonds become longer. This leads to repulsion between the two shells and thus weakens the RE-induced strong bonding of the outer shell.38
The main difference lies in the shell structure reported by Runhai Ouyang et al.,39 in which the outer shell of one of their isomers has two squares at the two ends (top and bottom) of the prolate spheroid and eight five-coordinated Au atoms symmetrically distributed on the shell. Nevertheless, with excellent agreement, the outer shell of the Dong and Gong38 DG structure has a diamond at one end and a square at the other end; there are 10 five-coordinated Au atoms on the shell. Therefore, we are sure that the higher symmetry of our structure leads to its higher stability.
Vibrational heat capacity of Au58
In Fig. 6, we have plotted Cvib vs. T at T = 0.75–300 K, in order to prove the influence of the size and the temperature effect upon the cluster. In particular, there is a sudden rise in the Cvib curve which is due to the low frequency starting point of the cluster. Our investigation has revealed that the Cvib curve is strongly influenced by the temperature, the size, the structure and the bond-order. The effect of the range of interatomic forces was studied; in particular, the lower frequencies make a significant contribution to the heat capacity at low temperatures. However, no experimental data is available for comparison. Surprisingly, the Cvib curve is a monotonously increasing function of T (which tends asymptotically). The temperature dependence of the individual modes leads to the total vibrational heat capacity for the cluster.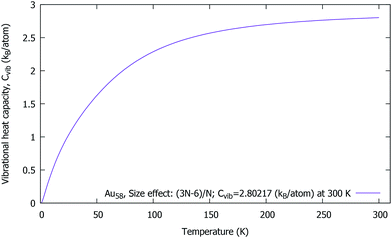 | ||
| Fig. 6 Au58 (C1/C4): the vibrational heat capacity Cvib vs. T of a neutral gold cluster at 0.75–300 K. | ||
Interestingly, we found that the Cvib curve of a neutral gold cluster increases smoothly towards the high temperatures and approaches a constant value, Cvib = 2.80 kB per atom at 300 K, and essentially becomes flat. Moreover, the expected absolute value (for size-dependence) should be Cvib = 2.90 kB per atom. In our study, the difference is only 0.10 kB per atom from the absolute value, which is very reasonable within the numerical approach. At the end, the Cvib curve almost reaches an excellent accurate value, 2.89 kB per atom when the temperature is high enough at 950 K. With this we can be sure that the structural symmetry can be C1 for Au58.
Interatomic forces and the disorder nature in the cluster
The most important contribution is from a short-range order in the disordered state of the atoms within the cluster. FC (stretching and bending mode) matrices, which are independent of symmetry and magnitudes, are strongly correlated to the bond lengths. A small change in the bond length upon disorder can have a large effect on the FCs and vibrational entropy. A general increase in the bond angle of this series indicates an increasing repulsion between the bonds which is consistent with the increasing bond order.The contribution of the vibrational free energy is related to the disorder in the FCs. In general, gold clusters are not so strongly disordered, having only minor positional disorder. We must remember that each normal mode acts like a simple harmonic oscillator, with the concerted motion of many atoms. The center of mass does not move. All atoms pass through their equilibrium positions simultaneously and normal modes are independent; they do not interact. This means that normal modes do not exchange energy. This is only true in the absence of anharmonic terms, which is a theoretical approximation that is never achieved in reality. For example, if the symmetric stretch is excited, the energy stays within the symmetric stretch.
Conclusion
In a first attempt, we have calculated the vibrational frequency (at ΔE = 0) and the heat capacity (at 0.75–300 K) of a larger sized cluster, Au58 – a shell-like structure. The model was combined with a numerical finite-differentiation method by using the DFTB approach. The numerical force constants were extracted through the re-optimization process. A useful feature of this method is that once the vibrational modes have been determined, the Raman and IR intensities can be obtained regardless of the size of system. Thus, the experimental frequency spectrum for C1/C4–Au58, is only a question of time.Our novel and reliable analysis model can be easily extended to even larger clusters, bi-metallic clusters, and certainly to biological molecules (e.g.: DNA sequences). This work gives a possible reason for the structure, size and temperature effect on Au atomic clusters. It is hoped that this work will encourage and help to interpret analogous measurements in nickel and platinum. In conclusion, our goal here was to develop a technique to reduce the computational cost and make the methods more user-friendly. In summary, we have demonstrated that structures which are composed of atomic shells can be important candidates for gold clusters, besides planar and hollow cage-like ones. For Au58, a double shell structure consisting of a hollow inner shell of ten atoms is found to be highly stable.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A part of this work was supported by the German Research Council (DFG) through project Sp 439/23-1. We gratefully acknowledge their very generous support.References
- R. H. M. Smit, et al., Phys. Rev. Lett., 2001, 87, 266102 CrossRef CAS PubMed.
- V. Rodrigues, J. Bettini, P. C. Silva and D. Ugarte, Phys. Rev. Lett., 2003, 91, 096801 CrossRef PubMed.
- D. J. Wales, Energy Landscapes with Applications to Clusters, Biomolecules and Glasses, Cambridge University, England, 2003 Search PubMed.
- Y. C. Choi, H. M. Lee, W. Y. Kim, S. K. Kwon, T. Nautiyal, D.-Y. Cheng, K. Vishwanathan and K. S. Kim, Phys. Rev. Lett., 2007, 98, 076101 CrossRef PubMed.
- R. Feynman, Science, 1991, 254, 1300–1301 Search PubMed.
- I. L. Garzón and A. Posada-Amarillas, Phys. Rev. B, 1996, 54, 11796 CrossRef.
- G. Bravo-Perez, I. L. Garzón and O. Novaro, J. Mol. Struct.: THEOCHEM, 1999, 493, 225–231 CrossRef CAS.
- G. Bravo-Perez, I. L. Garzón and O. Novaro, Chem. Phys. Lett., 1999, 313, 655–664 CrossRef CAS.
- H. E. Sauceda, D. Mongin, P. Maioli, A. Crut, M. Pellarin, N. del Fatti, F. Vallée and I. L. Garzón, J. Phys. Chem. C, 2012, 116, 25147–25156 CAS.
- H. E. Sauceda, J. J. Pelayo, F. Salazar, L. A. Pérez and I. L. Garzón, J. Phys. Chem. C, 2013, 117, 11393 CAS.
- H. E. Sauceda, F. Salazar, L. A. Pérez and I. L. Garzón, J. Phys. Chem. C, 2013, 117, 25160 CAS.
- H. E. Sauceda and I. L. Garzón, J. Phys. Chem. C, 2015, 119, 10876 CAS.
- H. E. Sauceda and I. L. Garzón, Phys. Chem. Chem. Phys., 2015, 17, 28054 RSC.
- A. J. Ballard, S. Martiniani, J. D. Stevenson, S. Somani and D. J. Wales, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 273–289 CrossRef CAS.
- S. Martiniani, J. D. Stevenson, D. J. Wales and D. Frenkel, Phys. Rev. X, 2014, 4, 031034 Search PubMed.
- V. A. Mandelshtam, P. A. Frantsuzov and F. Calvo, J. Phys. Chem. A, 2006, 110, 5326–5332 CrossRef CAS PubMed.
- V. A. Sharapov and V. A. Mandelshtam, J. Phys. Chem. A, 2007, 111, 10284–10291 CrossRef CAS PubMed.
- V. A. Sharapov, D. Meluzzi and V. A. Mandelshtam, Phys. Rev. Lett., 2007, 98, 105701 CrossRef PubMed.
- D. J. Wales, Chem. Phys. Lett., 2013, 584, 1–9 CrossRef CAS.
- N. Dugan and S. Erkoc, Phys. Status Solidi B, 2008, 245, 695 CrossRef CAS.
- N. Bolandhemat, M. Rahmana and A. Shuaibua, J. Mater. Sci. Eng., 2016, 5, 250, DOI:10.4172/2169-0022.1000250.
- W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611 CrossRef CAS.
- M. Brack, Rev. Mod. Phys., 1993, 65, 677 CrossRef CAS.
- B. X. Wang, L. P. Zhou and X. F. Peng, Int. J. Thermophys., 2006, 27, 139 CrossRef CAS.
- G. H. Comsa, D. Heitkamp and H. S. Räde, Solid State Commun., 1977, 24, 547 CrossRef CAS.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77(1), 371–421 CrossRef CAS.
- L. Wu, W. Fang and X. Chen, Phys. Chem. Chem. Phys., 2016, 18, 17320–17325, 10.1039/C6CP02770A.
- R. P. Andres, T. Bein, M. Dorogi, S. Feng, J. I. Henderson, C. P. Kubiak, W. Mahoney, R. G. Osifchin and R. Reifenberger, Science, 1996, 272, 1323–1325 CAS.
- P. Pyykkö, Chem. Rev., 1997, 97(3), 597–636 CrossRef.
- C. Lemire, R. Meyer, S. Shaikhutdinov and H.-J. Freund, Angew. Chem., Int. Ed., 2004, 43, 118 CrossRef PubMed.
- G. Mills, M. S. Gordon and H. Metiu, J. Chem. Phys., 2003, 118, 4198 CrossRef CAS.
- J. H. Teles, S. Brode and M. Chabanas, Angew. Chem., 1999, 99, 2589 Search PubMed.
- M. Valden, X. Lai and D. W Goodman, Science, 1998, 281, 1637 CrossRef.
- B. Yoon, H. Häkkinen, U. Landman, A. S. Wörz, J.-M. Antonietti, S. Abbet, K. Judai and U. Heiz, Science, 2005, 307, 403 CrossRef CAS PubMed.
- M.-C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293 CrossRef CAS PubMed.
- L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038–4053 RSC.
- D.-e. Jiang and M. Walter, Phys. Rev. B: Condens. Matter, 2011, 84, 193042 Search PubMed.
- C. D. Dong and X. G. Gong, J. Chem. Phys., 2010, 132, 104301 CrossRef CAS PubMed.
- R. Ouyang, Y. Xie and De-en Jiang, Nanoscale, 2015, 7, 14817 RSC.
- H. Häkkinen, M. Moseler, O. Kostko, N. Morgner, M. A. Hoffmann and B. V. Issendorff, Phys. Rev. Lett., 2004, 93, 093401 CrossRef PubMed.
- X. P. Xing, B. Yoon, U. Landman and J. H. Parks, Phys. Rev. B, 2006, 74, 165423 CrossRef.
- B. Yoon, P. Koskinen, B. Huber, B. Kostko, B. v. Issendorff, H. Häkkinen, M. Moseler and U. Landman, ChemPhysChem, 2007, 8, 157–161 CrossRef CAS PubMed.
- W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 2, 5 Search PubMed.
- L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038 RSC.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113, 2091–2109 CrossRef CAS.
- K. Bao, S. Goedecker, K. Koga, F. Lançon and A. Neelov, Phys. Rev. B: Condens. Matter, 2009, 79, 041405 CrossRef.
- J. L. F. Da Silva, H. G. Kim, M. J. Piotrowski, M. J. Prieto and G. Tremiliosi-Filho, Phys. Rev. B: Condens. Matter, 2010, 82, 205424 CrossRef.
- J. P. K. Doye and D. J. Wales, New J. Chem., 1998, 22, 733–744 RSC.
- N. T. Wilson and R. L. Johnston, Eur. Phys. J. D, 2000, 12, 161–169 CrossRef CAS.
- H. Li, L. Li, A. Pedersen, Y. Gao, N. Khetrapal, H. Jónsson and X. C. Zeng, Nano Lett., 2015, 15, 682–688 CrossRef CAS PubMed.
- K. Vishwanathan and M. Springborg, J. Mater. Sci. Eng., 2017, 6, 325 Search PubMed.
- K. Vishwanathan and M. Springborg, J. Phys. Chem. Biophys., 2016, 6, 232 Search PubMed.
- K. Vishwanathan and M. Springborg, J. Dev. Drugs, 2017, 6, 178, DOI:10.4172/2329-6631.1000178.
- K. Vishwanathan and M. Springborg, Archives in Chemical Research, 2017, 2 DOI:10.21767/2572-4657.100017.
- Y. Dong and M. Springborg, Eur. Phys. J. D, 2007, 43, 15–18 CrossRef CAS.
- D. Porezag, Th. Frauenheim, Th. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B, 1995, 51, 12947 CrossRef CAS.
- G. Seifert and R. Schmidt, New J. Chem., 1992, 16, 1145 CAS.
- G. Seifert, D. Porezag and Th. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185 CrossRef CAS.
- G. Seifert, J. Phys. Chem. A, 2007, 111, 5609–5613 CrossRef CAS PubMed.
- M. Dvornikov, Formulae of numerical differentiation, Preprint, arXiv:math.NA/0306092v3, 2004.
- V. Novotny, P. P. M. Meincke and J. H. P. Watson, Phys. Rev. Lett., 1972, 28, 901 CrossRef CAS.
- Q. Song, C. Zheng, S. Xia and S. Chen, Microelectron. J., 2004, 35, 817 CrossRef CAS.
- Y. Lu, Q. L. Song and S. H. Xia, Chin. Phys. Lett., 2005, 22, 2346 CrossRef CAS.
- J. Yu, Z. A. Tan, F. T. Zhang, G. F. Wei and L. D. Wang, Chin. Phys. Lett., 2005, 22, 2429 CrossRef CAS.
- K. J. Taylor, C. L. Pettiettehall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 96, 3319–3329 CrossRef CAS.
- X. Gu, S. Bulusu, X. Li, X. C. Zeng, J. Li, X. G. Gong and L. S. Wang, J. Phys. Chem. C, 2007, 111, 8228 CAS.
- M. Walter, J. Akola, O. L. Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157 CrossRef CAS PubMed.
- M. Z. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. C. Jin, J. Am. Chem. Soc., 2008, 130, 5883 CrossRef CAS PubMed.
- D. Karhánek, T. Bučko and J. Hafner, J. Phys.: Condens. Matter, 2010, 22, 265006 CrossRef PubMed.
Footnote |
| † Dedicated to Dr Valeri G. Grigoryan (A Retired Staff Scientist), University of Saarland, on the occasion of his 68th birthday, esteemed Professor Prasanta Kumar Panigrahi (FNASc), Department of Physical Sciences, IISER Kolkata, Mohanpur-741246, India, on the occasion of his 60th birthday, and Professor Asima Pradhan, Department of Physics and Center for Laser Technology, Indian Institute of Technology (IIT), Kanpur-208016, India, on the occasion of her forthcoming milestone 60th birthday. |
| This journal is © The Royal Society of Chemistry 2018 |