Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Copper-doped lanthanum manganite La0.65Ce0.05Sr0.3Mn1−xCuxO3 influence on structural, magnetic and magnetocaloric effects
M. Chebaanea,
R. Bellouz *a,
Ma. Oumezzine*a,
E. K. Hlilb and
A. Fouzria
*a,
Ma. Oumezzine*a,
E. K. Hlilb and
A. Fouzria
aLaboratory of Physical Chemistry of Materials, Faculty of Sciences of Monastir, University of Monastir, 5019 Monastir, Tunisia. E-mail: bellouzridha@yahoo.fr; Oumezzine@hotmail.co.uk
bInstitut Néel, CNRS–Université J. Fourier, B.P. 166, 38042 Grenoble, France
First published on 13th February 2018
Abstract
Bulk nanocrystalline samples of La0.65Ce0.05Sr0.3Mn1−xCuxO3 (0 ≤ x ≤ 0.15) manganites are prepared by the sol–gel based Pechini method. The effect of the substitution for Mn with Cu upon the structural and magnetic properties has been investigated by means of X-ray diffraction (XRD), Raman spectroscopy and dc magnetization measurements. The structural parameters obtained using Rietveld refinement of XRD data showed perovskite structures with rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) symmetry without any detectable impurity phase. Raman spectra at room temperature reveal a gradual change in phonon modes with increasing copper concentration. The analysis of the crystallographic data suggested a strong correlation between structure and magnetism, for instance a relationship between a distortion of the MnO6 octahedron and the reduction in the Curie temperature, Tc. A paramagnetic to ferromagnetic phase transition at TC is observed. The experimental results confirm that Mn-site substitution with Cu destroys the Mn3+–O2−–Mn4+ bridges and weakens the double exchange (DE) interaction between Mn3+ and Mn4+ ions, which shows an obvious suppression of the FM interaction in the La0.65Ce0.05Sr0.3Mn1−xCuxO3 matrix. The maximum magnetic entropy change −ΔSmaxM is found to decrease with increasing Cu content from 4.43 J kg−1 K−1 for x = 0 to 3.03 J kg−1 K−1 for x = 0.15 upon a 5 T applied field change.
c) symmetry without any detectable impurity phase. Raman spectra at room temperature reveal a gradual change in phonon modes with increasing copper concentration. The analysis of the crystallographic data suggested a strong correlation between structure and magnetism, for instance a relationship between a distortion of the MnO6 octahedron and the reduction in the Curie temperature, Tc. A paramagnetic to ferromagnetic phase transition at TC is observed. The experimental results confirm that Mn-site substitution with Cu destroys the Mn3+–O2−–Mn4+ bridges and weakens the double exchange (DE) interaction between Mn3+ and Mn4+ ions, which shows an obvious suppression of the FM interaction in the La0.65Ce0.05Sr0.3Mn1−xCuxO3 matrix. The maximum magnetic entropy change −ΔSmaxM is found to decrease with increasing Cu content from 4.43 J kg−1 K−1 for x = 0 to 3.03 J kg−1 K−1 for x = 0.15 upon a 5 T applied field change.
1. Introduction
Recently, perovskite manganites of R1−xAxMnO3 (where R and A are trivalent rare earth and divalent alkaline earth ions, respectively) have been the subject of intense research due to their interesting physical properties around the ferromagnetic (FM)–paramagnetic (PM) transition temperature (the Curie temperature, TC), such as the colossal magnetoresistance (CMR), the magnetocaloric effects (MCE) (related to a large magnetic entropy change) and the strong correlation between structural and magnetic properties. Doped lanthanum based manganites have been used in many technological applications, including magnetic recording, high-density data storage, hard disks, magnetic sensors, spin-electronic devices, and magnetic refrigerants.1–4These materials offer a high degree of chemical flexibility leading to complex interplay between structural, electrical and magnetic properties. The double exchange (DE) effect in which eg electrons transfer between adjacent Mn3+ and Mn4+ ions and the Jahn–Teller effect were used to understand FM–PM transition and CMR in manganites.5,6 A prominent feature of most manganites is that they will undergo a ferromagnetic–paramagnetic (FM–PM) phase transition at the Curie temperature TC associated with an metal–insulator (M–I) transition at temperature TMI, which explains the fact that there exists a close relationship between the electrical and magnetic properties of manganites.7,8 Average ionic radius, electronic configuration, valance state and the concentration of the doping element are important parameters for tuning the magnetic and electronic properties of these materials.9
On the other hand, the synthesis technique greatly influences the physical and chemical characteristics of the rare-earth perovskite materials. There are various methods to synthesize the manganites compounds among them the Pechini sol–gel method. This method has been used successfully to produce high-quality specimens due to these potential advantages such as better homogeneities, lower processing temperatures, short annealing times, high purity of materials and improved material properties.
In manganites, it is possible to dope at both R-site and Mn-site, much research has been done on the substitution at the R-site with transition elements10–12 and/or rare-earths Eu,13 Ce,14 Pr,15 which can modify the Mn3+–O2−–Mn4+ network and in turn will intensively affect the intrinsic physical properties, such as ferromagnetism and (MCE). The substitution at the Mn site in perovskite oxides, with other transition metal ions,16–20 is more important because it not only modifies the Mn3+–O2−–Mn4+ network but also brings about many new exchange interactions between the Mn ion and the doped transition metal ions. Amongst the doping at Mn sites with transition elements, Cu substitution has been particularly investigated because of the special nature of its variable valence.21–31 In particular, Kim et al.30,31 reported the coexistence of Cu2+ and Cu3+ ions with Cu2+ dominant was found in their samples, and was thought to be responsible for the variations of the lattice parameters, Mn/Cu–O bond length and Mn/Cu–O–Mn/Cu bond angle. The doping of Cu changes the Cu2+/Cu3+ ratio and therefore the Mn3+/Mn4+ ratio, which may affect the electron carrier density, causing an intrinsic effect on the Mn3+–O2−–Mn4+ DE network.
The objective of this work was to synthesize nanocrystalline samples of La0.65Ce0.05Sr0.3Mn1−xCuxO3 with an extended doping levels up to x = 0.15 and study the influence of copper-doping at Mn-site on the structural, magnetic and magnetocaloric properties.
2. Experimental procedure
2.1. Synthesis
Nanocrystalline samples of La0.65Ce0.05Sr0.3Mn1−xCuxO3 (0 ≤ x ≤ 0.15) were prepared using the Pechini sol–gel method and a mixture of oxides and precursors, La(NO3)3·6H2O, Sr(NO3)2, Ce(NO3)3·6H2O, Mn2O3 and Cu(NO3)2·3H2O. The stoichiometric amounts of precursors were dissolved in distilled water at 90 °C and then a suitable amount of citric acid and ethylene glycol as coordinate agents were added. The resulting gel was pre-calcined (673 K for 3 h) to eliminate the organic material, ground and calcined again (973 K for 15 h) to eliminate the residual organic material. The obtained powder was then pressed into pellets (13 mm in diameter and 2–3 mm thick under a pressure of 5 ton cm−2). After that, the powder was sintered at 1173 K for 12 h in air.2.2. Characterization
The morphological properties of the samples were investigated by scanning electron microscopy (SEM) on a JSM-6400 apparatus working at 20 kV. The structure and phase purity were checked by powder X-ray diffraction (XRD) using a "Panalytical X pert Pro" diffractometer with Cu Kα radiation (k = 1.5406 Å). Data for Rietveld refinement were collected in the range of 2 h from 10° to 120° with a step size of 0.017° and a counting time of 18 s per step. Raman scattering data was collected in the frequency range 100–1000 cm−1 using a Raman spectrometer. Magnetic measurements versus temperature and magnetic applied field were realized using a SQUID (Quantum Design) developed at Louis Neel Laboratory of Grenoble. The isothermals M versus H at various temperatures around TC have been measured in applied fields up to 5 T.3. Results and discussion
3.1. Structural properties
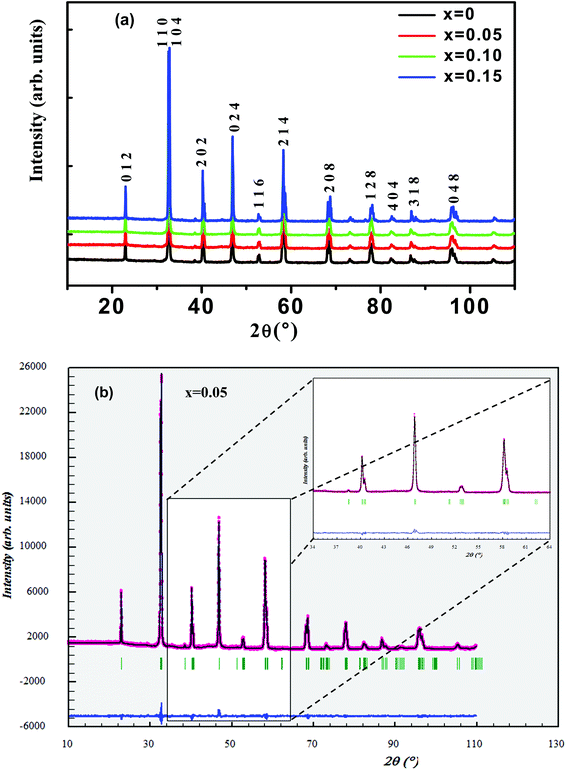
Fig. 1(a) shows the experimental XRD plots for the samples La0.65Ce0.05Sr0.3Mn1−xCuxO3 with x = 0, 0.05, 0.1 and 0.15. We first discuss the structural parameters of the studied samples in present work. Using the Rietveld refinement method, we noted that all samples are single-phase with a rhombohedral structure of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group (no. 167), in which the (La, Ce, Sr) atoms are at 6a (0, 0, 1/4) positions, (Mn, Cu) at 6b (0, 0, 0) and O at 18e (x, 0, 1/4). These results are consistent with the values of the Goldschmidt tolerance factor tG:
c space group (no. 167), in which the (La, Ce, Sr) atoms are at 6a (0, 0, 1/4) positions, (Mn, Cu) at 6b (0, 0, 0) and O at 18e (x, 0, 1/4). These results are consistent with the values of the Goldschmidt tolerance factor tG:
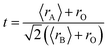 | (1) |
| x | 0 | 0.05 | 0.10 | 0.15 |
| Space group | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
| Lattice parameters | ||||
| a = b (Å) | 5.5037 (1) | 5.4995 (2) | 5.4979 (2) | 5.4954 (1) |
| c (Å) | 13.3691 (2) | 13.3549 (3) | 13.3452(1) | 13.3332 (3) |
| V (Å3) | 350.70 (2) | 349.79 (2) | 349.29 (2) | 348.71 (1) |
| (La, Ce, Sr) Biso (Å2) | 0.78 (3) | 0.64 (3) | 0.62 (3) | 0.35 (4) |
| (Mn, Cu) Biso (Å2) | 0.29 (4) | 0.18 (2) | 0.14 (4) | 0.13 (7) |
| (O) Biso (Å2) | 0.8 (1) | 0.65 (1) | 0.61 (1) | 0.32(1) |
| (O) x | 0.462 (1) | 0.462 (4) | 0.461 (2) | 0.459 (1) |
| d(Mn, Cu–O) (Å) | 1.9518 (4) | 1.9522 (5) | 1.9533 (8) | 1.9539 (8) |
| θ(Mn, Cu–O–Mn, Cu) (°) | 167.64 (2) | 167.53 (2) | 167.37 (3) | 167.11 (5) |
| W (× 10−2) (u.a.) | 9.570 | 9.562 | 9.554 | 9.552 |
| tG | 0.976 | 0.979 | 0.981 | 0.984 |
| TDRXG (nm) | 77 | 83 | 85 | 94 |
| Rwp (%) | 3.68 | 3.34 | 3.32 | 3.61 |
| Rp (%) | 2.90 | 2.61 | 2.60 | 3.36 |
| RF (%) | 1.71 | 1.55 | 1.49 | 2.39 |
| χ2 (%) | 1.71 | 1.54 | 1.53 | 2.79 |
The structural parameters were refined by the standard Rietveld refinement method using the FullProf program.32 We utilize the pseudo-Voigt function in order to fit parameters to the experimental data set. The parameters used are: a scale factor, a zero shifting factor, three cell parameters, five shapes and width of the peak factors, one global thermal factor and two asymmetric factors, the background was refined by a linear interpolation between a set background points with refinable heights. The weighted profile factor Rwp, the goodness of fit χ2, and the difference between the calculated and observed profiles were evaluated at each refinement cycle to determine the refinement quality. The final refinement analysis shows that the experimental spectra and the calculated values obtained by the Rietveld refinement are in good agreement with each other, and all observed peaks have been suitably indexed. The calculated results are shown in Fig. 1(b) and Table 1. One can see from Table 1 that both the lattice parameters (a = b, and c) and unit cell volume show a monotonous decrease with increasing Cu content. Similar structural variation with Cu doping at Mn sites was reported in ref. 24, 26, 29 and 30. (XPS) studies of Cu-doped manganites have shown that Cu ions exist in mixed-valence states: Cu2+ and Cu3+ with dominant Cu2+.30,31 The crystal structure and lattice parameters were affected because of the mismatch of ionic radius between the dopant and Mn ions. The B-site ionic radius of Cu2+ (0.73 Å) is larger than Mn3+ (Mn4+) and the ionic radius of Cu3+ (0.54 Å) is close to that of Mn4+ (0.53 Å) and smaller than the radius of the high spin state of Mn3+ (0.645 Å).33 Further, it is expected that Cu2+ ions substitute Mn3+ ions and Cu3+ ions substitute Mn4+ ions. Furthermore, substitution of Cu2+ for Mn3+ and Cu3+ for Mn4+ would lead to a proportionate conversion of Mn3+ to Mn4+ and Mn4+ to Mn3+. But the ionic state of Cu2+ is expected to be dominant in the samples, therefore, the overall copper doping effect leads to a change in the relative fraction of different valence Mn ions, which results an increase in the number of Mn4+ ions in order to preserve charge neutrality and therefore the unit cell volume is found to decrease.
Fig. 2(a and b) shows crystal structure of La0.65Ce0.05Sr0.3Mn1−xCuxO3 showing MnO6 octahedron generated with the help of program VESTA (Visualization for Electronic and Structural Analysis) using refined cell parameters, space group and positional parameters of atoms.34 It is represented from the figure that (La/Ce/Sr) cations occupies A-site in ABO3 type perovskite structure and are surrounded by 12 oxygen ions while Mn ion occupies the octahedral position (B site) surrounded by six oxygen ions, thus, forming a MnO6 octahedron Fig. 2(a).
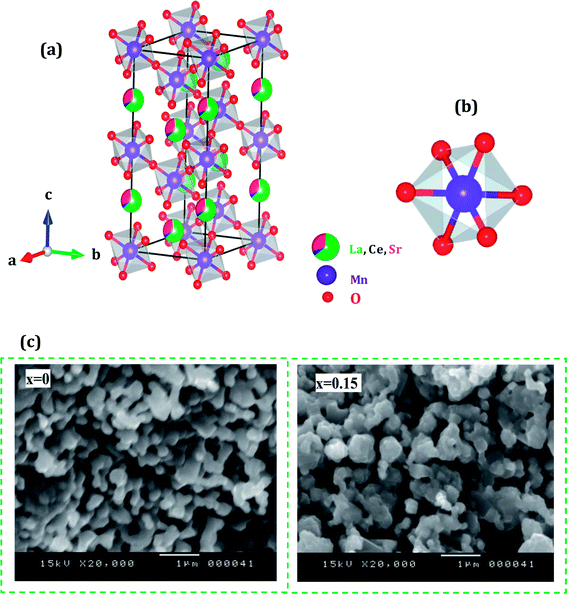 | ||
| Fig. 2 (a) Crystal structure of La0.65Ce0.05Sr0.3MnO3 (b) 3D view showing MnO6 octahedron (c) SEM images of (x = 0 and x = 0.15) samples. | ||
The surface morphology of samples examined by scanning electron microscopy (SEM) is illustrated in Fig. 2(c). The SEM images show that the particles have an almost homogeneous distribution. The average crystallite size of the samples are obtained by applying the following Rietveld refinement formula 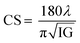 , where k is the X-ray wavelength and IG is the Gaussian size parameter given by Rietveld refinement. In all samples a nanometric size for the crystallites is found, between 77 nm and 94 nm (±2 nm), which is related to the moderate synthesis temperatures of these samples, obtained from very reactive precursors from sol–gel procedures. These values are close to those shown by SEM micrographs (the average particles size is ∼100 (±10 nm).
, where k is the X-ray wavelength and IG is the Gaussian size parameter given by Rietveld refinement. In all samples a nanometric size for the crystallites is found, between 77 nm and 94 nm (±2 nm), which is related to the moderate synthesis temperatures of these samples, obtained from very reactive precursors from sol–gel procedures. These values are close to those shown by SEM micrographs (the average particles size is ∼100 (±10 nm).
3.2. Raman spectroscopy
Raman spectroscopy is a powerful and sensitive tool for the non-destructive investigation and characterization of all kinds of materials. This technique is useful in understanding crystal symmetry, the local structural distortion and its dependence on doping. Our manganites samples shows rhombohedral crystal symmetry using the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group that assumes six equal distances of the Mn–O bonds of MnO6 octahedra (Fig. 2(b)). This structure can be described with respect to the ideal cubic structure by considering a rotation of MnO6 octahedra about the [111] pseudo cubic diagonal. According to the group theory, for R
c space group that assumes six equal distances of the Mn–O bonds of MnO6 octahedra (Fig. 2(b)). This structure can be described with respect to the ideal cubic structure by considering a rotation of MnO6 octahedra about the [111] pseudo cubic diagonal. According to the group theory, for R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (D3d6) rhombohedral structure, thirty vibrational degrees of freedom at the Γ point are distributed among the irreducible representation as:
c (D3d6) rhombohedral structure, thirty vibrational degrees of freedom at the Γ point are distributed among the irreducible representation as:| Γ (D3d6) = 2A1u + 3A2g + A1g + 4A2u + 4Eg + 6Eu |
The rhombohedral distortion gives rise to five Raman active modes.
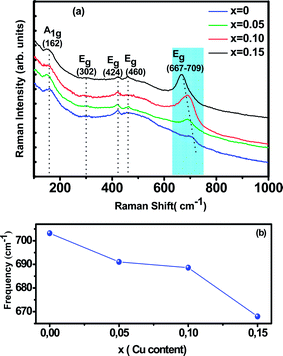
Room temperature Raman spectrum of as synthesized La0.65Ce0.05Sr0.3Mn1−xCuxO3 (x = 0, 0.05, 0.10 and 0.15) samples in the frequency range of 200–900 cm−1 is shown in Fig. 3(a). Five vibration modes have been identified, one (A1g) and four (Eg). These broad bands are located at 162 (A1g), 302 (Eg), 424 (Eg), 460 (Eg) and 667–703 (Eg) cm−1, which are associated with rotational-, bending-, and stretching-like vibrations of the MnO6 octahedra, respectively.35,36 It has been noticed from the graph that with increasing Cu concentration, the Raman scattering intensity of the phonon modes are increasing. The frequencies of the experimental peaks are plotted with doping level for the high-frequency mode Eg in Fig. 3(b). This mode shows a substantial shift toward lower frequencies (a downshift of about 30 cm−1) as a function of Cu concentration. These shifts are related to the change in the average (Mn/Cu)–O distance.37 Similar observations have been reported for some other perovskite compounds with distorted rhombohedral lattice.35,38,39
In this work, we underline the Eg mode allowed for the symmetric stretching vibration of oxygen in MnO6 octahedra. It is reasonable to relate the changes on the Eg mode frequency to the modifications of the oxygen octahedral MnO6. Moreover, the introduction of substitutional defect in the B-site (like Cu) has a strong effect in the structural changes of the lattice. Since Cu substitution induces a strong local stress, it can be expected that (Mn/Cu)O6 octahedra rotate, and the Mn–O bond lengths decrease under this compression.40
3.3. Magnetic properties
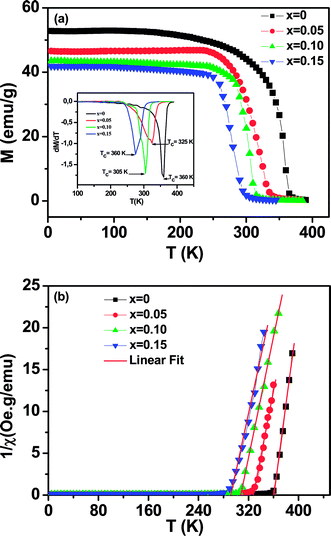
The magnetization of La0.65Ce0.05Sr0.3Mn1−xCuxO3 (0 ≤ x ≤ 0.15) as a function of temperature from 5 K to 400 K under an applied field of 100 Oe is shown in Fig. 4(a).All samples exhibit a clear transition from paramagnetic to ferromagnetic state with decreasing temperature. The Curie temperature TC is the temperature at which the absolute value of dM/dT is maximum (inset Fig. 4(a)), are summarized in Table 2.
| TC (K) | θP (K) | C | μeff (exp) (μB) | μeff (cal) (μB)a | μeff (cal) (μB)b | |
|---|---|---|---|---|---|---|
| a Under the assumption that all of the Cu ions exist in Cu2+ state.b Under the assumption that all of the Cu ions exist in Cu3+ state. | ||||||
| x = 0 | 360 | 353 | 2.777 | 4.71 | 4.61 | 4.61 |
| x = 0.05 | 330 | 323 | 2.607 | 4.56 | 4.45 | 4.52 |
| x = 0.10 | 305 | 300 | 2.769 | 4.70 | 4.27 | 4.43 |
| x = 0.15 | 275 | 270 | 2.894 | 4.81 | 4.09 | 4.34 |
One can see that TC decreases monotonically with increasing Cu-doping content. This behavior is consistent with those reported previously on Mn-site substitution of copper.22,26 However, the Mn site substitution of Cu2+/Cu3+ with localized electrons (Cu2+: t2g6 eg3, Cu3+: t2g6 eg2) reduces the amount of Mn3+ (t2g↑3eg↑1) with itinerate eg↑1 electron and converts Mn3+ (t2g↑3eg↑1) to Mn4+ (t2g↑3eg↑0) for charge neutrality, directly affecting the DE interaction, weakening the ferromagnetic coupling between Mn3+ and Mn4+ ions and leads to the lower ordering of FM transition temperature and suppresses the FM interaction. On the other hand, the decrease in TC is also closely related to the decrease in the one-electron band-width W of eg electron35 (Table 1) due to the increase of dMn/Cu–O bond length and the decrease of θ<Mn/Cu–O–Mn/Cu> bond angle caused by copper doping. The reduction of the parameter W is related to the weakening of the overlap between the O-2p and the Mn-3d orbital, which in turn decreases the (DE) interaction.
To get a clear knowledge about the magnetic interaction for the La0.65Ce0.05Sr0.3Mn1−xCuxO3, the magnetic susceptibility (χ) could be fitted to the Curie–Weiss law: χ = C/(T − θp); where θp is the Curie–Weiss temperature (the temperature at which χ−1 intercepts the temperature axis) and C is the Curie constant were determined by linear fitting of the temperature dependent χ−1 data in the high temperature paramagnetic region, as displayed in Fig. 4(b) and the values are given in Table 2.
The positive sign of θp values implies the ferromagnetic nature of the magnetic interactions between spins and are basically consistent with the values of TC.
From the estimated Curie constant (C), we have deduced the experimental effective moment (μexpeff) using the following relation: 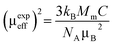 ; where NA = 6.023 × 1023 mol−1 is the number of Avogadro, μB = 9.274 × 10−21 emu is the Bohr magneton, Mm is the molecular weight and kB = 1.38016 × 10−16 erg K−1 is the Boltzmann constant.
; where NA = 6.023 × 1023 mol−1 is the number of Avogadro, μB = 9.274 × 10−21 emu is the Bohr magneton, Mm is the molecular weight and kB = 1.38016 × 10−16 erg K−1 is the Boltzmann constant.
The theoretical effective paramagnetic moment (μtheff) was calculated using the calculated Mn3+/Mn4+ contents under the assumption that all the Cu ions exist in either Cu2+ or Cu3+ state. The spin-only magnetic moments for free Mn3+, Mn4+, Cu2+ and Cu3+ are 4.89μB, 3.87μB, 1.73μB, 2.83μB, respectively. The obtained values of (μexpeff) and (μtheff) are listed in Table 2. The experimental (μexpeff) value is little larger than the calculated value using the spin-only moment. Such a difference in (μeff) value may be ascribed to the appearance of short-range FM interactions in the paramagnetic state. This result is commonly observed in manganites.8,41,42
In order to investigate the magnetic behavior at low temperatures, we have performed magnetization measurements as a function of the applied magnetic field μ0H up to 5 T at various temperatures. We plot in Fig. 5 the magnetization evolution versus the applied magnetic field obtained at different temperature (isothermal magnetization) for (a) x = 0, and (b) x = 0.15 samples. At a given lower fields, (M–H–T) curves show a rapid increase and get saturated at higher fields. For all the studied samples, the magnetization has been found to increase with decreasing temperature in the selected temperature range, where thermal fluctuation of spins decreases with decreasing temperature.
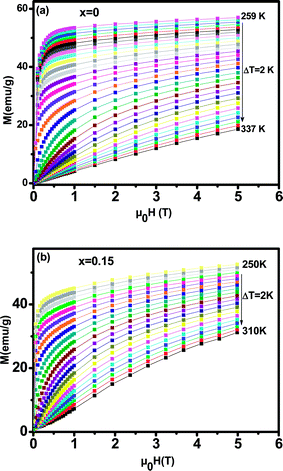 | ||
| Fig. 5 Isothermal magnetization versus magnetic field around TC of La0.65Ce0.05Sr0.3Mn1−xCuxO3, (a) for x = 0 and (b) for x = 0.15. | ||
To determine the nature of the FM–PM phase transition (first or second order) for our samples, we plotted in Fig. 6(a and b) the Arrott plot43 (μ0H/M versus M2) for x = 0 and x = 0.15. According to the Banerjee criterion,44 all of the M2 vs. μ0H/M curves show positive slopes without infection points, which is characteristic of second order transitions.
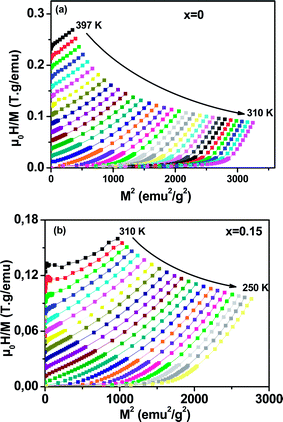 | ||
| Fig. 6 Arrott plot of μ0H/M vs. M2 at different temperatures for La0.65Ce0.05Sr0.3Mn1−xCuxO3, (a) x = 0 and (b) x = 0.15. | ||
3.4. Magnetocaloric effect and second-order magnetic phase transition
MCE is an intrinsic property of magnetic materials. It is the response of the material toward the application or removal of a magnetic field. This response is maximized when the material is near its magnetic ordering temperature. In an isothermal process, the magnetic entropy change of the materials can be derived from the Maxwell relation as shown below:45
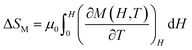 | (2) |
The magnetic entropy changes, ΔSM, of La0.65Ce0.05Sr0.3Mn1−xCuxO3 (x = 0, 0.05, 0.1 and 0.15) have been calculated using the Maxwell relation46 and are plotted in Fig. 7 as a function of temperature and field.
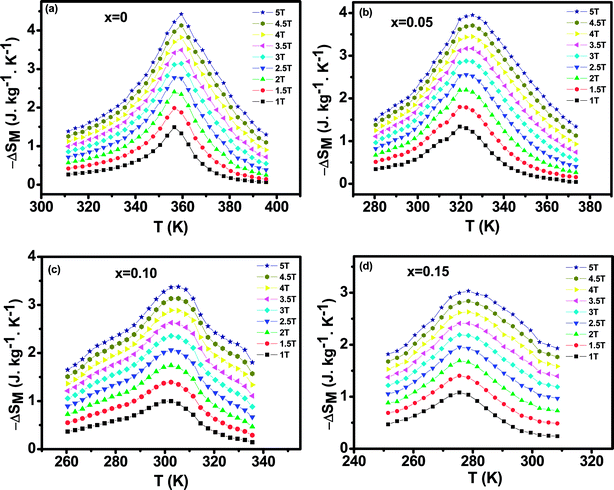 | ||
| Fig. 7 The temperature dependence of the magnetic entropy change (ΔSM) under different applied magnetic fields (a) for x = 0, (b) for x = 0.05, (c) for x = 0.10 and (d) for x = 0.15. | ||
The maximum value of magnetic entropy change ΔSM is found to be around TC and it increases with increasing the magnetic applied field due to the enhancement of FM interactions. As the Cu content increases the magnitude of ΔSM decreases under a given field strength. Indeed, under the magnetic field change from 0 to 5 T, the values of |ΔSmaxM| observed for x = 0.00, 0.05, 0.1 and x = 0.15 are found to be 4.43, 5.15, 3.37 and 3.03 J kg−1 K−1, respectively. The value of |ΔSmaxM| for μ0H = 1 and 5 T are listed in Table 2 along with related compounds47,48 for easy comparison.
Relative cooling power (RCP) is another important parameter to quantify the efficiency of the magnetocaloric material. It is a measure of how much heat can be transferred between the cold and the hot tanks in one ideal refrigeration cycle. It can be defined as
| RCP = −ΔSmaxM × δFWHM, | (3) |
The RCP values of the La0.65Ce0.05Sr0.3Mn1−xCuxO3 are evaluated under the magnetic field changes of 1 and 5 T. For a comparison TC and magnetocaloric parameters of some relevant manganites in the literature are listed in Table 3.
| Composition | TC (K) | ΔH (T) | |−ΔSmaxM (J kg−1 K−1)| | RCP (J kg−1) | Ref. |
|---|---|---|---|---|---|
| Gd | 293 | 1 | 3.25 | — | 47 |
| La0.77Sr0.23Mn0.9Cu0.1O3 | 325 | 1 | 4.41 | 57 | 26 |
| La0.7Sr0.3Mn0.9Cu0.1O3 | 347 | 1 | 3.24 | — | 21 |
| La0.65Ce0.05Sr0.3MnO3 | 360 | 1 | 1.49 | 33 | This work |
| La0.65Ce0.05Sr0.3Mn0.95Cu0.05O3 | 330 | 1 | 1.34 | 44 | This work |
| La0.65Ce0.05Sr0.3Mn0.9Cu0.1O3 | 305 | 1 | 1.5 | 36 | This work |
| La0.65Ce0.05Sr0.3Mn0.85Cu0.15O3 | 275 | 1 | 1.08 | 28 | This work |
| La0.67Ba0.33Mn0.98Ti0.02O3 | 310 | 1 | 0.93 | 45 | 17 |
| Gd | 293 | 5 | 9.5 | 410 | 48 |
| La0.65Ce0.05Sr0.3MnO3 | 360 | 5 | 4.43 | 132 | This work |
| La0.65Ce0.05Sr0.3Mn0.95Cu0.05O3 | 330 | 5 | 3.95 | 175 | This work |
| La0.65Ce0.05Sr0.3Mn0.9Cu0.1O3 | 305 | 5 | 3.37 | 102 | This work |
| La0.65Ce0.05Sr0.3Mn0.85Cu0.15O3 | 275 | 5 | 3.06 | 88 | This work |
| La0.65Eu0.05Sr0.3Mn0.9Cr0.1O3 | 310 | 5 | 3.35 | 207 | 16 |
| La0.67Ba0.33Mn0.98Ti0.02O3 | 310 | 5 | 3.19 | 307 | 17 |
The maximum value of RCP is obtained for x = 0.05, which is 43% of that of pure Gd, the prototype magnetic refrigerant material (RCP = 410 J kg−1).48 Our results indicate that this compound is promising for room temperature magnetic refrigeration.
For further clarification of the phase transition of the samples as an alternative to the Banerjee criterion44 we used the phenomenological universal curve method, proposed by Franco et al.,49,50 which is a general approach to determine the order of the phase transition. In order to construct this phenomenological universal curve, an analogous procedure to that described in ref. 51 has been used. It consists in normalizing the ΔSM curves with respect to their maximum and rescaling the temperature axis as
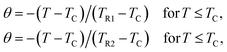 | (4) |
Fig. 8 shows the universal curves constructed for the experimental ΔSM (T, H) curves as a function of the rescaled temperature for La0.65Ce0.05Sr0.3Mn1−xCuxO3 (x = 0, 0.10 and 0.15) samples. It can be clearly seen from this figure that all normalized entropy change curves collapse into a single universal curve, which confirms that the PM–FM phase transition observed for our compounds is of a second-order. Hence, this result is consistent with the trends observed in the Arrott plots (Fig. 6).
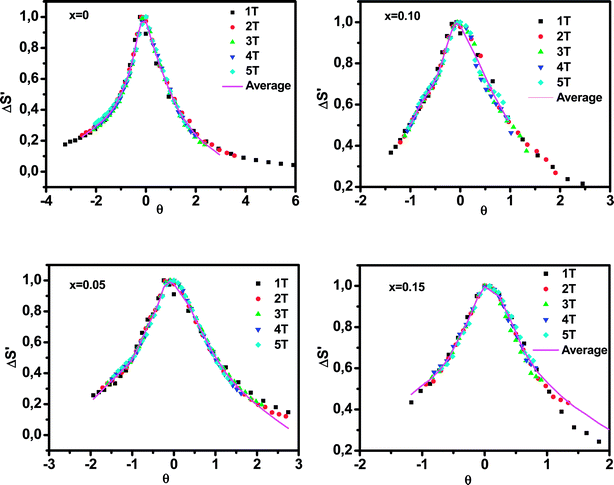 | ||
| Fig. 8 Normalized ΔSM versus rescaled temperature θ for La0.65Ce0.05Sr0.3Mn1−xCuxO3, the solid line is the average curve. | ||
The solid line corresponds to the average of the universal scaling. This average curve, once the temperature axis is back transformed from the reduced temperature to the unnormalized one, allows making extrapolations to lower temperatures for the high field data and obtaining a finer description of the peak for the low field curves.52,53
4. Conclusion
In summary, we have studied the effect of copper doping lanthanum manganite ions on structural, magnetic and magnetocaloric properties of La0.65Ce0.05Sr0.3Mn1−xCuxO3 (0 ≤ x ≤ 0.15) prepared using the Pechini sol–gel method. Rietveld refinement of XRD patterns shows that all samples crystallized in a rhombohedral structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. The Cu-doping induces the suppression of the one-electron band-width W of eg electron due the variations of the bond length and bond angle, leading to destruction of the DE interaction. The Curie temperature and the maximum magnetic entropy change decrease with the increase in the Cu content. This is attributed to the structural distortion of MnO6 octahedron and the changes in the valence states of the Cu and Mn ions upon Cu doping, weakening the ferromagnetic exchange interaction. A uniform phenomenological function that describes the magnetic entropy change is found for these materials, which provides good handle on designing of magnetocaloric materials for micro magnetic refrigerators.
c space group. The Cu-doping induces the suppression of the one-electron band-width W of eg electron due the variations of the bond length and bond angle, leading to destruction of the DE interaction. The Curie temperature and the maximum magnetic entropy change decrease with the increase in the Cu content. This is attributed to the structural distortion of MnO6 octahedron and the changes in the valence states of the Cu and Mn ions upon Cu doping, weakening the ferromagnetic exchange interaction. A uniform phenomenological function that describes the magnetic entropy change is found for these materials, which provides good handle on designing of magnetocaloric materials for micro magnetic refrigerators.
The La0.65Ce0.05Sr0.3Mn0.95Cu0.05O3 sample is found to have a comparable MCE around 330 K with a maximum ΔSM of 1.34 J kg−1 K−1 and a RCP of 44 J kg−1 under a magnetic field change of 1 T, and can be considered as competitive candidate for magnetic refrigerant materials operating near room temperature.
Conflicts of interest
There are no conflicts to declare.References
- A. P. Ramirez, J. Phys.: Condens. Matter, 1997, 9, 8171 CrossRef CAS.
- Z. B. Guo, Y. W. Du, J. S. Zhu, H. Huang, W. P. Ding and D. Feng, Phys. Rev. Lett., 1997, 78, 1142 CrossRef CAS.
- M. B. Salamon and M. Jaime, Rev. Mod. Phys., 2001, 73, 583 CrossRef CAS.
- E. Dagotto, T. Hotta and A. Moreo, Phys. Rep., 2001, 344, 1 CrossRef CAS.
- C. Zener, Phys. Rev. B: Condens. Matter Mater. Phys., 1951, 82, 403 CAS.
- A. J. Millis, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 8434 CrossRef CAS.
- M. Saleem and D. Varshney, RSC Adv., 2018, 8, 1600 RSC.
- M. Oumezzine, S. Kallel, O. Peña, N. Kallel, T. Guizouarn, F. Gouttefangeas and M. Oumezzine, J. Alloys Compd., 2014, 582, 640 CrossRef CAS.
- A. Coskun, E. Tasarkuyu, A. E. Irmak, M. Acet, Y. Samancıoglu and S. Akturk, J. Alloys Compd., 2015, 622, 796 CrossRef CAS.
- S. Zhao, X.-J. Yue and X. Liu, Ceram. Int., 2017, 43, 13240 CrossRef CAS.
- A. E.-M. A. Mohamed and B. Hernando, Phys. Lett. A, 2016, 380, 1763 CrossRef CAS.
- R. Thaljaoui, M. Pękała, J. F. Fagnard and P. Vanderbemden, J. of Rare Earths, 2017, 35, 875 CrossRef CAS.
- S. Vadnala and S. Asthana, J. Magn. Magn. Mater., 2018, 446, 68 CrossRef CAS.
- M. S. Anwar, F. Ahmed and B. Heun Koo, Ceram. Int., 2015, 41, 5821 CrossRef CAS.
- M. Zarifi, P. Kameli, M. Mansouri, H. Ahmadv and H. Salamati, Solid State Commun., 2017, 262, 20 CrossRef CAS.
- R. Bellouz, M. Oumezzine, E. K. Hlil and E. Dhahri, J. Magn. Magn. Mater., 2015, 375, 136 CrossRef CAS.
- M. Oumezzine, O. Peña, S. Kallel and M. Oumezzine, J. Alloys Compd., 2012, 539, 116 CrossRef CAS.
- I. Betancourt, L. Lopez Maldonado and J. T. Elizalde Galindo, J. Magn. Magn. Mater., 2016, 401, 812 CrossRef CAS.
- J. C. Debnath and J. Wang, Phys. B, 2017, 504, 58 CrossRef CAS.
- P. T. Phong, L. V. Bau, L. C. Hoan, D. H. Manh, N. X. Phuc and I.-J. Lee, J. Alloys Compd., 2016, 656, 920 CrossRef CAS.
- M. H. Phan, H. X. Peng, S. C. Yu, N. D. Tho and N. Chau, J. Magn. Magn. Mater., 2005, 285, 199 CrossRef CAS.
- M. S. Anwar, S. Kumar, F. Ahmed, S. Nae Heo, G. W. Kim and B. Heun Koo, J. Electroceram., 2013, 30, 46 CrossRef CAS.
- Q. T. Phung, V. K. Vu, A. B. Ngac, H. S. Nguyen and N. N. Hoang, J. Magn. Magn. Mater., 2012, 324, 2363 CrossRef CAS.
- C. Shang, Z. C. Xia, M. Wei, Z. Jin, B. R. Chen, L. R. Shi, Z. W. Ouyang, S. Huang and G. L. Xiao, J. Magn. Magn. Mater., 2016, 416, 357 CrossRef CAS.
- M. El-Hagary, Y. A. Shoker, S. Mohammad, A. M. Moustafa, A. Abd El-Aal, H. Michor, M. Reissner, G. Hilscher and A. A. Ramadan, J. Alloys Compd., 2009, 47, 468 Search PubMed.
- P. Thamilmaran, M. Arunachalam, S. Sankarrajan, K. Sakthipandi, E. James Jebaseelan Samuel and M. Sivabharathy, J. Magn. Magn. Mater., 2017, 443, 29 CrossRef CAS.
- K. Y. Wang, W. H. Song, J. M. Dai, S. L. Ye, S. G. Wang, J. Fang, J. L. Chen, B. J. Gao, J. J. Du and Y. P. Sun, J. Appl. Phys., 2001, 90, 6263 CrossRef CAS.
- T. L. Phan, P. Q. Thanh, N. H. Sinh, Y. D. Zhang and S. C. Yu, IEEE Trans. Magn., 2012, 48, 1293 CrossRef CAS.
- K. Yadav, M. P. Singh, F. S. Razavi and G. D. Varma, Mater. Chem. Phys., 2012, 137, 323 CrossRef CAS.
- M. S. Kim, J. B. Yang, J. Medvedeva, W. B. Yelon, P. E. Parris, W. J. James and J. Phys, Condens. Matter, 2008, 20, 255228 CrossRef.
- M. S. Kim, J. B. Yang, P. E. Parris, Q. Cai, X. D. Zhou, W. J. James, W. B. Yelon, D. Buddhikot and S. K. Malik, J. Appl. Phys., 2005, 97, 714 Search PubMed.
- T. Roisnel and J. Rodriguez-Carvajal, Computer Program FULLPROF, LLBLCSIM, May 2003 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- R. Bellouz, M. Oumezzine, A. Dinia, G. Schmerber, E. Hlil and M. Oumezzine, RSC Adv., 2015, 5, 64557 RSC.
- L. M. Carrón, A. de Andrés, M. J. Martínez-Lope, M. T. Casais and J. A. Alonso, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174303 CrossRef.
- N. Van Minh and I.-S. Yang, Vib. Spectrosc., 2006, 42, 353 CrossRef.
- M. Oumezzine, O. Hassayoun, R. Bellouz, H. B. Sales and E. K. Hlil, J. Alloys Compd., 2017, 729, 156 CrossRef CAS.
- D. Varshney and M. W. Shaikh, J. Alloys Compd., 2014, 589, 558 CrossRef CAS.
- G. De Marzi, H. J. Trodahl, J. Bok, A. Cantarero and F. Sapina, Solid State Commun., 2003, 127, 259 CrossRef CAS.
- B. Martinez, V. Laukhin, J. Fontcuberta, L. Pinsard and A. Revcolevschi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 054436 CrossRef.
- J. J. Blanco, M. Insausti, I. Gil de Muro, L. Lezama and T. Rojo, J. Solid State Chem., 2006, 179, 623 CrossRef CAS.
- L. M. R. Martinez and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5622 CrossRef.
- B. K. Banerjee, Phys. Lett., 1964, 12, 16 CrossRef.
- J. S. Amaral and V. S. Amaral, J. Magn. Magn. Mater., 2010, 322, 1552 CrossRef CAS.
- N. A. De Oliveira and P. J. Von Ranke, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214439 CrossRef.
- M. Földeàki, R. Chahine and T. K. Bose, J. Appl. Phys., 1995, 77, 3528 CrossRef.
- K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479 CrossRef.
- V. Franco and A. Conde, Int. J. Refrig., 2010, 33, 465 CrossRef CAS.
- V. Franco, R. Caballero-Flores, A. Conde, Q. Y. Dong and H. W. Zhang, J. Magn. Magn. Mater., 2009, 321, 1115 CrossRef CAS.
- V. Franco, A. Conde, J. M. Romero-Enrique and J. S. Blázquez, J. Phys.: Condens. Matter, 2008, 20, 285207 CrossRef.
- L. Zhang, J. Fan, W. Tong, L. Ling, L. Pi and Y. Zhang, Phys. B, 2012, 407, 3543 CrossRef CAS.
- V. M. Pridaa, V. Franco, V. Vega, J. L. Sanchez-Llamazares, J. J. Sunol, A. Conde and B. Hernand, J. Alloys Compd., 2011, 509, 190 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |