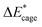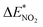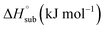Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Carbon-free energetic materials: computational study on nitro-substituted BN-cage molecules with high heat of detonation and stability†
Xin Zeng ,
Nan Li
,
Nan Li * and
Qingjie Jiao*
* and
Qingjie Jiao*
State Key Laboratory of Explosion Science and Technology, School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China. E-mail: leen04@bit.edu.cn; leen04@163.com; jqj@bit.edu.cn; jqjbit@126.com
First published on 18th April 2018
Abstract
A new series of high-energy density materials (HEDMs) B6N6H6−n(NO2)n (n = 1–6) are studied at the M06-2X/6-311++G**, ωB97XD/6-311++G** and B3LYP/6-311++G** levels. Analysis of the structural changes caused by substituting the NO2 and the electronic structures, such as electron localization function (ELF), Wiberg bond index (WBI), charge transfer and bond dissociation energies (BDE), provide important insights into the essence of the chemical characteristics and stability. Moreover, the Born–Oppenheimer molecular dynamic (BOMD) simulation is performed to verify their stability, which suggests that only the BN-cage derivatives with one and two nitro groups bonding with boron atoms (NO2-1-1 and NO2-2-1) can remain stable under ambient conditions. To predict the detonation performance and sensitivity of these two stable BN-cage energetic molecules accurately, the density, gas phase enthalpy of formation, enthalpy of sublimation, detonation performance, impact sensitivity and BDE are calculated systematically. The calculation results show that both NO2-1-1 and NO2-2-1 have a higher heat of detonation, higher value of h50, and larger BDE of trigger bonds than CL-20.
1. Introduction
High-energy density materials (HEDMs) with both superior detonation performance and low sensitivity have always drawn the attention of research scientists.1–11 The increased energy density often comes at the expense of molecular stability. Seeking new HEDMS with a fine balance between high detonation performance and low sensitivity remains to be an interesting, but very challenging task.It is recognized that the best known explosive with superior detonation performance is 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazatetracyclo[5.5.0.0.0]dodecane (HNIW or CL-20), which was successfully synthesized by Nielsen in 1987.12 Besides the energetic functional groups, the large strain energy of its cage skeleton also allows CL-20 to store a high amount of energy. Currently, boron containing energetic materials have captured a great deal of attention in energetic materials research.13–21 The addition of boron in both micro and nano sizes into energetic materials can increase the energy output effectively and improve the detonation properties due to its high heat of combustion (36.3 kJ mol−1, 1.9 times than that of aluminum).13–21 Thus, from the point of view of energy release during combustion, boron- and nitrogen-containing complexes could be a good choice for developing high energy materials.
Inspired by this, we attempted to replace the C atoms of CL-20 with B atoms to develop a new carbon-free BN-cage energetic system. The nitro (NO2) groups are bonded to the BN-cage structure to increase the nitrogen and oxygen content, which can achieve a good oxygen balance. In this theoretical study, the BN-cage and its NO2 derivates are systematically investigated to understand their stability, electronic structures, safety and detonation properties at the M06-2X/6-311++G**, ωB97XD/6-311++G** and B3LYP/6-311++G** levels of density functional theory (DFT). Through the systemic study of the above compounds, it is predicted that two BN-cage derivatives, NO2-1-1 and NO2-2-1, will have a superior detonation performance and low sensitivity, and could therefore potentially be new HEDMs.
2. Theoretical methods
All quantum mechanical calculations in this paper were performed using the Gaussian-09 software package22 at the M06-2X, ωB97XD and B3LYP level with the 6-311++G** basis set. The M06-2X meta-hybrid density functional developed by Zhao and Truhlar is an advanced method to calculate energies, which have shown a good performance for main group chemistry and kinetics studies.23,24 For comparison, the theoretical methods of ωB97XD and B3LYP were also employed with the basis set of 6-311++G**. The ωB97XD method includes a 100% long-range exact exchange, a small fraction (about 22%) of the short-range exact exchange, a modified B97 exchange density functional for a short-range interaction, and the B97 correlation density functional and empirical dispersion correction.25,26 ωB97XD yields satisfactory accuracy for thermochemistry and kinetics. The DFT method of B3LYP combines Becke's three-parameter (B3)27 functional with the Lee–Yang–Parr (LYP)28 correlation functional, which has been considered to be capable of accurately predicting the structural parameters and frequencies of many nitro-substituted compounds.29–31 Moreover, the 6-311++G** basis set can generally give satisfactory geometries.32 All of the optimized molecular structures in this paper belong to local minima on their singlet spin state potential surface and have no imaginary frequency. Structures of the nitro-substituted BN-cage compounds are denoted as NO2-n-N in the present article, where n is the number of energetic groups, N orders the structures according to their relative energies using the M06-2X method.Calculation of the electron localization function (ELF), deformation energies, net charge and charge transfer at the same level are used to analyze the electronic structure and stability of the NO2-n-N series. Moreover, Born–Oppenheimer molecular dynamic simulations (BOMD) are employed to exam the stability of the designed cage compounds to select the stable BN-cage derivates with a DFT in the level of M06-2X/6-311++G**. BOMD deals with the electronic and nuclear problems separately. In this method, the electronic structure in the ground state is calculated at each set of atomic positions, usually by optimization of the Kohn–Sham orbitals using an iterative method.33 The BOMD method in general needs more CPU time than for other MD software, but the method is more robust and stable.
Heat of detonation, detonation velocity and detonation pressure were calculated using EXPLO 5,34 using the density and solid phase enthalpy of formation (ΔfH°(s)). The gas phase enthalpy of formation (ΔfH°(g)) and the enthalpy of sublimation 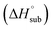 were used to calculate the solid phase enthalpy of formation (ΔfH°(s)).
were used to calculate the solid phase enthalpy of formation (ΔfH°(s)).
The following isodesmic reactions (1) combined with the computational Formula (2) were used to calculate the ΔfH°(g) of the studied compounds.
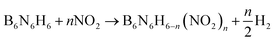 | (1) |
| ΔH298 = ΔE + ΔZPE + ΔHT | (2) |
In eqn (1) and (2), n is the number of nitro groups, ΔH298 is the enthalpy change of the reaction at 298 K, ΔE is the change in total energy between the products and the reactants, ΔZPE is the change of zero-point energy between the products and the reactants, and ΔHT is the thermal correction from 0 to 298 K.
Electrostatic potential analysis (ESP) is employed to analyze the molecular surface at the M06-2X/6-311++G level of theory. In the eqn (3)–(7), the electrostatic potential on the surface is characterized by Vs(r). V+s(ri), V−s(ri) and Vs(ri) represents the positive, negative and the overall value of Vs(r) at any point ri on the surface. The 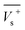 ,
, 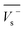 and
and 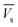 represent their averages, and σ+2, σ−2, and σtot2 are the corresponding variances. ν is the electrostatic balance parameter. m and n are the number of positions with positive and negative potentials on the molecular surface. The parameters mentioned above will be used to further calculate the enthalpy of sublimation, density and impact sensitivity in the corresponding equations.
represent their averages, and σ+2, σ−2, and σtot2 are the corresponding variances. ν is the electrostatic balance parameter. m and n are the number of positions with positive and negative potentials on the molecular surface. The parameters mentioned above will be used to further calculate the enthalpy of sublimation, density and impact sensitivity in the corresponding equations.
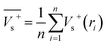 | (3) |
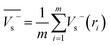 | (4) |
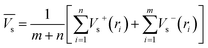 | (5) |
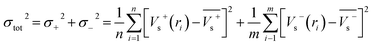 | (6) |
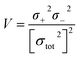 | (7) |
The enthalpy of sublimation 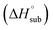 can be evaluated using the developed method by Rice and Politzer et al.35
can be evaluated using the developed method by Rice and Politzer et al.35
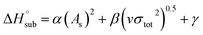 | (8) |
Then, the solid phase enthalpy of formation (ΔfH°(s)) can be calculated using eqn (9).
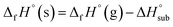 | (9) |
The crystal density (ρ) of the studied compounds can be calculated using 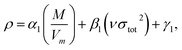 36 in which α1 = 0.9183, β1 = 0.0028, and γ1 = 0.0443.
36 in which α1 = 0.9183, β1 = 0.0028, and γ1 = 0.0443.
In order to understand the sensitivity and safety of the studied cage compounds, the impact sensitivity,37 Wiberg bond index (WBI),38,39 and bond dissociation energy (BDE)40 were calculated. Impact sensitivity can be tested using the drop hammer test, which is measured by dropping a given mass (2.5 kg) upon the compound and recording the height (h50) which has a 50% probability of producing an explosion. The value of h50 is calculated using eqn (10).37
| h50 = α2σ+2 + β2ν + γ2 | (10) |
The BDE is calculated using eqn (11). In general, if the value of BDE is greater than 84 kJ mol−1, the corresponding bond is considered to be stable.
| BDE(A–B) = [EA˙ + EB˙] − E(A–B) | (11) |
3. Results and discussion
3.1. Configuration
Fig. 1 shows an optimized structure of the designed BN-cage that was confirmed to be a global minimal without imaginary frequencies at the M06-2X level. The distances of B3-N7, B5-N6 and B16-N15 are 1.716 Å, 1.716 Å and 2.803 Å, respectively. The corresponding WBI, determined using natural bond orbital (NBO) analysis were 0.5085, 0.5085 and 0.0049, respectively. The relatively long distance and small WBI between B16 and N15 suggests the absence of the corresponding bond. Additionally, the bond lengths (WBI) of B1–N8, B2–N9 and B4–N10 were found to be 1.370 Å (1.2746), 1.403 Å (1.0820) and 1.403 Å (1.0820), respectively. The shorter bond lengths and larger WBI of these three bonds compared with the other B–N bonds are indicative that double bonds exist between B1–N8, B2–N9 and B4–N10. Also, the topological analysis of the ELF was performed to understand the bond character of the B–N bonds in the designed BN-cage. The corresponding color-filled maps and the curve maps of ELF for these bonds are shown in Fig. S1,† which further confirms the existence of the B3–N7, B5–N6, B1–N8, B2–N9, and B4–N10 covalent bonds, and the inexistence of the B16–N15 bond.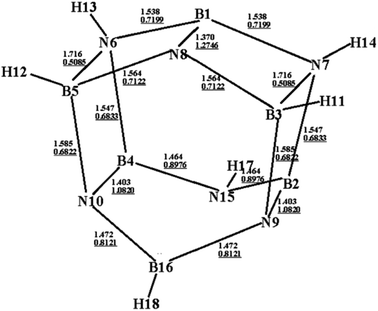 | ||
| Fig. 1 Optimized structure (bond lengths in Å) for the designed BN-cage at the M06-2X/6-311++G** level. Wiberg bond indexes are underlined. | ||
The H atoms in the designed BN-cage were replaced by nitro groups to construct a series of new energetic molecules. All of the optimized structures could retain the integrity of the BN-cages. Moreover, the calculation results indicated that the energetic groups bond with boron atoms in the cage led to lower-energy structures than that with nitrogen atoms. Fig. 2 shows the optimized geometries of the NO2-n-1 (n = 1–6).
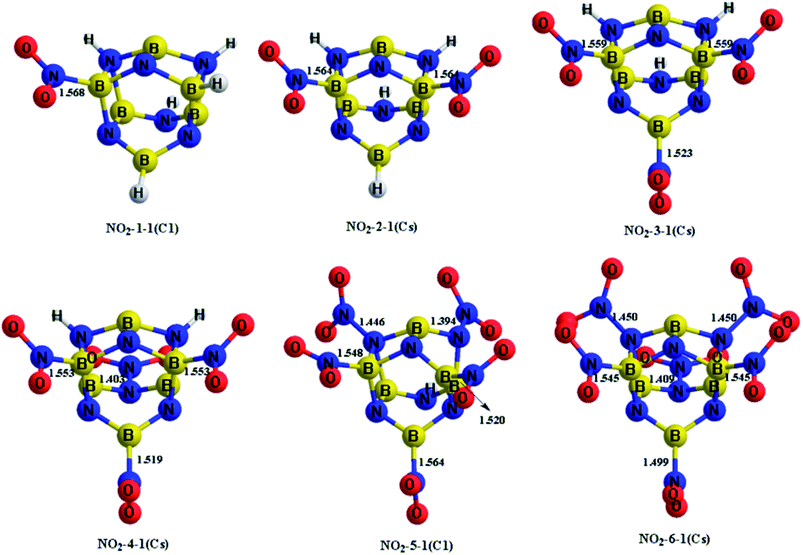 | ||
| Fig. 2 Optimized geometries (bond lengths in Å) at the M06-2X/6-311++G** level for the NO2-n-1 (n = 1–6). Symmetries are labeled in parentheses. | ||
The four mononitro-substituted BN-cage compounds shown in Fig. S1 and Table S2† were found to lie less than 200 kJ mol−1 in energy above the lowest-energy structure NO2-1-1. The nitro group in the lowest-lying structures NO2-1-1 is bonded to the B5 atom by replacing H12 in the BN-cage. It should be pointed out that the distance between B3 and N7 in NO2-1-3 is 2.621 Å, the long distance of the bond and the corresponding ELF analysis (shown in Fig. S3†) suggests that the B3–N7 bond does not exist.
The five dinitro-substituted BN-cage compounds shown in Fig. S2 and Table S3† are found to lie less than 200 kJ mol−1 in energy above NO2-2-1. Similar to the mononitro-substituted compounds, the nitro groups bond with B3 and B5 in NO2-2-1 to obtain the lowest-energy structure with the symmetry of the Cs. The NO2-2-2 lies at an energy of 27.2 kJ mol−1 above the NO2-2-1S at the M06-2X level, having the B5–NO2 and B16–NO2 bonds. However, the NO2-2-3, NO2-2-4 and NO2-2-5, with the N-NO2 bonds have much higher total energies than the NO2-2-1 and NO2-2-2 due to the high energy of the N–N bonds.
The four trinitro-substituted BN-cage compounds shown in Fig. S3 and Table S4† are found to lie less than 200 kJ mol−1 in energy above the lowest-energy structure NO2-3-1. The three nitro groups in NO2-3-1 with a Cs symmetry are bonded with the B3, B5 and B16 atoms. The NO2-3-2, NO2-3-3 and NO2-3-4 with one N–NO2 bond are, respectively, 126.0, 150.5 and 161.2 kJ mol−1 at the M06-2X level, higher than NO2-3-1.
As shown in Fig. S4 and Table S5,† three tetranitro-substituted BN-cages are found to lie less than 200 kJ mol−1 in energy above NO2-4-1. Both of the first two structures NO2-4-1 and NO2-4-2 have three B–NO2 bonds and one N–NO2 bonds, while the NO2 groups in NO2-4-3 bond with two B atoms and two N atoms. It should be pointed out that the distances between the B3 and N7 atoms in NO2-4-2 and NO2-4-3 are 2.534 and 2.491 Å, respectively. The relatively long distances and the corresponding ELF analysis shown in Fig. S7 and S8† suggests the absence of corresponding bonds.
Only the two pentanitro-substituted BN-cages were found, which are shown in Fig. S5 and Table S6.† In NO2-5-1, the five nitro groups bond with the three boron atoms and two nitrogen atoms. Additionally, the distance of B3⋯N7 and B16⋯N15 in NO2-5-1 are 2.608 and 2.629 Å respectively, which are about 1 Å longer than the other B–N bonds. This is indicative of the absence of these two bonds, combined with the color-filled map and the curve map of ELF (shown in Fig. S10†).
Finally, only one hexanitro-substituted BN-cage NO2-6-1 is found, as shown in Fig. S6 and Table S7.† All of the H atoms in the designed BN-cage are replaced by nitro groups leading to the Cs symmetry for NO2-6-1.
3.2. Electronic structure and thermal stability
To study the change caused by substituting the H of the designed BN-cage with NO2, the deformation energies of the skeleton (ΔEcage) and the relative (ΔBDE) are calculated and summarized in Table 1. ΔBDE can be calculated using eqn (12), which is the relative BDE of cage-NO2 bonds to the corresponding cage-H bonds in the designed BN-cage without substitution.| ΔBDE = BDEcage–NO2 − BDEcage–H | (12) |
| Compounds | Methods | NO2-1-1 | NO2-1-2 | NO2-1-3 | NO2-1-4 |
|---|---|---|---|---|---|
| ΔEcage | M06-2X | 0.5 | 1.6 | 53.4 | 44.4 |
| ωB97XD | 2.83 | 4.0 | 54.0 | 43.4 | |
| B3LYP | 3.9 | 1.6 | 55.5 | 30.5 | |
| ΔBDE | M06-2X | −24.6 | −55.4 | −212.8 | −226.8 |
| ωB97XD | −39.5 | −62.8 | −226.2 | −241.4 | |
| B3LYP | −37.0 | −61.0 | −225.5 | −228.2 |
To further study the stability of the mononitro-substituted BN-cage isomers, the deformation energies of the BN-cage skeletons 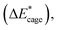 the deformation energies of the nitro groups
the deformation energies of the nitro groups 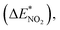 and the relative BDE of the cage-NO2 bonds (ΔBDE*) to NO2-1-1 are calculated and the results are shown in Table 2.
and the relative BDE of the cage-NO2 bonds (ΔBDE*) to NO2-1-1 are calculated and the results are shown in Table 2.
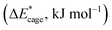 and nitro groups
and nitro groups 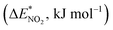 among the mononitro-substituted BN-cage compounds
among the mononitro-substituted BN-cage compounds
As shown in Table 2, comparing with NO2-1-1, the decrease of the BDE of the B–NO2 bond in the NO2-1-2 structure leads to an increase of its energy, and the deformation of its skeleton could be ignored due to its small 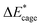 value. For the N-mononitrosubstituted isomers NO2-1-3 and NO2-1-4, the difference of the B–NO2 and N–NO2 bond is the primary reason leading to their energy increase. Compared to the global minimum of NO2-1-1, the NO2 bonding in the N atom brings the relative heavy deformation of the BN-cage skeletons, which is another reason for the lower NO2-1-3 and NO2-1-4 structural stability. For the nitro group, the isomers have a small
value. For the N-mononitrosubstituted isomers NO2-1-3 and NO2-1-4, the difference of the B–NO2 and N–NO2 bond is the primary reason leading to their energy increase. Compared to the global minimum of NO2-1-1, the NO2 bonding in the N atom brings the relative heavy deformation of the BN-cage skeletons, which is another reason for the lower NO2-1-3 and NO2-1-4 structural stability. For the nitro group, the isomers have a small 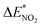 value and the change of the NO2 could be ignored, as shown in Table 2.
value and the change of the NO2 could be ignored, as shown in Table 2.
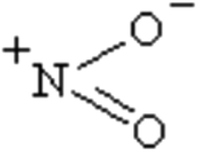
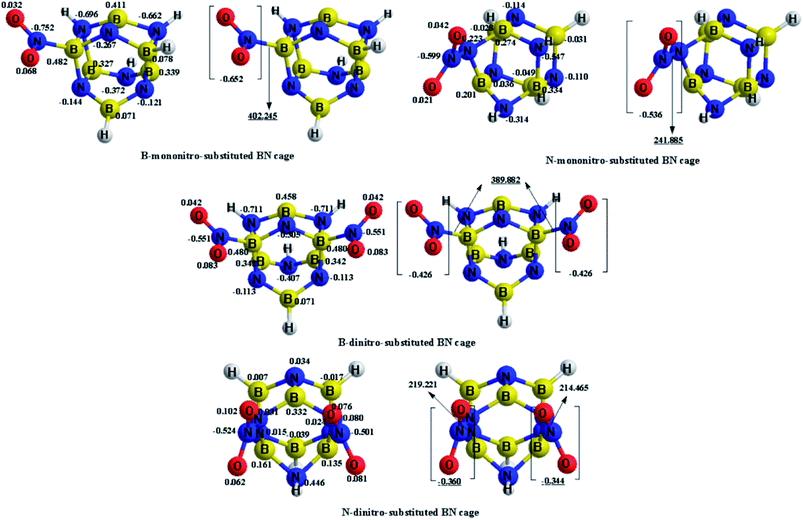
The charge transfer calculated using the NBO analysis is also employed to analyze the stability differences among the different substitution positions. The valence-bond structure of the nitro group, shown in Fig. 3, indicates that the nitro is an electrophilic group, in which the nitrogen atom tends to combine with the boron atom in the cage to provide a stable configuration. Fig. 4 and Table 3 describe the molecular structures, net charge, charge transfer and BDE of the cage-NO2 bonds for the mononitro or dinitro-substituted cages. As listed in Table 3, the results show that all the nitro groups in the B(N)-mononitro or dinitro-substituted cages are electron accepters, and the charge transfers of the B-mononitro or dinitro-substituted cage is always larger than those of the N-mononitro or dinitro-substituted cage, suggesting the higher dissociation energies of the B–NO2 bonds compared with the N–NO2 bonds.
| Compounds | Substitution positions | Net charge | ||
|---|---|---|---|---|
| M06-2X | ωB97XD | B3LYP | ||
| B-mononitro-substitution | B | −0.652 | −0.627 | −0.740 |
| N-mononitro-substitution | N | −0.536 | −0.497 | −0.504 |
| B-dinitro-substitution | B | −0.426 | −0.388 | −0.696 |
| B | −0.426 | −0.388 | −0.696 | |
| N-dinitro-substitution | N | −0.360 | −0.322 | −0.349 |
| N | −0.344 | −0.317 | −0.349 | |
The above calculations suggest that the B-nitrosubstituted cages have a relatively better stability than the N-nitrosubstituted cages. As such, the NO2-1-1, NO2-2-1 and NO2-3-1 structures were selected for further study, as discussed in the subsequent sections.
3.3. Dynamic simulation
Based on the above calculation results for the stability of these designed BN-cage derivatives, molecular dynamic calculations of the B-substituted NO2-n-1 (n = 1, 2, 3) structures were carried out to exam their dynamic stability. BOMD were employed to perform the molecular dynamic simulation. The static configurations calculated at the M06-2X/6-311++G** level were run as seeds for the BOMD trajectories using the Gaussian-09 program package. Equilibration steps were performed over 1 ps and production runs are 3 ps long with the time step of 1 fs.The simulation results of the NO2-n-1 (n = 1, 2, 3) structures show that the NO2-1-1 and NO2-2-1 remain stable at 298 K during the whole simulation, while the nitro groups in NO2-3-1 cannot remain stable at 298 K, as shown in Fig. 5. As can be seen from Fig. 5, the nitro groups in NO2-3-1 decompose from the cage with the cage-NO2 bond breaking. Oxygen atoms in the nitro groups in the NO2-3-1 bond with the cage directly at 298 K, with B–O bond lengths of 1.452 and 1.316 Å, while the NO groups decompose from the BN-cage compounds, with the distances between O and NO groups being ∼1.55 Å. Moreover, deformation of the cage skeleton occurs with the distance between B5 and N6 being 2.821 Å. Thus, the NO2-3-1 structure cannot remain stable at room temperature. Above all, the NO2-1-1 and NO2-2-1 structures have exhibited an attractive potential for application in the areas of energetic materials and the details are discussed in the following study on detonation performance.
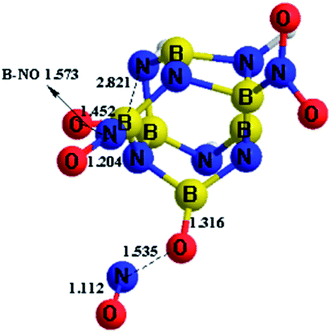 | ||
| Fig. 5 The dynamic simulation results of NO2-3-1 at 298 K, taken from the simulations performed at the M06-2X/6-311++G** level. | ||
3.4. Detonation performance
In order to quantitatively evaluate the detonation performance of the NO2-1-1 and NO2-2-1 structures, the predicted density (ρ), enthalpy of sublimation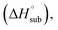 solid phase enthalpy of formation (ΔfH°(s)), oxygen balance and detonation parameters (Q, D, P) were calculated systematically using EXPLO 5. The results, together with the related information for CL-20, are listed in Table 4 for comparison.
solid phase enthalpy of formation (ΔfH°(s)), oxygen balance and detonation parameters (Q, D, P) were calculated systematically using EXPLO 5. The results, together with the related information for CL-20, are listed in Table 4 for comparison.
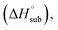 solid phase enthalpy of formation (ΔfH°(s)), detonation velocity (D), detonation pressure (P), heat of detonation (Q) and oxygen balance of the NO2-1-1 and NO2-2-1 structures. Experimental parameters of CL-20 are labeled in parentheses (the theoretical densities of CL-20 are 1.954 g cm−3 at M06-2X, 1.907 g cm−3 at ωB97XD and 2.022 g cm−3 at B3LYP)
solid phase enthalpy of formation (ΔfH°(s)), detonation velocity (D), detonation pressure (P), heat of detonation (Q) and oxygen balance of the NO2-1-1 and NO2-2-1 structures. Experimental parameters of CL-20 are labeled in parentheses (the theoretical densities of CL-20 are 1.954 g cm−3 at M06-2X, 1.907 g cm−3 at ωB97XD and 2.022 g cm−3 at B3LYP)
The results in Table 4 show that the ρ of NO2-1-1 and NO2-2-1 are 1.808 g cm−3 (1.789 g cm−3, 1.732 g cm−3) and 1.931 g cm−3 (1.871 g cm−3, 2.059 g cm−3) respectively at the M06-2X (ωB97XD, B3LYP)/6-311++G** level. In the meantime, the calculated densities of CL-20 are 1.954 g cm−3 at the M06-2X level, 1.907 g cm−3 at the ωB97XD level and 2.022 g cm−3 at the B3LYP level, which indicates the relatively high densities of these two newly proposed designed molecules. The Q of NO2-2-1 is 31.25% (M06-2X), 31.26% (ωB97XD) or 24.79% (B3LYP) higher than that of CL-20 (6314 kJ kg−1), with a D of over 6800 m s−1. The superior detonation heat of both the NO2-1-1 and NO2-2-1 structures indicate the great potential of these two energetic compounds to be HEDMs.
3.5. Sensitivity and safety
To test the sensitivity and safety of the above NO2-1-1 and NO2-2-1 structures, two methods have been employed in the present work: (1) impact sensitivity; and (2) BDE of the trigger bonds.| Compounds | Methods | NO2-1-1 | NO2-2-1 | CL-20 |
|---|---|---|---|---|
| σ+2 | M06-2X | 292.859 | 417.062 | 231.351 |
| ωB97XD | 302.761 | 437.273 | 233.923 | |
| B3LYP | 278.559 | 422.418 | 306.392 | |
| ν | M06-2X | 0.227 | 0.168 | 0.068 |
| ωB97XD | 0.220 | 0.167 | 0.065 | |
| B3LYP | 0.231 | 0.175 | 0.058 | |
| h50 (cm) | M06-2X | 49.498 | 34.459 | 11.506 |
| ωB97XD | 47.745 | 34.089 | 10.765 | |
| B3LYP | 50.555 | 36.115 | 8.611 |
To elucidate the pyrolysis mechanism and thermal stability of the NO2-1-1 and NO2-2-1 structures, the bond dissociation energies of the cage-NO2 bonds in NO2-1-1, NO2-2-1 and CL-20, as well as the corresponding WBI have been investigated in the present work, as shown in Table 6. Obviously, the BDE of the cage-NO2 bonds in the NO2-1-1 and NO2-2-1 structures are 402.245 kJ mol−1 (447.635 kJ mol−1, 393.573 kJ mol−1) and 389.882 kJ mol−1 (358.869 kJ mol−1, 381.905 kJ mol−1) with WBI of 0.6640 (0.6657, 0.6852) and 0.6716 (0.6731, 0.6916) respectively, at the M06-2X (ωB97XD, B3LYP)/6-311++G** level. Thus, the designed NO2-1-1 and NO2-2-1 BN-cage molecules meet the stability requirement suggested previously, that is, a molecule could be considered as a practical energetic material if it has its BDE larger than 84 kJ mol−1. Moreover, the BDE of the cage-NO2 bonds in NO2-1-1 and NO2-2-1 are much higher than that of CL-20 at the same calculation level, which implies that they have a better stability than CL-20.
| Compounds | WBI | BDE(kJ mol−1) | ||||
|---|---|---|---|---|---|---|
| Methods | M06-2X | ωB97XD | B3LYP | M06-2X | ωB97XD | B3LYP |
| NO2-1-1 | 0.6640 | 0.6657 | 0.6852 | 402.245 | 447.635 | 393.573 |
| NO2-2-1 | 0.6716 | 0.6731 | 0.6916 | 389.882 | 358.869 | 381.905 |
| CL-20 | 0.9421 | 0.9460 | 0.9318 | 153.092 | 127.022 | 148.656 |
4. Conclusions
Inspired by the high combustion heat of the boron atom and the large strain energy of the HNIW cage skeleton, we proposed several molecules with a new BN-cage skeleton by replacing C with B atoms in this study. A series of energetic molecules B6N6H6−n(NO2)n (n = 1–6) were subsequently constructed through systematically substituting NO2 groups for the H atoms of the BN-cage. Then, all the B6N6H6−n(NO2)n (n = 1–6) structures were optimized at the M06-2X/6-311++G**, ωB97XD/6-311++G** and B3LYP/6-311++G** level of DFT. Analysis of the structural changes caused by substituting the NO2 and the electronic structures including ELF, WBI, charge transfer and BDE reveal the essence of the stability and chemical characteristics of these B6N6H6−n(NO2)n (n = 1–6) molecules. The results show that these B-nitro substituted cages have a higher stability than the N-nitro substituted cages. The corresponding molecular dynamic simulations, which were performed to test the stability of NO2-1-1, NO2-2-1 and NO2-3-1, indicate that only the NO2-1-1 and NO2-2-1 structures remain stable under ambient conditions. Then, the density, detonation performance and safety of the NO2-1-1 and NO2-2-1 structures were calculated systematically. The results show that the two BN-cage energetic molecules have a much higher detonation heat than traditional energetic materials such as CL-20, due to their high densities and the particular characteristics of the “BN” groups. Calculations also showed much higher h50 values of NO2-1-1 (49.489 cm at the M06-2X level) and NO2-2-1 (34.459 cm at the M06-2X level) than CL-20 (11.506 cm at the M06-2X level) in the same level of calculation, as well as the high bond dissociation energies over 84 kJ mol−1. Above all, a new type of energetic material based on the BN-cage was put forward and could be a new field of research to find more HEDMs with a superior performance.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are indebted to the National Natural Science Foundation of China (21643015 and U1530262). We also acknowledge financial support from the Open Project (LHKF2014-C15) in the Key Laboratory of Theoretical Chemistry of Environment, Ministry of Education.References
- O. S. Bushuyev, P. Brown and A. Maiti, Ionic polymers as a new structural motif for high-energy-density materials, J. Am. Chem. Soc., 2012, 134(3), 1422–1425 CrossRef CAS PubMed.
- J. Song, Z. Zhou and X. Dong, Super-high-energy materials based on bis (2, 2-dinitroethyl) nitramine, J. Mater. Chem., 2012, 22(7), 3201–3209 RSC.
- Y. Zhang, D. A. Parrish and J. M. Shreeve, 4-Nitramino-3, 5-dinitropyrazole-Based Energetic Salts, Chem.–Eur. J., 2012, 18(3), 987–994 CrossRef CAS PubMed.
- J. Zhang and J. M. Shreeve, 3, 3′-Dinitroamino-4, 4′-azoxyfurazan and its derivatives: an assembly of diverse N–O building blocks for high-performance energetic materials, J. Am. Chem. Soc., 2014, 136(11), 4437–4445 CrossRef CAS PubMed.
- D. M. Badgujar, M. B. Talawar and S. N. Asthana, Advances in science and technology of modern energetic materials: an overview, J. Hazard. Mater., 2008, 151(2), 289–305 CrossRef CAS PubMed.
- W. J. Chi and Z. S. Li, Molecular design of prismane-based potential energetic materials with high detonation performance and low impact sensitivity, C. R. Chim., 2015, 18(12), 1270–1276 CrossRef CAS.
- D. E. Chavez, M. A. Hiskey and R. D. Gilardi, 3, 3′-Azobis (6-amino-1, 2, 4, 5-tetrazine): A Novel High-Nitrogen Energetic Material, Angew. Chem., 2000, 112(10), 1861–1863 CrossRef.
- M. A. Hiskey, N. Goldman and J. R. Stine, High-nitrogen energetic materials derived from azotetrazolate, J. Energ. Mater., 1998, 16(2–3), 119–127 CrossRef CAS.
- A. Hammerl, T. M. Klapötke and H. Nöth, [N2H5]+ 2 [N4C-N N-CN4] 2-: A New High-Nitrogen High-Energetic Material, Inorg. Chem., 2001, 40(14), 3570–3575 CrossRef CAS PubMed.
- E. G. Gillan, Synthesis of nitrogen-rich carbon nitride networks from an energetic molecular azide precursor, Chem. Mater., 2000, 12(12), 3906–3912 CrossRef CAS.
- C. Zhang, C. Sun and B. Hu, Synthesis and characterization of the pentazolate anion cyclo-N5 in (N5) 6 (H3O) 3 (NH4) 4Cl, Science, 2017, 355(6323), 374–376 CrossRef CAS PubMed.
- A. T. Nielsen, U.S. Department and Navy, US Pat. Office Application Case No. 70631, 24 June, 1987.
- K. K. Kuo, G. A. Risha and B. J. Evans, Potential usage of energetic nano-sized powders for combustion and rocket propulsion, MRS Online Proc. Libr., 2003, 800, 3–14 CAS.
- G. Risha, E. Boyer and R. Wehrman. Nano-sized aluminum and boron-based solid fuel characterization in a hybrid rocket engine, 39th AIAA/ASME/SAE/ASEE joint propulsion conference and exhibit, 2003, p. 4593 Search PubMed.
- P. D. McCrary, P. A. Beasley and O. A. Cojocaru, Hypergolic ionic liquids to mill, suspend, and ignite boron nanoparticles, Chem. Commun., 2012, 48(36), 4311–4313 RSC.
- A. MaČeic and J. M. K. Semple, Combustion of boron particles at atmospheric pressure, Combust. Sci. Technol., 1969, 1(3), 181–191 CrossRef.
- G. Young, K. Sullivan and M. R. Zachariah, Combustion characteristics of boron nanoparticles, Combust. Flame, 2009, 156(2), 322–333 CrossRef CAS.
- E. C. Koch and T. M. Klapötke, Boron-Based High Explosives, Propellants, Explos., Pyrotech., 2012, 37(3), 335–344 CrossRef CAS.
- V. I. Pepekin, M. N. Makhov and A. Y. Apin, The reactions of boron in the presence of an explosion, Combust., Explos. Shock Waves, 1972, 8(1), 109–111 CrossRef.
- L. N. Akimova, A. Y. Apin and L. N. Stesik, Detonation of explosives containing boron and its organic derivatives, Combust., Explos. Shock Waves, 1972, 8(4), 387–390 CrossRef.
- S. C. Li and F. A. Williams, Ignition and combustion of boron particles, Int. J. Energ. Mater. Chem. Propul., 1993, 2(1–6), 248–271 Search PubMed.
- J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09, Revision A.02, Gaussian Inc, Wallingford, 2009 Search PubMed.
- W. H. James III, E. G. Buchanan and C. W. Müller, Evolution of amide stacking in larger γ-peptides: triamide H-bonded cycles, J. Phys. Chem. A, 2011, 115(47), 13783–13798 CrossRef PubMed.
- Y. Zhao and G. T. Donald, Density functionals with broad applicability in chemistry, Acc. Chem. Res., 2009, 41(2), 157–167 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, Systematic Optimization of Long-range Corrected Hybrid Density Functionals, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; (b) J. Becke, Chem. Phys., 1993, 98, 5648 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785 CrossRef CAS.
- J. Zhang, Q. Zhang and T. T. Vo, Energetic salts with π-stacking and hydrogen-bonding interactions lead the way to future energetic materials, J. Am. Chem. Soc., 2015, 137(4), 1697–1704 CrossRef CAS PubMed.
- A. G. Roknabadi, M. H. Keshavarz and K. Esmailpour, Structural, thermochemical and detonation performance of derivatives of 1, 2, 4, 5-tetrazine and 1, 4 N-oxide 1, 2, 4, 5-tetrazine as new high-performance and nitrogen-rich energetic materials, J. Iran. Chem. Soc., 2017, 14(1), 57–63 CrossRef CAS.
- J. Yang, X. Gong and G. Wang, Structure, aromaticity, stability, and energetic performance of the analogues and derivatives of s-heptazine, J. Mol. Model., 2014, 20(8), 2379 CrossRef PubMed.
- K. B. Wiberg, Basis set effects on calculated geometries: 6-311++ G** vs. aug-cc-pVDZ, J. Comput. Chem., 2004, 25(11), 1342–1346 CrossRef CAS PubMed.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients, Rev. Mod. Phys., 1992, 64(4), 1045 CrossRef CAS.
- M. Suceska, EXPLO5 Program. Version 5.04, Brodarski Institute, Zagreb, Croatia, 2010 Search PubMed.
- P. Politzer and J. S. Murray, Some perspectives on estimating detonation properties of C, H, N, O compounds, Cent. Eur. J. Energ. Mater., 2011, 8(3), 209–220 CAS.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. ToroLabbe, An electrostatic interaction correction for improved crystal density prediction, Mol. Phys., 2009, 107(19), 2095–2101 CrossRef CAS.
- M. Pospíšil, P. Vávra, M. Concha, J. Murray and P. Politzer, A possible crystal volume factor in the impact sensitivities of some energetic compounds, J. Mol. Model., 2010, 16, 895–901 CrossRef PubMed.
- E. D. Glendening, J. K. Badenhoop and A. E. Reed, et al., NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001, there is no corresponding record for this reference, 2004 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88(6), 899–926 CrossRef CAS.
- S. J. Blanksby and G. B. Ellison, Bond dissociation energies of organic molecules, Acc. Chem. Res., 2003, 36(4), 255–263 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra13476b |
| This journal is © The Royal Society of Chemistry 2018 |