Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intrinsic structural distortion and exchange interactions in SmFexCr1−xO3 compounds†
Zhongcheng Xiang,
Wenping Li and
Yimin Cui *
*
Key Laboratory of Micro-nano Measurement-Manipulation and Physics, Ministry of Education, Beihang University, Beijing 100191, China. E-mail: cuiym@buaa.edu.cn
First published on 27th February 2018
Abstract
The effect of substituting different amounts of magnetic metal Fe on the magnetic properties of SmFexCr1−xO3 (0 < x < 0.5) is reported here in order to probe the relation between the structural distortion and magnetism in these materials. The structural properties of the samples were characterized using X-ray diffraction with Rietveld refinements, and Raman spectroscopy carried out at ambient temperature. Magnetization data reveals the Neel temperature (TN, where the Cr(Fe) ions order) increases with an increase in the average B-site ionic radius, and average Cr(Fe)–O–Cr(Fe) bond angle. By fitting the temperature dependence of the magnetic susceptibility to the Curie–Weiss law modified by the Dzyaloshinskii–Moriya (DM) interaction, the strengths of the symmetric and antisymmetric Cr(Fe)–Cr(Fe) exchange interactions (J and D) were determined. It was found that the strength of the symmetric interaction J (reflected in the changes in the Neel temperature) increases with the replacement of Cr3+ with Fe3+, which is ascribed to the changes in the average Cr(Fe)–O–Cr(Fe) bond angle and bond lengths. Meanwhile, the antisymmetric interaction D a slightly decreases, which may be ascribed to the displacement of oxygen ions (dO) away from their “original” middle point.
Introduction
Rare-earth (R) transition metal (M) orthorhombic perovskite materials with ABO3-type perovskite structures, such as orthochromites RCrO3, and orthoferrites RFeO3, have received great interest, and possess more than one ferroic order, for example, ferroelectricity (FE), ferromagnetism (FM), and ferroelasticity.1,2 Perovskite structures can demonstrate a variety of functions because of the wide selection of elements they can incorporate, driving structural distortions that influence the magnetic and electronic properties, and magnetoelectric properties.3 The structure can also accommodate various types of disorder such as point substitutions or vacancies in some cases. Element substitution in the A-site and B-site of rare-earth orthorhombic perovskite materials leads to changes in the average B–O–B bond angle and bond lengths. Naturally, the perovskite materials will suffer from structural deformation or tilting. Such tilting controls both the magnetic superexchange, J, and the orbital overlap between B and O ions, which thus determines the magnetic ordering temperature and the conductivity.4–6 It has been widely accepted that the B–O–B bond angle (B = transition metal), which is reduced from 180° due to the cooperative octahedral-site rotations in the orthorhombic perovskite, is a major factor in determining the B–O–B superexchange interaction. The empirical relationship between the superexchange coupling J and the superexchange angle for the RFeO3 family has been reported from J ∼ cosθ (ref. 7) to J ∼ cos2θ (ref. 8) and finally to J ∼ cos4 ((π − θ)/2)/d7 (ref. 9), where θ and d denote the average B–O–B bond angle and the average B–O bond length, respectively.In addition, RCrO3 and RFeO3 with ABO3-type perovskite structures exhibit antiferromagnetism with a weak ferromagnetic moment (WFM) due to the canted nature of the Cr3+ and Fe3+ moments below the Neel temperatures.10,11 In recent publications,12,13 the weak ferromagnetism of various antiferromagnetic compounds can mainly be explained by the Dzyaloshinskii–Moriya interaction, and the Hamiltonian can be expressed as  (Si × Sj). For a perovskite structure with bent B–O–B bonds, the vector Dij must be perpendicular to the B–O–B plane and determined by the symmetry restrictions.14,15 In other words, substitution in the A-site and B-site and a size mismatch between the A and B ions usually make the oxygen octahedra tilt and rotate, resulting in a distortion. Therefore, each oxygen ion sandwiched between two neighboring B ions may move away from the middle point, giving a bent B–O–B bond and breaking the B–B axis rotation symmetry. This bent B–O–B bond will change the DM interaction as a relativistic correction to the superexchange between the magnetic B ions. Through the above analysis, the strengths of the symmetric and antisymmetric B–B exchange interactions (J and D) are changed by structural deformation and tilting, which is caused by element substitution in perovskite materials.
(Si × Sj). For a perovskite structure with bent B–O–B bonds, the vector Dij must be perpendicular to the B–O–B plane and determined by the symmetry restrictions.14,15 In other words, substitution in the A-site and B-site and a size mismatch between the A and B ions usually make the oxygen octahedra tilt and rotate, resulting in a distortion. Therefore, each oxygen ion sandwiched between two neighboring B ions may move away from the middle point, giving a bent B–O–B bond and breaking the B–B axis rotation symmetry. This bent B–O–B bond will change the DM interaction as a relativistic correction to the superexchange between the magnetic B ions. Through the above analysis, the strengths of the symmetric and antisymmetric B–B exchange interactions (J and D) are changed by structural deformation and tilting, which is caused by element substitution in perovskite materials.
Interestingly, SmCrO3 is a representative rare-earth orthochromite that has been believed to possess canted G-type antiferromagnetism with a magnetic ordering temperature around 192 K.16 In recent years, it has been believed that a variety of interesting properties can be achieved by alloying different kinds of cation at the B-site of perovskite materials. According to the Goodenough–Kanamori theory, Fe3+ is the best choice for substituting Cr3+ in order to show superior magnetic properties, due to superexchange interactions.17 Studies on ABxB′1−xO3 perovskite compounds have shown that the structures and physical properties of these compounds strongly depend on the ionic size and charge differences of the B-site cations (B and B′).18,19
In this paper, polycrystalline samples SmFexCr1−xO3 (0 < x < 0.5) were compounded via a solid state reaction, and their structures were confirmed using XRD and Raman spectroscopy techniques, which reveal the evolution of the distorted perovskite structure with Fe substitution. The temperature dependent dc magnetic measurements reveal obvious changes to the Neel temperatures, TN, with substitution of rare-earth ions with Fe in SmFexCr1−xO3. We discuss the strength of the symmetric and antisymmetric Cr(Fe)–Cr(Fe) exchange interaction (J and D) effects with structural deformation and tilting, caused by changes in the average B–O–B bond angle and bond lengths.
Experimental
Polycrystalline samples SmFexCr1−xO3 (0 < x < 0.5) were compounded via a conventional solid-state reaction using high-purity (>99.99%) raw powders of Sm2O3, Cr2O3, and Fe2O3. Powder X-ray diffraction (XRD) measurements were performed using a Bruker D5 diffractometer using Cu-Kα radiation (λ = 1.5418 Å). X-ray diffraction (XRD) patterns were obtained from 10 to 120° with steps of 0.02° and a counting time of 2 s per step, using an X-ray diffractometer with Cu-Kα radiation at 40 kV and 40 mA. Raman spectroscopy measurements were taken using a 514 nm wavelength argon-ion laser. The particle size and micro-structural analyses were performed using scanning electron microscopy (SEM), and energy dispersive X-ray (EDX) analysis verified the chemical composition of SmFexCr1−xO3 (0 < x < 0.5). Magnetization data were collected using a Quantum Design Magnetic Property Measurement System (MPMS) SQUID magnetometer over the temperature range 5–400 K. Data were collected from field-cooled cooling (FCC) measurements made over this temperature range in an applied magnetic field of 100 Oe.Results and discussion
Sample characterization
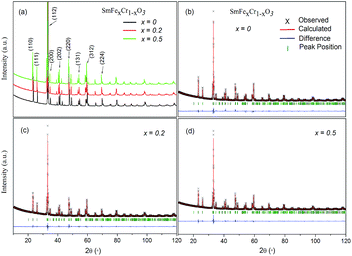
Fig. 1 shows the XRD patterns of the samples. X-ray diffraction (XRD) patterns were obtained from 10 to 120° with steps of 0.02° and a counting time of 2 s per step, using an X-ray diffractometer with Cu-Kα radiation (λ = 1.5418 Å) at 40 kV and 40 mA. All the major peaks for each sample could be indexed based on an orthorhombically distorted perovskite structure with the space group Pnma (no. 62).3 Thus, these samples were determined to be phase pure within the detection limit of laboratory XRD. The lattice parameters for the first member (x = 0) agree well with those in the literature for samples that have been made via both solid-state and hydrothermal syntheses,3,20 and the stability of the SmCrO3 structure was confirmed over the temperature range 88–300 K.21Rietveld refinement was used to analyze the XRD data for each composition. The Rietveld refined patterns of the SmFexCr1−xO3 (x = 0, 0.2 and 0.5) samples are shown in Fig. 1(b–d). The lattice parameters a, b, and c of the samples obtained from the Rietveld refinement are listed in Table 1. It was found that the unit cell lengths increase with increasing Fe3+ content, as seen in Table 1, meanwhile, the unit cell volume increases monotonically with increasing iron content. This difference could be interpreted as the effect of the dopant on the average B-site ionic radius Ravg = (x*(RFe3+)2 + 1 − x* (RCr3+)2)1/2 for the SmFexCr1−xO3 samples shown in Table 1. Here, RFe3+ and RCr3+ are 0.645 Å and 0.615 Å, respectively. From the Rietveld refinement, the in-plane (Cr(Fe)–O1–Cr(Fe)) and out-of-plane (Cr(Fe)–O2–Cr(Fe)) bond angles and their corresponding bond lengths were also determined (see Table 1). Note that the bond angles increase with increasing Ravg. For SmCrO3 and SmFeO3, the Goldschmidt tolerance factors (t) are 0.8332 and 0.82046, respectively. With increasing Ravg, t decreases for the SmCrO3 samples doped with Fe3+ at the B-site, which caused greater structural distortion.22 Along with the bond angles, the Cr(Fe)–O bond lengths are also slightly changed with changing Fe content, as seen in Table 1. The Cr(Fe)–O2 bond lies along the b direction of the unit cell, and both the Cr(Fe)–O1(1) and Cr(Fe)–O1(3) bonds are oriented in the ac plane. Increasing Fe content results in decreasing Cr(Fe)–O2 and Cr(Fe)–O1(1) bond lengths and increasing Cr(Fe)–O1(3) bond lengths. The overall result is that the average Cr(Fe)–O bond length slightly decreases, see Table 1. For the first member, SmCrO3, the values agree well with those reported previously.3,23
| Sample | X = 0 | X = 0.2 | X = 0.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Fig. 1 The XRD patterns for La1−xFexTiO3+δ (x = 0, 0.05, 0.1, 0.3, 0.4) at room temperature. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a (Å) | 5.48197 | 5.48841 | 5.52444 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| b (Å) | 7.63202 | 7.63921 | 7.65942 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| c (Å) | 5.36321 | 5.36779 | 5.37575 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V (Å3) | 224.389 | 225.056 | 227.470 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ravg (Å) | 0.615 | 0.621 | 0.630 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cr(Fe)–O1–Cr(Fe) (deg) | 147.418(0) | 152.330(27) | 155.710(31) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cr(Fe)–O2–Cr(Fe) (deg) | 146.833(1) | 150.600(5) | 152.300(5) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cr(Fe)–O1(1) (Å) | 1.99889(3) | 1.95400(6) | 1.95000(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cr(Fe)–O1(3) (Å) | 1.99609(3) | 1.99900(6) | 2.00900(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cr(Fe)–O2 (Å) | 1.99081(4) | 1.97440(16) | 1.97030(17) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| φ[010] | 14.3329 | 14.9384 | 16.1057 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| θ[101] | 11.9479 | 12.0344 | 13.3234 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Fig. 2 shows scanning electron microscopy (SEM) images of the as-synthesized SmFexCr1−xO3 (x = 0, 0.2 and 0.5) samples. Fig. 2(a and b) shows SEM images of the SmCrO3 samples, clearly showing a large amount of small spherical grains with a uniform distribution. The diameters of the spheres are in the range of 1 μm to 5 μm. The enlarged magnification SEM image (Fig. 2(a)) clearly shows that two grains are connected by a grain boundary. Fig. 2(c and d) shows SEM images of the SmFe0.2Cr0.8O3 and SmFe0.5Cr0.5O3 samples, respectively. From Fig. 2(b–d), it can been seen that the boundaries of the spheres become increasingly blurred with increasing Fe content, and the samples finally change to have hill-shaped morphologies, as shown in Fig. 2(d) (x = 0.5). In addition, the energy dispersive X-ray (EDX) spectra reveal that the relative compositional ratios of Fe to Cr atoms in the SmFexCr1−xO3 samples are about 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 1
4 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, for the samples where x = 0, 0.2 and 0.5, respectively (Fig. S1–3, ESI†). The results confirmed the different Fe dopant concentrations with x = 0, 0.2 and 0.5 in the SmFexCr1−xO3 samples.
1, for the samples where x = 0, 0.2 and 0.5, respectively (Fig. S1–3, ESI†). The results confirmed the different Fe dopant concentrations with x = 0, 0.2 and 0.5 in the SmFexCr1−xO3 samples.
 | ||
| Fig. 2 SEM images of (a and b) the as-synthesized SmCrO3 samples, (c) SmFe0.2Cr0.8O3, and (d) SmFe0.5Cr0.5O3. | ||
In order to further examine the phase purity and structural characteristics of the samples, their Raman spectra were recorded at room temperature, and are shown in Fig. 3(a). The orthorhombic space group Pnma, distorted from an ideal cubic perovskite in which Raman scattering is formally forbidden, is predicted to have 24 Raman-active modes (7Ag + 5B1g + 7B2g + 5B3g) according to group theory,26 however, 12 modes are present within a 100–600 cm−1 range for the orthorhombic Pnma perovskite structure for RCrO3 systems.27,28 The others are either too weak in intensity or have energies below the experimental cutoff.
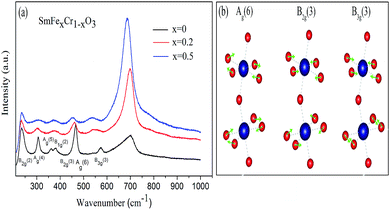 | ||
| Fig. 3 (a) Raman spectra of the SmCrO3, SmFe0.2Cr0.8O3, and SmFe0.5Cr0.5O3 samples. (b) Atomic-displacement patterns of the perovskite structure Ag(6), B2g(3), and B3g(3) Raman modes. | ||
The positions of the Raman modes of the three samples investigated here are plotted in Fig. 3(a). In Raman scattering the frequencies of the specific lattice vibrational modes are directly related to structural distortion. The phonon modes in RCrO3 can be attributed to different symmetry operations: (1) those below 200 cm−1 are related to lattice modes involving Sm atom vibrations, and (2) the modes in the region above 200 cm−1 consist of various modes involving vibrations of the Sm atom and oxygen. To be specific, (1) B1g(1) and Ag(3) are octahedral rotations around the crystallographic y-axis and Ag(5) is a rotation around the x-axis (Pnma setting); (2) the singlet Ag(4) is related to Sm–O vibrations; (3) Ag(6) and B2g(3) arise due to bending of the CrO6 octahedra; (4) the B3g(3) mode is related to the antisymmetric stretching vibrations of the O2 and O1 atoms.27
Fig. 3(b) shows that the phonon frequency changes of the Ag(6), B2g(3) and B3g(3) modes are more obvious than the others measured at room temperature. It is observed that with increasing Fe content, the phonon frequencies of the Ag(6) and B2g(3) modes change from 466.01 cm−1 and 461.03 cm−1 (x = 0) to 461.03 cm−1 and 456.21 cm−1 (x = 0.2) and finally decrease to 453.56 cm−1 and 448.40 cm−1 (x = 0.5), respectively. The phonon frequency of the B3g(3) mode decreases from 573.05 cm−1 (x = 0) to 548.15 cm−1 (x = 0.2) and finally down to 533.22 cm−1 (x = 0.5). The others are almost unchanged. The changes of the mode vibration frequencies are directly related to the degree of structural distortion.26,27 We note that those modes discussed above show a greater dependence than others on the octahedral tilt angles θ and φ, shown in Table 1, leading to the structural distortion of the perovskite structure. This is not hard to understand: the Ag(6) and B2g(3) modes are associated with the bending of the CrO6 octahedra, which results in rotations of the CrO6 octahedra in the [010] plane. Thus, the rotations lead to changes in the octahedral tilt angles φ.
In addition, the B3g(3) mode is associated with the antisymmetric stretching vibrations of the O2 and O1 atoms. Because the radius of an Fe ion is larger than that of a Cr ion, it is natural to have Raman peak shifts caused by the movement of the O2 and O1 atoms, leading to rotations of the CrO6 octahedra in the [101] plane.27,29 Therefore, the octahedral tilt angles θ increase with Fe content giving rise to the change of the B3g(3) mode. These results are in agreement with the results from the XRD data, which revealed a weak distortion of the CrO6 octahedra, leading to a buckling angle, by increasing the Fe doping content.
Magnetic properties
The temperature dependence of the magnetization of the pure and rare-earth ion substituted SmCrO3 samples in a measuring field H = 100 Oe for the field cooled (FC) cases is shown in Fig. 4. From the χ vs. T graph it is evident that indeed there exist various transitions pertinent to antiferromagnetic coupling (AFM), spin re-orientation transitions (SR) and Sm3+ ordering.30,31 However, the above transitions exist at various temperature ranges. Below we mainly discuss the antiferromagnetic coupling and the strength of the symmetric and antisymmetric Cr(Fe)–Cr(Fe) exchange interaction (J and D) effects with structural deformation or tilting. From Fig. 4 it is evident that a sudden jump occurs at 193 K for the compound where x = 0 , which can be attributed to the antiferromagnetic ordering of the Cr3+ moments in SmCrO3.3,20 The increase in the magnetization below this transition indicates a weak ferromagnetic moment (WFM), which arises due to the canted nature of the Cr3+ moments. With increasing Fe content, the samples behave as weak ferrimagnets for all concentrations of x below this transition temperature (TN) as shown in Fig. 4(b and c). The Neel temperature (TN) is varied in a sequential manner for the SmFexCr1−xO3 (0 ≤ x ≤ 0.5) compounds.32 The χ vs. T graphs demonstrated TN values of 193 K, 228 K, and 285 K for the compounds in which x = 0, 0.2, and 0.5, respectively. Such a variation of TN with Fe content could be due to the smaller ionic radius of Cr3+ (0.615 Å) in comparison to that of Fe3+ (0.645 Å). In this work, since we substituted Cr3+ for Fe3+, there is a contraction of the lattice and hence a distortion in the crystal structure. The variation of the lattice parameters with Fe3+ addition has been confirmed using XRD and Raman spectroscopy, measured by our group and reported elsewhere.33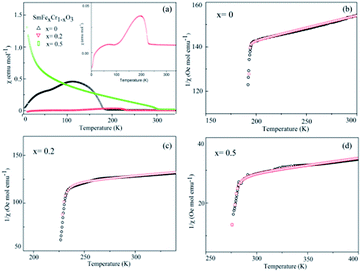 | ||
| Fig. 4 (a) The temperature dependence of the molar magnetic susceptibility (χ) measured in an applied field of 100 Oe for the SmCrO3, SmFe0.2Cr0.8O3, and SmFe0.5Cr0.5O3 samples. The inset in (a) shows the χ vs. T graph for the SmFe0.2Cr0.8O3 sample. (b–d) The temperature dependence of the inverse of the susceptibility (1/χ) of the SmCrO3, SmFe0.2Cr0.8O3, and SmFe0.5Cr0.5O3 samples, where the black circles are data points and the red circles fit to the modified Curie–Weiss law in eqn (1), which includes the DM interaction. | ||
According to the effect of t–e hybridization reported by Zhou et al.34 the change in TN was shown to be strongly dependent on: (1) the Cr(Fe)–O–Cr(Fe) bond angle and (2) the t–e orbital hybridization introduced by intrinsic distortions in orthorhombic RCrO3 and RFeO3 perovskites. The relationship between the superexchange coupling Ja and the superexchange angle (the Cr(Fe)–O–Cr(Fe) bond angle) for the RFeO3 and RCrO3 families was based on the formula Ja ∼ cos4(ω/2)/d7,35 where d and θ are the B–O bond length and the averaged Cr(Fe)–O–Cr(Fe) bond angle, and ω = 180 − θ. In addition, the symmetric Cr(Fe)–Cr(Fe) exchange interactions J were obtained by fitting the experimental data to the modified Curie–Weiss (CW) law,12,13 as shown in Table 2. The values of the Cr(Fe)–Cr(Fe) exchange interactions J obtained from fitting the experimental data, and the Ja determined using the formula above, were investigated here and compared in Table 2. It was revealed that the change in J was almost in line with that of Ja, and the difference between the two could be attributed to the t–e hybridization, as explained in more detail later. From the above, we believe that the increase in TN with decreasing Cr3+ content is not only due to the weakening of the Fe (Cr)–O–Fe(Cr) AFM exchange interaction, but is also due to the t–e hybridization as a result of the structural distortion. The octahedral-site tilting not only reduces the t-orbital overlap integral that is considered but also introduces orbital overlap between the π (t3–O–t3) and the σ (e2–O–e2) bonds. However, the influence on the overall exchange interaction of the intersite t–e orbital hybridization is very different in Fe3+: t3 e2 versus Cr: t3 e0. For RFeO3, t–e orbital hybridization doesn’t give any extra magnetic phase component to the overall superexchange interaction. On the other hand, in RCrO3, t–e hybridization gives a ferromagnetic (FM) component in addition to the existing AFM interaction in the t3–O–t3 orbitals though a superexchange interaction.34–36 As there exist both FM and AFM competing interactions due to t–e hybridization in SmFexCr1−xO3 compounds, by the substitution of Cr3+ for Fe3+, the strength of the FM interactions increases and the AFM interactions diminish, which may result in the increase of TN. The results are in good agreement with the report by Kotnana et al.18
| Samples | X = 0 | X = 0.2 | X = 0.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a 3/2 all J/kB values were calculated assuming a full spin-only moment S = 3/2 (Cr) on the B site.b 5/2 all D/kB values were calculated assuming a full spin-only moment S = 5/2 (Fe) on the B site. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TN (K) | 193.45(6) | 228.32(4) | 284.75(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T0 (K) | 192.76(4) | 227.83(3) | 284.64(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| J/kB (K)a3/2 | 12.851(7) | 15.189(5) | 18.976(6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D/kB (K)a3/2 | 2.175(10) | 1.993(10) | 1.065(10) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| J/kB (K)b5/2 | 5.507(7) | 6.509(5) | 8.133(6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D/kB (K)b5/2 | 0.932(10) | 0.854(10) | 0.456(10) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ja | 6.72 × 10−3 | 7.50 × 10−3 | 7.65 × 10−3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TN − T0 | 0.69(5) | 0.49(4) | 0.11(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| θ | −1102(7) | −824(6) | −276(7) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| C | 7.9(4) | 8.8(2) | 14.2(3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| μeff | 7.95(10) | 8.82(9) | 10.66 (10) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| μeffa | 3.960 | 4.438 | 5.071 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| dO | 0.5682 | 0.5010 | 0.4898 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Now we discuss the Dzyaloshinskii–Moriya (DM) antisymmetric exchange interaction of the SmFexCr1−xO3 samples with weak ferromagnetism. The weak ferromagnetism due to the canted nature of the Cr3+ (Fe3+) moments of the samples below this transition temperature (TN) can be explained by considering the Dzyaloshinskii–Moriya (DM) interaction, which was elaborated as a consequence of spin–orbit coupling.13 In most materials, the temperature dependence of the magnetic susceptibility data well above TN can be fitted to the Curie–Weiss law. However, in the present material, near TN, the susceptibility can deviate from the behavior described by the Curie–Weiss law. This deviation was modeled by Moriya13 for the case of weak ferromagnets (canted antiferromagnets) to now account for the DM antisymmetric exchange interaction. According to this theory, the susceptibility in the easy-axis direction obeys the CW law, whereas the susceptibility perpendicular to the easy axis must account for the DM interaction. Since the present samples are powdered (polycrystalline) samples, it is not possible to independently measure parallel and perpendicular susceptibilities, thus, the effect of the perpendicular χ will be dominant for the powdered sample. Therefore, we have modeled the measured powder susceptibility using eqn (1) with (T − T0)/(T − TN) resulting from the effect of the DM interaction.13
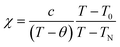 | (1) |
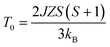 | (2) |
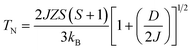 | (3) |
For the data for each sample above TN, the data of the inverse χ vs. T was fitted to eqn (1); the fitting is shown in Fig. 4 and the evaluated parameters are listed in Table 2. The Weiss constants obtained from fitting to the aforementioned modified Curie–Weiss law are negative for each of the present samples, indicating AFM ordering as expected. The effective magnetic moment μeff (μB) is calculated using the equation3
| μeff2 = 3kBC/NAμB2 | (4) |
| μeffa = [μSm2 + (x)μFe2 + (1 − x)μCr2]1/2 | (5) |
The value of μeff is much higher than the theoretical value of μeffa (shown in Table 2) and an ab initio calculation suggested that the pressure produced by the tilting of the oxygen octahedra causes the difference between μeff and μeffa.37,38 These results are in agreement with the results of XRD and Raman spectroscopy, which revealed a weak distortion of the CrO6 octahedra by increasing the Fe doping content. In addition, the evaluated magnetic parameters obtained in other work3,20,37–39 are given in the ESI (Table S1†). The magnetic parameters (TN and μeff) of the as-synthesized SmCrO3 agree well with those3,38 in the literature.
From the fitting shown in Fig. 4 and the evaluated parameters listed in Table 2, it is noted that the effect of the (T − T0)/(T − TN) term in eqn (1) is important only near TN, resulting in the sharp drop in the inverse χ, because the difference between TN and T0 is less than 1°. The above analysis shows that for S = 3/2 (S = 5/2) the antisymmetric exchange constant D/kB is 2.175 K (0.9322 K), 1.993 K (0.8543 K), and 1.06 K (0.4563 K), respectively, for the SmCrO3, SmFe0.2Cr0.8O3, and SmFe0.5Cr0.5O3 samples discussed here. The results show that the antisymmetric interaction D slightly decreases with Fe content, and the difference between TN and T0 could well be relevant to the exchange constant D/kB, as seen in Table 2.
Moreover, according to the theory presented by Sergienko and Dagotto,15 the size mismatch between A and B ions usually makes the oxygen octahedra tilt and rotate, resulting in a distortion. Therefore, each oxygen ion sandwiched between two neighboring B ions may move away from the middle point, giving a bent B–O–B bond and breaking the B–B axis rotation symmetry. This bent B–O–B bond will induce a DM interaction between magnetic B ions; this is shown schematically in Fig. 5 and can be expressed as HDM = 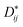 (Si × Sj), where Dij is the coefficient of the DM interaction between spins Si and Sj. For a perovskite structure with bent B–O–B bonds, the vector Dij must be perpendicular to the B–O–B plane. In a first-order approximation, the magnitude of Dij is proportional to the displacement of the oxygen ion (dO) away from the “original” middle point, and is defined as Dij = βeij × dO, where β is a coefficient and eij is the unit vector pointing from site i to site j.40–44 Finally, we obtained the displacement of the oxygen ion (dO) away from the middle point according to the trigonometric identities, using the averaged Cr(Fe)–O bond length and the Cr(Fe)–O–Cr(Fe) bond angle determined using X-ray diffraction with Rietveld refinements, as shown in Table 2. By qualitatively studying the contrast between the exchange constant D/kB and the displacement of the oxygen ion (dO), it was revealed that the change in D/kB was almost in line with the change in dO, which was in good agreement with the theory of Sergienko and Dagotto mentioned previously.
(Si × Sj), where Dij is the coefficient of the DM interaction between spins Si and Sj. For a perovskite structure with bent B–O–B bonds, the vector Dij must be perpendicular to the B–O–B plane. In a first-order approximation, the magnitude of Dij is proportional to the displacement of the oxygen ion (dO) away from the “original” middle point, and is defined as Dij = βeij × dO, where β is a coefficient and eij is the unit vector pointing from site i to site j.40–44 Finally, we obtained the displacement of the oxygen ion (dO) away from the middle point according to the trigonometric identities, using the averaged Cr(Fe)–O bond length and the Cr(Fe)–O–Cr(Fe) bond angle determined using X-ray diffraction with Rietveld refinements, as shown in Table 2. By qualitatively studying the contrast between the exchange constant D/kB and the displacement of the oxygen ion (dO), it was revealed that the change in D/kB was almost in line with the change in dO, which was in good agreement with the theory of Sergienko and Dagotto mentioned previously.
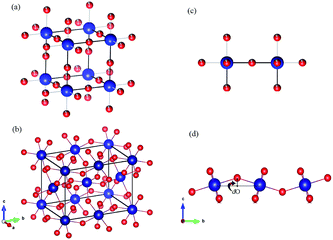 | ||
| Fig. 5 (a and b) The crystal structures of an ABO3 perovskite where blue = B and red = O. (a) An ideal cubic perovskite. All the nearest-neighbor B–O–B bonds are straight. (b) An orthorhombic perovskite lattice, which is the result of a size mismatch between the A and B ions. All the nearest-neighbor B–O–B bonds are bent. (c and d) Representative B–B axes from the crystal structures in (a) and (b), respectively. The dO is the displacement of the oxygen ion away from the middle point. The illustrations were created using VESTA.45 | ||
Conclusions
In summary, polycrystalline samples SmFexCr1−xO3 (0 < x < 0.5) were compounded via a solid state reaction and their structures were confirmed using XRD and Raman spectroscopy techniques, which reveal the evolution of the distorted perovskite structure with Fe substitution. Note that the bond angles increase with increasing Ravg. Magnetization data reveal that the Neel temperature (TN) increases with an increase in the average B-site ionic radius, and average Cr(Fe)–O–Cr(Fe) bond angle. By fitting the temperature dependence of the magnetic susceptibility to a Curie–Weiss law modified by the Dzyaloshinskii–Moriya (DM) interaction, it was found that the strength of the symmetric interaction J (reflected in the changes in the Neel temperature) increases with the replacement of Cr3+ with Fe3+, which is ascribed to changes in the average Fe(Cr)–O–Fe(Cr) bond angle and bond lengths, as a result of structural distortion. Meanwhile, the strength of the antisymmetric interaction D slightly decreased. This was mainly attributed to the displacement of the oxygen ion (dO) away from the original middle point.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the National Natural Science Foundation of China (No. 51571006).References
- C. N. R. Rao, A. Sundaresan and R. Saha, J. Phys. Chem. Lett., 2012, 3, 2237 CrossRef CAS PubMed.
- S. W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13 CrossRef CAS PubMed.
- L. M. Daniels, M. C. Weber, M. R. Lees, M. Guennou, R. J. Kashtiban, J. Sloan, J. Kreisel and R. I. Walton, Inorg. Chem., 2013, 52, 12161–12169 CrossRef CAS PubMed.
- S. Yin, M. S. Seehra, C. J. Guild, S. L. Suib, N. Poudel, B. Lorenz and M. Jain, Phys. Rev. B, 2017, 95, 184421 CrossRef.
- A. McDannald, L. Kuna, M. S. Seehra and M. Jain, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224415 CrossRef.
- B. Rajeswaran, P. Mandal, R. Saha, E. Suard, A. Sundaresan and C. N. R. Rao, Chem. Mater., 2012, 24, 3591–3595 CrossRef CAS.
- M. Eibschütz and D. Treves, Phys. Rev., 1967, 156, 562 CrossRef.
- C. Boekema and G. A. Sawatzky, Int. J. Magn., 1972, 3, 341–348 CAS.
- J. S. Zhou and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 132104 CrossRef.
- J. H. Lee, Y. K. Jeong, J. H. Park, M. Oak, H. M. Jang, J. Y. Son and J. F. Scott, Phys. Rev. Lett., 2011, 107, 117201 CrossRef PubMed.
- L. G. Marshall, J. G. Cheng, J. S. Zhou, J. B. Goodenough, J. Q. Yan and D. G. Mandrus, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 064417 CrossRef.
- I. Dzialoshinski, J. Phys. Chem. Solids, 1958, 4, 241 CrossRef.
- T. Moriya, Phys. Rev., 1960, 120, 91 CrossRef CAS.
- F. Keffer, Phys. Rev., 1962, 126, 896 CrossRef CAS.
- I. A. Sergienko and E. Dagotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094434 CrossRef.
- K. S. P. Meher, C. Martin, V. Caignaert, F. Damay and A. Maignan, Chem. Mater., 2014, 26, 830 CrossRef CAS.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564 CrossRef CAS.
- G. Kotnana, V. R. Reddy and S. N. Jammalamadaka, J. Magn. Magn. Mater., 2017, 429, 353–358 CrossRef CAS.
- M. A. Pena and J. G. Fierro, Chem. Rev., 2001, 101, 1981 CrossRef CAS PubMed.
- K. Sardar, M. R. Lees, R. J. Kashtiban, J. Sloan and R. I. Walton, Chem. Mater., 2011, 23, 48–56 CrossRef CAS.
- M. E. Amrani, M. Zaghrioui, V. T. Phuoc, F. Gervais and N. E. Massa, J. Magn. Magn. Mater., 2014, 361, 1–6 CrossRef.
- H. Zhao, S. Cao, R. Huang, W. Ren, S. Yuan, B. Kang, B. Lu and J. Zhang, J. Appl. Phys., 2013, 114, 113907 CrossRef.
- J. P. Gonjal, R. Schmidt, J. J. Romero, D. Avila, U. Amador and E. Moran, Inorg. Chem., 2013, 52, 313–320 CrossRef PubMed.
- Y. Zhao, D. J. Weidner, J. B. Parise and D. E. Cox, Phys. Earth Planet. Inter., 1993, 76, 1–16 CrossRef CAS.
- Y. Zhao, D. J. Weidner, J. B. Parise and D. E. Cox, Phys. Earth Planet. Inter., 1993, 76, 17–34 CrossRef CAS.
- M. N. Iliev, M. V. Abrashev, H. G. Lee and V. N. Popov, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 2872 CrossRef CAS.
- M. C. Weber, J. Kreisel, P. A. Thomas, M. Newton, K. Sardar and R. I. Walton, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054303 CrossRef.
- M. C. Weber, M. Guennou, H. J. Zhao, J. Iniguez, R. Vilarinho and J. Kreisel, Phys. Rev. B, 2016, 94, 214103 CrossRef.
- M. N. Iliev, M. V. Abrashev, J. Laverdière, S. Jandl, M. M. Gospodinov, Y. Q. Wang and Y. Y. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064302 CrossRef.
- S. Chaturvedi, P. Shyam, A. Apte, J. Kumar, A. Bhattacharyya, A. M. Awasthi and S. Kulkarni, Phys. Rev. B, 2016, 93, 174117 CrossRef.
- L. H. Yin, Y. Liu, S. G. Tan, B. C. Zhao, J. M. Dai, W. H. Song and Y. P. Sun, Mater. Res. Bull., 2013, 48, 4016–4021 CrossRef CAS.
- A. M. adomtseva, A. S. Moskvin, I. G. Bostrem, B. M. Wanklyn and N. A. Khafizova, Zh. Eksp. Teor. Fu., 1977, 72, 2286–2298 Search PubMed.
- G. Kotnana and S. N. Jammalamadaka, J. Magn. Magn. Mater, 2016, 418, 81–85 CrossRef CAS.
- J. S. Zhou, J. A. Alonso, V. Pomjakushin, J. B. Goodenough, Y. Ren, J. Q. Yan and J. G. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214115 CrossRef.
- X. Qian, L. Chen, S. Cao and J. Zhang, Solid State Commun., 2014, 195, 21–25 CrossRef CAS.
- L. Ding, P. Manuel, D. D. Khalyavin, F. Orlandi, Y. Kumagai, F. Oba, W. Yi and A. A. Belik, Phys. Rev. B, 2017, 95, 054432 CrossRef.
- H. J. Zhao, W. Ren, X. M. Chen and L. Bellaiche, J. Phys.: Condens. Matter, 2013, 25, 385604 CrossRef PubMed.
- A. Ghosh, K. Dey, M. Chakraborty, S. Majumdar and S. Giri, Europhys. Lett., 2014, 107, 47012 CrossRef.
- B. Dash and S. Ravi, J. Magn. Magn. Mater., 2016, 405, 209–213 CrossRef CAS.
- A. S. Moskvin, J. Magn. Magn. Mater., 2016, 400, 117–120 CrossRef CAS.
- Y. Cui, Y. Tian, W. Liu, Y. Li, R. Wang and T. Wu, AIP Adv., 2011, 1, 042129 CrossRef.
- S. Dong, J. M. Liu, S. W. Cheong and Z. Ren, Adv. Phys., 2015, 64, 519–626 CrossRef CAS.
- Y. M. Cui, Y. F. Tian, A. Shan, C. Chen and R. M. Wang, Appl. Phys. Lett., 2012, 101, 122406 CrossRef.
- P. Zhang and Y. M. Cui, RSC Adv., 2014, 102, 58337–58341 RSC.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra13615c |
| This journal is © The Royal Society of Chemistry 2018 |