Comparative conformational analyses and molecular dynamics studies of glycylglycine methyl ester and glycylglycine N-methylamide

Abstract

Compared to their amide analogs, peptidic esters have a lower propensity for intramolecular hydrogen bonding, and thus most likely quite different stable geometries. On the other hand, their similarity and facile conversion to peptides has led to their broad use in synthetic and biological applications. This dichotomy creates a need to understand their conformational properties. Here, we study the geometries of glycylglycine methyl ester (GGMe, the simplest dipeptide ester) and its amide counterpart (GGAm) using density functional methods. The optimized conformational states were analysed in gas phase and also using a dielectric continuum aqueous phase model. In addition, molecular dynamics studies were carried out to explore effects of molecular water solvation on structure and conformational flexibility. The two atom change, from amide to ester, results in significantly different conformational profiles and solvation characteristics. In gas phase calculations, the strength of the CO–HN (3→1) intramolecular hydrogen bond in GGAm determines its minimum energy conformation, while GGMe is extended; cis-geometries are more energetic by 6 or 5 kcal mol⁻¹ for the two molecules, respectively. The addition of a continuum dielectric to model an aqueous phase environment weakens hydrogen bonding such that the intramolecular H-bonds are replaced by geometries with less internal strain and more ideal chemical topologies. As a further consequence of the electrostatic shielding, the relative energies of the cis-geometries are reduced by more than half. Molecular dynamics simulations predict GGAm to be more flexible and more extensively solvated than GGMe. Roughly 40% of the increased solvation is due to the additional hydrogen bond donor NH group of the amide; the rest is due to increased hydrogen bonding to the amide oxygen. These analyses of the solvent dependent structural characteristics of simple peptides and peptide esters provide a basis for understanding and design applications in biological recognition, drug design, and synthetic chemistry.

---

Introduction

Peptides and peptide-like molecules have long been of interest for chemists worldwide.^1,2 As methods have advanced, attempts have been made regularly to rationalize local conformations of amino acid residues and relative stabilities of peptide chains using theoretical chemistry and small prototypes such as dipeptides^3–8 of glycine and/or alanine. Such studies have successfully established the importance of amidic hydrogen bonds in peptide chain folding, for example, the greater stability of C₇-type conformations^4,6,7 compared to the fully extended (C₅-type) ones. In contrast, peptidic esters lack amidic hydrogen bonding capabilities at the ester group, leading to an expectation^9,10 of significantly different conformational stability profiles. Indeed, the replacement of amide groups by ester groups has often been used to study the role of amidic hydrogen bonding experimentally^11–19 in peptide folding and protein–protein interactions. However, peptidic esters have not received as much attention for theoretical studies, despite their wide use in peptidomimetic chemistry^20–24 and as starting materials^25–27 for synthesis of cyclic peptides. Thus, theoretical studies describing the implications of amide-to-ester alteration on a peptidic scaffold can be useful for various purposes, including peptidomimetic drug design and synthetic chemistry applications involving cis/trans isomerization or cyclization reactions. Such studies would benefit from a solid foundation of detailed conformational studies on simple peptidic esters, including analyses of trans and cis geometries, conformational flexibility and solvent interactions.

Recently, we reported²⁸ theoretical studies on cis/trans isomerization in secondary amides using density functional calculations, where we used N-methylacetamide (NMA) and glycylglycine methyl ester (GGMe) as model molecules to understand peptide bond isomerization. We found systematic theoretical studies on conformational properties of GGMe, its substituted derivatives, or other dipeptide esters or peptidic esters to be lacking. As the simplest peptidic ester, theoretical studies and conformational analyses on GGMe should provide a solid foundation for detailed comparative studies on substituted dipeptide esters. NMA provides a good comparison to study the properties and geometry of the amide functionality,^29,30 while comparison with its amide counterpart glycylglycine N-methylamide (GGAm) would demonstrate the effect of the change from amide to ester in terms of conformational stability. With this background, we present our theoretical studies on GGMe, and compare the findings with NMA and GGAm (molecules shown in Fig. 1).

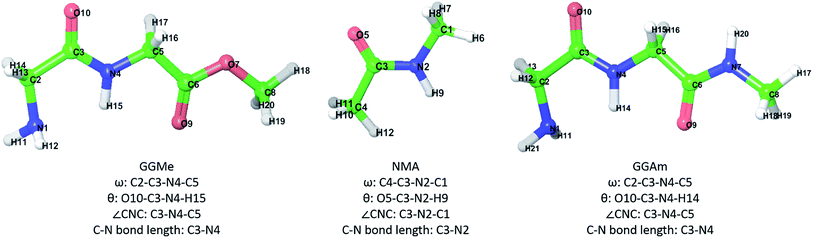Fig. 1 GGMe, NMA and GGAm structures, atom numbers and important measurements that will be used in the following discussion.

Experimental

Generation of structures

NMA, GGMe and GGAm structures were initially generated as 2D structures with trans orientations using MarvinSketch (ChemAxon, Budapest, Hungary) and were imported to the Maestro³¹ module of the Schrodinger suite (Schrödinger, LLC. New York City, USA) from which all further studies were performed. The cis geometries were generated by manual adjustment of ω dihedral.

Conformational search

Initial rotamer sets for both the trans and cis geometries were generated with the MacroModel³² conformational search algorithm using the MMFFs force-field. The resultant conformational search geometries with energies less than 21 kJ mol⁻¹ were subjected to geometric optimization. For gas phase calculations, the conformational search gave 39 trans and 30 cis rotamers of GGMe, and 12 trans and 39 cis rotamers of GGAm. For the water phase, the conformational search gave 37 trans and 29 cis rotamers of GGMe, and 32 trans and 37 cis of GGAm.

Geometric optimization

Geometric optimizations were performed using Jaguar.^33,34 The conformational search rotamers were subjected to geometric optimization at B3LYP/6-31++G** level with maximum grid density and the “accurate” accuracy level of SCF. Frequency analyses were carried out to confirm convergence to optimized minimum energy geometries with no imaginary frequencies. For NMA, “tight” convergence criteria were required to determine the optimized geometry. For GGMe and GGAm, default convergence criteria were sufficient. Besides these settings, the PBF solvent model with the default setting for water was used for optimization in a water dielectric continuum. For GGMe, 18 trans and 20 cis unique optimized geometries were found for the gas phase, and 23 trans and 14 cis unique optimized geometries were found for the water phase. For GGAm, 12 trans and 20 cis unique optimized geometries were found for the gas phase, and 21 trans and 18 cis unique optimized geometries were found for the water phase.

Single point energy calculations

Accurate single point energies were calculated using Jaguar^33,34 for all optimized geometries at the B3LYP/6-311++G (3df, 3pd) level, with maximum grid density and the “accurate” accuracy level of SCF. Along with these settings, the PBF solvent model with the default settings for water was used for the calculations in water dielectric continuum. Vibrational analyses were carried out at the B3LYP/cc-pVTZ(-f)++ level and the free energy values obtained for 298.15 K were used to calculate relative free energies.

Molecular dynamics

The molecular dynamics simulations were carried out using the program Desmond. Using the optimized minimum energy geometry of GGMe/GGAm, the MD systems were generated with System Builder module based on TIP4Pew solvent model as a 20 Å × 20 Å × 20 Å orthorhombic box with default settings. The systems thus generated were then subjected to NPT molecular dynamics simulation at 300 K and 1.01325 bar for total 12 ns with 1.2 ps recording time and trajectory spanning 4.8 ps, resulting into 2500 frames each.

Results and discussion

Conformations in gas phase

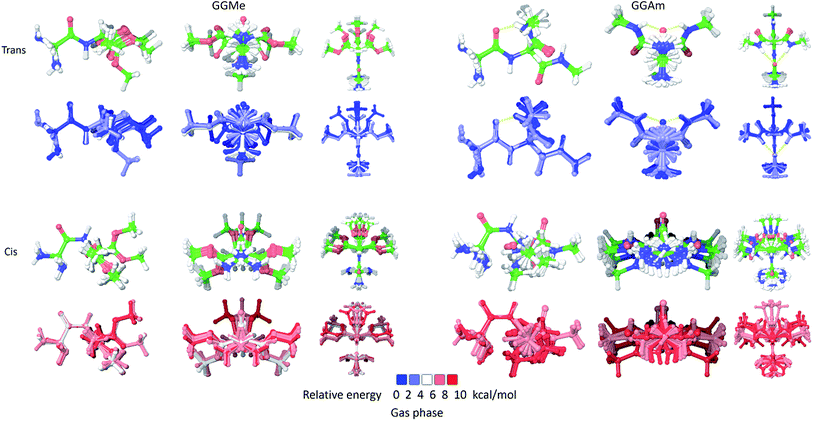
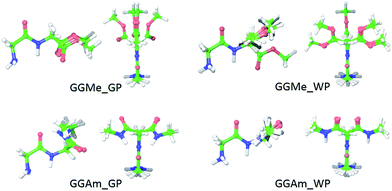
The most stable trans and cis geometries of GGMe, NMA and GGAm in the gas phase are shown in Fig. 2, and their key structural parameters have been tabulated in Table 1. As we have reported²⁸ recently, the optimized trans and cis geometries of NMA were found to be more planar than those reported previously³⁵ at SCF and MP2 levels, and the relative stabilities of trans and cis geometries were in excellent agreement.^29,36 With the absence of amidic hydrogen on C-terminal, GGMe was found to be most stable in an extended (C₅) trans form, which is in sharp contrast to GGAm, whose most stable conformation was the trans form with usual C₇-type (γ-turn) folding.^7,37 The characteristics of the C₇-form of GGAm, e.g. an intramolecular hydrogen bond between O10 and H20 (2.05 Å), were consistent with previously reported C₇-forms of similar compounds, such as the glycine dipeptide. Other folding geometries (such as β-turn, α-turn, δ-turn etc.) require longer peptide chains.^37,38 Instead, both GGMe and GGAm showed 2→1 hydrogen bonding (2.24 Å and 2.18 Å, respectively) between the pyramidal amino nitrogen of N-terminal and the amide hydrogen of the peptide bond. The extended C₅-form of GGMe also implied a 2→2 intramolecularly H-bonded conformation, and thus the hydrogen bond here (2.35 Å) for the C-terminal glycine residue appeared bifurcated (and therefore longer than 2.3 Å) because of simultaneous 2→1 hydrogen bonding.³⁷ In contrast, with no such bifurcation, the cis form of GGMe (also in an extended conformation) showed a clearer 2→2 intramolecular hydrogen bonding (2.27 Å).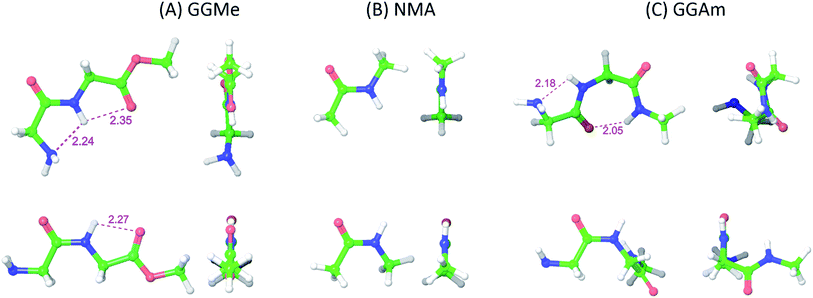

Fig. 2 trans (upper) and cis (lower) optimized minimum energy geometries of (A) GGMe, (B) NMA and (C) GGAm, each geometry has been projected from side (left) and C-terminal end (right).

Table 1 Optimized minimum energy geometries of trans and cis GGMe, NMA and GGAm

Geometry	cis/trans	ω (degree)	θ (degree)	C–N bond length (Å)	C=O bond length (Å)	∠CNC	Relative energy^a	ΔG^b
a Gas phase energy relative to the minimum energy trans geometries, calculated in kcal mol^−1 at B3LYP/6-311++G (3df, 3pd) level.b Relative free energy at 298.15 K relative to minimum energy trans geometries, calculated in kcal mol^−1 at B3LYP/cc-pVTZ(-f)++ level.
GGMe	trans	178.3	180.7	1.354	1.231	121.5	0.0	0.0
GGMe	cis	0.1	−0.1	1.367	1.228	127	4.6	4.5
NMA	trans	178.7	176.8	1.366	1.229	121.7	0.0	0.0
NMA	cis	5.3	3.0	1.370	1.229	127.1	2.3	2.2
GGAm	trans	−175.5	−178.4	1.349	1.238	123.4	0.0	0.0
GGAm	cis	−3.0	5.9	1.376	1.227	127.7	6.3	5.6

---

While the “peptide backbone” in both trans and cis isomers of GGMe and NMA remained largely planar, in contrast to GGAm, it deviated only somewhat from ideal planarity, with all consecutive dihedral angles within a range of ±5° of perfect planarity (dihedral values of ±180° or 0°). The cis and trans forms represent two distinct peptide geometries, each of which is similar for all three compounds. The C–N peptide bond lengths as well as bond angles ∠CNC were larger for the cis forms than those for the trans forms, reflecting the repulsion between two carbons on the two sides of the peptide unit. The ester group in GGMe shows two distinct bond-lengths for carbonyl C=O and methoxy C–O bonds, with a shorter C=O bond (1.21 Å) and a longer C–O bond (1.34 Å) for both cis and trans geometries. The bond angles ∠C₅–C₆–O₇ and ∠C₆–O₇–C₈ are measured ∼111° and ∼116° respectively. The most stable cis geometry for GGMe is less unstable than that for GGAm relative to the respective trans isomers.

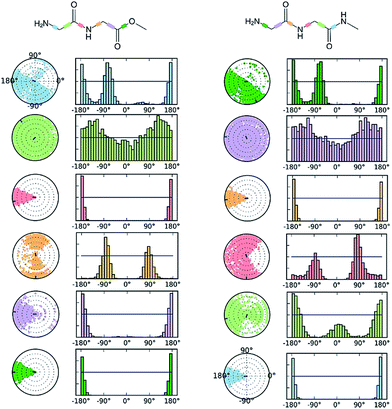
As we have analysed previously,²⁸ NMA is a small and simple molecule with only methyl groups attached to the amide moiety, and lacks asymmetric rotatable bonds and substitutions that create multiple local minima rotamers. Hence, a particular optimized state (such as trans or cis) can be effectively represented by a single respective geometry. However, this is not the case for larger molecules, such as GGMe and GGAm, as multiple rotatable bonds give rise to multiple local minimum rotamers (see Experimental). Fig. 3 shows the ensembles of such optimized structures of GGMe and GGAm in gas phase. This serves as an illustration of a first level of complexity in real peptidic and peptidomimetic systems, with far more rotatable bonds, giving rise to multiple rotamers.

Fig. 3 The ensembles of optimized rotamers of trans (upper two rows) and cis geometries (lower two rows) of GGMe (left group) and GGAm (right group) in gas phase calculations. The geometries are aligned at the amide bond and projected from side (left), N-terminus (middle) and above (right) within each group. The second and fourth rows display the conformers colored according to their relative stabilities. The 3→1 hydrogen bond in C₇-geometries of trans GGAm is shown as yellow dashed lines.

As shown in Fig. 3, the cis geometries are significantly unstable compared to the trans geometries (by >4 kcal mol⁻¹), so conformational analysis of major forms requires detailed discussion of only trans geometries.

For the trans GGAm geometries, the C₇-type conformation is characterized by an intramolecular 3→1 amidic hydrogen bond, while C₅-type conformations are characterized by weaker 2→2 intramolecular hydrogen bonding. Among the 12 optimized conformations identified for trans GGAm (Table 2), only 2 are C₅ (entries 5 and 6), and other 10 are C₇ geometries. The most stable C₅ conformer was predicted to be ∼1.63 kcal mol⁻¹ more energetic than the most stable C₇ conformer of GGAm. Additionally, the 2→1 hydrogen bonding also appeared to be important, as all 5 conformers of GGAm with such hydrogen bonding were found to be more stable than the other 7, which lack the hydrogen bond. In terms of energy, this additional stabilization seemed to affect the C₇ conformation more than C₅. While the lack of 2→1 hydrogen bonding destabilized the C₅ geometry by only 0.5 kcal mol⁻¹ (entries 5 vs. 6), the same difference among C₇ conformers resulted in destabilization by ∼2.9 kcal mol⁻¹ (entries 1–4 vs. 11 and 12).

Table 2 Intramolecular hydrogen bonds for the optimized conformations of trans GGAm in gas phase^a

a HB: hydrogen bond between two atoms; “+”: present; “−”: absent.

---

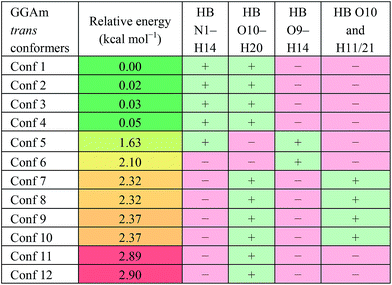GGMe, lacking of the amidic hydrogen on C-terminus, shows no C₇-type stable conformation, leaving the most stable conformer to be a C₅ conformer. As listed in Table 3, the ψ dihedral of the C-terminal glycine residue (dihedral 4-5-6-7) was observed to be energetically decisive, with values close to ±180° or within 10° of 0°. The 7 geometries with dihedral 4-5-6-7 values close to ±180° were more stable than the other 11 geometries with the value close to 0°. The absence of 2→1 hydrogen bonding destabilized the extended forms by ∼1 kcal mol⁻¹ (entries 1 and 2 vs. 4 and 5 in Table 3).

Table 3 Intramolecular hydrogen bonds for the optimized conformations of trans GGMe in gas phase^a

a HB: hydrogen bond between two atoms; “+”: present; “−”: absent.

---

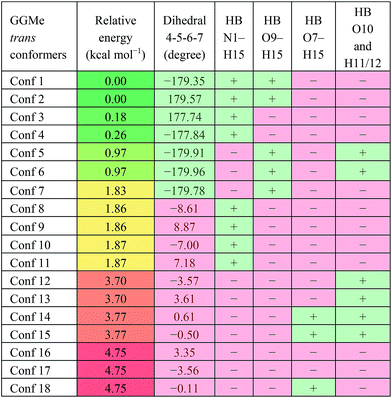Conformations in water phase

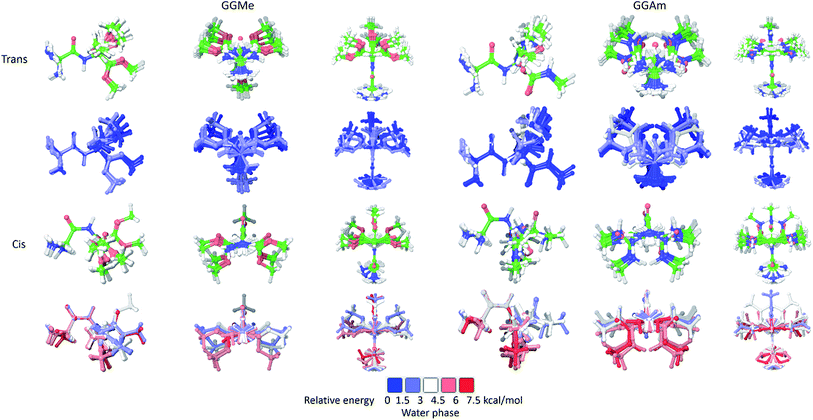
The calculations in a solvent phase require consideration of solvent interactions. Because QM studies with explicit solvent molecules are not feasible, such calculations are typically carried out with implicit solvent models, whereby a solvent is modelled as a dielectric continuum. However, this simplification eliminates any consideration of the effects of molecular water, especially hydrogen bonding into the water structure. Therefore, such studies may be used to evaluate a low energy set of conformational states, rather than identification of a specific minimum energy conformation.

For initial evaluation of aqueous phase geometries, 23 trans and 14 cis optimized rotamers of GGMe, as well as 21 trans and 18 cis optimized rotamers of GGAm (Fig. 4) were identified using a PBF solvent model. From the geometries, it is evident that intramolecular H-bonds are no longer decisively important conformational determinants in the polar water dielectric continuum. The conformations with higher propensity to interact with solvent molecules are estimated to be more stable than the conformations with intramolecular H-bonding, thereby resulting in a significantly different conformational profile compared to the gas phase. Thus, in striking contrast to the gas phase geometries (see above), none of the optimized GGAm geometries showed a C₇ conformation, and only one optimized geometry showed an extended C₅ conformation (relative energy: 0.68 kcal mol⁻¹). Similarly, a C₅ conformation of GGMe is no longer the most stable conformation (relative energy: 0.53 kcal mol⁻¹). The solvent interactions also stabilize the cis geometries, and hence the most stable cis geometry is estimated to be <2 kcal mol⁻¹, compared to >4 kcal mol⁻¹ in the gas phase. Overall, the geometries of GGMe and GGAm show very different conformational properties in both the gas phase and the aqueous dielectric continuum model, especially for stable geometries (up to relative energies ∼0.6 kcal mol⁻¹) at room temperature (Fig. 5).

Fig. 4 The ensembles of optimized rotamers of trans (upper two rows) and cis geometries (lower two rows) of GGMe (left group) and GGAm (right group) in the water phase dielectric continuum model. The geometries are aligned at the amide bond and projected from side (left), N-terminus (middle) and above (right) within each group. The second and fourth rows display the conformers colored according to their relative stabilities.

Fig. 5 Optimized geometries of GGMe (upper row) and GGAm (lower row) with energies less than 0.6 kcal mol⁻¹ (equiv. to 1 RT at 300 K) in gas phase (left) and in water dielectric continuum (right).

Solvation and hydrogen bonding with water

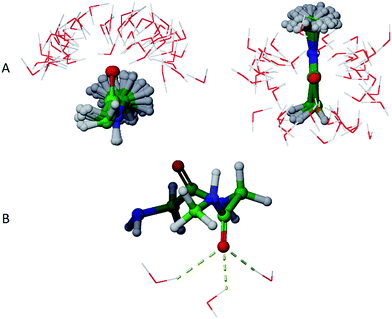
Physical aqueous phases involve interactions with molecular water, requiring modelling techniques beyond simple continuum dielectric models, especially when hydrogen bonding with water occurs. A major question thus becomes the average structure of hydrogen bonding interactions. For this study, we addressed this question in terms of average hydrogen bonding over time using molecular dynamics simulations of GGMe and GGAm solvated by TIP4Pew water at 300 K.

The average hydrogen bonding values were calculated over the simulation times as a ratio of total number of hydrogen bonds observed for a specific atom to the total number of frames. Different atoms showed different propensities to form hydrogen bonds (Table 4). Overall, for an average frame, GGMe showed moderate solvation by the water phase with an average total of 5.6 hydrogen bonds. In contrast, GGAm is better solvated, with a total of 6.5 hydrogen bonds on average. On a closer look, it is evident that the difference results from the altered hydrogen bond forming capabilities of amide and ester functionalities. The amide group in GGAm provides an additional hydrogen with a higher hydrogen bond forming propensity (0.46) relative to the ester sp³ oxygen (0.09) of GGMe. The remainder of the difference can be explained by the relative propensities of the amide and ester carbonyl oxygen atoms to form hydrogen bonds with water. The GGMe O9 atom appears in 1364, 993, and 57 frames (of the total 2500 frames) as singly, doubly, or triply hydrogen bonded to water, whereas GGAm structures show these frequencies to be 313, 1798, and 377 frames, respectively. (The OPLS3 force field assigns a more negative charge to the amide carbonyl oxygen compared to the ester carbonyl oxygen; whether this or other parameterization differences are decisive cannot be evaluated, as the details are proprietary.) The triply hydrogen bonded structures reflect a tetrahedral geometry (Fig. 6) of the oxygen atom, consistent with an amide resonance structure that places greater negative charge on it. Overall, the force field parameterization, in combination with structural details, predict the stronger solvation of carbonyl O9 of GGAm (2.03) compared to the carbonyl oxygen of the ester group in GGMe (1.41).

Table 4 Atom-wise distribution of hydrogen bonds formed by GGMe and GGAm with surrounding water molecules during NPT molecular dynamics at 300 K for 12 ns, analyzed in terms of 2500 frames. Each frame corresponds to 4.8 ps

GGMe			GGAm
Atom	Total H-bonds in 2500 frames	Average H-bond per frame	Atom	Total H-bonds in 2500 frames	Average H-bond per frame
H11	1217	0.49	H11	1170	0.47
H12	1185	0.47	H21	1153	0.46
H15	1195	0.48	H14	1427	0.57
N1	1812	0.72	N1	1764	0.71
O7	233	0.09	H20	1144	0.46
O9	3521	1.41	O9	5084	2.03
O10	4798	1.92	O10	4544	1.82
Total	13 961	5.58	Total	16 286	6.51

---

Fig. 6 (A) Clustering of water molecules for the 17 of the first 100 frames that show simultaneously three solvent hydrogen bond interactions with O9 of GGAm. The geometries are aligned at the C-terminal amide groups (only the atoms neighbouring the amide groups are shown). (B) The amide carbonyl O9 of GGAm displays tetrahedral geometry while making simultaneously three hydrogen bonds with water molecules.

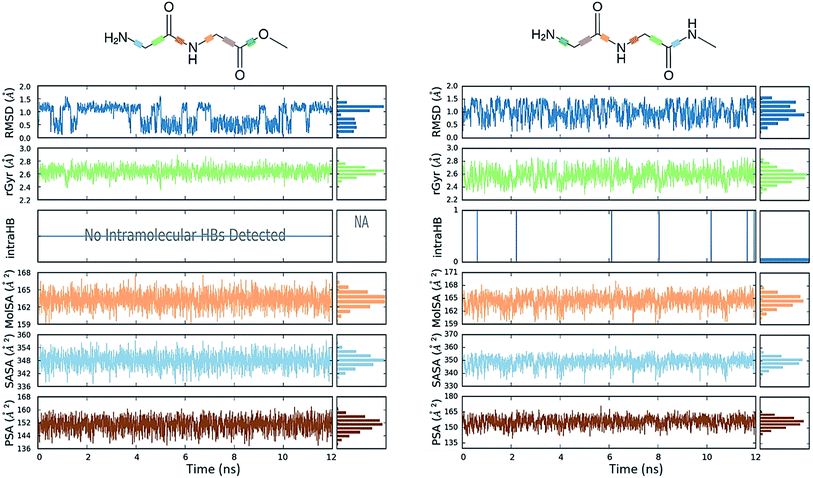
Conformational flexibility

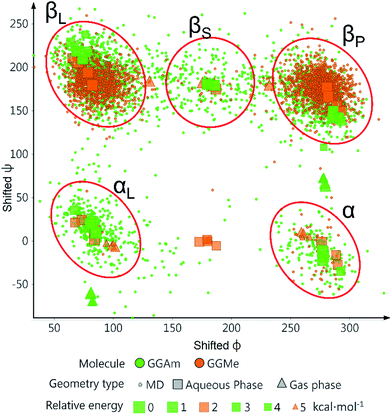
The comparative conformational flexibility of peptidic esters is an important consideration for their use as peptidomimetics. Conformational flexibility is also related to the reactivity for intramolecular cyclization. As shown in Fig. 7, the MD studies revealed a high degree of conformational variability for GGAm, represented by frequent transitions between low RMSD (<0.5) geometries and high RMSD (∼1.5) geometries, as well as a broader distribution of radius of gyration (rGyr). On the other hand, GGMe geometries displayed relatively lower conformational variability, represented by less frequent transitions between one cluster of low RMSD (<0.5) geometries and another of high RMSD (∼1.5) geometries, as well as a narrower distribution of radius of gyration (rGyr).

Fig. 7 Different properties of GGMe (left) and GGAm (right) geometries observed during 300 K NPT molecular dynamics simulation plotted along time as well as displayed as frequency distribution histogram. MolSA: molecular surface are calculated with 1.4 Å probe radius, equivalent to a van der Waals surface area; SASA: solvent accessible surface area; PSA: polar surface area i.e. solvent accessible surface area contributed only by oxygen and nitrogen atoms.

This difference in conformational flexibility was analysed in terms of specific scaffold dihedrals, i.e. frequency histograms of the scaffold dihedral angles for the MD geometries (Fig. 8). Here also, GGMe showed less flexibility than GGAm. The most noteworthy difference was observed for dihedral 4-5-6-7 (ψ dihedral of the C-terminal glycine residue, row 5), where GGAm showed many more structures with the dihedral values between −90° to 90°; GGMe had virtually none. Interestingly, this is also consistent with the observations from the gas phase geometries, that the dihedral 4-5-6-7 values near 0 are unfavourable compared to values near ±180°. GGMe also demonstrates relatively restricted preference for dihedral 3-4-5-6 values (ϕ dihedral of the C-terminal glycine residue, row 4) close to ±90°, having few geometries with the dihedral values close to 0° or ±180°. On the other hand, GGAm shows a considerable proportion of geometries close to ±180°. This is clearly reflected in the Ramachandran plot for the C-terminal glycine residue of GGMe and GGAm geometries (Fig. 9). GGAm geometries are spread across all 5 regions (α, α_L, β_P, β_L, β_S), and predominantly within the β_P and β_L regions (unlike the distribution in proteins, which is predominantly within the α and α_L regions³⁹). In contrast, the GGMe conformations are almost exclusively within the β_P and β_L regions. Interestingly, QM studies with the aqueous dielectric continuum model for GGMe provide a few moderately stable geometries in (180, 0) region, but no such geometries are observed in molecular dynamics.

Fig. 8 Distribution of scaffold dihedrals during the molecular dynamics studies on GGMe and GGAm. The plots summarize the conformational evolution throughout the simulation trajectory (0.00–12.00 ns). The colour-coded scaffold dihedrals are highlighted on 2D structures of GGMe and GGAm on top. Each dihedral is accompanied by a dial plot and bar plots of the same color. Dial plots describe the conformation of the torsion throughout the course of the simulation. The beginning of the simulation is in the center of each dial plot and the time evolution is plotted radially outwards. The bar plots represent the frequency distribution of the dihedral angle values.

Fig. 9 Ramachandran plot in terms of shifted ϕ (0° to 360°) and ψ (−90° to 270°) dihedral coordinates of the C-terminal glycine residue in GGMe and GGAm geometries observed in molecular dynamics at 300 K for 12 ns as well as in the QM derived geometries in gas phase and water dielectric continuum. The relative energy scale is applicable to the QM derived geometries only.

Conclusions

Peptidic esters are important, as prodrugs or peptidomimetics, and also as precursors of cyclic peptides. Here we have described conformational studies of the simplest peptidic ester, glycylglycine methyl ester (GGMe) using density functional studies and compared the results with its amide counterpart (GGAm). Multiple optimized rotamers of trans and cis geometries in gas phase and water dielectric continuum were identified, showing how intramolecular hydrogen bonding determined lowest energy conformations in the gas phase, but not in the water phase. To study effects of molecular water, solvation properties and conformational flexibility were analysed with molecular dynamics. These simulations predicted weaker solvation at both oxygen atoms of the ester group, along with lower flexibility of GGMe. These analyses of the solvent dependent structural characteristics of simple peptides and peptide esters provide a basis for further theoretical studies, such as on substituted derivatives of GGMe or other larger peptidic esters, with potential implications for the overall extent of flexibility and reactivity. Such studies are important for understanding and design applications in biological recognition, drug design, and synthetic chemistry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Department of Chemistry, UiT The Arctic University of Norway for supporting this research work.

References

1. L. Gentilucci, A. Tolomelli and F. Squassabia, Curr. Med. Chem., 2006, 13, 2449–2466.
2. J. Vagner, H. Qu and V. J. Hruby, Peptidomimetics, Curr. Opin. Chem. Biol., 2008, 12, 292–296.
3. B. Maigret, B. Pullman and D. Perahia, J. Theor. Biol., 1971, 31, 269–285.
4. L. Schäfer, C. Van Alsenoy and J. N. Scarsdale, J. Chem. Phys., 1982, 76, 1439–1444.
5. W. F. Lau and B. Montgomery Pettitt, Biopolymers, 1987, 26, 1817–1831.
6. H. J. Boehm and S. Brode, J. Am. Chem. Soc., 1991, 113, 7129–7135.
7. T. Head-Gordon, M. Head-Gordon, M. J. Frisch, C. L. Brooks and J. A. Pople, J. Am. Chem. Soc., 1991, 113, 5989–5997.
8. J. Hermans, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3095–3096.
9. X. Yang, M. Wang and M. C. Fitzgerald, Bioorg. Chem., 2004, 32, 438–449.
10. A. Choudhary and R. T. Raines, ChemBioChem, 2011, 12, 1801–1807.
11. G. S. Beligere and P. E. Dawson, J. Am. Chem. Soc., 2000, 122, 12079–12082.
12. T. E. Wales and M. C. Fitzgerald, J. Am. Chem. Soc., 2001, 123, 7709–7710.
13. P. Silinski and M. C. Fitzgerald, Biochemistry, 2003, 42, 6620–6630.
14. S. Deechongkit, P. E. Dawson and J. W. Kelly, J. Am. Chem. Soc., 2004, 126, 16762–16771.
15. J. A. Scheike, C. Baldauf, J. Spengler, F. Albericio, M. T. Pisabarro and B. Koksch, Angew. Chem., Int. Ed. Engl., 2007, 46, 7766–7769.
16. J. Gao and J. W. Kelly, Protein Sci. Publ. Protein Soc., 2008, 17, 1096–1101.
17. K. N. Vijayadas, H. C. Davis, A. S. Kotmale, R. L. Gawade, V. G. Puranik, P. R. Rajamohanan and G. J. Sanjayan, Chem. Commun., 2012, 48, 9747–9749.
18. K. N. Vijayadas, R. V. Nair, R. L. Gawade, A. S. Kotmale, P. Prabhakaran, R. G. Gonnade, V. G. Puranik, P. R. Rajamohanan and G. J. Sanjayan, Org. Biomol. Chem., 2013, 11, 8348–8356.
19. J. N. N. Eildal, G. Hultqvist, T. Balle, N. Stuhr-Hansen, S. Padrah, S. Gianni, K. Strømgaard and P. Jemth, J. Am. Chem. Soc., 2013, 135, 12998–13007.
20. J. S. Goldberg, Perspect. Med. Chem., 2011, 5, 19–26.
21. E. Jensen and H. Bundgaard, Int. J. Pharm., 1991, 71, 117–125.
22. M. Rabinovitch, Parasitol. Today, 1989, 5, 299–301.
23. H. Kaur, P. W. R. Harris, P. J. Little and M. A. Brimble, Org. Lett., 2015, 17, 492–495.
24. O. S. Søgaard, M. E. Graversen, S. Leth, R. Olesen, C. R. Brinkmann, S. K. Nissen, A. S. Kjaer, M. H. Schleimann, P. W. Denton, W. J. Hey-Cunningham, K. K. Koelsch, G. Pantaleo, K. Krogsgaard, M. Sommerfelt, R. Fromentin, N. Chomont, T. A. Rasmussen, L. Østergaard and M. Tolstrup, PLoS Pathog., 2015, 11, e1005142.
25. K. D. Kopple, J. Pharm. Sci., 1972, 61, 1345–1356.
26. C. J. White and A. K. Yudin, Nat. Chem., 2011, 3, 509–524.
27. A. D. Borthwick, Chem. Rev., 2012, 112, 3641–3716.
28. B. S. Thakkar, J.-S. M. Svendsen and R. A. Engh, J. Phys. Chem. A, 2017, 121, 6830–6837.
29. V. Villani, G. Alagona and C. Ghio, Mol. Eng., 1998, 8, 135–153.
30. N. G. Mirkin and S. Krimm, J. Mol. Struct.: THEOCHEM, 1991, 236, 97–111.
31. Schrödinger Release 2016-1, Maestro, Schrödinger, LLC, New York, NY, 2016.
32. Schrödinger Release 2016-1, MacroModel, Schrödinger, LLC, New York, NY, 2016.
33. A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142.
34. Schrödinger Release 2016-1, Jaguar, Schrödinger, LLC, New York, NY, 2016.
35. J. L. Katz and B. Post, Acta Crystallogr., 1960, 13, 624–628.
36. Y. K. Kang and H. S. Park, J. Mol. Struct.: THEOCHEM, 2004, 676, 171–176.
37. C. Toniolo, Crit. Rev. Biochem., 1980, 9, 1–44.
38. M. Crisma, M. De Zotti, A. Moretto, C. Peggion, B. Drouillat, K. Wright, F. Couty, C. Toniolo and F. Formaggio, New J. Chem., 2015, 39, 3208–3216.
39. B. K. Ho and R. Brasseur, BMC Struct. Biol., 2005, 5, 14.

---

Footnote

† Electronic supplementary information (ESI) available: A supporting information file with Cartesian coordinates for all geometries. See DOI: 10.1039/c7ra13712e

---