Open Access Article
Open Access ArticleAn ab initio study on coinage atom-inserted cyanide/isocyanide: XMCN/XMNC (M = coinage atoms; X = halogen)†
Zhengguo Huang *,
Xiaohong Wang,
Jingbo Zhang*,
Yuqing Li and
Yuying Li
*,
Xiaohong Wang,
Jingbo Zhang*,
Yuqing Li and
Yuying Li
Tianjin Key Laboratory of Structure and Performance for Functional Molecules, Key Laboratory of Inorganic–Organic Hybrid Functional Materials Chemistry (Tianjin Normal University), Ministry of Education, College of Chemistry, Tianjin Normal University, Tianjin 300387, People's Republic of China. E-mail: hsxyhzg@126.com; hxxyzjb@mail.tjnu.edu.cn
First published on 18th April 2018
Abstract
The coinage atom-inserted cyanide/isocyanide compounds, XMCN and XMNC (X = halogens) formed by the insertion of a coinage atom into the X–C(N) bonds of XCN (or XNC), were investigated by ab initio methods. XMCN was predicted to be more stable than XMNC, which is different from the case of XUCN/XUNC reported previously. Based on the analyses on the ionization dissociation pathways, the M–C (or M–N) bond is more easily broken than the X–M bond. Moreover, the order of the M–C (or M–N) bond energy in XMCN (or XMNC) is XAuCN (XAuNC) > XCuCN (XCuNC) > XAgCN (XAgNC). The shift characters of vC–N in XMCN (or XMNC) with respect to the concerning precursor can be used to identified XMCN and XMNC experimentally. The results of charge decomposition analysis (CDA) and atoms-in-molecule (AIM) illustrate that the X–M and M–C(N) bond behaves as a coordination bond, while the C–N bond is a typical polar covalent bond. The higher thermodynamic stability of XMCN is the result of the –CN group having better coordination ability than the –NC group.
1. Introduction
The reactions of metal atoms with species containing a CN group are very interesting because the CN group can bond at either C or N, leading to cyanides and isocyanides, respectively. The theoretical research on the uranyl–CN/NC bonding showed that the U–NC and U–CN bonding have comparable energies, which depend intimately on the local environment.1 Previous study showed that UF4(NC)2 is slightly more exothermic than UF4(CN)2, and the stretching frequency of the isocyanide ligand is about 200 cm−1 lower than that of the cyanide ligand.2 The isocyanide CH3UNC is the dominant product in the reaction of CH3CN + U in solid argon matrices.3 Laser-ablated uranium atoms react with HCN to produce HUNC, which has higher stability than the cyanide isomers (HUCN).4 Similarly, the major products of the reactions of laser–ablated uranium atoms with (CN)2 are also isocyanides including UNC, U(NC)2, and U(NC)4.5 Recently, our research on the reaction of U + XCN/XNC (X = halogens) showed that XUNC is stable than XUCN.6 However, it is an open question whether the isocyanides of other transition metal are stable than the cyanides as well, which motivates us to further explore the nature of cyanides/isocyanides of other transition metals.Group 11 metals, the so-called coinage metals, are at the borderline between the main group elements and transition metals, and have high electronegativity and catalytic activity due to their d10 electronic configuration and single valence electron (s1).7,8 CH3MH (M = Cu, Ag and Au) and its negative ion form have been identified in low-temperature matrix isolation experiments by the insertion of coinage metals into C–H bond of methane.9 The insertion of the coinage metal atoms into the C–X bonds of halogenated methane (CH3X, X = F, Cl, Br and I) have been systemic studied theoretically, which provides useful information of CH3MX molecules and is helpful for the preparation and characterization of CH3MX.10
To our best knowledge, no researches on the cyanides/isocyanides of coinage metals were reported so far. Therefore, we systematically investigate the possible products, XMCN and XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au), of the reaction of XCN/XNC with coinage metal atoms in this paper. As mentioned, previous researches showed that XUNC is stable than XUCN,6 therefore, this article focuses on the following issues: Is XMNC stable than XMCN (X = F, Cl, Br and I; M = Cu, Ag and Au) as well? What are the differences (e.g. structures, energies, vibrational frequencies and electronic structures) between XMCN and XMNC? What is the reason for such differences? We hope that this research will be helpful for the preparation of XMCN/XMNC molecules in cryogenic noble-gas matrices.
2. Theoretical calculations
The structures, energies and spectroscopic properties of XMCN and XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au) have been calculated by ab initio methods using ORCA software.11 To reduce the computation cost, the Def2-ECP effect core potential with corresponding basis sets were used for heavy elements (Ag, Au and I),12,13 in which 25 and 19 explicit electrons for halogen (I) and coinage atoms (Ag and Au) are retained, respectively. The minimally augmented def2 basis sets of the Karlsruhe group, ma-def2-SVP,14,15 were used for other atoms (C, N, F, Cl, Br and Cu). In order to generate one valid initial wave function, the stability of Hartree–Fock wave function for each molecule was tested prior to the structural optimization, and the wave function would be reoptimized if it has internal instabilities. Based on the optimized wave function, each of molecules was optimized by CCSD(T) method, follow by the numerical vibrational frequency calculation to ensure that the optimized structure is the minima and evaluate zero-point vibrational energies (ZPVE). To ensure that no serious spin contaminations were involved, the expectation value of the total spin (S2) for CCSD(T) calculation was checked. Moreover, the multi-reference character of each of molecules was checked by T1 diagnostics performed at the CCSD(T) level.16To under the bonding characters of XMCN and XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au), charge decomposition analysis (CDA)17,18 and Bader's atoms-in-molecule (AIM)19,20 analyses were performed by Multiwfn software.21 To obtain the chemical sense results of AIM analysis, the segmented all-electron relativistically contracted (SARC-ZORA-TZVPP) basis sets22 were used for Au atom, in which the g function was removed because the Multiwfn software cannot deal with it. The recontracted scalar relativistic all-electron basis sets (old-ZORA-TZVPP)22,23 were used for other atoms. To consider the relativistic effect and the spin–orbit coupling (SOC) effect,24,25 scalar relativistic all-electron single-point energies calculations for each of XMCN/XMNC molecules were performed with the 0th order regular approximation (ZORA).26,27
3. Results and discussions
3.1 Structures
The selected structural parameters, the expectation values of the total spins (S2) and T1 diagnostic values of XMCN/XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au) obtained at the CCSD(T) level were listed in Table 1. Each of XMCN/XMNC with possible electronic states was optimized, and the results show that all ground-state XMCN/XMNC are doublet. As shown in Table 1, the spin contamination is negligible due to the small S2. Moreover, the T1 diagnostic values are larger than 0.02, which indicates that XMCN/XMNC molecules have remarkable multireference character, and multireference methods (MRCI, MRPT2, and so on) are required to study their reaction dynamics. Because the focuses of this paper are not the reaction dynamics but the structures, vibrational frequencies and electronic structures of XMCN/XMNC which are influenced slightly by multireference character, CCSD(T) is reliable enough to be used for the optimization of XMCN/XMNC, but even so, the computational amount is still very large. It is impractical to optimize the structures of XMCN/XMNC molecules using MRCI due to the huge computational amount.| F | Cl | Br | I | F | Cl | Br | I | |
|---|---|---|---|---|---|---|---|---|
| XCuCN | XCuNC | |||||||
| RX–Cu | 1.753 | 2.131 | 2.260 | 2.437 | 1.751 | 2.121 | 2.264 | 2.422 |
| RCu–C(N) | 1.898 | 1.902 | 1.904 | 1.901 | 1.832 | 1.831 | 1.831 | 1.845 |
| RC–N | 1.176 | 1.176 | 1.176 | 1.180 | 1.190 | 1.191 | 1.191 | 1.190 |
| AX–Cu–C(N) | 180.0 | 180.0 | 180.0 | 179.5 | 180.0 | 180.0 | 180.0 | 180.0 |
| ACu–C(N)–N(C) | 180.0 | 180.0 | 180.0 | 177.8 | 180.0 | 180.0 | 180.0 | 180.0 |
| δRX–Cu | −0.007 | 0.021 | 0.000 | −0.013 | −0.009 | 0.011 | 0.004 | −0.028 |
| δRCu–C(N) | 0.028 | 0.032 | 0.034 | 0.031 | 0.002 | 0.001 | 0.001 | 0.015 |
| T1 | 0.050 | 0.023 | 0.048 | 0.026 | 0.024 | 0.053 | 0.025 | 0.059 |
| S2 | 0.761 | 0.762 | 0.796 | 0.758 | 0.755 | 0.758 | 0.766 | 0.758 |
| XAgCN | XAgNC | |||||||
|---|---|---|---|---|---|---|---|---|
| RX–Ag | 1.935 | 2.309 | 2.481 | 2.692 | 1.926 | 2.310 | 2.473 | 2.655 |
| RAg–C(N) | 1.994 | 2.011 | 2.034 | 2.045 | 1.972 | 1.999 | 2.018 | 2.028 |
| RC–N | 1.175 | 1.179 | 1.178 | 1.179 | 1.190 | 1.191 | 1.190 | 1.189 |
| AX–Ag–C(N) | 180.0 | 139.1 | 160.2 | 180.0 | 180.0 | 159.6 | 178.3 | 180.0 |
| AAg–C(N)–N(C) | 180.0 | 176.7 | 177.5 | 180.0 | 180.0 | 175.7 | 179.0 | 180.0 |
| δRX–Ag | 0.175 | 0.199 | 0.221 | 0.242 | 0.006 | 0.040 | 0.053 | 0.045 |
| δRAg–C(N) | −0.036 | −0.019 | 0.004 | 0.015 | −0.018 | 0.009 | 0.028 | 0.038 |
| T1 | 0.025 | 0.028 | 0.030 | 0.028 | 0.032 | 0.023 | 0.030 | 0.025 |
| S2 | 0.757 | 0.804 | 0.758 | 0.754 | 0.761 | 0.765 | 0.771 | 0.753 |
| XAuCN | XAuNC | |||||||
|---|---|---|---|---|---|---|---|---|
| RX–Au | 1.954 | 2.267 | 2.417 | 2.620 | 1.936 | 2.225 | 2.360 | 2.556 |
| RAu–C(N) | 1.967 | 1.960 | 1.972 | 1.977 | 1.950 | 1.942 | 1.957 | 1.970 |
| RC–N | 1.174 | 1.175 | 1.179 | 1.178 | 1.190 | 1.197 | 1.193 | 1.191 |
| AX–Au–C(N) | 180.0 | 147.1 | 175.2 | 180.0 | 180.0 | 152.5 | 179.3 | 180.0 |
| AAu–C(N)–N(C) | 180.0 | 178.7 | 179.4 | 180.0 | 180.0 | 179.6 | 179.7 | 180.0 |
| δRX–Au | 0.074 | 0.037 | 0.037 | 0.050 | 0.056 | −0.005 | −0.020 | −0.014 |
| δRAu–C(N) | −0.023 | −0.030 | −0.018 | −0.013 | 0.000 | −0.008 | 0.007 | 0.020 |
| T1 | 0.022 | 0.024 | 0.022 | 0.023 | 0.052 | 0.019 | 0.051 | 0.020 |
| S2 | 0.755 | 0.760 | 0.766 | 0.754 | 0.758 | 0.757 | 0.761 | 0.757 |
| XCN | XNC | |||||||
|---|---|---|---|---|---|---|---|---|
| RX–C(N) | 1.273 | 1.650 | 1.804 | 2.023 | 1.309 | 1.647 | 1.801 | 2.012 |
| RC–N | 1.171 | 1.173 | 1.174 | 1.174 | 1.189 | 1.190 | 1.191 | 1.192 |
As shown in Table 1, most of XMCN/XMNC molecules are linear, and other XMCN/XMNC molecules are planar structures with Cs symmetry. The C–N bond (ca. 1.18 Å) of XMCN is slightly shorter than that of XMNC (ca. 1.19 Å), which indicates that their bond strengths are almost the same. Compared with the C–N bond of their precursor (XCN/XNC), the C–N bond of XMCN/XMNC almost keeps unchanged, so the insertion of M atom into XCN/XNC has little effect on the C–N bond. In most cases, the X–M bond of XMCN might be weaker than that of XMNC because the former is slightly longer than the latter. For XMCN (or XMNC) containing the same metal element, the M–C (or M–N) bond is weakened as X varies from F to I (except for individual cases) because the RM–C (or RM–N) is lengthened. Meanwhile, although the RM–C of XMCN is longer than the RM–N of XMNC containing the same metal atom, we cannot infer that the former is weaker than the latter because the radius of carbon atom is larger than that of nitrogen atom. Similarly, it is inappropriate to compare directly the strengths of the X–M bonds concerning different halogen (or coinage) atoms using the bond length because the radius of different halogen (or coinage) atoms are different. To compare the strength of A–B bond containing different atoms, the structural parameter δR is defined as:28,29
| δRA–B = RA–B − RA − RB | (1) |
3.2 Energies
Based on the optimized structures, the single point energies with zero-point vibrational energy (ZPVE) corrections of XMCN/XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au) were calculated at the CCSD(T) level. The fragmentation energies of four possible fragmentation pathways were considered to study the thermodynamic stabilities of these molecules:| ΔE1 = E(M) + E(XCN) − E(XMCN) or ΔE1 = E(M) + E(XNC) − E(XMNC) | (2) |
| ΔE2 = E(X) + E(M) + E(CN) − E(XMCN) or ΔE2 = E(X) + E(M) + E(NC) − E(XMNC) | (3) |
| ΔE3 = E(XM+) + E(CN−) − E(XMCN) or ΔE3 = E(XM+) + E(NC−) − E(XMNC) | (4) |
| ΔE4 = E(X−) + E(MCN+) − E(XMCN) or ΔE4 = E(X−) + E(MNC+) − E(XMNC) | (5) |
| XMCN | XMNC | ΔEa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔE1 | ΔE2 | ΔE3 | ΔE4 | ΔE1 | ΔE2 | ΔE3 | ΔE4 | |||
| a ΔE = E(XMCN) − E(XMNC). | ||||||||||
| FCuCN | 59.0 | 176.6 | 226.1 | 243.6 | FCuNC | 121.5 | 167.9 | 217.4 | −8.7 | |
| ClCuCN | 55.5 | 151.4 | 214.3 | 215.5 | ClCuNC | 93.3 | 143.7 | 206.6 | −7.6 | |
| BrCuCN | 58.0 | 143.9 | 190.7 | 208.1 | BrCuNC | 88.1 | 135.6 | 182.4 | −8.3 | |
| ICuCN | 53.4 | 130.6 | 172.0 | 199.9 | ICuNC | 75.6 | 123.1 | 164.5 | −7.5 | |
| FAgCN | 2.3 | 120.0 | 202.2 | 208.8 | FAgNC | 60.1 | 106.5 | 188.7 | 174.3 | −13.5 |
| ClAgCN | 8.2 | 104.1 | 170.4 | 189.9 | ClAgNC | 40.7 | 91.1 | 157.5 | 156.0 | −12.9 |
| BrAgCN | 17.1 | 103.0 | 165.3 | 189.0 | BrAgNC | 43.6 | 91.1 | 153.5 | 156.1 | −11.9 |
| IAgCN | 28.2 | 105.4 | 161.2 | 196.5 | IAgNC | 46.1 | 93.6 | 149.3 | 163.6 | −11.8 |
| FAuCN | 6.2 | 123.9 | 234.3 | 224.7 | FAuNC | 58.3 | 104.7 | 215.2 | 201.2 | −19.1 |
| ClAuCN | 19.2 | 115.1 | 223.2 | 212.9 | ClAuNC | 46.4 | 96.8 | 204.9 | 190.4 | −18.2 |
| BrAuCN | 28.4 | 114.2 | 201.3 | 212.2 | BrAuNC | 49.1 | 96.6 | 183.6 | 190.3 | −17.7 |
| IAuCN | 38.4 | 115.5 | 191.1 | 218.7 | IAuNC | 49.4 | 96.9 | 172.5 | 195.7 | −18.6 |
XCN is more stable thermodynamically than XNC, and XMCN has higher thermodynamic stability than XMNC as well, therefore, the comprehensive effects of both factors result in that the ΔE1 of XMNC is remarkably smaller than that of XMCN. All XMCN (or XMNC) are endothermic with respect to the two-body decomposition pathway (2), which confirms that XMCN (or XMNC) is thermodynamic stable with respect to M + XCN (or M + XNC). By comparing the ΔE1 of XMCN (or XMNC) containing different metal atoms, we found that XCuCN (or XCuNC) has the highest thermodynamic stability with respect to the two-body decomposition pathway (2), followed by XAuCN (or XAuNC), and the thermodynamic stability of XAgCN (or XAgNC) are the least. Because XMCN is more stable than XMNC, only the cases of XMCN are discussed below. As X varies from F to I, the thermodynamic stabilities of both XAuCN and XAgCN increase due to the increasing ΔE1, while the thermodynamic stability of XCuCN shows a decreasing trend. Therefore, FCuCN, IAgCN and IAuCN are the most stable XCuCN, XAgCN and XAuCN, respectively.
As shown in Table 2, the positive ΔE2 of XMCN (or XMNC) indicates that the three-body decomposition pathways are endothermic, and XMCN (or XMNC) is thermodynamic stable with respect to M + X + CN. The order of thermodynamic stability concerning the three-body decomposition pathways is XCuCN (or XCuNC) > XAuCN (or XAuNC) > XAgCN (or XAgNC). In addition, for each XMCN (or XMNC) molecule, ΔE2 is remarkably larger than ΔE1, which attribute to the excess energy for the decomposing XCN (or XNC) into X + CN.
As shown in Table 2, the two ionization dissociation pathways of XMCN (or XMNC) are endothermic as well, moreover, the bond energies of the M–C (or M–N) and X–M bonds can be evaluated approximately according to ΔE3 and ΔE4. Although some data of ΔE4 are missed, it can be learned from Table 2 that the ΔE4 of XMCN (or XMNC) is generally larger than the ΔE3, which demonstrates that the M–C (or M–N) bond is easier to be broken than the X–M bond. For the ionization dissociation pathway (4), the M–C (or M–N) bond of XMCN (or XMNC) is weakened as X varies from F to I due to the decreasing ΔE3, which agrees with the above-mentioned results of structures analyses. Moreover, the bond energy of the M–C (or M–N) bond in XMCN/XMNC generally meets the following order: XAuCN (XAuNC) > XCuCN (XCuNC) > XAgCN (XAgNC). For the ionization dissociation pathway (5), the analysis is affected to a certain extent by the lack of ΔE4 (XCuNC). The X–Cu bond of XCuCN is weakened as X varies from F to I due to the decreasing ΔE4; for other systems (XAgCN, XAgNC, AuCN and XAuNC), the F–M bond is the strongest among counterparts containing the same metal atom due to the largest ΔE4, and other X–M bond are relatively less affected by the substitution of halogens.
3.3 Frequencies
IR spectroscopy is one of powerful tools to characterize active species in matrix isolation experiments, and the vibrational fingerprints can provide important information for the identifications and analyses of products. The selected vibrational frequencies of XCuCN/XCuNC (X = F, Cl, Br and I) and precursors were listed in Table 3, and the selected vibrational frequencies of XAgCN/XAgNC and XAuCN/XAuNC were listed in Table S1 in the ESI.† As shown in Tables 3 and S1,† the C–N bond in XCN (or XNC) is one typical triple bond, and its stretching vibrational frequency (vC–N) is in the range of 2110–2370 cm−1. It is well known that the vC–N of XCN is larger than that of XNC. Similarly, the vC–N of XMCN is about 2086–2430 cm−1 and is obviously larger than that of XMNC. Such difference can be used to identify XMCN and XMNC in matrix isolation experiments. Compared with the vC–N of XCN, the vC–N of XMCN shows small red-shift or blue-shift character, which indicates that the C–N bond is less affected by the insertion of metal atom.| XMCN | XMNC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| vC–N | ΔvC–Nb | vM–C | vX–M | vC–N | ΔvC–Nb | vM–N | vX–M | ||
| a Frequencies are in cm−1 and intensities (in parentheses) are in km mol−1.b ΔvC–N is the difference of the vC–N between XMCN (or XMNC) and XCN (or XNC). | |||||||||
| FCuCN | 2303.8 | −64.0 | 460.0 | 687.1 | FCuNC | 2133.8 | −58.0 | 491.9 | 692.8 |
| ClCuCN | 2338.4 | 74.8 | 358.8 | 515.2 | ClCuNC | 2129.7 | −7.7 | 385.9 | 552.6 |
| BrCuCN | 2337.1 | 96.5 | 490.4 | 286.5 | BrCuNC | 2140.1 | 20.5 | 546.4 | 260.1 |
| ICuCN | 2187.1 | −33.3 | 448.7 | 192.7 | ICuNC | 2130.2 | 17.6 | 485.7 | 187.3 |
| FCN | 2367.8 | FNC | 2191.9 | ||||||
| ClCN | 2263.6 | ClNC | 2137.4 | ||||||
| BrCN | 2240.6 | BrNC | 2119.7 | ||||||
| ICN | 2220.4 | INC | 2112.6 | ||||||
The vC–N cannot provide sufficient evidence for the identification of XMCN/XMNC in experiments because it is involved in not only XMCN/XMNC but also their precursors. The stretching vibrational modes of both X–M and M–C (or M–N) are the fingerprints of XMCN/XMNC because they involve metal atoms, and can be used to identify these studied molecules. Except few cases, the vX–M of XMCN is close to that of XMNC, which indicates that the strengths of the X–M bonds in both XMCN and XMNC are approximately the same. Moreover, the vX–M of XMCN (or XMNC) decreases as X varies from F to I, which is attributed to two factors, one is the increasing reduced mass of such vibrational mode, and the other is the weakening X–M bond. Among XMCN (or XMNC) containing the same metal atom, the vF–M of FMCN (or FMNC) and the vCl–Cu of ClCuCN (or ClCuNC or ClAuNC) are larger than 500 cm−1. The other vX–M are too low (<350 cm−1) to be detected experimentally because they is beyond the detection limit of infrared spectrometer. Although the vM–C (or vM–N) of XMCN (or XMNC) is usually larger than 400 cm−1, it is hard to be detected by IR spectrum in some cases, one reason is that such vibrational mode is weak, and the other reason is that the anharmonic effect was not taken into account during the vibrational frequencies calculation.
3.4 AIM analyses
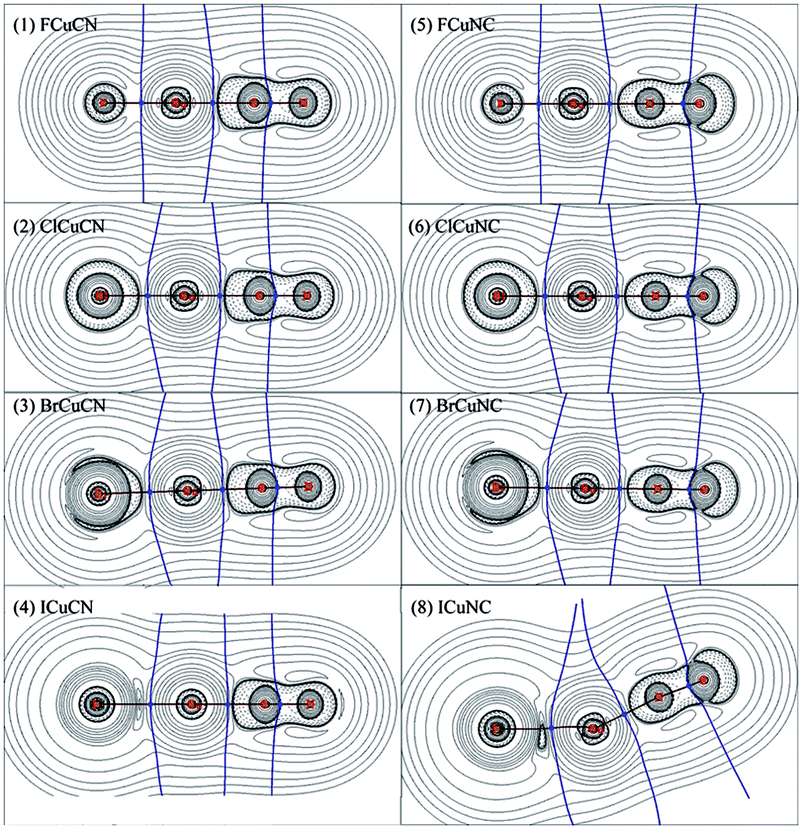
The bonding of XMCN/XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au) was investigated by AIM method, the results of XCuCN/XCuNC were presented in Table 4, and the results of XAgCN/XAgNC and XAuCN/XAuNC were listed in Table S3 and S4 in the ESI,† respectively. The contour line diagrams of the Laplacian of electron density (∇2ρ(r)) for XCuCN/XCuNC were shown in Fig. 1, and the contour line diagrams of ∇2ρ(r) for XAgCN/XAgNC and XAuCN/XAuNC were presented in Fig. S1 and S2 in the ESI,† respectively. As shown in Fig. 1 and S1 and S2,† for each of XMCN/XMNC, there is one charge concentration region around C–N bond, and the bond critical point (BCP) locates at the boundary of the valence shell of carbon atom, which illustrates that it is one typical polar covalent bond. Unlike XMCN, the charge concentration region around carbon atom of XMNC is discontinuous, which may be caused by the charge of CN group shifts to the nitrogen atom bonded to metal atom. The X–M and M–C (or M–N) bond of XMCN/XMNC behave like closed-shell interaction because there exist charge depletion regions among these bonds. In FMCN/FMNC and ClMCN/ClMNC, the circular charge concentration region around X (F or Cl) atom illustrates that X− is the result of the extra electron transfer from metal atom to X atom. The charge concentration region around Br atom in BrMCN/BrMNC is smaller obviously than those of F (or Cl) atoms, and charge concentrates toward to metal atom along Br–M bond, which shows that the charge transfer becomes weak. In IMCN/IMNC, the charge concentration region around I atom is replaced by the charge depletion regions, so the direction of charge transfer changed. In conclusion, for different XMCN/XMNC containing different halogen atom, there are large differences among the contour line diagrams of ∇2ρ(r), which indicates that the nature of X–M bond is affected by the substitution of halogen atom to a large extent. On the contrary, for XMCN/XMNC containing the same halogen atom, the contour line diagrams of ∇2ρ(r) are similar, which demonstrates that the nature of bonds in these molecules are similar.| molecule | bond | ρ(r) | ∇2ρ(r) | H(r) | |V(r)|/G(r) | molecule | bond | ρ(r) | ∇2ρ(r) | H(r) | |V(r)|/G(r) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The recontracted scalar relativistic def2-TZVPP basis sets were used for all atoms. | |||||||||||
| FCuCN | F–Cu | 0.138 | 1.033 | −0.045 | 1.148 | FCuNC | F–Cu | 0.139 | 1.045 | −0.045 | 1.148 |
| Cu–C | 0.124 | 0.420 | −0.063 | 1.375 | Cu–N | 0.127 | 0.706 | −0.050 | 1.221 | ||
| C–N | 0.488 | 0.146 | −0.953 | 1.963 | C–N | 0.465 | −0.267 | −0.897 | 2.080 | ||
| ClCuCN | Cl–Cu | 0.101 | 0.363 | −0.043 | 1.321 | ClCuNC | Cl–Cu | 0.102 | 0.368 | −0.043 | 1.321 |
| Cu–C | 0.124 | 0.414 | −0.062 | 1.376 | Cu–N | 0.126 | 0.695 | −0.049 | 1.221 | ||
| C–N | 0.488 | 0.142 | −0.952 | 1.964 | C–N | 0.464 | −0.274 | −0.896 | 2.083 | ||
| BrCuCN | Br–Cu | 0.086 | 0.242 | −0.035 | 1.366 | BrCuNC | Br–Cu | 0.087 | 0.244 | −0.035 | 1.366 |
| Cu–C | 0.123 | 0.410 | −0.062 | 1.376 | Cu–N | 0.126 | 0.690 | −0.049 | 1.221 | ||
| C–N | 0.487 | 0.141 | −0.952 | 1.964 | C–N | 0.464 | −0.275 | −0.896 | 2.083 | ||
| ICuCN | I–Cu | 0.070 | 0.171 | −0.022 | 1.344 | ICuNC | I–Cu | 0.083 | 0.123 | −0.033 | 1.518 |
| Cu–C | 0.125 | 0.319 | −0.065 | 1.450 | Cu–N | 0.127 | 0.697 | −0.050 | 1.222 | ||
| C–N | 0.489 | 0.053 | −0.958 | 1.986 | C–N | 0.464 | −0.290 | −0.896 | 2.088 | ||
The AIM parameters presented in Tables 4, S2 and S3† can provide more useful information about the nature of bonds in XMCN/XMNC (X = F, Cl, Br and I; M = Cu, Ag and Au).31–36 It is well known that both total energy density (H(r)) and Laplacian of electron density (∇2ρ(r)) at BCPs are usually used to evaluate the type of interactions between the atoms.37–40 H(r) < 0 and ∇2ρ(r) < 0 correspond to covalent interaction between the interacting atoms because of the accumulation of charge density at the BCP; H(r) > 0 and ∇2ρ(r) > 0 correspond to closed-shell interaction between the interacting atoms due to the depleting of charge density at BCP; H(r) < 0 but ∇2ρ(r) > 0 correspond to partially covalent interaction. The absolute ratio of potential and kinetic energy densities, namely |V(r)|/G(r), is usually used to discriminate interaction type as well: |V(r)|/G(r) < 1 corresponds to a pure closed-shell interaction, |V(r)|/G(r) > 2 corresponds to a pure covalent (open-shell) interaction, while 1 < |V(r)|/G(r) < 2 corresponds to an intermediate interaction.37
As shown in Tables 4, S2 and S3,† the C–N bond in XMNC behaves like covalent interaction because both H(r) and ∇2ρ(r) at C–N BCP are negative. On the contrary, H(r) at the C–N BCP in XMCN is about −0.95, while ∇2ρ(r) is positive, so the C–N bond in XMCN seems to be partially covalent interaction. However, Fig. 1, S1 and S2† show that the C–N BCP in XMCN just locates at the boundary of the shell structure of carbon atom, which demonstrates that the C–N bond is strong polar covalent bond, and the positive ∇2ρ(r) is not enough to prove that the C–N bond belongs to closed-shell interaction. Meanwhile, the covalent interaction character of the C–N bond in XMCN is further confirmed by the |V(r)|/G(r) ratio of ca. 2.0.
The X–M, M–C and M–N bonds exhibit closed-shell interaction character along with partially covalent character due to the positive ∇2ρ(r) and the small negative H(r), which is further confirmed by the |V(r)|/G(r) ratios of ca. 1.1–1.5. In consideration of Fig. 1, S1 and S2,† the X–M, M–C and M–N bonds are considered as coordination bonds. As shown in Tables 4, S2 and S3,† for each XMCN, the H(r) of the X–M bond is larger than that of the M–C bond, while the |V(r)|/G(r) ratio is the opposite, which indicates that the M–C bond seems to be more covalent than the X–M bond. However, considering that both X–M and M–C bonds are coordination bonds, we think that these cases demonstrate the better coordination ability of –CN rather than halogen atoms. Furthermore, the |V(r)|/G(r) ratio of the X–M bond in most of XMNC molecules is larger than that of the M–N bond, which indicates that the coordination ability of –NC is relatively weak than –CN group. Therefore, the higher thermodynamic stability of XMCN is the result of that the –CN group has better coordination ability than –NC group.
3.5 CDA analyses
CDA calculations were performed to analyze the interactions between molecular fragments on a quantitative basis. The X−, M2+ and CN− (or NC−) were defined as three fragments. Three terms including d (the amount of electron donation), b (the amount of electron back donated) and r (repulsive polarization) were calculated by CDA. The term (d − b) is the amount of net transferred electrons from the electron donator to the acceptor. In addition, the (b + d) term is also defined, the larger the (b + d) term, the greater the interaction between the two fragments, and the more significant the orbital mixing is.41 The CDA results of XCuCN/XCuNC (X = F, Cl, Br and I) were presented in Table 5, while the results of XAgCN/XAgNC and XAuCN/XAuNC were listed in Tables S4 and S5 in the ESI,† respectively. As shown in Tables 5, S4 and S5,† it is clear that there occurs an electron flow from the halogens and the cyanide (or isocyanide) to the metal atom (M). Because the b term is small, the net electron transfer term (d − b) mainly depends on the d term. The d term of CN→M in XMCN is remarkably larger than that of NC→M in XMNC, which leads to that the (d − b) term of CN→M in XMCN is obviously larger than that of NC→M in XMNC. Therefore, the –CN group exhibits better coordination ability than the –NC group, which result in that the M–C bond in XMCN is stronger than the concerning M–N bond in XMNC. Such conclusion is further supported by the (d + b) term. The (d + b) term of CN→M in XMCN is larger than that of NC→M in XMNC, which indicates the orbital mixing of M with cyanide is more significant than that of M with isocyanide. In one word, the –CN group exhibits better coordination ability than the –NC group, which is the root cause of the difference between XMCN and XMNC.| FCuCN | ClCuCN | BrCuCN | ICuCN | |||||
|---|---|---|---|---|---|---|---|---|
| F→Cu | CN→Cu | Cl→Cu | CN→Cu | Br→Cu | CN→Cu | I→Cu | CN→Cu | |
| d | 0.2215 | 0.2920 | 0.3415 | 0.2899 | 0.3541 | 0.2900 | 0.3777 | 0.2917 |
| b | −0.0010 | 0.0053 | 0.0040 | 0.0056 | 0.0062 | 0.0047 | 0.0065 | 0.0028 |
| d − b | 0.2225 | 0.2868 | 0.3376 | 0.2843 | 0.3478 | 0.2853 | 0.3711 | 0.2890 |
| r | −0.0609 | −0.0685 | −0.0278 | −0.0500 | −0.0280 | −0.0483 | −0.0309 | −0.0633 |
| b + d | 0.2205 | 0.2973 | 0.3455 | 0.2955 | 0.3603 | 0.2946 | 0.3842 | 0.2945 |
| FCuNC | ClCuNC | BrCuNC | ICuNC | |||||
|---|---|---|---|---|---|---|---|---|
| F→Cu | NC→Cu | Cl→Cu | NC→Cu | Br→Cu | NC→Cu | I→Cu | NC→Cu | |
| d | 0.2150 | 0.2491 | 0.3334 | 0.2430 | 0.3465 | 0.2456 | 0.3876 | 0.2626 |
| b | −0.0018 | 0.0006 | 0.0034 | 0.0014 | 0.0053 | 0.0016 | 0.0056 | 0.0013 |
| d − b | 0.2168 | 0.2485 | 0.3300 | 0.2417 | 0.3412 | 0.2440 | 0.3820 | 0.2613 |
| r | −0.0630 | −0.0672 | −0.0244 | −0.0475 | −0.0226 | −0.0460 | −0.0311 | −0.0672 |
| b + d | 0.2132 | 0.2497 | 0.3368 | 0.2444 | 0.3518 | 0.2472 | 0.3932 | 0.2639 |
4. Conclusions
The structures, vibrational frequencies and energies of XMCN and XMNC (M = Cu, Ag and Au; X = F, Cl, Br and I) were studied by DFT and ab initio methods, and the bonding properties of the studied molecules were analyzed by AIM and CDA methods. The main conclusions are as follows:(1) XMCN/XMNC (M = Cu, Ag and Au; X = F, Cl, Br and I) have different nature from XUCN/XUNC reported previously. XMCN has higher thermodynamic stability than XMNC. AIM and CDA results show that the higher thermodynamic stability of XMCN is the result of that the –CN group has better coordination ability than –NC group. The order of thermodynamic stability of XMCN (or XMNC) is XCuCN (or XCuNC) > XAuCN (or XAuNC) > XAgCN (or XAgNC).
(2) The M–C (or MN) bond is easier to be broken than the X–M bond, and the bond energy of the M–C (or M–N) bond in XMCN (or XMNC) is XAuCN (XAuNC) > XCuCN (XCuNC) > XAgCN (XAgNC).
(3) The vC–N of XMCN is obviously larger than that of XMNC, and such difference can be used to identified XMCN and XMNC experimentally. Due to the low frequencies or intensities, some vX–M and vM–C (or vM–N) cannot be detected by IR spectrum.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21273160) and the Program for Innovative Research Team in University of Tianjin (TD13-5074).References
- C. Clavaguera-Sarrio, S. Hoyau, N. Ismail and C. J. Marsden, J. Phys. Chem. A, 2003, 107, 4515–4525 CrossRef CAS.
- M. Straka, M. Patzschke and P. Pyykko, Theor. Chem. Acc., 2003, 109, 332–340 CrossRef CAS.
- H.-G. Cho and L. Andrews, Organometallics, 2012, 31, 535–544 CrossRef CAS.
- Y. Gong, H.-G. Cho and L. Andrews, Eur. J. Inorg. Chem., 2015, 18, 2974–2981 CrossRef.
- Y. Gong, L. Andrews, B. K. Liebov, Z. T. Fang, E. B. Garner and D. A. Dixon, Chem. Commun., 2015, 51, 3899–3902 RSC.
- Z. Huang, L. Sun, Y. Yuan, Y. Li and X. Wang, Inorg. Chem., 2016, 55, 12559–12567 CrossRef CAS PubMed.
- H.-G. Cho and L. Andrews, Organometallics, 2013, 32, 2753–2759 CrossRef CAS.
- H.-G. Cho and L. Andrews, Inorg. Chem., 2011, 50, 10319–10327 CrossRef CAS PubMed.
- H. G. Cho and L. Andrews, Dalton Trans., 2011, 40, 11115–11124 RSC.
- Z. Huang, Y. Yuan, L. Sun, X. Wang and Y. Li, RSC Adv., 2016, 6, 84016–84024 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Quantum Chem. Symp., 1989, 199–207 CAS.
- S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352–9362 CrossRef CAS.
- M. Xiao and T. Lu, J. Adv. Phys. Chem., 2015, 4, 111–124 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, U.K., 1990 Search PubMed.
- C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, 2007 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- F. Neese, J. Chem. Phys., 2003, 118, 3939–3948 CrossRef CAS.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- H. K. Wang, Z. G. Huang, T. T. Shen and L. F. Guo, Struct. Chem., 2012, 23, 1163–1172 CrossRef CAS.
- Q. Wang, B. Zhang and Z. Huang, Chem. Phys. Lett., 2014, 614, 5–9 CrossRef CAS.
- P. Pyykko and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197 CrossRef PubMed.
- J. L. McDonagh, A. F. Silva, M. A. Vincent and P. L. A. Popelier, J. Phys. Chem. Lett., 2017, 8, 1937–1942 CrossRef CAS PubMed.
- L. R. Domingo, RSC Adv., 2014, 4, 32415–32428 RSC.
- R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396 CrossRef CAS PubMed.
- N. O. J. Malcolm and P. L. A. Popelier, Faraday Discuss., 2003, 124, 353–363 RSC.
- P. L. A. Popelier, Coord. Chem. Rev., 2000, 197, 169–189 CrossRef CAS.
- R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- S. Jenkins and I. Morrison, Chem. Phys. Lett., 2000, 317, 97–102 CrossRef CAS.
- S. J. Grabowski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. A, 2006, 110, 4772–4779 CrossRef CAS PubMed.
- X. Meng and L. Tian, J. Adv. Phys. Chem., 2015, 4, 111–124 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra00397a |
| This journal is © The Royal Society of Chemistry 2018 |