Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of octahedral distortions on the electronic properties and magnetic interactions in O3 NaTMO2 compounds (TM = Ti–Ni & Zr–Pd)
M. Hussein N. Assadi * and
Yasuteru Shigeta
* and
Yasuteru Shigeta
Center for Computational Sciences, University of Tsukuba, Tennodai 1-1-1, Tsukuba, Ibaraki 305-8577, Japan. E-mail: h.assadi.2008@ieee.org
First published on 13th April 2018
Abstract
The interplay between the coordination environment and magnetic properties in O3 layered sodium transition metal oxides (NaTMO2) is a fascinating and complex problem. Through detailed and comprehensive density functional investigations on O3 NaTMO2 compounds, we demonstrate that the TM ions in O3 NaMnO2, NaFeO2 and NaCoO2 adopt a high spin state. Structurally, NaMnO2 and NaPdO2 undergo Jahn–Teller distortions while NaNbO2 undergoes puckering distortion. Furthermore, in addition to Jahn–Teller distortion, NaPdO2 exhibits charge disproportionation as it contains Pd2+, Pd3+ and Pd4+ species. These distortions stabilize the inter-plane ferromagnetism. Additionally, the inter-plane ferromagnetic coupling is stabilized by kinetic p–d exchange mechanism in undistorted NaCoO2, NaNiO2 and NaTcO2. The intra-plane coupling in this family of compounds on the other hand was found to be generally weak. Only NaMnO2, NaNiO2 and NaTcO2 are predicted to show bulk ferromagnetism with estimated Curie temperatures below ∼50 K.
1. Introduction
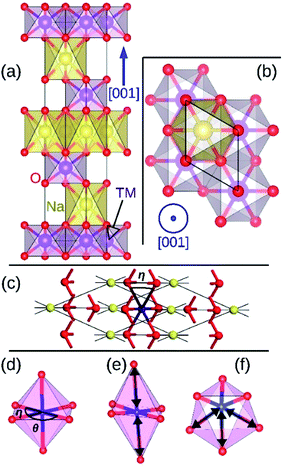
Layered hexagonal compounds with formula NaTMO2 in which TM is a transition metal often exhibit interesting magnetic,1–3 thermoelectric,4 and electrochemical properties.5 One obstacle in studying these compounds is the rich variety of their polymorphs each with distinct symmetry and local coordination for the transition metal ions which complicates finding general property trends for this family of materials. One such area of research that lacks a concise overview is the magnetic properties of the NaTMO2 compounds. For instance, reports of conflicting experimental observations of the magnetic properties for the same compound is not unheard of.6,7 Such contradictions oftentimes stem from coarse structural characterization, restricted by instruments' range and resolution, which falls short in capturing the delicate structural details that dictate the magnetic ground state in these compounds.8,9 This study therefore presents a detailed and focused density functional insight into one important family of such layered materials, namely O3 NaTMO2 compounds in which TM is a fourth or fifth row transition metal element.We start our investigations with compounds of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry which is a common symmetry group among layered compounds.10 As shown in Fig. 1(a) and (b), the hexagonal representation of this structure consists of three alternating TMO2 and Na layers. The notion “O3” indicates that oxygen ions are stacked in ABCABC order and Na ions occupy the octahedral site with respect to the surrounding O ions. The primitive cell of the R
m symmetry which is a common symmetry group among layered compounds.10 As shown in Fig. 1(a) and (b), the hexagonal representation of this structure consists of three alternating TMO2 and Na layers. The notion “O3” indicates that oxygen ions are stacked in ABCABC order and Na ions occupy the octahedral site with respect to the surrounding O ions. The primitive cell of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m O3 structure, presented in Fig. 1(c), has rhombohedral symmetry and the TM ion is located in the center of the primitive cell coordinated by six oxygen ions. The O–TM–O angles, marked η in Fig. 1(c), depend on the lattice parameters of the rhombohedral primitive cell (a and α) and the fractional coordinates of oxygen. If this angle is not exactly 90°, then it follows that the O–TM–O angles alternate between values smaller and larger than 90° resulting in a rhombohedral distortion to the TMO6 octahedra. These angles are marked η and θ in Fig. 1(d). This distortion decreases the octahedral symmetry and splits the energy levels of the t2g orbitals of the TM ions into a single a1g orbital and doubly degenerate
m O3 structure, presented in Fig. 1(c), has rhombohedral symmetry and the TM ion is located in the center of the primitive cell coordinated by six oxygen ions. The O–TM–O angles, marked η in Fig. 1(c), depend on the lattice parameters of the rhombohedral primitive cell (a and α) and the fractional coordinates of oxygen. If this angle is not exactly 90°, then it follows that the O–TM–O angles alternate between values smaller and larger than 90° resulting in a rhombohedral distortion to the TMO6 octahedra. These angles are marked η and θ in Fig. 1(d). This distortion decreases the octahedral symmetry and splits the energy levels of the t2g orbitals of the TM ions into a single a1g orbital and doubly degenerate 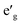 orbitals. The sequence of stabilization of the a1g and
orbitals. The sequence of stabilization of the a1g and 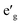 orbitals is not however trivial.11 In addition to the rhombohedral distortion which is inherent to the R
orbitals is not however trivial.11 In addition to the rhombohedral distortion which is inherent to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, NaTMO2 compounds may also experience additional distortions that further reduce the overall symmetry and influence the electronic structure. We will thoroughly examine all such distortions and determine how they influence the electronic and magnetic properties of O3 NaTMO2 compounds.
m symmetry, NaTMO2 compounds may also experience additional distortions that further reduce the overall symmetry and influence the electronic structure. We will thoroughly examine all such distortions and determine how they influence the electronic and magnetic properties of O3 NaTMO2 compounds.
2. Computational and system settings
Spin polarized density functional theory (DFT) calculations were carried out within augmented plane-wave potential12 formalism as implemented in VASP code.13,14 Brillouin zone was sampled using a mesh generated by Monkhorst–Pack scheme with spacing of ∼0.02 Å−1 among k points while the energy cut-off was set to 550 eV. The threshold for energy convergence was set to 10−7 eV per atom. Orbital population and bonding characteristics were examined using LOBSTER code.15The exchange-correlation functional was approximated by the Perdew–Burke–Ernzerhof method.16,17 To improve the electronic description of the compounds in term of localizing the d shell electrons of the transition metal elements, an orbital dependent Hubbard term18 was applied to the d orbitals. The value of Ueff(U − J) was set to 5 eV for 3d TM elements and 2 eV for 4d TM elements. Weaker localization effects of the 4d electrons justifies the smaller Ueff value for the 4d elements. Among the different elements of the 3d and the 4d rows, a small variation in Ueff is naturally expected. However, the choice of constant Ueff for each row allows a more straightforward comparison.19 This procedure is further justified by the fact that the localization effects in NaVO2 are not affected by slight variation of Ueff.11 Furthermore, as shown in Table 1, the applied Ueff values reproduce the lattice constants reported in earlier experiments within ∼1% deviation indicating the adequacy of the chosen values.
| System | Calculated a (Å) | Calculated c (Å) | Experimental a (Å) | Experimental c (Å) | Ref. | TM–O (Å) | η (°) |
|---|---|---|---|---|---|---|---|
| a The lattice parameter a of the supercell has been divided by the number of hexagonal unit cells in corresponding dimensions of the supercell.b These values correspond to the angles closest in value to 90° in distorted systems. | |||||||
| NaTiO2 | 3.042 | 16.551 | 3.037 | 16.260 | 10 | 2.11 | 92.25 |
| NaVO2 | 3.055 | 16.242 | 2.996 | 16.100 | 11 | 2.10 | 95.57 |
| NaCrO2 | 3.052 | 16.146 | 3.030 | 16.000 | 20 | 2.06 | 95.66 |
| NaMnO2 | 3.087a | 16.234 | — | — | — | 2.01, 2.26 | 92.16b |
| NaFeO2 | 3.061 | 16.286 | 3.029 | 16.113 | 21 | 2.03 | 94.86 |
| NaCoO2 | 2.908 | 15.776 | 2.891 | 15.612 | 21 | 1.95 | 96.13 |
| NaNiO2 | 3.000 | 15.899 | 2.960 | 15.780 | 6 | 2.02 | 95.89 |
| NaZrO2 | 3.206 | 17.217 | — | — | — | 2.24 | 90.63 |
| NaNbO2 | 2.998a | 17.817 | — | — | — | 2.22 (unpuckered), 2.18 (puckered), 2.23 (puckered) | 91.15b |
| NaMoO2 | 3.272 | 16.128 | — | — | — | 2.19 | 96.90 |
| NaTcO2 | 3.111 | 16.466 | — | — | — | 2.14 | 93.12 |
| NaRuO2 | 3.121 | 15.968 | 3.124 | 16.037 | 22 | 2.11 | 96.29 |
| NaRhO2 | 3.151 | 15.725 | 3.097 | 15.527 | 23 | 2.10 | 97.03 |
| NaPdO2 | 3.235a | 15.854 | — | — | — | 2.07 (Pd4+), 2.10 (Pd3+), 2.32 (Pd3+), 2.27 (Pd2+) | 90.00b |
O3 NaTMO2 structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry in hexagonal representation, as shown in Fig. 1(a) and (b), was initially used for all compounds. To find the final geometries of NaTMO2 compounds, the lattice parameters and all internal coordinates of the primitive cell were allowed to relax to forces smaller than 0.001 eV Å−1. Furthermore, the geometry optimization was repeated with 2a × 2a × 1c, 3a × 3a × 1c and 4a × 4a × 1c supercells with symmetry restrictions turned off, to detect any possible distortion that may lower the total energy by breaking the symmetry.
m symmetry in hexagonal representation, as shown in Fig. 1(a) and (b), was initially used for all compounds. To find the final geometries of NaTMO2 compounds, the lattice parameters and all internal coordinates of the primitive cell were allowed to relax to forces smaller than 0.001 eV Å−1. Furthermore, the geometry optimization was repeated with 2a × 2a × 1c, 3a × 3a × 1c and 4a × 4a × 1c supercells with symmetry restrictions turned off, to detect any possible distortion that may lower the total energy by breaking the symmetry.
The magnetic phase stability was examined by comparing the total energies of the ferromagnetic system (EtFM) with those of competing antiferromagnetic phases. The energy of the ferromagnetic state was calculated by aligning the spin of the all TM ions in the hexagonal cell parallel. The total energy of the C-type antiferromagnetic state (EtCAFM) was calculated by aligning the spin of adjacent TM ions within the basal planes of a 2a × 1a × 1c supercell antiparallel. ΔECAFM is defined as the difference between total energies EtCAFM and EtFM the per TM ion:
| ΔECAFM = [(EtCAFM/2) − EtFM]/n | (1) |
Here, n is the total number of the TM ions in the ferromagnetic supercell which is 3 for systems without distortions but larger for distorted systems. The energy of the A-type antiferromagnetic states (EtAAFM) calculated by aligning the spin of TM ions in a 1a × 1a × 2c supercell antiparallel in alternating manner. ΔEAAFM is defined as the difference between EtAAFM and EtFM the per TM ion:
| ΔEAAFM = [(EtAAFM/2) − EtFM]/n | (2) |
Positive ΔECAFM values indicate the preference of TM ion to align ferromagnetically within a TMO2 plane (inter-plane) while positive EtAAFM indicate the preference of ferromagnetic coupling across TMO2 planes (intra-plane).
3. Results and discussions
3.1. TM spin state
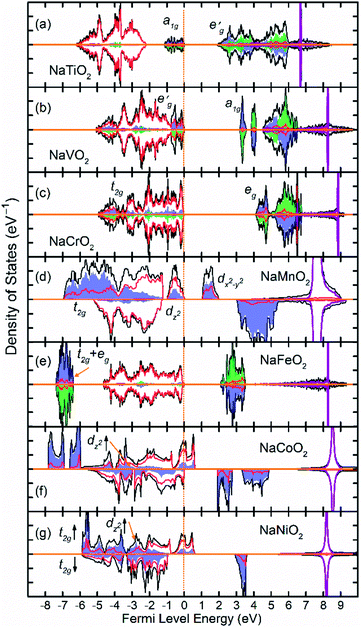
Based on the calculated spin populations presented in Table 2, the early 3d TM ions in NaTiO2, NaVO2 and NaCrO2 generally conform to the octahedral crystal field splitting t2geg. However, as we will see later, there are finer splittings among t2g states caused by symmetry considerations. Later TM ions in NaMnO2, NaFeO2 and NaCoO2 compounds stabilize in high spin configuration. We found that the total energy of the NaMnO2 compound rose by 1.306 eV/f.u. (f.u. is formula unit) when the Mn ion was set to low spin configuration (t2g4e0g). Similarly, the total energy of low spin NaFeO2 (t2g5e0g) rose by 0.889 eV/f.u. and the total energy of low spin NaCoO2 (t2g6e0g) rose by 0.157 eV/f.u. with respect to their corresponding high spin configurations. Ni ions in NaNiO2, nonetheless, are stabilized in low spin configuration as setting Ni to high spin configuration (t2g5eg2) raised the total energy by 0.777 eV/f.u. Our calculations for Ni is agreement with the experimental observation of low spin NaNiO2.24| Compound | Nominal configu-ration | Calculated unpaired d electrons | ΔECAFM (mEV) | ΔEAAFM (mEV) | Magnetic ground state | Conduction |
|---|---|---|---|---|---|---|
| NaTiO2 | t2g1e0g | 0.897 | −395.365 | −0.228 | GAFM | Insulator |
| NaVO2 | t2g2e0g | 1.879 | −18.163 | −3.204 | GAFM | Insulator |
| NaCrO2 | t2g3e0g | 2.925 | −4.341 | −0.323 | GAFM | Insulator |
| NaMnO2 | t2g3eg1 | 3.922 | 51.657 | 0.197 | FM | Insulator |
| NaFeO2 | t2g3eg2 | 4.277 | −4.738 | −1.894 | GAFM | Insulator |
| NaCoO2 | t2g4eg2 | 3.149 | 152.238 | −2.410 | AAFM | Half metallic |
| NaNiO2 | t2g6eg1 | 1.378 | 24.564 | 0.826 | FM | Half metallic |
| NaZrO2 | t2g1e0g | 0.000 | — | — | Nonmagnetic | Metallic |
| NaNbO2 | t2g2e0g | 1.110, 0.350 | 14.468 | −1.240 | AAFM | Metallic |
| NaMoO2 | t2g3e0g | 2.567 | −117.673 | −2.272 | GAFM | Insulator |
| NaTcO2 | t2g4e0g | 1.721 | 65.860 | 2.565 | FM | Half metallic |
| NaRuO2 | t2g5e0g | 0.858 | −13.462 | −5.030 | GAFM | Insulator |
| NaRhO2 | t2g6e0g | 0.000 | — | — | Nonmagnetic | Insulator |
| NaPdO2 | t2g6eg2 | 1.339 | 11.315 | −2.750 | AAFM | Insulator |
| t2g6eg1 | 0.621 | |||||
| t2g6e0g | 0.015 |
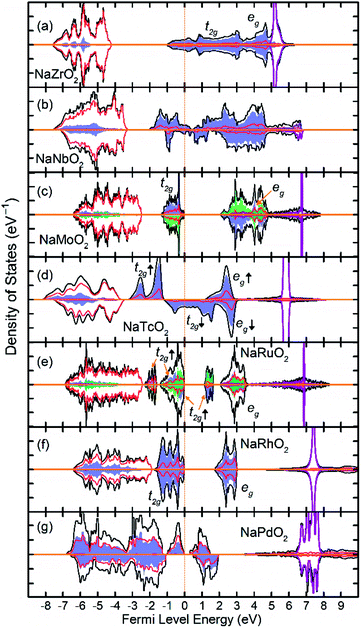
Unlike their 3d counterparts, early 4d TM ions in NaZrO2 and NaNbO2, deviate from t2geg splitting as Zr bears no magnetic moment and Nb adopts two distinct magnetic moments both significantly smaller than the anticipated t2g2e0g. NaZrO2 in which Zr set to t2g1e0g was 0.317 eV/f.u. higher in energy than non-magnetic NaZrO2 while NaNbO2 with Nb fixed to t2g2e0g configuration was 0.649 eV/f.u. higher than the presented ground state. Moreover, contrarily to the 3d TM ions, the later 4d TM ions in NaTMO2 stabilized in low spin configuration. The total energy of NaTcO2 rose by 1.086 eV/f.u. when Tc was set to high spin configuration (t2g2eg2). Similarly, the high spin NaRuO2 (t2g3eg2) and NaRhO2 (t2g4eg2) were higher in energy than their low spin counterpart by 1.937 eV/f.u. and 4.642 eV/f.u. respectively.
3.2. Electronic structures
Fig. 2 shows the total and partial density of states (DOS) of 3d TM containing NaTMO2 compounds. In the NaTiO2, rhombohedral distortion in the TiO6 octahedra splits the t2g orbitals of the spin-up channel into lower single fold a1g orbital which is occupied by Ti3+’s lone 3d electron and higher empty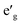 orbitals. Furthermore, a1g orbital is detached from the lower O 2p states and creates a pseudo-gap within the valence band. Consequently, the complete separation of Ti 3d states from O 2p states implies that Ti–O bond is highly ionic. In NaVO2, the rhombohedral splitting is still dominant. However, contrary to the Ti case, the occupied
orbitals. Furthermore, a1g orbital is detached from the lower O 2p states and creates a pseudo-gap within the valence band. Consequently, the complete separation of Ti 3d states from O 2p states implies that Ti–O bond is highly ionic. In NaVO2, the rhombohedral splitting is still dominant. However, contrary to the Ti case, the occupied 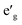 orbitals have lower energy than the empty a1g orbital. Moreover, since the gap between
orbitals have lower energy than the empty a1g orbital. Moreover, since the gap between 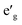 states and O 2p states is now closed, there is a greater hybridization between
states and O 2p states is now closed, there is a greater hybridization between 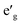 and O 2p states which reduces the ionicity of the V–O bond compared to that of Ti–O bond. In NaCrO2, through the merging of the
and O 2p states which reduces the ionicity of the V–O bond compared to that of Ti–O bond. In NaCrO2, through the merging of the 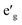 and a1g states in the spin-up channel, the band structure resembles conventional octahedral splitting where the spin-up t2g states in the valence band are all occupied while the empty eg states constitute the bottom of the conduction band. The DOS of NaMnO2 corresponds to the elongated Jahn–Teller distortion. The lower region of the valence band (∼−7 eV < E < ∼−4 eV) is occupied by dxz and dyz states while the middle part (∼−4 eV < E < ∼−1.2) is occupied by dxy states. The top of valence band is nevertheless occupied by dz2 states. As inferred from the DOS, the proximity of dxy and dz2 favors the high spin configuration for the Mn ions.
and a1g states in the spin-up channel, the band structure resembles conventional octahedral splitting where the spin-up t2g states in the valence band are all occupied while the empty eg states constitute the bottom of the conduction band. The DOS of NaMnO2 corresponds to the elongated Jahn–Teller distortion. The lower region of the valence band (∼−7 eV < E < ∼−4 eV) is occupied by dxz and dyz states while the middle part (∼−4 eV < E < ∼−1.2) is occupied by dxy states. The top of valence band is nevertheless occupied by dz2 states. As inferred from the DOS, the proximity of dxy and dz2 favors the high spin configuration for the Mn ions.
The DOS of the half-filled Fe 3d shell (t32ge2g) in NaFeO2 exhibits a different arrangement when compared to earlier compounds. Here, due to strong electron–electron repulsion between the half-filled Fe 3d5 states and O 2p states, all of the occupied Fe 3d states are shifted downwards below O 2p states. The proximity of the t32g and e2g states in the spin-up channel to one another favors the high spin configuration for Fe ions as the spin-down t2g states are ∼11 eV higher in energy than spin-up eg states. In NaCoO2, the t2g states of the spin-up channel, although mainly concentrate at the bottom of the valence band, still stretch over the entire valence band width and strongly hybridize with O 2p states. Furthermore, the tale of the spin-up t2g states crosses the Fermi level creating half metallic conduction. Similarly, in NaNiO2, the spin-up t2g states stretch over the valence band and cross the Fermi level while the spin-down t2g states and dz2 states remain confined within the middle of the valence band without crossing the Fermi level.
Fig. 3 show the total and partial DOS in 4d TM containing compounds. NaZrO2 exhibits strong metallic character as its Fermi level intercepts the Zr 4d states in the conduction band. Metallicity in NaZrO2 is facilitated by a metallic Zr–Zr bond which is caused by extraordinarily large Zr3+ ionic radius of ∼0.89 Å (ref. 25) and the Zr–Zr distance of 3.21 Å which is comparable to that in Zr metal. The metallic character of NaZrO2 explains the lack of magnetic moment as there is no significant hybridization between Zr with O. NaNbO2 also exhibits metallic conduction as the Fermi level crosses through the 4d states in the conduction band. However, as we will discuss later, due to puckering distortion, there are two distinct Nb species in this compound each with different levels of metallicity. The band structure of the NaMoO2 shows a conventional octahedral distortion where the half-filed t2g states constitute the top of the valence band while the empty eg states are separated by ∼1 eV above the Fermi level. In NaTcO2, NaRuO2 and NaRhO2 compounds the spin-down channel of the t2g states is progressively filled as expected for the TM ions in low spin configuration. As will be discussed in detail in the next section, Pd in NaPdO2 undergoes charge disproportionation and form Pd2+, Pd3+, Pd4+ species. The t2g states of all Pd species occupy the lower part of the conduction band while the filled eg occupy the top of the valence band.
3.3. Octahedral distortions
The geometry optimization conducted with larger supercells revealed that NaMnO2, NaNbO2 and NaPdO2 compounds, each to a different extent, exhibits additional distortions in their TMO6 octahedra. In NaMnO2, as indicated by purple arrows in Fig. 4, two out of six Mn–O bonds in all MnO6 octahedra are elongated causing a deviation from perfect R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. This distortion is similar to the Jahn–Teller distortion depicted in Fig. 1(e). The long Mn–O bond is 2.26 Å while the short Mn–O bonds is 2.01 Å implying a 12.4% elongation. We found that perfectly R
m symmetry. This distortion is similar to the Jahn–Teller distortion depicted in Fig. 1(e). The long Mn–O bond is 2.26 Å while the short Mn–O bonds is 2.01 Å implying a 12.4% elongation. We found that perfectly R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetric NaMnO2 primitive cell with no elongation had a total energy 0.763 eV/f.u. higher than the distorted compound indicating that this distortion leads to significant stabilization.
m symmetric NaMnO2 primitive cell with no elongation had a total energy 0.763 eV/f.u. higher than the distorted compound indicating that this distortion leads to significant stabilization.
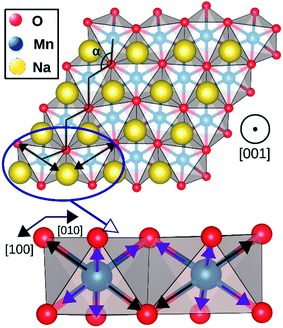 | ||
| Fig. 4 Jahn–Teller distortion in NaMnO2 system. The elongated bonds are marked with black arrows while the shorter bonds are marked with purple arrows. | ||
NaNbO2 showed puckering distortion [Fig. 1(f)] in half of its NbO6 octahedra. As marked by blue arrows in Fig. 5(a), NbO6 octahedra on every second row in [100] direction are alternately puckered to the left and the right along [010] direction while the octahedra on the adjacent row only had rhombohedral distortion. In the puckered NbO6 octahedra, the short Nb–O bond was 2.18 Å while the long Nb–O bond was 2.23 Å indicating a 2.2% puckering distortion in bond lengths. The bond length in unpuckered NbO6 octahedra had a median value of 2.22 Å. The puckering altered the electronic structure of the NaNbO2 compound as ions in the puckered and unpuckered octahedra had distinct spin populations of 1.051e and 0.350e respectively. According to Fig. 5(b), Nb ions in the puckered octahedra has a significantly larger spin-up population (marked with red arrow) and smaller spin-down population (marked with blue arrow) compared to the Nb ions in unpuckered octahedra. To examine the stability induced by this distortion, we once set all Nb ions to low magnetization equal to that in the unpuckered octahedra and once again to high magnetization equal to that in the puckered octahedra and recalculated the total energy. The earlier setting raised the total energy of NaNbO2 compound by 0.230 eV/f.u. while the latter setting raised the total energy by 0.649 eV/f.u. demonstrating the stabilizing effect of puckering distortion. Given that Nb's total electronic population does not significantly depend on the puckering of NbO6 octahedra, we infer that this relatively minor distortion does not cause charge disproportionation but rather only alters the magnetization of Nb ions.
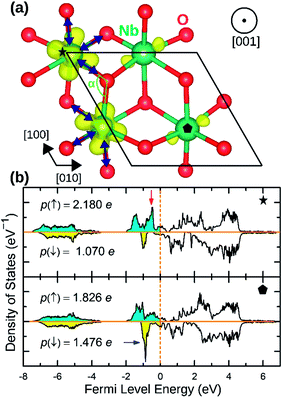
The distortion in PdO6 octahedra in NbPdO2 were accompanied with charge disproportionation among Pd ions. As shown in Fig. 6(a), within a Pd containing plane perpendicular to the [001] direction in the 2a × 2a × 1c supercell, two Pd3+ ions transform into a pair of Pd4+ and Pd2+ along [110] direction while the other two Pd3+ ions along [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] direction remain unchanged. The Pd2+O6 and Pd4+O6 octahedra had perfect octahedral symmetry however each with a different Pd–O bond length. Pd2+–O bond was 2.27 Å long while Pd4+–O bond was 2.07 Å long. The two Pd3+O6 octahedra, on the other hand, showed elongated Jahn–Teller distortion with long bonds of 2.32 Å and short bonds of 2.09 Å accounting for an elongation of 11.0%. The stability of this distortion was verified by the fact that the NaPdO2 in which all Pd ions were fixed to +3 oxidation state had a total energy 0.381 eV/f.u. higher than the presented ground state. Furthermore, this distortion pattern and the accompanying charge disproportionation prevailed in larger 4a × 4a × 1c supercell and persisted under different Ueff values.
0] direction remain unchanged. The Pd2+O6 and Pd4+O6 octahedra had perfect octahedral symmetry however each with a different Pd–O bond length. Pd2+–O bond was 2.27 Å long while Pd4+–O bond was 2.07 Å long. The two Pd3+O6 octahedra, on the other hand, showed elongated Jahn–Teller distortion with long bonds of 2.32 Å and short bonds of 2.09 Å accounting for an elongation of 11.0%. The stability of this distortion was verified by the fact that the NaPdO2 in which all Pd ions were fixed to +3 oxidation state had a total energy 0.381 eV/f.u. higher than the presented ground state. Furthermore, this distortion pattern and the accompanying charge disproportionation prevailed in larger 4a × 4a × 1c supercell and persisted under different Ueff values.
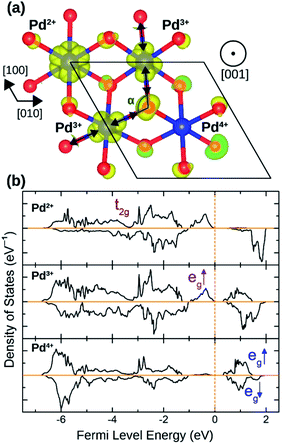 | ||
| Fig. 6 (a) The spin density isosurface in NaPdO2 drown at 0.025 e Å−2 demonstrating charge disproportionation. (b) The site-projected 4d states for Pd2+, Pd3+ and Pd4+ species. | ||
Fig. 6(b) shows how Pd eg states are occupied as charge disproportionation occurs. For Pd2+, eg's spin-up states are all occupied while the empty spin-down states are entirely located ∼1 eV above the Fermi level. For Pd3+, the spin-up peak decreases (marked with a red arrow) while an empty spin-up eg peak appears above the Fermi level. Finally, for Pd4+, all eg states are now located above the Fermi level.
3.4. Magnetic coupling
The magnetic ground state of a compound can be predicted by comparing the total energies corresponding to different spin alignments among the TM ions that is ΔECAFM and ΔEAAFM.26 If different spin alignments result in the same energy, the compound is paramagnetic.27 Furthermore, ΔECAFM and ΔEAAFM are functions of the magnetic exchange integrals (J) which determine the Curie and Néel temperatures (TC and TN) in compounds with long range magnetic ordering.28 According to the mean field approximation these critical temperatures depends linearly on the J.29 For instance, room temperature ferromagnetism requires positive ΔECAFM and ΔEAAFM values of ∼12 meV.30As presented in Table 2, NaMnO2, NaCoO2, NaNiO2, NaNbO2 NaTcO2 and NaPdO2 have positive ΔECAFM values indicating inter-plane ferromagnetism which is defined as the ferromagnetic coupling among TM ions within the basal TMO2 planes. This ferromagnetic coupling can be attributed to one of two distinct mechanisms: the kinetic p–d exchange interaction and the superexchange interaction. The density of states in Fig. 2(f)–(g) and Fig. 3(d) reveals a special p–d hybridization in NaCoO2, NaNiO2 and NaTcO2 compounds. Because of this hybridization, the spin majority p states are shifted to higher energies, while the spin minority p states are shifted to lower energies. This hybridization scheme therefore creates spin polarized p states which mediate the ferromagnetic coupling.29 In NaMnO2, NaNbO2 and NaPdO2, on the other hand, positive ΔECAFM values are caused by ferromagnetic superexchange. The prerequisite for ferromagnetic superexchange is a ∼90° TM–O–TM angle which stabilizes the ferromagnetic coupling through π TM–O bonds in TM–O–TM trimer.31 The octahedral distortions in these compounds orient the TM–O–TM angles in these compounds to ∼90°. Under perfect R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, as shown in Fig. 1(c), the TM–O–TM angle is determined by O's fractional coordinates and alternates between the supplementary angles η and θ [defined in Fig. 1(c) and (d)] preventing the stabilization of the ferromagnetic phase.9,11,32,33 If a distortion, however, breaks the symmetry and brings the TM–O–TM angle closer to 90°, ferromagnetic superexchange can prevail. One should note that, as indicated in Table 1, the octahedral distortions in these compounds basically bring the O–TM–O angle closer to 90°. However, since these compounds do not have any octahedral tilting, the TM–O–TM angle, at least in certain planes, also approaches 90° due to the similar distortion in neighbouring TMO6 octahedra. Those TM–O–TM angles assisting the ferromagnetic superexchange are marked α in Fig. 4–6. α is 91.67° in NaMnO2, 89.86° in NaNbO2 and 88.48° in NaPdO2. Contrary to our results, earlier DFT calculation of the NaMnO2 compound using a small supercell restricted to C2/m symmetry, predicted weak frustrated antiferromagnetic ground state.34 This discrepancy shows the importance of taking into account the octahedral distortions that stabilizes the ferromagnetic ground state. Inferred from ΔECAFM values, the kinetic p–d exchange interaction seems to be generally stronger than the ferromagnetic superexchange interaction.
m symmetry, as shown in Fig. 1(c), the TM–O–TM angle is determined by O's fractional coordinates and alternates between the supplementary angles η and θ [defined in Fig. 1(c) and (d)] preventing the stabilization of the ferromagnetic phase.9,11,32,33 If a distortion, however, breaks the symmetry and brings the TM–O–TM angle closer to 90°, ferromagnetic superexchange can prevail. One should note that, as indicated in Table 1, the octahedral distortions in these compounds basically bring the O–TM–O angle closer to 90°. However, since these compounds do not have any octahedral tilting, the TM–O–TM angle, at least in certain planes, also approaches 90° due to the similar distortion in neighbouring TMO6 octahedra. Those TM–O–TM angles assisting the ferromagnetic superexchange are marked α in Fig. 4–6. α is 91.67° in NaMnO2, 89.86° in NaNbO2 and 88.48° in NaPdO2. Contrary to our results, earlier DFT calculation of the NaMnO2 compound using a small supercell restricted to C2/m symmetry, predicted weak frustrated antiferromagnetic ground state.34 This discrepancy shows the importance of taking into account the octahedral distortions that stabilizes the ferromagnetic ground state. Inferred from ΔECAFM values, the kinetic p–d exchange interaction seems to be generally stronger than the ferromagnetic superexchange interaction.
The magnetic coupling across the TMO2 planes or intra-plane coupling, in principle, can be mediated a by second nearest neighbour superexchange interaction through TM–O–Na–O–TM chain via by O's p orbitals and Na sp2 hybrid orbitals.35 Because of anisotropy in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m crystal structure which prevents the hybridization of TM d states with the p states of adjacent TMO2 layers, p–d kinetic exchange is not expected to result in significant intra-plane coupling. Among all compounds only NaMnO2, NaNiO2 and NaTcO2 had small positive ΔEAAFM values indicating weak ferromagnetic intra-plane coupling resulting in TC values lower than ∼50 K. This prediction, particularly for the NaNiO2 compound, is agreement with the earlier observation that measured a TC of ∼20 K.7 In the case of NaNbO2, NaPdO2 and NaCoO2 compounds, the negative ΔEAAFM values along with positive ΔECAFM values predict A-type antiferromagnetic ground state. For the rest of compounds for which both ΔEAAFM and ΔECAFM are negative, G-type antiferromagnetic ground state prevails. Such antiferromagnetism has been observed in NaCrO2 with TN = 40–50 K,36,37 NaVO2 (ref. 11 and 38) and NaTiO2 (ref. 39).
m crystal structure which prevents the hybridization of TM d states with the p states of adjacent TMO2 layers, p–d kinetic exchange is not expected to result in significant intra-plane coupling. Among all compounds only NaMnO2, NaNiO2 and NaTcO2 had small positive ΔEAAFM values indicating weak ferromagnetic intra-plane coupling resulting in TC values lower than ∼50 K. This prediction, particularly for the NaNiO2 compound, is agreement with the earlier observation that measured a TC of ∼20 K.7 In the case of NaNbO2, NaPdO2 and NaCoO2 compounds, the negative ΔEAAFM values along with positive ΔECAFM values predict A-type antiferromagnetic ground state. For the rest of compounds for which both ΔEAAFM and ΔECAFM are negative, G-type antiferromagnetic ground state prevails. Such antiferromagnetism has been observed in NaCrO2 with TN = 40–50 K,36,37 NaVO2 (ref. 11 and 38) and NaTiO2 (ref. 39).
Last, note that relativistic spin–orbit interaction can play a significant role in determining the structural and magnetic properties of isolated TM octahedral complexes.40–43 However, in the context of bulk NaTMO2 compounds that have been studied here, the role of spin–orbit interaction on the calculated ΔECAFM and ΔEAAFM values is negligibly small. Spin–orbit interaction constant is proportional to the mass of the interacting ions and can be significant in 5d TM oxides such as iridates.44 However, experimental studies have shown that the magnitude of the spin–orbit interaction in 3d and 4d TM oxides such as cobaltates45 and rhoates46 is generally small. To verify this notion, we recalculated the ΔECAFM and ΔEAAFM for NaPdO2 with the inclusion of the spin–orbit calculation and obtained ΔECAFM = 11.492 meV and ΔEAAFM = −2.841 meV. These values differ only by ∼0.1 meV from the values of Table 2 which have been obtained without including spin–orbit interaction. The role of spin–orbit interaction is expected to be even smaller for the rest of the compounds, especially for 3d NaTMO2, as their molecular mass is considerably smaller than that of NaPdO2.
4. Conclusions
We demonstrated that the rhombohedral distortion inherent to the 3![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) m symmetry stabilizes G-type antiferromagnetism in NaTiO2, NaVO2, NaCrO2, NaFeO2, NaMoO2 and NaRuO2 compounds. Inter-plane ferromagnetism however can be stabilized if the 3
m symmetry stabilizes G-type antiferromagnetism in NaTiO2, NaVO2, NaCrO2, NaFeO2, NaMoO2 and NaRuO2 compounds. Inter-plane ferromagnetism however can be stabilized if the 3![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) m symmetry breaks due to additional octahedral distortions which is the case for NaMnO2, NaNbO2 and NbPdO2. Here, because of favorable orbital orientation, the superexchange interaction stabilizes ferromagnetism instead of antiferromagnetism among the TM ions of the same TMO2 plane. Additionally, strong p–d hybridization, as in NaCoO2, NaNiO2 and NaTcO2 can also result in inter-plane ferromagnetism. In this case, due to its strength, the kinetic p–d exchange mechanism overcomes the underlying inter-plane antiferromagnetism. The intra-plane ferromagnetic coupling is mediated by a weak second neighbor coupling which prevails only in NaMnO2, NaTcO2 and NaNiO2 giving rise to bulk ferromagnetism with low TC.
m symmetry breaks due to additional octahedral distortions which is the case for NaMnO2, NaNbO2 and NbPdO2. Here, because of favorable orbital orientation, the superexchange interaction stabilizes ferromagnetism instead of antiferromagnetism among the TM ions of the same TMO2 plane. Additionally, strong p–d hybridization, as in NaCoO2, NaNiO2 and NaTcO2 can also result in inter-plane ferromagnetism. In this case, due to its strength, the kinetic p–d exchange mechanism overcomes the underlying inter-plane antiferromagnetism. The intra-plane ferromagnetic coupling is mediated by a weak second neighbor coupling which prevails only in NaMnO2, NaTcO2 and NaNiO2 giving rise to bulk ferromagnetism with low TC.
The weak intra-plane coupling appears to be a general feature of O3 compounds. This is in contrast to the P2 structures in which the magnitudes of inter-plane and intra-plane coupling are of the same order.35 This is probably because this interaction strongly depends on Na's coordination environment. This line of enquiry warrants further research.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported in part by MEXT as a social and scientific priority issue: creation of new functional devices and high-performance materials to support next-generation industries to be tackled by using post-K computer. Computational resources were provided by Kyushu University's high performance computing center and supercomputers at the Institute for Solid State Physics at the University of Tokyo and at the Center for Computational Sciences at University of Tsukuba.References
- M. V. Mostovoy and D. I. Khomskii, Phys. Rev. Lett., 2002, 89, 227203 CrossRef CAS PubMed.
- O. I. Velikokhatnyi, C.-C. Chang and P. N. Kumta, J. Electrochem. Soc., 2003, 150, A1262–A1266 CrossRef CAS.
- L. Viciu, J. W. G. Bos, H. W. Zandbergen, Q. Huang, M. L. Foo, S. Ishiwata, A. P. Ramirez, M. Lee, N. P. Ong and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 174104 CrossRef.
- S. Walia, S. Balendhran, H. Nili, S. Zhuiykov, G. Rosengarten, Q. H. Wang, M. Bhaskaran, S. Sriram, M. S. Strano and K. Kalantar-zadeh, Prog. Mater. Sci., 2013, 58, 1443–1489 CrossRef CAS.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS.
- E. Chappel, M. D. Nunez-Regueiro, F. Dupont, G. Chouteau, C. Darie and A. Sulpice, Eur. Phys. J. B, 2000, 17, 609–614 CrossRef CAS.
- S. d. Brion, M. Bonda, C. Darie, P. Bordet and I. Sheikin, J. Phys.: Condens. Matter, 2010, 22, 126001 CrossRef PubMed.
- T. A. Kaplan and N. Menyuk, Philos. Mag., 2007, 87, 3711–3785 CrossRef CAS.
- N. Terada, Y. Ikedo, H. Sato, D. D. Khalyavin, P. Manuel, A. Miyake, A. Matsuo, M. Tokunaga and K. Kindo, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 035128 CrossRef.
- D. Wu, X. Li, B. Xu, N. Twu, L. Liu and G. Ceder, Energy Environ. Sci., 2015, 8, 195–202 CAS.
- T. Jia, G. Zhang, Z. Zeng and H. Q. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045103 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- P. Gopal and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094418 CrossRef.
- Y.-N. Zhou, J.-J. Ding, K.-W. Nam, X. Yu, S.-M. Bak, E. Hu, J. Liu, J. Bai, H. Li, Z.-W. Fu and X.-Q. Yang, J. Mater. Chem. A, 2013, 1, 11130–11134 CAS.
- K. Kubota, T. Asari, H. Yoshida, N. Yaabuuchi, H. Shiiba, M. Nakayama and S. Komaba, Adv. Funct. Mater., 2016, 26, 6047–6059 CrossRef CAS.
- K. M. Mogare, K. Friese, W. Klein and M. Jansen, Z. Anorg. Allg. Chem., 2004, 630, 547–552 CrossRef CAS.
- K. Hobbie and R. Hoppe, Z. Anorg. Allg. Chem., 1988, 565, 106–110 CrossRef CAS.
- E. Chappel, M. D. Núñez-Regueiro, G. Chouteau, O. Isnard and C. Darie, Eur. Phys. J. B, 2000, 17, 615–622 CrossRef CAS.
- S. Jeon, J. Ryu, H.-G. Shin, J. Lee and H. Lee, Mater. Charact., 2017, 131, 374–379 CrossRef CAS.
- K. Sato, L. Bergqvist, J. Kudrnovský, P. H. Dederichs, O. Eriksson, I. Turek, B. Sanyal, G. Bouzerar, H. Katayama-Yoshida, V. A. Dinh, T. Fukushima, H. Kizaki and R. Zeller, Rev. Mod. Phys., 2010, 82, 1633–1690 CrossRef CAS.
- M. H. N. Assadi and H. Katayama-Yoshida, Funct. Mater. Lett., 2015, 08, 1540016 CrossRef CAS.
- J. Lee, PhD thesis, The University of Texas at Austin, 2010.
- B. Belhadji, L. Bergqvist, R. Zeller, P. H. Dederichs, K. Sato and H. Katayama-Yoshida, J. Phys.: Condens. Matter, 2007, 19, 436227 CrossRef.
- P. W. Anderson, in Solid State Physics, ed. F. Seitz and D. Turnbull, Academic Press, 1963, vol. 14, pp. 99–214 Search PubMed.
- J. M. D. Coey, M. Venkatesan and H. Xu, in Functional Metal Oxides, Wiley-VCH Verlag GmbH & Co. KGaA, 2013, pp. 1–49, DOI:10.1002/9783527654864.ch1.
- K. Takada, H. Sakurai, E. Takayama-Muromachi, F. Izumi, R. A. Dilanian and T. Sasaki, Nature, 2003, 422, 53–55 CrossRef CAS PubMed.
- S. P. Bayrakci, I. Mirebeau, P. Bourges, Y. Sidis, M. Enderle, J. Mesot, D. P. Chen, C. T. Lin and B. Keimer, Phys. Rev. Lett., 2005, 94, 157205 CrossRef CAS PubMed.
- G. R. Zhang, L. J. Zou, Z. Zeng and H. Q. Lin, J. Appl. Phys., 2009, 105, 07E512 CrossRef.
- M. D. Johannes, I. I. Mazin and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 214410 CrossRef.
- D. Hsieh, D. Qian, R. F. Berger, R. J. Cava, J. W. Lynn, Q. Huang and M. Z. Hasan, Phys. B, 2008, 403, 1341–1343 CrossRef CAS.
- A. Olariu, P. Mendels, F. Bert, B. G. Ueland, P. Schiffer, R. F. Berger and R. J. Cava, Phys. Rev. Lett., 2006, 97, 167203 CrossRef CAS PubMed.
- T. M. McQueen, P. W. Stephens, Q. Huang, T. Klimczuk, F. Ronning and R. J. Cava, Phys. Rev. Lett., 2008, 101, 166402 CrossRef CAS PubMed.
- I. Yamada, K. Ubukoshi and K. Hirakawa, J. Phys. Soc. Jpn., 1985, 54, 3571–3576 CrossRef CAS.
- J. David and A. Restrepo, Phys. Rev. A, 2007, 76, 052511 CrossRef.
- J. David, P. Fuentealba and A. Restrepo, Chem. Phys. Lett., 2008, 457, 42–44 CrossRef CAS.
- A. Pérez-Villa, J. David, P. Fuentealba and A. Restrepo, Chem. Phys. Lett., 2011, 507, 57–62 CrossRef.
- J. David, D. Guerra and A. Restrepo, Inorg. Chem., 2011, 50, 1480–1483 CrossRef CAS PubMed.
- Y. Singh, S. Manni, J. Reuther, T. Berlijn, R. Thomale, W. Ku, S. Trebst and P. Gegenwart, Phys. Rev. Lett., 2012, 108, 127203 CrossRef PubMed.
- Y. Yanase, M. Mochizuki and M. Ogata, J. Phys. Soc. Jpn., 2005, 74, 2568–2578 CrossRef CAS.
- I. I. Mazin, S. Manni, K. Foyevtsova, H. O. Jeschke, P. Gegenwart and R. Valentí, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035115 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |