Open Access Article
Open Access ArticleTune the chemical activity of graphene via the transition metal substrate†
Yuan
Ma
,
Lei
Gao
 *,
Yu
Yan
,
Yanjing
Su
and
Lijie
Qiao
*,
Yu
Yan
,
Yanjing
Su
and
Lijie
Qiao
Corrosion and Protection Center, Key Laboratory for Environmental Fracture (MOE), University of Science and Technology Beijing, Beijing 100083, China. E-mail: gaolei@ustb.edu.cn
First published on 27th March 2018
Abstract
To achieve the chemical modification of graphene efficiently is desirable and essential to promote the technological applications of graphene. In this study, the density functional theory (DFT) calculations have been carried out to investigate the hydrogenation and fluorination activities of graphene on Ni(111), Re(0001) and Pt(111). The calculation results indicate that the chemical activity of graphene is related to both the characteristics of the graphene–substrate interfacial interaction and the local atomic stacking, namely the chemical activity of graphene is position-dependent. The strong covalently interacting substrates Ni(111) and Re(0001) will remarkably enhance the chemical activity of graphene, while the modulation effects from the weak van der Waals interacting substrate Pt(111) is trivial. Electronic structure studies reveal that the intensive graphene–substrate interfacial interaction can gain in chemical energy to offset the strain energy caused by the C atom sp2–sp3 transition and stabilize the absorbing state.
1. Introduction
Graphene with a honeycomb lattice has attracted intensive interest, mostly due to its extraordinary physical, chemical, mechanical, and electrical properties that enable a wide range of applications.1,2 However, the graphene still suffers from several shortcomings,3e.g., the giant delocalized π electron orbitals lead the graphene to be chemically inert and the zero band gap limits its applications in functional nanoscale devices.To achieve the chemical modification of graphene efficiently is desirable and essential to promote the technological applications of graphene. Recently, many functionalization methods such as chemical bonding, functional groups and free radicals on graphene have been utilized to improve the surface activity of graphene, which will render it with more novel properties through modifying the chemical, structural and electronic properties of graphene.3–7 One simple and effective method is to adsorb H or F atoms on graphene, which changes the hybridization of C atoms from sp2 into sp3 to open the band gap of graphene.8–10 Previous studies demonstrated that a negative perpendicular electric field can act as a catalyst to facilitate the molecular H2 dissociative adsorption on graphene.11 The layer-dependent chemical activity of n-layer graphene on SiO2/Si substrate has been reported. The Raman spectrum indicated that monolayer graphene was much more feasible to being fluorinated and hydrogenated than multilayer graphene, which was attributed to the lack of π-stacking due to the out-of-plane deformation caused by the substrate.12–14
In addition, graphene epitaxially grown on transition metal substrate usually forms various superstructures according to the interfacial interaction and lattice constants mismatch between the graphene and its supporting substrate. Previous studies illustrated that the graphene on Ni(111) will form a commensurate superstructure with fcc stacking,15 while for the cases of graphene on other transition metal substrates, e.g., Pt(111), Ir(111), Au(111), Re(0001), and Ru(0001) et al., the moiré superstructures will be formed.16 As a result, the periodically geometrical corrugation will be introduced into the graphene, and the chemically inert delocalized π electron orbitals will be broken. The distributions of fluorinated sites on graphene/Ge(111) with the moiré superstructure seems to be slightly more regular than that without the moiré superstructure.17 Whether we can tune the chemical activity of graphene via the modulation from the transition metal substrate is still unknown. Meanwhile, if the chemical activity of graphene could be tuned by the supporting substrate, the underlying mechanism needs to be clarified.
In this study, the density functional theory calculations have been performed to investigate the hydrogenation and fluorination activities of graphene on Ni(111), Re(0001) and Pt(111). The calculation results indicate that the strong covalently interacting substrates Ni(111) and Re(0001) will remarkably enhance the chemical activity of graphene, while the modulation effects from the weak van der Waals interacting substrate Pt(111) on the graphene is trivial. Electronic structure studies reveal that the chemical activity enhancement of graphene on transition metal substrate arises from the intensive graphene–substrate interfacial interaction, as it can gain in chemical energy to offset the strain energy caused by the C atom sp2–sp3 transition and stabilize the adsorbing state. Meanwhile the chemical activity of graphene on its supporting substrate is position-dependent. Thus, the chemical activity of graphene is related to both the characteristic of the graphene–substrate interfacial interaction and the local atomic stacking.
2. Calculation methods
The DFT calculations were performed in the Vienna ab initio Simulation Package (VASP).18 The projector-augmented-wave (PAW) method was utilized to model the core electrons.19 A nonlocal optB86b-vdW exchange–correlation functional20,21 was used to describe the dispersion interaction (van der Waals forces) approximately, as it has been demonstrated to be among the most accurate vdW functions.22 The plane-wave basis kinetic energy cut off was set to 400 eV.The calculation supercells were selected as the 4 × 4 graphene unit cells siting on the 4 × 4 unit cells of Ni(111) (9.96 Å × 9.96 Å × 30 Å) according to the relaxed Ni lattice constant (a = 3.521 Å), and 8 × 8 graphene unit cells siting on 7 × 7 unit cells of Re(0001) (19.37 Å × 19.37 Å × 30 Å) and Pt(111) (19.59 Å × 19.59 Å × 30 Å) according to the relaxed Re lattice constants (a = 2.767 Å, c = 4.466 Å) and Pt lattice constant (a = 3.958 Å).23–25 The relaxed graphene lattice constant was 2.464 Å. In each supercell, it contained three layers of substrate and monolayer graphene. During the geometrical relaxations, only the graphene and the top layer of transition metal substrate were allowed to relax until the forces on all the relaxed atoms were less than 0.02 eV Å−1. All calculations for the Ni(111) were carried out as spin-polarized.
3. Results and discussion
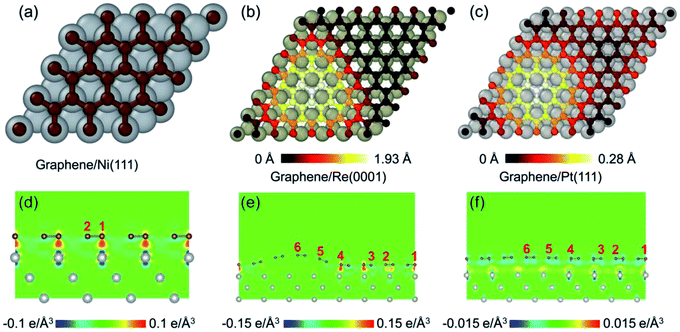
Fig. 1 illustrates the morphologies of graphene on the transition metal substrates Ni(111), Re(0001), and Pt(111) after the geometrical optimizations. The graphene on Ni(111) shown in Fig. 1a remains flatten as the commensurate stacking between the graphene and Ni(111). With respect to the graphene on Re(0001) and Pt(111), the lattice mismatch leads to the formation of moiré superstructure, and the geometrical corrugation with a moiré scale periodicity can be observed in Fig. 1b and c. Then the interfacial charge transfer distributions between the graphene and transition metal substrates Ni(111), Re(0001), and Pt(111) are shown in Fig. 1d–f respectively. The results indicate that the interfacial interaction between the graphene and Ni(111) or Re(0001) is covalent, which is much stronger than the van der Waals interfacial interaction between graphene and Pt(111).15,23–25 Due to the strong interfacial interaction, a much more obvious morphological corrugation of graphene on Re(0001) is formed as shown in Fig. 1e.To investigate the hydrogenation and fluorination activities of graphene on the transition metal substrate, two distinct adsorbing sites were selected in the graphene/Ni(111) superstructure as shown in Fig. 1d. With respect to moiré superstructures of graphene/Re(0001) and graphene/Pt(111), six representative adsorbing sites ranging from the hump to the flat region were selected as shown in Fig. 1e and f.
Then the chemical activities were estimated by the calculations of the Gibbs free energies of adsorbing H or F atom at the selected sites. The Gibbs free energies of the adsorption of H or F atom were obtained by eqn (1).26
| ΔGX = ΔEX + ΔEZPE − TΔSX | (1) |
Here, we set T = 0 K and did not consider the effect of temperature, then the eqn (1) was simplified as eqn (2).
| ΔGX = ΔEX + ΔEZPE | (2) |
| ΔEX = EX-substrate − Esubstrate − 1/2EX2 | (3) |
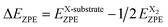 | (4) |
The Gibbs free energies of one H atom on graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) at the selected sites are presented in Fig. 2a and b, and the Gibbs free energies of one F atom on graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) at the selected sites are presented in Fig. 2c and d. Comparing with the chemical activities of monolayer graphene, we can observe that all the transition metal substrates could enhance the chemical activity of graphene. Specifically, the Ni(111) substrate could remarkably improve the hydrogenation and fluorination activity, meanwhile due to the distinction of the local atomic stacking, the chemical activity at site 2 is obviously larger than that at site 1 as shown in Fig. 2. With respect to the Re(0001) substrate, the chemical activities of graphene range from close to monolayer graphene (sites 5 and 6) to lower than site 2 of graphene/Ni(111) (site 3) as shown in Fig. 2a and c, illustrating the chemical activity of graphene is variable on the Re(0001) and related with the local atomic stacking of C atoms and Re atoms. Especially the free energy of H atom at site 3 is negative, which indicates a much enhanced reaction activity to the hydrogen atom comparing to the monolayer graphene. However, for the cases of graphene on the Pt(111), the modulation effects from the substrate on the graphene is limited, and the chemical activities are close to the monolayer graphene and differ trivially from sites 1 to 6 as shown in Fig. 2b and d.
 | ||
| Fig. 2 The hydrogenation and fluorination activities of graphene on transition metal substrates. In each substrate, the free energy of the initial state without chemical modification was set to zero as reference. (a) and (b) represent the free energies of one H atom on graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) at the selected hydrogenation sites in Fig. 1. (c) and (d) represent the free energies of one F atom on graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) at the selected fluorination sites in Fig. 1. The chemical activities of the monolayer graphene have been used as comparison. If several free energies are very close, the sites numbers are listed from high energy to low energy. | ||
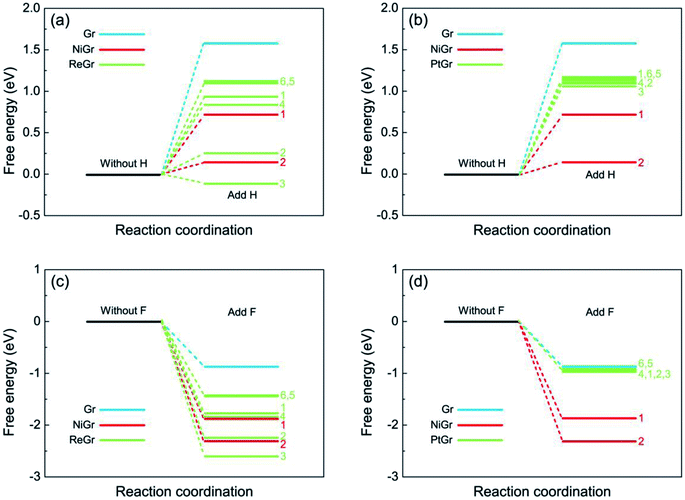
As mentioned above the chemical activities of graphene on transition metals behave as position-dependent, especially for the graphene on Re(0001), the chemical activities on graphene are quite different for the selected sites ranging from the hump to flat region. Then we firstly investigate which kinds of local geometrical atomic stacking are beneficial to enhance the chemical activity of graphene. Fig. 3 show the atomic structures of graphene–transition metal substrate after adding one H or F atom with the maximum hydrogenation and fluorination activity. The H or F atom is favorite to be adsorbed at site 2 of the Ni(111) (Fig. 3a and d), while for the Re(0001) and Pt(111), they are favorite to be adsorbed at site 3 (Fig. 3b and e, Fig. 3c and f) of the selected six sites. From Fig. 3 we can observe that the H or F atom attracts up the C atom beneath to perform the sp2–sp3 transition, meanwhile the three nearest neighbor C atoms are pressed downwards, which will dramatically increase the local strain energy in the graphene. The bond lengths and bond angles in Fig. 3 are consistent with the free energy calculations in Fig. 2, that the minimum free energy favors shorter bond length and larger bond angle. Furthermore the general characteristic of energy favorable sites for the H and F atoms on graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) is that three metal atoms in the top layer of the substrates are just beneath the three nearest neighbor C atoms of the adsorbing sites. With respect to the C atoms at the hump of the moiré superstructure (sites 5 and 6 in the graphene/Re(0001) and graphene/Pt(111)), where are free graphene like, the chemical activities are quite weak and similar to the monolayer graphene.
 | ||
| Fig. 3 The morphologies of graphene on transition metal substrates after hydrogenation and fluorination. (a)–(c) illustrate the morphologies of graphene after adding one H atom at the minimum free energy sites of graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) according to Fig. 2. The cyan atom represents the H atom. (d)–(f) illustrate the morphologies of graphene after adding one F atom at the minimum free energy sites of graphene/Ni(111), graphene/Re(0001), and graphene/Pt(111) according to Fig. 2. The green atom represents the F atom. The C–H and C–F bond lengths, and the bond angles are listed. | ||
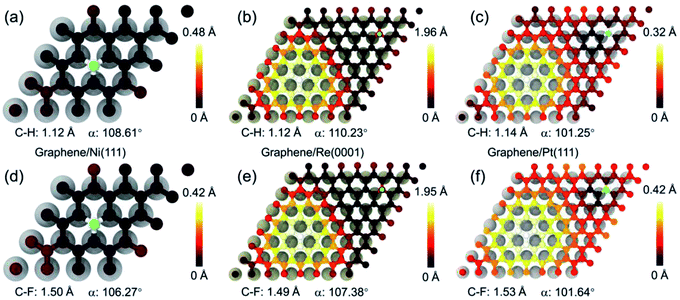
From the perspective of geometrical atomic stacking, the stacking of the C atoms and metal atoms are quite similar at the site 2 of graphene on Ni(111), and site 3 of graphene on Re(0001) and Pt(111), while the chemical activities behave quite differently for them. To interpret the origin of this distinction, we should consider the characteristic of the substrate, i.e., the interfacial interaction between the graphene and transition metal substrate. Corresponding to the atomic structures in Fig. 3, Fig. 4 illustrates the interfacial charge transfer distributions between the graphene and supporting substrates after adding a H or F atom at the free energy favorable positions of the selected sites. For the cases of Ni(111) and Re(0001), the stronger charge transfer behaviors between the graphene and substrates (Fig. 4a and d, Fig. 4b and e) indicate the intensive interactions between the C atoms and substrate metal atoms, which could decrease the chemical energy to compensate the increase in the strain energy of graphene after sp2–sp3 transition. However, with respect to the Pt(111), the interaction between graphene and Pt(111) was recognized as weak van der Waals interaction, and the charge transfer between the three nearest C atoms and the substrate Pt atoms were quite weak as shown in Fig. 4c and f. As a result, the gained chemical energy is not sufficient to offset the large strain energy induced by the sp2–sp3 transition of the C atom. The variations of the interfacial charge transfer between the C atoms and substrate metal atoms after the adsorption of H or F atom are further verified by the calculations of density of state (DOS) in ESI.† Therefore, the driving force for the sp2–sp3 transition of the graphene on transition metal substrate is largely dependent on the characteristics of the interfacial interaction between graphene and substrate. The intensive interfacial interaction will obtain more chemical energy to offset the strain energy in graphene and stabilize the adsorbing state. As the variety of the local atomic stacking for moiré superstructure of graphene on a strongly interacting covalent substrate, the tune of the chemical activity of graphene in a wide range can be achieved.
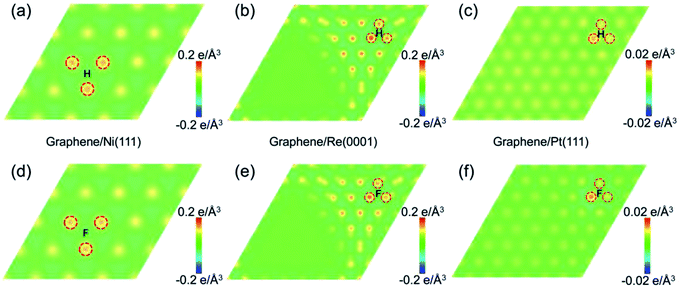 | ||
| Fig. 4 The charge transfer distributions between the graphene and transition metal substrates after the hydrogenation and fluorination. (a)–(c) represent the charge transfer between the graphene and Ni(111), Re(0001), and Pt(111) after adding one H atom at the minimum free energy sites according to Fig. 2. (d)–(f) represent the charge transfer between the graphene and Ni(111), Re(0001), and Pt(111) after adding one F atom at the minimum free energy sites according to Fig. 2. | ||
4. Conclusion
In summary, the DFT calculations have been carried out to investigate the chemical activities of graphene on transition metal substrates. The calculation results indicate that the chemical activity of graphene is related to both the characteristics of the graphene–substrate interfacial interaction and the local atomic stacking. The intensive graphene–substrate interfacial interaction can gain in the chemical energy to offset the strain energy caused by the C atom sp2–sp3 transition and stabilize the adsorbing state. Thus the strong covalently interacting substrates Ni(111) and Re(0001) will remarkably enhance the chemical activity of graphene, while the modulation effects from the weak van der Waals interacting substrate Pt(111) on the graphene is trivial. In addition, the moiré superstructure formed by the graphene and transition metal substrate could introduce various types atomic stacking between the C atoms and metal atoms. Therefore, the tune of the chemical activity of the graphene in a wide range could be achieved by the formation of moiré superstructure between the graphene and transition metal substrate. This study deepens our understanding about the effects of the interfacial interaction between the graphene and the substrate on the chemical activity of graphene, and provides with a promising method to enhance and tune the chemical activity of the graphene.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the support of the National Key Research and Development Program of China (Grant No. 2017YFB0702100), the National Natural Science Foundation of China (Grant No. 51705017, U1706221) and the Fundamental Research Funds for the Central Universities (06500069).References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS
.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS
.
- W. Feng, P. Long, Y. Feng and Y. Li, J. Adv. Sci., 2016, 3, 1500413 CrossRef
.
- L. Yan, Y. B. Zheng, F. Zhao, S. Li, X. Gao, B. Xu, P. S. Weiss and Y. Zhao, Chem. Soc. Rev., 2012, 41, 97–114 RSC
.
- Z. Wang, J. Wang, Z. Li, P. Gong, X. Liu, L. Zhang, J. Ren, H. Wang and S. Yang, Carbon, 2012, 50, 5403–5410 CrossRef CAS
.
- Q. Feng, N. Tang, F. Liu, Q. Cao, W. Zheng, W. Ren, X. Wan and Y. Du, ACS Nano, 2013, 7, 6729–6734 CrossRef CAS
.
- S.-H. Cheng, K. Zou, F. Okino, H. R. Gutierrez, A. Gupta, N. Shen, P. C. Eklund, J. O. Sofo and J. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205435 CrossRef
.
- L. Liao, H. Peng and Z. Liu, J. Am. Chem. Soc., 2014, 136, 12194–12200 CrossRef CAS
.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS
.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef
.
- Z. M. Ao and F. M. Peeters, Appl. Phys. Lett., 2010, 96, 253106 CrossRef
.
- M. Chen, H. Zhou, C. Qiu, H. Yang, F. Yu and L. Sun, Nanotechnology, 2012, 23, 115706 CrossRef
.
- H. Yang, M. Chen, H. Zhou, C. Qiu, L. Hu, F. Yu, W. Chu, S. Sun and L. Sun, J. Phys. Chem. C, 2011, 115, 16844–16848 CrossRef CAS
.
- S. Ryu, M. Y. Han, J. Maultzsch, T. F. Heinz, P. Kim, M. L. Steigerwald and L. E. Brus, Nano Lett., 2008, 8, 4597–4602 CrossRef CAS PubMed
.
- A. Dahal and M. Batzill, Nanoscale, 2014, 6, 2548–2562 RSC
.
- H. Tetlow, J. Posthuma de Boer, I. J. Ford, D. D. Vvedensky, J. Coraux and L. Kantorovich, Phys. Rep., 2014, 542, 195–295 CrossRef CAS
.
- X. Zheng, L. Gao, Q. Yao, Q. Li, M. Zhang, X. Xie, S. Qiao, G. Wang, T. Ma, Z. Di, J. Luo and X. Wang, Nat. Commun., 2016, 7, 13204 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef
.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef
.
- T. Björkman, J. Chem. Phys., 2014, 141, 074708 CrossRef
.
- C. Tonnoir, A. Kimouche, J. Coraux, L. Magaud, B. Delsol, B. Gilles and C. Chapelier, Phys. Rev. Lett., 2013, 111, 246805 CrossRef CAS
.
- L. Gao, Y. Liu, R. Shi, T. Ma, Y. Hu and J. Luo, RSC Adv., 2017, 7, 12179–12184 RSC
.
- M. Gao, Y. Pan, L. Huang, H. Hu, L. Z. Zhang, H. M. Guo, S. X. Du and H.-J. Gao, Appl. Phys. Lett., 2011, 98, 033101 CrossRef
.
- Y. Jia, L. Zhang, A. Du, G. Gao, J. Chen, X. Yan, C. L. Brown and X. Yao, Adv. Mater., 2016, 28, 9532–9538 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra00735g |
| This journal is © The Royal Society of Chemistry 2018 |