Open Access Article
Open Access ArticleEffects of anions on the underpotential deposition behavior of Cu on polycrystalline Pt†
Jiao Liuab,
Zhen Xu b,
Benfeng Zhub,
Xiaoqing Dub,
Yumeng Yangb,
Chenxi Yib,
Zhao Zhang
b,
Benfeng Zhub,
Xiaoqing Dub,
Yumeng Yangb,
Chenxi Yib,
Zhao Zhang *b,
Chao Caic and
Jianmei Lic
*b,
Chao Caic and
Jianmei Lic
aCollege of Chemistry and Chemical Engineering, Hunan University, Changsha 410082, China
bDepartment of Chemistry, Zhejiang University, Hangzhou 310027, China. E-mail: eaglezzy@zju.edu.cn; Tel: +86-13305816563
cCollege of Chemistry and Chemical Engineering, Ningxia University, Yinchuan 750021, China
First published on 23rd May 2018
Abstract
The process of Cu underpotential deposition (UPD) on polycrystalline Pt (pc Pt) has been investigated by cyclic voltammetry, chronoamperometry and electrochemical impedance spectroscopy techniques using (bi)sulfate and perchlorate (with/without the addition of a small amount of NaCl) as supporting electrolytes, respectively. The results showed that the adsorption capacity of the anions influences both the reversibility and charge transfer resistance (Rct) of Cu UPD reactions on pc Pt. With a negative shift of the applied potential, Rct of the (bi)sulfate system decreases monotonously, whereas Rct of the perchlorate system (with/without Cl− ions) decreases at first and then increases. Cu UPD on pc Pt follows Langmuir-type adsorption and two-dimensional nucleation/growth mechanisms. The specific adsorption anions ((bi)sulfate and chloride ions) can not only enhance the Cu UPD process by decreasing Rct, but also favor instantaneous 2D nucleation and subsequent grain growth. Finally, the possible deposition mechanisms of the Cu UPD process in the presence of specific adsorption anions were proposed.
1. Introduction
As an opposite concept to overpotential deposition (OPD), underpotential deposition (UPD) has received extensive research interest over many years due to its theoretical and pragmatical significance.1,2 Generally, the UPD process forms a (sub)monolayer of foreign species on a substrate; therefore, it is especially sensitive to the interfacial state of the electrode/solution and electrolyte composition. Many factors involved in the UPD process (such as the temperature, substrate crystallographic orientation, deposition potential, and the type and concentration of anions or other organic additives) can significantly influence the deposition behavior of UPD species. Among these factors, the effects of anions have attracted great attention and have been extensively studied.Anions may induce an enhanced Cu UPD process (CuUPD) or change the electrosorption valency of CuUPD ad-atoms determined by their adsorption/desorption characteristics;3 also, the formation of CuUPD-anion pairs due to anion coadsorption can reduce the coulombic repulsion generated by the partially charged CuUPD ad-atoms.3,4 Specific adsorption anions (such as Cl−, Br− and SO42−) can accelerate the UPD process due to local electrostatic effects,5,6 the decrease of positive potential in the dense part of the electric double layer (EDL),7 and possible deformation of the highly stable Cu2+ hydration shell caused by the weakly hydrated (bi)sulfate and halide anions (in contrast with perchlorate anions), which can enhance the electron transfer reaction.5,8 Moreover, the halide adlayer has a significant stabilizing effect on the UPD monolayer.9 The density and structure of UPD copper on Pt is definitely affected or even dominated by the electrolytic environment; the presence of Cl− in the electrolyte causes shrinkage of the Cu–Cu distance from 0.285 nm in a pure sulfuric acid environment to 0.259 nm.10
To date, considerable studies have concentrated on UPD of Cu on monocrystalline Pt substrates, especially Pt(111)4,8,11–17 and Pt(110);5,11 one important aspect of this process is the effects of specific adsorption anions on the structures of the CuUPD deposits (as well as the anion coadsorption layers) and on the kinetics of the CuUPD process in acid aqueous solution. In the case of Cu UPD on polycrystalline Pt (pc Pt) substrates, previous studies mainly focused on the effects induced by nonionic additives.10,18–20 Some nonionic additives (such as acetonitrile and thiourea) influence the Cu UPD processes via forming a charged copper-additive complex.10,18,19 At small concentrations of acetonitrile in a copper sulfate solution ([ACN] ≤ 4 mM), adsorbed ACN molecules promote copper underpotential deposition (UPD) on pc Pt.19 Azo-heterocyclic compounds that bind primarily through a ring nitrogen atom delay UPD processes depending on the bond strength of the adsorbed layer.20 However, the effect of anions on Cu UPD on pc Pt substrates is also an important aspect for practical applications. Therefore, this paper aims to investigate the effects of anions on CuUPD behavior on pc Pt using cyclic voltammetry (CV), chronoamperometry (CHR), and electrochemical impedance spectroscopy (EIS) techniques.
2. Experimental
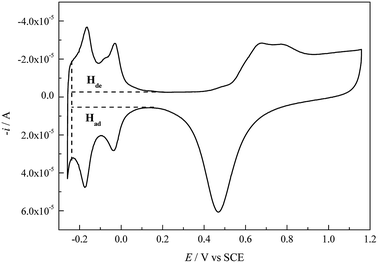
Cu UPD on pc Pt was studied in different aqueous solutions containing (bi)sulfate and perchlorate (with/without the addition of NaCl) ions, respectively. Copper(II) oxide (Alfa Aesar, 99.9995%, metals basis), CuSO4 (Aldrich, ≥99.99%, trace metals basis), H2SO4 (Sinopharm, GR), HClO4 (Sinopharm, GR), NaCl (Aladdin, 99.99%, metals basis) and ultrapure water (Millipore Water, resistivity ρ ≥ 18.2 MΩ cm at 25 °C) were used to prepare the solutions. Unless otherwise stated, all the used ultrapure water was prepared using a Millipore-Q system (Millipore-Q Academic, Millipore, USA) whose source water was doubly distilled in our lab. Immediately before each experiment, all the glassware used was soaked in a chromic mixture overnight and then rinsed with ultrapure water, and all solutions were purged by bubbling with high-purity N2 for 30 minutes to remove dissolved oxygen.All experiments were performed in a conventional three-compartment cell at 30 ± 0.1 °C controlled by a thermostatic bath. A pc Pt disk (Pine Research Instrumentation Inc., USA, 99.99%) with a geometric area of 0.1962 cm2 (the diameter of the circular working area is 5.0 mm) was used as the working electrode, a large platinum foil was used as the counter electrode, and a double liquid junction saturated calomel electrode (SCE) was used as the reference electrode in order to prevent contamination of Cl− ions. In this paper, all the potentials are referred to SCE. Before each experiment, the pc Pt working electrode was pretreated according to the following procedure: (1) the pc Pt electrode was mechanically polished with 0.5 μm diamond polishing paste to obtain a mirror surface and was then ultrasonically cleaned for 5 min in acetone and ultrapure water, respectively. (2) The pc Pt electrode was transferred into 0.5 M H2SO4 to carry out electrochemical polishing (−0.255 V to 1.160 V vs. SCE) until the normal CV profile (Fig. 1) appeared. (3) Lastly, the activated pc Pt electrode with a layer of 0.5 M H2SO4 solution covering its surface was transferred into the working solution as quickly as possible. After each experiment, the Cu UPD layer was electrochemically stripped; then, the pc Pt electrode was pretreated again according to the above procedure but without mechanical polishing.
 | ||
| Fig. 1 CV profile obtained for the pc Pt electrode in 0.5 M H2SO4 solution at a scan rate (v) of 100 mV s−1. | ||
CV and CHR measurements were carried out using a commercial model electrochemical analyzer/workstation (CHI750D, China). EIS measurements were carried out using an impedance measurement unit (PARSTAT 2273, Advanced Electrochemical System, USA) at different potential biases after the working electrode reached a steady state (∼10 minutes). The frequency sweep was always initiated from 100 kHz to 10 MHz with a voltage amplitude of 5.0 mV.
3. Results and discussion
3.1 Cyclic voltammetry
The cleanness of the pc Pt electrode surface was examined by performing CV cycles in 0.5 M H2SO4 (Fig. 1). The CV profile is in accordance with that in the literature,2,21 indicating a clean Pt surface. According to the electric quantity of the H adsorption region (Had) in Fig. 1 and a theoretical value of 210 μC cm−2, the electrochemical surface area (ECSA) and roughness factor (rf) of the pc Pt electrode were calculated to be 0.3728 cm−2 and 1.9 (all the calculations involving the electrode area refer to the apparent area unless otherwise specified), respectively.Fig. 2 shows the voltammograms for Cu deposition on pc Pt in 1.0 mM Cu2+ solutions containing different anions (the CV characteristics of pc Pt in the 5.0 mM Cu2+ solutions showed similar behavior to those in the 1.0 mM Cu2+ solutions; therefore, they are not shown here). The potential scan always started in the negative direction, and the potential range was between 0.650 V and −0.225 V. In Fig. 2, peak A and B are designated as the bulk deposition and stripping process of Cu deposits, respectively; meanwhile, the enlarged UPD peaks are shown in the insets. The different CV profiles (Fig. 2a–e) reflect significant distinctions of inter-atomic forces between the Cu–Cu and Cu–Pt bondings as well as the distinct energy states of different active sites on the pc Pt surface. From Fig. 2, the potential ranges of the OPD and UPD stripping peaks cover around 100 mV and 500 mV, respectively. Meanwhile, it can also be observed that OPD and its stripping peaks are generally unimodal, whereas UPD and its stripping peaks usually display some humps or broad curves.
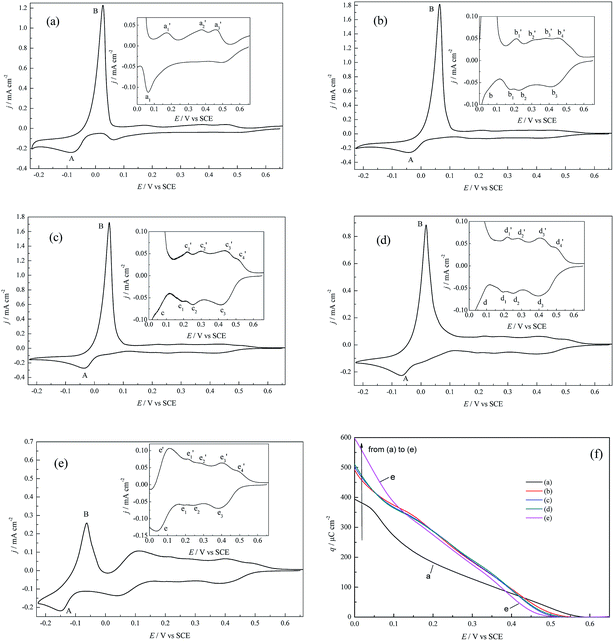 | ||
| Fig. 2 CV profiles for Cu deposition on pc Pt in (a) 0.5 M H2SO4 + 1.0 mM CuSO4, (b) 0.5 M HClO4 + 1.0 mM Cu(ClO4)2, (c) 0.5 M HClO4 + 1.0 mM Cu(ClO4)2 + 1.0 mM NaCl, (d) 0.5 M HClO4 + 1.0 mM Cu(ClO4)2 + 10 mM NaCl, and (e) 0.5 M HClO4 + 1.0 mM Cu(ClO4)2 + 50 mM NaCl. v = 30 mV s−1. The insets show partial enlarged details of the UPD region. (f) The UPD charge density (q) variation as a function of the applied potentials (E) (the calculations refer to the ECSA), estimated by integrating the voltammograms in Fig. 2a–e. | ||
Under the conditions of identical Cu2+ concentrations, anions exert prominent impacts on both the OPD and UPD processes. With regard to OPD, peaks A and B for the (bi)sulfate supporting electrolyte (Fig. 2a) both appear at more negative potentials than that for the perchlorate supporting electrolyte (Fig. 2b), and the peak current densities of the former are smaller than the latter; this suggests that Cu bulk deposition is more facile in the perchlorate supporting electrolyte. The above phenomena can be attributed to the weaker coordination and adsorption capacity of perchlorate with respect to (bi)sulfate. With increasing Cl− ions concentration in perchlorate electrolyte (Fig. 2b–e), the peak potentials of A and B shift negatively and the corresponding peak current densities decrease, whilst the peak shapes experience a gradual change. The above results can be attributed to the strong specific adsorption of Cl− and the complexation of Cl− with Cu2+ species at higher Cl− concentrations.22
For the UPD process, the CV profiles are much more complicated than for the OPD process; this is attributed to the fact that pc Pt is composed of different crystallographic planes, crystal defects and grain boundaries, and therefore different active sites are in strikingly different energetic states.23 In (bi)sulfate supporting electrolyte (Fig. 2a), there is only one UPD peak and three stripping peaks, which agrees well with the studies of Alonso et al.24 and also indicates the irreversibility of the Cu UPD process. However, obviously different CV profiles appear in perchlorate supporting electrolyte, and at least three UPD peaks and four stripping humps/peaks appear. For example, in Fig. 2c, in the assignments of UPD and its stripping peaks, peak c1 should correspond to c1′, peak c2 to c2′, and peak c3 to c3′ and c4′. In the case of the perchlorate supporting electrolyte and Cl− concentration c(Cl−) ≤ 10 mM (Fig. 2b–d), the addition of Cl− results in more distinct UPD stripping humps and shifts the UPD peak positions towards more positive potentials, suggesting that the CuUPD process tends to be more facile; however, when c(Cl−) increases to 50 mM, the boundaries of the UPD humps become inconspicuous and peak e becomes more significant (Fig. 2e).
Fig. 2f shows the variation of the charge density (q) as a function of the applied potential (E). It can be observed that the UPD onset potential is ca. 0.56 V for (bi)sulfate electrolyte and ca. 0.50 V for perchlorate electrolyte containing 50 mM Cl−; for q, slight differences can be observed for the perchlorate electrolytes containing lower Cl− concentrations (0 to 10 mM). In addition, it is interesting to note that the magnitude of q follows the order of q((bi)sulfate) > q(perchlorate) > q(chloride) in the higher potential region (0.43 V to 0.5 V), while the order is q(chloride) > q(perchlorate) > q((bi)sulfate) in the lower potential region (0.05 V to 0.0 V). Furthermore, almost a full Cu monolayer is completed prior to 0.00 V for perchlorate electrolyte with or without Cl− according to the q–E relationships (Fig. 2f) (hypothesizing the theoretical charge density needed to form a full Cu monolayer of 420 μC cm−2), which is similar to that of Cu UPD on polycrystalline Au.25 The differences in q between the (bi)sulfate and perchlorate (with or without Cl−) systems may synchronously result from the following factors: (1) stronger inductive effects (such as a stronger local electrostatic effect,5,6 greater potential decrease in the dense part of EDL,7 possible greater deformation of the hydrated Cu2+ hydration shell5,8), and more favorable replacement of (bi)sulfate with CuUPD ad-atoms than perchlorate.26 (2) Both the different lattice structures in different supporting electrolytes and the different specific adsorption capacities of (bi)sulfate and chloride ions on pc Pt, as well as the complexation of Cu2+ species with Cl− ions, especially at higher Cl− concentrations. (3) The influence of the electrode potential on the rate and mechanisms of Cu2+ charge transfer as well as the desorption rate of the pre-adsorbed anions. For example, in the lower potential region, the perchlorate electrolyte system of 50 mM Cl− shows the largest q, which may arise from the transition of charge transfer mechanisms due to the complexation of Cl− ions with Cu2+, such as the transition from single electron transfer (Cu2+ + e → Cu+, Cu+ + e → Cu) to electron transfer coupled with comproportionation (Cu+ + Cu+ → Cu + Cu2+). Shao and his coworkers22 also reported that the transition between two different mechanisms (direct two-step reduction and the chloride-mediated route) depends on the amount of chloride ions for Cu OPD.
3.2 EIS measurements
With regard to the UPD process, the current density (jUPD) can be expressed as a function of the electrode potential (E), state variables of the electrode surface (Xi), and the surface concentration of UPD species (Csk),27| jupd = f(E, Xi, Csk) | (1) |
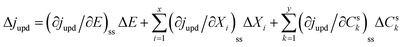 | (2) |
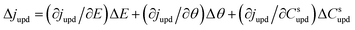 | (3) |
Ragoisha's research group28,29 elaborated several possible equivalent electric circuits (EECs) of EIS when studying the UPD process according to eqn (3). In brief, the right-hand side of eqn (3) indicates the current changes caused by the charge transfer resistance (Rct), adsorption capacitance (CUPD) and mass transfer impedance (ZT) of the UPD species from left to right, respectively. In view of the reversibility of the UPD process, it can be divided into two different situations. For reversible UPD, the mathematical model of interfacial impedance is expressed as29–31
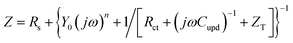 | (4) |
For irreversible UPD, it can be expressed as29
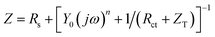 | (5) |
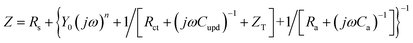 | (6) |
For an irreversible UPD process,
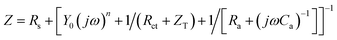 | (7) |
Potentiodynamic electrochemical impedance spectroscopy (PDEIS) has been applied to study UPD kinetics, of which the ac response must be confined to a limited frequency range while leaving out certain EEC elements, such as mass transfer impedance at low or infralow frequencies.29 In this study, we adopted the classical EIS technique and decomposed the ac response through the whole EEC in the frequency range between 100 kHz and 10 mHz as much as possible.
| E (V) | Rs (Ω cm2) | CPEdl-T (μF cm−2) | CPEdl-P | Rct (Ω cm2) | W1-R (Ω cm2) | Ra (Ω cm2) | CPEa-T (μF cm−2) | CPEa-P |
|---|---|---|---|---|---|---|---|---|
| 0.16 V | 0.921 | 51.779 | 0.906 | 377.881 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915.744 915.744 |
738.104 | 337.151 | 0.912 |
| 0.12 V | 0.846 | 58.588 | 0.916 | 143.069 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685.405 685.405 |
265.459 | 595.158 | 0.884 |
| 0.08 V | 0.922 | 55.708 | 0.927 | 23.878 | 9705.425 | 95.844 | 565.240 | 0.802 |
| 0.04 V | 0.895 | 60.112 | 0.927 | 13.134 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956.428 956.428 |
19.973 | 548.012 | 0.769 |
| 0.02 V | 0.890 | 40.004 | 0.962 | 6.530 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 519.294 519.294 |
11.256 | 673.853 | 0.778 |
| 0.00 V | 0.852 | 42.203 | 0.967 | 6.263 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 243.233 243.233 |
7.913 | 1098.012 | 0.778 |
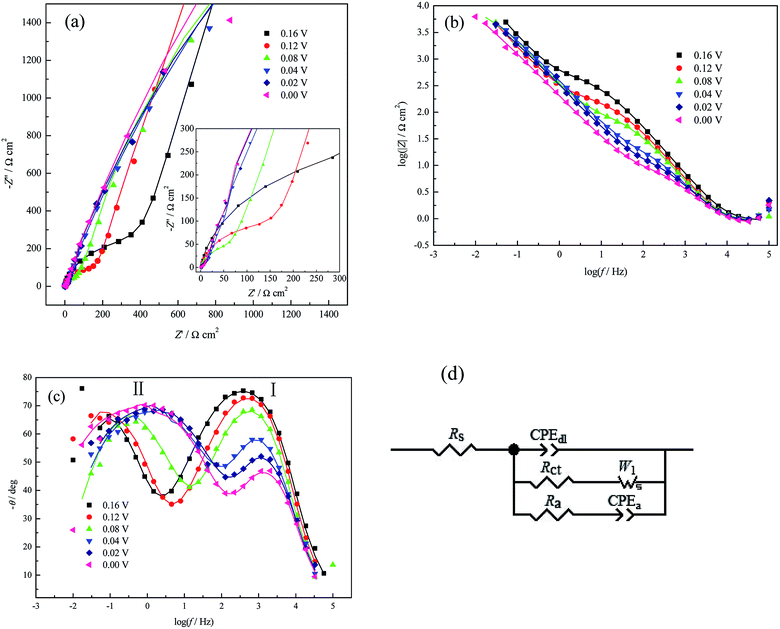
With the negative shift of the applied potentials from 0.16 V to 0.0 V, the diameters of both the high-frequency arc (Fig. 3a) and the impedance module (Fig. 3b) decrease. The frequency of peak I in the Bode plot (Fig. 3c) shifts towards the higher frequency region and the analyzed Rct decreases monotonously (Table 1), which is similar to H UPD in 0.1 M H2SO4 solution;32 this indicates that the UPD process (nucleation/growth) is accelerated and that the formation of CuUPD-anion pairs due to (bi)sulfate coadsorption decreases the coulombic repulsion caused by the partially charged CuUPD ad-atoms.3,4 Meanwhile, two phase angle peaks obviously exist in the Bode plot (Fig. 3c) at all applied potentials, which cannot be observed in PDEIS measurements to a large extent due to its limited sweep frequency range.28,33–35
The phase angle value of peak I (Fig. 3c) decreases as the applied potential bias increases (vs. open circuit potential (OCP), approximately 0.65 V), which proves that the UPD process becomes more and more nonuniform or inhomogeneous36 due to the dispersive surface energetic states of pc Pt and the increasing potential bias. The increasing inhomogeneity can also be proved by the decrease of the surface fractal dimensions Df (Df = 3 − n or Df = 1/n + 1, where n is the power exponent of the constant phase element, which is CPEdl-P here)37,38 as the applied potential bias increases. The UPD process caused a slight decrease of the Cu2+ concentration (or a slight concentration polarization) based on Faraday's law and the electric quantity consumed by forming a CuUPD monolayer; meanwhile, the electrode surface should be rationally composed of more CuUPD and fewer Pt atoms at a higher potential bias (vs. OCP) (Fig. 2f). In this case, because both the specific resistance and the area of Pt were smaller than those of the CuUPD layer, the activity of the residual nude Pt increased gradually with decreasing applied potential; this would certainly accelerate the diffusion process of the UPD species and consequently result in a shift of the low frequency phase angle peak II related to the diffusion process towards the higher frequency region (Fig. 3c). The EIS measurements results at 0.00 V present no sign of inductive components (the shrinkage phenomenon of the real part) in the entire frequency range, which suggests that the H UPD process (or hydrogen evolution reaction, HER) is suppressed by Cu UPD. This type of inhibiting phenomenon was also observed for low Cu ad-atoms coverage by Machado and his coworkers.39
The fitting results (Table 1) also show that the magnitude of CPEdl-T (i.e. Y0 in eqn (4)) fluctuates within the measurement uncertainties and is much smaller than that of CPEa-T. This result agrees well with the fact that the former process takes place at the whole electrode/solution interface, while the latter may prefer some active sites for easier adsorption/desorption of (bi)sulfate. Due to the above reasons, it can also be observed that the dispersion index CPEdl-P (i.e. n in eqn (4)) is slightly larger than CPEa-P, and the former is closer to the behavior of pure capacitance. Moreover, the simultaneous increase of CPEa-T and the applied potential bias (Table 1) further suggests the occurrence of (bi)sulfate adsorption/desorption onto the CuUPD surface.
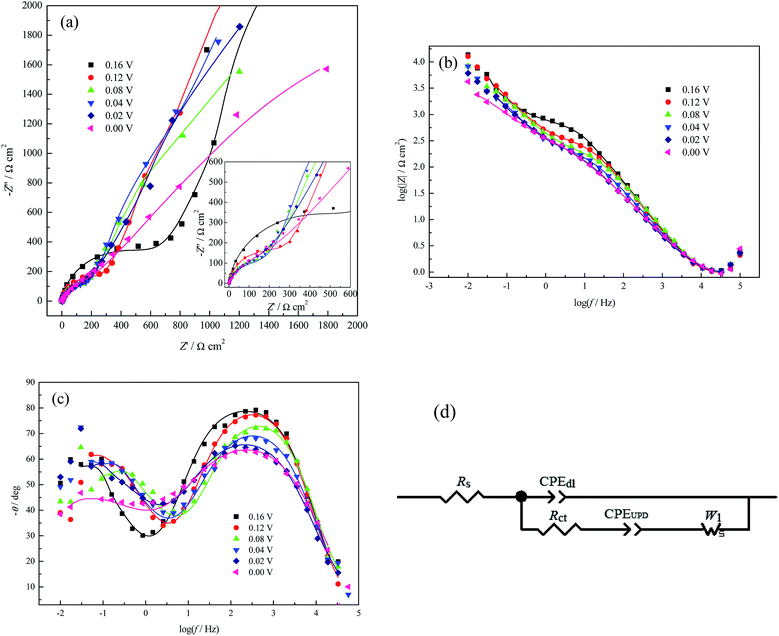
However, for pure the perchlorate electrolyte system, with increasing applied potential bias, the peak frequency of the phase angle (Fig. 4c) initially shows a tendency of a very small shift towards a higher frequency (0.08 V ≤ E ≤ 0.16 V), then to a lower frequency (0.00 V ≤ E ≤ 0.08 V); this indicates that the Cu UPD process becomes easier in the range of 0.08 V ≤ E ≤ 0.16 V and more difficult in the range of 0.00 V ≤ E ≤ 0.08 V, similar to a recent report.31 The more difficult UPD process at a larger potential bias may be caused by strong lateral interactions among the partially charged Cu ad-atoms; this can be verified by the q–E dependence (Fig. 2f), where Cu ad-atoms have already reached a relatively large coverage at 0.08 V (∼0.926 monolayer).
The deviation of the inclination angles of the diffusion impedance (Fig. 4a) from π/4 suggests that the Cu UPD process is affected by other surface state variables in addition to the applied potentials.27 However, due to the weak adsorption capacity of perchlorate depicted above, the deviation should be mainly attributed to the coverage of the Cu UPD adlayer. Therefore, when simultaneously considering the weak adsorption capacity of perchlorate and the relative reversibility of Cu UPD in the range of 0.00 V ≤ E ≤ 0.50 V (Fig. 2b, according to the potential difference between the reduction and oxidation peaks40), the EEC model (Fig. 4d) proposed by Huang and his coworkers for Cu UPD on polycrystalline Pd30 was adopted to analyze the EIS data in Fig. 4a–c; the best fitting results are listed in Table 2.
| E (V) | Rs (Ω cm2) | CPEdl-T (μF cm−2) | CPEdl-P | Rct (Ω cm2) | CPEUPD-T (μF cm−2) | CPEUPD-P | W1-R (Ω cm2) |
|---|---|---|---|---|---|---|---|
| 0.16 V | 0.922 | 49.878 | 0.921 | 718.681 | 843.629 | 0.746 | 275.072 |
| 0.12 V | 0.914 | 50.177 | 0.929 | 322.749 | 693.323 | 0.761 | 755.174 |
| 0.08 V | 0.900 | 60.810 | 0.895 | 197.573 | 1045.056 | 0.774 | 618.030 |
| 0.04 V | 0.872 | 113.216 | 0.848 | 206.206 | 1595.872 | 0.905 | 790.294 |
| 0.02 V | 0.873 | 203.252 | 0.797 | 272.129 | 1381.244 | 0.693 | 1132.663 |
| 0.00 V | 0.783 | 242.243 | 0.769 | 275.465 | 1222.477 | 0.571 | 2811.546 |
From Table 2, Rct initially decreases and then increases with increasing applied potential bias, which is consistent with the variation of the peak frequency of the phase angle (Fig. 4c). Higher values of Rct are observed in HClO4 solution than in H2SO4 solution (Tables 1 and 2), which indicates that the Cu UPD rate in HClO4 solution is slower. This phenomenon is consistent with that observed by Łosiewicz and his coworkers;32 they also found that H UPD in H2SO4 solutions is faster than that in HClO4 solutions. CPEdl-T is much smaller than CPEUPD-T, whilst both CPEdl-T and CPEUPD-T (the fluctuations of their values are within the measurement uncertainties) increase with increasing applied potential bias. The former may be caused by the following synergistic effects: (1) the adsorption capacity of perchlorate is much weaker than that of (bi)sulfate, as proved by the q–E dependence (Fig. 2f), so the Cu UPD process occurs more readily in the perchlorate system with increasing applied potential bias; (2) the strong lateral interactions between the partially charged Cu ad-atoms in the perchlorate system (depicted above) result in a more inhomogeneous (or rougher) electrode surface than the (bi)sulfate system, which can be verified by the decrease of CPEdl-P (Table 2). Meanwhile, CPEdl-T may also be interpreted as the charge–discharge process of the whole electrode/solution interface; however, CPEUPD-T only represents the faradaic pseudo-capacitance occurring at the active sites of the pc Pt surface.
It should be mentioned that the EEC model in Fig. 4d omitting CPEUPD and W1 was used to fit the PDEIS data31 when using PDEIS to study Cu UPD on Pt. The obtained Rct values are much larger than those in this paper. The above discrepancies may result from both the dynamic potential scan in the PDEIS measurements and the Cu2+ concentration difference.
| E (V) | Rs (Ω cm2) | CPEdl-T (μF cm−2) | CPEdl-P | Rct (Ω cm2) | CPEUPD-T (μF cm−2) | CPEUPD-P | W1-R (Ω cm2) | Ra (Ω cm2) | CPEa-T (μF cm−2) | CPEa-P |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.16 | 0.926 | 119.893 | 0.850 | 13.065 | 82.768 | 0.906 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 060.642 060.642 |
17.162 | 590.826 | 0.950 |
| 0.12 | 1.052 | 80.459 | 0.887 | 11.674 | 349.725 | 0.720 | 6876.810 | 20.424 | 359.516 | 0.938 |
| 0.08 | 1.055 | 28.836 | 0.997 | 3.588 | 538.481 | 0.666 | 2505.866 | 10.614 | 558.716 | 0.922 |
| 0.04 | 0.925 | 75.474 | 0.918 | 4.573 | 624.720 | 0.601 | 1235.079 | 13.987 | 811.009 | 0.914 |
| 0.02 | 0.950 | 142.961 | 0.864 | 14.697 | 605.861 | 0.526 | 1988.487 | 17.020 | 1202.548 | 0.866 |
| 0.00 | 0.929 | 280.133 | 0.810 | 26.153 | 1980.581 | 0.784 | 1146.200 | 36.297 | 2482.875 | 0.463 |
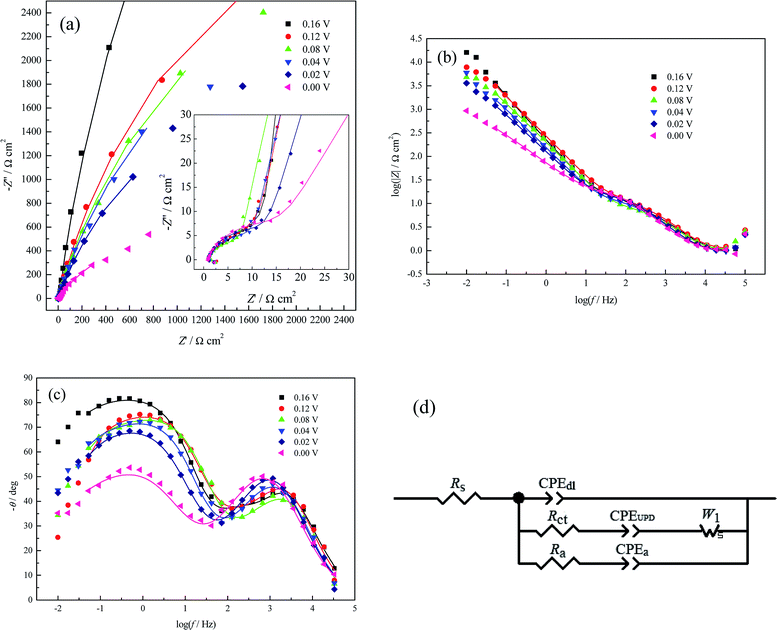
From Table 3, Rct initially decreases and then increases with increasing applied potential bias. This variation trend of Rct is very similar to that in a pure perchlorate electrolyte bath (Table 2); the reason for this has been elucidated in Section 3.2.2. However, this variation trend of Rct is very different from that in (bi)sulfate electrolyte (Table 1), which can be attributed to the different effects of perchlorate and (bi)sulfate ions on the Cu UPD process. Table 3 also clearly shows that Rct is slightly smaller than Ra, indicating more facile adsorption of CuUPD adatoms than Cl− ions. From Table 3, CPEdl-T is much smaller than both CPEUPD-T and CPEa-T; this is because CPEdl-T, CPEUPD-T and CPEa-T originate from the whole electrode/solution interface, the fast charge transfer reaction (i.e. pseudo-capacitance) and the strong adsorption/desorption of Cl− ions at the active sites, respectively.
3.3 Potentiostatic current transient measurements
The aim of this section is to investigate the effects of anions (SO42−, ClO4− and Cl−) on the nucleation and growth features of the Cu UPD process, and solutions containing 5.0 mM Cu2+ with specific anions were chosen to perform chronoamperometric (CHR) experiments (Fig. 6). Additionally, in order to avoid the pre-adsorption of dissolved oxygen species and Cu UPD adatoms, the potential for the remaining CHR tests was selected as 0.65 V. Potentiostatic current density transients were obtained by voltage stepping from the rest potential to the UPD potentials.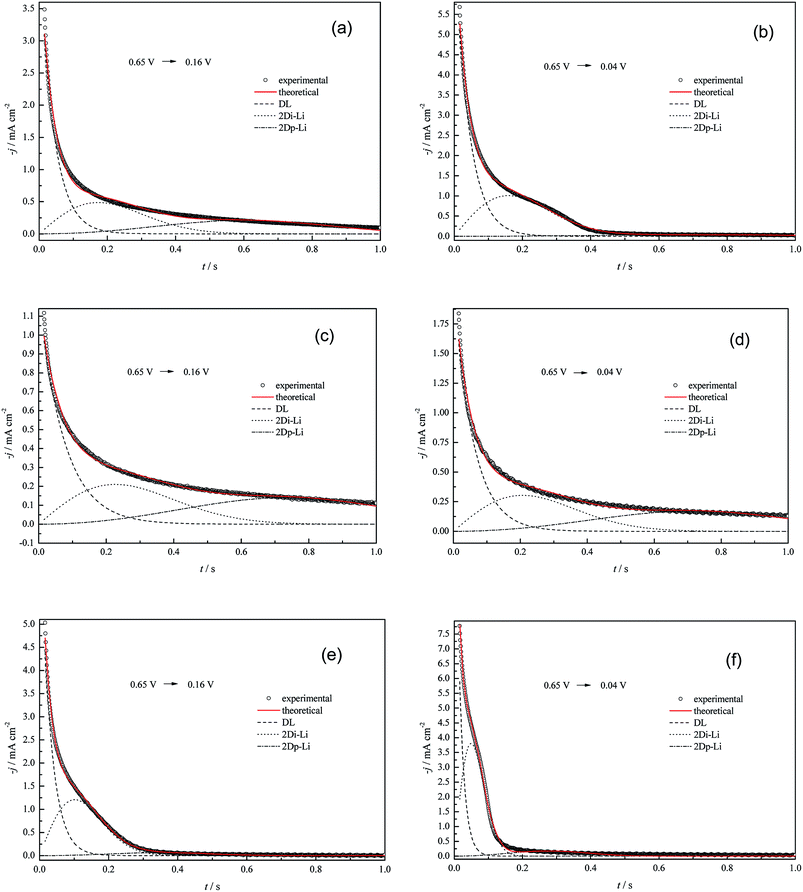 | ||
| Fig. 6 Experimental current density transients recorded for Cu UPD at pc Pt in (a) and (b) 5.0 mM CuSO4 + 0.5 M H2SO4, (c) and (d) 5.0 mM Cu(ClO4)2 + 0.5 M HClO4, (e) and (f) 5.0 mM Cu(ClO4)2 + 0.5 M HClO4 + 1.0 mM NaCl, and theoretical non-linear fitting with eqn (15) at some selected potentials. Other current density transients with non-linear fitting results shown in the ESI (Fig. S1–S3†). | ||
There are two typical differences between the “j–t” curves of different electrolyte systems (Fig. 6). One is that an obvious shoulder peak always exists for all the “j–t” curves obtained in the perchlorate electrolyte system containing 1.0 mM Cl− ions, whereas this peak does not appear in the pure perchlorate electrolyte system or only exists at higher potential biases for the (bi)sulfate electrolyte system. The other difference is that the current density (after the initial marked drop, which is simultaneously related to charging of the adsorption pseudo-capacitance, i.e. the discharging of copper ions in the copper electrodeposition process,41,42 or the shoulder peak) is much larger than zero for the pure perchlorate electrolyte system, whereas it always levels off to zero for the perchlorate electrolyte system containing 1.0 mM Cl− ions or for the (bi)sulfate electrolyte system at higher potential biases (the critical potential is ca. 0.04 V).
Currently, it is widely accepted that the UPD process generally follows the two-dimensional (2D) nucleation/growth mechanism.43,44 According to the jp–v1/2 relationship in Fig. 7, linear fitting results reveal that the rate-controlling step of Cu UPD with diffusion control was converted to non-diffusion control as a result of the increase of the Cu2+ concentration from 1.0 mM to 5.0 mM. On the other hand, based on the fact that the formation of even an integrated CuUPD monolayer only consumes 8.11 × 10−7 mM Cu2+ in our experimental conditions (hypothesizing a two-electron transfer mechanism), the Cu UPD process should be mostly controlled by charge transfer. Therefore, the theoretical models proposed by Bewick–Fleischmann–Thirsk (BFT) were adopted to analyze the current density transients shown in Fig. 6. In the BFT model, the overlapping effects between crystal nuclei are taken into consideration, and the growth of the 2D circular island nuclei proceeds with lattice incorporation of adatoms into the periphery of the growing nuclei as the rate-controlling step.45,46 According to the BFT model, the nucleation/growth current densities of 2D instantaneous nucleation (2Di-Li) and 2D progressive nucleation (2Dp-Li) are given by the following equations, respectively.25,45,46
j2Di-Li(t) = k1t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k2t2) exp(−k2t2)
| (8) |
j2Dp-Li(t) = k3t2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k4t3) exp(−k4t3)
| (9) |
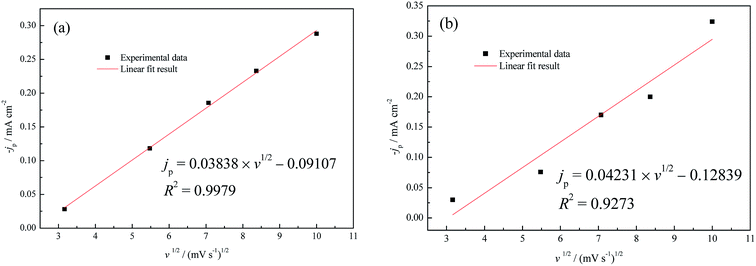 | ||
| Fig. 7 UPD peak maxima jp of CV in (a) 0.5 M H2SO4 + 1.0 mM CuSO4, (b) 0.5 M H2SO4 + 5.0 mM CuSO4 as a function of the square root of the scan rate (v). | ||
The deposition process should accompany the deposition/dissolution of metal ions/metal adatoms, namely, the copper ion discharge process. Milchev et al.41,42 have shown that discharge of the copper ions takes place in two steps:
| Cu2+ + e → Cu+ | (10) |
| Cu+ + e → Cu | (11) |
Meanwhile, assuming that the deposition/dissolution of a (sub)monolayer at defect sites mostly resembles a Langmuir-type adsorption/desorption process, the current density can be expressed as:41–43,45,47
jad(t) = k5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k6t) exp(−k6t)
| (12) |
For the deposition of metal ions associated with a charge transfer,43
k6 = k0a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(1 − β)nFE/RT] exp[−(1 − β)nFE/RT]
| (13) |
For the dissolution of metal adatoms,43
k6 = k0d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(βnFE/RT) exp(βnFE/RT)
| (14) |
| jtotal(t) = jad(t) + j2Di-Li(t) + j2Dp-Li(t) | (15) |
The experimental current density transients were deconvolved by non-linear fitting with eqn (15), and the fitted lines are also shown in Fig. 6. Based on the best fitting parameters k1 to k6 (shown in the ESI of this paper, Tables S1–S3†), the electric quantities of the different contributions (Qad, Q2Di-Li and Q2Dp-Li) were calculated according to expressions (16)–(18)25 and are listed in Tables 4–6
| k5 = Qadk6 | (16) |
| k1 = 2Q2Di-Lik2 | (17) |
| k3 = 3Q2Dp-Lik4 | (18) |
In eqn (16)–(18) and Tables 4–6, Qad, Q2Di-Li and Q2Dp-Li are the charge densities of adsorption, 2D instantaneous nucleation/growth and progress nucleation/growth, respectively; Qnucl = Q2Di-Li + Q2Dp-Li, Qtotal = Qad + Qnucl; qad and qnucl are the contributions of adsorption and nucleation to the total charge density, respectively.
For Cu UPD in the above three systems, Qtotal always increases with increasing applied potential bias (Tables 4–6). However, comparing the values of Qtotal, Qad and qad of different systems, it is interesting to observe that all of them are directly related to the anionic specific adsorption capacity. Briefly, the stronger the adsorption capacity of the anions in the supporting electrolyte, the larger the parameters (Qtotal, Qad and qad). For the systems containing SO42− (Table 4) and Cl− (Table 6) ions with stronger adsorption capacity, Q2Di-Li is generally larger than Q2Dp-Li (except at the potentials adjacent to the Nernst potential; the reason for this is under further investigation), and the differential of Q2Di-Li and Q2Dp-Li increases with increasing anionic specific adsorption capacity. Meanwhile, for the pure perchlorate supporting electrolyte system (Table 5), Q2Di-Li is always slightly smaller than Q2Dp-Li, and the differential of qnucl and qad is significantly larger than that obtained in the systems containing SO42− or Cl− ions. The above results undoubtedly indicate that the process of Cu UPD on pc Pt is always coupled with adsorption and replacement of the used anions, and the anions with stronger adsorption capacity facilitate the process of instantaneous nucleation and subsequent growth. When simultaneously taking into account the results shown in Fig. 2, it is rational to consider that co-adsorbed CuUPDn+ – anions (n = 0 to 2) of some specific structures should exist on the pc Pt surface and influence the deposition rate to some extent.
| E (V) | Qad (μC cm−2) | Q2Di-Li (μC cm−2) | Q2Dp-Li (μC cm−2) | Qnucl (μC cm−2) | Qtotal (μC cm−2) | qad (%) | qnucl (%) |
|---|---|---|---|---|---|---|---|
| 0.16 | 186.110 | 138.844 | 123.901 | 262.745 | 448.855 | 41.463 | 58.537 |
| 0.12 | 210.807 | 173.477 | 138.821 | 312.298 | 523.105 | 40.299 | 59.701 |
| 0.08 | 218.230 | 187.258 | 163.011 | 350.269 | 568.499 | 38.387 | 61.613 |
| 0.04 | 315.751 | 263.973 | 26.615 | 290.588 | 606.339 | 52.075 | 47.925 |
| 0.02 | 247.359 | 170.395 | 211.423 | 381.818 | 629.177 | 39.315 | 60.685 |
| 0.00 | 307.161 | 300.887 | 33.151 | 334.038 | 641.199 | 47.904 | 52.096 |
| E (V) | Qad (μC cm−2) | Q2Di-Li (μC cm−2) | Q2Dp-Li (μC cm−2) | Qnucl (μC cm−2) | Qtotal (μC cm−2) | qad (%) | qnucl (%) |
|---|---|---|---|---|---|---|---|
| 0.16 | 91.034 | 78.841 | 100.757 | 179.598 | 270.632 | 33.637 | 66.363 |
| 0.12 | 78.721 | 69.486 | 82.852 | 152.338 | 231.059 | 34.070 | 65.930 |
| 0.08 | 111.169 | 95.960 | 114.182 | 210.141 | 321.310 | 34.599 | 65.401 |
| 0.04 | 122.454 | 103.243 | 119.615 | 222.858 | 345.312 | 35.462 | 64.538 |
| 0.02 | 133.165 | 108.358 | 117.791 | 226.149 | 359.314 | 37.061 | 62.939 |
| 0.00 | 179.900 | 147.879 | 152.242 | 300.122 | 480.022 | 37.478 | 62.522 |
| E (V) | Qad (μC cm−2) | Q2Di-Li (μC cm−2) | Q2Dp-Li (μC cm−2) | Qnucl (μC cm−2) | Qtotal (μC cm−2) | qad (%) | qnucl (%) |
|---|---|---|---|---|---|---|---|
| 0.16 | 225.323 | 202.359 | 22.257 | 224.616 | 449.939 | 50.079 | 49.921 |
| 0.12 | 237.648 | 240.819 | 16.953 | 257.772 | 495.420 | 47.969 | 52.031 |
| 0.08 | 245.331 | 286.739 | 24.954 | 311.692 | 557.024 | 44.043 | 55.957 |
| 0.04 | 256.258 | 309.797 | 47.260 | 357.057 | 613.315 | 41.782 | 58.218 |
| 0.02 | 276.591 | 305.269 | 64.873 | 370.142 | 646.734 | 42.767 | 57.233 |
| 0.00 | 586.859 | 47.097 | 95.063 | 142.160 | 729.019 | 80.500 | 19.500 |
The UPD process is highly complicated, and the deposition mechanisms should be mainly related to both the spatial structures of the adsorbed anions and the electrostatic interactions of the anions with the substrate and UPD species. Based on the above results and the previous reports of Cu UPD on single crystal Pt concurrent with coadsorption of specific adsorption anions,5,8,12,13,48 it is rational to deduce that Cu UPD on a pc Pt surface in the presence of specific adsorption anions may proceed via the following mechanisms. Firstly, before the onset potential of Cu UPD, the specific adsorption anions adsorb onto the Pt substrate and gradually translate into specific adlayers of certain lattice structures (the structures may transform along with the negative potential scan), which will also deform the hydration shell of the pre-adsorbed Cu2+ (some specific adsorption anions can even insert into the Cu2+ hydration shells) and cause a decrease of the positive potential in the dense part of the EDL region.7 Meanwhile, the electrostatic interaction of the specific adsorption anions with Cu2+ ions causes the latter to gather in the dense part of the EDL. Secondly, when the UPD potential is suddenly applied, Cu UPD proceeds with simultaneous replacement of the adsorbed anions at certain active sites,26 and some uniform structures of co-adsorbed CuUPDn+ – anion (n = 0 to 2) may form at some critical potentials. Here, it should be mentioned that in the presence of halide ions, Pb UPD on pc Au may proceed via the reduction of Pb2+ adsorbed on the pre-adsorbed halide ions.49 Finally, as the potential becomes more negative, the UPD process continues until the integrated Cu UPD monolayer is formed; this process is always coupled with the adsorption of specific adsorption anions onto the Cu UPD monolayer (a sandwiched structure), which may inhibit the continuous deposition of Cu2+ on the CuUPD layer, thereby stabilizing the UPD film.10,13
4. Conclusions
The CV plot of pc Pt in a (bi)sulfate system shows only one significant UPD peak and three corresponding stripping peaks; this differs from the plots of perchlorate systems, which contain at least three UPD peaks and four stripping peaks. In contrast to the irreversibility of the Cu UPD process in the (bi)sulfate system, better reversibility was observed in the perchlorate system, and the reversibility was further improved by the addition of a small amount of Cl− ions.Anions with stronger adsorption capacity facilitate the process of 2D instantaneous nucleation and subsequent grain growth, and specific adsorption anions ((bi)sulfate and chloride) can enhance the Cu UPD process by decreasing the charge transfer resistance (Rct). With decreasing applied potential, Rct of the (bi)sulfate system decreases monotonously, whereas Rct shows a trend of initial decrease and subsequent increase for perchlorate systems with or without Cl− ions. Finally, the possible mechanisms of Cu UPD on pc Pt in the presence of specific adsorption anions were proposed; these reveal the intrinsic relationships between specific adsorption anions and the Cu UPD process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Project 21273199, 51771173, 51741107).References
- Z. Xu, Y. Chen, Z. Zhang and J. Zhang, Acta Phys.-Chim. Sin., 2015, 31, 1219–1230 Search PubMed.
- Z. Xu, D. M.Qi, L. Jiang, Y. Chen, Z.Zhang and J. Zhang, Acta Phys.-Chim. Sin., 2015, 31, 1231–1250 Search PubMed.
- C. Wang, C. S. Chung and S. C. Chang, J. Electroanal. Chem., 1995, 395, 317–321 CrossRef.
- H. S. Yee and H. D. Abruna, Langmuir, 1993, 9, 2460–2469 CrossRef.
- B. Grgur, C. Lucas and P. Ross, Electrochim. Acta, 1998, 44, 1009–1017 CrossRef.
- A. I. Danilov, E. B. Molodkina, Y. M. Polukarov, V. Climent and J. M. Feliu, Electrochim. Acta, 2001, 46, 3137–3145 CrossRef.
- A. Danilov, E. Molodkina and Y. M. Polukarov, Russ. J. Electrochem., 2000, 36, 976–986 CrossRef.
- N. M. Markovic, H. A. Gasteiger and P. N. J. Ross, Langmuir, 1995, 11, 4098–4108 CrossRef.
- Y. Gründer, P. Thompson, A. Brownrigg, M. Darlington and C. A. Lucas, J. Phys. Chem. C, 2012, 116, 6283–6288 Search PubMed.
- M. Wünsche, H. Meyer and R. Schumacher, Electrochim. Acta, 1995, 40, 629–635 CrossRef.
- N. Markovic and P. Ross, Langmuir, 1993, 9, 580–590 CrossRef.
- N. M. Markovic, C. Lucas, H. A. Gasteiger and P. Ross, Solid-Liquid Electrochemical Interfaces, 1997, vol. 656, pp. 87–105 Search PubMed.
- H. Ogasawara, J. Inukai and M. Ito, Surf. Sci., 1994, 311, L665–L670 CrossRef.
- Y. Soldo, E. Sibert, G. Tourillon, J. L. Hazemann, J. Lévy, D. Aberdam, R. Faure and R. Durand, Electrochim. Acta, 2002, 47, 3081–3091 CrossRef.
- C. Lucas, N. Marković, I. Tidswell and P. Ross, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 221, 245–250 CrossRef.
- N. M. Marković, H. A. Gasteiger, C. A. Lucas, I. M. Tidswell and P. N. Ross Jr, Surf. Sci., 1995, 335, 91–100 CrossRef.
- I. Tidswell, C. Lucas, N. Marković and P. Ross, Phys. Rev. B, 1995, 51, 10205 CrossRef.
- A. V. Rudnev, T. Zapryanova, E. B. Molodkina, A. I. Danilov and Y. M. Polukarov, Russ. J. Electrochem., 2008, 44, 840–846 CrossRef.
- A. V. Rudnev, E. B. Molodkina, A. I. Danilov and Y. M. Polukarov, Russ. J. Electrochem., 2006, 42, 689–698 CrossRef.
- C. Alonso, M. J. Pascual and H. D. Abruna, Electrochim. Acta, 1997, 42, 1739–1750 CrossRef.
- B. Conway, H. Angerstein-Kozlowska, W. Sharp and E. Criddle, Anal. Chem., 1973, 45, 1331–1336 CrossRef.
- W. Shao, G. Pattanaik and G. Zangari, J. Electrochem. Soc., 2007, 154, D201–D207 CrossRef.
- L. Mascaro, S. S. Machado and L. Avaca, J. Chem. Soc., Faraday Trans., 1997, 93, 2577–2582 RSC.
- C. Alonso, M. Pascual and H. Abruna, Electrochim. Acta, 1997, 42, 1739–1750 CrossRef.
- M. Palomar-Pardavé, E. Garfias-García, M. Romero-Romo, M. Ramírez-Silva and N. Batina, Electrochim. Acta, 2011, 56, 10083–10092 CrossRef.
- L. J. Buller, E. Herrero, R. Gómez, J. M. Feliu and H. D. Abruña, J. Phys. Chem. B, 2000, 104, 5932–5939 CrossRef.
- C. Cao and J. Zhang, An introduction to electrochemical impedance spectroscopy, Science Press, Beijing, 2002 Search PubMed.
- G. A. Ragoisha and A. S. Bondarenko, Electrochim. Acta, 2005, 50, 1553–1563 CrossRef.
- G. Ragoisha, Electroanalysis, 2015, 27, 855–863 CrossRef.
- M. Huang, J. B. Henry, P. Fortgang, J. Henig, N. Plumeré and A. S. Bandarenka, RSC Adv., 2012, 2, 10994–11006 RSC.
- B. B. Berkes, A. Maljusch, W. Schuhmann and A. S. Bondarenko, J. Phys. Chem. C, 2011, 115, 9122–9130 Search PubMed.
- B. Łosiewicz, R. Jurczakowski and A. Lasia, Electrochim. Acta, 2012, 80, 292–301 CrossRef.
- G. A. Ragoisha and A. S. Bondarenko, Electrochem. Commun., 2003, 5, 392–395 CrossRef.
- G. Ragoisha, A. Bondarenko, N. Osipovich and E. Streltsov, J. Electroanal. Chem., 2004, 565, 227–234 CrossRef.
- G. A. Ragoisha and A. S. Bondarenko, Surf. Sci., 2004, 566, 315–320 CrossRef.
- X. Huang, Y. Chen, T. Fu, Z. Zhang and J. Zhang, J. Electrochem. Soc., 2013, 160, D530–D537 CrossRef.
- L. Zhang, J. Fan, Z. Zhang, F. Cao, J. Zhang and C. Cao, Electrochim. Acta, 2007, 52, 5325–5333 CrossRef.
- L. Zhang, Doctoral Dissertation, Zhejiang University, 2008.
- S. Machado, A. Tanaka and E. Gonzalez, Electrochim. Acta, 1991, 36, 1325–1331 CrossRef.
- A. J. Bard and L. R. Faulkner, Electrochemical methods fundamentals and applications, Y. H. Shao, G. Y. Zhu, X. D. Dong and B. L. Zhang, Chemical Industry Press, Beijing, 2nd edn, 2005 Search PubMed.
- A. Milchev and T. Zapryanova, Electrochim. Acta, 2006, 51, 2926–2933 CrossRef.
- A. Milchev and T. Zapryanova, Electrochim. Acta, 2006, 51, 4916–4921 CrossRef.
- M. Hölzle, U. Retter and D. Kolb, J. Electroanal. Chem., 1994, 371, 101–109 CrossRef.
- M. Alanyalioglu, H. Çakal, E. Öztürk and Ü. Demir, J. Phys. Chem. B, 2001, 105, 10588–10593 CrossRef.
- M. Palomar-Pardave, I. González and N. Batina, J. Phys. Chem. B, 2000, 104, 3545–3555 CrossRef.
- A. Martínez-Ruíz, M. Palomar-Pardavé, J. Valenzuela-Benavides, M. H. Farías and N. Batina, J. Phys. Chem. B, 2003, 107, 11660–11665 CrossRef.
- L. H. Mendoza-Huizar, J. Robles and M. Palomar-Pardavé, J. Electroanal. Chem., 2002, 521, 95–106 CrossRef.
- Y. Shingaya, H. Matsumoto, H. Ogasawara and M. Ito, Surf. Sci., 1995, 335, 23–31 CrossRef.
- B. Y. Chang, E. Ahn and S. M. Park, J. Phys. Chem. C, 2008, 112, 16902–16909 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra00921j |
| This journal is © The Royal Society of Chemistry 2018 |