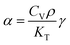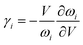Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Negative thermal expansion and electronic structure variation of chalcopyrite type LiGaTe2†
V. V. Atuchin*ab,
Fei Liang c,
S. Grazhdannikov
c,
S. Grazhdannikov de,
L. I. Isaenko
de,
L. I. Isaenko de,
P. G. Krinitsin
de,
P. G. Krinitsin de,
M. S. Molokeev
de,
M. S. Molokeev efg,
I. P. Prosvirinh,
Xingxing Jiangc and
Zheshuai Lin*c
efg,
I. P. Prosvirinh,
Xingxing Jiangc and
Zheshuai Lin*c
aLaboratory of Optical Materials and Structures, Institute of Semiconductor Physics, SB RAS, Novosibirsk 630090, Russia. E-mail: atuchin@isp.nsc.ru
bLaboratory of Semiconductor and Dielectric Materials, Novosibirsk State University, Novosibirsk 630090, Russia
cKey Laboratory of Functional Crystals and Laser Technology, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zlin@mail.ipc.ac.cn
dLaboratory of Crystal Growth, Institute of Geology and Mineralogy, SB RAS, Novosibirsk 630090, Russia
eLaboratory of Functional Materials, Novosibirsk State University, Novosibirsk 630090, Russia
fLaboratory of Crystal Physics, Kirensky Institute of Physics, Federal Research Center KSC SB RAS, Krasnoyarsk 660036, Russia
gDepartment of Physics, Far Eastern State Transport University, Khabarovsk 680021, Russia
hSurface Science Laboratory, Boreskov Institute of Catalysis, SB RAS, Novosibirsk 630090, Russia
First published on 12th March 2018
Abstract
The LiGaTe2 crystals up to 5 mm in size were grown by the modified Bridgman–Stockbarger technique and the cell parameter dependence on temperature in the range of 303–563 K was evaluated by the X-ray diffraction analysis. The thermal behavior of LiGaTe2 is evidently anisotropic and a negative thermal expansion is found along crystallographic direction c with coefficient −8.6 × 10−6. However, the normal thermal expansion in two a directions with coefficient 19.1 × 10−6 is dominant providing unit cell volume increase on heating. The atomic mechanism is proposed to describe this pronounced anisotropic expansion effect. The electronic structure of LiGaTe2 is measured by X-ray photoelectron spectroscopy and the band structure is obtained by DFT calculations. The pressure response from 0 to 5 GPa was calculated and a normal crystal compression is found. This work indicates that LiGaTe2 is promising as an IR NLO or window material for many practical applications because the thermal expansion coefficients of this telluride are not big. We believe that these results would be beneficial for the discovery and exploration of new IR optoelectronic polyfunctional metal tellurides.
1. Introduction
Telluride crystalline materials are of great importance in modern microelectronics and photonics.1–12 Because of specific features of metal-tellurium chemical bonds, tellurides possess narrow-bandgap semiconductor or metallic properties.1,2,6–8,11,12 Due to their low-wavenumber phonon spectrum, semiconductor tellurides are transparent in the mid-IR range and they can be used as optical window materials. However, the number of known noncentrosymmetric tellurides is not big and, only for several crystals, the linear and nonlinear properties are obtained.13–22 The high potential of LiGaTe2 for the optical frequency conversion in the mid-IR spectral range has been demonstrated in several studies, and the structural and optical properties of this material were measured.13,16,17,20,23 LiGaTe2 is a positive uniaxial crystal and it has a chalcopyrite type structure (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d with the closest packing).24 The structure of LiGaTe2 is shown in Fig. 1.16,25 Each Li, Ga and Te atom occupies only one crystallographic position, the Li–Te bond distance is 2.736 Å and, for the Ga–Te bond, the value is 2.611 Å. For comparison, in the LiGaSe2 structure (wurtzite type, Pna21) there are two positions of Se. The Li–Se bond distance changes from 2.493 to 2.565 Å, while the Ga–Se bonds range from 2.389 to 2.405 Å. The nonlinear crystal LiGaTe2 is characterized by the biggest band-gap energy of Eg = 2.41 eV among tellurides, which is essentially bigger than those of LiInTe2 (1.5 eV), AgGaTe2 (1.32 eV) and AgInTe2 (1.03 eV). A sufficiently large birefringence (0.094) for LiGaTe2 allows one to obtain its room-temperature phase-matching in the whole transparency range (1.66–21 μm). Its nonlinear coefficient d36 was estimated by the phase-matched second harmonic generation to be 43 pm V−1, which is about 7 times higher than that of the related orthorhombic LiGaS2 and about 4.5 times relative to LiGaSe2. The conversion efficiency in LiGaTe2 for SHG 10.6 μm was found to be higher than that of AgGaSe2.16 Besides, this telluride is considered as a promising crystal for neutron detection.26,27 However, in several studies, it was reported on that crystal growth of LiGaTe2 is not trivial because of its high tellurium volatility and pronounced chemical activity of lithium at high temperatures.20,28–30 This may result in the defect generation and stoichiometry deviations, and these effects should be accounted to reach the optical quality crystals.
3d with the closest packing).24 The structure of LiGaTe2 is shown in Fig. 1.16,25 Each Li, Ga and Te atom occupies only one crystallographic position, the Li–Te bond distance is 2.736 Å and, for the Ga–Te bond, the value is 2.611 Å. For comparison, in the LiGaSe2 structure (wurtzite type, Pna21) there are two positions of Se. The Li–Se bond distance changes from 2.493 to 2.565 Å, while the Ga–Se bonds range from 2.389 to 2.405 Å. The nonlinear crystal LiGaTe2 is characterized by the biggest band-gap energy of Eg = 2.41 eV among tellurides, which is essentially bigger than those of LiInTe2 (1.5 eV), AgGaTe2 (1.32 eV) and AgInTe2 (1.03 eV). A sufficiently large birefringence (0.094) for LiGaTe2 allows one to obtain its room-temperature phase-matching in the whole transparency range (1.66–21 μm). Its nonlinear coefficient d36 was estimated by the phase-matched second harmonic generation to be 43 pm V−1, which is about 7 times higher than that of the related orthorhombic LiGaS2 and about 4.5 times relative to LiGaSe2. The conversion efficiency in LiGaTe2 for SHG 10.6 μm was found to be higher than that of AgGaSe2.16 Besides, this telluride is considered as a promising crystal for neutron detection.26,27 However, in several studies, it was reported on that crystal growth of LiGaTe2 is not trivial because of its high tellurium volatility and pronounced chemical activity of lithium at high temperatures.20,28–30 This may result in the defect generation and stoichiometry deviations, and these effects should be accounted to reach the optical quality crystals.
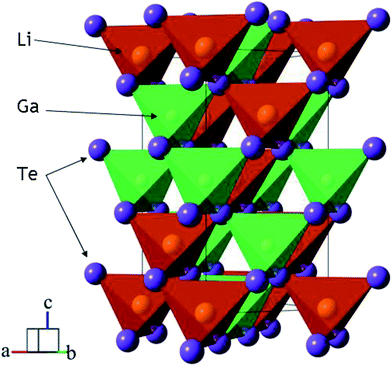 | ||
| Fig. 1 The crystal structure of LiGaTe2 chalcopyrite. The unit cell is outlined. Lone lithium and gallium atoms are omitted for clarity. | ||
For a practical NLO crystal, the crystal growth and optical response are equally important. Consequently, the thermal and chemical properties, including electronic structure analysis, play the most crucial role. However, only a few theoretical studies focus on these issues.31–36 To date, there are no reports about the dependence of structural parameters of LiGaTe2 on temperature and experimental measurements of electronic structure. Thus, the present study is aimed at the LiGaTe2 crystals growth and observation of the electronic structure in parallel by the X-ray photoelectron spectroscopy (XPS) and theoretical methods, where XPS is extremely sensitive to chemical state of the crystal surface and theoretical model is a power tool to consider the relations between crystal structure and physical properties. Besides, the dependence of structural parameters of LiGaTe2 on temperature is explored combining experimental and theoretical methods.
2. Experimental methods
LiGaTe2 crystals were obtained in three stages.37 At the first stage, we obtained the charge by fusing the elementary components Li, Ga, and Te in a glass carbon crucible inside the sealed quartz ampoule. The ampoule was evacuated to the residual pressure of 10−3 atm. The synthesis temperature was 1250 K, the initial components purity was Li 99.99%, for Ga and Te – 99.9999%. All the metal reagents were supplied by Alfa Aesar. The accuracy of reagent mass measurements was ±4 mg. The pyrosynthesis reaction proceeds with the liberation of a large amount of heat. At the conditions, Li reacts with the crucible walls and it is partially consumed. To compensate this effect, we introduced an excess of Li2Te to the starting stoichiometric composition at the level up to 16 at%. To avoid the material contamination by lithium oxide and/or nitride, the sample handling was produced in the Ar atmosphere in a specialized dry box. Upon the completion of the active synthesis stage, the melt was maintained at the melting temperature for 24 h.The second stage was the melt homogenization in a sealed quartz ampoule with an inner pyrolytic carbon coating. The homogenization temperature did not exceed 50 K above the melting point of LiGaTe2. This level was selected because the incongruent evaporation of the melt appeared above this temperature.29,30 The LiGaTe2 crystals up to 5 mm in size were grown from the homogenized melt by the Bridgman–Stockbarger technique in the two-zone vertical resistance furnace with the diaphragm in a sealed pyrocarbon inner-coated quartz ampoule. The ampoule was first evacuated to the residual pressure of 10−3 atm and then filled with a high purity Ar (P = 0.2–0.5 atm). The temperature at the start of crystallization was a few degrees below the LiGaTe2 melting point. The maximum gradient near the crystallization front was 2 K mm−1 and the ampoule movement rate to the cold zone was 2.5 mm per day. The crystal growth was performed for 20 days. The photo image of the grown crystal is shown in Fig. 2.
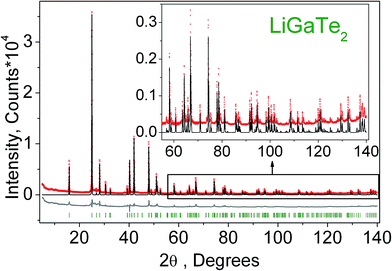
The powder diffraction data of LiGaTe2 were collected at room temperature with a Bruker D8 ADVANCE powder diffractometer (Cu-Kα radiation) and linear VANTEC detector. The step size of 2θ was 0.016° and the counting time was 1.5 s per step. The 2θ range of 5–70° was measured with the 0.6 mm divergence slit, but the 2θ range of 70–140° was measured with the 2 mm divergence slit. The intensities and obtained esd's were further normalized: Ii norm = Ii × 0.6/(slit width), σnorm(Ii) = σ(Ii) × 0.6/(slit width), taking into account the actual divergence slit width value which was used to measure each particular intensity Ii, and saved in the xye-type file. So, the transformed powder pattern had a usual view over the whole 2θ range of 5–140°, but all high-angle points had small esd values.
Additionally, to see the structural parameters dependence on temperature, fourteen X-ray diffraction (XRD) patterns in the range of 2θ = 5–120° were collected at fourteen different temperatures in the range from 303 K to 563 K spending 35 min for each pattern. The measurements were carried out using the temperature set TTK450 (Anton Paar). The recorded XRD patterns are shown in Fig. 3. It was found that the sample decomposes at a low rate in the temperature range of 303–443 K, but, after that, the rate increases and the impurity peaks prevent a good fitting. Therefore, the XRD patterns from 443 K to 563 K were recorded from a new LiGaTe2 powder sample. However, the decomposition at 583 K also leads to a large amount of Te impurity, and a further heating leads to the total sample decomposition and we stop the experiment.
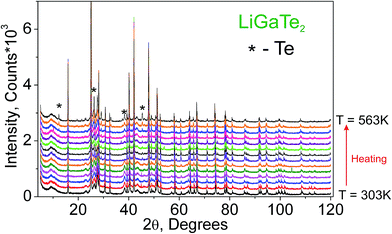 | ||
| Fig. 3 The XRD patterns recorded from the LiGaTe2 sample in the range from 303 K to 563 K. The impurity peaks related to the Te component are marked by the asterisk. | ||
The XPS spectra were recorded using a SPECS (Germany) photoelectron spectrometer equipped with a hemispherical PHOIBOS-150-MCD-9 analyzer and FOCUS-500 (Al Kα radiation, hν = 1486.74 eV, 200 W) monochromator. Just before the measurements, the binding energy (BE) scale was calibrated using the positions of the peaks of Au 4f7/2 (BE = 84.0 eV) and Cu 2p3/2 (BE = 932.67 eV) core levels. The LiGaTe2 powder sample was prepared for the XPS experiment. To decrease a possible contamination by air agents, the LiGaTe2 crystal was ground in agate mortar into the glove box filled with high-purity argon. In this way, however, the chemical reaction between LiGaTe2 and agate species can not be excluded. The LiGaTe2 powder sample was loaded onto a conducting double-sided copper scotch and transfered into the input vacuum chamber without a contact with the air environment. The details of the sample handling and BE energy scale calibration methods can be found elsewhere.38–40 The base pressure of a sublimation ion-pumped chamber of the system was less than 5 × 10−10 mbar during the present experiments. Besides the survey photoelectron spectra, the narrow spectral regions Li 1s, Te 3d, Ga 2p, Ga 3d, Te 4d and the valence band were recorded. The survey spectra were taken at the analyzer pass energy of 50 eV and the detailed spectra were registered at 20 eV. The concentration ratios of the elements on the sample surface were calculated from the integral photoelectron peak intensities which were corrected with the theoretical sensitivity factors based on Scofield photoionization cross sections.41 For the peak fitting procedure, a mixture of Lorentzian and Gaussian functions was used together with the Shirley background subtraction method.
3. Ab initio calculation methods
The electronic band structures calculations for LiGaTe2 were performed by a CASTEP package.42 The generalized gradient approximation (GGA-PBE) functionals43 were selected to be the exchange–correlation (XC) functional. The ion–electron interactions were described by optimized norm-conserving pseudopotentials.44 The orbital electrons of Li 2s1, Ga 3d104s24p1, Te 5s25p4 were treated as valence electrons and the correlation energy (U = 5.0 eV) was used to describe the Hubbard U of Ga 3d electrons. The kinetic energy cutoff of 880 eV and Monkhorst–Pack k-point meshes45 spanning less than 0.04 Å−3 (4 × 4 × 2) in the Brillouin zone were chosen to ensure the sufficient accuracy of current methods. The hydrostatic pressure (from 0 to 5 GPa; step 0.5 GPa) was applied on the LiGaTe2 crystal and geometry optimization calculations were performed until the energy change, the maximum force and maximum displacement were less than 5.0 × 10−6 eV per atom, 0.01 eV Å−1, and 5.0 × 10−4 Å, respectively. The convergence tests revealed that the above computational parameters are accurate enough for the purposes of this study. The phonon dispersion spectra of LGT were calculated by the linear response method.46 Notably, the primitive cell constants under different temperatures were fixed in phonon calculations.4. Results and discussion
4.1. Temperature effect
The crystal structure refinement was performed by the package DDM which accounts the esd values of each point by a special weight scheme.47 The powder pattern has a complex background curve due to the existence of an amorphous phase in the sample, and this was the reason for applying the DDM program instead of commonly used Rietveld programs. All diffraction peaks were indexed by the tetragonal cell (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d) with parameters close to those of LiGaTe2.16 Therefore, the crystal structure shown in Fig. 1 was taken as a starting model for the refinement. The thermal parameter of Li was not refined and other ions were refined with isotropic thermal parameters. The refinement was stable and it gave low R-factors, as evident from Table 1 and Fig. 4. The atom coordinates and main bond lengths are summarized in Tables S1 and S2,† respectively.
2d) with parameters close to those of LiGaTe2.16 Therefore, the crystal structure shown in Fig. 1 was taken as a starting model for the refinement. The thermal parameter of Li was not refined and other ions were refined with isotropic thermal parameters. The refinement was stable and it gave low R-factors, as evident from Table 1 and Fig. 4. The atom coordinates and main bond lengths are summarized in Tables S1 and S2,† respectively.
| Compound | LiGaTe2 |
| Space group | I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d 2d |
| a, Å | 6.33757 (2) |
| c, Å | 11.70095 (5) |
| V, Å3 | 469.966 (4) |
| Z | 4 |
| 2θ-interval, ° | 5–140 |
| RDDM, % | 9.48 |
| Rexp, % | 6.98 |
| χ2 | 1.36 |
| RB, % | 4.74 |
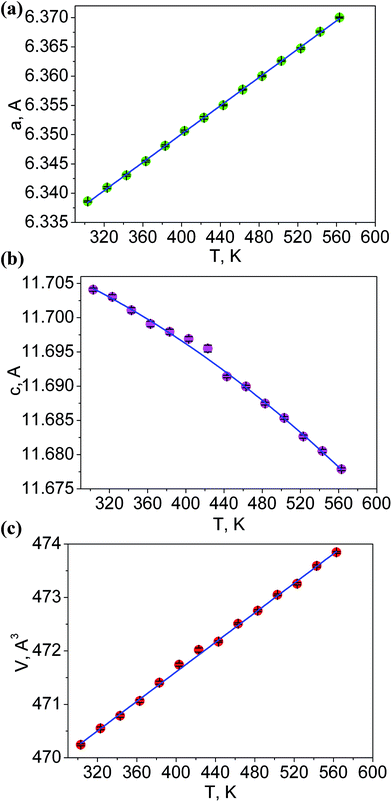
The additional fourteen powder patterns recorded at the temperatures from 303 K to 563 K were also treated by the DDM program and this gave the thermal dependencies of unit cell parameters and cell volume with a good reliability (Fig. 5, Table S3†). With the temperature increase, one can see a strong increase of a cell parameter, but cell parameter c noticeably decreases. This means that the thermal behavior of LiGaTe2 is evidently anisotropic and the negative thermal expansion is found in crystallographic direction c. However, the normal thermal expansion in two a directions is dominant; thereby, the cell volume still increases on heating, as shown in Fig. 5c. The thermal expansion coefficients obtained for LiGaTe2 are summarized in Table 2. Thus, this telluride should be classified as an anisotropic positive thermal expansion (APTE) material.
| Crystallographic parameter | Thermal expansion coefficient, K−1 |
|---|---|
| a | 19.1 × 10−6 |
| c | −8.6 × 10−6 |
| V | 29.4 × 10−6 |
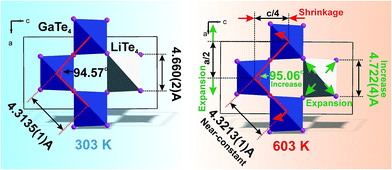
It is interesting to consider the atomic mechanism of this pronounced anisotropic expansion effect. The dependences of d(Ga–Te) and d(Li–Te) bond lengths on temperature are shown in Fig. 6. Accordingly, as the temperature increase from 303 to 563 K, the Ga–Te bond length fluctuation is only 0.2% (Fig. 6a). This implies that the Ga–Te bond length is almost persistent, manifesting the rigidity of GaTe4 tetrahedra when being heated. In comparison, the Li–Te bond length exhibits a higher flexibility and it increases from 2.751 to 2.775 Å (by 0.9%, almost five times than that of the Ga–Te bond, Fig. 6b). Coupled with the Li–Te bond elongation, the neighboring rigid GaTe4 tetrahedra rotate with each other, leading to the enlargement of the Ga–Ga–Ga angle from 94.57° to 95.06° (Fig. 6c). This effect directly results in the increase of the projection along the a-axis and the contraction of that along c-axis in the Ga–Ga distance with the increasing temperature, giving rise to the positive and negative thermal expansions of these two dimensions, respectively. Therefore, the APTE behavior of LiGaTe2 is mainly ascribed to the synergetic effect between the configuration modification of “rigid” GeTe4 and “flexible” LiTe4 tetrahedra, as depicted in Fig. 7.
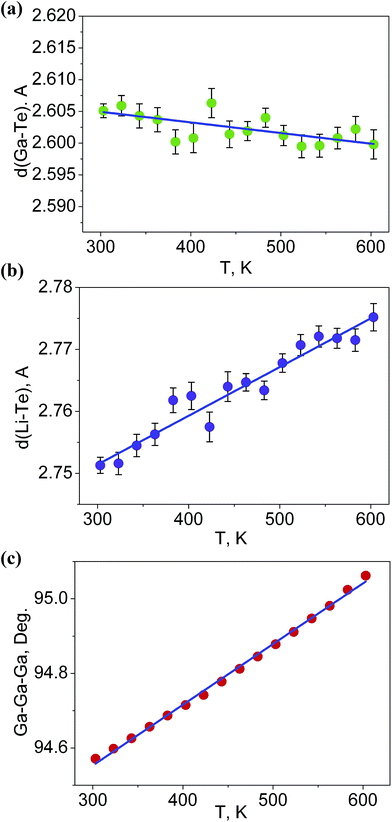 | ||
| Fig. 6 The dependences of (a) d(Ga–Te), (b) d(Li–Te) bond lengths and (c) Ga–Ga–Ga angle on temperature. | ||
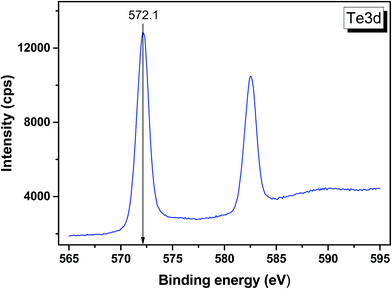
As it is known, the thermal expansion response is strongly related to intrinsic phonon vibrational modes. In order to elucidate the mechanism of negative thermal expansion along the c axis, we performed the phonon calculations of LGT at different temperatures (303, 403, 503 and 603 K) (Table 3). The lattice parameters are fixed and the atomic positions are fully relaxed in calculations. The relationship between the Grüneisen parameter and thermal expansion coefficient is given as:
and V is the volume. So, if the frequency of a vibrational mode increases with the increasing volume (increasing temperature), this phonon mode would contribute to the negative thermal expansion (NTE).
| Mode | 303 K | 403 K | 503 K | 603 K |
|---|---|---|---|---|
| E | 54.099 | 54.249 | 54.379 | 54.346 |
| E | 54.099 | 54.249 | 54.379 | 54.346 |
| B2 | 75.147 | 75.198 | 75.308 | 75.321 |
| E | 79.036 | 79.157 | 79.263 | 79.381 |
| E | 79.036 | 79.157 | 79.263 | 79.381 |
| B1 | 84.277 | 84.360 | 84.508 | 84.643 |
| A2 | 94.289 | 93.849 | 93.444 | 93.083 |
| A2 | 117.890 | 117.494 | 117.150 | 116.817 |
| A1 | 139.510 | 139.153 | 138.849 | 138.488 |
| B2 | 186.916 | 186.231 | 185.674 | 185.160 |
| B1 | 192.383 | 191.624 | 191.000 | 190.352 |
| E | 199.834 | 199.356 | 198.992 | 198.668 |
| E | 199.834 | 199.356 | 198.992 | 198.668 |
| E | 208.451 | 208.116 | 207.867 | 207.655 |
| E | 208.451 | 208.116 | 207.867 | 207.655 |
| B2 | 300.283 | 297.476 | 294.839 | 292.215 |
| E | 306.310 | 303.520 | 300.971 | 298.416 |
| E | 306.310 | 303.520 | 300.971 | 298.416 |
| E | 311.169 | 308.399 | 305.858 | 303.364 |
| E | 311.169 | 308.399 | 305.858 | 303.364 |
| B1 | 312.970 | 310.324 | 307.852 | 305.353 |
For a chalcopyrite structure with space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d, symmetry allows the optical vibrations to be classified into 15 normal modes: Γ = A1+ 2A2 + 3B1 + 3B2 + 6E, where B2 and E are polar Raman active modes having transverse optical (TO) and longitudinal optical (LO) modes, A1 and B1 are nonpolar Raman active modes, and A2 is an optically inactive mode. As seen in Table 3, six vibrational modes (low frequency region) exhibit an anomalous wavenumber increase on the increasing temperature. So, we can assigned the negative thermal expansion of LGT to these vibration modes. As shown in Fig. S1,† the B2 modes located at 75.14 cm−1 (300 K) mainly contribute to the rotation of (GaTe4) tetrahedra, coupling the Li+ slide migration along the c axis. Therefore, the negative thermal expansion of LGT along the c axis can be attributed to the tetrahedra rotation, combining the experimental measurements and theoretical calculations.48
2d, symmetry allows the optical vibrations to be classified into 15 normal modes: Γ = A1+ 2A2 + 3B1 + 3B2 + 6E, where B2 and E are polar Raman active modes having transverse optical (TO) and longitudinal optical (LO) modes, A1 and B1 are nonpolar Raman active modes, and A2 is an optically inactive mode. As seen in Table 3, six vibrational modes (low frequency region) exhibit an anomalous wavenumber increase on the increasing temperature. So, we can assigned the negative thermal expansion of LGT to these vibration modes. As shown in Fig. S1,† the B2 modes located at 75.14 cm−1 (300 K) mainly contribute to the rotation of (GaTe4) tetrahedra, coupling the Li+ slide migration along the c axis. Therefore, the negative thermal expansion of LGT along the c axis can be attributed to the tetrahedra rotation, combining the experimental measurements and theoretical calculations.48
4.2. Comparison between XPS spectra and band structure
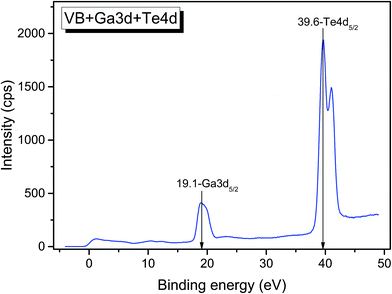
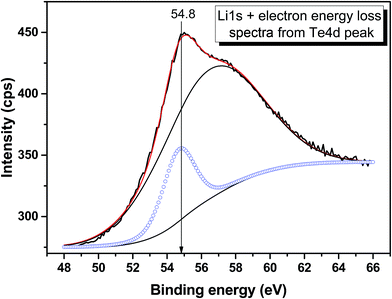
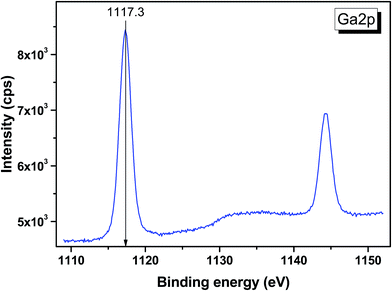
The survey photoemission spectrum recorded from the LiGaTe2 sample is shown in Fig. S2.† All detected spectral features were successfully attributed to constituent element core levels and Auger lines, except for the weak C 1s and O 1s bands shown in Fig. S3 and S4,† respectively. A comparatively narrow dominant component of the C 1s line (284.8 eV) was related to adventitious hydrocarbons adsorbed at the surface from the air, and the low-intensity additive component at 289.7 eV was attributed to carbonate species. In the O 1s line, two components can be revealed. The lower binding energy component at ∼530.4 could be attributed to the surface oxide, and a higher binding energy component appeared at ∼531.5 eV could be related to the initial stages of surface hydration. Thus, it can be concluded that LiGaTe2 is not chemically inert and it actively interacts with atmospheric agents. From the technological point of view, this should be accounted for at crystal cutting and polishing stages.The valence band spectrum and the nearest constituent element core levels are shown in Fig. 8. The mixed-states bands with several less pronounced components are found over the binding energy range of 0–17 eV. At ∼19.5 and ∼40 eV, the bands related to Ga 3d and Te 4d are observed, respectively. In Fig. 9–11, the representative element core levels Li 1s, Te 3d and Ga 2p are shown. The Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga
Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te ratio was estimated by Li 1s, Te 4d and Ga 3d peak areas and tabulated atomic sensitivity factors.41 The relative element ratio for the powder sample is Li
Te ratio was estimated by Li 1s, Te 4d and Ga 3d peak areas and tabulated atomic sensitivity factors.41 The relative element ratio for the powder sample is Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ga
Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te = 0.38
Te = 0.38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.22
0.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.40 and that indicates a noticeable enrichment of the LiGaTe2 surface by Li. Previously, a similar effect was observed for closely related compound LiGaS2.49 Thus, the Li segregation to the crystal surface may be a general feature of compounds LiGaX2 (X = S, Se, Te). The ratio Ga
0.40 and that indicates a noticeable enrichment of the LiGaTe2 surface by Li. Previously, a similar effect was observed for closely related compound LiGaS2.49 Thus, the Li segregation to the crystal surface may be a general feature of compounds LiGaX2 (X = S, Se, Te). The ratio Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te = 0.55 is in reasonable consistence with nominal composition Ga
Te = 0.55 is in reasonable consistence with nominal composition Ga![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te = 0.50. The calculations were made without carbon signal accounting. The set of the element core levels measured for LiGaTe2 is shown in Table 4. Comparatively, the BE values obtained for Li 1s, Te 3d and Ga 2p core levels in LiGaTe2 are in a good relation with the BE values obtained earlier in several other representative compounds.49–52
Te = 0.50. The calculations were made without carbon signal accounting. The set of the element core levels measured for LiGaTe2 is shown in Table 4. Comparatively, the BE values obtained for Li 1s, Te 3d and Ga 2p core levels in LiGaTe2 are in a good relation with the BE values obtained earlier in several other representative compounds.49–52
| Core level | Binding energy, eV | ||||
|---|---|---|---|---|---|
| LiGaTe2 | LiGaS2 | GaTe | PbTe(100) | Bi2Te3(001) | |
| Ga 3d | 19.1 | 19.7 | 19.5 | — | — |
| Te 4d5/2 | 39.6 | — | — | — | — |
| Te 4d3/2 | 41.0 | — | — | — | — |
| Li 1s | 54.8 | 54.9 | — | — | — |
| C 1s | Fixed at 284.8, 289.7 | Fixed at 284.6, 288.4 | — | — | Fixed at 284.8 |
| O 1s | 531.5 | 531.5 | 530.8 | 530.0 | — |
| Te 3d5/2 | 572.1 | — | 573.1 | 571.9 | 572.5 |
| Te 3d3/2 | 582.5 | — | 583.5 | — | 582.8 |
| Ga 2p3/2 | 1117.3 | 1117.6 | 1117.9 | — | — |
| Ga 2p1/2 | 1144.2 | 114.5 | — | — | — |
| Reference | This study | 49 | 50 | 51 | 52 |
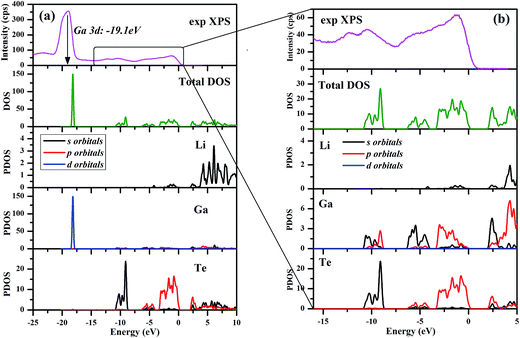
The calculated electronic total and partial densities of states (DOS and PDOS) projected on the constituent elements in LiGaTe2 are displayed in Fig. 12. LiGaTe2 is non-magnetic compound, so it spin-up and spin-down band structure (and DOS) are degenerated. Therefore, we only plotted one spin tunnel component for clarity. It is noted that the Te 4d orbitals cannot be simulated by DFT because they are inner-shell electron levels and there are no suitable pseudopotentials that take them into account. As displayed in Fig. 12a, the XPS spectrum and electron density of states are reasonably matched in the energy region from −20 to 0 eV. This confirms the validity of the plane-wave pseudopotential method in its application to LiGaTe2. Some bond characteristics can be deduced from the PDOS: (i) the Ga 3d orbitals are strongly localized at −19.1 eV, which is consistent with the calculated strong DOS peak at −18.16 eV. It hybridizes little with the orbitals of other elements, suggesting that Ga 3d electrons are not bonded with Te orbitals. Notably, the Hubbard U values mainly changes the position of Ga 3d orbitals (from −15.2 eV at U = 0 eV to −18.16 eV at U = 5 eV); (ii) the Te 5s orbitals are relatively localized at the inner energy level around −10 eV, which is slightly hybridized with Ga 4s and 4p electrons; (iii) from 10 to 0 eV, the electron states are mainly composed of Ga 4s/4p and Te 5s/5p orbitals. The strong hybridization in the wide energy range between these orbitals indicates the strong covalent interaction between Ga and Te atoms. From −10 to −8 eV, Te 5s orbitals play a crucial role. Meanwhile, Ga 4s and Te 5p orbitals make the main contribution to the hybridization interaction. Notably, the valence band maximum is mainly composed of Ga 3p and Te 5p orbitals. In addition, Li 1s orbitals are only located at the valence band maximum with a negligible contribution; (iv) the bottom of the conduction band minimum is mainly contributed from the Ga 4s and Te 5p orbitals. Since the optical effects of a crystal are mainly determined by the optical transition between the electronic states close to the bandgap, it is anticipated that they are dominantly contributed from [GaTe4] tetrahedra, and the contribution from the orbitals of Li+ cations is negligibly small.
4.3. Optical properties
LiGaTe2 is a direct gap crystal with the calculated bandgap (1.85 eV) (Fig. S5†), which is slightly smaller than the experimental value (2.30 eV) owing to the well-known band gap underestimation by the GGA exchange–correlation (XC) functional.53 Therefore, a scissors operator54 is usually introduced to shift all the conduction bands in order to agree to the experimental band gap value for calculating the optical coefficients. The calculated second order NLO coefficient is d36 = −52.7 pm V−1, which is comparable to other calculated results.55 If adopting GGA+U method, the calculated d36 is −49.6 pm V−1. The Hubbard U mainly changes the position of Ga 3d orbitals but no influence on the electric bands near forbidden gap (see Fig. S6†). Because the optical effects of a crystal are mainly determined by the optical transition between the electronic states close to the band gap, accordingly, it is anticipated that the effects of Hubbard U are negligibly small on optical properties. In addition, the birefringence is calculated to be 0.035 (see Fig. S7†), which is smaller than the experimental results,16 but it agrees well to other calculated results.34,554.4. Pressure effect
The SHG coefficients of NLO materials are highly dependent on the band gap energy. Band gap engineering is generally achieved through lattice distortion by the impurity doping that results in changing the material composition. Since this method often leads to some negative change that could not be controlled well, material compression under high pressure is a remarkable alternative for changing the lattice parameters while keeping the element composition. To identify the high pressure effects on the properties of the LiGaTe2 crystal, the lattice constants and band gap energy dependence on the pressure applied uniformly is also investigated. The crystal lattice constants (a and c axis) and the band gap energy of the LiGaTe2 at different pressures are shown in Fig. 13. The a and c axes compression up to 5% and 3%, respectively, refers to the pressure uniformly applied on the crystal in the range of 0–5 GPa. The LiGaTe2 band gap decreases monotonically with the increasing pressure, which is similar to that of Li2S56 and As2S3.57 For the As2S3 crystal, the optical band gap red-shifts rapidly with the increasing pressure, decreasing from 2.7 eV at the ambient condition to 1.6 eV at 10 GPa. Owing to a positive correlation between the band gap and laser induced damage threshold (LIDT), it indicates that the LIDT value of LiGaTe2 will decrease with applying the external pressure.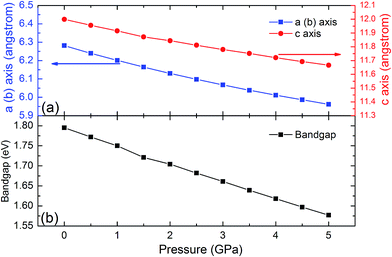 | ||
| Fig. 13 The crystal lattice constants (a and c) and band gap energy of LiGaTe2 as a function of pressure. | ||
5. Conclusions
In this study, the big-sized high-quality LiGaTe2 crystal was grown by the Bridgman–Stockbarger method. The anisotropic thermal expansion behavior of the LiGaTe2 crystal was measured for the first time. Combining the experimental characterization and theoretical calculations, the negative thermal expansion along the c axis was assigned to the rotational vibration mode of (GaTe4) tetrahedra. The negative thermal expansion was first found in chalcopyrite-type chalcogenides and, respectively, searching for similar structural effects in other materials from this wide crystal family is topical. In addition, the electronic structure of LiGaTe2 crystal was measured by XPS and the recorded valence band is in a good agreement with the theoretical electronic density of states. Moreover, the optical properties and pressure response from 0 to 5 GPa were also calculated in the theory. These results indicate that LiGaTe2, besides its well known pronounced linear and nonlinear optical properties in IR spectral range, possesses the specific structural effects that may be a way to new applications of this telluride material.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the state assignment project (0330-2016-0008), Russian Foundation for Basic Research (Grant No. 17-45-540775, 16-52-48010, 17-52-53031), National Natural Science Foundation of China under Grant No. 91622118, 91622124, 11174297, 51602318, 11611530680 and China “863” project (Grant No. 2015AA034203). Besides, this study was partly supported by the Russian Science Foundation (Grant No. 17-12-01047, in the part of XPS measurements).References
- A. Rogalski, Rep. Prog. Phys., 2005, 68, 2267–2336 CrossRef CAS.
- J.-F. Li, W.-S. Liu, Li-D. Zhao and M. Zhou, NPG Asia Mater., 2010, 2, 152–158 CrossRef.
- L. Isaenko, A. Yelisseyev, S. Lobanov, A. Titov, V. Petrov, J.-J. Zondy, P. Krinitsin, A. Merkulov, V. Vedenyapin and J. Smirnova, Cryst. Res. Technol., 2003, 38, 379–387 CrossRef CAS.
- W. Yin, W. Wang, L. Bai, K. Feng, Y. o Shi, W. Hao, J. Yao and Y. Wu, Inorg. Chem., 2012, 51, 11736–11744 CrossRef CAS PubMed.
- V. V. Atuchin, T. A. Gavrilova, K. A. Kokh, N. V. Kuratieva, N. V. Pervukhina and N. V. Surovtsev, Solid State Commun., 2012, 152, 1119–1122 CrossRef CAS.
- Y. Tanaka, Z. Ren, T. Sato, K. Nakayama, S. Souma, T. Takahashi, K. Segawa and Y. Ando, Nat. Phys., 2012, 8, 800–803 CrossRef CAS.
- C. D. Malliakas, D. Young Chung, H. Claus and M. G. Kanatzidis, J. Am. Chem. Soc., 2013, 135, 14540–14543 CrossRef CAS PubMed.
- A. Yasuda, K. Suto and J.-i. Nashizawa, Mater. Sci. Semicond. Process., 2014, 27, 159–162 CrossRef CAS.
- K. A. Kokh, V. V. Atuchin, T. A. Gavrilova, N. V. Kuratieva, N. V. Pervukhina and N. V. Surovtsev, Solid State Commun., 2014, 177, 16–19 CrossRef CAS.
- S. A. Avanesov, D. V. Badikov, V. V. Badikov, V. L. Panyutin, V. Petrov, G. S. Shevyrdyaeva, A. A. Martynov and K. V. Mitin, J. Alloys Compd., 2014, 612, 386–391 CrossRef CAS.
- S. Welzmiller, F. Hennersdorf, R. Schlegel, A. Fitch, G. Wagner and O. Oekler, Inorg. Chem., 2015, 54, 5745–5756 CrossRef CAS PubMed.
- V. V. Atuchin, V. A. Golyashov, K. A. Kokh, I. V. Korolkov, A. S. Kozhukhov, V. N. Kruchinin, I. D. Loshkarev, L. D. Pokrovsky, I. P. Prosvirin, K. N. Romanyuk and O. E. Tereshchenko, J. Solid State Chem., 2016, 236, 203–208 CrossRef CAS.
- L. I. Isaenko and A. P. Yelisseyev, Semicond. Sci. Technol., 2016, 31, 123001 CrossRef.
- M. C. Ohmer, J. T. Goldstein, D. E. Zelton, A. W. Saxler, S. M. Hegde, J. D. Wolf, P. G. Schuneman and T. M. Pollak, J. Appl. Phys., 1999, 86, 94–99 CrossRef CAS.
- A. H. Reshak, Linear, nonlinear optical properties and birefringence of AgGaX2 (X = S, Se, Te) compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 369, 243–253 CrossRef CAS.
- L. Isaenko, P. Krinitsin, V. Vedenyapin, A. Yelisseyev, A. Merkulov, J.-J. Zondy and V. Petrov, Cryst. Growth Des., 2005, 5, 1325–1329 CAS.
- J.-J. Zondy, F. Bielsa, A. Douillet, L. Helico, O. Acef, V. Petrov, A. Yelisseyev, L. Isaenko and P. Krinitsin, Opt. Lett., 2007, 32, 1722–1724 CrossRef CAS PubMed.
- S. Avanesov, V. Badikov, A. Tyazhev, D. Badikov, V. Panyutin, G. Marchev, G. Shevyrdyaeva, K. Mitin, F. Noack, P. Vinogradova, N. Schebetova, V. Petrov and A. Kwasniewski, Opt. Mater. Express, 2011, 1, 1286–1291 CrossRef CAS.
- S. Wang, G. Liu, Q. Shi, X. Zhang, X. Zhang, C. Li, Z. Gao, C. Dong, Q. Lu and X. Tao, RSC Adv., 2014, 4, 27830–27836 RSC.
- A. Yelisseyev, P. Krinitsin, L. Isaenko and S. Grazhdannikov, Opt. Mater., 2015, 42, 276–280 CrossRef CAS.
- A. A. Ionin, I. O. Kinyaevskiy, Y. M. Klimachev, A. A. Kotkov, V. V. Badikov and K. V. Mitin, Opt. Lett., 2016, 41, 2390–2393 CrossRef CAS PubMed.
- H. Lin, Y. Liu, L.-J. Zhou, H.-J. Zhao and L. Chen, Inorg. Chem., 2016, 55, 4470–4475 CrossRef CAS PubMed.
- V. Petrov, L. Isaenko, A. Yelisseyev, P. Krinitsin, V. Vedenyapin, A. Merkulov and J.-J. Zondy, J. Non-Cryst. Solids, 2006, 352, 2434–2438 CrossRef CAS.
- F. Liang, L. Kang, Z. Lin, Y. Wu and C. Chen, Coord. Chem. Rev., 2017, 333, 57–70 CrossRef CAS.
- T. C. Ozawa and S. J. Kang, J. Appl. Crystallogr., 2014, 37, 679 CrossRef.
- A. C. Stowe, J. S. Morrell, P. Bhattacharya, E. Tupitsyn and A. Burger, Proc. SPIE, 2011, 8142, 81421H CrossRef.
- E. Tupitsyn, P. Bhattacharya, E. Rowe, L. Matei, Y. Cui, V. Buliga, M. Groza, B. Wiggins, A. Burger and A. Stowe, J. Cryst. Growth, 2014, 393, 23–27 CrossRef CAS.
- L. Isaenko, I. Vasilieva, A. Merkulov, A. Yelisseyev and S. Lobanov, J. Cryst. Growth, 2005, 275, 217–223 CrossRef CAS.
- L. I. Isaenko and I. G. Vasilyeva, J. Cryst. Growth, 2008, 310, 1954–1960 CrossRef CAS.
- I. G. Vasilyeva, R. E. Nikolaev, P. G. Krinitsin and L. I. Isaenko, J. Phys. Chem. C, 2017, 121, 17429–17435 CAS.
- Yu. M. Basalaev, Yu. N. Zhuravlev, E. B. Kitova and A. S. Poplavnoi, J. Struct. Chem., 2007, 48, 1001–1005 CrossRef CAS.
- V. V. Atuchin, L. I. Isaenko, V. G. Kesler, S. Lobanov, H. Huang and Z. S. Lin, Solid State Commun., 2009, 149, 572–575 CrossRef CAS.
- A. V. Kosobutsky, Y. M. Basalaev and A. S. . Poplavnoi, Phys. Status Solidi B, 2009, 246, 364–371 CrossRef CAS.
- A. V. Kosobutsky and Y. M. Basalaev, J. Phys. Chem. Solids, 2010, 71, 854–861 CrossRef CAS.
- T. Ma, L. Sun, C. Xu and Y. Chen, J. Alloys Compd., 2011, 509, 9733–9741 CrossRef CAS.
- M. Tian-Hui, Z. Zhi-Ping and R. n Yu-Lan, Acta Phys. Sin., 2012, 61, 197101 Search PubMed.
- S. A. Grazhdannikov, P. G. Krinitsyn, A. F. Kurus', L. I. Isaenko, A. P. Yelisseyev and M. S. Molokeev, Mater. Sci. Semicond. Process., 2017, 72, 52–59 CrossRef CAS.
- D. V. Demidov, I. P. Prosvirin, A. M. Sorokin and V. I. Bukhtiyarov, Catal. Sci. Technol., 2011, 1, 1432–1439 CAS.
- V. V. Atuchin, V. A. Golyashov, K. A. Kokh, I. V. Korolkov, A. S. Kozhukhov, V. N. Kruchinin, S. V. Makarenko, L. D. Pokrovsky, I. P. Prosvirin, K. N. Romanyuk and O. E. Tereshchenko, Cryst. Growth Des., 2011, 11, 5507–5514 CAS.
- E. J. Rubio, V. V. Atuchin, V. N. Kruchinin, L. D. Pokrovsky, I. P. Prosvirin and C. V. Ramana, J. Phys. Chem. C, 2014, 118, 13644–13651 CAS.
- J. H. Scofield, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 129–137 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- L. A. Solovyov, J. Appl. Crystallogr., 2004, 37, 743–749 CrossRef CAS.
- J. Haines, C. Chateau, J. M. Léger, C. Bogicevic, S. Hull, D. D. Klug and J. S. Tse, Phys. Rev. Lett., 2003, 91, 015503 CrossRef CAS PubMed.
- V. V. Atuchin, L. I. Isaenko, V. G. Kesler and S. I. Lobanov, J. Alloys Compd., 2010, 497, 244–248 CrossRef CAS.
- K. S. Mandal, R. M. Krishna, T. C. Hayes, P. G. Muzykov, S. Das, T. S. Sudarshan and S. Ma, IEEE Trans. Nucl. Sci., 2011, 58, 1981–1986 CrossRef CAS.
- L. V. Yashina, E. V. Tikhonov, V. S. Neudachina, T. S. Zyubina, A. N. Chaika, V. I. Shtanov, S. P. Kobeleva and Yu. A. Dobrovolsky, Surf. Interface Anal., 2004, 36, 993–996 CrossRef CAS.
- V. V. Atuchin, V. A. Golyashov, K. A. Kokh, I. V. Korolkov, A. S. Kozhukhov, V. N. Kruchinin, I. D. Loshkarev, L. D. Pokrovsky, I. P. Prosvirin, K. N. Romanyuk and O. E. Tereshenko, J. Solid State Chem., 2016, 236, 203–208 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef.
- C. S. Wang and B. M. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 3417–3429 CrossRef CAS.
- L. Bai, Z. S. Lin, Z. Z. Wang and C. T. Chen, J. Appl. Phys., 2008, 103, 083111 CrossRef.
- R. D. Eithiraj, G. Jaiganesh, G. Kalpana and M. Rajagopalan, Phys. Status Solidi B, 2007, 244, 1337–1346 CrossRef CAS.
- R. Zallen, High Pressure Res., 2004, 24, 117–118 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra01079j |
| This journal is © The Royal Society of Chemistry 2018 |