Theoretical research on novel orthorhombic tungsten dinitride from first principles calculations

Abstract

Tungsten nitrides have been intensely studied for technological applications owing to their unique mechanical, chemical, and thermal properties. Combining first-principles calculations with an unbiased structural searching method (CALYPSO), we uncovered a novel orthorhombic structure with a space group Cmc2₁ as the thermodynamically most stable phase for tungsten dinitride (WN₂) between 46–113 GPa. The computed elastic constants and phonons reveal that the Cmc2₁-WN₂ structure is dynamically stable at atmospheric pressure. Moreover, hardness calculations indicate that this structure is likely to become a hard material. Our current results may stimulate further experimental work on synthesizing these technologically important materials and improve the understanding of the pressure-induced phase transitions of other transition-metal light-element compounds.

---

1. Introduction

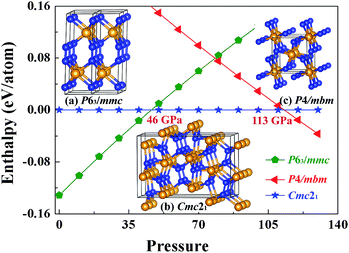
Tungsten nitrides have greater potential than other nitrides not only due to their mechanical, catalytic, optical, electronic, and hardness properties but also due to tungsten's wide availability, their economical synthesis and their varied possible stoichiometric compositions.^1–4 These qualities make them practically useful in industrial applications such as in cutting tools, super-abrasive materials, and wear-resistant coatings, all leading them to be the subject of considerable research interest.^5–15 In particular, tungsten nitrides (WN, W₃N₄, W_2.25N₃, W₂N₃) were recently successfully synthesized through new approaches involving metathesis reaction, solid-state ion exchange and nitrogen degassing under high pressure and high temperature (5 GPa, 880–2570 K;¹⁶ 7.7 GPa, 1373–1973 K;¹⁷ 600–675 °C (ref. 18)), which could be quenched and stabilized to ambient conditions. These have attracted significant attentions on these compounds and motivated considerable interest in searching for new tungsten nitrides. Theoretical researches also show that in nitrogen-rich materials the chemical bonding is strongly covalent so that they have high bulk modulus and high hardness such as Zr₃N₄,¹⁹ Hf₃N₄,¹⁹ PtN₂,^20,21 OsN₂,²² and IrN₂,²² synthesized under high pressure. Therefore, it is advantageous to choose nitrogen-enriched compounds using high-pressure methods in searching for new superhard materials. It is noteworthy that, in a very recent work, Lu et al. suggested WN is likely to become a superhard material (>40 GPa).¹⁵ Tungsten dinitride (WN₂) is thus expected to be a good candidate for high hardness materials, since it possessed one more N atom per formula unit compared to WN.

For a long time, WN₂ has been theoretically suggested to adopt P6₃/mmc¹⁰ structure at atmosphere pressure. Other researchers proposed a tetragonal phase of WN₂ through replacing the P4/mbm-ReN₂ structure.¹¹ In this work, we established thermodynamically stable structures of WN₂ over a wide range of pressures combining the first-principles calculations with unbiased structural searching methods. A novel orthorhombic WN₂ with a space group Cmc2₁ is predicted which is energetically superior to the previously proposed P6₃/mmc phase above 46 GPa and P4/mbm phase below 113 GPa. This structure is incompressible and has not been reported before. As this newly found structure is dynamically stable, it can be prepared at high-pressure and high-temperature and quenched recovered under atmospheric conditions. This work not only revised the phase diagram of WN₂ at high pressures, but also provided useful information and important guidance for the further experimental synthesis and theoretical study of WN₂.

2. Computational details

Our global structural prediction used the unbiased intelligence based on CALYPSO^23–25 methods which have successfully predicted structures of various systems.^26–30 The structural relaxations, electron localization function (ELF) and electronic band structure calculations were performed using the density functional theory within the local density approximation (LDA)^31,32 as implemented in the Vienna ab initio simulation package (VASP) code.³³ The electron–ion interaction was described by means of projector augmented wave (PAW)³⁴ with 5d⁴6s² and 2s²2p³ electrons as valence for tungsten and nitrogen atoms, respectively. The PAW³⁴ method was adopted with a plane-wave kinetic-energy cutoff of 520 eV to give excellent convergence on the total energies and structural parameters. The Monkhorst–Pack (MP) k meshes³⁵ 0.025 Å⁻¹ were chosen to ensure the energies of all structures were well converged to be better than 1 meV per atom. The phonon frequencies were calculated using the direct supercell method, which uses the forces obtained by the Hellmann–Feynman theorem calculated from the optimized supercell.³⁶ Accurate crystal elastic constants and modulus were calculated by using the Voigt–Reuss–Hill approximation.³⁷ The simulated micro hardness^38,39 were used to evaluate the mechanical properties for these WN compounds.

3. Results and discussion

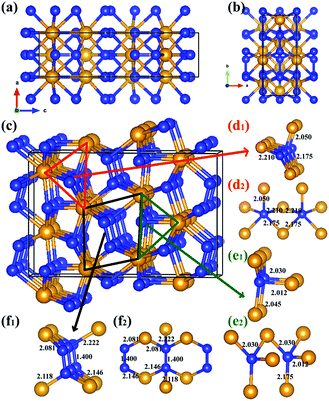
In the previous theoretical studies, Wang et al. predicted a hexagonal structure with space group P6₃/mmc¹⁰ which is potential ultra-incompressible and energetically superior to the previously proposed phase hence it is regarded as the ground state of WN₂ up to 60 GPa. Yan et al.¹¹ put forward a tetragonal phase of WN₂ through replace the P4/mbm-ReN₂ structure which exhibits an unusual incompressibility along the c axis on a par with diamond. This P4/mbm phase is dynamically stable, nevertheless, metastable compared to P6₃/mmc at 0 GPa.¹¹ Due to the potential importance of this material, we have performed the systematical structural prediction for WN₂ compound in the pressure range of 0–150 GPa (3–24 atoms for each pressure) using unbiased intelligence structural searches. Here, we found that three structures could exist in different pressure ranges [Fig. 1(a)–(c)]. Besides the ground state phase (P6₃/mmc)¹⁰ and high-pressure phase (P4/mbm)¹¹ which fits well with previous researches, our structural search also successfully identified a new orthorhombic structure with a space group Cmc2₁ [Fig. 1(b)] as the thermodynamically most stable phase for WN₂ between 46 and 113 GPa as shown in Fig. 1. It is noteworthy that this structure is more complex than the other two previous structures with higher symmetry. The present results revised the phase diagram of WN₂ at high pressures.

Fig. 1 Enthalpy of WN₂ versus pressure. Pentagons, triangles and pentagonal stars represent P6₃/mmc, P4/mbm and Cmc2₁ structures respectively. The illustrations are the structures of the P6₃/mmc (a), Cmc2₁ (b) and P4/mbm (c) phases of WN₂. The large orange and small blue spheres represent W and N atoms, respectively.

The equilibrium lattice parameter of the Cmc2₁-WN₂ structure are a = 2.909 Å, b = 6.875 Å, c = 10.517 Å at 0 GPa while a = 2.802 Å, b = 6.721 Å, c = 10.153 Å at 50 GPa. There are eight WN₂ formula units in the unit cell, and the tungsten atoms occupied the Wyckoff 4d(0, 0.150, 0.581), 4d(0.500, 0.942, 0.792), while the nitrogen atoms at the 8b(0.500, 0.774, 0.231), 8b(0.000, 0.247, 0.947) positions. The density of Cmc2₁-WN₂ is 13.383 g cm⁻³ at 0 GPa. Through observation of Cmc2₁-WN₂ along the A axis, we prove that the structure is arranged in a neat layer while disordered along other directions [Fig. 2(a) and (b)]. Besides, this phase consists of a fundamental building block connected by irregular rings [Fig. 2(c)]. We have selected three representative bonding modalities of nitrogen atoms in the Cmc2₁-WN₂ structure and exhibited in different crystallographic planes. The first kind of nitrogen atom has five neighboring tungsten atoms [Fig. 2(d)] with W–N bond lengths of 2.050 Å, 2.175 Å and 2.210 Å. The other two kinds of nitrogen atoms have four neighboring atoms. By contrast, one of them is adjacent to four tungsten atoms [Fig. 2(e)] while another one has a neighboring nitrogen atom [Fig. 2(f)]. The bond lengths are shown in the Fig. 2. It is worth noting that the N–N bond length is 1.400 Å at 0 GPa while 1.364 Å at 50 GPa [Fig. 2(f)].

Fig. 2 The Cmc2₁-WN₂ structure is shown in different crystallographic planes in order to perceive the structures more clearly (a)–(c). The bond lengths are pinpoints as shown in (d), (e) and (f). The large orange and small blue spheres represent W and N atoms, respectively.

We calculated the charge density distribution and Electron Localization Function (ELF) that enables an effective and reliable analysis of the interaction between atoms. Here, we use a high isosurface value of 0.8 which indicates the possible formation of strong covalent bonds.^40,41 Previous studies have shown that an important ultra-incompressible effect comes from strong covalent N–N bonding.^20,21 High electron localization can be clearly seen in the region between adjacent N–N and W–N bonds, indicative of strong covalent bonding (Fig. 3). As shown in the Fig. 3, the bonding environment of nitrogen atoms is much more complex. The calculated ELF exhibits that some nitrogen atoms in Cmc2₁-WN₂ structure are fourfold coordinated with three near-neighbor tungsten atoms and one nitrogen atom hence forming a three-dimensional covalently bonded framework. Some nitrogen atoms are five-coordinated with neighboring tungsten atoms. The other nitrogen atoms are four-coordinated and forming a stable sp³ bonding state with tungsten atoms. These strong three-dimensional covalent bonds could reasonably lead to super hardness properties of Cmc2₁-WN₂ structure. The calculated charge of Cmc2₁-WN₂ showed there is the charge transfer between W (∼2.774) and N (1.449 and 1.327) atoms.

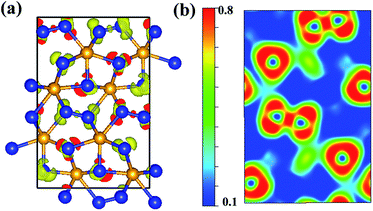Fig. 3 Contours of the ELF of Cmc2₁-WN₂with isosurface = 0.8. The 2D-ELF is given for better observation.

As the strong covalent W–N and N–N bonding play a key role in the ultra-incompressibility, Cmc2₁-WN₂ may become one of the potential candidates for superhard materials. It is of the fundamental importance to compute the mechanical properties and hardness of WN₂. The computed elastic constants (C_ij) are listed in Table 1 as well as the previously predicted P6₃/mmc and P4/mbm for comparison. It is well known that, for orthogonal structure, the mechanical stability requires that the elastic constants have to satisfy the following conditions:⁴² C_ii >0 (i = 1–6), C₁₁ + C₂₂ + C₃₃ + 2(C₁₂ + C₁₃ + C₂₃) > 0, C₁₁ + C₂₂ − 2C₁₂ > 0, C₁₁ + C₃₃ − 2C₁₃ > 0, C₂₂ + C₃₃ − 2C₂₃ > 0. For tetragonal and hexagonal structures, the C_ij's need satisfy the following conditions: C₁₁ > 0, C₃₃ > 0, C₄₄ > 0, C₆₆ > 0, (C₁₁ − C₁₂) > 0, (C₁₁ + C₃₃ − 2C₁₃) > 0, 2(C₁₁ + C₁₂) + C₃₃ + 4C₁₃ > 0 and C₄₄ > 0, C₁₁ > |C₁₂|, (C₁₁ + C₁₂) × C₃₃ > 2C₁₂,² respectively. The elastic constants in Table 1 satisfy all of the conditions above, indicating they are mechanically stable.

Table 1 The theoretical elastic constants C_ij (GPa), bulk modulus B (GPa), shear modulus G (GPa) Young's modulus Y (GPa), and hardness (GPa) of Cmc2₁, P6₃/mmc and P4/mbm are given at atmospheric pressure

	C11	C12	C13	C23	C33	C44	C66	B	G	Y	Hv^tian	Hv^chen
Cmc21	641	311	298	232	728	298	251	437	252	596	21.9	23.6
P63/mmc^10	579	195	211		973	233		364	228	695		24.7
P4/mbm^11	785	188	165		894	275	308	389	300	716		38.5

---

The bulk moduli (B) of Cmc2₁-WN₂ (437 GPa) is larger than the other two structures, which is comparable to the experimental value of diamond of 446 GPa (ref. 43) and indicate its ultra-incompressible nature. The ratio of B and shear modulus G for these structures are found lower than 1.75 (threshold for a material becoming ductile), indicating that these three WN₂ compounds are brittle material. In addition, the calculated Young's modulus for novel Cmc2₁-WN₂ is much lower than that of other two phases. The Vickers hardness of the Cmc2₁-WN₂ was calculated both using a semiempirical model designed for covalency dominant crystals in particular transition-metal carbides and nitrides (eqn (1))³⁸ and a theoretical model which establishes a robust correlation between hardness and elasticity (eqn (2)),³⁹

H_v (GPa) = 1051 N_e^2/3d^−2.5e^{−1.191f_i−32.2f_m0.55} (1)

H_v = 2(k²G)^0.585 − 3 (2)

In eqn (1), N_e is the valence electron density (Å⁻³), d is the bond length, f_i is the ionicity of the chemical bond in the crystal on the Phillips scale, and f_m is a factor of metallicity. In eqn (2), k is the Pugh's ratios (k = G/B). The calculated Vickers hardness (ambient pressure values) for the Cmc2₁-WN₂ structures is 21.9 GPa and 23.6 GPa, respectively indicates that it is a hard material (20 GPa). The hardness of the other two structures are also listed for comparison.^10,11

Furthermore, we have investigated the electronic properties of the predicted structure. The band structure of Cmc2₁-WN₂ is plotted in Fig. 4(a) together with the corresponding partial density of states (PDOS). It is found that the Cmc2₁-WN₂ structure is shown to be metallic with the majority of the DOS near the Fermi level contributed by p-states of nitrogen and d-states of tungsten. Strong hybridization between the W-d and N-p orbitals suggests the strong covalent bonding between the W and N atoms, in satisfactory agreement with the ELF analysis. The pronounced peaks in the DOS of Cmc2₁-WN₂ correspond to flat bands in the band structure. Phonon calculation played a key role in understanding the dynamic stabilities of the predicted structures. The calculations on phonon dispersion clearly show that there is no imaginary phonon frequency in the whole Brillouin zones of Cmc2₁-WN₂ [Fig. 4(b)], indicating this structure is dynamically stable at ambient pressure that thus suggest the predicted structure could in principle be experimentally synthesized and quenched recovered to atmospheric conditions. We have also investigated the P6₃/mmc and P4/mbm as well, and the results reveal the both structures are dynamically stable.^10,11

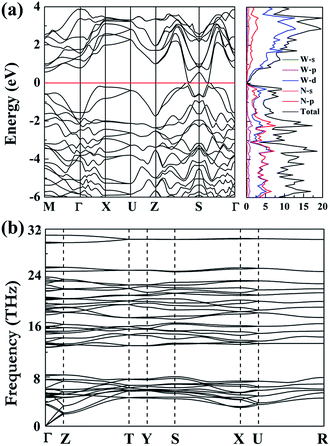Fig. 4 Calculated band, dos (a) and phonon dispersion curves (b) of the Cmc2₁-WN₂ at the atmospheric conditions.

4. Conclusion

In summary, we have performed the simulations on the thermodynamically stable structures of WN₂ over a wide range of pressures combining the first-principles calculations with unbiased structural searching method. We uncovered a novel orthorhombic structure with a space group Cmc2₁ as the thermodynamically most stable phase for WN₂ between 46–113 GPa. A comprehensive study of the elastic properties, ELF and hardness demonstrated that the novel Cmc2₁-WN₂ exhibit excellent mechanical and ultra-incompressible properties. No imaginary phonon frequencies indicate that the structure is dynamically stable therefore it can be prepared at high-pressure and high-temperature and quenched recovered to atmospheric conditions. These findings will inevitably stimulate extensive experimental works on synthesizing these technologically important materials and theoretical work to explore the rich and complex phases of transition-metal and light-element compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Natural Science Foundation of China under No. 11747049, Shandong Provincial Natural Science Foundation of China under Grant No. ZR2017LA008, Science Foundation of Binzhou University under Grant No. 2016Y03.

References

1. S. Anwar, Surf. Eng., 2017, 33, 276.
2. P. Nayak, S. Anwar, S. Bajpai and S. Anwar, in AIP Conference Proceedings, 2017, vol. 1832, p. 080063.
3. N. Schönberg, Acta Chem. Scand., 1954, 8, 204.
4. M. Zhang, Y. Qiu, Y. Han, Y. Guo and F. Cheng, J. Power Sources, 2016, 322, 163.
5. Y. Shen, Y. Mai, D. R. McKenzie, Q. Zhang, W. D. McFall and W. E. McBride, J. Appl. Phys., 2000, 88, 1380.
6. M. J. Mehl, D. Finkenstadt, C. Dane, G. L. Hart and S. Curtarolo, Phys. Rev. B, 2015, 91, 184110.
7. P. Hones, N. Martin, M. Regula and F. Lévy, J. Phys. D: Appl. Phys., 2003, 36, 1023.
8. Y. Dong and J. Li, Chem. Commun., 2015, 51, 572.
9. Q. Li, L. Sha, C. Zhu and Y. Yao, Europhys. Lett., 2017, 118, 46001.
10. H. Wang, Q. Li, Y. Li, Y. Xu, T. Cui, A. R. Oganov and Y. Ma, Phys. Rev. B, 2009, 79, 132109.
11. H. Yan, M. Zhang, Q. Wei and P. Guo, J. Alloys Compd., 2013, 581, 508.
12. Z. Zhao, K. Bao, D. Duan, F. Tian, Y. Huang, H. Yu, Y. Liu, B. Liu and T. Cui, Phys. Chem. Chem. Phys., 2015, 17, 13397.
13. Z. Liu, X. Zhou, D. Gall and S. Khare, Comput. Mater. Sci., 2014, 84, 365.
14. D. Suetin, I. Shein and A. Ivanovskii, Russ. Chem. Rev., 2010, 79, 611.
15. C. Lu, Q. Li, Y. Ma and C. Chen, Phys. Rev. Lett., 2017, 119, 115503.
16. S. Wang, X. Yu, Z. Lin, R. Zhang, D. He, J. Qin, J. Zhu, J. Han, L. Wang, H. Mao, J. Zhang and Y. Zhao, Chem. Mater., 2012, 24, 3023.
17. F. Kawamura, H. Yusa and T. Taniguchi, J. Am. Ceram. Soc., 2018, 101, 949.
18. D. Choi and P. N. Kumta, J. Am. Ceram. Soc., 2007, 90, 3113.
19. A. Zerr, G. Miehe and R. Riedel, Nat. Mater., 2003, 2, 185.
20. E. Gregoryanz, M. Sanloup, J. Badro, G. Fiquet, H. K. Mao and R. J. Hemley, Nat. Mater., 2004, 3, 294.
21. J. Crowhurst, A. Goncharov, B. Sadigh, C. Evans, P. Morrall, J. Ferreira and A. Nelson, Science, 2006, 311, 1275.
22. A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. H. Hemley and H. K. Mao, Phys. Rev. Lett., 2006, 96, 155501.
23. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063.
24. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B, 2010, 82, 094116.
25. X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101.
26. Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, J. Chem. Phys., 2014, 140, 174712.
27. M. Zhang, H. Liu, Q. Li, B. Gao, Y. Wang, H. Li, C. Chen and Y. Ma, Phys. Rev. Lett., 2015, 114, 015502.
28. L. Zhang, Y. Wang, J. Lv and Y. Ma, Nat. Rev. Mater., 2017, 2, 17005.
29. L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Nat. Chem., 2014, 6, 644.
30. X. Yong, H. Liu, M. Wu, Y. Yao, J. S. Tse, R. Dia and C. S. Yoo, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11110.
31. D. M. Ceperley and B. Alder, Phys. Rev. Lett., 1980, 45, 566.
32. J. Ihm, A. Zunger and M. L. Cohen, J. Phys. C: Solid State Phys., 1979, 12, 4409.
33. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169.
34. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758.
35. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.
36. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B, 2008, 78, 134106.
37. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
38. X. Guo, L. Li, Z. Liu, D. Yu, J. He, R. Liu, B. Xu, Y. Tian and H. Wang, J. Appl. Phys., 2008, 104, 023503.
39. X. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275.
40. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397.
41. B. Silvi and A. Savin, Nature, 1994, 371, 683.
42. M. Born and R. D. Misra, On the stability of crystal lattices, Cambridge University Press, 1940, vol. 36, p. 466.
43. F. Occelli, D. L. Farber and R. L. Toullec, Nat. Mater., 2003, 2, 151.

---