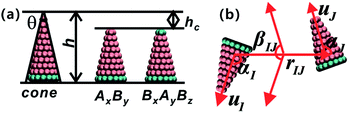Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-assembly of amphiphilic truncated cones to form hollow nanovesicles†
Yali Wanga and
Xuehao He *abc
*abc
aDepartment of Chemistry, School of Science, Tianjin University, Tianjin 300350, China. E-mail: xhhe@tju.edu.cn
bDemonstration Centre for Experimental Chemistry & Chemical Engineering Education, Tianjin University, Tianjin 300350, China
cNational Virtual Simulation Experimental Teaching Centre for Chemistry & Chemical Engineering Education, Tianjin University, Tianjin 300350, China
First published on 10th April 2018
Abstract
To mimic the unique properties of capsid (protein shell of a virus), we performed Brownian dynamics simulations of the self-assembly of amphiphilic truncated cone particles with anisotropic interactions. The particle shape of a truncated cone in our simulations depended on the cone angle θ, truncated height hc and particle type (AxBy and BxAyBz). The hydrophobic A moieties and hydrophilic B moieties are responsible for attractive and repulsive interactions, respectively. By varying the particle shape, truncated cones can assemble into hollow and vesicle-like clusters with a specific cluster size N. To assemble into hollow vesicles, the truncated height hc must be below a critical value. When hc exceeds this critical value, malformation will occur. The dynamics shows that the vesicle formation occurs in three stages: initially the growth is slow, then rapid, and finally it slows down. The truncated height hc has a stronger impact on the growth kinetics than the cone angle θ or the particle type. We explored how the cluster packing depended on the cooling rate and particle number as well as discussing the relationship between the cluster geometry and the interparticle interactions. Further, we also discuss possible methods to experimentally prepare the truncated cones. The results of our work deepen our understanding of the self-assembly behavior of truncated cones and our results will aid the effective design of particle building blocks for novel nanostructures.
1. Introduction
Nanoparticle self-assembly imitates the organization of atoms or molecules into crystals or supramolecular structures1 and it has attracted intense research interest owing to its usefulness for the design and fabrication of novel nanostructured materials.2–4 In the nanoparticle self-assembly process the particle shape plays a key role and is particularly important for exploring new nanostructures and their functionalities.5,6 In addition to the shape of building blocks, the interactions between individual subunits is also vital for the assembly process. The subunit interactions are mainly determined by the shape, surface properties, and inherent physical properties (e.g., charge, polarizability, dipole, and mass) of the subunits. A key aim in the field of nanoparticle self-assembly is the exploitation of highly specific and directional interactions in combination with an anisotropic building block shape to achieve precisely ordered structures to broaden the range of applications.In biological systems, peptides and proteins have the ability to assemble into advanced structures.7 Ionic self-complementary peptides can form nanofibers8 and short peptides can self-assemble into semiflexible nanotapes,9 while surfactant-like peptides can form nanotubes, nanovesicles10,11 and supramolecular structures.12,13 Recent experiments have demonstrated that recombinant fusion proteins can form an amphiphilic complex to further self-assemble into globular protein vesicles by fine turning the protein concentration or temperature;14 and both vesicle size and vesicle geometry can be well-controlled. Beside vesicles, solid particles and hierarchical supraparticles can also be formed through rational protein design.15 Peptides and proteins were treated as cone-like molecules in above mentioned studies, which inspired us to understand their assembly mechanism in more depth and helped us to more effectively design novel building blocks for assembly. With regard to non-biological systems, several assembly systems such as amphiphilic block copolymers,16 metal-polymer amphiphiles17 and patchy colloidal dumbbells18,19 have often been regarded as a cone-like molecules and they can assemble into various structures (e.g., spherical micelles, cylindrical micelles and vesicles) owing to the inherent curvature of building blocks. Cone-like particles or molecules are typical building blocks for assembly and they generally have a nonsymmetrical shape with regard to their two ends. Although much experimental progress has been made in the self-assembly of cone-shaped molecules and particles, some issues such as assembly pathways and the influence of building blocks' parameters including shape and interparticle interaction are not yet exhaustively understood.20
Compared with experimental methods, computer simulations are powerful tools for exploring the self-assembly of specific-shaped particles, although it is difficult to simultaneously consider the particle shapes and interparticle interactions.21–24 Because of computational limitations, the direct calculation of nanoparticle self-assembly using an all-atom model is not feasible; instead one must consider coarse-grained model systems. The widely adopted coarse-grained model is the Kern–Frenkel model25 of patchy spherical particles with short-ranged directional attraction. The whole particle is treated as a “bead” and the patch is either attached to the bead's surface or part of it. Models of this class are formulated in terms of spherical particles with symmetric, regular patches because the interparticle attractions are restricted to orientations in which two patches face each other. In Kern–Frenkel model, the anisotropy of interactions strongly depends on the number of patches and their size.25–27 Another general model with anisotropic interactions was proposed by Zhang et al.,28 who used a more complex coarse-grained model in which the whole particle was constructed from a large number of coarse-grained beads. This coarse-grained model greatly reduced the overall number of interactions that must be calculated compared with an all-atom model. The same or complementary beads within the patches interacted with either attractive or repulsive interactions. This coarse-grained model is capable of describing particles and patches with irregular shape and size and it can easily be modified to study the assembly of nonspherical particles.29,30 In this work, the simplified coarse-grained model was used to characterize the shape of the truncated cone, and a truncated cone included two types of coarse-grained beads to separately represent hydrophobicity and hydrophilicity.
Gaining a quantitative description of a particle's shape and interparticle interactions is a critical and challenging task in assembly simulation of nonspherical particles. Recently, we developed an effective simulation method for the assembly of nonspherical particle with the help of tabulated potential technology.30 Utilizing this model, the self-assembly of two kinds of cone-like particles with a series of cone angles was studied, and various spherical structures with a precise cluster size were formed.24 In that system it was found that clusters began to form simultaneously and the formed clusters aggregated uncontrollably. Those formed clusters were not hollow structures, which considerably prohibits their potential applications,13,31 especially for drug delivery which requires dispersed hollow clusters in solutions.13 In this study, a truncated cone with an amphiphilic surface was designed. Meanwhile, purely repulsive interactions were introduced for hydrophilic coarse-grained beads, which imitates the hydrophilic parts of amphiphilic molecules and it can avoid the cluster–cluster aggregation. The aim of this work was to reveal how the shapes of truncated cone particles affect the self-assembly process and to explore the relationship between complex particle shapes and simple cluster geometry. We employed a quantitative Brownian dynamics (BD) simulation framework for nonspherical particles that was proposed in our prior work.30 This BD framework applied the tabulated potential and the interpolation techniques, and it has advantages of being highly efficient at calculating anisotropic interparticle interactions. This force field between two interacting assembly particles has been calculated before the BD simulations begin. This BD simulation framework not only ensures the precise description of the particle shape and anisotropic interparticle interactions, and it also significantly improves the simulation's efficiency.
Herein, we employ the novel BD simulation framework to study the self-assembly of a series of truncated cones with different particle shapes. General descriptions involved in coarse-grained model of the truncated cones and detailed information on the simulation method are introduced in section 2. The influence of the particle shape on assembled structures, cluster size, cluster geometry, aggregation temperature and cluster growth kinetics are discussed in section 3; the dependence of cooling rate and particle number on the self-assembly and the relationship between interparticle interaction and cluster morphology are also discussed in this section. Furthermore, possible synthesis methods for cone-like particles are suggested, and finally a brief summary of this work is presented in the conclusion section.
2. Model and method
The coarse-grained model of truncated cones is illustrated in Fig. 1a. Particles are composed of two types of spherical coarse-grained beads. Pink A beads and cyan B beads indicate hydrophobicity and hydrophilicity, respectively. Truncation was used for the particle shape transformation. Truncated cones were designed by cutting complete cones to a certain height, and the truncated height is defined as hc. The full height h of a cone was set to 1.0 nm, and the spacing of adjacent beads and layers within a single particle is 0.1 nm. Present simulation only shows the general rules of self-assembly of the truncated cones. The particle size used don't correspond to the real system. A particle's shape is characterized by the two-dimensional cone angle θ (i.e., θ = 25°, 30°, 35°), truncated height hc (e.g., hc = 0.2, 0.4, 0.5, 0.6, 0.7 nm) and particle type. Two particle types, namely AxBy and BxAyBz, were constructed. The subscript x, y, z represents the number of coarse-grained beads of type A and B. The bottom layer in an AxBy type particle consists of B beads. Unlike in an AxBy type, both the top and bottom layers of a BxAyBz type particle are composed of B beads. We studied whether replacing one layer of B beads to the “tail” end would affect the cluster size and cluster growth kinetics. The length and overall hydrophobicity of a particle can be fine-tuned by modifying the number of A coarse-grained beads. The hydrophobic tails of the particles contained an increasing number of A beads and thus had higher hydrophobicity. The number of coarse-grained beads in the various truncated cones is listed in Table S1.†For hydrophobic A components, the interaction between A beads is Lennard-Jones potential and that is Uij = 4εAA[(σ/rij)12 − (σ/rij)6], while for the hydrophilic B components purely repulsive interactions are used to reflect its hydrophilicity, Uij = εBB(σ/rij)5. The interaction between two unlike A and B beads is the arithmetic mean of like beads, which is
Here, εAA and εBB are interaction strength parameters, σ is interaction range, which is equal to the diameter of a coarse-grained bead (σ = σAA = σBB = σAB = 0.1 nm), and rij is the distance between the centre of two interacting beads. The interaction strength parameters are defined to ensure that the A beads are strongly hydrophobic and the B beads are weakly hydrophilic (εAA = 2.0 KJ mol−1 and εBB = 0.2 KJ mol−1).
According to the interactions used above, the interaction between two truncated cones (I and J) is the sum of the interactions between coarse-grained beads within the truncated cones,
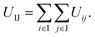 | (1) |
Here, the truncated cones are treated as rigid bodies and the interparticle interactions are directionally dependent. The computation cost for UIJ is high in every simulation step. Instead of this, we used an alternative anisotropic potential, given by
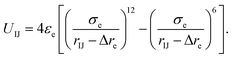 | (2) |
The strength parameter εe, range parameter σe and shape parameter re were calculated using a numerical matching method.30 These three parameters are orientation-dependent and the orientation between two particles is represented with three angles αI ∈ [0,π], αJ ∈ [0,π] and βIJ ∈ [0,π], as shown in Fig. 1b. Each orientation angle is divided into 99 equal parts when calculating the tabulated potentials.
The three interaction parameters in eqn (2) can be solved only when eqn (1) yields a potential curve with a negative local minimum.30 However, in the present system UIJ maybe positive without local minimum due to the introduction of the purely repulsive interaction between B beads. The potential fitting method must be modified accordingly, and thus we added an additional attractive interaction Uadd = −1.0/(rIJ − 0.1) to UIJ in eqn (1) in the potential calculation. The additional attraction Uadd can lead to the existence of a negative local minimum in new potential curves at all orientation directions. Consequently, the UIJ in eqn (1) can be well fitted with the anisotropic potential in eqn (2). Note that the additional attractive potential Uadd is excluded in the calculation of translation force and torque in BD simulations. Examples of potential calculation are shown in Fig. S1.†
Because there is a short-ranged interparticle interaction expressed in eqn (2), and to further improve the potential calculation efficiency and to increase the calculation convergence rate, a soft-core potential is introduced when rIJ < rm and the potential calculation is paused at rIJ > rm. Thus, the final form of the anisotropic interparticle interactions can be written as
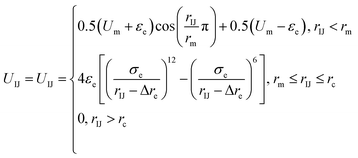 | (3) |
In present coarse-grained model, we only consider the global interactions between particles is attractive or repulsive. Such interaction does not correspond to any real interaction type. In our BD simulation, hydrodynamic interactions is also ignored and the random force represents the randomly fluctuating force exerted on a particle by the surrounding fluid. An implicit solvent model was used here. Our tabulated potential method has an advantage in quantitatively describing specific particle shapes and anisotropic interparticle interactions, unlike other methods such as the patch model which presents anisotropy via the patch size and patch position. The direction-dependent interactions between particles arise from all attractive and/or repulsive beads that make up the particles, not from the “atoms” within the patches. This potential computation method is not only suitable for symmetric, regular particle shape but in principle also for arbitrary shapes. In a BD simulation, the computation cost is entirely unrelated to the number of coarse-grained beads within a particle because the interparticle interactions in BD simulations are calculated with interpolation methods based on tabulated potentials.
To study the self-assembly of truncated cones, a rigid body BD simulation in the canonical ensemble was applied. The simulated box was cubic with a box side l; periodic boundary conditions were used. At each BD step, each particle attempts to move and rotate according to the following equations of motion:
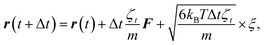 | (4) |
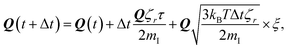 | (5) |
All BD simulations were cooled from a high-temperature, initially disorder conformation of M particles to a target temperature with stable structures. The low target temperature of each simulation was chosen to allow sufficient time for the particles to assemble into stable structures with unnoticeable change of the system's total energy (the annealing temperature range for each simulation is listed in Table S1†). Unless otherwise stated, an annealing rate, 2.0 × 105 step per K, was applied to avoid kinetically trapped structures. This cooling rate was proved to be affordably slow and yet also fast and efficient enough, compared with using 1.0 × 105 step per K or 3.0 × 105 step per K to produce stable clusters. The specific heat capacity Cv was used to monitor changes of the system's energy. Our studies were restricted to the dilute solution regime, i.e., M = 100 particles were dispersed in a cubic simulation box with a box side l = 10 nm, mainly to reduce the computational time.
3. Results
3.1 Truncated cone shapes and assembled structures
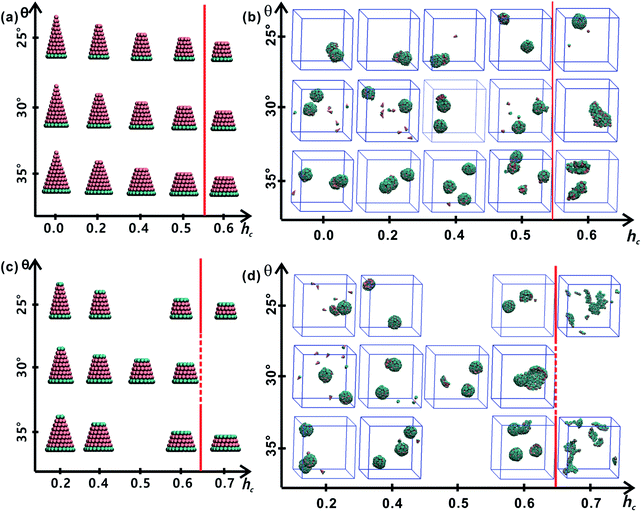
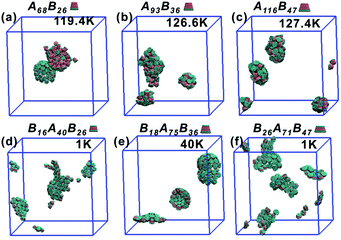
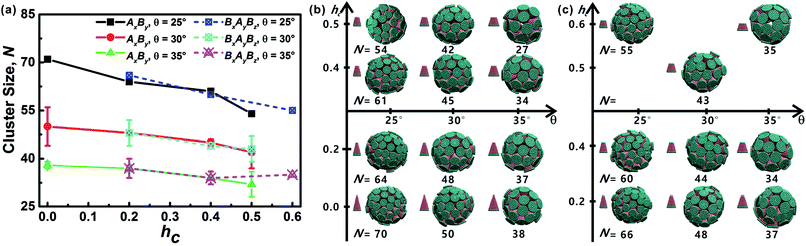
All truncated cone-shaped particles studied in this work are listed in Fig. 2a and c. The self-assembly process of twenty-four truncated cones and three complete cones were simulated using the annealing method. The initial state of system was obtained at a high enough temperature where all particles are randomly distributed in solution owing to thermal motion. As the system temperature gradually decrease, truncated cones strive for the maximum number of nearest neighbours and they are bound tightly to each other. Meanwhile, repulsive interactions between the ends of the truncated cones propel the assembled particles into curved, closed structures. Fig. 2 shows the final assembled structures generated in the simulations for each particle shape in simulations. Notably, most of the truncated cones self-assemble into discrete vesicle-like structures. As expected, the geometric arrangement of the cluster mainly depends on building block shape and interparticle interactions. The assembled clusters were hollow, and for those constructed with AxBy particles, the inner wall was composed of A component and was thus hydrophobic; for BxAyBz type particles, B component made up the hydrophilic cavity wall.As the truncated height hc increased, the inner diameter of the hollow structures also increased. However, the increase of hc was unfavourable for forming ordered clusters. When the truncated height hc was very large, order packing was difficult to achieve and malformations were observed. There exists a critical border for each set of truncated cone at the same θ to assemble into vesicle (see Fig. 2). For AxBy particles, the critical value of hc is 0.5 (Fig. 2b) and for BxAyBz particles the critical values of hc is 0.6, except for θ = 30° (Fig. 2d). The disparity of the critical value of hc at θ = 30° was caused by the fluctuation of simulation data. A truncated cone was evolved from a complete cone by cutting several layers from its top tip. It is not a smooth evolution of particle shape, which may lead to the error of the statistical data in a certain particle shape. The source of the malformations of A68B26 particles at θ = 25°and hc = 0.6 was the development of small local errors in the growing micelles. The clusters continue to grow when there is a malformation, and finally a malformed structure is generated and it is similar to a correct vesicle (Fig. 3a). For A93B36 and A116B47 particles at θ = 30°, 35°and hc = 0.6, the source of the malformation is the inability of malformed clusters to correct themselves after the occurrence of a malformation (Fig. 3b and c). While for BxAyBz particles, the origin of malformations of B18A75B36 particles at θ = 30° and hc = 0.6 is interactions of incomplete clusters; two incomplete clusters can connect together into a single malformed structure and the malformed structure can continue to attract free particles (Fig. 3e). For B16A40B26 and B26A71B47 particles at θ = 25°, 35° and hc = 0.7 the interparticle attractive interactions are not sufficient to counterbalance the repulsive volume effect in the assembly when hc is large enough (Fig. 3d and f).
3.2 Cluster sizes and cluster geometries
As mentioned above, truncated cones can assemble into a series of unique vesicle-like clusters with a specific cluster size N; the cluster size is defined as the number of particles that form a single cluster. Cluster size of each assembled aggregates was calculated. The cluster size N is shown in Fig. 4a as a function of the particle shape. It was found that the cluster size N increases with decreasing cone angle θ, and the cluster size N decreases gradually with increasing hc. The downward trend is most pronounced at θ = 25°. But the dependence of the cluster size N on particle type is not significant. These results indicate that cone angle θ and truncated height hc, rather than particle type, determine the cluster size N of the assembled vesicles and the most critical factor is the cone angle θ. The conclusion in this work is in agreement with the conclusions of previous studies21,22,24,32 and the previous conclusion is that the cluster size of cone-shaped particles increases as the cone angle decreases.Cluster geometries with their corresponding particle shapes and cluster size are shown in Fig. 4b and c. There are chemical similarities between amphiphilic molecules and the truncated cones, because both amphiphilic molecules and the truncated cones consist of hydrophobic and hydrophilic parts. The hydrophobic parts of truncated cones pack closely to form hollow and spheroid structure, and the formed structures resemble vesicles comprised of amphiphilic molecules. However, the spheroid structure does not agree with the prediction results of the “critical packing parameter” (CPP).33 Truncated cones with 1/3 < CPP ≤ 1/2 should assemble into cylinders. The difference between the CPP expected structures and the actual assembled structures was also been observed by other groups.21,22,32 Tsonchev et al.32 argued that the relationship between CPP values and the aggregation shapes is not unique and the CPP method should merely be reviewed as a guide. Spherical structures are energetically preferred because there is always a higher number density of cones or truncated cones for spherical structures than for cylinders.32 Thus, it is clear that the problem is to find the densest structure that can be formed using truncated cones. Additionally, Chen et al.21 suggested that the disparity may be limited to rigid cone systems, because the CPP method is suitable for the soft amphiphiles.
In this work, the hydrophobic A components are responsible for hydrophobic attractive interactions and the attractive interactions lead to effective self-assembly, and the hydrophilic “heads” (i.e., B components) only interact with repulsive interactions and the repulsive interactions are unfavourable to effective self-assembly. When the truncation height hc is larger than the critical hc illustrated in Fig. 2, the hydrophilic area of each particle will obviously increase; the result is that the repulsive force between particles also increases significantly, which is not favourable for the effective self-assembly of spherical structures because the attractions between particles are not large enough to inhibit malformed self-assembly. Thus, the densest structures ought to be the results of the balance between the hydrophobic attractive interactions and hydrophilic repulsive interactions. Here, entropic effects were not considered because our previous work24 suggested that the contributions of entropic effect on self-assembly can be omitted, because the entropic effect is very small compared with the interparticle interactions. Furthermore, truncated cones are regarded as rigid bodies and all simulations were carried out in dilute systems (particle number density of 0.1 nm−3). The CPP packing rule is actually more suitable for predicting the behaviour of amphiphiles with soft tails,17,34 and for soft amphiphiles by increasing the tail length, the cluster geometries can transform from spherical micelles to cylinders to bilayers. It is obvious that our current model of truncated cones is not suitable for the CPP packing rule because our hydrophobic “tails” are rigid.
In addition, it is instructive to compare the packing of our truncated cones to the virus capsid (protein shell of a virus) assembly. Most studies of virus capsid assembly process usually impose symmetry constraint, e.g., spherical or icosahedral,35,36 to the cluster geometry before assembly. Thus, the problem is limited to an optimal packing for a few subunits constrained to the surface of a spherical or icosahedral shell.37,38 Our simulation have no special approximation or limitation with regard to the assembly of the truncated cones. We found some cases for which the assembled vesicles (cluster size N = 34, N = 42 and N = 70) are very similar to several virus capsid protein, i.e., cowpea chlorotic mottle virus39 capsid with T = 3 Caspar and Klug (CK) structure (N = 32), a NωV virus40 capsid with T = 4 CK structure (N = 42) and a polyoma virus41 capsid with T = 7 CK structure (N = 72).
3.3 Self-assembly process of truncated cones
The specific heat capacity Cv was chosen as the second criterion to estimate the assembly process and it can accurately reflect the energy fluctuation in assembly process. The Cv can be calculated with| Cv = ∂E/∂T = 1/kBT(〈E2〉 − 〈E〉2). |
The temperature that corresponds to the first maximum Cv value is defined as aggregation temperature, Ta and the influence of particle shape on Ta is shown in Fig. 5. It can be seen that the Ta of AxBy particles is higher than that of BxAyBz particles at the same θ and hc. At the same θ, Ta decreases with increasing hc; furthermore, the decrease of Ta for the BxAyBz particles occurs at an obviously higher rate than for AxBy particles. For the same hc, Ta increases with increasing θ for both AxBy and BxAyBz particles. All these phenomena can be explained by considering the differences in the particle hydrophobicity and hydrophilicity. The stronger the hydrophobicity, the better the effective self-assembly, and the more effective self-assembly leads to a higher Ta.
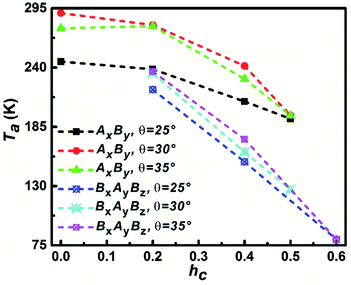 | ||
| Fig. 5 The dependence of aggregation temperature Ta on the particle shape. The Ta is defined as the temperature corresponding to the first specific capacity heat Cv peak. | ||
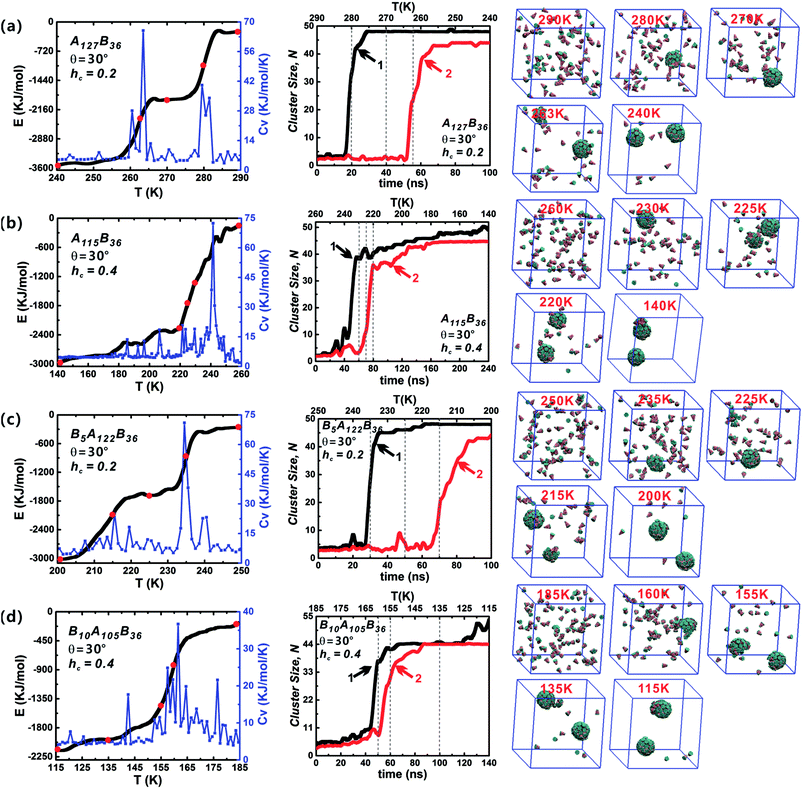
Both the success of forming discrete clusters and the growth kinetics depend delicately on the aggregation energies of the free truncated cones. The influence of hc on the self-assembly process was investigated for AxBy and BxAyBz particles at θ = 30°, as shown in Fig. 6 (the date of other particle shapes is shown in Fig. S2–S4†). The sharp changes in energy are reflected in the Cv curves. At hc = 0.2, the decline in energy is stairs-like with obvious plateaus. When hc is 0.4 and 0.5, the system' total energy decreases continuously and the stairs-like downward trend of energy is no longer obvious; accordingly, there is only one distinct sharp peak in the Cv curve. Compared with the effects of particle type and cone angle θ, the truncated height hc has a strong impact on system energy fluctuations. With the increase of hc, the hydrophobicity of particles weakens and the hydrophilicity of particles becomes stronger, that is, the repulsive interactions between particles increase with the increment of hc, which is not favourable to minimizing the system energy, and thus the system rapidly enters the growth stage of second cluster. The typical configurations of the particles at various temperatures are shown in Fig. 6. Initially, particles are randomly distributed, followed by the formation of curved partial structures, and then a well-packed cluster is generated; thereafter, the remaining free particles begin to grow to form the second cluster until its completion. In the whole assembly process, clusters are formed one-by-one, not together. The reason is that when the temperature decreases to a critical value, a stable nucleus starts to create and particles aggregate into the nucleus till a complete vesicle forms. When a vesicle is formed, the concentration of the free particles in system decreases. It becomes difficult to form a new stable nucleus. Only when the temperature is further decreased, the second stable nucleus can be formed. So, clusters are formed one-by-one in such annealing process.
The role of particle type in the assembly kinetics at θ = 30° was also studied (Fig. 6, and the data for other shapes is shown in Fig. S2–S4†). Three distinct periods are visible: (1) initial lag, closely followed by (2) rapid growth, and finally (3) growth slow-down. Such growth kinetics traits resemble classical nucleation and growth mechanism of virus capsids.42 Stage (1) clearly defines the time range in which nucleation occurs, i.e., in which particles diffuse and collide freely, thus producing the critical growth nucleus. Once the growth nucleus has been formed, the system enters a period of fast growth and the number of free particle decreases rapidly until a robust cluster has been formed. For the same hc value, the role of particle type in the assembly kinetics is not obvious. However, increasing hc has a significant impact on the growth kinetics: a distinct lag period for the growth of the second vesicle is observable at hc = 0.2. But this distinct lag stage vanishes when hc is 0.4 or 0.5, and the second clusters (red curves) begin to grow immediately once the generation of the first clusters (black curves) is complete. In addition, it was found that there are some fluctuations in the cluster size, and these fluctuations indicate the merger of clusters. The merger of clusters will creates oversize misassembled structures, and they are usually generated from complete vesicles and partial vesicles. Fortunately, these oversize misassembled structures can be corrected immediately and they are different to the malformation mentioned in Fig. 3. In brief, varying particle shape, especially hc, changes the interparticle interaction significantly and plays an important role in the vesicle growth kinetics.
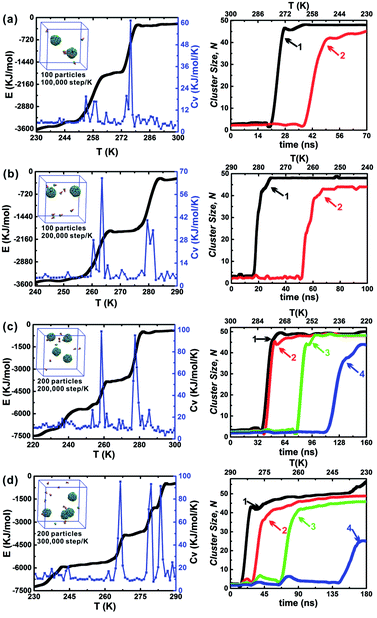
The influence of the annealing rate on the assembled structure, energy evolution, and cluster growth kinetics were explored at θ = 30° and hc = 0.2. Three cooling rates were used including 1 × 105 step per K, 2 × 105 step per K and 3 × 105 step per K. When 100 particles were in a 10 nm cubic box, only the cooling rates 1 × 105 step per K and 2 × 105 step per K were considered (Fig. 7a and b); this is because an annealing rate 2 × 105 step per K has been proved to be slow enough for the formation of the final two clusters and the energy change related to the formation of each cluster was evident. The slower cooling rate (3 × 105 step per K) was more useful for distinguishing the formation of the first and second clusters. However, using this cooling rate tripled the computation time (Fig. 7c and d). Thus, the moderate cooling rate of 2 × 105 step per K was used for almost all simulations in this work. The larger system, which comprised 200 particles in a 12.6 nm cubic box with an equal particle number density was also tested under these conditions (Fig. 7b and c). Using the larger system did not alter the specific cluster size N, but it did accelerate the growth of the second cluster (red line). This demonstrates that the specific cluster sizes N for each particle shape is robust and independent of system's particle number. There is a sharp increase of cluster size of cluster 1 in Fig. 7d, and it is due to the contact of a partial vesicle structure and the complete vesicle cluster 1. Because the interaction of A and B beads is attractive, the partial vesicle structure (some side surfaces with A beads are exposed) can contact with the B beads of the complete vesicle (where only B beads on the bottoms of particles can be exposed). Finally, all aggregation structures should be vesicle structures with the maximum A–A contacts corresponding to the lowest energy of the system.
3.4 Interaction potential of two truncated cones
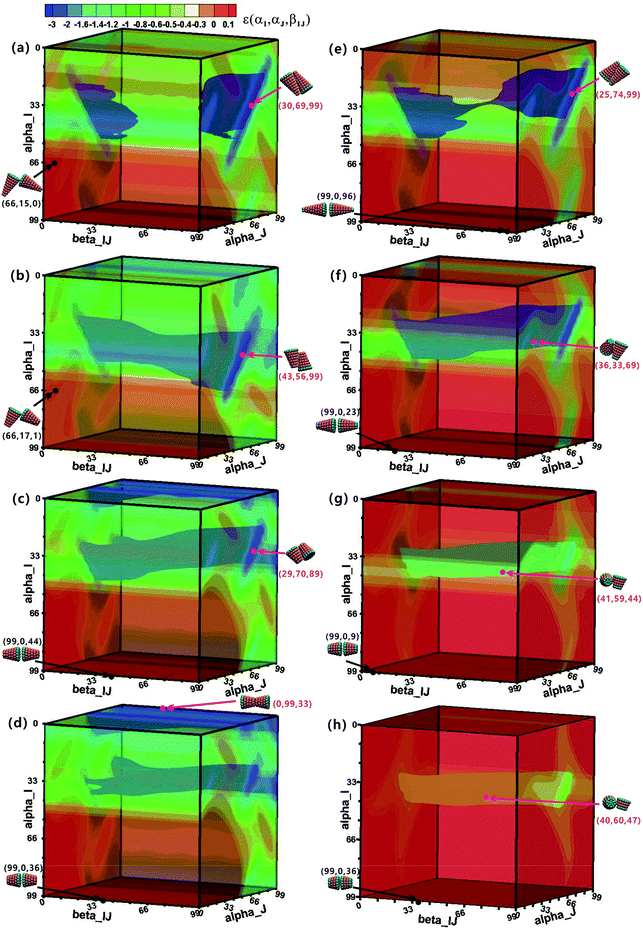
To understand the assembly mechanism of various truncated cone in depth, the effect of the particle shape on the potential energy surfaces (PESs) between two interacting particles was discussed (see Fig. 8 and S5–S6† in which the colour legends are all the same to facilitate comparisons of the potential energies). In the PES data, orange and red indicate a positive potential energy, i.e., two particles in these orientational zones will repulse each other. Pink points and black points indicate minimum and maximum energies on the PES, respectively, and their corresponding configurations are also shown. The orientational range in the near blue regions (lower potential energy) on the PESs is approximately the same at the same hc, but the potential energy increases with increasing θ. The same is true in the near red region (higher potential energy). The minimum-energy conformations of AxBy type particles change from antiparallel side–side packing to tail–tail stacking with increasing hc (Fig. 8), but the transformation of minimum-energy conformations of BxAyBz type particles is different: they change from antiparallel side–side packing to orthonormal side–side packing with increasing hc (Fig. 8 and S5–S6†). However, the final assembled vesicle structures with a lower energy have a higher packing number density (see cluster structures in Fig. 2) and they are not constructed based on these minimum-energy configurations between two particles. The minimization of the system's total energy, rather than the local energy, must be ensured at all times to encourage effective self-assembly. Self-assembly is a multi-body interaction process, and the system's total energy is the sum of the interactions of any two interacting particles. In our simulations, once a free truncated cone attempts to join the structure, it alters its orientation to find the best position, and all particles constituting the structure modify their orientations to achieve the most stable equilibrium conformation. This is akin to the local rule-based theory43,44 for virus capsid assembly in which a protein possesses enough local information to know where to bind to the growing cluster. To assemble into the global vesicle structure, the attractive forces between particles should be large enough to induce effective aggregation, but also weak enough to form complete vesicle structure for global energy minimization during the assembly process via thermal fluctuations.4. Discussion
The self-assembly of truncated cones reported here generates nanoscale vesicles with a range of cluster sizes, and all formed vesicles are with similar spherical cluster geometries. The resultant unique cluster sizes and spherical cluster geometries can be explained by the particle shapes and interparticle interactions. Our study reveals that truncated cones with different shapes undergo the classical nucleation and growth pathway to form ordered structures. Thus cone-shaped particles possess ideal characteristics for self-assembly. Particles with such cone-like shape may be prepared by various experimental methods including mechanical stretching,45,46 soft lithography47,48 and phase separation.49,50 Mechanical stretching method can enhance particle shape diversity when using more complex starting materials,46 such as using Janus polymeric particles. After stretching, Janus ellipsoidal particles can be formed and subsequently half of each particle can be removed via selective solubilisation to obtain cone-like particle. Moreover, bullet-like structures has been created from single component particles through stretching-liquefaction method.46 The key advantages of the mechanical stretching method are its high throughput and precise control over particle size in three dimensions; it is also easy to scale up production through increased film thicknesses and particle loadings in the films. Beside the stretching method, soft lithography technology is also a feasible method to fabricate conical-shaped particles47 and, in principle, any shape particle.48 Surface modification can be realized using glancing angle deposition.51–53 Further, pinecone-shaped particles can be generated by phase separation of binary blends of block copolymer and homopolymer by varying the interfacial properties of polymers and aqueous solution; in such particles the cone side of a particle will consist of diblock copolymer.50 Therefore, conical particles can be produced by selectively dissolving homopolymer components. The resultant cone-shaped particle have amphiphilic top and bottom surfaces owing to the comparable interactions of the blocks with the aqueous solution. Thus, a simple fabrication method can be used to make a remarkable large variation of cone-shaped particles.5. Conclusions
The self-assembly of a series of truncated cones was systematically studied by applying a BD simulation. Cones or truncated cones are important models to understand the aggregation structures of amphiphilic or surfactant-like molecules. In this work, two kinds of truncated cones (AxBy and BxAyBz types) with different cone angle θ and truncated height hc were designed. Our simulations show that truncated cones can assemble into highly ordered nanoscale vesicles with a specific cluster size and inner interface properties. The simulations reveal that the cluster size, cluster geometry and cluster growth kinetics greatly rely on the particle shape. Cluster size is mainly determined by cone angle θ, while the truncated height hc and particle types have little effect on the cluster size. The geometry of all formed clusters was spherical, as this is energetically most favourable. The effect of particle type (AxBy or BxAyBz) on the assembly process was found to be insignificant, while the truncated height hc has a strong influences on the cluster growth kinetics. Our results show that the truncated cones with different particle shapes undergo similar ordering pathways. Nanoscale vesicles formed from truncated cones have potential applications including serving as carrier for molecules delivery, forming a bioreactor for cell encapsulation and providing a scaffold for nanocrystals growth to grow on. The available methods to fabricate truncated cones were also discussed in this paper. This work not only provides novel insights into the self-assembly processes of nonspherical particles, but also broadens our knowledge of how to design the building unit particles for the formation of nanovesicles structures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors appreciate the financial support from the National Natural Science Foundation of China (21474075).References
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- H. R. Vutukuri, A. Imhof and A. van Blaaderen, Angew. Chem., Int. Ed., 2014, 53, 13830–13834 CrossRef CAS PubMed.
- J. Gong, R. S. Newman, M. Engel, M. Zhao, F. Bian, S. C. Glotzer and Z. Tang, Nat. Commun., 2017, 8, 14038 CrossRef CAS PubMed.
- S. Ravaine and E. Duguet, Curr. Opin. Colloid Interface Sci., 2017, 30, 45–53 CrossRef CAS.
- S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–105 CrossRef CAS.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colon-Melendez, S.-H. Kim, D. J. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
- S. Zhang, Interface Focus, 2017, 7, 20170028 CrossRef PubMed.
- T. C. Holmes, S. de Lacalle, X. Su, G. S. Liu, A. Rich and S. G. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 6728–6733 CrossRef CAS.
- A. Aggeli, I. A. Nyrkova, M. Bell, R. Harding, L. Carrick, T. C. B. McLeish, A. N. Semenov and N. Boden, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11857–11862 CrossRef CAS PubMed.
- S. Vauthey, S. Santoso, H. Y. Gong, N. Watson and S. G. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5355–5360 CrossRef CAS PubMed.
- X. Wang, K. Corin, P. Baaske, C. J. Wienken, M. Jerabek-Willemsen, S. Duhr, D. Braun and S. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9049–9054 CrossRef CAS PubMed.
- J. D. Hartgerink, E. Beniash and S. I. Stupp, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5133–5138 CrossRef CAS PubMed.
- D. M. Leite, E. Barbu, G. J. Pilkington and A. Lalatsa, Curr. Top. Med. Chem., 2015, 15, 2277–2289 CrossRef CAS PubMed.
- Y. Jang, W. T. Choi, W. T. Heller, Z. Ke, E. R. Wright and J. A. Champion, Small, 2017, 13, 1700399 CrossRef PubMed.
- Y. Jang and J. A. Champion, Acc. Chem. Res., 2016, 49, 2188–2198 CrossRef CAS PubMed.
- A. Blanazs, S. P. Armes and A. J. Ryan, Macromol. Rapid Commun., 2009, 30, 267–277 CrossRef CAS PubMed.
- S. Park, J. H. Lim, S. W. Chung and C. A. Mirkin, Science, 2004, 303, 348–351 CrossRef CAS PubMed.
- D. J. Kraft, R. Ni, F. Smallenburg, M. Hermes, K. Yoon, D. A. Weitz, A. van Blaaderen, J. Groenewold, M. Dijkstra and W. K. Kegel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10787–10792 CrossRef CAS PubMed.
- G. Avvisati, T. Vissers and M. Dijkstra, J. Chem. Phys., 2015, 142, 084905 CrossRef PubMed.
- S. F. Tan, S. W. Chee, G. Lin and U. Mirsaidov, Acc. Chem. Res., 2017, 50, 1303–1312 CrossRef CAS PubMed.
- T. Chen, Z. Zhang and S. C. Glotzer, Langmuir, 2007, 23, 6598–6605 CrossRef CAS PubMed.
- T. Chen, Z. Zhang and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 717–722 CrossRef CAS PubMed.
- J. Zhao, S. Li, P. Lu, L. Meng, T. Li and H. Zhu, Powder Technol., 2011, 214, 500–505 CrossRef CAS.
- Y. Wang and X. He, RSC Adv., 2016, 6, 66108–66119 RSC.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS.
- Z.-W. Li, Z.-Y. Lu, Z.-Y. Sun and L.-J. An, Soft Matter, 2012, 8, 6693–6697 RSC.
- R. Guo, J. Mao, X.-M. Xie and L.-T. Yan, Sci. Rep., 2014, 4, 7021 CrossRef PubMed.
- Z. L. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- J. P. Mahalik and M. Muthukumar, J. Chem. Phys., 2012, 136, 135101 CrossRef CAS PubMed.
- J. Xu, Y. Wang and X. He, Soft Matter, 2015, 11, 7433–7439 RSC.
- V. Noireaux and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17669–17674 CrossRef CAS PubMed.
- S. Tsonchev, G. C. Schatz and M. A. Ratner, Nano Lett., 2003, 3, 623–626 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic press, 2011 Search PubMed.
- C. R. Iacovella, M. A. Horsch, Z. Zhang and S. C. Glotzer, Langmuir, 2005, 21, 9488–9494 CrossRef CAS PubMed.
- R. Zandi, D. Reguera, R. F. Bruinsma, W. M. Gelbart and J. Rudnick, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15556–15560 CrossRef CAS PubMed.
- D. G. Angelescu and P. Linse, Soft Matter, 2008, 4, 1981–1990 RSC.
- R. F. Bruinsma, W. M. Gelbart, D. Reguera, J. Rudnick and R. Zandi, Phys. Rev. Lett., 2003, 90, 248101 CrossRef PubMed.
- J. Wagner and R. Zandi, Biophys. J., 2015, 109, 956–965 CrossRef CAS PubMed.
- J. E. Johnson and J. A. Speir, J. Mol. Biol., 1997, 269, 665–675 CrossRef CAS PubMed.
- S. Munshi, L. Liljas, J. Cavarelli, W. Bomu, B. McKinney, V. Reddy and J. E. Johnson, J. Mol. Biol., 1996, 261, 1–10 CrossRef CAS PubMed.
- R. C. Liddington, Y. Yan, J. Moulai, R. Sahli, T. L. Benjamin and S. C. Harrison, Nature, 1991, 354, 278–284 CrossRef CAS PubMed.
- R. Zandi, P. van der Schoot, D. Reguera, W. Kegel and H. Reiss, Biophys. J., 2006, 90, 1939–1948 CrossRef CAS PubMed.
- B. Berger, P. W. Shor, L. Tucker-Kellogg and J. King, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 7732–7736 CrossRef CAS.
- R. Schwartz, P. W. Shor, P. E. Prevelige and B. Berger, Biophys. J., 1998, 75, 2626–2636 CrossRef CAS PubMed.
- A. Mohraz and M. J. Solomon, Langmuir, 2005, 21, 5298–5306 CrossRef CAS PubMed.
- J. A. Champion, Y. K. Katare and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11901–11904 CrossRef CAS PubMed.
- J. P. Rolland, B. W. Maynor, L. E. Euliss, A. E. Exner, G. M. Denison and J. M. DeSimone, J. Am. Chem. Soc., 2005, 127, 10096–10100 CrossRef CAS PubMed.
- D. Dendukuri, D. C. Pregibon, J. Collins, T. A. Hatton and P. S. Doyle, Nat. Mater., 2006, 5, 365–369 CrossRef CAS PubMed.
- S. Mei, L. Wang, X. Feng and Z. Jin, Langmuir, 2013, 29, 4640–4646 CrossRef CAS PubMed.
- R. Deng, S. Liu, F. Liang, K. Wang, J. Zhu and Z. Yang, Macromolecules, 2014, 47, 3701–3707 CrossRef CAS.
- A. B. Pawar and I. Kretzschmar, Langmuir, 2008, 24, 355–358 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Langmuir, 2009, 25, 9057–9063 CrossRef CAS PubMed.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The details of particle shapes, examples of potential calculation and additional data of cluster kinetics and potential energy surface. See DOI: 10.1039/c8ra01100a |
| This journal is © The Royal Society of Chemistry 2018 |