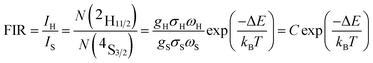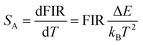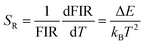Open Access Article
Open Access ArticleUnderstanding differences in Er3+–Yb3+ codoped glass and glass ceramic based on upconversion luminescence for optical thermometry
Yingxin Haoa,
Shichao Lva,
Zhijun Maa and
Jianrong Qiu *ab
*ab
aState Key Laboratory of Luminescent Materials and Devices, Institute of Optical Communication Materials, South China University of Technology, Guangzhou 510641, China
bState Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Hangzhou 310027, China. E-mail: qjr@scut.edu.cn
First published on 28th March 2018
Abstract
Optical thermometry has attracted growing consideration due to its outstanding performance. In this research, precursor glass with compositions of 50SiO2–20Al2O3–30CaF2–0.5ErF3–1YbF3 and the corresponding CaF2 glass ceramic were prepared for optical temperature sensing comparison. A large enhancement in upconversion luminescence originated from thermally coupled energy levels (2H11/2 and 4S3/2) and 4F9/2 was confirmed in the transparent glass ceramic (GC). Importantly, the temperature-dependent upconversion fluorescence intensity ratios of glass and GC were investigated from 303 K to 573 K under a 980 nm laser with constant pumping power. It was found that GC shows weaker optical thermometry ability than the precursor glass in terms of temperature sensitivity, the maximum relative sensitivity of GC reached to 10.6 × 10−3 K−1 at 303 K while that of the glass is 11.15 × 10−3 K−1 at 303 K, the thermally coupled energy gap reduced about 34.2 cm−1 after crystallization, we attribute this change to the crystal field effect. Furthermore, the FIR value variation of glass shows weaker pumping power dependence than GC in terms of thermal effect induced by laser. The temperature-cycle measurements suggest that both glass and GC exhibit favorable thermal stability. Consequently, our results may contribute to enriching our understanding of the optical temperature sensing properties of glass and glass ceramic in other systems and provide a comprehensive perspective to design practical optical thermometry materials.
Introduction
Life is closely linked with the temperature, whether it is macroscopic ambient temperature or microscopic life activities, temperature monitoring is extremely significant in many applications.1–5 Recently, a new non-contact temperature sensor, optical thermometry, has attracted growing interest due to possessing superior properties such as high sensitivity, rapid response time and immunity to harsh environment when compared to traditional contact thermometers.6–8 The temperature-sensitive optical techniques based on fluorescence lifetime and fluorescence intensity ratio (FIR) are two main mechanisms, relevant investigations concentrate on transition metal (TM)9–11 ions and rare earth (RE)12–15 ones. Notably, benefited from self-calibrated capacity and high reliability, improved measurement accuracy,16,17 FIR technique has been widely applied to determine temperature and regarded as a promising way for optical thermometry. It makes use of emission bands from thermally coupled energy levels (TCEL), the ratio of which can avoid the influences originated from spectral losses and fluctuations in excitation intensity.14,15,18,19 So far, the materials that have thermally coupled energy levels are rare earth ions,12,14,20–22 for instance, Er3+, Tm3+, Ho3+, Eu3+, Sm3+.Especially, Er3+ ion is one of most studied sensitive probe in optical temperature sensing,13,15,22–24 which ascribes to remarkable fluorescence intensities change from thermally coupled energy levels (TCEL) consisting of 2H11/2 and 4S3/2, as a sensitizer, Yb3+ is always adopted as codoped ion to improve up-conversion emission. Within the last few decades, optical thermometry based on FIR technique in non-crystalline materials doped with Er3+ have been growingly investigated, such as glass systems,25–29 oxyfluoride glass ceramic.13,16,22,24,30 Generally, transparent oxyfluoride glass ceramic exhibits more excellent luminescence property than glass for combining the merits of oxide glass' good stability and fluoride nanocrystals' low phonon energy environment.31,32 Additionally in terms of temperature sensing, hosts with lower phonon energy will show higher luminescence efficiencies, which will contribute to improving measurement accuracy,22,33 thus various glass ceramic materials for optical thermometry are widely explored currently. However, as we know, the energy gap between two thermally coupled levels will make a big difference on temperature sensitivity in fact, the improvement of luminescence efficiencies and measurement accuracy has no necessary relation with elevation of temperature sensitivity, and it is also ambiguous that what influence the different crystal field of glass ceramic has on rare earth ions' thermally coupled levels after crystallization. Therefore, understanding variation about temperature sensitivity in glass and glass ceramic is greatly essential to design optical thermometry materials with optimized properties. Unfortunately, the report concerning comparison on temperature sensing property between them is scarce, as far as we know.
In this sense, Er3+–Yb3+ codoped silicate glass and transparent oxyfluoride glass ceramic were successfully prepared by conventional melt-quenching method and successive heat treatment. Their structural, photoluminescence properties and temperature-dependent optical behaviors were systematically investigated to explore the possible application based on FIR technique. It was found that, compared to glass, glass ceramic show stronger upconversion luminescence and higher measurement accuracy while the temperature sensitivity decreased to a certain extent after crystallization, and in the aspect of thermal effect induced by 980 nm NIR laser, the upconversion emission spectra of glass show a weaker pumping power dependence than glass ceramic, finally, both of them exhibit favorable thermal stability. All results may provide comprehensive way to design practical optical thermometry materials.
Experimental procedure
The glass sample was prepared with the following composition (mol%): 50SiO2–20Al2O3–30CaF2–1YbF3–0.5ErF3 in an electric furnace (with MoS2 heating elements) by the conventional melt-quenching method. A 30 g reagent-grade mixture of SiO2 (99.99%), Al2O3 (99.99%) CaF2 (99.9%), YbF3 (99.99%) and ErF3 (99.99%) was mixed thoroughly in an agate mortar and melted in a covered corundum crucible at 1450 °C for 40 min. The glass samples were fabricated by pouring the melt into a preheated stainless steel plate and then pressed it into a slice with another cool iron plate immediately, then the precursor glasses were annealed at 400 °C for 2 h to release inner stress and cool to room temperature naturally. Finally based on the thermal analysis result, glass slices with the thickness of 2 mm were cut and heat-treated at 650 °C for 2 h to obtain transparent glass ceramic (GC).The crystal structures of prepared GC samples were determined by X-ray diffraction (XRD, PANalytical, Netherlands) with Cu/Kα (λ = 0.1541 nm) radiation in the 2 Theta range from 10° to 90°. The morphology and crystal size of the nanocrystals in glass-ceramic were obtained by high-resolution transmission electron microscope (HRTEM, 2100F, JEOL, Japan), GC samples were ground into a very fine powder which was placed onto a carbon coated copper grid and introduced into the microscope. Upconversion fluorescence measurement of the as-prepared glass and GC was investigated on a Triax (iHR 320, JobinYvon, France) fluorescence spectrometer with an adjustable fiber laser (980 nm) as the excitation. Temperature-dependent luminescence measurements of glass and GC were recorded on the same fluorescence spectrometer with a homemade temperature controlling apparatus and a 980 nm laser by means of designing light path.
Results and discussion
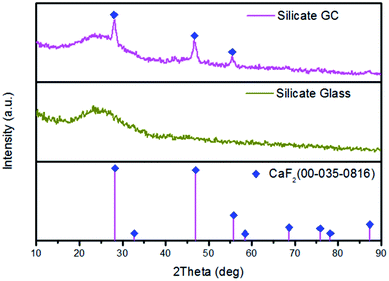
To identify the amorphous state and crystalline phase in precursor glass and GC, samples were ground into powders for XRD measurement, as is shown in Fig. 1. There is no any sharp diffraction peaks in precursor glass due to high cooling rate. In contrast, several specific diffraction peaks are detected in the GC pattern after heat treatment, and the sharp peaks appeared in GC match well with the diffraction peaks of CaF2 (PDF no. 00-035-0816) crystal. These characteristic peaks at 2θ = 28.2°, 47°, 55.7°, 68.6°, 75.8°, 87.3° are all ascribed to the diffractions of the (111), (220), (311), (400), (331) and (422) crystal facets of CaF2, respectively. Meanwhile, no other sharp peaks were observed in the XRD pattern of GC, which indicates that only CaF2 crystals are precipitated after the heat treatment.TEM and HRTEM are measured to intuitively confirm the precipitation of CaF2 crystals in silicate glass after heat treatment, as is presented in Fig. 2(a) lots of darker particles dispersed in the glassy matrix with average crystal diameters about 7 nm. According to Rayleigh scattering theory, the transmission loss caused by light scattering is negligible when the emission wavelength of upconversion is much larger than the size of crystals. Thus it can be inferred the optical transmission loss in GC cannot be affected seriously for application compared with precursor glass. Fig. 2(b) illustrates the HRTEM image of an individual nanoparticle. The crystal lattice fringes is very obvious and spacing d values of about 0.158 nm are assigned to the (222) crystal facets of the cubic face structure of CaF2 crystal. Additionally from the inset of Fig. 2(a), the pattern consists of amorphous diffuse rings and some bright diffraction spots from CaF2 crystalline grain. All these results indicate that only CaF2 nanocrystals have successfully precipitated in the silicate glass.
 | ||
| Fig. 2 (a) TEM micrograph of the GC sample and corresponding SAED patterns. (b) HRTEM micrograph of an individual CaF2 nanoparticle in silicate GC. | ||
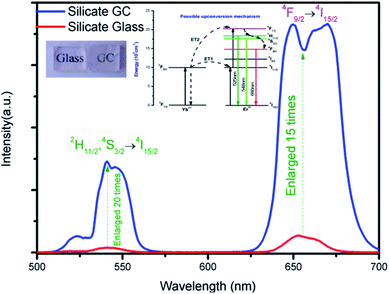
Fig. 3 displays the visible upconversion emission spectra of glass and glass ceramic under 980 nm laser excitation at room temperature. The emissions spectra in glass and GC are composed of several peaks located at 525 nm (2H11/2 → 4I15/2), 547 nm (4S3/2 → 4I15/2) and 660 nm (4F9/2 → 4I15/2), the green emission bands originated from 2H11/2 and 4S3/2 which is the thermally coupled energy levels will be responsible for temperature-dependent luminescence. Obviously, both emission intensity of green and red bands of GC increased enormously compared to that of precursor glass, thus it can be inferred that rare earth ions have been located in CaF2 crystal field, and the enhancement of luminescence intensity could be ascribed to the lower phonon energy environment and local symmetry site of CaF2 crystal. Notably, the upconversion spectra of GC appeared some sharp overlapping peaks, which is due to that Stark energy level splitting occurred in Er3+ under the effect of crystal field, the phenomenon also demonstrate rare earth ions have been contained in CaF2 crystals. Compared with precursor glass, these results confirm the luminescence emission efficiency of GC have been improved remarkably after rare earth ions participate in CaF2 crystal field.
The inset of Fig. 3 presents possible upconversion mechanisms, when excited by 980 nm laser, Er3+ at 4I15/2 ground state are firstly pumped to 4I11/2 intermediate excited state by ground state absorption, subsequently, the excited-state 4I11/2 level of Er3+ can be populated to higher emitting levels 4F7/2 by means of two most common excitation processes: (a) ESA, where an excited Er3+ ion absorbs a second 980 nm photon, raising the electrons to the highest energy level immediately, and (b) energy transfer34 (ET) of 2F5/2 (Yb3+) + 4I11/2 (Er3+) → 2F7/2 (Yb3+) + 4F7/2 (Er3+). Then excited electrons in the 4F7/2 level of Er3+ non-radioactively relax to lower 2H11/2, 4S3/2, 4F9/2 immediately after the previous population, which produce the final green emissions and red emission by radioactive transitions of 2H11/2 → 4I15/2 (525 nm) and 4S3/2 → 4I15/2 (547 nm) and 4F9/2 → 4I15/2 (660 nm) respectively.
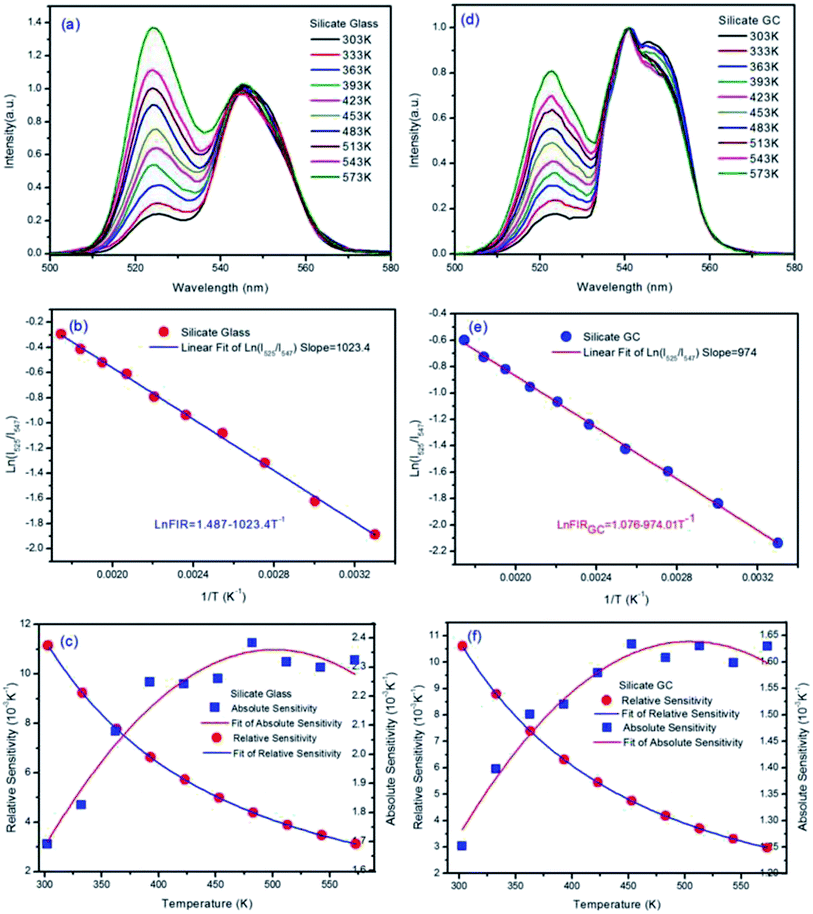
The temperature-dependent normalized green upconversion spectra of precursor glass collected at different temperature from 303 K to 573 K under 980 nm excitation with constant 340 mW are shown in Fig. 4(a). It is obvious that the luminescence intensity ratio of 525 nm versus 547 nm increases monotonously as the temperature raises, which is due to the increased population of 2H11/2 level at the expensive of that of 4S3/2 level by thermally coupled.
Based on the two thermally coupled level following the Boltzmann distribution, namely 2H11/2 and 4S3/2, the FIR of two thermally coupled energy levels (TCELs) can be described as follows:
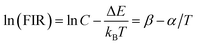 | (1) |
The natural logarithmic FIR about glass of emissions at 525 nm and 547 nm as a function of inverse absolute temperature is plotted in Fig. 4(b), the fitted straight line matches well with original data plots, whose result can be expressed by the following equation.
| ln(FIRglass) = 1.487 − 1023.4T−1 | (2) |
According to eqn (2) above, the effective energy gap in precursor glass between 2H11/2 and 4S3/2 can be inferred to 710.8 cm−1 in principle.
There are two indispensible parameters evaluating the temperature sensing applications based on FIR technique, one of which is the absolute temperature sensitivity SA and the other is relative sensitivity SR. Actually the relative sensitivity SR is more objective compared with the absolute temperature sensitivity because the SA is always affected by FIR value which can be obtained diversely from materials using different procedures. The feature is reflected by their definitions:
The SR and SA values are in proportion to the effective energy gap ΔE. According to eqn (1), ΔE/kB represents slope value in linear function, so the slope value can represent temperature sensitivity in fact. Fig. 4(c) describes the obtained experimental data of absolute temperature sensitivity (SA) together with relative sensitivity (SR) and corresponding fitting curves as a function of temperature from 303 K to 573 K. It is obvious that the SR becomes small and small as the temperature increases while the tendency of SA keeps increasing initially and decreasing finally. Derived from original data plots, the maximum SA and SR of silicate glass samples are 2.38 × 10−3 K−1 at 483 K and 11.15 × 10−3 K−1 at 303 K, respectively. Especially the maximum relative sensitivity is 11.15 × 10−3 K−1 at 303 K, note that it will keep increasing with the temperature descending. Derived from eqn (2), the slope value (E/kB) of fitted logarithmic FIR curve is 1023.56 ± 14.20.
The normalized upconversion spectra and series of characterization analysis of silicate GC, similar to those of precursor glass, were collected in Fig. 4(d–f). The fluorescence intensity ratio of 525 nm versus 547 nm also increases monotonously as the temperature raises, according to previous theoretical analysis, the logarithmic FIR about GC as a function of inverse absolute temperature is well fitted with the expression:
| ln(FIRGC) = 1.076 − 974.01T−1 | (3) |
From the eqn (3), the slope of GC fitted line is 974.01 ± 9.55, we can deduced that the effective energy gap in GC between 2H11/2 and 4S3/2 is 676.6 cm−1, notably the value have changed after crystallization when compared with precursor glass. Moreover, it gets smaller than precursor glass instead of bigger. Because the slope value can represent relative temperature sensitivity, this phenomenon means that, although upconversion emission efficiency of silicate GC enhanced greatly, its relative temperature sensitivity decreased on the contrary. As we know, rare earth ions have special electronic structure, the fluorescence emission of them originated from 4f–4f orbits does not affected easily by external environment for the reason of shielding effect by 5s–5d orbit electrons. However, the cubic face structure CaF2 crystal fields were formed in GC around rare earth ions after heat treatment, the energy level of rare earth ions will be affected still due to strong electrostatic interaction of crystal field, such as Stark energy level splitting, which can be demonstrated from the upconversion spectra in Fig. 3. According to crystal field theory, there is a J mixed effect after Stark splitting, namely different J state about spectral items mix with each other, which will result in the movement of orthocenter of J energy level. It is the same with the thermally coupled energy level (2H11/2 and 4S3/2) under the effect of crystal field, the orthocenter interval in GC between 2H11/2 and 4S3/2 energy bands gets closer than that of precursor glass. In short, compared with glass, the relative temperature sensitivity of GC decreased a little, which could be attributed to the crystal field effect.
Then Fig. 4(f) describes the obtained experimental data about GC of SA and SR as a function of variable temperature. According to the experimental data plots, the maximum SA and SR of silicate GC samples are 1.63 × 10−3 K−1 at 453 K and 10.6 × 10−3 K−1 at 303 K, respectively. Table 1 lists the optical temperature sensing ability of glass and corresponding GC for better comparison. In conclusion, whether it is relative sensitivity or absolute sensitivity, silicate CaF2 GC shows weaker optical thermometry ability than precursor glass in terms of temperature sensitivity.
| Sample | SR-MAX (10−3 K−1) | SA-MAX (10−3 K−1) | ΔE/kB | Standard error |
|---|---|---|---|---|
| Silicate glass | 11.15 at 303 K | 2.38 at 483 K | 1023.56 | 14.20 |
| Silicate GC | 10.6 at 303 K | 1.63 at 453 K | 974.02 | 9.55 |
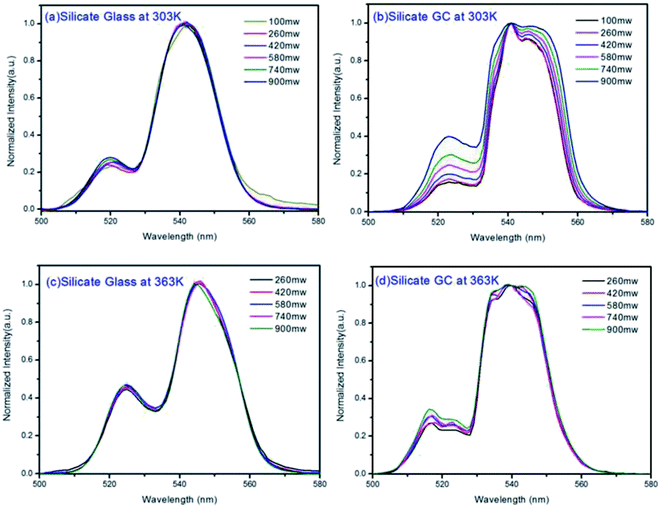
Considering the thermal effect caused by laser excitation, the pumping power dependent upconversion emission spectra of precursor glass and GC samples at different temperature were studied in Fig. 5. If the thermal effect induced by light source is serious, the surface temperature of sample will elevate dramatically, which can cause evident error between the test temperature and practical temperature for application. From the results collected at 303 K of Fig. 5(a) and (b), as the pumping power increases from 100 mW to 900 mW, the normalized emissions spectra of silicate glass located at 525 nm (2H11/2 → 4I15/2) and 547 nm (4S3/2 → 4I15/2) changed slightly while that of GC varied obviously. This means the integrated emission intensities ratio in glass and GC corresponding to thermally coupled energy levels, namely FIR, will be quiet different as a function of pumping power. Meanwhile we also monitored the similar upconversion emission spectra of precursor glass and GC at 363 K for further investigation, as is displayed in Fig. 5(c) and (d), the measurement range of pumping power was adjusted from 260 mW to 900 mW because of the weaker upconversion emission in precursor glass, which could be attributed to the more drastic non-radioactive transitions at the higher temperature. Note that the variation tendencies of glass and GC at 363 K are similar to those of pumping power dependent upconversion spectra at 303 K respectively, but the influence of pumping power on upconversion emission at higher temperature become weaker, we deduced that the higher temperature environment makes the materials less sensitive to the thermal effect caused by laser.
Fig. 6(a) displays the pumping power dependent FIR variation in glass and GC according to Fig. 5(a) and (b) collected at 303 K. Obviously, the thermal effect have already made a difference on FIR of GC when the pumping power is above 100 mW, it increases as the pumping power rises, actually this is a big challenge for practical application of optical thermometer as the thermal effect will induce a deviation between the measured temperature and actual one. In comparison, a more favorable result is achieved in silicate glass. Note that the FIR value variation is negligible when pumping power is under 420 mW, it implies that the thermal effect in glass induced by laser within a certain power is suppressed, but with the increase continuously of pumping power, FIR value still enhanced for the reason of unavoidable thermal effect. Fig. 6(b) exhibits the result of corresponding FIR variation at 363 K based on Fig. 5(c) and (d). In terms of silicate GC, the FIR also keeps increasing initially as the pumping power rises, while the FIR value of precursor glass is basically unchanged before the pumping power reaches to 740 mW, and then it has an increasing tendency, however whether it is GC or glass, the range of FIR fluctuation induced by thermal effect at 363 K becomes smaller than that of 303 K, we attributed this difference to the less sensitivity to thermal effect when temperature increases. In conclusion, FIR value has a close relation with pumping power, therefore previous temperature-dependent green upconversion spectra of glass and GC in Fig. 4 are all monitored at the 340 mW considering the upconversion emission intensity and weaker thermal effect as much as possible. In the present samples, the FIR variation of glass induced by thermal effect shows weaker pumping power dependence than that of GC, in another word, the laser pumping power in precursor glass triggering thermal effect is much bigger than GC.
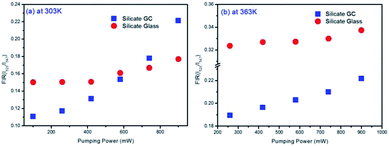 | ||
| Fig. 6 (a) Comparison of pumping power dependent FIR variation in glass and GC collected at 303 K and (b) at 363 K. | ||
In order to measure the repeatability of the temperature dependent FIR, the thermal cycling processes between 303 K and 573 K were displayed in Fig. 7. Evidently whether it is glass or GC, FIR value at the same temperature remains almost invariable even with a process of heating and cooling, it implies that electron distribution on thermally couple energy levels can restore to their original states when cooling from 573 K to 303 K. On the other hand, the little fluctuations in FIR value of the corresponding same temperature could be ascribed to a faint difference between the real temperature of measured samples and the monitoring temperature of copper heating plate. Subsequently, the FIR fluctuation is still negligible during a reheating process. These results indicate that such switching between heating and cooling of temperature dependent FIR is reversible and repeatable, we conclude that both silicate glass and GC exhibit favorable thermal stability.
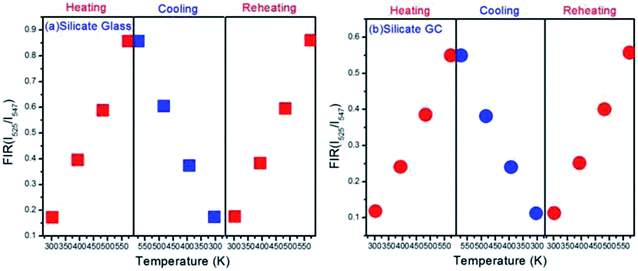 | ||
| Fig. 7 (a) Plots of FIR versus temperature upon the thermal cycling process with the varied temperature from 303 K to 573 K in glass and (b) GC. | ||
Conclusion
Transparent silicate glass and corresponding CaF2 glass ceramic were successfully fabricated, their structural, upconversion spectra and temperature-dependent luminescence measurement were investigated systematically. It was found that there are pros and cons to both of the precursor glass and glass ceramic. The upconversion luminescence intensity of GC enhanced enormously compared to that of glass. Impressively, the temperature sensitivity of GC decreased to a certain extent after crystallization, the maximum absolute sensitivity and relative sensitivity of GC reached to 1.63 × 10−3 K−1 at 453 K and 10.6 × 10−3 K−1 at 303 K, respectively, while the glass is 2.38 × 10−3 K−1 at 483 K and 11.15 × 10−3 K−1 at 303 K, it means the interval between thermally couple energy levels varied from 710.8 cm−1 in glass to 676.6 cm−1 in GC. We ascribe it to the J mixed effect of crystal field after Stark energy level splitting. Moreover, in the aspect of thermal effect induced by NIR laser, the FIR variation of glass shows weaker pumping power dependence than GC. Finally, both of glass and GC exhibit favorable thermal stability. As a consequence, these results may enrich our understanding toward the optical temperature sensing properties between glass and glass ceramic in other systems and provide comprehensive perspective to design practical optical thermometry materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Guangdong Natural Science Foundation (Grants S2011030001349, 2014A030306045), and Guangdong Science and Technology Department (Grant No. 2015B090901038) and Shenzhen science & technology innovation commission (Grant No. GJHS20160330152111138).References
- J. Brübach, C. Pflitsch, A. Dreizler and B. Atakan, Prog. Energy Combust. Sci., 2013, 39, 37–60 CrossRef.
- H. J. Seo, J. Wang, L. Qin, P. Cai, T. Vu, X. Wang, X. Yan and Y. Bu, Opt. Lett., 2016, 41, 5314–5317 CrossRef PubMed.
- H. Suo, C. Guo, Z. Yang, S. Zhou, C. K. Duan and M. Yin, J. Mater. Chem. C, 2015, 3, 7379–7385 RSC.
- X. D. Wang, O. S. Wolfbeis and R. J. Meier, Chem. Soc. Rev., 2013, 42, 7834 RSC.
- S. Zheng, W. Chen, D. Tan, J. Zhou, Q. Guo, W. Jiang, C. Xu, X. Liu and J. Qiu, Nanoscale, 2014, 6, 5675 RSC.
- X. Li, G. Jiang, S. Zhou, X. Wei, Y. Chen, C. K. Duan and M. Yin, Sens. Actuators, B, 2014, 202, 1065–1069 CrossRef CAS.
- B. Dong, B. Cao, Y. He, Z. Liu, Z. Li and Z. Feng, Adv. Mater., 2012, 24, 1987 CrossRef CAS PubMed.
- Y. Tian, B. Tian, C. e. Cui, P. Huang, L. Wang and B. Chen, Opt. Lett., 2014, 39, 4164–4167 CrossRef CAS PubMed.
- D. Chen, Z. Wan and S. Liu, Anal. Chem., 2016, 88, 4099–4106 CrossRef CAS PubMed.
- D. Chen, Z. Wan and Y. Zhou, Sens. Actuators, B, 2016, 226, 14–23 CrossRef CAS.
- D. Chen, Y. Zhou and Z. Wan, Opt. Lett., 2015, 40, 3607–3610 CrossRef CAS PubMed.
- Z. Cao, X. Wei, Z. Lu, Y. Chen and Y. Min, ACS Appl. Mater. Interfaces, 2016, 8, 34546 CAS.
- X. Wang, Q. Liu, P. Cai, J. Wang, L. Qin, T. Vu and H. J. Seo, Opt. Express, 2016, 24, 17792 CrossRef CAS PubMed.
- S. Zhou, S. Jiang, X. Wei, Y. Chen, C. Duan and M. Yin, J. Alloys Compd., 2014, 588, 654–657 CrossRef CAS.
- A. Pandey, V. K. Rai, V. Kumar, V. Kumar and H. C. Swart, Sens. Actuators, B, 2015, 209, 352–358 CrossRef CAS.
- S. Jiang, P. Zeng, L. Liao, S. Tian, H. Guo, Y. Chen, C. Duan and M. Yin, J. Alloys Compd., 2014, 617, 538–541 CrossRef CAS.
- F. Vetrone, R. Naccache, A. Zamarrón, A. Juarranz, F. Sanz-Rodríguez, L. M. Maestro, E. M. Rodríguez, D. Jaque, J. G. Sole and J. Capobianco, ACS Nano, 2010, 4, 3254 CrossRef CAS PubMed.
- X. Wang, RSC Adv., 2015, 5, 86219–86236 RSC.
- S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743–4756 CrossRef CAS.
- D. Chen, M. Xu, S. Liu and X. Li, Sens. Actuators, B, 2017, 246, 756–760 CrossRef CAS.
- W. Xu, X. Gao, L. Zheng, Z. Zhang and W. Cao, Sens. Actuators, B, 2012, 173, 250–253 CrossRef CAS.
- X. M. Li, J. K. Cao, Y. L. Wei, Z. R. Yang and H. Guo, J. Am. Ceram. Soc., 2016, 98, 3824–3830 CrossRef.
- X. Cheng, K. Yang, J. Wang, L. Yang and X. Cheng, Opt. Mater., 2016, 58, 449–453 CrossRef CAS.
- D. Chen, Z. Wan, Y. Zhou, P. Huang, J. Zhong, M. Ding, W. Xiang, X. Liang and Z. Ji, J. Alloys Compd., 2015, 638, 21–28 CrossRef CAS.
- L. Feng, B. Lai, J. Wang, G. Du and Q. Su, J. Lumin., 2010, 130, 2418–2423 CrossRef CAS.
- T. Wu, R. Tong, L. Liao, L. Huang, S. Zhao and S. Xu, Sensors, 2017, 17, 1253 CrossRef PubMed.
- Z. Q. Feng, L. Bai, B. S. Cao, L. D. Gong and B. Dong, Sci. China: Phys., Mech. Astron., 2010, 53, 848–851 CrossRef CAS.
- W. A. Pisarski, J. Pisarska, R. Lisiecki and W. Ryba-Romanowski, Sens. Actuators, A, 2016, 252, 54–58 CrossRef CAS.
- A. Pandey, S. Som, V. Kumar, V. Kumar, K. Kumar, V. K. Rai and H. C. Swart, Sens. Actuators, B, 2014, 202, 1305–1312 CrossRef CAS.
- W. P. Chen, F. F. Hu, R. F. Wei, Q. G. Zeng, L. P. Chen and H. Guo, J. Lumin., 2017, 192, 303–309 CrossRef CAS.
- F. Liu, E. Ma, D. Chen, Y. Yu and Y. Wang, J. Phys. Chem. B, 2006, 110, 20843–20846 CrossRef CAS PubMed.
- D. Chen, Y. Wang, Y. Yu and P. Huang, Appl. Phys. Lett., 2007, 91, 139 Search PubMed.
- L. Xing, W. Yang, D. Ma and R. Wang, Sens. Actuators, B, 2015, 221, 458–462 CrossRef CAS.
- H. Guo and Y. M. Qiao, Opt. Mater., 2009, 31, 583–589 CrossRef CAS.
- K. Zheng, Z. Liu, C. Lv and W. Qin, J. Mater. Chem. C, 2013, 1, 5502–5507 RSC.
| This journal is © The Royal Society of Chemistry 2018 |