Role of NH₄ ions in successive phase transitions of perovskite type (NH₄)₂ZnX₄ (X = Cl, Br) by ¹H MAS NMR and ¹⁴N NMR

Abstract

The ¹H chemical shifts and the spin-lattice relaxation time, T_1ρ, in the rotating frame of (NH₄)₂ZnX₄ (X = Cl, Br) are observed in order to investigate local phenomena related to successive phase transitions. The temperature dependence of T_1ρ values for ¹H showed a minimum, and the T_1ρ values for ¹H appeared to be governed by tumbling molecular motions at high temperatures. In addition, ¹⁴N NMR spectra are studied in each phase of (NH₄)₂ZnX₄ single crystals in the laboratory frame. The phase transition temperatures strongly affect the ¹⁴N number of symmetry related nitrogen centers within the unit cell. The ¹H MAS NMR and ¹⁴N NMR results are discussed to elucidate the roles of NH₄ ions during the phase transitions of (NH₄)₂ZnX₄.

---

1. Introduction

Perovskite A₂BX₄ type (A = NH₄, K, Rb, Cs; B = Zn, Co, Cu, Fe, Zn, Cd; X = Cl, Br) crystals have received a great deal of attention because of their nonlinear optical properties, and also because of the significant diversity of their structural phase transitions.^1–10 The prototype of the crystal structures of this family is that of β-K₂SO₄, which consists of isolated BX₄²⁻ tetrahedra and monovalent A⁺ cations placed in two inequivalent cavities. Ammonium tetrachlorozincate, (NH₄)₂ZnCl₄, and ammonium tetrabromozincate, (NH₄)₂ZnBr₄, belong to the family of crystals of the perovskite A₂BX₄ type and are known to undergo several phase transitions. Although the physical properties of (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ have been studied by several research groups, the structural geometry changes during the phase transitions of the two compounds have not been fully understood. Here, the phase transition temperatures and dynamics of the cations in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ are important. The potential applications of these materials are strongly affected by the phase transitions and dynamics of the cations.¹¹

(NH₄)₂ZnCl₄ undergoes five phase transitions: those between phases I and II at 406 K (=T_C1) and phases II and III at 364 K (=T_C2) are well-known, and the successive phase transitions at 319 K (=T_C3), 271 K (=T_C4), and 266 K (=T_C5) have also been reported;^12–14 the phases involved in these transitions are denoted by VI, V, IV, III, II, and I in order of increasing temperature, as shown in Table 1. The structure of (NH₄)₂ZnCl₄ in the normal phase, phase I (above 406 K), is orthorhombic with a_o = 9.274 Å, b_o = 12.620 Å, and c_o = 7.211 Å, and space group Pnma.¹² Upon cooling, there is a phase transition at 406 K to an incommensurate phase that is stable down to 364 K.¹⁵ The structure in phase III between 364 K and 319 K is orthorhombic with a = a_o, b = b_o, c = 4c_o, and the space group Pn2₁a.^12,16,17 The room temperature phase, phase IV, is antiferroelectric with a pseudo-orthorhombic monoclinic structure and space group Pa.¹² The region between 271 K and 266 K is mixed phase.¹⁴ Below 266 K, the lattice is constant with an orthorhombic structure, where a = a_o, b = b_o, and c = 3c_o.^12,17

Table 1 Phase transition temperatures, crystal structures, space groups, and lattice constants of (NH₄)₂ZnX₄ (X = Cl, Br)

(NH4)2ZnCl4
Transition temperature	TC5 (=266K)	TC4 (=271 K)	TC3 (=319 K)	TC2 (=364 K)	TC1 (=406 K)
Phase	VI	V	IV	III	II	I
Structure	Orthorhombic	Mixed phase	Monoclinic	Orthorhombic	Incommensurate	Orthorhombic
Space group	Pna21		Pa	Pn21a		Pnma
Lattice constant	a = ao		a = ao	a = ao		ao = 9.274 Å
	b = bo		b = bo	b = bo		bo = 12.620 Å
	c = 3co		c = 4co	c = 4co		co = 7.211 Å
			β = 89.992°
	Z = 12	Z = 12, 14, 16	Z = 16	Z = 16		Z = 4
Reference	12 and 17	14	12	12, 16 and 17	15	12

---

(NH4)2ZnBr4
Transition temperature	TC3 (=216 K)	TC2 (=395 K)	TC1 (=432 K)
Phase	IV	III	II	I
Structure	Orthorhombic	Monoclinic	Incommensurate	Orthorhombic
Space group	P21cn	P21/c11		Pmcn
Lattice constant	a = ao	a = ao		ao = 7.649 Å
	b = bo	b = bo		bo = 13.353 Å
	c = 3co	c = 4co		co = 9.727 Å
		β = 90.00(3)°
	Z = 12	Z = 16		Z = 4
Reference	22	22	20	21 and 22

---

On the other hand, the successive phase transitions of (NH₄)₂ZnBr₄ have been reported at 216 K (=T_C3), 395 K (=T_C2), and 432 K (=T_C1),^18–20 as shown in Table 1; the phases involved in these transitions are represented by IV, III, II, and I in order of increasing temperature. The structures of (NH₄)₂ZnBr₄ crystals in phases I, III, and IV are shown in Fig. 1. In phase I (above 432 K), the structure of (NH₄)₂ZnBr₄ is orthorhombic with a_o = 7.649 Å, b_o = 13.353 Å, c_o = 9.727 Å, and space group Pmcn.^21,22 Upon cooling, there is a phase transition at 432 K to an incommensurate phase II that is stable down to 395 K. The structure in phase III, between 395 K and 216 K, is monoclinic with a = a_o, b = b_o, c = 4c_o, β = 90.00(3)°, and space group P2₁/c11.²² The low-temperature phase IV is orthorhombic with a = a_o, b = b_o, c = 3c_o, and space group P2₁cn.²²

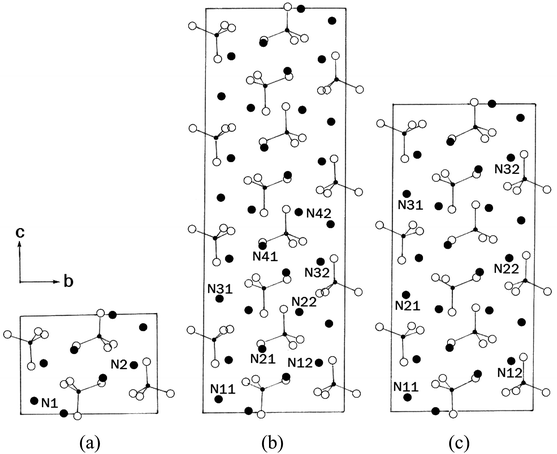Fig. 1 Projection of the structure along the a-axis in phases (a) I, (b) III, and (c) IV of (NH₄)₂ZnBr₄ crystal.

The ¹H spin-lattice relaxation times of (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ crystals have been obtained in the laboratory frame by Lim et al.^23–25 and Ramesh et al.,²⁶ respectively. The molecular dynamics and phase transitions of (NH₄)₂ZnCl₄ single crystals were reported previously. There were two crystallographically inequivalent NH₄ sites, namely NH₄(1) and NH₄(2), in the (NH₄)₂ZnCl₄. The ¹H spin-lattice relaxation time T₁ in the laboratory frame was observed to vary continuously with temperature without jumps or changes. The ¹H T₁ passes through a minimum value near 220 K; the presence of this minimum was attributed to the reorientation of the NH₄ groups. In addition, the ¹⁴N nuclear magnetic resonance (NMR) results in phase I of (NH₄)₂ZnCl₄ were reported for the two inequivalent sites N(1) and N(2): the quadrupole coupling constant, e²qQ/h, and asymmetry parameter, η, were e²qQ/h = 105.5 kHz and η = 0.96 for N(1), and e²qQ/h = 48.2 kHz and η = 0.087 for N(2).²⁷

The NMR method enables the study of a lattice's local properties, and is particularly useful in those cases that require information on the behavior of individual structural groups. Measurements of T_1ρ obtained by magic angle spinning (MAS) NMR in the rotating frame are advantageous in that they allow for probing of molecular motion in the kHz range, whereas T₁ values obtained by state NMR in a laboratory frame reflect motion in the MHz range.²⁸

The aim of this paper is to clarify the structural changes associated with the successive phase transitions in (NH₄)₂ZnX₄ (X = Cl, Br). Detailed studies of the molecular motions are necessary in order to explain the mechanisms of the phase transitions of (NH₄)₂ZnX₄. The temperature dependences of the MAS NMR spectra and the spin-lattice relaxation times, T_1ρ, in the rotating frame for the ¹H nuclei in (NH₄)₂ZnX₄ were investigated using a pulsed NMR spectroscopy. In addition, the ¹⁴N NMR spectra in (NH₄)₂ZnX₄ single crystals were obtained by static NMR in the laboratory frame, as a function of temperature. The ¹H MAS NMR and ¹⁴N static NMR results were analyzed to elucidate the roles of NH₄ ions during the phase transitions of (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄. The T_1ρ values by ¹H MAS NMR obtained here and the previously reported T₁ values by ¹H static NMR are compared. In addition, the information regarding the structural geometry of nitrogen environments in NH₄⁺ is discussed as a function of temperature.

2. Experimental method

Single crystals of (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ were obtained by the slow evaporation of aqueous solutions with the appropriate molar ratios of NH₄Cl and ZnCl₂, and NH₄Br and ZnBr₂, respectively, at 298 K.^12,29,30 These single crystals exhibited hexagonal shapes that were transparent and colorless.

¹H MAS NMR spectra and the spin-lattice relaxation times, T_1ρ, in the rotating frame in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ were measured in a static magnetic field of 9.4 T and Larmor frequency of ω₀/2π = 400.13 MHz, using a Bruker 400 MHz NMR spectroscopy at the Korea Basic Science Institute, Western Seoul Center. The chemical shifts were measured with respect to tetramethylsilane (TMS). Powder samples were placed inside a 4 mm cross-polarization (CP)/MAS probe, and the MAS rate was set to 5 kHz to minimize spinning sideband overlap. ¹H T_1ρ values were determined using a π/2–t sequence by varying the duration of spin-locking pulses. The widths of the π/2 pulse used to measure the T_1ρ values of ¹H in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ were 4.35 μs and 3.7 μs, respectively, with the spin-locking field equaling 57.47 kHz and 67.56 kHz.

In addition, the ¹⁴N NMR spectra of the (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ single crystals in the laboratory frame were measured using a Unity INOVA 600 NMR spectroscopy at the Korea Basic Science Institute, Western Seoul Center. The static magnetic field was 14.1 T, and the Larmor frequency was set to ω₀/2π = 43.342 MHz. The ¹⁴N NMR experiments were performed using a solid echo sequence of π/2–t–π/2–t. The widths of the π/2 pulse for ¹⁴N in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ were 4 μs and 3.7 μs, respectively. The measurements of ¹H MAS NMR in the rotating frame and ¹⁴N NMR in the laboratory frame were obtained over the temperature range of 180–430 K. Sample temperatures on MAS NMR and static NMR were held constant within ±0.5 K by controlling the helium gas flow and heater current.

3. Experimental results and discussion

3.1 Phase transition temperatures

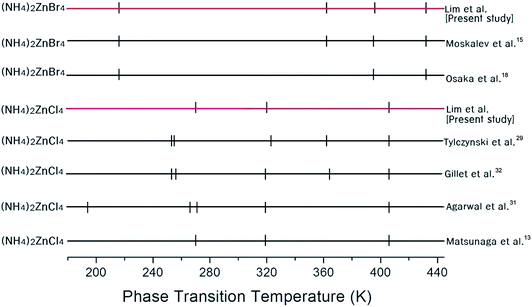
The phase transition temperatures for (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ single crystals have not yet been accurately established, as shown in Fig. 2. Here, the small vertical bars were represented the phase transition temperatures reported by several groups. In the case of (NH₄)₂ZnCl₄, this crystal exhibits three temperature dependence anomalies in the dielectric, thermal, and X-ray diffraction measurements at 270 K, 319 K, and 406 K, respectively, as reported by Matsunaga et al.¹³ Furthermore, anomalies characteristic of phase transitions reported by Agarwal et al.³¹ have been found in the Raman spectra investigations at 194 K, 266 K, 271 K, 319 K, and 406 K. According to Gillet et al.,³² the occurrence of phase transitions at 253 K, 256 K, 319 K, 364 K, and 406 K was also confirmed on the basis of the Brillouin investigation.³² In addition, thermal expansion changes at temperatures of 253 K, 255 K, 323 K, 362 K, and 406 K were reported by Tylczynski et al.²⁹ In the case of (NH₄)₂ZnBr₄, phase transition temperatures have been reported at 216 K, 395 K, and 432 K by Osaka et al.,¹⁸ and an additional phase transition at 365 K was reported by Moskalev et al.¹⁵ in their investigation of a (NH₄)₂ZnBr₄ crystal using ⁸¹Br nuclear quadrupole resonance (NQR), differential thermal analysis (DTA), and dielectric measurements. Fig. 2 shows that the phase transition temperatures obtained by several experiments are inconsistent for (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄, respectively.

Fig. 2 Phase transition temperatures (K) for (NH₄)₂ZnX₄ (X = Cl, Br) reported by several groups.

In order to determine the phase transition temperatures for the (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ single crystals obtained here, differential scanning calorimetry (DSC) measurements were taken with a DuPont 2010 DSC instrument at a heating rate of 10 °C min⁻¹. The DSC measurements revealed three endothermic peaks at 270 K, 320 K, and 406 K for (NH₄)₂ZnCl₄, and four endothermic peaks at 216 K, 362 K, 396 K, and 432 K for (NH₄)₂ZnBr₄, as shown in Fig. 3. These endothermic peaks were related to the phase transitions, and the temperatures were consistent with those previously reported by Matsunaga et al.¹³ and Moskalev et al.¹⁵ The phase transition temperatures of (NH₄)₂ZnX₄ may vary according to the conditions of crystal growth.

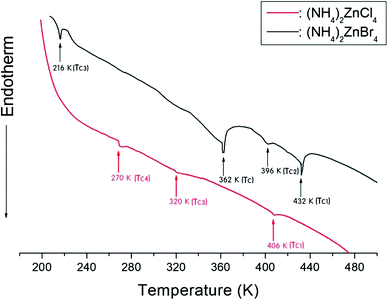Fig. 3 Differential scanning calorimetry (DSC) thermograms of (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ single crystals.

3.2 Molecular motion near phase transition temperatures from ¹H MAS NMR

The ¹H MAS NMR spectra in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ were measured as a function of temperature. At room temperature, (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ showed only one peak each, at chemical shifts of δ = 6.53 ppm and δ = 6.66 ppm, respectively, as shown in Fig. 4. The phase transition temperatures of (NH₄)₂ZnCl₄ are denoted by solid lines, and those of (NH₄)₂ZnBr₄ are denoted dash lines. The chemical shifts of the two materials did not change near the phase transition temperatures. The ¹H chemical shifts of (NH₄)₂ZnCl₄ decreased with increasing temperature, whereas the ¹H chemical shift of (NH₄)₂ZnBr₄ increased with increasing temperature. From the chemical shift for ¹H, the proton environments in N–H⋯Cl bond and the proton environments in N–H⋯Br bond were very different. This difference of chemical shifts was possibly due to the difference between the electron structures of halogen ions.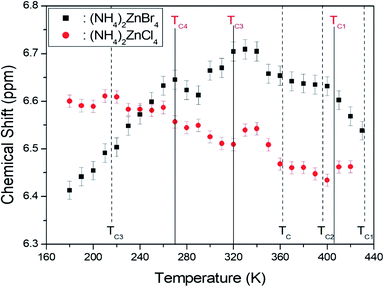

Fig. 4 Chemical shifts of ¹H MAS NMR spectra in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ as a function of temperature ((NH₄)₂ZnCl₄: solid lines, (NH₄)₂ZnBr₄: dash lines).

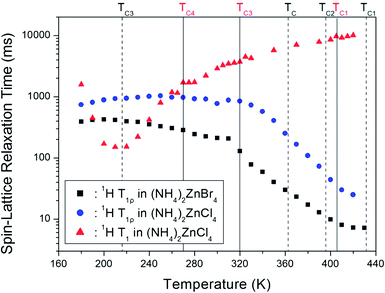
The decay traces for the ¹H resonance line in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ are represented by a single exponential function of M(t) = M(∞)exp(−t/T_1ρ), where M(t) is the magnetization as a function of the spin-locking pulse duration t, and M(∞) is the total nuclear magnetization of ¹H at thermal equilibrium.¹⁴ The decay traces for the ¹H nuclei varied with the delay time, and these decay traces also varied depending upon the temperature. The decay traces fitted with the single exponential function for delay times. From the slopes of the decay traces, the ¹H spin-lattice relaxation times, T_1ρ, in the rotating frame for the (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ were obtained as a function of temperature, as shown in Fig. 5. The T_1ρ values of ¹H were significantly different in the high-temperature and low-temperature regions. The significant difference in the T_1ρ values indicates that (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ are strongly affected, which considered to be mainly the result of molecular motions. The ¹H T_1ρ data showed no evidence of a change near the phase transition temperatures. The trend of ¹H T_1ρ in (NH₄)₂ZnCl₄ resembled that of ¹H T_1ρ in (NH₄)₂ZnBr₄. The two T_1ρ series displayed similar trends, both decreasing quickly above 310 K. The variation of T_1ρ with temperature exhibited a shallow minimum of 7.2 ms at 430 K in the case of (NH₄)₂ZnBr₄, indicating that distinct molecular motion is present. The T_1ρ minimum is considered to be clearly attributable to the tumbling motion of NH₄⁺ ions. The T_1ρ values are related to the corresponding values of the rotational correlation time, τ_C, which directly measures the rate of motion. The experimental T_1ρ value can be expressed in terms of τ_C using molecular motion, as suggested by the Bloembergen–Purcell–Pound (BPP) theory.³³ The T_1ρ value in the rotating frame can also be expressed in terms of τ_C using molecular motion.^28,34

1/T_1ρ = (n/20)(γ_Hγ_Nħ/r_H–N³)²[4f(ω₁) + f(ω_H − ω_N) + 3f(ω_N) + 6f(ω_H + ω_N) + 6f(ω_H)] (1)

Fig. 5 Temperature dependences of the spin-lattice relaxation time, T_1ρ, in the rotating frame and the spin-lattice relaxation time, T₁, in the laboratory frame of the ¹H nuclei in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ ((NH₄)₂ZnCl₄: solid lines, (NH₄)₂ZnBr₄: dash lines).

Here:

f(ω₁) = τ_C/[1 + ω₁²τ_C²]

f(ω_H − ω_N) = τ_C/[1 + (ω_H − ω_N)²τ_C²]

f(ω_N) = τ_C/[1 + ω_N²τ_C²]

f(ω_H + ω_N) = τ_C/[1 + (ω_H + ω_N)²τ_C²]

f(ω_H) = τ_C/[1 + ω_H²τ_C²]

In the equation, γ_H and γ_N are the gyromagnetic ratios for the ¹H and ¹⁴N nuclei, respectively; n is the number of directly bound protons; r_H–N is the H–N internuclear distance; ħ is the reduced Planck constant; ω_H and ω_N are the Larmor frequencies of ¹H and ¹⁴N, respectively; and ω₁ is the spin-lock field frequency of 67.56 kHz. Here, the f(ω₁) is non-zero, i.e., the τ_C is much less than the Larmor frequencies, therefore all of the other terms is far smaller than the f(ω₁) term. We analyzed our data by assuming that T_1ρ would show a minimum when ω₁τ_C = 1, and that the relation between T_1ρ and the characteristic frequency of motion, 1/τ_C, could be applied. The coefficient in eqn (1) can be determined because the T_1ρ curve displays a minimum and because the value of τ_C can be obtained from ω₁τ_C = 1; thus, (n/20)(γ_Hγ_Nħ/r_H–N³)² ≈ 4.66 × 10⁶ in the BPP formula. We were then able to calculate the correlation time τ_C as a function of temperature. The temperature dependence of τ_C follows a simple Arrhenius expression:^34,35

τ_C = τ_o exp(−E_a/RT), (2)

where τ_o is a pre-exponential factor, T is the temperature, R is the gas constant, and E_a is an activation energy. Thus, the slope of the linear portion of a semi-logarithmic plot should yield E_a. The value of E_a for the tumbling motion can be obtained from a plot of log τ_C versus 1000/T. We obtained E_a = 36.69 ± 0.66 kJ mol⁻¹ for the tumbling motion of ¹H in (NH₄)₂ZnBr₄ at high temperature. This value is very similar to that for ¹H in (NH₄)₂ZnCl₄, and is the same within the error range. And, the E_a for (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ at low temperature is 0.32 ± 0.30 kJ mol⁻¹ and 2.25 ± 0.37 kJ mol⁻¹, respectively.

On the other hand, the ¹H spin-lattice relaxation time T₁ in the laboratory frame in (NH₄)₂ZnCl₄ previously reported was obtained as a function of temperature, as shown in Fig. 5.^23–25 In the high temperature region, T₁ increases monotonically with temperature, and T₁ was continuous at the phase transition temperatures. However, the T₁ undergoes a change in slope near T_C4. ¹H T₁ passes through a minimum value in the vicinity of 220 K, and the presence of this minimum was attributed to the effects of molecular motion. The relaxation process from the ¹H T₁ curve was affected by molecular motion, as described by the BPP theory.³³ The activation energy in the low and high temperatures was reported 29.95 ± 0.85 kJ mol⁻¹ and 10.99 ± 0.37 kJ mol⁻¹, respectively.

3.3 Structural changes near phase transition temperatures from ¹⁴N NMR

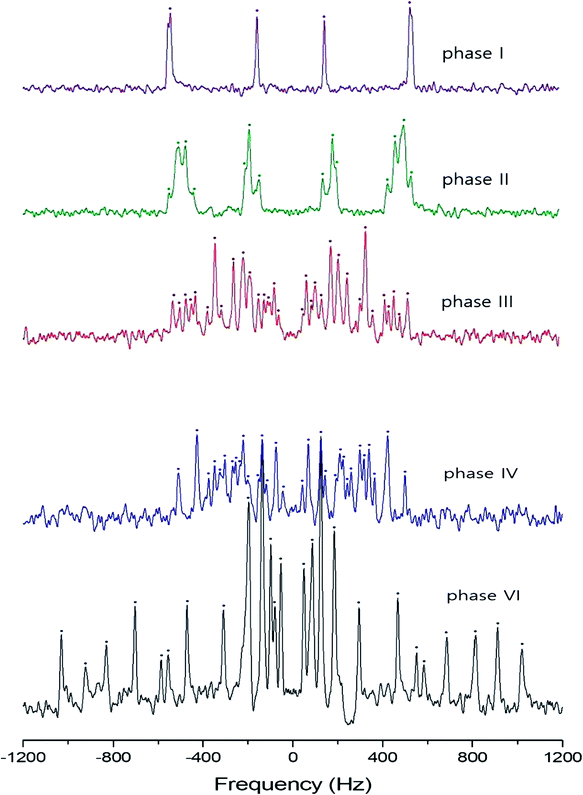
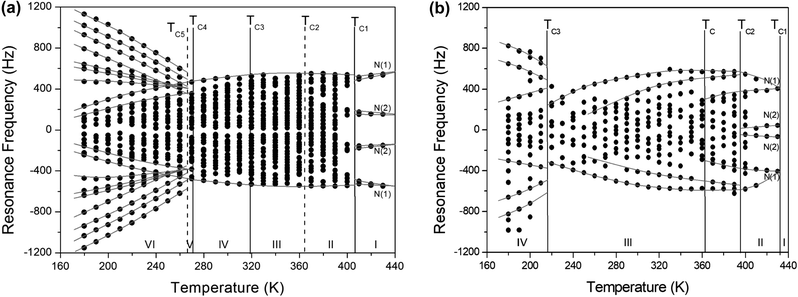
In order to investigate local phenomena related to successive phase transitions, the NMR spectra of ¹⁴N (I = 1) was obtained as a function of temperature using static NMR at a Larmor frequency of ω₀/2π = 43.342 MHz. ¹⁴N (I = 1) NMR is a sensitive method for probing local structural properties in each phase. The ¹⁴N NMR spectra consisted of pairs of lines at frequencies corresponding to the transitions Δm = ±1 ↔ Δm = 0. The crystal was oriented such that the magnetic field was aligned with the crystallographic c-axis. Temperature-dependent changes in the ¹⁴N resonance frequency are generally attributed to changes in the structural geometry, indicating a change in the quadrupole coupling constant of the ¹⁴N nuclei. The ¹⁴N NMR spectra at phase I, II, III, IV, and VI in (NH₄)₂ZnCl₄ crystals were plotted in Fig. 6. Here, the ¹⁴N peaks positions were denoted by close circles. Two resonance lines were expected because of the quadrupole interaction of the ¹⁴N nucleus. However, many resonance lines were observed, and they were much narrower in line width.

Fig. 6 ¹⁴N NMR spectra in (NH₄)₂ZnCl₄ single crystal at phase I, II, III, IV, and VI.

The resonance frequencies of ¹⁴N signals in (NH₄)₂ZnCl₄ and (NH₄)₂ZnBr₄ single crystals are respectively plotted in Fig. 7(a) and (b) as a function of temperature. In the case of (NH₄)₂ZnCl₄, the phase transitions occurring at T_C1, T_C3, and T_C4 were observed from our DSC results, whereas those at T_C2 and T_C5 were not observed. Therefore, T_C1, T_C3, and T_C4 are denoted by solid lines, and T_C2 and T_C5 are denoted dotted lines in Fig. 7(a). The resonance frequencies near T_C1, T_C4, and T_C5 changed, whereas those near T_C2 and T_C3 did not change. In phase I, each unit cell contains four formula units, and there are also two different kinds of ¹⁴N nuclei, termed N(1) and N(2). Therefore, the ¹⁴N NMR spectra exhibited eight resonance lines in four pairs. Here, the two inequivalent sites N(1) and N(2) are distinguished by the quadrupole coupling constant previously reported: e²qQ/h = 105.5 kHz and η = 0.96 for N(1), and e²qQ/h = 48.2 kHz and η = 0.087 for N(2).²⁷ Additional lines in phases II, III, and IV were obtained, although they exhibited very small intensities compared with phase I. In phases III and IV, the unit cell is quadrupoled along the c-direction of phase I. The unit cell of phases III and IV contains 16 formula units, and thus 32 resonance lines of 16 pairs are expected. According to the crystallography results shown in Fig. 1(b), eight atoms N(11), N(21), N(31), and N(41) are surrounded by five Cl atoms, while the other atoms N(12), N(22), N(32), and N(42), which are located between the layers created by the ZnCl₄ tetrahedra, are surrounded by eight Cl atoms. From the NMR spectra results of 16 pairs of ¹⁴N, the approximately 32 resonance lines in phases III and IV were measured, as shown in Fig. 7(a). The 32 resonance lines from the 16 pairs of ¹⁴N in the NH₄ ion were consistent with the previously reported crystallography structure.^12,16,17 In addition, phase VI, below T_C5, contains Z = 12 formula units, N(11), N(12), N(21), N(22), N(31), and N(32), as shown in Fig. 1(c). Therefore, approximately 24 resonance lines in 12 pairs were obtained. In these results, the splitting of the ¹⁴N resonance lines for seven of the pairs slightly decreased with increasing temperature, whereas those of the ¹⁴N resonance lines for the other five pairs slightly increased with increasing temperature. On the other hand, the resonance frequencies in phases I, II, III, and IV for the case of (NH₄)₂ZnBr₄ are shown in Fig. 7(b). The ¹⁴N NMR spectra from (NH₄)₂ZnBr₄ could not be easily observed in detail because of their very low intensity. However, the resonance frequencies near T_C2 and T_C3 changed discontinuously.

Fig. 7 (a) Resonance frequency of ¹⁴N NMR spectra in (NH₄)₂ZnCl₄ single crystal as a function of temperature. (b) Resonance frequency of ¹⁴N NMR spectra in (NH₄)₂ZnBr₄ single crystal as a function of temperature.

As mentioned above, in the case of (NH₄)₂ZnCl₄, four pairs of lines ascribed to N(1) and N(2) nuclei appeared in phase I, above 406 K. Because the frequency distributions in phase II discontinuously emerged from these high-temperature lines, the notations N(1) and N(2) were not retained. Based on this temperature dependence, the assignment of the resonance lines in phases III and IV are also not denoted. The resonance frequency from phase V cannot be distinguished because of the much narrower temperature range. The resonance frequencies in phase VI, below T_C4, changed discontinuously from those of phases V and IV. The changes in the resonance lines near T_C4 for (NH₄)₂ZnCl₄ and T_C3 for (NH₄)₂ZnBr₄ also indicated a phase transition where the new phase exhibited orthorhombic symmetry, which equates to a higher degree of symmetry compared with monoclinic symmetry. Abrupt changes in the resonance frequencies for ¹⁴N near the phase transition temperatures are generally attributed to structural phase transitions.

4. Conclusion

Data on structural geometries near successive phase transition temperatures of (NH₄)₂ZnX₄ (X = Cl, Br) were obtained by ¹H MAS NMR and ¹⁴N NMR as a function of temperature. We studied the molecular motions in (NH₄)₂ZnX₄, based on the ¹H chemical shifts and spin-lattice relaxation time, T_1ρ, in the rotating frame. The ¹H chemical shifts near the phase transition temperatures for the two materials did not show any drastic change, and this result might be related to proton ordering near the phase transition temperatures. From the ¹H T_1ρ results, the activation energies for the tumbling motion of ¹H had very similar values, and the tumbling motion of NH₄⁺ ions occurred within the high-temperature range.

We compared the ¹H MAS NMR in the rotating frame measured here and the previously reported ¹H static NMR results in the laboratory frame^23–25 for (NH₄)₂ZnCl₄. The trends in T_1ρ values for ¹H in (NH₄)₂ZnCl₄ are different from the trends in the T₁ values. The molecular motion by T_1ρ in the rotating frame was dominant at high temperature, whereas that by T₁ in the laboratory frame was dominant at low temperature. The activation energy values extracted from T_1ρ and T₁ measurements are different for the molecular motions in the kHz and MHz ranges.

The ¹⁴N NMR spectra exhibited a sudden shift in the ¹⁴N peak positions and number of peaks at the phase transition temperatures. The electric field gradient (EFG) tensors at the N sites varied, reflecting the changing atomic configurations around the ¹⁴N nuclei. This is because the phase transition temperature strongly affect the ¹⁴N number of symmetry related nitrogen centers within the unit cell. Therefore, ¹⁴N NMR provides insight into changes in crystal symmetry and cation reorientation rates induced by heating and phase transitions.

The two crystals have different phase transition temperatures, but seemingly similar phase transition mechanisms. Although (NH₄)₂ZnX₄ has different bond lengths in the Zn–X (X = Cl, Br) structure, and different X atomic radii, the different halide ions (X = Cl, Br) do not appear to significantly influence the ¹H relaxation time.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science, and Technology (2016R1A6A1A03012069 and 2015R1A1A3A04001077).

References

1. C. Griset, S. Head, J. Alices and O. A. Starykh, Phys. Rev. B, 2011, 84, 245108.
2. T. Ono, H. Tanaka, Y. Shirata, A. Kindo, F. Ishikawa, O. Kolomiyets, H. Mitamura, T. Goto, N. Nakano, N. A. Fortune, S. T. Hannahs, Y. Yoshida and Y. Takano, J. Phys.: Conf. Ser., 2011, 302, 12003.
3. M. Vachon, G. Koutroulakis, V. F. Mitrovic, O. Ma, J. B. Marston, A. P. Reyes, P. Kuhns, R. Coldea and Z. Tylczynski, New J. Phys., 2011, 13, 93029.
4. K. Foyevtsova, I. Opahle, Y.-Z. Ahang, H. O. Jeschke and R. Valenti, Phys. Rev. B, 2011, 83, 125126.
5. T. Coletta, M. E. Zhitomirsky and F. Mila, Phys. Rev. B, 2013, 87, 60407.
6. S. A. Zvyagin, D. Kamenskyi, M. Ozerov, J. Wosnitza, M. Ikeda, T. Fujita, M. Hagiwara, A. I. Smirnov, T. A. Soldatov, A. Ya Shapiro, J. Krzystek, R. Hu, H. Ryu, C. Petrovic and M. E. Zhitomirsky, Phys. Rev. B, 2014, 112, 77206.
7. A. Yamada, Phys. Rev. B, 2014, 90, 235138.
8. J. Merino, Phys. Rev. B, 2014, 89, 245112.
9. S. A. Zvyagin, M. Ozerov, D. Kamenskyi, J. Wosnitza, J. Krzystek, D. Yoshizawa, W. Hagiwara, R. Hu, H. Ryu, C. Petrovic and M. E. Zhitomirsky, New J. Phys., 2015, 17, 113059.
10. B. Schmidt and P. Thalmeier, New J. Phys., 2015, 17, 73025.
11. D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Pechy, S. M. Zakeeruddin, M. Gratzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10055.
12. H. Matsunaga, J. Phys. Soc. Jpn., 1982, 51, 864.
13. H. Matsunaga and E. Nakamura, J. Phys. Soc. Jpn., 1981, 50, 2789.
14. T. Sata, T. Osaka and Y. Makita, J. Phys. Soc. Jpn., 1984, 53, 1907.
15. A. K. Moskalev, I. A. Belobrova, L. I. Zherebtsova and I. P. Aleksandrova, Phys. Status Solidi A, 1982, 72, k19.
16. I. Mikhail, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2126.
17. H. Matsunaga, K. Ithoh and E. Nakamura, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 898.
18. T. Osaka, M. Komukae and Y. Makita, J. Phys. Soc. Jpn., 1982, 51, 3409.
19. H. V. Koningsveld, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 15.
20. T. Sato, T. Osaka and Y. Makita, J. Phys. Soc. Jpn., 1983, 52, 3297.
21. W. J. Asker, D. E. Scaife and J. A. Watts, Aust. J. Chem., 1972, 25, 2301.
22. H. Shigematsu, H. Kasano and H. Mashiyama, J. Phys. Soc. Jpn., 1993, 62, 3929.
23. A. R. Lim, Solid State Commun., 2011, 151, 1631.
24. A. R. Lim and K.-Y. Lim, J. Solid State Chem., 2013, 200, 227.
25. A. R. Lim, Chem. Phys., 2012, 400, 39.
26. K. P. Ramesh, N. Devaraj, D. Vijayaraghavan and J. Ramakrishna, Phase Transitions, 1992, 37, 203.
27. D. Michel, B. Muller, J. Petersson, A. Trampert and R. Walisch, Phys. Rev. B, 1991, 43, 7507.
28. J. L. Koenig, Spectroscopy of Polymers, Elsevier, New York, 1999.
29. Z. Tylczynski and P. Piskunowicz, Phys. Status Solidi A, 1990, 118, 441.
30. J. P. Strivastava and A. Kulshreshtha, J. Opt. Soc. Am. B, 1991, 8, 2379.
31. A. Agarwal, M. B. Patel, M. Pal and H. D. Bist, Spectrochim. Acta, Part A, 1984, 40, 1063.
32. A. M. Gillet, Y. Luspin and G. Hauret, Solid State Commun., 1987, 64, 797.
33. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679.
34. A. R. Lim, AIP Adv., 2016, 6, 35307.
35. A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, 1961.

---