Multifunctional Nd³⁺ substituted Na_0.5Bi_0.5TiO₃ as lead-free ceramics with enhanced luminescence, ferroelectric and energy harvesting properties

Abstract

Herein, we present comprehensive investigations of the optical and electrical properties of Nd³⁺ substitution in sodium bismuth titanate ceramics (NBNT) with varying Nd³⁺ concentration. The room temperature photoluminescence (PL) emission for both unpoled and poled samples is observed to be a maximum for an Nd³⁺ substitution of 1 mol%. Upon poling, the PL intensity is observed to be quenched, consistent with the obtained XRD data, indicating an electric-field induced structural ordering towards higher symmetry, confirmed with the help of structural refinement. The evaluated ferroelectric to relaxor and antiferroelectric relaxor T_(F–R) was observed clearly from the poled dielectric–loss curve for the 1 mol% of Nd³⁺ substitution. Furthermore, the optimized NBNT exhibited a lower E_c and a higher off-resonance figure of merit (FOM_off) for energy harvesting by 12% and 30%, respectively, in comparison with un-doped NBT.

---

1. Introduction

Multifunctional ceramics, exhibiting two or more properties from among magnetic, ferroelectric, pyroelectric, piezoelectric and optoelectronic properties have received a remarkable amount of interest.^1–3 Sodium bismuth titanate, Na_0.5Bi_0.5TiO₃ (NBT), with a lead-free perovskite structure is a proven candidate showing excellent ferroelectric properties.^4,5 Enhanced piezoelectric properties of NBT and its solid solutions by cation substitution at the A and B-sites have been reported.^6–9 In particular, it was observed that site-specific substitution with optically active rare-earth (RE) ions resulted in enhanced electrical properties with the additional functionality of photoluminescence (PL), making them attractive for promising applications.^10–15 Recent reports on RE substituted NBT ceramics indicated that both PL and electrical properties can be modified upon electrical poling.^16,17 Among all the optically active RE ions, Nd³⁺ with emission in the near IR spectral region has found a plethora of optoelectronics applications. M. Zannen et al.¹³ reported the best emission together with better ferroelectric properties for 5 mol% substitution of Nd³⁺ for NBT ceramics. Another investigation¹⁸ revealed better piezoelectric coefficients with 2 mol% substitution of Nd³⁺. These contradictory reports, however, did not deliberate on the effect of electrical poling.

In this report, we focus our attention on obtaining the optimal substitution of Nd³⁺ for enhanced properties and multifunctionality. Here, we relate the role of structural changes in the host lattice to the obtained PL intensity from Nd³⁺ substituted [Na_0.5Bi_0.5−xNd_x]TiO₃ (referred to hereafter as NBNT) ceramics with varying Nd³⁺ concentration in the range of x = 0.003–0.1 [≅(0.3–10) mol%] by photo excitation at 532 nm. We observed the maximum PL intensity for x = 0.01 (≅1 mol%), which is the critical concentration for the onset of PL quenching. Upon poling, the applied electric-field induces structural order that is manifested in further PL quenching. The obtained hysteresis (P–E) data for NBNT showed a reduced coercive electric field (E_c) with almost identical remnant-polarization (P_r), implying that optimized NBNT maintains a ferroelectric behaviour similar to that of NBT. Further, the estimated off-resonance figure of merit (FOM_off) for energy harvesting showed an increase of ≈30%, compared to NBT, making the optimised NBNT a promising candidate for multifunctional applications. The literature reports multifunctionality achieved in different solid-solutions which, no doubt provide better properties. Yet processing these materials from simple bulk ceramic compounds to thin-film devices is challenging. Thus, advances in simple perovskite compounds are useful in this respect and this communication aims to show that simple substitution of Nd³⁺ into the A-site of NBT enhances the ferroelectric, piezoelectric, and energy harvesting properties with the added functionality of it being photo-luminescent.

2. Experimental details

Polycrystalline NBT compounds with different Nd³⁺ substitutions were synthesized by a conventional solid-state route using high-quality powders of Na₂CO₃, Bi₂O₃, TiO₂, and Nd₂O₃ (99.99% Sigma-Aldrich Chemicals, USA). Considering the loss on ignition, the precursors are weighed carefully according to stoichiometric ratios given as [Na_0.5Bi_0.5−xNd_x]TiO₃ where x = 0, 0.003, 0.005, 0.007, 0.01, 0.02, 0.03, 0.04, 0.05, 0.07, and 0.1) and subsequently milled and calcined at 800 °C for 3 h. The calcined powders are further milled, sieved, and compacted into a circular pellet (ϕ = 10 mm) and finally sintered at 1150 °C for 3 h in air with a heating rate of 5°C min⁻¹. Phase analysis of the obtained ceramic pellets was performed by using a powder X-ray diffractometer (PANalyticalX'pertpro; CuK_α radiation λ = 1.5406 Å) over the angles 20° < 2θ < 80°. The relative density (RD) of the NBNTs was measured using the Archimedes method and was estimated to be in the range of 94–95% relative to the theoretical density of 5.94 g cm³ (ref. 19 and 20) for pure NBT ceramics. Diffused-reflectance measurements were performed using a Shimadzu UV-3600 spectrometer. The room temperature PL spectrum was measured by photo-excitation at 532 nm from a cw-DPSS laser (LSR532NL-300, Lasever) and the subsequent PL was collected by a fiber coupled spectrometer (AvaSpec-ULS2048L-RS, Avantes) with a spectral resolution of 1.4 nm.²¹ The PL spectrum, averaged over 3 spots on the sample, is presented as obtained. All the ceramics are thinned down to a thickness of 0.5 mm to get enough dense silver electrodes on both sides of the pellets. The samples were electrically poled at room temperature in a silicon oil (DOW CORNING 704) bath by applying a DC electric field of (0–10–50) kV cm⁻¹ for 30 min and all the measurements were repeated thereafter. The hysteresis (P–E) data were obtained with a TF-Analyzer 2000 (aixACCT systems, GmbH) from samples of 0.5 mm thickness, using silver-coated electrodes on both sides. The temperature- and frequency-dependent dielectric measurements on the silver-coated pellets were performed with an impedance analyzer (Wayne Kerr 6500B). The piezoelectric harvesting parameters were obtained using a Piezometer System PM300 (Piezotest Ltd.) operated at a frequency of 100 Hz.

3. Results and discussion

The prepared NBNT ceramics with Nd³⁺ substitution [x = 0.003–0.1] allowed a sufficient number of samples to get the optimized NBNT with the best multifunctionality. The absorption spectra of the NBNTs, shown in Fig. 1, had the specific signature of Nd³⁺ in an ordered host medium, even though the peak intensities differ in different hosts.²² With an increase in x these bands are observed to be getting stronger, with no absorption feature for pure NBT in the visible spectral region (inset).

Fig. 1 Representative absorption spectra of NBNTs for x = 0, 0.01, 0.03, 0.05, 0.07 and 0.1 (inset) showing the magnified 450–800 nm spectral region highlighting the signature absorption of Nd³⁺ ions.

Fig. 2 shows the measured PL spectra of NBNT ceramics exhibiting multiple peaks within the possible detection range. Evidently, the best PL intensity is observed for x = 0.01 substitution and the PL intensity decreases with an increase in the Nd³⁺ substitution. Importantly, the PL peak position is not influenced by x. PL is not observed from the pure NBT sample, as expected. The spectroscopic terms related to the radiative relaxation of Nd³⁺ are well known.²² The observed PL spectrum consists of overlapping lines arising from transitions between the crystal field split ⁴F_3/2 level and various sublevels of ⁴I_9/2 and ⁴I_11/2. The inset of Fig. 2 shows the PL spectrum from NBNT with x = 0.01 substitution, at a log-scale to highlight the various peaks, the maxima being at 880 nm and 910 nm. The choice of rejection color filters at detection enabled observation of the peaks at 808 nm and 832 nm, which were not presented in earlier reports.^14,15 The measured spectrum in (1000–1100) nm with a maximum at 1064 nm is weak since the detector sensitivity²¹ drops sharply in this spectral region. The shoulder at 1083 nm can be conjectured to be the effect of structural disorder, which could be due to the individual excitation of Nd³⁺ ions in the Bi³⁺ site.

Fig. 2 PL spectra of unpoled NBNTs showing the variation in the PL intensity as a function of Nd³⁺ substitution. Inset shows the log-plot of PL spectrum for x = 0.01 clearly showing the emission peaks from different transitions.

Considering NBNT is a ferroelectric ceramic, it will be subjected to electric fields during routine device operation, making it vital to understand the effect of an applied electric field on the PL. Upon electrical poling, PL is observed to have been quenched in intensity compared to the respective unpoled samples. Nonetheless, the variation in emission with respect to substitution is similar to the trend seen for unpoled ceramics, with the best emission for x = 0.01 substitution, similar to emission from unpoled samples. To make a quantitative comparison, we calculated the area under the PL spectra of poled and unpoled ceramics in the spectral range of (800–1000) nm. Fig. 3 demonstrates the effect of electrical poling, with a reduction in PL spectral intensity of ≈30% upon poling to 50 kV cm⁻¹ being observed. It is interesting to note that the shapes of the PL spectral profiles remain unchanged upon poling, unlike a similar report¹² on Eu³⁺ doped NBT ceramics for which the formation of a new spectral peak was observed. The PL intensity is found to be a maximum for x = 0.01 substitution.

Fig. 3 Quenching of PL for optimized NBNT (x = 0.01) with different electric fields.

Considering the paucity of reports on the computational study of crystal-field effects on rare-earth emission in doped perovskite material systems, we try to elucidate our observation qualitatively. It is well known that the Nd³⁺ emission is extremely sensitive to the local host symmetry. The Judd–Ofelt theory, which is widely used to estimate the intensities of transitions for the RE ions, defines a set of three intensity parameters Ω_t (t = 2, 4 and 6) that are sensitive to the local environment of the luminescent centers.^23,24 Here, the important factors affecting the local environments of Nd³⁺ in NBT pertain to fluctuations in the Na : Bi ratio from 1 : 1 as a result of substitution, different chemical ordering at the local scale and disorder associated with atomic displacements. With a solid matrix with fixed lattice positions for Na and Bi, the external electric field is expected to induce long-range order in the polar displacements of the atoms. This in turn affects the transition intensities. Therefore, in line with an earlier report¹⁶ for Pr-doped BNT-BT, where there was an enhancement in PL intensity upon poling, the observed reduction in PL can be conjectured to be a result of electric-field induced structural order towards higher symmetry.

To confirm the role of structural ordering, XRD measurements were performed in different poling fields (0–50) kV cm⁻¹ with the interval of the poling field 10 kV cm⁻¹ to identify the structural symmetry variation in the optimal specimen, i.e. NBT-0.01Nd. Unpoled NBNTs exhibited a single phase structure stabilizing into a monoclinic structure with Cc space group symmetry in the substitution range 0 ≤ x ≤ 0.1, with no co-existing secondary phases within the sensitivity of XRD.²² Fig. 4 shows the variation in the XRD pattern for various poling fields. The poling field induces a distinct broadness in the main prominent peak (110)_PC of the perovskite structure, as shown in the left panel of Fig. 4. Notably, the structurally induced changes we observe upon electrical poling are in line with the reduction in PL intensity presented in Fig. 3.

Fig. 4 X-Ray diffraction pattern of NBT-0.01Nd under different poling fields (0–10–50) kV cm⁻¹, showing the enlarged portion of (110)_PC.

Further analysis of this prominent peak presented the structural evolution of other phases from the peak broadening as well the change in peak profile. In order to extract the possible structural evolution under the poling field in (110)_PC, the obtained peak is deconvoluted by using Lorentzian multi-peak fits, as shown in Fig. 5. The new structural phase rhombohedral (R3c) gradually evolves over the poling fields (represented by the blue shaded portion of the area under the curve). From the 40 kV cm⁻¹ spectrum we can observe a prominent doublet instead of a singlet, representing the effect of electrical poling on the crystal structure. The XRD data showing the effect of poling throughout the series is provided in the ESI.†

Fig. 5 Deconvolution of the (110)_PC peak for extracting the rhombohedral R3c phase along with monoclinic Cc under different electrical poling fields (0–50) kV cm⁻¹.

To strengthen the above arguments, further structural refinement of the XRD measurements was carried out by Rietveld refinement for the poled and unpoled [Na_0.5Bi_0.5−xNd_x]TiO₃ (x = 0.01) using Fullproof software, as presented in Fig. 6. Notably, the shape of the Bragg profile was modified upon poling, suggesting a gradual change throughout the series [Na_0.5Bi_0.5−xNd_x]TiO₃ (x = 0 and 0.1). The structure throughout the series stabilizes to monoclinic with the Cc space group. Upon poling the induced structural modification from Cc to R3c changes, observed as clear splitting at the (110)_PC reflection. The unpoled XRD pattern of [Na_0.5Bi_0.5−xNd_x]TiO₃ (x = 0.01) has fitted reasonably well with the recently proposed monoclinic Cc structure. The poled pattern of the same composition could be fitted well with the pure rhombohedral (R3c) structure. The goodness of fit is depicted in the inset of Fig. 6 for the Bragg reflection at 40°. The right panel of Fig. 6 illustrates the proposed crystal structure corresponding to poled and unpoled ceramics, using the refined parameters as input to the Diamond-Crystal and Molecular Structure Visualization software. Evidently distinct structural modulation can be observed upon poling. Further, the XRD patterns of the poled compositions x = 0.04 onwards could be fitted well with the Cc model, showing a reduced contribution of the fraction of the R3c phase upon poling the compounds with increased Nd³⁺ substitution. Table 1 shows the refined crystal parameters and corresponding positions.

Fig. 6 (Top panel) The structural refinement of unpoled NBT-0.01Nd with monoclinic Cc and corresponding crystal structure. (Bottom panel) The structural refinement of poled NBT-0.01Nd with rhombohedral R3c and corresponding crystal structure.

Table 1 Refined parameters and atomic positions of monoclinic Cc and rhombohedral R3c of NBT-0.01Nd

Unpoled (Cc)	x	y	z
Na/Bi/Nd	0.0000	0.2517	0.0000
Ti	0.2519	0.2504	0.7386
O1	−0.0016	0.2521	0.5107
O2	0.1982	0.4906	−0.0686
O3	0.3013	0.0296	0.0614
Lattice parameters (Å)	a = 9.518, b = 5.4876, c = 5.4982, α = γ = 90°, β = 125.331°, χ^2 = 1.85

---

Poled (R3c)	x	y	z
Na/Bi/Nd	0.0000	0.0000	0.2713
Ti	0.0000	0.0000	0.0068
O	0.1335	0.3379	0.0838
Lattice parameters (Å)	a = 5.4789, b = 5.4789, c = 13.5465, α = β = 90°, γ = 120°, χ^2 = 2.45

---

In order to understand the difference in the state of dipolar ordering in unpoled and poled specimens of NBT-0.01Nd, we performed temperature-dependent studies of the dielectric constant and loss tangent (tan δ) at different frequencies within the range of 5–100 kHz, as shown in Fig. 7. There are two prominent dielectric anomalies, corresponding to the temperatures T_d (the depolarization temperature) and T_m (the maximum temperature), which are responsible for the phase transitions from ferroelectric to antiferroelectric and antiferroelectric to paraelectric over the temperature range. The T_d and T_m were found to be 140 °C and 360 °C, respectively, from the poled and unpoled samples. In the case of the poled specimen, the dielectric constant improved compared to the unpoled specimen and a strong frequency dispersion with frequency dependence was observed at broad maxima of T_d and T_m. After poling, a new dielectric anomaly, which is associated with the transition from ferroelectric to relaxor and antiferroelectric relaxor at T_(F–R), can be observed clearly from the dielectric and loss curve at 110 °C in the poled specimen.

Fig. 7 The dielectric constant and tangent loss with temperature of NBT-0.01Nd for (top) unpoled and (bottom) poled samples.

The PL intensity variation and subsequent PL quenching with higher Nd³⁺ substitution can be understood by invoking concentration quenching.^25,26,27 Theoretically, the rate of relaxation due to concentration quenching varies as r⁻⁶ (where r denotes the inter-ion distance). As the concentration increases, the distance between neighboring Nd³⁺ ions reduces, leading to an energy exchange among Nd³⁺ ions. The inter-ionic radius for different x is estimated by using the relation.²⁸ Here, N_Nd³⁺ is the Nd³⁺ concentration in ions per cm³. As expected, an increase in x leads to a reduction in R_Nd. For the unpoled NBNT with x = 0.01, the estimated R_Nd ≈ (23.2 ± 1.3) Å. Similar calculations can be made for the poled NBNTs. From Fig. 2, we deduce the critical concentration X_Critical = 0.01, after which concentration quenching by energy transfer begins. The theoretical transfer distance, R_C (defined as the distance for which the energy transfer probability between neighboring Nd³⁺ ions is equal to the emission probability of the Nd³⁺ ions) is estimated using the relation²⁹ , where V is the volume of one unit cell, X_Critical is the optimal concentration of the activator ion and Z is the number of cations present in the unit cell. Using the values, V = 234.1 ų, Z = 4 for a monoclinic structure (Cc, unpoled), we estimated R_C ≈ (22.3639 ± 1.5) Å which is in the vicinity of the value of R_Nd for x = 0.01. Similarly, for the poled compound, using V = 351.5 ų, Z = 6 for the rhombohedral (R3c) structure, and we estimated R_C ≈ (22.3612 ± 1.5) Å, which is similar to the value for the unpoled structure and in the vicinity of the value of R_Nd for x = 0.01. From our calculations we deduce that the critical energy transfer radius (R_C) and the inter-ionic radius (R_Nd) are equal within the error limits for x = 0.01 substitution and beyond this concentration quenching begins.

To achieve multifunctionality, it is vital to have this PL functionality without compromising on the existing ferroelectric nature of the parent NBT compound. Fig. 8(a) presents a comparison of the hysteresis (P–E) loops obtained for the parent NBT and the optimized NBNT (x = 0.01). These hysteresis loops are well saturated, which is characteristic of ferroelectric behavior. We performed the measurement on two devices of each composition and estimated the average coercive electric fields (E_c) to be ≈65 kV cm⁻¹ and 59 kV cm⁻¹ and the remnant polarization values (P_r) to be 32.7 μC cm⁻² and 33.8 μC cm⁻² for NBT and NBT-0.01Nd, respectively. NBT-0.01Nd exhibits a slightly higher P_r and much lower E_c values by 3% and 12%, respectively, relative to pure NBT, confirming the better suitability of NBNT for possible applications in piezochromic devices. The requirement for such NBT based devices is lower coercivity (for easy switching) without compromising P_r. Thus, it can be inferred that the NBT-0.01Nd compound can be considered as a possible candidate for optimizing future piezochromic devices.

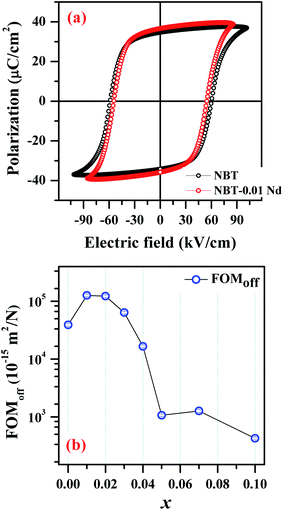Fig. 8 (a) Room temperature polarization (P)–electric field (E) measurement of NBT and NBT-0.01Nd. (b) Plot showing the variation of FOM_off as a function of x (Nd³⁺ substitution).

The best enhancement in terms of device functionality upon substitution was observed for piezoelectric energy harvesting. The measured d₃₃ were 84 pC N⁻¹ and 95 pC N⁻¹ for NBT and NBT-0.01Nd, suggesting an increase of 13%, implying that substitution of Nd³⁺ in NBT favors the mobility of domain walls (corroborated by the softer ferroelectric nature). From the same measurements we estimated the piezoelectric voltage coefficient (g₃₃) to be 26.7 mV N⁻¹, 48.4 mV N⁻¹ and the dielectric loss (tan δ) to be 0.0572, 0.0362 for NBT and NBT-0.01Nd, respectively. Together with the three quantities estimated so far, the off-resonance figure of merit (FOM_off) for energy harvesting can be estimated using the relation.^30,31 The estimated values of FOM_off were 39 209.8 × 10⁻¹⁵ m² N⁻¹ and 127 016.6 × 10⁻¹⁵ m² N⁻¹ for NBT and NBNT, implying an enhancement of ≈30%. Fig. 8(b) shows the variation in FOM_off for all the various composition used in the study. Interestingly, the variation in FOM_off follows the trend in PL emission for the varying amounts of Nd³⁺ substituted in NBT.

4. Conclusions

To conclude, we presented a comprehensive investigation of the effect of Nd³⁺ in Na_0.5Bi_0.5−xNd_xTiO₃ (NBNT) in order to obtain various functionalities. The optimal concentration of Nd³⁺ for the best PL emission was found to be x = 0.01 (≅1 mol%). Upon electrical poling, there was a significant quenching of PL intensity. We elucidated this to be a result of electric-field induced structural ordering to higher symmetry. Structural studies from XRD data corroborated this hypothesis, as the electrical poling resulted in the transformation of the stabilized NBNT phase from a monoclinic to a rhombohedral structure which has higher symmetry. Estimation of the critical radius (R_C) for energy transfer and inter-ionic distance (R_Nd) suggested the onset of a concentration quenching effect after the substitution of x = 0.01. For the optimized NBNT the electrical characterization revealed a reduction in the coercive electric field (E_c) by 12% compared to undoped NBT. The piezoelectric characterization of the samples studied showed an enhanced d₃₃coefficient for the optimized NBNT and therefore the estimated off-resonance figure of merit (FOM_off) for energy harvesting revealed ≈30% enhancement for NBT-0.01Nd. From a computational knowledge point of view, the effect of perovskite structure symmetry on Nd³⁺ emission has not been studied to date. Thus, we hope our results will encourage such investigations as the very possibility of having multifunctionality in a simple material system is elegant. The results presented here convey a simple material system, but with elegant multifunctional properties. Therefore, the optimally substituted NBNT displayed convincing reasons for it to be a potential multifunctional material exhibiting simultaneous ferroelectric, luminescent and energy harvesting properties.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from various funding sources, namely, DST Project No. EMR/2014/000761 & YSS/2015/000008, CSIR project no. 03(1348)/16/EMR-II and DAE-CSR project no. CRS-M-250. Authors acknowledge helpful discussions with Dr Premkiran and Dr Venugopal Rao, ACRHEM, University of Hyderabad, Hyderabad, Telangana, India.

References

1. X. Wang, C. N. Xu, H. Yamada and K. Nishikubo, Adv. Mater., 2005, 17(10), 1254–1258.
2. D. Peng, X. Wang, C. Xu, X. Yao, J. Lin and T. Sun, J. Am. Ceram. Soc., 2013, 96(1), 184–190.
3. P. Du, L. Luo, Q. Yue and H. Chen, Appl. Phys. Lett., 2014, 104(15), 152902.
4. M. K. Niranjan, T. Karthik, S. Asthana, J. Pan and U. V. Waghmare, J. Appl. Phys., 2013, 113, 194106.
5. K. Reichmann, A. Feteira and M. Li, Materials, 2015, 8(12), 8467–8495.
6. Y. Hiruma, H. Nagata and T. Takenaka, Appl. Phys. Lett., 2008, 92(26), 262904.
7. K. R. Kandula, S. S. K. Raavi and S. Asthana, Ferroelectrics, 2017, 518(1), 23.
8. H. Sun, D. Peng, X. Wang, M. Tang, Q. Zhang and X. Yao, J. Appl. Phys., 2011, 110, 016102.
9. H. Zhou, X. Liu, N. Qin and D. Bao, J. Appl. Phys., 2011, 110(3), 034102.
10. X. Tian, Z. Wu, Y. Jia, R. K. Zheng, Y. Zhang and H. Luo, Appl. Phys. Lett., 2013, 102(4), 042907.
11. L. Luo, P. Du, W. Li, W. Tao and H. Chen, J. Appl. Phys., 2013, 114(12), 124104.
12. A. Kalaskar, B. N. Rao, T. Thomas and R. Ranjan, J. Appl. Phys., 2015, 117(24), 244106.
13. M. Zannen, A. Lahmar, M. Dietze, H. Khemakhem and M. Es-Souni, Mater. Chem. Phys., 2012, 134(2), 829–833.
14. C. He, Y. Zhang, T. Wu and Y. Liu, J. Phys. D: Appl. Phys., 2013, 46(24), 245104.
15. Q. Yao, F. Wang, F. Xu and W. Shi, ACS Appl. Mater. Interfaces, 2015, 7(9), 5066–5075.
16. D. K. Khatua, A. Kalaskar and R. Ranjan, Phys. Rev. Lett., 2016, 116(11), 117601.
17. V. Pal, R. Dwivedi and O. P. Thakur, Mater. Res. Bull., 2014, 51, 189–196.
18. W. Krupke, IEEE J. Quantum Electron., 1974, 10(4), 450–457.
19. K. R. Kandula, S. S. K. Raavi and S. Asthana, Phys. Status Solidi A, 2018, 1700915.
20. Y. Huan, X. Wang, J. Fang and L. Li, J. Eur. Ceram. Soc., 2014, 34(5), 1445–1448.
21. https://www.avantes.com/support/theoretical-background/spectrometers.
22. K. Kandula, S. S. K. Raavi and S. Asthana, J. Alloys Compd., 2018, 732, 233–239.
23. J. Azkargorta, R. Balda and J. Fernández, Opt. Express, 2008, 16(16), 11894–11906.
24. G. Singh, R. Selvamani, V. S. Tiwari and A. K. Karnal, J. Lumin., 2017, 1(192), 1084–1088.
25. Lanthanide luminescence: photophysical, analytical and biological aspects, ed. P. Hänninen and H. Härmä, Springer Science & Business Media, 2011, vol. 7.
26. H. G. Danielmeyer and P. Balmer, Appl. Phys. A: Mater. Sci. Process., 1973, 1(5), 269–274.
27. A. Tarafder, K. Annapurna, R. S. Chaliha, V. S. Tiwari, P. K. Gupta and B. Karmakar, J. Alloys Compd., 2010, 489(1), 281–288.
28. J. Hur, I. T. Seo, D. H. Kim, S. Nahm, J. Ryu, S. H. Han and S. J. Yoon, J. Am. Ceram. Soc., 2014, 97(10), 3157–3163.
29. G. Blasse, J. Solid State Chem., 1986, 62(2), 207–211.
30. M. Weber and T. E. Varitimos, J. Appl. Phys., 1971, 42(12), 4996–5005.
31. I. Iparraguirre, J. Azkargorta, R. Balda and J. Fernández, Opt. Mater., 2015, 27(11), 1697–1703.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra01349g

---