 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The A·T(rWC)/A·T(H)/A·T(rH) ↔ A·T*(rwWC)/A·T*(wH)/A·T*(rwH) mutagenic tautomerization via sequential proton transfer: a QM/QTAIM study
Ol'ha O. Brovarets' ab,
Kostiantyn S. Tsiupa
ab,
Kostiantyn S. Tsiupa a and
Dmytro M. Hovorun
a and
Dmytro M. Hovorun *ab
*ab
aDepartment of Molecular and Quantum Biophysics, Institute of Molecular Biology and Genetics, National Academy of Sciences of Ukraine, 150 Akademika Zabolotnoho Str., 03680 Kyiv, Ukraine. E-mail: dhovorun@imbg.org.ua
bDepartment of Molecular Biotechnology and Bioinformatics, Institute of High Technologies, Taras Shevchenko National University of Kyiv, 2-h Akademika Hlushkova Ave., 03022 Kyiv, Ukraine
First published on 10th April 2018
Abstract
In this study for the first time we have revealed by QM and QTAIM calculations at the MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of QM theory the novel routes of the mutagenic tautomerization of three biologically important A·T DNA base pairs – reverse Watson–Crick A·T(rWC), Hoogsteen A·T(H) and reverse Hoogsteen A·T(rH) – followed by their rebuilding into the wobble (w) A·T*(rwWC), A·T*(wH) and A·T*(rwH) base mispairs by the participation of the mutagenic tautomers of the DNA bases (denoted by asterisk) and vice versa, thus complementing the physico-chemical property of the canonical A·T(WC) Watson–Crick DNA base pair reported earlier (Brovarets' et al., RSC Adv., 2015, 5, 99594–99605). These non-dissociative tautomeric transformations in the classical A·T(rWC), A·T(H) and A·T(rH) DNA base pairs proceed similarly to the canonical A·T(WC) DNA base pair via the intrapair sequential proton transfer with shifting towards major or minor grooves of DNA followed by further double proton transfer along the intermolecular H-bonds and are controlled by the plane symmetric and highly stable transition states – tight ion pairs formed by the A+ nucleobase, protonated by the N1/N7 nitrogen atoms, and T− nucleobase, deprotonated by the N3H imino group. Comparison of the estimated populations of the tautomerised states (10−21 to 10−14) with similar characteristics for the canonical A·T(WC) DNA base pair (10−8 to 10−7) leads authors to the conclusion, that only a base pair with WC architecture can be a building block of the DNA macromolecule as a genetic material, which is able for the evolutionary self-development. Among all four classical DNA base pairs, only A·T(WC) DNA base pair can ensure the proper rate of the spontaneous point errors of replication in DNA.
Introduction
Clarification of the microstructural mechanisms of the mutagenic tautomerization of the DNA base pairs is a classical problem of molecular biophysics, biochemistry and structural biology, which remain topical up to now.1–5 Literature analysis shows that the so-called tautomeric hypothesis formulated by Watson and Crick,1 soon after their discovery of the spatial architecture of DNA – a macromolecule that is the carrier of the genetic information,2 represents itself the most vivid theoretical platform for the conduction of these studies. At that time, this hypothesis became a real breakthrough in the understanding of the nature of the origin of the spontaneous point mutations – transitions and transversions5 – and also involvement in this biologically important phenomenon of the prototropic tautomerism of the DNA bases.6,7Advances in technology eventually led to numerous as experimental investigations,8–13 in particular X-ray analysis8,9 and NMR, in particular relaxation dispersion, measurements,10–13 so theoretical examinations14–19 of this discovery. However, these results do not clarify the physico-chemical mechanisms of the arising of the rare or mutagenic tautomeric forms of the DNA bases20–23 (here and below marked by an asterisk).
It was established for sure that generally accepted mechanism of the double proton transfer (DPT) along intermolecular H-bonds in the Watson–Crick (WC) (so-called Löwdin's mechanism),24–29 wobble (w) base pairs,30,31 biologically important A·G,32 A·C*,33 G*·T,34 C·T,35 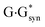 ,36 A*·Asyn,37
,36 A*·Asyn,37 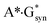 ,38 H·C,39,40 H·H39,40 and H·A39,42 base mispairs and also in the protein–DNA complexes26,43,44 can't be considered as the source of the mutagenic tautomers formations due to the dynamical instability of the terminal complexes containing mutagenic tautomers of the DNA bases.26–29,31–42,44
,38 H·C,39,40 H·H39,40 and H·A39,42 base mispairs and also in the protein–DNA complexes26,43,44 can't be considered as the source of the mutagenic tautomers formations due to the dynamical instability of the terminal complexes containing mutagenic tautomers of the DNA bases.26–29,31–42,44
For the first time, we have proposed a novel theoretical approach to the elucidation of the microstructural mechanisms of the incorporation and replication errors arising at the DNA replication due to the intrinsic ability of the purine·pyrimidine (A·T, G·C, G·T and A·C), purine·purine (A·A and G·G) and pyrimidine·pyrimidine (C·C and T·T) DNA base mispairs to perform WC ↔ w tautomeric transitions via the sequential proton transfer (PT).45–53 It was revealed that all these non-dissociative tautomerisations are controlled by the highly stable, highly polar and zwitterionic transition states of the type (protonated base)·(deprotonated base). These interconversions are accompanied by a significant rebuilding of the base mispairs with Watson–Crick architecture into the mismatches wobbled towards minor or major grooves of DNA. Moreover, it was established that these tautomerisation reactions occur non-dissociatively and are accompanied by the consequent replacement of the unique patterns of the intermolecular specific interactions along intrinsic reaction coordinate (IRC).
Thus, in particular, it was found out that the A·T(WC) Watson–Crick DNA base pair exists simultaneously in three other biologically important hypostasis45 – short-lived wobble A*·T(w) (population = 5.4 × 10−8), 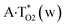 (9.9 × 10−9) and A·T*(w) (2.5 × 10−10) H-bonded mismatches, containing mutagenic tautomers of the nucleotide bases. Their forced separation by the DNA-polymerase machinery into the monomers with necessity generates mutagenic tautomers of the DNA bases, which are long-lived structures causing spontaneous point mutations – transitions and transversions.53–55
(9.9 × 10−9) and A·T*(w) (2.5 × 10−10) H-bonded mismatches, containing mutagenic tautomers of the nucleotide bases. Their forced separation by the DNA-polymerase machinery into the monomers with necessity generates mutagenic tautomers of the DNA bases, which are long-lived structures causing spontaneous point mutations – transitions and transversions.53–55
Presented approach clarifies the microstructural mechanisms of the mutations induced by the classical mutagens, in particular 2-aminopurine, for which frequencies agree well with the experimental data.56–61
The aim of the current study is to extend the approach launched in our previous work for the canonical DNA base pairs45 to the other classical A·T DNA base pairs – reverse Watson–Crick A·T(rWC), Hoogsteen A·T(H) and reverse Hoogsteen A·T(rH).
At this point, the question arises according the urgency of this investigation.
First, the A·T(rWC), A·T(H) and A·T(rH) DNA base pairs have a remarkable biological meaning (see works62–79 and the bibliography cited therein). Second, as of today, the mutagenic tautomerization of these biologically important pairs has not even mentioned in the literature. Thirdly, we are interested in the investigation of the evolutionary aspect of the problem, in particular, why Nature chose precisely Watson–Crick DNA base pairs for the construction of the genetic material, among which the A·T(WC) DNA base pair is the most evolutionarily distant, since it was the first to appear evolutionary.6,80,81
So, in this regard, we can make an assumption that exactly the A·T(WC) base pair provides necessary frequency of the spontaneous point replication errors in DNA, which lies in the range of 10−9 to 10−11 per nucleotide, incorporated during one replication cycle.82,83
Such statement of the problem except merely academic value has also practical assignment, e.g. for the biomolecular electronics, which are used for the DNA-based carriers of the digital information,84,85 since it allows, in principle, to understand how the complementary bases should be modified in order to suppress the tautomeric instability of their pair. This is extremely important for increasing of the accuracy of such molecular devices.86
As a result of the systematic quantum-mechanical calculations, we managed to establish the microstructural mechanisms of the mutagenic tautomerisation of the studied A·T DNA base pairs and to reach the conclusion about a unique place of the canonical Watson–Crick A·T(WC) DNA base pair among them. Only this base pair able to provide the necessary rate of the spontaneous point mutations, which, as it is well known, are the source of the genome self-development.6,80–83
Computational methods
Geometries of the investigated DNA base pairs and transition states (TSs) of their mutual tautomeric transformations, as well as their harmonic vibrational frequencies have been calculated at the B3LYP/6-311++G(d,p) level of theory,87–91 using Gaussian'09 package92 followed by the IRC calculations in the forward and reverse directions from each TS using Hessian-based predictor-corrector integration algorithm.93 Applied level of theory has proved itself successful for the calculations of the similar systems.94–96 A scaling factor that is equal to 0.9668 (ref. 97–100) has been applied in the present work for the correction of the harmonic frequencies for all DNA base pairs and TSs of their tautomeric transitions. We have confirmed the local minima and TSs, localized by Synchronous Transit-guided Quasi-Newton method,101 on the potential energy landscape by the absence or presence, respectively, of the imaginary frequency in the vibrational spectra of the complexes. We applied standard TS theory for the estimation of the activation barriers of the tautomeric transformations.102 Electronic energy calculations have been performed at the MP2/aug-cc-pVDZ level of theory.103,104The Gibbs free energy G for all structures was obtained in the following way:
| G = Eel + Ecorr, | (1) |
The time τ99.9% necessary to reach 99.9% of the equilibrium concentration of the reactant and product in the system of reversible first-order forward (kf) and reverse (kr) reactions can be estimated by the formula:102
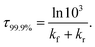 | (2) |
The lifetime τ of the formed mismatches has been calculated using the formula (1)/kr, where the values of the reverse kr and forward kf rate constants for the tautomerisation reactions were obtained as:102
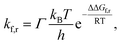 | (3) |
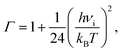 | (4) |
Electronic interaction energies ΔEint have been calculated at the MP2/6-311++G(2df,pd) level of theory as the difference between the total energy of the base pair and energies of the monomers and corrected for the basis set superposition error (BSSE)106,107 through the counterpoise procedure.108,109
Bader's quantum theory of atoms in molecules (QTAIM),110–115 using program package AIMAll,116 was applied to analyse the electron density distribution. The presence of the bond critical point (BCP), namely the so-called (3,−1) BCP, and a bond path between hydrogen donor and acceptor, as well as the positive value of the Laplacian at this BCP (Δρ > 0), were considered as criteria for the H-bond formation.117,118 Wave functions were obtained at the level of theory used for geometry optimisation.
The energies of the AH⋯B conventional H-bonds were evaluated by the empirical Iogansen's formula:119
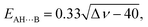 | (5) |
The energies of the weak CH⋯O/N H–bonds123,124 were calculated by the empirical Espinosa–Molins–Lecomte formula125,126 based on the electron density distribution at the (3,−1) BCPs of the H-bonds:
| EHB = 0.5 V(r), | (6) |
The energies of the NH⋯O H-bonds in the TSs of the DPT tautomerisations containing loosened covalent bridge have been estimated by the Nikolaienko–Bulavin–Hovorun formula:127
| ENH⋯O = −2.03 + 225ρ, | (7) |
The atomic numbering scheme for the DNA bases is conventional.128
Results and their discussion
In this work based on the results obtained in the pioneering publication,45 devoted to the novel WC ↔ w mutagenic tautomerization of the canonical A·T(WC) and G·C(WC) DNA base pairs, we have investigated for the first time the microstructural mechanisms of the mutagenic tautomerisation of the three other biologically important A·T DNA base pairs62–79 – A·T(rWC)/A·T(H)/A·T(rH) ↔ A·T*(rwWC)/A·T*(wH)/A·T*(rwH) – as their intrinsically inherent property (Fig. 1, Tables 1 and 2).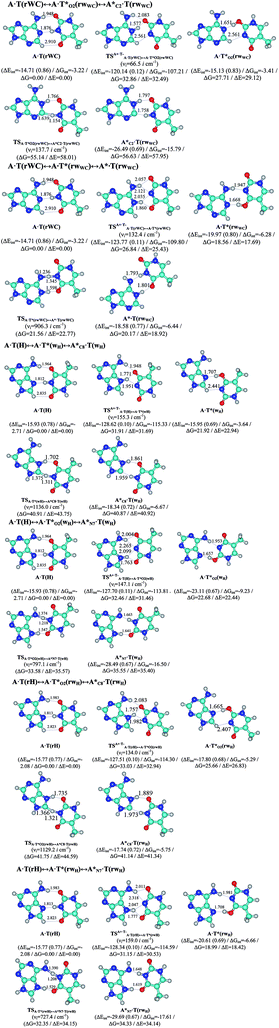 | ||
| Fig. 1 Geometrical structures of the stationary points on the pathways of the tautomerization of the classical A·T DNA base pairs into the wobble base mispairs via the sequential PT followed by DPT. Electronic ΔEint (contribution of the total energy of the H-bonds) and Gibbs free ΔGint energies of the interaction (MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of theory, in kcal mol−1), relative Gibbs free energies ΔG and electronic energies ΔE (in kcal mol−1), imaginary frequencies νi at the TSs of the tautomeric transitions (MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of theory in the continuum with ε = 1 at T = 298.15 K) are presented below complexes in brackets. Dotted lines indicate AH⋯B H-bonds – their lengths H⋯B are presented in angstroms (for their more detailed physico-chemical characteristics see Table 2); carbon atoms are in light-blue, nitrogen – in dark-blue, hydrogen – in grey and oxygen – in red. | ||
| Tautomeric transition | νia | ΔGb | ΔEc | ΔΔGTSd | ΔΔETSe | ΔΔGf | ΔΔEg | τ99.9%h | τi | Pj |
|---|---|---|---|---|---|---|---|---|---|---|
| a The imaginary frequency at the TS of the tautomeric transition, cm−1.b The Gibbs free energy of the product relatively the reactant of the tautomeric transition (T = 298.15 K).c The electronic energy of the product relatively the reactant of the tautomeric transition.d The Gibbs free energy barrier for the forward tautomeric transition.e The electronic energy barrier for the forward tautomeric transition.f The Gibbs free energy barrier for the reverse tautomeric transition.g The electronic energy barrier for the reverse tautomeric transition.h The time necessary to reach 99.9% of the equilibrium concentration between the reactant and the product of the tautomerisation reaction, s.i The lifetime of the product of the tautomerisation reaction, s.j The thermal population of the tautomerised structures, which is situated on the right in the first row of the table. | ||||||||||
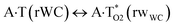 |
66.5 | 27.71 | 29.12 | 32.86 | 32.49 | 5.15 | 3.37 | 6.62 × 10−9 | 9.58 × 10−10 | 4.72 × 10−21 |
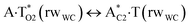 |
137.7 | 28.92 | 29.23 | 27.43 | 29.29 | −1.49 | 0.06 | 8.83 × 10−14 | 1.28 × 10−14 | 2.91 × 10−42 |
| A·T(rWC) ↔ A·T*(rwWC) | 132.4 | 18.56 | 17.69 | 26.84 | 25.43 | 8.29 | 7.74 | 1.31 × 10−6 | 1.90 × 10−7 | 2.45 × 10−14 |
| A·T*(rwWC) ↔ A*·T(rwWC) | 906.3 | 1.61 | 1.24 | 3.00 | 5.08 | 1.39 | 3.85 | 1.08 × 10−11 | 1.67 × 10−12 | 1.60 × 10−15 |
| A·T(H) ↔ A·T*(wH) | 155.3 | 21.92 | 22.94 | 31.91 | 31.69 | 9.99 | 8.75 | 2.31 × 10−5 | 3.35 × 10−6 | 8.39 × 10−17 |
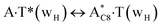 |
1136.0 | 18.95 | 17.97 | 18.99 | 20.81 | 0.04 | 2.84 | 5.56 × 10−13 | 8.04 × 10−14 | 1.06 × 10−30 |
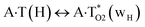 |
147.1 | 22.68 | 22.44 | 32.46 | 31.63 | 9.78 | 9.19 | 1.62 × 10−5 | 2.34 × 10−6 | 2.32 × 10−17 |
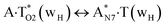 |
797.1 | 12.87 | 12.96 | 10.90 | 13.14 | −1.97 | 0.18 | 2.54 × 10−14 | 3.68 × 10−15 | 8.45 × 10−27 |
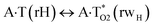 |
134.0 | 25.66 | 26.83 | 33.03 | 32.94 | 7.38 | 6.11 | 2.81 × 10−7 | 4.07 × 10−8 | 1.52 × 10−19 |
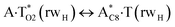 |
1129.2 | 15.49 | 14.51 | 16.09 | 17.76 | 0.60 | 3.25 | 1.43 × 10−12 | 2.08 × 10−13 | 6.61 × 10−31 |
| A·T(rH) ↔ A·T*(rwH) | 159.0 | 18.99 | 18.42 | 31.15 | 30.53 | 12.17 | 12.11 | 9.13 × 10−4 | 1.32 × 10−4 | 1.18 × 10−14 |
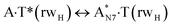 |
727.4 | 15.34 | 15.73 | 13.36 | 15.73 | −1.98 | 0.01 | 3.86 × 10−14 | 5.58 × 10−15 | 6.65 × 10−26 |
| Complex | AH⋯B H-bond | ρa | Δρb | 100εc | dA⋯Bd | dH⋯Be | ∠AH⋯Bf | EAH⋯Bg | μh |
|---|---|---|---|---|---|---|---|---|---|
| a The electron density at the (3,−1) BCP of the H-bond, a.u.b The Laplacian of the electron density at the (3,−1) BCP of the H-bond, a.u.c The ellipticity at the (3,−1) BCP of the H-bond.d The distance between the A and B atoms of the of the AH⋯B H-bond, Å.e The distance between the H and B atoms of the AH⋯B H-bond, Å.f The H-bond angle, degree.g Energy of the H-bond, calculated by Iogansen's,119 Espinose–Molins–Lecomte125,126 (marked with an asterisk) or Nikolaienko–Bulavin–Hovorun127 (marked with double asterisk) formulas, kcal mol−1.h The dipole moment of the complex, D. | |||||||||
| A·T(rWC) | N6H⋯O2 | 0.024 | 0.088 | 5.26 | 2.962 | 1.949 | 172.9 | 4.38 | 2.40 |
| N3H⋯N1 | 0.039 | 0.093 | 6.51 | 2.887 | 1.843 | 177.7 | 7.55 | ||
| C2H⋯O4 | 0.004 | 0.014 | 3.32 | 3.696 | 2.872 | 132.8 | 0.77* | ||
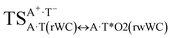 |
N6+H⋯O2− | 0.017 | 0.073 | 8.71 | 2.910 | 2.083 | 136.9 | 2.99 | 9.34 |
| N1+H⋯O2− | 0.067 | 0.133 | 1.76 | 2.614 | 1.577 | 159.6 | 10.16 | ||
| C2+H⋯N3− | 0.011 | 0.034 | 18.55 | 3.207 | 2.561 | 117.3 | 1.81* | ||
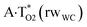 |
O2H⋯N7 | 0.058 | 0.100 | 4.73 | 2.682 | 1.665 | 179.7 | 10.35 | 5.10 |
| C8H⋯N3 | 0.013 | 0.043 | 2.29 | 3.131 | 2.407 | 123.1 | 2.21* | ||
| TSA·T*O2(rwWC)↔A*C2·T(rwWC) | N1H⋯O2 | 0.040 | 0.125 | 4.34 | 2.761 | 1.766 | 159.5 | 6.91** | 5.36 |
| A*C2·T(rwWC) | N1H⋯O2 | 0.037 | 0.120 | 4.38 | 2.787 | 1.797 | 159.5 | 5.77 | 5.21 |
| N3H⋯C2− | 0.061 | 0.033 | 103.30 | 2.840 | 1.758 | 164.3 | 12.53 | ||
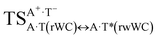 |
N6+H⋯O2− | 0.020 | 0.067 | 12.45 | 3.026 | 2.057 | 155.7 | 2.86 | 6.11 |
| N6+H⋯N3− | 0.020 | 0.069 | 13.99 | 2.971 | 2.121 | 138.4 | 2.82 | ||
| N1+H⋯N3− | 0.024 | 0.081 | 32.39 | 2.932 | 2.035 | 141.8 | 2.92 | ||
| N1+H⋯O4− | 0.034 | 0.098 | 5.50 | 2.805 | 1.860 | 148.0 | 4.45 | ||
| A·T*(rwWC) | N6H⋯N3 | 0.030 | 0.087 | 7.07 | 2.682 | 1.668 | 170.4 | 5.76 | 2.52 |
| O4H⋯N1 | 0.059 | 0.096 | 5.10 | 2.955 | 1.947 | 167.0 | 10.21 | ||
| TSA·T*(rwWC)↔A*·T(rwWC) | N1H⋯O4 | 0.061 | 0.142 | 3.32 | 2.663 | 1.598 | 179.3 | 11.61** | 3.78 |
| A*·T(rwWC) | N3H⋯N6 | 0.044 | 0.095 | 6.22 | 2.844 | 1.793 | 174.7 | 8.53 | 3.23 |
| N1H⋯O4 | 0.035 | 0.117 | 3.55 | 2.832 | 1.801 | 177.3 | 5.82 | ||
| A·T(H) | N6H′⋯O4 | 0.023 | 0.086 | 3.93 | 2.972 | 1.963 | 170.6 | 4.18 | 6.16 |
| N3H⋯N7 | 0.041 | 0.099 | 5.75 | 2.853 | 1.811 | 175.9 | 7.39 | ||
| C8H⋯O2 | 0.005 | 0.016 | 7.71 | 3.524 | 2.835 | 121.7 | 0.83* | ||
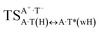 |
N6+H′⋯O4− | 0.022 | 0.091 | 1.81 | 2.936 | 1.948 | 161.7 | 4.76 | 2.09 |
| N7+H⋯O4− | 0.041 | 0.112 | 6.15 | 2.749 | 1.771 | 152.5 | 5.03 | ||
| N7+H⋯N3− | 0.029 | 0.097 | 35.39 | 2.784 | 1.951 | 133.5 | 3.27 | ||
| A·T*(wH) | O4H⋯N7 | 0.052 | 0.102 | 4.74 | 2.717 | 1.707 | 178.5 | 8.99 | 4.74 |
| C8H⋯N3 | 0.012 | 0.040 | 2.99 | 3.149 | 2.441 | 121.9 | 2.08* | ||
| TSA·T*(wH)↔A*C8·T(wH) | N7H⋯O4 | 0.047 | 0.133 | 2.94 | 2.678 | 1.702 | 153.3 | 8.55** | 3.56 |
| A*C8·T(wH) | N7H⋯O4 | 0.031 | 0.109 | 3.24 | 2.810 | 1.861 | 152.7 | 5.00 | 6.08 |
| N3H⋯C8− | 0.035 | 0.061 | 4.38 | 2.975 | 1.959 | 161.6 | 8.30 | ||
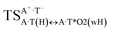 |
N6+H′⋯O4− | 0.024 | 0.079 | 2.31 | 2.887 | 2.004 | 142.4 | 3.64 | 6.54 |
| N6+H′⋯N3− | 0.014 | 0.049 | 67.29 | 3.218 | 2.265 | 153.9 | 1.84 | ||
| N7+H⋯N3− | 0.021 | 0.076 | 382.35 | 3.022 | 2.099 | 144.8 | 2.36 | ||
| N7+H⋯O2− | 0.042 | 0.115 | 3.62 | 2.688 | 1.763 | 143.9 | 5.72 | ||
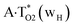 |
N6H′⋯N3 | 0.029 | 0.086 | 7.38 | 2.974 | 1.953 | 176.4 | 5.38 | 8.23 |
| O2H⋯N7 | 0.059 | 0.100 | 4.48 | 2.664 | 1.657 | 168.0 | 10.16 | ||
| TSA·T*O2(wH)↔A*N7·T(wH) | N7H⋯O2 | 0.067 | 0.152 | 3.15 | 2.615 | 1.547 | 176.3 | 12.95** | 9.46 |
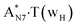 |
N3H⋯N6 | 0.060 | 0.092 | 5.58 | 2.743 | 1.663 | 175.7 | 10.97 | 10.35 |
| N7H⋯O2 | 0.051 | 0.145 | 3.17 | 2.689 | 1.641 | 176.3 | 8.09 | ||
| A·T(rH) | N6H′⋯O2 | 0.022 | 0.082 | 4.95 | 2.994 | 1.986 | 170.9 | 3.90 | 5.67 |
| N3H⋯N7 | 0.041 | 0.099 | 5.80 | 2.856 | 1.815 | 176.9 | 7.34 | ||
| C8H⋯O4 | 0.005 | 0.017 | 7.97 | 3.517 | 2.825 | 121.9 | 0.86* | ||
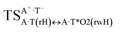 |
N6+H′⋯O2− | 0.016 | 0.066 | 0.24 | 3.064 | 2.083 | 161.1 | 4.06 | 3.41 |
| N7+H⋯O2− | 0.042 | 0.114 | 5.64 | 2.757 | 1.757 | 157.6 | 5.05 | ||
| N7+H⋯N3− | 0.028 | 0.098 | 49.28 | 2.758 | 1.982 | 128.1 | 3.02 | ||
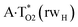 |
O2H⋯N7 | 0.058 | 0.100 | 4.73 | 2.682 | 1.665 | 179.7 | 9.20 | 5.10 |
| C8H⋯N3 | 0.013 | 0.043 | 2.29 | 3.131 | 2.407 | 123.1 | 2.21* | ||
| TSA·T*O2(rwH)↔A*C8·T(rwH) | N7H⋯O2 | 0.043 | 0.129 | 3.56 | 2.698 | 1.735 | 151.8 | 7.70** | 4.79 |
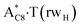 |
N7H⋯O2 | 0.029 | 0.104 | 3.92 | 2.829 | 1.889 | 151.4 | 4.61 | 6.47 |
| N3H⋯C8− | 0.034 | 0.061 | 4.31 | 2.984 | 1.973 | 160.5 | 8.12 | ||
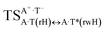 |
N6+H′⋯O2− | 0.023 | 0.078 | 1.54 | 2.902 | 2.011 | 143.9 | 3.51 | 4.80 |
| N6+H′⋯N3− | 0.013 | 0.045 | 127.55 | 3.263 | 2.318 | 152.9 | 1.65 | ||
| N7+H⋯N3− | 0.023 | 0.078 | 82.90 | 2.987 | 2.047 | 146.7 | 2.64 | ||
| N7+H⋯O4− | 0.041 | 0.113 | 4.62 | 2.686 | 1.776 | 141.6 | 5.65 | ||
| A·T*(rwH) | N6H′⋯N3 | 0.027 | 0.082 | 7.62 | 3.000 | 1.981 | 175.7 | 5.09 | 7.36 |
| O4H⋯N7 | 0.052 | 0.102 | 4.48 | 2.702 | 1.708 | 166.4 | 9.18 | ||
| TSA·T*(rwH)↔A*N7·T(rwH) | N7H⋯O4 | 0.070 | 0.151 | 2.34 | 2.603 | 1.529 | 175.7 | 13.76** | 8.37 |
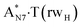 |
N3H⋯N6 | 0.062 | 0.090 | 5.55 | 2.731 | 1.648 | 174.5 | 11.26 | 9.42 |
| N7H⋯O4 | 0.055 | 0.147 | 2.33 | 2.671 | 1.619 | 175.8 | 8.61 | ||
It was found that the mutagenic tautomerization of each of these classical base pairs is controlled by the two TSs, representing itself tight (electronic energy of the bases interaction ∼120–129 kcal mol−1) ion pairs (A+ nucleobase, protonated by the N1/N7 nitrogen atoms)·(T− nucleobase, deprotonated by the N3H imino group) with plane symmetric (Cs symmetry) quasi-wobble structure. The term “quasi-wobble” means that these structures are no longer rWC/H/rH, but are not yet wobble. Notably, they differ from each other by the shifting direction of the T− respectively A+ (towards major or minor groove of DNA) and also by the number of the H-bonds, which participate in their stabilization, – three or four, – one or two of them are characterized by the increased ellipticity (Fig. 1, Table 2). The latter points to the dynamic instability of these H-bonds.31,97 Thus, the 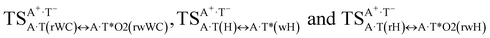 transition states, in which the T− deprotonated by the N3H imino group, is shifted towards the minor groove of DNA relatively A+, are stabilized by the participation of three H-bonds: (A)N6+H⋯O2−(T) (2.99), (A)N1+H⋯O2−(T) (10.16) and (A)C2+H⋯N3−(T) (1.81 kcal mol−1); (A)N6+H′···O4−(T) (4.76), (A)N7+H⋯O4−(T) (5.03) and (A)N7+H⋯N3−(T) (3.27 kcal mol−1); (A)N6+H′···O2−(T) (4.06), (A)N7+H⋯O2−(T) (5.05) and (A)N7+H⋯N3−(T) (3.02 kcal mol−1) (their energies are presented in brackets), accordingly (Table 2). At this, in each TS only one H-bond has increased ellipticity (its value is presented in brackets) – (A)C2+H⋯N3−(T) (18.55); (A)N7+H⋯N3−(T) (35.39); (A)N7+H⋯N3−(T) (49.28), respectively (Fig. 1, Table 2).
transition states, in which the T− deprotonated by the N3H imino group, is shifted towards the minor groove of DNA relatively A+, are stabilized by the participation of three H-bonds: (A)N6+H⋯O2−(T) (2.99), (A)N1+H⋯O2−(T) (10.16) and (A)C2+H⋯N3−(T) (1.81 kcal mol−1); (A)N6+H′···O4−(T) (4.76), (A)N7+H⋯O4−(T) (5.03) and (A)N7+H⋯N3−(T) (3.27 kcal mol−1); (A)N6+H′···O2−(T) (4.06), (A)N7+H⋯O2−(T) (5.05) and (A)N7+H⋯N3−(T) (3.02 kcal mol−1) (their energies are presented in brackets), accordingly (Table 2). At this, in each TS only one H-bond has increased ellipticity (its value is presented in brackets) – (A)C2+H⋯N3−(T) (18.55); (A)N7+H⋯N3−(T) (35.39); (A)N7+H⋯N3−(T) (49.28), respectively (Fig. 1, Table 2).
Three other 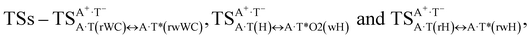 in which the T− deprotonated by the N3H imino group, is shifted towards major groove of DNA relatively A+, are joined by the participation of the four H-bonds: (A)N6+H⋯O2−(T) (2.86), (A)N6+H⋯N3−(T) (2.82), (A)N1+H⋯N3−(T) (2.92) and (A)N1+H⋯O4−(T) (4.45 kcal mol−1); N6+H′⋯O4− (3.64), N6+H′⋯N3− (1.84), N7+H⋯N3− (2.36) and N7+H⋯O2− (5.72 kcal mol−1); N6+H′⋯O2− (3.51), N6+H′⋯N3− (1.65), N7+H⋯N3− (2.64) and N7+H⋯O4− (5.65 kcal mol−1). Two H-bonds have increased ellipticity for each of these TSs – (A)N6+H⋯N3−(T) (13.99) and (A)N1+H⋯N3−(T) (32.39); N6+H′⋯N3− (67.29) and N7+H⋯N3− (382.35); N6+H′⋯N3− (127.55) and N7+H⋯N3− (82.90), accordingly (Fig. 1, Table 2).
in which the T− deprotonated by the N3H imino group, is shifted towards major groove of DNA relatively A+, are joined by the participation of the four H-bonds: (A)N6+H⋯O2−(T) (2.86), (A)N6+H⋯N3−(T) (2.82), (A)N1+H⋯N3−(T) (2.92) and (A)N1+H⋯O4−(T) (4.45 kcal mol−1); N6+H′⋯O4− (3.64), N6+H′⋯N3− (1.84), N7+H⋯N3− (2.36) and N7+H⋯O2− (5.72 kcal mol−1); N6+H′⋯O2− (3.51), N6+H′⋯N3− (1.65), N7+H⋯N3− (2.64) and N7+H⋯O4− (5.65 kcal mol−1). Two H-bonds have increased ellipticity for each of these TSs – (A)N6+H⋯N3−(T) (13.99) and (A)N1+H⋯N3−(T) (32.39); N6+H′⋯N3− (67.29) and N7+H⋯N3− (382.35); N6+H′⋯N3− (127.55) and N7+H⋯N3− (82.90), accordingly (Fig. 1, Table 2).
Values of the Gibbs free energies of activation of the processes of the dipole-active tautomerization of the investigated A·T DNA base pairs are quite high and lie within the range 27–33 kcal mol−1 under normal conditions (Fig. 1, Table 1).
The 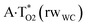 , A·T*(rwWC), A·T*(wH),
, A·T*(rwWC), A·T*(wH), 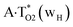 ,
, 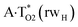 and A·T*(rwH) base mispairs, which are the products of the mutagenic tautomerization of classical A·T DNA base pairs, represent themselves wobble structures with plane symmetric architecture (Cs symmetry), stabilized by two anti-parallel intermolecular H-bonds. They are noticeably more stable than the starting A·T(rWC), A·T(H) and A·T(rH) DNA base pairs and have quite high relative energies, lying in the range 19–28 kcal mol−1, and hence – insignificant population (≤1.2 × 10−14 under normal conditions). It is interesting to note, that these wobble base mispairs are figuratively speaking “terminal stations” on the way of the mutagenic tautomerization of the investigated DNA base pairs, since they do not tautomerise further (Fig. 1, Tables 1 and 2).
and A·T*(rwH) base mispairs, which are the products of the mutagenic tautomerization of classical A·T DNA base pairs, represent themselves wobble structures with plane symmetric architecture (Cs symmetry), stabilized by two anti-parallel intermolecular H-bonds. They are noticeably more stable than the starting A·T(rWC), A·T(H) and A·T(rH) DNA base pairs and have quite high relative energies, lying in the range 19–28 kcal mol−1, and hence – insignificant population (≤1.2 × 10−14 under normal conditions). It is interesting to note, that these wobble base mispairs are figuratively speaking “terminal stations” on the way of the mutagenic tautomerization of the investigated DNA base pairs, since they do not tautomerise further (Fig. 1, Tables 1 and 2).
Really, the 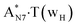 and
and 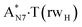 complexes, which are formed from the
complexes, which are formed from the 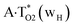 and A·T*(rwH) base pairs via the DPT, respectively, return without any barrier into the initial pairs due to the asynchronous DPT along the intermolecular H-bonds via the TSA·T*O2(wH)↔A*N7·T(wH) and TSA·T*(rwH)↔A*N7·T(rwH), accordingly. The same situation also takes place for the complex by the participation of the yilidic form20,39,129 of A –
and A·T*(rwH) base pairs via the DPT, respectively, return without any barrier into the initial pairs due to the asynchronous DPT along the intermolecular H-bonds via the TSA·T*O2(wH)↔A*N7·T(wH) and TSA·T*(rwH)↔A*N7·T(rwH), accordingly. The same situation also takes place for the complex by the participation of the yilidic form20,39,129 of A – 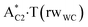 . Two other
. Two other 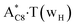 and
and 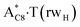 complexes involving yilidic forms of the A DNA base, which are formed from the A·T*(wH) and
complexes involving yilidic forms of the A DNA base, which are formed from the A·T*(wH) and 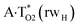 by the asynchronous DPT along the intermolecular H-bonds, one of which (A)C8H⋯N3(T) H-bond is non-canonical,123,124 are short-lived (∼0.1 ps), dynamically-unstable systems. Low-frequency intermolecular normal vibrations, lying in the range 20–83 cm−1, could not develop during their lifetimes. From the other side, the lifetime of the A*·T(rwWC) complex (1.7 ps), which is formed from the A·T*(rwWC) pair by the asynchronous DPT along the intermolecular H-bonds, is significantly less than the time (10−9 s)27,28, spent by the DNA-polymerase for the forced dissociation of the complementary pairs of the DNA bases into the monomers. As a result, this complex “slips out of its hands” and canonical tautomeric status of the A DNA base does not change (Table 1).
by the asynchronous DPT along the intermolecular H-bonds, one of which (A)C8H⋯N3(T) H-bond is non-canonical,123,124 are short-lived (∼0.1 ps), dynamically-unstable systems. Low-frequency intermolecular normal vibrations, lying in the range 20–83 cm−1, could not develop during their lifetimes. From the other side, the lifetime of the A*·T(rwWC) complex (1.7 ps), which is formed from the A·T*(rwWC) pair by the asynchronous DPT along the intermolecular H-bonds, is significantly less than the time (10−9 s)27,28, spent by the DNA-polymerase for the forced dissociation of the complementary pairs of the DNA bases into the monomers. As a result, this complex “slips out of its hands” and canonical tautomeric status of the A DNA base does not change (Table 1).
Base pairs remain plane symmetric structures during the entire PT and DPT tautomerization processes along the IRC. The methyl group of the T DNA base does not change its orientation during these tautomerization processes via the PT and DPT. Moreover, the heterocycles of the A and T DNA bases remain planar, despite their ability for the out-of-plane bending130–133 (Fig. 1).
Interestingly, that the total energy of the intermolecular H-bonds only partially contributes to the electron energy of the monomers interactions among all without any exceptions H-bonded structures investigated in this work (see Fig. 1). In particular, in the TSs of mutagenic tautomerization, which are ion pairs, contribution of the H-bonds into the energy of their stabilization consist only 10–12% in comparison with the background of strong electrostatic (Coulomb) interactions. In other complexes it is much higher – from 67 to 86% (Fig. 1). These regularities agree well with the previously reported data for the other H-bonded pairs of nucleotide bases.31–42
Conclusions
So, revealed microstructural mechanisms of the mutagenic tautomerization of the A·T DNA base pairs provide the generation of the mutagenic tautomers of only one among two DNA bases, in particular T DNA base, within the pair of bases. However, this generation is much more slower in comparison with the classical A·T(WC) DNA base pair and does not provide adequate population of the mutagenic tautomers (10−9 to 10−11).Finally, these results lead us to a conclusion, which is very interesting from an evolutionary point of view:6,80,81 among all classical pairs of the DNA bases only the Watson–Crick A·T(WC) DNA base pair can pretend on the role of the building block of the genetic material – DNA macromolecule with antiparallel strands, able for the self-development during large time intervals.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully appreciate technical support and computational facilities of joint computer cluster of SSI “Institute for Single Crystals” of the National Academy of Sciences of Ukraine (NASU) and Institute for Scintillation Materials of the NASU incorporated into Ukrainian National Grid. DrSci Ol'ha O. Brovarets' expresses sincere gratitude to organizing committee headed by Prof. Karl Kuchler (Medical University Vienna, Austria) for the kind invitation and support (ABC fellow) of the participation in the 7th FEBS Special Meeting “ATP-Binding Cassette (ABC) Proteins: From Multidrug Resistance to Genetic Disease” (March 6–12, 2018, Innsbruck, Austria) and to Chemistry Biological Interface Division of the RSC (Royal Society of Chemistry, UK) for the RSC Travel Grant for the participation at the “3rd Green and Sustainable Chemistry Conference” (May 13–16, 2018, Hotel Intercontinental, Berlin, Germany).References
- J. D. Watson and F. H. C. Crick, The Structure of DNA, Cold Spring Harbor Symp. Quant. Biol., 1953, 18, 123–131 CrossRef CAS PubMed.
- J. D. Watson and F. H. C. Crick, Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid, Nature, 1953, 171, 737–738 CrossRef CAS PubMed.
- P.-O. Löwdin, Proton tunneling in DNA and its biological implications, Rev. Mod. Phys., 1963, 35, 724–732 CrossRef.
- P.-O. Löwdin, Quantum genetics and the aperiodic solid: Some aspects on the biological problems of heredity, mutations, aging, and tumors in view of the quantum theory of the DNA molecule, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, Academic Press, New York, USA, London, UK, 1966, vol. 2, pp. 213–360 Search PubMed.
- M. D. Topal and J. R. Fresco, Complementary base pairing and the origin of substitution mutations, Nature, 1976, 263, 285–289 CrossRef CAS PubMed.
- B. Pullman and A. Pullman, Electronic delocalization and biochemical evolution, Nature, 1962, 196, 1137–1142 CrossRef CAS PubMed.
- B. Pullman, and A. Pullman, Quantum biochemistry, Interscience Publishers, New York, NY, 1963 Search PubMed.
- K. Bebenek, L. C. Pedersen and T. A. Kunkel, Replication infidelity via a mismatch with Watson−Crick geometry, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1862–1867 CrossRef CAS PubMed.
- W. Wang, H. W. Hellinga and L. S. Beese, Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17644–17648 CrossRef CAS PubMed.
- A. N. Nedderman, M. J. Stone, P. K. T. Lin, D. M. Brown and D. H. Williams, Base pairing of cytosine analogues with adenine and guanine in oligonucleotide duplexes: evidence for exchange between Watson-Crick and wobble base pairs using 1H NMR spectroscopy, J. Chem. Soc., Chem. Commun., 1991, 1357–1359 RSC.
- A. N. Nedderman, M. J. Stone, D. H. Williams, P. K. Y. Lin and D. M. Brown, Molecular basis for methoxyamine-initiated mutagenesis: 1H nuclear magnetic resonance studies of oligonucleotide duplexes containing base-modified cytosine residues, J. Mol. Biol., 1993, 230, 1068–1076 CrossRef CAS PubMed.
- I. J. Kimsey, K. Petzold, B. Sathyamoorthy, Z. W. Stein and H. M. Al-Hashimi, Visualizing transient Watson-Crick-like mispairs in DNA and RNA duplexes, Nature, 2015, 519, 315–320 CrossRef CAS PubMed.
- E. S. Szymanski, I. J. Kimsey and H. M. Al-Hashimi, Direct NMR evidence that transient tautomeric and anionic states in dG·dT form Watson-Crick-like base pairs, J. Am. Chem. Soc., 2017, 139, 4326–4329 CrossRef CAS PubMed.
- J. Florian, V. Hrouda and P. Hobza, Proton transfer in the adenine-thymine base pair, J. Am. Chem. Soc., 1994, 116, 1457–1460 CrossRef CAS.
- L. Gorb, Y. Podolyan, P. Dziekonski, W. A. Sokalski and J. Leszczynski, Double-proton transfer in adenine−thymine and guanine−cytosine base pairs. A post-Hartree-Fock ab initio study, J. Am. Chem. Soc., 2004, 126, 10119–10129 CrossRef CAS PubMed.
- J. Bertran, L. Blancafort, M. Noguera, and M. Sodupe, Proton transfer in DNA base pairs, in Computational studies of RNA and DNA, ed. J. Šponer and F. Lankaš, Springer, Dordrecht, 2006, pp. 411–432 Search PubMed.
- J. P. Cerón-Carrasco, A. Requena, C. Michaux, E. A. Perpète and D. Jacquemin, Effects of hydration on the proton transfer mechanism in the adenine-thymine base pair, J. Phys. Chem. A, 2009, 113, 7892–7898 CrossRef PubMed.
- J. P. Cerón-Carrasco and D. Jacquemin, Electric field induced DNA damage: an open door for selective mutations, Chem. Commun., 2013, 49, 7578–7580 RSC.
- S. N. Maximoff, Sh. C. L. Kamerlin and J. D. N. A. Florián, Polymerase λ active site favors a mutagenic mispair between the enol form of deoxyguanosine triphosphate substrate and the keto form of thymidine template: a free energy perturbation study, J. Phys. Chem. B, 2017, 121, 7813–7822 CrossRef CAS PubMed.
- I. V. Kondratyuk, S. P. Samijlenko, I. M. Kolomiets' and D. M. Hovorun, Prototropic molecular-zwitterionic tautomerism of xanthine and hypoxanthine, J. Mol. Struct., 2000, 523, 109–118 CrossRef CAS.
- S. P. Samijlenko, O. M. Krechkivska, D. A. Kosach and D. M. Hovorun, Transitions to high tautomeric states can be induced in adenine by interactions with carboxylate and sodium ions: DFT calculation data, J. Mol. Struct., 2004, 708, 97–104 CrossRef CAS.
- V. I. Danilov, V. M. Anisimov, N. Kurita and D. Hovorun, MP2 and DFT studies of the DNA rare base pairs: the molecular mechanism of the spontaneous substitution mutations conditioned by tautomerism of bases, Chem. Phys. Lett., 2005, 412, 285–293 CrossRef CAS.
- M. O. Platonov, S. P. Samijlenko, O. O. Sudakov, I. V. Kondratyuk and D. M. Hovorun, To what extent can methyl derivatives be regarded as stabilized tautomers of xanthine?, Spectrochim. Acta, Part A, 2005, 62, 112–114 CrossRef CAS PubMed.
- P.-O. Löwdin, Isotope effect in tunneling and its influence on mutation rates, Mutat. Res. Fundam. Mol. Mech. Mutagen., 1965, 2, 218–221 CrossRef.
- V. I. Danilov and G. F. Kventsel, Electronic representations in the point mutation theory, Naukova Dumka, Kyiv, 1971 Search PubMed.
- O. O. Brovarets', I. M. Kolomiets' and D. M. Hovorun. Elementary molecular mechanisms of the spontaneous point mutations in DNA: A novel quantum-chemical insight into the classical understanding, in Quantum chemistry – molecules for innovations, ed. Tomofumi Tada, InTech Open Access, Rijeka, Croatia, 2012 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Can tautomerisation of the A·T Watson-Crick base pair via double proton transfer provoke point mutations during DNA replication? A comprehensive QM and QTAIM analysis, J. Biomol. Struct. Dyn., 2014, 32, 127–154 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Why the tautomerization of the G·C Watson–Crick base pair via the DPT does not cause point mutations during DNA replication? QM and QTAIM comprehensive analysis, J. Biomol. Struct. Dyn., 2014, 32, 1474–1499 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Proton tunneling in the A·T Watson-Crick DNA base pair: myth or reality?, J. Biomol. Struct. Dyn., 2015, 12, 2716–2720 Search PubMed.
- A. Padermshoke, Y. Katsumoto, R. Masaki and M. Aida, Thermally induced double proton transfer in GG and wobble GT base pairs: a possible origin of the mutagenic guanine, Chem. Phys. Lett., 2008, 457, 232–236 CrossRef CAS.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, DPT tautomerisation of the wobble guanine·thymine DNA base mispair is not mutagenic: QM and QTAIM arguments, J. Biomol. Struct. Dyn., 2015, 33, 674–689 Search PubMed.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, Is the DPT tautomerisation of the long A·G Watson-Crick DNA base mispair a source of the adenine and guanine mutagenic tautomers? A QM and QTAIM response to the biologically important question, J. Comput. Chem., 2014, 35, 451–466 CrossRef PubMed.
- O. O. Brovarets' and D. M. Hovorun, The physicochemical essence of the purine·pyrimidine transition mismatches with Watson-Crick geometry in DNA: A·C* versa A*·C. A QM and QTAIM atomistic understanding, J. Biomol. Struct. Dyn., 2015, 33, 28–55 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, The nature of the transition mismatches with Watson-Crick architecture: the G*·T or G·T* DNA base mispair or both? A QM/QTAIM perspective for the biological problem, J. Biomol. Struct. Dyn., 2015, 33, 925–945 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Atomistic understanding of the C·T mismatched DNA base pair tautomerization via the DPT: QM and QTAIM computational approaches, J. Comput. Chem., 2013, 34, 2577–2590 CrossRef PubMed.
- O. O. Brovarets' and D. M. Hovorun, Does the G·G*syn DNA mismatch containing canonical and rare tautomers of the guanine tautomerise through the DPT? A QM/QTAIM microstructural study, Mol. Phys., 2014, 112, 3033–3046 CrossRef.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, Does the tautomeric status of the adenine bases change upon the dissociation of the A*·Asyn Topal-Fresco DNA mismatch? A combined QM and QTAIM atomistic insight, Phys. Chem. Chem. Phys., 2014, 16, 3715–3725 RSC.
- O. O. Brovarets' and D. M. Hovorun, DPT tautomerisation of the G·Asyn and A*·G*syn DNA mismatches: a QM/QTAIM combined atomistic investigation, Phys. Chem. Chem. Phys., 2014, 16, 9074–9085 RSC.
- O. O. Brovarets' and D. M. Hovorun, Prototropic tautomerism and basic molecular principles of hypoxanthine mutagenicity: An exhaustive quantum-chemical analysis, J. Biomol. Struct. Dyn., 2013, 31, 913–936 Search PubMed.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, The physico-chemical "anatomy" of the tautomerisation through the DPT of the biologically important pairs of hypoxanthine with DNA bases: QM and QTAIM perspectives, J. Mol. Model., 2013, 19, 4119–4137 CrossRef PubMed.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, The physico-chemical mechanism of the tautomerisation via the DPT of the long Hyp*·Hyp Watson-Crick base pair containing rare tautomer: a QM and QTAIM detailed look, Chem. Phys. Lett., 2013, 578, 126–132 CrossRef.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, A QM/QTAIM microstructural analysis of the tautomerisation via the DPT of the hypoxanthine·adenine nucleobase pair, Mol. Phys., 2014, 112, 2005–2016 CrossRef.
- P. Strazewski and C. Tamm, Replication experiments with nucleotide base analogues, Angew. Chem., Int. Ed., 1990, 29, 36–57 CrossRef.
- O. O. Brovarets', Y. P. Yurenko, I. Y. Dubey and D. M. Hovorun, Can DNA-binding proteins of replisome tautomerize nucleotide bases? Ab initio model study, J. Biomol. Struct. Dyn., 2012, 29, 1101–1109 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, New structural hypostases of the A·T and G·C Watson-Crick DNA base pairs caused by their mutagenic tautomerisation in a wobble manner: a QM/QTAIM prediction, RSC Adv., 2015, 5, 99594–99605 RSC.
- O. O. Brovarets' and D. M. Hovorun, Wobble↔Watson-Crick tautomeric transitions in the homo-purine DNA mismatches: a key to the intimate mechanisms of the spontaneous transversions, J. Biomol. Struct. Dyn., 2015, 33, 2710–2715 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Novel physico-chemical mechanism of the mutagenic tautomerisation of the Watson–Crick-like A·G and C·T DNA base mispairs: a quantum-chemical picture, RSC Adv., 2015, 5, 66318–66333 RSC.
- O. O. Brovarets' and D. M. Hovorun, A novel conception for spontaneous transversions caused by homo-pyrimidine DNA mismatches: a QM/QTAIM highlight, Phys. Chem. Chem. Phys., 2015, 17, 21381–21388 RSC.
- O. O. Brovarets' and D. M. Hovorun, Physicochemical mechanism of the wobble DNA base pairs Gua·Thy and Ade·Cyt transition into the mismatched base pairs Gua*·Thy and Ade·Cyt* formed by the mutagenic tautomers, Ukr. Bioorg. Acta, 2009, 8, 12–18 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Tautomeric transition between wobble A·C DNA base mispair and Watson-Crick-like A·C* mismatch: miscrostructural mechanism and biological significance, Phys. Chem. Chem. Phys., 2015, 17, 15103–15110 RSC.
- O. O. Brovarets' and D. M. Hovorun, By how many tautomerisation routes the Watson-Crick-like A·C* DNA base mispair is linked with the wobble mismatches? A QM/QTAIM vision from a biological point of view, Struct. Chem., 2016, 27, 119–131 CrossRef.
- O. O. Brovarets' and D. M. Hovorun, How many tautomerisation pathways connect Watson-Crick-like G*·T DNA base mispair and wobble mismatches?, J. Biomol. Struct. Dyn., 2015, 33, 2297–2315 Search PubMed.
- O. O. Brovarets', Microstructural mechanisms of the origin of the spontaneous point mutations, DrSci Thesis, Taras Shevchenko National University of Kyiv, Kyiv, Ukraine, 2015.
- O. O. Brovarets' and D. M. Hovorun, Stability of mutagenic tautomers of uracil and its halogen derivatives: the results of quantum-mechanical investigation, Biopolym. Cell, 2010, 26, 295–298 CrossRef.
- O. O. Brovarets' and D. M. Hovorun, Intramolecular tautomerization and the conformational variability of some classical mutagens – cytosine derivatives: Quantum chemical study, Biopolym. Cell, 2011, 27, 221–230 CrossRef.
- O. O. Brovarets', H. E. Pérez-Sánchez and D. M. Hovorun, Structural grounds for the 2-aminopurine mutagenicity: A novel insight into the old problem of the replication errors, RSC Adv., 2016, 6, 99546–99557 RSC.
- O. O. Brovarets' and H. E. Pérez-Sánchez, Whether 2-aminopurine induces incorporation errors at the DNA replication? A quantum-mechanical answer on the actual biological issue, J. Biomol. Struct. Dyn., 2017, 35, 3398–3411 Search PubMed.
- O. O. Brovarets' and H. E. Pérez-Sánchez, Whether the amino-imino tautomerism of 2-aminopurine is involved into its mutagenicity? Results of a thorough QM investigation, RSC Adv., 2016, 110, 108255–108264 RSC.
- O. O. Brovarets', I. Voiteshenko, H. E. Pérez-Sánchez and D. M. Hovorun, A QM/QTAIM detailed look at the Watson-Crick↔wobble tautomeric transformations of the 2-aminopurine·pyrimidine mispairs, J. Biomol. Struct. Dyn., 2017 DOI:10.1080/07391102.2017.1331864.
- O. O. Brovarets', I. S. Voiteshenko, H. E. Pérez-Sánchez and D. M. Hovorun, A QM/QTAIM research under the magnifying glass of the DPT tautomerisation of the wobble mispairs involving 2-aminopurine, New J. Chem., 2017, 41, 7232–7243 RSC.
- O. O. Brovarets', I. S. Voiteshenko and D. M. Hovorun, Physico-chemical profiles of the wobble↔Watson-Crick G*·2AP(w)↔G·2AP(WC) and A·2AP(w)↔A*·2AP(WC) tautomerisations: A QM/QTAIM comprehensive survey, Phys. Chem. Chem. Phys., 2018, 20, 623–636 RSC.
- N. A. Tchurikov, B. K. Chernov, Y. B. Golova and Y. D. Nechipurenko, Parallel DNA: Generation of a duplex between two Drosophila sequences in vitro, FEBS Lett., 1989, 257, 415–418 CrossRef CAS PubMed.
- E. Cubero, F. J. Luque and M. Orozco, Theoretical studies of d(A: T)-based parallel-stranded DNA duplexes, J. Am. Chem. Soc., 2001, 123, 12018–12025 CrossRef CAS PubMed.
- V. R. Parvathy, S. R. Bhaumik, K. V. Chary, G. Govil, K. Liu, F. B. Howard and H. T. Miles, NMR structure of a parallel-stranded DNA duplex at atomic resolution, Nucleic Acids Res., 2002, 30, 1500–1511 CrossRef CAS PubMed.
- V. I. Poltev, V. M. Anisimov, C. Sanchez, A. Deriabina, E. Gonzalez, D. Garcia, N. Rivas and N. A. Polteva, Analysis of the conformational features of Watson–Crick duplex fragments by molecular mechanics and quantum mechanics methods, Biophysics, 2016, 61, 217–226 CrossRef CAS.
- M. Y. Ye, R. T. Zhu, X. Li, X. S. Zhou, Z. Z. Yin, Q. Li and Y. Shao, Adaptively recognizing parallel-stranded duplex structure for fluorescent DNA polarity analysis, Anal. Chem., 2017, 89, 8604–8608 CrossRef CAS PubMed.
- M. Szabat and R. Kierzek, Parallel-stranded DNA and RNA duplexes: structural features and potential applications, FEBS J., 2017, 284, 3986–3998 CrossRef CAS PubMed.
- O. O. Brovarets', Under what conditions does G·C Watson-Crick DNA base pair acquire all four configurations characteristic for A·T Watson-Crick DNA base pair?, Ukr. Biochem. J., 2013, 85, 98–103 CrossRef.
- O. O. Brovarets', Structural and energetic properties of the four configurations of the A·T and G·C DNA base pairs, Ukr. Biochem. J., 2013, 85, 104–110 CrossRef.
- K. Hoogsteen, The crystal and molecular structure of a hydrogen-bonded complex between 1-methylthymine and 9-methyladenine, Acta Crystallogr., 1963, 16, 907–916 CrossRef CAS.
- N. G. Abrescia, A. Thompson, T. Huynh-Dinh and J. A. Subirana, Crystal structure of an antiparallel DNA fragment with Hoogsteen base pairing, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 2806–2811 CrossRef CAS PubMed.
- N. G. Abrescia, C. Gonzalez, C. Gouyette and J. A. Subirana, X-ray and NMR studies of the DNA oligomer d(ATATAT): Hoogsteen base pairing in duplex DNA, Biochemistry, 2004, 43, 4092–4100 CrossRef CAS PubMed.
- J. Pous, L. Urpi, J. A. Subirana, C. Gouyette, J. Navaza and J. L. Campos, Stabilization by extra-helical thymines of a DNA duplex with Hoogsteen base pairs, J. Am. Chem. Soc., 2008, 130, 6755–6760 CrossRef CAS PubMed.
- L. Campos, N. Valls, L. Urpí, C. Gouyette, T. Sanmartín, M. Richter, E. Alechaga, A. Santaolalla, R. Baldini, M. Creixell, R. Ciurans, P. Skokan, J. Pous and J. A. Subirana, Overview of the structure of all AT oligonucleotides: organization in helices and packing interactions, Biophys. J., 2006, 91, 892–903 CrossRef CAS PubMed.
- E. N. Nikolova, H. Zhou, F. L. Gottardo, H. S. Alvey, I. J. Kimsey and H. M. Al-Hashimi, A historical account of Hoogsteen base-pairs in duplex DNA, Biopolymers, 2014, 99, 955–968 Search PubMed.
- H. S. Alvey, F. L. Gottardo, E. N. Nikolova and H. M. Al-Hashimi, Widespread transient Hoogsteen base-pairs in canonical duplex DNA with variable energetics, Nat. Commun., 2014, 5, 4786–4794 CrossRef CAS PubMed.
- F. J. Acosta-Reyes, E. Alechaga, J. A. Subirana and J. L. Campos, Structure of the DNA duplex d(ATTAAT)2 with Hoogsteen hydrogen bonds, PLoS One, 2015, 10, e0120241 Search PubMed.
- C. Yang, E. Kim and Y. Pak, Free energy landscape and transition pathways from Watson–Crick to Hoogsteen base pairing in free duplex DNA, Nucleic Acids Res., 2015, 43, 7769–7778 CrossRef CAS PubMed.
- H. Zhou, Occurrence and function of Hoogsteen base pairs in nucleic acids, PhD Thesis, Department of Biochemistry, Duke University, Durham, North Carolina, USA, 2016.
- S. Kaur, P. Sharma and S. D. Wetmore, Structural and electronic properties of barbituric acid and melamine-containing ribonucleosides as plausible components of prebiotic RNA: implications for prebiotic self-assembly, Phys. Chem. Chem. Phys., 2017, 19, 30762–30771 RSC.
- A. Rich, On the problems of evolution and biochemical information transfer, in Horizons in Biochemistry, ed. M. Kasha and B. Pullman, Academic Press, New York, USA, 1962, pp. 103–126 Search PubMed.
- J. W. Drake, B. Charlesworth, D. Charlesworth and J. F. Crow, Rates of spontaneous mutation, Genetics, 1998, 148, 1667–1686 CAS.
- M. Lynch, Rate, molecular spectrum, and consequences of human mutation, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 961–968 CrossRef CAS PubMed.
- E. Del Grosso, A.-M. Dallaire, A. Vallée-Bélisle and F. Ricci, Enzyme-operated DNA-based nanodevices, Nano Lett., 2015, 15, 8407–8411 CrossRef CAS PubMed.
- T. Liedl, T. L. Sobey and F. C. Simmel, DNA-based nanodevices, Nanotoday, 2007, 2, 36–41 CrossRef.
- M. Piccolino, Biological machines: from mills to molecules, Nat. Rev. Mol. Cell Biol., 2000, 1, 149–153 CrossRef CAS PubMed.
- J. Tirado-Rives and W. L. Jorgensen, Performance of B3LYP Density Functional Methods for a large set of organic molecules, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- R. G. Parr, and W. Yang, Density-functional theory of atoms and molecules, Oxford University Press, Oxford, 1989 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman and J. A. Pople, GAUSSIAN 09 (Revision B.01), Gaussian Inc, Wallingford CT, 2010 Search PubMed.
- H. P. Hratchian, and H. B. Schlegel, Finding minima, transition states, and following reaction pathways on ab initio potential energy surfaces, in Theory and applications of computational chemistry: The first 40 years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. Scuseria, Elsevier, Amsterdam, 2005, pp. 195–249 Search PubMed.
- C. F. Matta, How dependent are molecular and atomic properties on the electronic structure method? Comparison of Hartree-Fock, DFT, and MP2 on a biologically relevant set of molecules, J. Comput. Chem., 2010, 31, 1297–1311 CAS.
- O. O. Brovarets' and D. M. Hovorun, Quantum-chemical investigation of tautomerization ways of Watson-Crick DNA base pair guanine-cytosine, Ukr. Biochem. J., 2010, 82, 55–60 Search PubMed.
- O. O. Brovarets' and D. M. Hovorun, Quantum-chemical investigation of the elementary molecular mechanisms of pyrimidine·purine transversions, Ukr. Biochem. J., 2010, 82, 57–67 Search PubMed.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, Is there adequate ionization mechanism of the spontaneous transitions? Quantum-chemical investigation, Biopolym. Cell, 2010, 26, 398–405 CrossRef.
- O. O. Brovarets' and D. M. Hovorun, DPT tautomerization of the long A·A* Watson-Crick base pair formed by the amino and imino tautomers of adenine: combined QM and QTAIM investigation, J. Mol. Model., 2013, 19, 4223–4237 CrossRef PubMed.
- O. O. Brovarets' and D. M. Hovorun, How does the long G·G* Watson-Crick DNA base mispair comprising keto and enol tautomers of the guanine tautomerise? The results of a QM/QTAIM investigation, Phys. Chem. Chem. Phys., 2014, 16, 15886–15899 RSC.
- M. A. Palafox, Molecular structure differences between the antiviral nucleoside analogue 5-iodo-2′-deoxyuridine and the natural nucleoside 2′-deoxythymidine using MP2 and DFT methods: conformational analysis, crystal simulations, DNA pairs and possible behavior, J. Biomol. Struct. Dyn., 2014, 32, 831–851 Search PubMed.
- A. A. El-Sayed, A. Tamara Molina, M. C. Alvarez-Ros and M. A. Palafox, Conformational analysis of the anti-HIV Nikavir prodrug: comparisons with AZT and thymidine, and establishment of structure-activity relationships/tendencies in other 6′-derivatives, J. Biomol. Struct. Dyn., 2015, 33, 723–748 CAS.
- C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, Using redundant internal coordinates to optimize equilibrium geometries and transition states, J. Comput. Chem., 1996, 17, 49–56 CrossRef CAS.
- P. W. Atkins, Physical chemistry, Oxford University Press, Oxford, 1998 Search PubMed.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Semi-direct algorithms for the MP2 energy and gradient, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- E. Wigner, Über das Überschreiten von Potentialschwellen bei chemischen Reaktionen [Crossing of potential thresholds in chemical reactions], Zeitschrift für Physikalische Chemie, 1932, B19, 203–216 CAS.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- M. Gutowski, J. H. Van Lenthe, J. Verbeek, F. B. Van Duijneveldt and G. Caahalasinski, The basis set superposition error in correlated electronic structure calculations, Chem. Phys. Lett., 1986, 124, 370–375 CrossRef CAS.
- J. A. Sordo, S. Chin and T. L. Sordo, On the counterpoise correction for the basis set superposition error in large systems, Theor. Chim. Acta, 1988, 74, 101–110 CrossRef CAS.
- J. A. Sordo, On the use of the Boys–Bernardi function counterpoise procedure to correct barrier heights for basis set superposition error, J. Mol. Struct., 2001, 537, 245–251 CrossRef CAS.
- R. F. W. Bader, Atoms in molecules: A quantum theory, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- C. F. Matta and J. Hernández-Trujillo, Bonding in polycyclic aromatic hydrocarbons in terms of the electron density and of electron delocalization, J. Phys. Chem. A, 2003, 107, 7496–7504 CrossRef CAS.
- C. F. Matta, N. Castillo and R. J. Boyd, Atomic contributions to bond dissociation energies in aliphatic hydrocarbons, J. Chem. Phys., 2006, 125(20), 204103 CrossRef PubMed.
- I. Cukrowski and C. F. Matta, Hydrogen–hydrogen bonding: A stabilizing interaction in strained chelating rings of metal complexes in aqueous phase, Chem. Phys. Lett., 2010, 499, 66–69 CrossRef CAS.
- C. F. Matta, Modeling biophysical and biological properties from the characteristics of the molecular electron density, electron localization and delocalization matrices, and the electrostatic potential, J. Comput. Chem., 2014, 35, 1165–1198 CrossRef CAS PubMed.
- C. Lecomte, E. Espinosa and C. F. Matta, On atom–atom ‘short contact’ bonding interactions in crystals, IUCrJ, 2015, 2, 161–163 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 10.07.01), retrieved from aim.tkgristmill.com, 2010 Search PubMed.
- C. F. Matta, N. Castillo and R. J. Boyd, Extended weak bonding interactions in DNA: π-stacking (base-base), base-backbone, and backbone-backbone interactions, J. Phys. Chem. B, 2006, 110, 563–578 CrossRef CAS PubMed.
- C. F. MattaR. J. Boyd, The Quantum Theory of Atoms in Molecules: from solid state to DNA and drug design, Wiley-VCH Verlag GmbH & Co. KGaA, 2007 Search PubMed.
- A. V. Iogansen, Direct proportionality of the hydrogen bonding energy and the intensification of the stretching ν(XH) vibration in infrared spectra, Spectrochim. Acta, Part A, 1999, 55, 1585–1612 CrossRef.
- O. O. Brovarets' and D. M. Hovorun, IR vibrational spectra of H-bonded complexes of adenine, 2-aminopurine and 2-aminopurine+ with cytosine and thymine: quantum-chemical study, Opt. Spectrosc., 2010, 111, 750–757 CrossRef.
- O. O. Brovarets', R. O. Zhurakivsky and D. M. Hovorun, Structural, energetic and tautomeric properties of the T·T*/T*·T DNA mismatch involving mutagenic tautomer of thymine: a QM and QTAIM insight, Chem. Phys. Lett., 2014, 592, 247–255 CrossRef.
- O. O. Brovarets' and D. M. Hovorun, Atomistic nature of the DPT tautomerisation of the biologically important C·C* DNA base mispair containing amino and imino tautomers of cytosine: a QM and QTAIM approach, Phys. Chem. Chem. Phys., 2013, 15, 20091–20104 RSC.
- O. O. Brovarets’, Y. P. Yurenko and D. M. Hovorun, Intermolecular CH···O/N H-bonds in the biologically important pairs of natural nucleobases: A thorough quantum-chemical study, J. Biomol. Struct. Dyn., 2013, 32, 993–1022 Search PubMed.
- O. O. Brovarets', Y. P. Yurenko and D. M. Hovorun, The significant role of the intermolecular CH···O/N hydrogen bonds in governing the biologically important pairs of the DNA and RNA modified bases: a comprehensive theoretical investigation, J. Biomol. Struct. Dyn., 2015, 33, 1624–1652 Search PubMed.
- E. Espinosa, E. Molins and C. Lecomte, Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- I. Mata, I. Alkorta, E. Espinosa and E. Molins, Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields, Chem. Phys. Lett., 2011, 507, 185–189 CrossRef CAS.
- T. Y. Nikolaienko, L. A. Bulavin and D. M. Hovorun, Bridging QTAIM with vibrational spectroscopy: The energy of intramolecular hydrogen bonds in DNA-related biomolecules, Phys. Chem. Chem. Phys., 2012, 14, 7441–7447 RSC.
- W. Saenger, Principles of nucleic acid structure, Springer, New York, 1984 Search PubMed.
- D. M. Govorun and I. V. Kondratyuk, The quantum mechanical calculations evidence molecular-zwitterionic features of prototropic tautomerism of canonical nucleotide bases. 2. Purines, Biopolym. Cell, 1996, 12, 49–52 CrossRef CAS.
- D. M. Govorun, V. D. Danchuk, Y. R. Mishchuk, I. V. Kondratyuk, N. F. Radomsky and N. V. Zheltovsky, AM1 calculation of the nucleic acid bases structure and vibrational spectra, J. Mol. Struct., 1992, 267, 99–103 CrossRef CAS.
- T. Y. Nikolaienko, L. A. Bulavin and D. M. Hovorun, How flexible are DNA constituents? The quantum-mechanical study, J. Biomol. Struct. Dyn., 2011, 29, 563–575 CAS.
- D. M. Hovorun, L. Gorb and J. Leszczynski, From the nonplanarity of the amino group to the structural nonrigidity of the molecule: a post-Hartree-Fock ab initio study of 2-aminoimidazole, Int. J. Quantum Chem., 1999, 75, 245–253 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |
