 Open Access Article
Open Access ArticleFirst-principles analysis of a molecular piezoelectric meta-nitroaniline
Fu Wang a,
Zelin Daia,
Yu Gua,
Xiaomeng Chenga,
Yadong Jianga,
Fangping Ouyangb,
Jimmy Xuac and
Xiangdong Xu
a,
Zelin Daia,
Yu Gua,
Xiaomeng Chenga,
Yadong Jianga,
Fangping Ouyangb,
Jimmy Xuac and
Xiangdong Xu *a
*a
aState Key Laboratory of Electronic Thin Films and Integrated Devices, School of Optoelectronic Science and Engineering, University of Electronic Science and Technology of China (UESTC), Chengdu 610054, P. R. China. E-mail: xdxu@uestc.edu.cn
bSchool of Physics and Electronics, Central South University, Changsha 410083, P. R. China
cSchool of Engineering, Brown University, Providence, Rhode Island 02912, USA
First published on 9th May 2018
Abstract
The piezoelectric and elastic properties of a molecular piezoelectric meta-nitroaniline (mNA) in its single-crystal form were investigated in the framework of first-principles density functional perturbation theory (DFPT). Results support the recent experimental findings those despite being soft and flexible, mNA's piezoelectric coefficients are an order of magnitude greater than that of ZnO and LiNbO3. A molecular-level insight into the piezoelectric properties of mNA is provided. These results are helpful not only for better understanding mNA, but also for developing new piezoelectric materials.
1. Introduction
Piezoelectric materials are ideally suited for electromechanical transductions. By producing dielectric polarization with a mechanical strain and, conversely, a mechanical response with an applied electric field, they have found applications in sensors,1 energy harvesting,2,3 actuators,4 oscillators,5,6 and many other fields. Most recent studies have focused on inorganic piezoelectric materials, such as AlN,7 ZnO,8 LiNbO3,9 and lead zirconate titanate (PZT).10 These inorganic piezoelectric ceramics have large piezoelectric coefficients, but are generally stiff and brittle, and some even contain environmentally unfriendly elements, including the champion piezoelectric PZT.11 For many applications, flexible, thin, lightweight, scalable, low processing temperature, and biophilic piezoelectrics are more desirable. These are difficult challenges for conventional piezoelectric ceramics, but can be met with molecular piezoelectrics, in the form of either an organic composite film or crystal. On the other hand, the piezoelectricity of commonly known organic piezoelectrics such as poly(vinylidene fluoride) (PVDF)12,13 is rather low.14 The electromechanical conversion efficiency of the PVDF has only reached 17.8%,15 limiting its applications. However, given the numerous possibilities of synthesizing (engineering) highly polarizable molecules with non-centrosymmetry, it is rational to speculate that there exist molecular structures of greater piezoelectricity or ones that could be specially made by informed designs. Experimentally, findings are still few, but at least two16,17 have emerged as especially promising, one of which is meta-nitroaniline (mNA).Structurally, mNA is a relatively simple molecular species, but still complex by the standard of piezoelectrics. It has long been known for its large second or third optical nonlinearities,18–21 in accompany with its non-centrosymmetry. The non-centrosymmetry is also suggestive of piezoelectricity. Indeed, piezoelectricity of mNA crystal has been experimentally measured by Avanci,17 Bain,22 and Isakov et al.23 In fact, these experimental reports presented rather impressive piezoelectric coefficients, comparable to or even larger than some of the well-known inorganic piezoelectric ceramics. Among them, some of the measured results reported by Bain22 and Isakov23 are similar. Therefore, the measured results of Avanci and Bain will be mainly discussed in this work. But the numerical values measured by Avanci17 are about one order of magnitude larger than those by Bain,22 which could result from various experimental constraints and measurement errors as pointed out in ref. 17 and is reasonable at the early stage of discovery. One source of uncertainty in accuracy could be in the shear force applied to the mNA crystal in measurements and therefore in determining the pertinent tangential components of the piezoelectric tensor. While discrepancies in experimental findings are natural in the early phase and will narrow down as the methods refine along with the material itself, a first-principles based computational model could add value by serving as a reference framework and shedding light on the origins of factors contributing to the piezoelectric responses and on the complex relationships between the macroscopic properties and the underlying molecular structure.
In this paper, the piezoelectric and elastic properties of organic mNA crystal were modeled in the framework of the density functional perturbation theory (DFPT). Results support the experimental findings that the piezoelectric coefficients of mNA d33 is about one order of magnitude larger than that of some well-known conventional inorganic piezoelectric ceramics such as ZnO8 and LiNbO3,9 and comparable to the poled BaTiO3. As it is conventionally defined, d33 is a measure of the material's response in terms of surface charge density to a normal strain, its value depends on both the molecular orbital charge density redistribution, dipolar reorientation, and the elastic deformation of the material. In the case of a molecular piezoelectric both are much more complex than in an inorganic piezoelectric and more difficult to compute.
2. Computational model
The piezoelectric and elastic constants of mNA crystals were calculated based on the DFPT24 together with the generalized gradient approximation revised Perdew–Burke–Ernzerhof (GGA-rPBE) functional implemented in the Vienna Ab-initio Simulation Package (VASP).25 The PBE pseudopotential file was used in this work, PREC is set to accurate mode, and the accuracy of the calculation are set as EDIFF = 2 × 10−6 and EDIFFG = −1 × 10−3. The Brillouin zone integration is obtained by a 1 × 3 × 3 Monkhorst–Pack k-points mesh and the energy cutoff was set to 800 eV. In our calculations, the DFT-D3 method proposed by Grimme and co-workers26 was employed to introduce the dispersion correction term into the calculations, in which the van der Waals interactions were described via a pair-wise force field. The DFPT method is known as an efficient way for calculating various physical response properties of insulating crystals, including elastic, dielectric, Born charge, and piezoelectric tensors. It has been successfully applied to calculations of piezoelectricity of many materials, such as BaTiO3 (ref. 27) and poly(lactic acid) (PLA) polymorphs.28 Compared with the alternative popular Berry phase method, the DFPT method can avoid the so-called “improper piezoelectricity”,29 and automatically produce the proper piezoelectric constants. The initial mNA crystal structure for geometry optimization was determined by Kanoun et al.30 at room temperature.3. Results and discussion
The mNA crystal belongs to the orthorhombic space group Pbc21, point group mm2 with a unit cell containing four mNA molecules. The molecule of the mNA unit cell is drawn with atom label in Fig. 1a and the crystal configuration is displayed in Fig. 1b. Considering that the piezoelectric properties are ground-state properties, a full relaxation or optimization of the molecular structure is needed. The optimized lattice parameters by our set-up are summarized in Table 1, and are compared with those experimentally measured.17,30,31 They are in good agreement with each other. The maximum deviation of the optimized structural parameters is 6.29% in comparison with those previously reported.17,30,31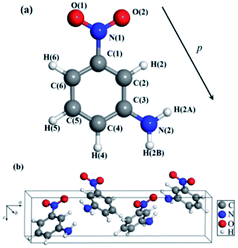 | ||
| Fig. 1 The optimized structure of mNA: (a) single isolated mNA molecule, (b) the unit cell of mNA crystal. | ||
The piezoelectric coefficients of materials can be described in two forms: one is the piezoelectric stress coefficient eαj, another is the piezoelectric strain coefficient dαi. The piezoelectric stress coefficient eαj is defined as:32,33
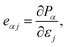 | (1) |
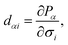 | (2) |
| eαj = dαiCij | (3) |
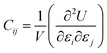 | (4) |
The elastic constant Cij tensor can be expressed in a 6 × 6 square matrix, with 36 components. Given the symmetry of the mNA crystal, there are only 9 independent elastic tensor components, which are C11, C12, C13, C22, C23, C33, C44, C55, and C66. Similarly, of the piezoelectric stress constants and the piezoelectric strain constants only 5 (e15, e24, e31, e32, e33) are independent. Hence, for mNA, eqn (3) can be written as:
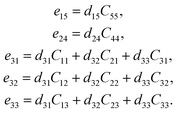 | (5) |
Assume
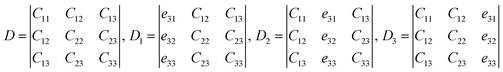 | (6) |
Thus,
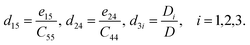 | (7) |
To obtain the strain tensor dij, we need to calculate the stress tensor eij and elastic tensor Cij, which can be directly obtained in the DFPT approach without multiple ground-state calculations as required in the Berry Phase framework.
For checking the feasibility and correctness of the DFPT approach in calculating the piezoelectric properties of materials, we further applied the DFPT approach to calculate the properties of the well-studied and matured piezoelectric ZnO. As shown in Table 2, the calculated results at zero temperature are in good agreement with those previously measured35 and calculated.32 While the DFPT calculations are subject to several approximates, such as the GGA-rPBE itself which is associated with the errors of lattice parameters (Table 1), and the frozen-core approximation originated from the use of pseudopotentials, the calculated results are consistent with the experiment data at room temperature.
| Our results | Previous calc.a | Previous expt.b | ||
|---|---|---|---|---|
| a Ref. 32.b Ref. 35. | ||||
| Elastic constant (GPa) | C11 | 205 | 226(+10.24) | 209(+1.95) |
| C12 | 138 | 139(+0.72) | 120(−13.04) | |
| C13 | 122 | 123(+0.82) | 104(−14.75) | |
| C33 | 202 | 242(+19.80) | 211(+4.46) | |
| C44 | 33 | 40(+21.21) | 44(+33.33) | |
| C66 | 33 | 44(+33.33) | — | |
| Stress coefficients (C m−2) | e15 | −0.50 | −0.53(+6.00) | −0.37(−26.00) |
| e31 | −0.74 | −0.67(−9.46) | −0.62(−16.22) | |
| e33 | 1.41 | 1.28(−9.22) | 0.96(−31.91) | |
To the best of our knowledge, no prior analysis of the piezoelectric properties of mNA crystal has been reported in literatures, aside from the experimental findings of the longitudinal components (d31, d32, d33) of the piezoelectric tensor of the mNA crystal17,22,23 in the past twenty years.
The calculated elastic stiffness constants of the mNA crystal and the experimentally measured ones are summarized in Table 3. The relaxed-ion elastic constants are of the same order of magnitude as those experimentally measured.17 Especially, the computed C12, C33, C44, C55, C66 are in good agreement with the experimental values.
| Elastic components | Clamped-ion (GPa) | Relaxed-ion (GPa) | |
|---|---|---|---|
| This work | Experimenta | ||
| a Ref. 17. | |||
| C11 | 295.955 | 16.320 | 10.47(−35.8) |
| C12 | 97.694 | 7.225 | 6.27(−13.2) |
| C13 | 105.091 | 8.874 | 14.07(+58.6) |
| C22 | 348.615 | 35.071 | 13.91(−60.3) |
| C23 | 84.171 | 19.870 | 9.73(−51.0) |
| C33 | 155.558 | 16.425 | 22.07(+34.4) |
| C44 | 122.356 | 16.264 | 12.17(−25.2) |
| C55 | 137.926 | 6.956 | 4.64(−33.3) |
| C66 | 157.735 | 3.212 | 4.26(+32.6) |
The computed results also naturally satisfy the Born mechanical stability criteria:22
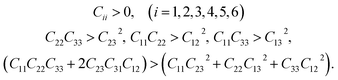 | (8) |
This indirectly reconfirms that the optimized lattice structure of the mNA crystal generated from the computational optimization process described earlier is stable.
It is also worth noting that the elastic constants of mNA are approximately one order of magnitude smaller than that of inorganic piezoelectric materials such as GaN36 and AlN,37,38 providing a relative measure of the flexibility of mNA crystal.
The piezoelectric stress coefficients of the mNA crystal, as defined in eqn (1), were calculated and are shown in Table 4.
| Stress constant | Clamped-ion (C m−2) | Relaxed-ion (C m−2) |
|---|---|---|
| e15 | 0.001 | −0.059 |
| e24 | −0.048 | −0.022 |
| e31 | 0.046 | −0.339 |
| e32 | 0.164 | −0.257 |
| e33 | 0.083 | 0.168 |
The piezoelectric strain coefficients were calculated according to eqn (3) and listed in Table 5. As can be seen from the Table 5, the piezoelectric strain coefficients are of the same order of magnitude as those experimentally measured by Avanci.17 In particular, the calculated and experimental results of d31 and d33 are very close, of which d33 is frequently cited as a primary measure of piezoelectricity of the material.
| Strain constant | Clamped-ion (pC/N) | Relaxed-ion (pC/N) | |||
|---|---|---|---|---|---|
| This work | Expt.a | Expt.b | Expt.c | ||
| a Ref. 17.b Ref. 22.c Ref. 23. | |||||
| d15 | 0.010 | −8.488 | — | — | — |
| d24 | −0.395 | −1.359 | — | — | — |
| d31 | −0.061 | −64.950 | 73.1(+12.5) | 30.79(−52.6) | 20(−69.2) |
| d32 | 0.493 | −49.949 | 165.7/149.5(+231.7/+199.3) | 2.55(−94.9) | — |
| d33 | 0.232 | 115.757 | 103.8(−10.3) | 6.81(−94.1) | 4.0(−95.5) |
It is noteworthy that the piezoelectric strain constants d33 measured by Bain22 and Isakov23 are about one twentieth of that by Avanci.17 A possible reason for the large difference in the two experiments is that molecular rotation, vibration, and deformation require different times and energies, and the energy coupled into the crystal from external forces also depends on sample shapes and configurations. Consequently, it is reasonable to expect the vibration frequency of the applied stress would affect the results in direct piezoelectric measurements. In Bain's experiment, a brass was placed on the top of the crystal, and the changes in charge produced by the application and removal of the weights were recorded. The averages of 20–30 measurements were taken to obtain the piezoelectric coefficients.
As Table 5 reveals, the piezoelectric coefficient d33 of mNA is impressively large and promising for future applications. It could be understood from the molecular structure features of mNA, as illustrated in Fig. 1. The mNA molecule contains a benzene ring, a nitro group (–NO2) and an amino group (–NH2). The –NO2 and –NH2 are attached to the benzene ring in the meta positions, forming a push–pull electronic structure. The –NO2 behaves as an electron-acceptor negatively charged, while the –NH2 behaves as an electron-donor positively charged. Thus, the dipole moment of the mNA molecule is directed from the –NO2 group towards the –NH2 group,39 as illustrated in Fig. 1a, providing a strong dipole moment of 4.9 debye.40 It can be seen from Fig. 1b that the dipole moments of the four molecules in one unit cell vary in orientations, but generally point to the same direction (i.e. along the reverse direction of the c-axis). Accordingly, if the strain occurs in the c-axis direction, the change in the polarization along the c-axis direction is larger than those along the a-axis and b-axis directions in an elastic material. From eqn (2), the piezoelectric strain coefficient dij is the derivative of the polarization of the direction i to the strain in the direction j. If a compressive stress is applied in the c-axis direction, the thickness of the mNA crystal along the c-axis will be decreased. Such a thickness decrease leads to an increase of the dipole density and decrease of the dipole moment of a single mNA molecule along the c-axis direction, thus resulting in a significant decrease of the macroscopic dipole moment. Therefore, d33 that is defined as the measurement of the surface charge on the (001) plane produced by the longitudinal strain along the c-axis direction is large and positive. In contrast, the thickness of the mNA crystal along the c-axis slightly decreases if a tensile stress is applied to the mNA crystal along the a-axis or the b-axis, due to the slight decrease of the dipole moment along the c-axis, thus resulting in negative d31 and d32 (Table 5). These suggest that from the microcosmic point of view, larger d33 of mNA is mainly attributed to its large dipole moment. Thus, we provide a molecular-level insight into the piezoelectric properties of mNA crystal. Based on this, one can easily deduce that for seeking new piezoelectric materials, the materials with large dipole moments are likely to exhibit excellent piezoelectric properties.
Both our calculated and previously experimental results17 similarly reveal that mNA is superior in its piezoelectric responses, even if its properties are compared with those measured results of the bulk piezoelectric materials of GaN,36 AlN,7 ZnO,8 PVDF14 and LiNbO3.9 As a visual comparison, the relative piezoelectric responses are displayed in Fig. 2. It is worth noting that the experimentally-measured results reflect the combined effects of electrons and ions in the materials, so the relaxed-ion piezoelectric coefficient is generally chosen when the calculated piezoelectric properties of a material are compared with those of others. Compared with the well-known inorganic piezoelectric material of AlN (C33 = 373 GPa, e33 = 1.55 C m−2),41,42 the piezoelectric stress coefficient e33 (0.168 C m−2 as shown in Table 4) of mNA calculated in this work is about one ninth of AlN, while the elastic coefficient C33 of the latter (16.425 GPa as shown in Table 3) is much more smaller, just about one twentieth of the former. This suggests that from the macroscopic view, the larger d33 for mNA crystal can be mainly attributed to its smaller elastic coefficient C33, rather than to a large piezoelectric stress coefficient e33.
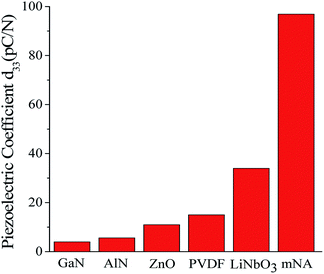 | ||
| Fig. 2 A visual comparison of d33 of some well-known piezoelectric materials and mNA. The piezoelectric coefficient of GaN,36 AlN,7 ZnO,8 PVDF14 and LiNbO3 (ref. 9) were obtained from experiments. | ||
Based on the results presented in this work, one can deduce that the theoretical calculations can provide valuable information beyond the experiments. First, the calculation results can provide effective supplements to the experimental results and verify the correctness of the latter if the calculation conditions are well considered. Second, the theoretical calculations can efficiently avoid some unwanted errors caused by the experimental measurements and/or instruments. Third, the theoretical calculations can be used specially as an independent criterion for predicting the piezoelectric properties before experiments. This is critical in seeking new high-performance piezoelectric materials.
4. Conclusions
In summary, the elasticity and piezoelectric properties of the mNA crystal were analyzed through numerical modeling based on the first-principles density functional perturbation theory (DFPT). The calculated results confirm the experimental findings that the relatively simple molecular material of mNA is capable of superior piezoelectric responses. While experimental findings are still few and varied, which is natural in an early phase of discovery, the theoretical modeling analysis provides an independent framework of reference and assessment. It also offers molecular structural insights to the highly anisotropic piezoelectric and elastic properties of the mNA crystal. The DFPT method as an efficient method for predicting the piezoelectricity and elastic properties of molecular piezoelectrics is extendable to more complex organic materials. While the theoretical analysis is in general agreement with the experimental findings, however still few and varied, it also can provide a more complete assessment in details and guidance for possible molecular modifications. In the case of a simpler and well-established piezoelectric material such as ZnO, the calculated results are in excellent agreement with the experimental data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial supports of this work by the National Natural Science Foundation of China (NSFC 61377063, 61071032, 61235006, and 61421002) and by the Chang-Jiang Chair Professor program are acknowledged.References
- S. Zhang and F. Yu, J. Am. Ceram. Soc., 2011, 94, 3153–3170 CrossRef CAS.
- H. D. Akaydin, N. Elvin and Y. Andreopoulos, J. Intell. Mater. Syst. Struct., 2010, 21, 1263–1278 CrossRef.
- H. D. Akaydin, N. Elvin and Y. Andreopoulos, Exp. Fluids, 2010, 49, 291–304 CrossRef.
- M. Rakotondrabe and I. A. Ivan, IEEE Trans. Autom. Sci. Eng., 2011, 8, 824–834 CrossRef.
- X. Chu, J. Wang, S. Yuan, L. Li and H. Cui, Rev. Sci. Instrum., 2014, 85, 065002 CrossRef PubMed.
- S. H. Zhang, J. P. Zhou, Z. Shi, P. Liu and C. Y. Deng, J. Alloys Compd., 2014, 590, 46–49 CrossRef CAS.
- Y. Oshima, M. Nakamura, Y. Masa, G. Villora, K. Shimamura and N. Ichinose, J. Electrochem. Soc., 2012, 27, 2455 Search PubMed.
- T. J. Bukowski, K. McCarthy, F. McCarthy, G. Teowee, T. P. Alexander, D. R. Uhlmann, J. T. Dawley and B. J. J. Zelinski, Integr. Ferroelectr., 1997, 17, 339–347 CrossRef CAS.
- M. M. Fejer, G. A. Magel and E. J. Lim, SPIE-Int. Soc. Opt. Eng., Proc., 1990, 1148, 213–225 CAS.
- Y. Li, W. Chen, Q. Xu, J. Zhou, Y. Wang and H. Sun, Ceram. Int., 2007, 33, 95–99 CrossRef CAS.
- M. D. Maeder, D. Damjanovic and N. Setter, J. Electroceram., 2004, 13, 385–392 CrossRef CAS.
- B. Mohammadi, A. A. Yousefi and S. M. Bellah, Polym. Test., 2007, 26, 42–50 CrossRef CAS.
- Y. Jiang, H. Hamada, S. Shiono, K. Kanda, T. Fujita, K. Higuchi and K. Maenaka, Procedia Eng., 2010, 5, 1466–1469 CrossRef CAS.
- G. D. Jones, R. A. Assink, T. R. Dargaville, P. M. Chaplya, R. L. Clough, J. M. Elliott, J. W. Martin, D. M. Mowery and M. C. Celina, J. Electron. Packag., 2005, 131, 51–55 Search PubMed.
- F. Pan, Z. Xu, L. Jin, P. Pan and X. Gao, IEEE Trans. Ind. Appl., 2017, 53, 3890–3897 CrossRef CAS.
- S. Gilmour, R. A. Pethrick, D. Pugh and J. N. Sherwood, Philos. Mag. B, 1993, 67, 855–868 CAS.
- L. H. Avanci, L. P. Cardoso, S. E. Girdwood, D. Pugh, J. N. Sherwood and K. J. Roberts, Phys. Rev. Lett., 1998, 81, 5426–5429 CrossRef CAS.
- J. L. Oudar, D. S. Chemla and E. Batifol, J. Chem. Phys., 1977, 67, 1626–1635 CrossRef CAS.
- A. C. Fantoni, C. G. Pozzi and G. Punte, J. Phys. Chem. A, 2009, 113, 9527–9532 CrossRef CAS PubMed.
- T. Kanagasekaran, M. Gunasekaran, P. Srinivasan, D. Jayaraman, R. Gopalakrishnan and P. Ramasamy, Cryst. Res. Technol., 2010, 40, 1128–1133 CrossRef.
- P. V. Adhyapak, M. Islam, R. C. Aiyerb, U. P. Mulik, Y. S. Negi and D. P. Amalnerkar, J. Cryst. Growth, 2008, 310, 2923–2927 CrossRef CAS.
- A. M. Bain, N. Ei-Korashy, S. Gilmour, R. A. Pethrick and J. N. Sherwood, Philos. Mag. B, 1992, 66, 293–305 CAS.
- D. Isakov, S. Vasilev, E. D. M. Gomes, B. Almeida, V. Y. Shur and A. L. Kholkin, Appl. Phys. Lett., 2016, 109, 162903 CrossRef.
- X. Gonze, Phys. Rev. A, 1995, 52, 1096–1114 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- H. Takahashi, Y. Numamoto, J. Tani and S. Tsurekawa, Jpn. J. Appl. Phys., 2006, 45, 7405–7408 CrossRef CAS.
- T. Lin, X. Y. Liu and C. He, J. Phys. Chem. B, 2012, 116, 1524–1535 CrossRef CAS PubMed.
- D. Vanderbilt, J. Phys. Chem. Solids, 2000, 61, 147–151 CrossRef CAS.
- M. B. Kanoun, E. Botek and B. Champagne, Chem. Phys. Lett., 2010, 487, 256–262 CrossRef CAS.
- A. E. Goeta, C. C. Wilson, J. C. Autino, J. Ellena and G. Punte, Chem. Mater., 2000, 12, 3342–3346 CrossRef CAS.
- X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B, 2005, 72, 035105 CrossRef.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- W. F. Perger, J. Criswell, B. Civalleri and R. Dovesi, Comput. Phys. Commun., 2009, 180, 1753–1759 CrossRef CAS.
- A. S. Bhalla, W. R. Cook jr. and S. T. Liu, Low Frequency Properties of Dielectric Crystals: Piezoelectric, Pyroelectric and Related Constants, Springer, Berlin, 1993 Search PubMed.
- G. Irmer, C. Röder, C. Himcinschi and J. Kortus, Phys. Rev. B, 2016, 94, 195201 CrossRef.
- K. Kim, W. R. L. Lambrecht and B. Segall, Phys. Rev. B, 1996, 53, 16310–16326 CrossRef CAS.
- F. Peng, D. Chen, H. Fu and X. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 403, 4259–4263 CrossRef CAS.
- G. Ryu and C. S. Yoon, J. Cryst. Growth, 1998, 191, 190–198 CrossRef CAS.
- J. L. Oudar, D. S. Chemla and E. Batifol, J. Chem. Phys., 1977, 67, 1626–1635 CrossRef CAS.
- A. F. Wright, J. Appl. Phys., 1997, 82, 2833–2839 CrossRef CAS.
- J. G. Gualtieri, J. A. Kosinski and A. Ballato, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 1994, 41, 53–59 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |
