Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate global potential energy surface for the ground state of CH2+ by extrapolation to the complete basis set limit†
Lu Guoa,
Hongyu Maa,
Lulu Zhangb,
Yuzhi Song*b and
Yongqing Li *a
*a
aDepartment of Physics, Liaoning University, Shenyang 110036, China. E-mail: yqli@lnu.edu.cn
bSchool of Physics and Electronics, Shandong Normal University, Jinan 250014, China. E-mail: yzsong@sdnu.edu.cn
First published on 11th April 2018
Abstract
A full three-dimensional global potential energy surface is reported for the ground state of CH2+ by fitting accurate multireference configuration interaction energies calculated using aug-cc-pVQZ and aug-cc-pV5Z basis sets with extrapolation of the electron correlation energy to the complete basis set limit. The topographical characteristics have been compared in detail with a potential energy surface of the same type recently reported [J. Chem. Phys., 2015, 142, 124302] based on a least-squares fit to accurate high level ab initio MRCI(Q) energies, calculated using AV6Z basis set. The new three-dimensional global potential energy surface is then used in quasiclassical trajectory calculations for H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) reaction. The integral cross sections, differential cross sections and the rate coefficients have been computed. A comparison shows that our potential energy surface can be applied to any type of dynamic study.
1. Introduction
The C+ + H2, ion-molecule reaction has been the research core of extensive experimental and theoretical study owing to its important role in astrophysics and atmospheric chemistry. Particularly, the CH2+ complex formed by the reaction is a crucial intermediate in interstellar matter and combustion process.1 Hence the reaction C+ + H2 has been widely researched.The cation CH2+ belongs to a class of molecules which are termed ‘‘quasilinear’’. From the spectroscopic side, the linear and bending problems of CH2+ attracted the researchers' interest in the 1960s.2 This issue was first solved theoretically due to the lack of spectral data, Schaefer and Bender3 predicted a bent equilibrium geometry for the electronic ground state (12A′) of CH2+ in 1971. Later, the bent equilibrium geometry was confirmed by the Coulomb explosion imaging experiment.4,5 Then, extensive research on CH2+ has been carried out theoretically.
Among a series of theoretical studies, Stoecklin and Halvick6 reported the theoretical research result of the caption reaction for the first time, which fitting a precise 3-D single-valued potential energy surface (PES). Utilizing an extensive multiconfigurational wave function with the augmented Dunning correlation consistent basis set (aug-cc-pVQZ) to calculate large ab initio points. Then Halvick et al.7 based on this PES to study quasiclassical trajectory (QCT) calculations, along with phase space theory and quantum rigid rotor calculations for H + CH+. And the PES was used by Zanchet et al.8 for the state-to-state rate constant study with quantum wave packet analysis of the H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) reaction. Recently, Schneider and Warmbier9 constructed the CH2+ ground state PES by fitting internuclear distances polynomials with the multireference configuration interaction (MRCI) and aug-cc-pVTZ ab initio points. And for verifying this PES, they have performed quantum scattering and QCT calculations. Additionally, Herráez–Aguilar et al.10 have performed a dynamical study of the endothermic and barrierless C+ + H2(1Σg+) → CH+(1Σg+) + H reaction for different initial rotational states of the H2(v = 0) and H2(v = 1) manifolds, with the QCT and the Gaussian binning methodology on Schneider and Warmbier's9 PES. Most recently, Li et al.11 reported a new many-body expansion (MBE) PES by fitting MRCI/aug-cc-pV6Z ab initio energies. This PES is used by Guo et al.12 to analyze the effect of isotopic substitution on three-dimensional dynamic properties of the reactions C+ + H2/HD/HT → CH+ + H/D/T. In addition, the time-dependent wave packet propagation approach was used to compute thermal rate constants and integral cross sections of the H + CH+ reaction in the coupled states approximation by Sundaram et al.13 Faure et al. also presents a detailed theoretical study of state-to-state and initial-state-specific rate coefficients are computed in the kinetic temperature range 10–3000 K.14
The purpose of present study is to build a high quality global PES for the ground state(12A′) of CH2+ from MRCI(Q)15 ab initio energies based on the reference full valence complete active space (FVCAS)16 wave function, the aug-cc-pV5Z(AV5Z) and aug-cc-pVQZ(AVQZ) basis sets of Dunning17,18 have been applied. We all know that in order to get a highly precise PES, it usually requires a large basis sets. But, we did not use such a large basis sets in this work, instead we have extrapolated the total energy to the complete basis set (CBS) limit by using a uniform single-pair and triple-pair (USTE).19,20 For verifying this PES, the QCT has been performed on H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+), the differential cross sections (DCSs), integral cross sections (ICSs) and the rate coefficients will be computed.
The paper is organized as follows. Section 2 introduces the theoretical approaches, such as ab initio calculations and the application of extrapolation. Section 3 introduces the analytic expression of CH2+(12A′) PES. Main topographical features are discussed in section 4. Section 5 describes the QCT calculations. Finally, the conclusion is presented in section 6.
2. Ab initio calculations and extrapolation scheme
The MRCI(Q)15 approach is one of the best methods to obtain the precise PESs. All ab initio calculations are performed at the MRCI(Q) level with the FVCAS16 as reference. MOLPRO 2012 (ref. 21) is a kind of program package about the quantum chemistry, in association with the Dunning et al.17,18 correlation-consistent basis sets have been applied during our work. This procedure involves 6 active orbitals (5A′ + 1A′′), with a total of 443 (166A′ + 177A′′) configuration state functions at AV5Z and AVQZ basis sets, respectively. In all 3255 ab initio grid points have been computed for C+–H2 channels, the region was defined by 1.2 ≤ RH2/a0 ≤ 4.4, 1.4 ≤ rC+–H2/a0 ≤ 10 and 0 ≤ γ/deg ≤ 90, while, for H–CH+, they cover geometries defined by 1.8 ≤ RCH+/a0 ≤ 3.6, 1.4 ≤ rH–CH+/a0 ≤ 10 and 0 ≤ γ/deg ≤ 180, R, r and γ are atom-diatom Jacobi coordinates for both channels. To get more precise energy points, the USTE19,20 method is adopted. During the calculations, the core is frozen and ignoring the relativistic effect.In order to carry out the extrapolation, electronic energy in the MRCI(Q) calculation is expressed by a sum of two terms19
| Ex = ECASx + Edcx, | (1) |
Using a two-point extrapolation program suggested by Karton and Martin(KM),22 the CAS energies are extrapolated to the CBS limit
| ECASx = ECAS∞ + B/Xα, | (2) |
The USTE protocol19,20 has been triumphantly implemented to extrapolate the dynamical correlation energies in MRCI(Q) calculations, which is extrapolated by the formula
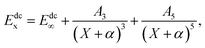 | (3) |
| A5 = A5(0) + cA35/4 | (4) |
With α = −3/8, c = −1.17847713 and A5(0) = 0.0037685459 are “universal-like” parameters.19 Eqn (3) could be converted to (E∞, A3) two-parameter rule, which has access to the actual extrapolation process.
3. Analytical potential energy function of CH2+(12A′)
The analytical function of CH2+(12A′) PES can be represented as a MBE23,24 form
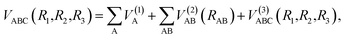 | (5) |
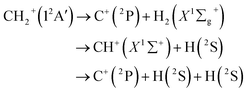 | (6) |
A. Two-body energy terms
The analytic energy function of the two-body terms VAB(2) for CH+(X1Σ+) and H2(X1Σg+) are imitated employing the Aguado and Paniagua25,26 approach, which the function for title diatomic systems can be represented as summation of the short-range and long-range potentials| V(2)AB = V(2)short + V(2)long | (7) |
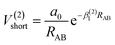 | (8) |
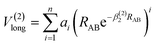 | (9) |
B. Three-body energy term
For the calculation of three-body term, the method of three-body distributed polynomial is adopted,27,28 which was applied to calculate ground and excited states of FH2,29 NH2 (ref. 30–32) and NH3.33,34
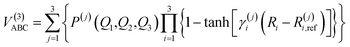 | (10) |
4. Features of the PES
Table 1 presents the results of Re, De, ωe, ωeχe, αe and Be of CH+(X1Σ+) and H2(X1Σg+) together with the other theoretical11,35–37,40–42 and experimental38–42 data. The equilibrium internuclear Re of CH+(X1Σ+) to be 2.135a0, which is only 0.002a0 shorter than the experimental result38 and 0.001a0 shorter than the latest result computed by Li et al.,11 while for the case of H2, all the results are 1.401a0,40,42−44 it shows a high precision. For the dissociation energies De, CH+(X1Σ+) differs from the theoretical and experimental results by less than 0.005 eV.11,39 For the H2 (X1Σg+) has dissociation energy De = 4.749 eV, this compares well with the corresponding theoretical values are De = 4.748 eV (ref. 11) and corresponding experimental values De = 4.478 eV.45 Overall, it can be concluded that the other spectroscopic constants are in good agreement with these literature results. Fig. 1 shows the potential energy curves (PECs) of CH+(X1Σ+) and H2(X1Σg+). In order to evaluate the quality of the fitting, we calculate the rmsd. The rmsd of CH+(X1Σ+) and H2(X1Σg+) PECs are 0.05 kcal mol−1 and 0.005 kcal mol−1, respectively. As a whole, it reveals a high quality fitting process. Shown in Fig. 1, the PECs at the CBS/USTE(Q,5) calculations nicely, showing accurate and smooth behavior both in short and long regions.| Re | De | ωe | ωeχe | αe | βe | |
|---|---|---|---|---|---|---|
| CH+(X1Σ+) | ||||||
| This work | 2.135 | 4.257 | 2861.948 | 59.629 | 0.447 | 14.311 |
| Theor.11 | 2.136 | 4.252 | 2853.027 | 58.515 | 0.489 | 14.201 |
| Theor.35 | 2.136 | 4.244 | 2851 | 58.1 | 0.489 | 14.199 |
| Theor.36 | 2.144 | — | 2849.03 | 66.448 | 0.490 | 14.094 |
| Theor.37 | 2.127 | 4.660 | 3111.0 | 38.44 | — | — |
| Exp.38 | 2.137 | 4.26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 39 |
2857.56 | 59.32 | 0.495 | 14.178 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| H2(X1Σg+) | ||||||
| This work | 1.401 | 4.749 | 4404.613 | 126.636 | 2.233 | 60.861 |
| Theor.40 | 1.401 | 4.748 | 4403.60 | 126.602 | 2.232 | 60.864 |
| Theor.41 | 1.403 | 4.748 | 4395.22 | 126.119 | 2.221 | 60.735 |
| Theor.42 | 1.401 | 4.711 | 4389.66 | 121.560 | 3.162 | 60.826 |
| Exp.43 | 1.401 | 4.478![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 45 |
4401.21 | 121.33 | 3.062 | 60.853 |
| Exp.44 | 1.401 | 4.476 | 4395.20 | 117.99 | 2.993 | 60.809 |
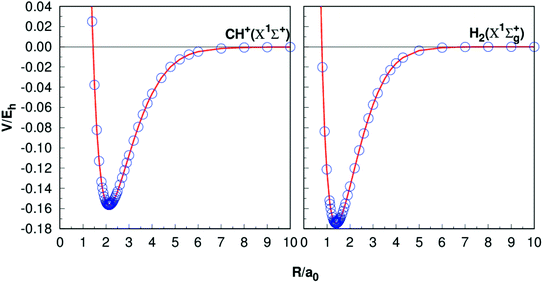 | ||
| Fig. 1 Potential energy curves of CH+(X1Σ+) and H2(X1Σg+). The circles indicate the CBS(Q,5) energies. | ||
Table 2 collects all known stationary points (geometry, energy and vibrational frequencies) of the new PES for ground state of CH2+. For better comparisons, the results of other theoretical and experimental work reports are also gathered in Table 2. A global minimum (GM) is found to local at θHC+H = 138.6°, R1 = 3.859a0 and R2 = R3 = 2.063a0 with the minimum energy −0.333Eh relative to the all dissociation asymptote (R1 represents the H2 interatomic separation, while R2 and R3 represent the two CH+ interatomic separations), its maximum deviation is only 0.004a0 for the CH+ bond length (R2 and R3) when compared to the data of the MRCI(Q)/AV6Z PES11 with the θHC+H = 141.0°, R1 = 3.896a0 and R2 = R3 = 2.067a0. Comparing with the theoretical works of Stoecklin and Halvick,6 R1 = 3.865a0 is 0.006a0 longer than our results. This compares well with the corresponding experimental values2,46 of θHC+H = 139.8°. For the harmonic frequencies, the PES from this work computes values of 3048 cm−1, 3272 cm−1 and 921 cm−1, there is good consistency with the theoretical results calculated by Brinkmann et al.47, which are 3011 cm−1, 3260 cm−1 and 965 cm−1, respectively. Table 2 also collects the attributes of a local minimum (LM) and three transition states: TS1(D∞h), TS2(C2v) and TS3(C∞v) barriers.
| Feature | R1 | R2 | R3 | θHCH | ΔVa | ω1 | ω2 | ω3 |
|---|---|---|---|---|---|---|---|---|
| a Relative to the C+ + H2 asymptote. | ||||||||
| Global minimum | ||||||||
| This work | 3.859 | 2.063 | 2.063 | 138.6 | −99.64 | 3048 | 3272 | 921 |
| Theor.11 | 3.896 | 2.067 | 2.067 | 141.0 | −99.54 | 2983 | 3283 | 957 |
| Theor.47 | 3.890 | 2.067 | 2.067 | 140.39 | — | 3011 | 3260 | 965 |
| Theor.6 | 3.865 | 2.075 | 2.075 | 137.3 | — | — | — | — |
| Exp.2,46 | 3.922 | 2.088 | 2.088 | 139.8 | — | — | 3133.4 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Local minimum | ||||||||
| LM(C2v) | 1.648 | 2.757 | 2.757 | 34.8 | −29.63 | 3254 | 1317 | 1220 |
| Theor.11 | 1.666 | 2.645 | 2.645 | 36.7 | −29.28 | 2937 | 1444 | 1307 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Transition state | ||||||||
| TS1(D∞h) | 4.099 | 2.050 | 2.050 | 180.0 | −97.13 | 3083 | 5489 | 1077i |
| Theor.11 | 4.127 | 2.064 | 2.064 | 180.0 | −96.54 | 2939 | 5431 | 1319i |
| TS2(C2v) | 2.106 | 2.362 | 2.362 | 52.9 | −21.44 | 2265i | 1766 | 1493 |
| Theor.11 | 2.170 | 2.435 | 2.435 | 52.9 | −23.41 | 2149i | 2179 | 1745 |
| TS3(C∞v) | 1.525 | 2.660 | 4.185 | 0.0 | −15.96 | 3557 | 664i | 1527 |
| Theor.11 | 1.511 | 2.645 | 4.156 | 0.0 | −16.89 | 3676 | 172i | 1769 |
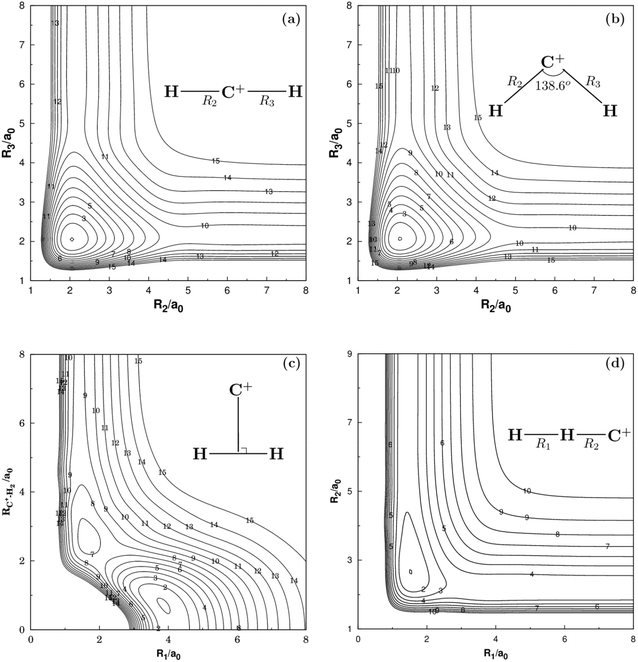
Fig. 2 and 3 show the main topographical characteristics of the new CH2+ PES computed in this work. Obviously, there is a correct and smooth behavior in the entire configuration space. The salient features of these contour maps corresponding to several important stationary points for the main reaction. Fig. 2(a) illustrates a contour map for linear [H–C–H]+ stretch. The significant characteristic of this map is that there is a TS1(D∞h) linear transition state at R2 = R3 = 2.050a0 with an energy of 878 cm−1 above the GM of CH2+ but still 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972 cm−1 below the energy of the C+ + H2 asymptote. This compares well with the MRCI(Q)/AV6Z PES,11 where the transition state is computed to local at R2 = R3 = 2.064a0 with an energy of 1050 cm−1 above the GM and 33
972 cm−1 below the energy of the C+ + H2 asymptote. This compares well with the MRCI(Q)/AV6Z PES,11 where the transition state is computed to local at R2 = R3 = 2.064a0 with an energy of 1050 cm−1 above the GM and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 765 cm−1 below the reactants asymptote. The corresponding infrared spectrum48 result for this linear barrier is 1089 cm−1.
765 cm−1 below the reactants asymptote. The corresponding infrared spectrum48 result for this linear barrier is 1089 cm−1.
Fig. 2(b) plots for the bond stretching in [H–C–H]+ which the angle is fixed at138.6°. It can be found from Fig. 2(b) that there is a deep well for CH2+ PES, which is GM. Fig. 2(c) shows the contour plots to the insertion of C+ + H2 reaction. In this figure, the stationary points which are corresponding to TS1(D∞h), TS2(C2v), the LM and the GM. As shown in Table 2, the LM is predicted to locate at R1 = 1.648a0 and R2 = R3 = 2.757a0, so agreeing with MRCI(Q)/AV6Z PES.11 The main characteristics of the new PES for collinear [H–H–C]+ stretch are shown in the contour map of Fig. 2(d). The collinear TS3(C∞v) is found to locate at R1 = 1.525a0 and R2 = 2.660a0 with the energy of 15.96 kcal mol−1. This compares well with the R1 = 1.511a0 and R2 = 2.645a0 and 16.89 kcal mol−1 for the MRCI(Q)/AV6Z PES.11
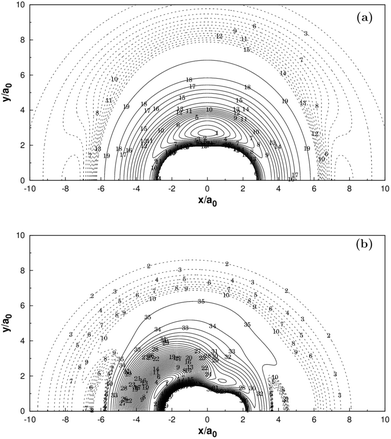
Panel (a) of Fig. 3 illustrates the contour plot of C+ atom moving around H2(X1Σg+) which the bond length at equilibrium geometry RH2 = 1.401a0. Diatoms follow the X-axis centered on the origin. In addition, the corresponding contour plot of H atom moving around a fixed CH+(X1Σ+) is shown in (b) of the same figure, which the bond length is fixed at equilibrium geometry RCH+ = 2.135a0, which is in very good agreement with the MRCI(Q)/AV6Z PES.11 The two plots clearly show that there is a smooth behavior both in the long and short range.
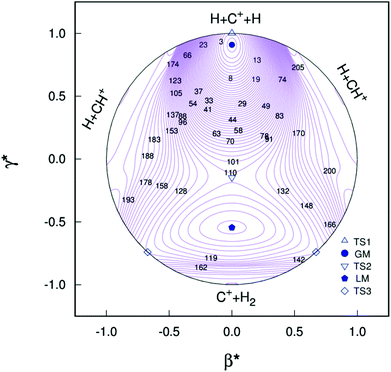
All the main topographical characteristics of CH2+ PES can be also viewed in a relaxed triangular plot49 using scaled hyper-spherical coordinates (γ* = γ/Q and β* = β/Q), where the Q, γ and β are written as
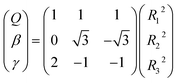 | (11) |
Clearly visible in Fig. 4 are all stationary points discussed above, which correspond to a GM, a LM and three transition states: TS1(D∞h), TS2(C2v) and TS3(C∞v) barriers.
Fig. 5 shows the minimum energy paths (MEPs) for H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) reaction obtained from both the new PES and MRCI(Q)/AV6Z PES11 for the collinear configuration ∠HC+H = 180°. The MEPs indicate the potential energy of CH2+ as a function for corresponding reaction coordinate of RCH+–RH2, RCH+ and RH2 as the internuclear distance between C+–H and H–H, respectively. As shown Fig. 5, there is a little barrier connecting a deep well and a shallow well. For the new PES, the relatively deeper well is found to locate at RCH+ = 2.660a0 and RH2 = 1.525a0 and the little barrier locates at RCH+ = 2.210a0 and RH2 = 2.972a0. The well depth and the barrier height are computed to be 1.184 eV and 0.016 eV. Comparing with the MRCI(Q)/AV6Z PES,11 the relatively deeper well locates at RCH+ = 2.645a0 and RH2 = 1.511a0 and the little barrier is found to locate at RCH+ = 2.196a0 and RH2 = 3.044a0. The well depth and the barrier height are computed to be 1.223 eV and 0.006 eV. Moreover, the reaction H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) is exoergic by 0.49 eV base on the both PESs. It can be seen from Fig. 5, the results of the two PESs are in good agreement.
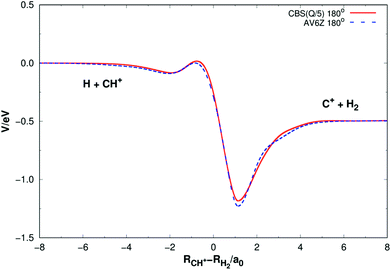 | ||
| Fig. 5 Minimum energy paths for H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) reaction obtained from both the new PES and MRCI(Q)/AV6Z PES11 as a function of RCH+–RH2. Collinear configuration ∠HC+H = 180°. | ||
5. Dynamics of H + CH+ reaction
On the new PES, QCT50,51 calculation was performed for the H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) reaction. In this work, we computed the ICSs, DCSs and rate constants. A total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories have been run for each of the collision energy. The time integration step is chosen to be 0.1 fs of classical motion equations, with H atom and the center of mass of the CH+ initially separated by 15.0 Å. The ICS is then written as
000 trajectories have been run for each of the collision energy. The time integration step is chosen to be 0.1 fs of classical motion equations, with H atom and the center of mass of the CH+ initially separated by 15.0 Å. The ICS is then written as
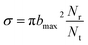 | (12) |
As shown Fig. 6, the ICSs are expressed as a collision energy function. For comparison our results with the quantum wave packet calculations11 and a modified version of the ABC52 quantum scattering code method have also been performed for the same reaction. We can find that the ICS based on our surface smaller than the results based on MRCI(Q)/AV6Z PES11 when the collision energy is less than about 40 meV. But when the collision energy is larger than about 40 meV, our results are consistency with quantum wave packet results. Overall, our results are reasonably good consistency with previous results.11,52
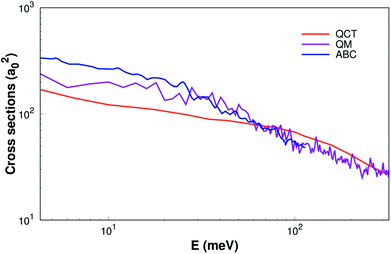 | ||
| Fig. 6 Integral cross sections of reaction of H(2S) + CH+(X1Σ+) → C+(2P)+ H2(X1Σg+) as a function of collision energy. The QM and ABC from Li11 and Schneider9 are shown as well. | ||
DCS is mainly used to study product and reagent relative velocity k–k′, which is the most common vector correlation. The global angular distributions of H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) reaction at collision energies of 10, 20, 30 and 40 kcal mol−1 based on the new PES are shown in Fig. 7. We can find that with the collision energies increase, the backward scattering phenomenon becomes more and more obvious. The enhanced phenomenon of backward scattering may be caused by an insertion reaction mechanism proposed by Pino et al.53
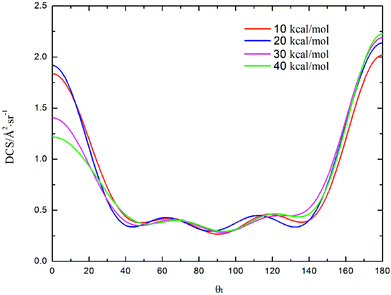 | ||
| Fig. 7 Differential cross section as a function of the scattering angle θt for the title reaction at the collision energy of 10, 20, 30 and 40 kcal mol−1. | ||
Finally, rate constants for the reaction H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+) are computed over the temperature range 10–1000 K by running QCT on the new PES of this work. By supposing a Maxwell–Boltzmann distribution on the collision energies, the rate constant is written as54
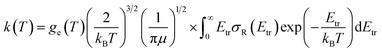 | (13) |
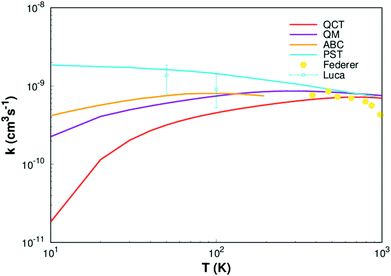 | ||
| Fig. 8 Rate constant for H(2S)+ CH+(X1Σ+) → C+(2P)+ H2(X1Σg+) reaction calculated in this work. Other theoretical works of Li,11 Warmbier and Schneider9 and Halvick et al.,7 as well as experimental data from Luca et al.55 and Federer et al.56 are also included. | ||
6. Conclusions
In our research process, we have constructed a high quality global PES for the ground state of CH2+(12A′) from MRCI ab initio energies based on the reference FVCAS wave function, both AVQZ and AV5Z basis sets subsequently extrapolated to the CBS limit. All known stationary points including geometries, energies and vibrational frequencies can be obtained, and all the results are consistency with the corresponding theoretical and experimental values. The consistency and accuracy of the CBS method have also been affirmed by comparing the MRCI(Q)/AV6Z PES.11 Finally, QCT calculation has been performed on H(2S) + CH+(X1Σ+) → C+(2P) + H2(X1Σg+), the ICS, DCS and the rate coefficients are computed in detail and compared to the MRCI(Q)/AV6Z and other PESs, as well as experimental values in the literature. In summary, the new PES built here can be used for any type of dynamic study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11474141), the Natural Science Foundation of Liaoning Province (Grant No. 20170540408) and the Science and Technology Plan Project of Shenyang City (Grant No. 17-231-1-06).References
- E. Herbst, Annu. Rev. Phys. Chem., 1995, 46, 27 CrossRef CAS.
- S. Willitsch and F. Merkt, J. Chem. Phys., 2003, 118, 2235 CrossRef CAS.
- C. F. Bender and H. F. Schaefer, J. Mol. Spectrosc., 1971, 37, 423 CrossRef CAS.
- T. Graber, E. P. Kanter, Z. Vager and D. Zajfman, J. Chem. Phys., 1993, 98, 7725 CrossRef CAS.
- A. Baer, M. Grieser, L. Knoll, J. Levin, R. Repnow, D. Schwalm, Z. Vager, R. Wester, A. Wolf and D. Zajfman, Phys. Rev. A, 1999, 59, 1865 CrossRef CAS.
- T. Stoecklin and P. Halvick, Phys. Chem. Chem. Phys., 2005, 7, 2446 RSC.
- P. Halvick, T. Stoecklin, P. Larrgaray and L. Bonnet, Phys. Chem. Chem. Phys., 2007, 9, 582 RSC.
- A. Zanchet, B. Godard, N. Bulut, O. Roncero, P. Halvick and J. Cernicharo, Astrophys. J., 2013, 76, 80 CrossRef.
- R. Warmbier and R. Schneider, Phys. Chem. Chem. Phys., 2011, 13, 10285 RSC.
- D. Herráez-Aguilar, P. G. Jambrina, M. Menéndez, J. Aldegunde, R. Warmbier and F. J. Aoiz, Phys. Chem. Chem. Phys., 2014, 16, 24800 RSC.
- Y. Q. Li, P. Y. Zhang and K. L. Han, J. Chem. Phys., 2015, 142, 124302 CrossRef CAS PubMed.
- L. Guo, Y. F. Yang, X. X. Fan, F. C. Ma and Y. Q. Li, Commun. Theor. Phys., 2017, 67, 549 CrossRef CAS.
- P. Sundaram, V. Manivannan and R. Padmanaban, Phys. Chem. Chem. Phys., 2017, 19, 20172 RSC.
- A. Faure, P. Halvick, T. Stoecklin, P. Honvault, M. D. Epée Epée, J. Z. Mezei, O. Motapon, I. F. Schneider, J. Tennyson, O. Roncero, N. Bulut and A. Zanchet, MNRAS, 2017, 469, 612 CrossRef CAS PubMed.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803 CrossRef CAS.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1985, 115, 259 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- D. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 2007, 126, 244105 CrossRef CAS PubMed.
- A. J. C. Varandas, J. Chem. Phys., 2007, 127, 114316 CrossRef CAS PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutzand others, MOLPRO Version 2012.1, 2012, see http://www.molpro.net.
- A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2006, 115, 330 CrossRef CAS.
- J. N. Murrell, S. Carter, S. C. Farantos, P. Huxley and A. J. C. Varandas, Molecular potential energy functions, Wiley, Chichester, 1984 Search PubMed.
- A. J. C. Varandas, Adv. Chem. Phys., 1988, 74, 255 CAS.
- A. Aguado and M. Paniagua, J. Chem. Phys., 1992, 96, 1265 CrossRef CAS.
- A. Aguado, C. Tablero and M. Paniagua, Comput. Phys. Commun., 1998, 108, 259 CrossRef CAS.
- A. J. C. Varandas and L. A. Poveda, Theor. Chem. Acc., 2006, 116, 404 CrossRef CAS.
- E. Martínez-Núñez and A. J. C. Varandas, J. Phys. Chem. A, 2001, 105, 5923 CrossRef.
- Y. Q. Li, Y. Z. Song and A. J. C. Varandas, Eur. Phys. J. D, 2015, 69, 22 CrossRef.
- Y. Q. Li and A. J. C. Varandas, J. Phys. Chem. A, 2010, 114, 9644 CrossRef CAS PubMed.
- Y. Q. Li, F. C. Ma and M. T. Sun, J. Chem. Phys., 2013, 139, 154305 CrossRef CAS PubMed.
- Y. Q. Li, J. C. Yuan, M. D. Chen, F. C. Ma and M. T. Sun, J. Comput. Chem., 2013, 34, 1686 CrossRef CAS PubMed.
- Y. Q. Li and A. J. C. Varandas, J. Phys. Chem. A, 2010, 114, 6669 CrossRef CAS PubMed.
- Y. Q. Li, Y. Z. Song, P. Song, Y. Z. Li, Y. Ding, M. T. Sun and F. C. Ma, J. Chem. Phys., 2012, 136, 194705 CrossRef CAS PubMed.
- Z. Biglari, A. Shayesteh and A. Maghari, Comput. Theor. Chem., 2014, 1047, 22 CrossRef CAS.
- R. R. Reddy, Y. Nazeer Ahammed, K. Rama Gopal and D. Baba Basha, J. Quant. Spectrosc. Radiat. Transfer, 2004, 85, 105 CrossRef CAS.
- K. Kowalski and P. Piecuch, J. Chem. Phys., 2001, 115, 643 CrossRef CAS.
- R. Hakalla, R. Kepa, W. Szajna and M. Zachwieja, Eur. Phys. J. D, 2006, 38, 481 CrossRef CAS.
- U. Hechtfischer, C. J. Williams, M. Lange, J. Linkemann, D. Schwalm, R. Wester, A. Wolf and D. Zajfman, J. Chem. Phys., 2002, 117, 8754 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 1996, 105, 3524 CrossRef CAS.
- Y. Z. Song, Y. Zhang, L. L. Zhang, S. B. Gao and Q. T. Meng, Chin. Phys. B, 2015, 24, 063101 CrossRef.
- C. L. Yang, Y. J. Huang, X. Zhang and K. L. Han, J. Mol. Struct.: THEOCHEM, 2003, 625, 289 CrossRef CAS.
- K. P. G. H. Huber, NIST Chemistry WebBook69, 2001, see http://webbook.nist.gov/chemistry.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules, Van Nostrand Reinhold, New York, 1979 Search PubMed.
- A. Balakrishnan, V. Smith and B. P. Stoicheff, Phys. Rev. Lett., 1992, 68, 2149 CrossRef CAS PubMed.
- R. M. Badger, J. Chem. Phys., 1935, 3, 710 CrossRef CAS.
- N. R. Brinkmann, N. A. Richardson, S. S. Wesolowski, Y. Yamaguchi and H. F. Schaefer III, Chem. Phys. Lett., 2002, 352, 505 CrossRef CAS.
- P. Jensen, M. Brumm, W. P. Kraemer and P. R. Bunker, J. Mol. Spectrosc., 1995, 172, 194 CrossRef CAS.
- A. J. C. Varandas, Chem. Phys. Lett., 1987, 138, 455 CrossRef CAS.
- K. L. Han, G. Z. He and N. Q. Lou, J. Chem. Phys., 1996, 105, 8699 CrossRef CAS.
- M. D. Chen, K. L. Han and N. Q. Lou, J. Chem. Phys., 2003, 118, 4463 CrossRef CAS.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128 CrossRef CAS.
- I. Pino, R. Martinazzob and G. F. Tantardini, Phys. Chem. Chem. Phys., 2008, 10, 5545 RSC.
- M. Karplus, R. N. Porter and R. D. Sharma, J. Chem. Phys., 1965, 43, 3259 CrossRef CAS.
- A. Luca, G. Borodi and D. Gerlich, Photonic, Electronic and Atomic Collisions, World Scientific, Singapore, 2006 Search PubMed.
- W. Federer, H. Villinger, F. Howorka, W. Lindinger, P. Tosi, D. Bassi and E. Ferguson, Phys. Rev. Lett., 1984, 52, 2084 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02228c |
| This journal is © The Royal Society of Chemistry 2018 |