Open Access Article
Open Access ArticleEffect of ionic size compensation by Ag+ incorporation in homogeneous Fe-substituted ZnO: studies on structural, mechanical, optical, and magnetic properties
Gaurav Bajpaia,
Tulika Srivastavaa,
N. Patrac,
Igamcha Moirangthemd,
S. N. Jhac,
D. Bhattacharyya c,
Sk Riyajuddin
c,
Sk Riyajuddin e,
Kaushik Ghosh
e,
Kaushik Ghosh e,
Dharma R. Basaulaf,
Mahmud Khanf,
Shun-Wei Liu
e,
Dharma R. Basaulaf,
Mahmud Khanf,
Shun-Wei Liu g,
Sajal Biring*g and
Somaditya Sen
g,
Sajal Biring*g and
Somaditya Sen *abg
*abg
aMetallurgical Engg. and Material Sciences, Indian Institute of Technology Indore, India. E-mail: sens@iiti.ac.in
bDepartment of Physics, Indian Institute of Technology Indore, India
cAtomic & Molecular Physics Division, Bhabha Atomic Research Centre, Mumbai, India
dAmity Institute of Nanotechnology, Noida, U.P., India
eInstitute of Nano Science and Technology, Mohali, Punjab, India
fDepartment of Physics, Miami University, Oxford, Ohio 45056, USA
gElectronic Engg., Ming Chi University of Technology, New Taipei City, Taiwan. E-mail: biring@mail.mcut.edu.tw
First published on 5th July 2018
Abstract
Substituting an ion of different size from that of the host element introduces lattice strain and defects. However, this mismatch may be significantly reduced by substituting an additional ion with a compensating size relative to the dopant. Such a double substitution might offer better solubility irrespective of the local distortions as well as the formation of defects in the valence states. Fe-substituted ZnO has been widely reported with conflicting results primarily arising from lack of chemical and structural homogeneity originating from preparation techniques, compositional fluctuations, and equivocal comprehension of actual solubility limits of the dopants. In this study, Ag ion has been incorporated in Fe-substituted ZnO to compensate the ionic size of Zn1−x[Fe0.8Ag0.2]xO (0 ≤ x ≤ 0.03125) by determining the solubility limit of the homogeneous material and their corresponding structural, mechanical, optical and magnetic properties have been investigated thoroughly. Co-substitution rearranges the lattice and leads to better crystal structures with tunable properties related to the amount of substitution.
Introduction
Zinc oxide (ZnO) is a II–VI group semiconductor with a direct band gap energy of 3.37 eV. It has a large exciton binding energy of 60 meV at room temperature. It has attracted much attention due to its unique properties and various technological applications. Applications include optics, optoelectronics, magneto-electronics, highly efficient blue LEDs and microwave devices.1–5 Nanostructured ZnO materials can also behave as a dilute magnetic semiconductor (DMSs). This has attracted great attention in the design of devices with spin based electronics (spintronics).1 There are many reports on ZnO doped with transition metal (TM) ions which point to many applications including room temperature ferromagnetic semiconductor nanomaterials and room temperature nano-lasers.6–10 Dietl et al.11 and Sato et al.12 indicate the possibility of room temperature ferromagnetism (RTFM) in transition metal doped ZnO, and there has been a great deal of research work carried out on ZnO based dilute magnetic semiconductors (DMS). There have been many claims from numerous researches that there is a presence of ferromagnetism in transition metals (Co, Mn, Fe, Ni, Cr, etc.) doped ZnO using defect related mechanisms, hole mediated exchange interactions, secondary phases, bound magnetic polarons (BMPs), clusters, organic capping agents, synthesis methods etc. at low and high Curie temperatures.13–20 However, others have claimed the contrary.21,22 Ferromagnetism in ZnO without doping of transition metal ions has also been discussed.23 Magnetic properties of multiple ions doped (or) co-doped ZnO nanomaterials are also studied.24,25 However, the real origin of ferromagnetism is still controversial as magnetism appears in pure ZnO, TM doped ZnO and non-TM doped ZnO.26There are various types of physical and chemical methods for synthesizing samples such as simple vapor transport and chemical co-precipitation method,27 solid state reaction method,28 radio-frequency (rf) magnetron sputtering technique,29 facile low temperature synthesis,30 sol–gel method,31–33 etc. Among these methods, sol–gel method is a simple, inexpensive and high yield method providing uniform homogeneous powders. In the present work, we have chosen Fe-substituted ZnO, Zn1−xFexO with 0 < x < 0.03125 (ZFO), to investigate the existence of magnetism in a homogenously substituted material. Silver (Ag) acts as an excellent neutralizer of native defect states in ZnO, thereby enhancing optical properties.27 In general, Fe-substituted ZnO lattice strain keeps on increasing due to growing differences in crystalline sizes of Zn and Fe. Also, there is a charge difference between the dopant and the host. Attempts are being made to minimize native defect states by substitution with Ag in a Fe-substituted ZnO lattice. A Zn1−x[Fe0.8Ag0.2]xO (ZFAO), with 0 ≤ x ≤ 0.03125, series is synthesized using a similar sol–gel method. There are lots of conflicting results about solubility limits of Fe doped ZnO nanomaterials. Some authors reported solubility limit of Fe in ZnO to be less than 4% using different methods.34,35 Hence, this study limits substitution to x ∼ 0.03125. Structural, local structural and magnetic properties have been investigated to rule out impurity and homogeneity factors.
Experimental
Zn1−xFexO (ZFO) and Zn1−x[Fe0.8Ag0.2]xO (ZFAO) (0 ≤ x ≤ 0.03125) nanoparticles have been synthesized by sol–gel process followed by solid state sintering. The choice of sol–gel route was because dopant/substituent elements can be distributed in a modified lattice in different concentrations in different regions due to improper mixing of constituent elements. This concentration gradient in the lattice will give rise to different functionalities at different regions. By mixing the constituent elements in the liquid phase and then letting them react, we have ensured the formation of the desired homogeneous solid solution.Dissolving ZnO powder (zinc oxide, Alfa Aesar, purity 99.9%) in HNO3 (Alfa Aesar, purity 70%) and adding appropriate number of dopants AgNO3 (silver nitrate, Alfa Aesar, purity 99.9%) and Fe(NO3)3·9H2O (ferric nitrate nonahydrate, Alfa Aesar, purity 99.9%), a homogeneous solution molar ratio of Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe (128
Fe (128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and molar ratio of Zn
1) and molar ratio of Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe : Ag (64
Fe : Ag (64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4: 1) was prepared by prolonged stirring. A solution of citric acid and glycerol were added to serve as fuel and gelling agent. Burnt gels were de-carbonized and denitrified at 450 °C for 6 h to get fine ZFO and ZFAO nanoparticles. These nanoparticles were further annealed at 600 °C for 2 h. From previous experience, a change in slope of Thermo Gravimetric Analysis (TGA) plots of as prepared samples was observed at ∼450–550 °C. The flatness of TGA data beyond this temperature did not vary for most of the samples, irrespective of the dopant/substituent. It is some internal atomic rearrangement, may be related to reduction of crystal defects and improved crystal quality that stabilizes structure beyond 550 °C. Hence, to avoid such issues of instability, a choice of annealing the samples at 600 °C was taken. It has also been reported that the intensity of the UV peak becomes stronger after annealing at ∼600 °C.36–38 Also oxygen defects related to green emission reduces, indicating much better crystal quality.39,40 Similar results were reiterated on previously reported series from this lab. Hence, samples were annealed at 600 °C to maintain uniformity in crystal quality of all samples.
4: 1) was prepared by prolonged stirring. A solution of citric acid and glycerol were added to serve as fuel and gelling agent. Burnt gels were de-carbonized and denitrified at 450 °C for 6 h to get fine ZFO and ZFAO nanoparticles. These nanoparticles were further annealed at 600 °C for 2 h. From previous experience, a change in slope of Thermo Gravimetric Analysis (TGA) plots of as prepared samples was observed at ∼450–550 °C. The flatness of TGA data beyond this temperature did not vary for most of the samples, irrespective of the dopant/substituent. It is some internal atomic rearrangement, may be related to reduction of crystal defects and improved crystal quality that stabilizes structure beyond 550 °C. Hence, to avoid such issues of instability, a choice of annealing the samples at 600 °C was taken. It has also been reported that the intensity of the UV peak becomes stronger after annealing at ∼600 °C.36–38 Also oxygen defects related to green emission reduces, indicating much better crystal quality.39,40 Similar results were reiterated on previously reported series from this lab. Hence, samples were annealed at 600 °C to maintain uniformity in crystal quality of all samples.
X-ray diffraction (XRD) patterns of samples were obtained using a Bruker D2 Phaser X-ray diffractometer. Lattice parameters were calculated from Rietveld refinement of XRD data using GSAS Software. Surface morphology and chemical homogeneity have been investigated by Field Emission Scanning Electron Microscopy and Energy Dispersive X-ray Spectroscopy using a Carl Zeiss FESEM Supra-55 Spectrometer.
XANES and EXAFS measurements of samples have been carried out at room temperature at Energy Scanning EXAFS beamline (BL-9) at INDUS-2 Synchrotron source (2.5 GeV, 100 mA), Raja Ramanna Centre for Advanced Technology (RRCAT), Indore, India.41,42 Photon energy range of the beamline is 4–25 keV. Beamline optics consists of a Rh/Pt coated collimating meridional cylindrical mirror used for collimation of beam. Collimated beam is monochromatized by a Si (111) (2d = 6.2709 Å) double crystal monochromator (DCM). The Rh/Pt mirror is used prior to the DCM for higher harmonic rejection. Second crystal of DCM is a sagittal cylindrical crystal, used for horizontal focusing of beam. Another Rh/Pt coated bendable post mirror facing downwards is used for vertical focusing of beam at sample position. EXAFS measurements at Zn K-edge (9659 eV) were performed in transmission mode while those at Fe K-edge (7112 eV) were performed in fluorescence mode. It should be noted that measurements at Ag K-absorption edge (25.514 keV) could not be done due to limitations of the above beamline (works in the range of 5–25 keV).
For data collection in transmission mode two ionization chambers, each of 30 cm length have been used. First and second ionization chambers measure incident flux (I0) and transmitted flux (It) 70–90%, respectively. X-ray absorption co-efficient is determined using relation, μ = ln(I0/It). Appropriate gas mixtures with optimized pressures were chosen to achieve 10–20% and 70–90% absorption in first and second ionization chambers, respectively, to improve signal to noise ratio. Rejection of higher harmonics of X-ray source was performed by 30% detuning of second crystal of DCM using piezo motor. To obtain a proper edge jump, samples of appropriate weight were taken in powder form and were pelletized (diameter ∼ 15 mm) by mixing with 100 mg cellulose and were kept in a Teflon tape. For EXAFS measurement in fluorescence mode, samples were placed at 45° to incident X-ray beam. Fluorescence signal (If) is detected using a Si drift detector placed at 90° to incident beam. First ionization chamber was placed prior to sample to measure incident beam (I0). X-ray absorption co-efficient of sample was determined by μ = (If/I0), and spectra were obtained as a function of energy by scanning a specific energy range using an appropriate monochromator.
Vickers micro-hardness measurements were carried out at room temperature using a digital micro-hardness tester (VHL) on pellets sintered at 600 °C. Load ∼0.249–4.9 N was applied for 10 seconds. A diamond pyramid with square bottom with 136° angle between opposite surfaces has been used as indenter.
Optical transmittance data was obtained using Shimadzu UV-vis spectrometer (model UV-2600). Room-temperature photoluminescence (PL) of ZFO and ZFAO samples was performed using Dongwoo-Optron DM 500i spectrometer (excitation wavelength 325 nm).
Magnetic field dependent magnetization of the samples was examined using a Quantum Design Physical Property Measurement System (PPMS).
Results and discussion
Structural analysis
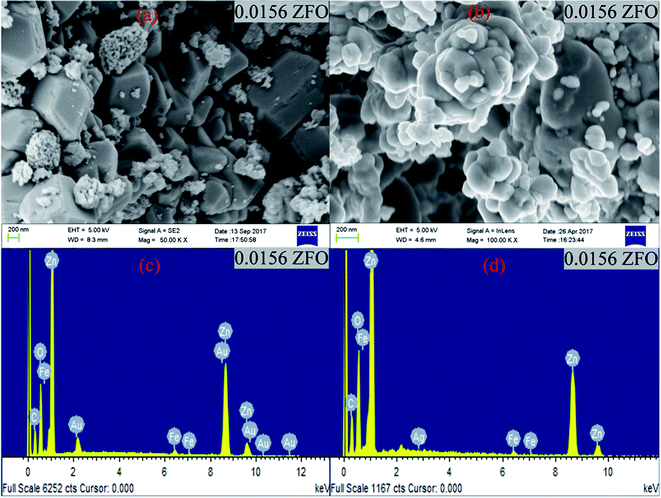 | ||
| Fig. 1 (a) and (b) FESEM images of 0.0156 ZFO & 0.0156 ZFAO, (c) and (d) EDX of 0.0156 ZFO & 0.0156 ZFAO. | ||
| Sample | Particle Size (nm) | Sample | Particle Size (nm) |
|---|---|---|---|
| Pure ZnO | 50.158 ± 0.00021 | Pure ZnO | 50.158 ± 0.00021 |
| 0.0078 ZFO | 74.256 ± 0.00034 | 0.0078 ZFAO | 70.235 ± 0.00037 |
| 0.0156 ZFO | 82.671 ± 0.00056 | 0.0156 ZFAO | 65.354 ± 0.00037 |
| 0.0234 ZFO | 72.245 ± 0.00048 | 0.0234 ZFAO | 59.738 ± 0.00061 |
| 0.03125 ZFO | 68.164 ± 0.00058 | 0.03125 ZFAO | 55.535 ± 0.00029 |
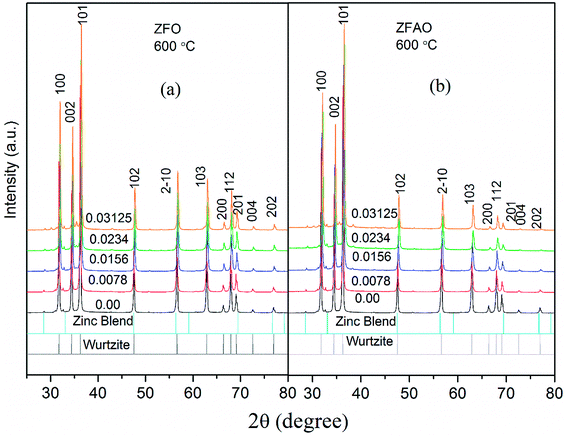
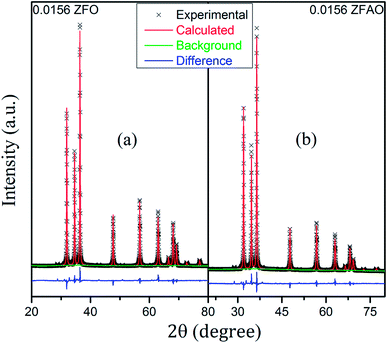
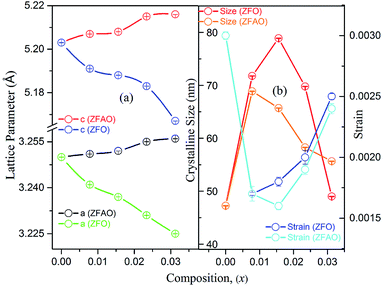
Rietveld refinement of XRD data using GSAS software reveals that lattice parameters, ‘a’ and ‘c’ decrease in ZFO with increasing x, but increase in ZFAO samples [Fig. 4(a)]. Using Scherrer formula,
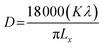 | (1) |
Lattice strain (S) was calculated from refinement parameters using formula equation:
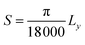 | (2) |
In ZFAO, strain initially decreases for x < 0.0156 but increases for x > 0.0156. However, in ZFO, strain initially decreases for x < 0.0078 but thereafter increases.
For lower substitution x < 0.0156, strain decreases and thereafter increases for x > 0.0156. As a result of decreasing and increasing strain in the lattice crystallinity is affected. A longer range of structural order is expected for a better crystalline sample with lesser strain.43 Hence a reverse trend of strain and crystallite size is observed in the samples. It is to be noted that strain reduces and then enhances both for ZFAO and ZFO. Note that the ratio of Fe3+ to Ag+ is ∼4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Hence 3 out of 4 Fe ions atoms will add to the extra charge of the lattice. This will invite more oxygen to the lattice. The latent oxygen defects will be annihilated by such addition initially. But growing oxygen population will then add up to generation of strain for higher substitution after neutralization of latent O defects. O interstitial starts to form. This will create extra pressure leading to a strained lattice. The increased pressure in ZFAO results in the increase of lattice parameters in all directions in spite of ionic size compensation by Fe/Ag combination. However in ZFO samples, this cannot happen due to the size difference of Fe3+(IV) (∼0.63 Å) and Zn2+(IV) (∼0.74 Å). In ZFO samples the latent oxygen defect compensation is faster and starts at x = 0.0078.
1. Hence 3 out of 4 Fe ions atoms will add to the extra charge of the lattice. This will invite more oxygen to the lattice. The latent oxygen defects will be annihilated by such addition initially. But growing oxygen population will then add up to generation of strain for higher substitution after neutralization of latent O defects. O interstitial starts to form. This will create extra pressure leading to a strained lattice. The increased pressure in ZFAO results in the increase of lattice parameters in all directions in spite of ionic size compensation by Fe/Ag combination. However in ZFO samples, this cannot happen due to the size difference of Fe3+(IV) (∼0.63 Å) and Zn2+(IV) (∼0.74 Å). In ZFO samples the latent oxygen defect compensation is faster and starts at x = 0.0078.
X-ray absorption near edge structure (XANES)
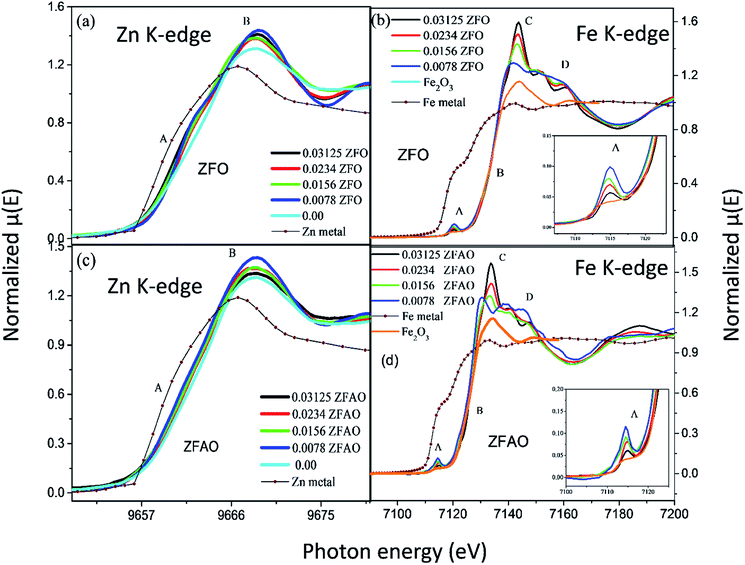
Significant increase in white line intensity labeled as point ‘B’ for both ZFO/ZFAO samples have been observed compared to that of pure ZnO. This mainly arises due to the charge transfer of Fe and Ag, suggesting significant increase in oxygen vacancies/holes near Zn sites due to substitution which is also reflected from EXAFS results.45
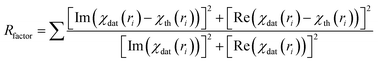 | (3) |
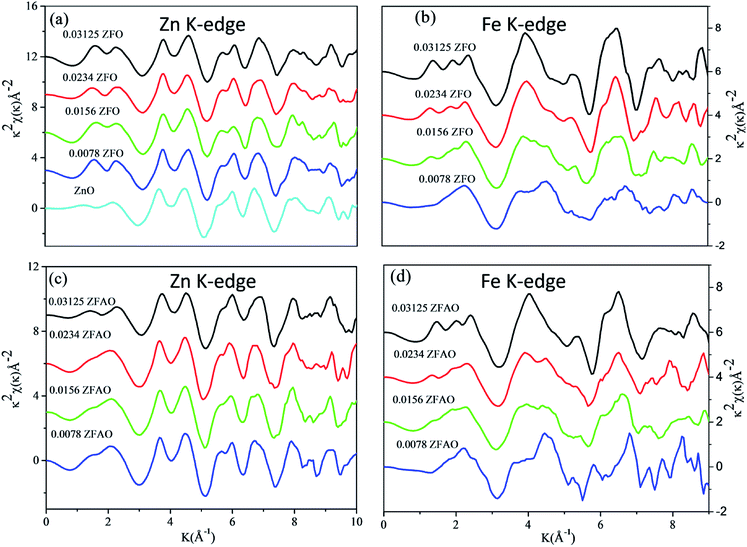 | ||
| Fig. 6 k2 weighted χ(k) spectra at (a) Zn K-edge of ZFO, (b) Fe K-edge of ZFO, (c) Zn K-edge of ZFAO and (d) Fe K-edge of ZFAO. | ||
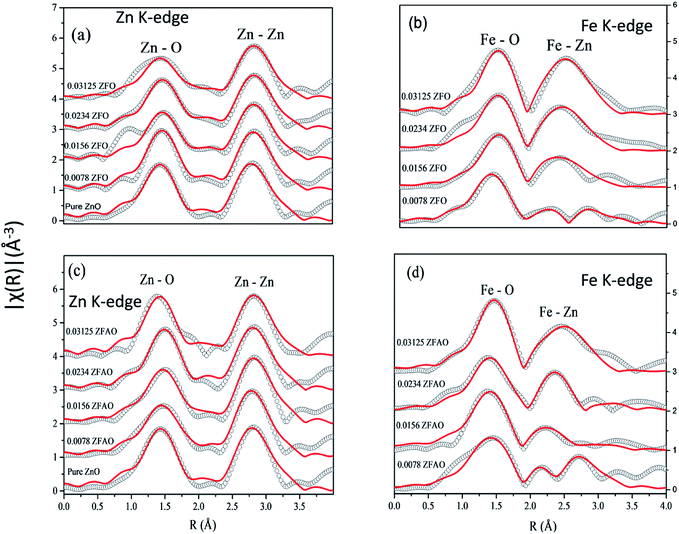 | ||
| Fig. 7 Theoretically generated χ(R) vs. (R) plot fitted with experimental data (a) Zn K-edge of ZFO, (b) Fe K-edge of ZFO, (c) Zn K-edge of ZFAO and (d) Fe K-edge of ZFAO. | ||
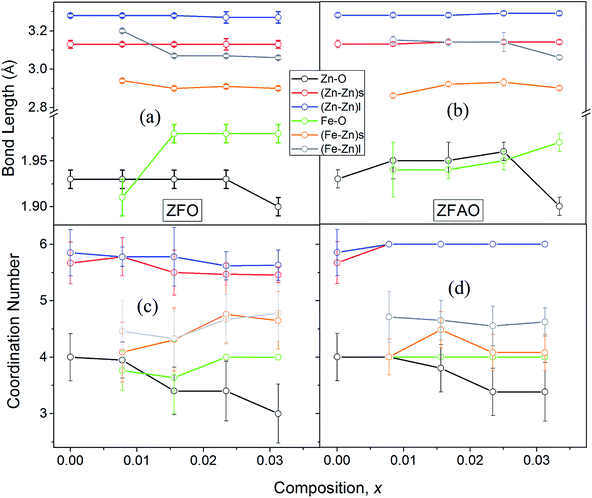
A notable difference is observed between CN values of Zn–Zn and Fe–Zn shells. CN values are lower by 15–30% for Fe–Zn than Zn–Zn paths. This implies that there is ample Zn loss in neighborhood of Fe atoms. Loss is less in case of higher substitutions. At the same time it is observed that both (Fe–Zn)s and (Fe–Zn)l bond lengths are shorter than the corresponding (Zn–Zn)s and (Zn–Zn)l counterparts. Shorter bonds are ∼6–7% while longer ones are 2–7% lesser. This may arise due to availability of space from longer Fe–O bonds than Zn–O. All bond lengths are shorter than bulk materials.54,55 Values of Zn–O and (Zn–Zn)s CN's and bond lengths reported here are lower than values reported by Jeong et al. (∼1.98 Å and ∼3.20 Å).50 (Zn–Zn)l bond lengths are higher than previously reported results.51–53 Values of σ2 Zn–O and Zn–Zn paths for ZFO samples are lower than that of Fe–O and Fe–Zn paths. However, σ2of Zn–O and Zn–Zn paths appears to increase nominally with substitution while for Fe–O and Fe–Zn paths it shows decrements in ZFO from pure samples. Hence, disorder is lesser at Zn-site than Fe-site but increases with substitution at the neighborhood of Zn-sites but decreases near Fe-sites. This implies a incremental structural distortion throughout the entire lattice along with condensation of a different structure at local points of vicinity of Fe. This is an indication that structural changes are prone beyond x = 0.03125. Such changes may also happen upon provision of thermal energy. Difference between two Zn–Zn bond lengths suggests elongation and contraction of bonds in two different orientations to maintain shell volume. This is a big contrast with previous studies where expansion of bonds happens for all atomic pairs.56
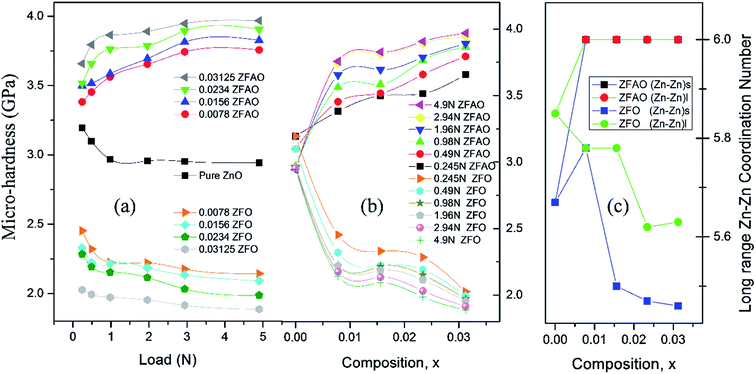
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(136°/2) = d2/1.8544; where d (μm), calculated using a microscope, is length of diagonals of the trace created by indentation for a definite load. Vickers micro-hardness, Hv, is calculated using, Hv = (1854.4F/d2) (GPa). In ZFO samples hardness decreased with increasing load [Fig. 9(a)]. This is known as indentation size effect (ISE). Hardness decreased with increasing Fe-substitution as well [Fig. 9(b)]. However, for ZFAO samples a reverse nature is observed. Hardness increased with increasing load and with substitution. This is generally termed as reverse indentation size effect (RISE). Hardness may be related to packing of atoms in a lattice. If a lattice is well packed and not with vacancies then with applied pressure chances of rearrangements are less. However, in presence of vacant sites rearrangements are possible. An estimation of vacant sites can be done from coordination number of constituent elements. It was discussed that CN of Zn–Zn paths reduced with substitution in case of ZFO, while for ZFAO, CN reached a maximum of 6 for both the short and long paths [Fig. 9(c)]. Hence it is evident that in case of ZFAO the lattice becomes extremely regular and hardness increases whereas in ZFO, excess oxygen ions create Zn vacancies which decrease hardness. With increasing load ZFO lattice becomes more and more deformed leading to breaking of bonds and therefore reduction of hardness. On the other hand, in absence of relocation sites ZFAO lattice becomes more compact and difficult to be compressed, thereby increasing hardness.
sin(136°/2) = d2/1.8544; where d (μm), calculated using a microscope, is length of diagonals of the trace created by indentation for a definite load. Vickers micro-hardness, Hv, is calculated using, Hv = (1854.4F/d2) (GPa). In ZFO samples hardness decreased with increasing load [Fig. 9(a)]. This is known as indentation size effect (ISE). Hardness decreased with increasing Fe-substitution as well [Fig. 9(b)]. However, for ZFAO samples a reverse nature is observed. Hardness increased with increasing load and with substitution. This is generally termed as reverse indentation size effect (RISE). Hardness may be related to packing of atoms in a lattice. If a lattice is well packed and not with vacancies then with applied pressure chances of rearrangements are less. However, in presence of vacant sites rearrangements are possible. An estimation of vacant sites can be done from coordination number of constituent elements. It was discussed that CN of Zn–Zn paths reduced with substitution in case of ZFO, while for ZFAO, CN reached a maximum of 6 for both the short and long paths [Fig. 9(c)]. Hence it is evident that in case of ZFAO the lattice becomes extremely regular and hardness increases whereas in ZFO, excess oxygen ions create Zn vacancies which decrease hardness. With increasing load ZFO lattice becomes more and more deformed leading to breaking of bonds and therefore reduction of hardness. On the other hand, in absence of relocation sites ZFAO lattice becomes more compact and difficult to be compressed, thereby increasing hardness.
α = αo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(hν/Eu) exp(hν/Eu)
| (4) |
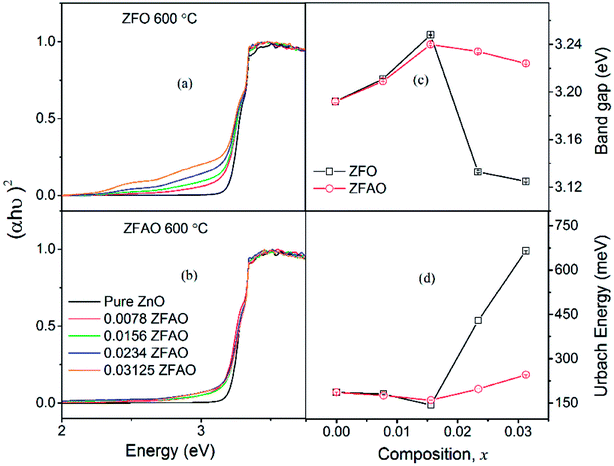 | ||
| Fig. 10 (a) and (b) Optical transmittance of ZFO & ZFAO, (c) and (d) bandgap and Urbach energy versus composition (x). | ||
Urbach energy decreases with increase in ZFO and ZFAO incorporation up to x = 0.0156, thereafter increases [Fig. 10(d)]; a trend commensurate with bandgap. However, from our EXAFS studies such a behavior is hard to explain. Hence, most probably these defects may be related to new electronic states created near the band edge by dopant ions. Note that the lattice becomes more crystalline with Fe/Ag substitution. This is evident from the strain values calculated from the XRD data as discussed before. Urbach energy is related to lattice strain. Hence, a commensurate behavior between strain and Urbach energy is observed.
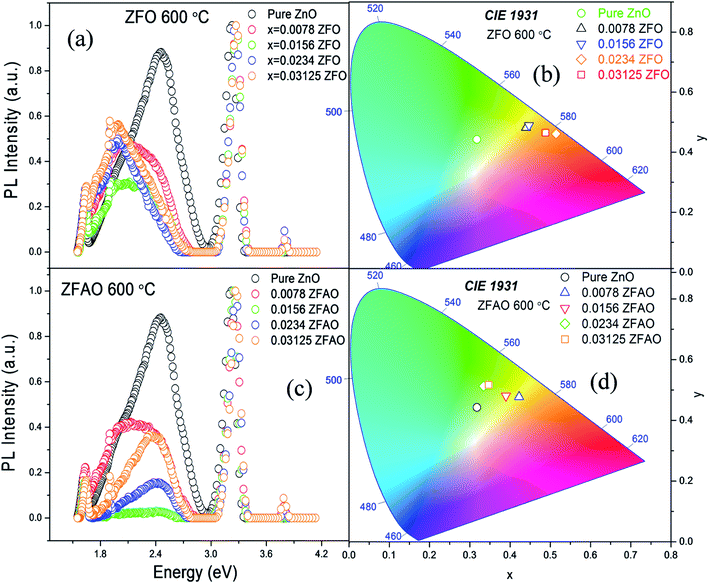
Room temperature photoluminescence (PL) [Fig. 11(a) and (c)] was studied to understand role of Ag+ and Fe3+ ion in ZnO structure. A sharp NBE centered at ∼382 nm is observed. A wider and broader DLE extending from 450 nm to 750 nm is observed in all samples. Relative intensity of DLE keeps on decreasing with substitution while NBE increases. Fig. 12(c) shows the intensities of NBE and DLE that were calculated conventionally. A marked increase in I(NBE)/I(DLE) ratio from 1.13424 for x = 0.00 to 3.35 for x = 0.0156 is observed in Fe substituted samples and also same trend follows in Fe/Ag samples. For x > 0.0156 the ratio decreases in both ZFO and ZFAO [Fig. 12(c)]. An increase in I(NBE)/I(DLE) ratio is related to decrement of defect states62 and increment in optical transparency of ZnO nano-particles.
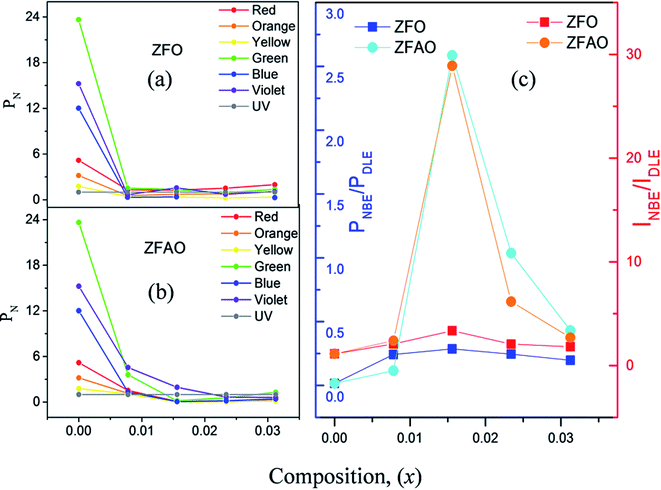 | ||
| Fig. 12 (a) and (b) PN of ZFO & ZFAO with respect to composition (x), (c) INBE/IDLE and PNBE/PDLE with respect to composition (x). | ||
Note that DLE of pure ZnO is centered at 500 nm whereas other Fe & Fe/Ag substituted samples are centered at ∼530 to 560 nm for x = 0.0078 to x = 0.03125: a clear red shift in ZFO and ZFAO also. Red shift is more in ZFO than ZFAO. The ZFO PL data (plotted using 1931 standard) further confirms this red shift behavior [Fig. 11(b)]. The values are (0.3177, 0.4427) for pure, (0.4398, 0.4816) for x = 0.0078, (0.447, 0.4893) for x = 0.0156, (0.514, 0.4613) for x = 0.0234 and (0.488, 0.4652) for x = 0.03125. Decrement of green emission up to x = 0.0156 followed by an enhancement for higher substitution is observed. Chromaticity coordinates of ZFAO PL data (on 1931 standard) [Fig. 11(d)], can be expressed as (0.3177, 0.4427), (0.4224, 0.4774) (0.3898, 0.4807), (0.3342, 0.5123) and (0.3469, 0.5168) in the same order.
PL spectra including both broad DLE as well as NBE were de-convoluted into several peaks belonging to individual colors. Areas were calculated of each fitted peak and added up in groups, AUV, AV, AB, AG, AY, AO, AR for six color ranges corresponding to UV, violet, blue, green, yellow & orange-red. Contribution of each component color in total spectrum was estimated by calculating color fraction, Pcolor, defined by Pcolor = Acolor/Atotal, where, Atotal = ΣAcolor, the total area under the spectrum. Hence, for each sample ΣPcolor = 1. Various defect states in the sample's PL spectrum may be estimated from the color fraction, Pcolor. However, for different compositions Atotal varies. Although the samples were prepared with care, the total intensity of the PL spectrum may differ for various reasons. Therefore, the sample preparatory factors must be normalized. Being significantly small, the difference in the bandgap and Urbach energies may be neglected. Thus, the total UV emission may be normalized to one and the contribution of all colors from other transitions can be estimated by defining the normalized color fraction, PN = Pcolor/PUV for each sample.
The NBE of pure ZnO is a contribution of three peaks: UV (3.16 eV [for donor acceptor pair] and 3.25 eV [due to free excitons (FX)]) and violet (3.05 eV); while DLE is a contribution of 9 peaks: blue (2.69 eV), green (2.25 eV, 2.4 eV, and 2.54 eV), yellow (2.08 eV and 2.15 eV) and orange-red range (1.85 eV, 1.95 eV, and 2.02 eV). Similarly, for substituted samples each color range is composed of similar sets of peaks contributing to the same ranges as above.
From composition dependence of PN, amount of green emission is observed to decrease with increasing substitution up to x = 0.00156 in Fe substituted samples; thereafter PN increases [Fig. 12(b)]. Similar to I(NBE)/I(DLE), the ratio PNBE/PDLE initially increases after that it decreases. [Fig. 12(c)].
Green and red emission decreases in PN vs. x plots upto x = 0.0156 followed by increase beyond x = 0.0156. This hints at reduction and increment of oxygen vacancy and interstitials with increasing substitution. On the other hand, a similar trend of reduction followed by enhancement of blue and violet emissions indicates similar facts about Zn vacancies and interstitials. Thus Ag+ and Fe3+ substitution, results in initial reduction of defect states, created by Zn and O vacancies and interstitials, up to x = 0.0156, followed by increase of all types of defects for x > 0.0156. Note that this trend of decrease and increase of defects states is similar to trends in strain and also Urbach energy of these materials.
We observe VZn/VO in pure ZnO centered at ∼2.5 eV (wavelength 500 nm). When Fe3+ incorporates in lattice in ZFO, there is red shift in photoluminescence spectra, that means, reduction in oxygen vacancy but enhances oxygen interstitial defects in that lattice. This implies that lattice is strained and defects are created in system, also supported by EXAFS study. On the other hand, in ZFAO there is size compensation of dopants in lattice and defects are reduced. Hence, Ag+ plays an important role in reducing defects.
Crystal radius of Ag+(IV) (∼1.14 Å) is bigger than Zn2+(IV) (∼0.74 Å). On the other hand, Ag+, having lower charge, tends to retain less oxygen compared to Zn2+. In Ag-substituted ZnO it has been reported that oxygen defects decrease with Ag+ incorporation. This is in contrary to what is expected for a substitution by a lesser charged Ag+. This may happen if Ag+ions are incorporated as interstitials.63 Interstitial Ag+ adds extra charge to lattice. This may attract extra oxygen, thereby reducing oxygen defects. However, Ag+ being larger in size, lattice cannot accommodate without getting distorted. Hence, interstitials lead to defects and voids.
On the other hand, Fe3+(IV) (∼0.63 Å) is smaller than Zn2+. Smaller size and extra positive charge of Fe3+ as compared to Zn2+ attract more oxygen to lattice. Hence, for Fe-substituted ZnO reports show decrement of oxygen defects. However, excess oxygen may lead to oxygen interstitials and thereby lattice distortion. Thus, both Fe3+ and Ag+ individually, tend to reduce oxygen defects initially. However, increased incorporation of dopant creates lattice distortion and thereby impurity phase.
In Zn(1−x)Fe(0.8x)Ag(0.2x)O, i.e. Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ag = 4
Ag = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, was intentionally chosen, so that the combination of bigger Ag+ and smaller Fe3+ ions can result in an equivalent crystal radii of Zn2+. This helped maintain solubility of dopant elements in the compositions. However, as the proportion of Fe3+ is more than Ag+ ions, effective added charge is positive. This extra charge helps attract more oxygen to the lattice. Note that the unit cell lattice parameters and volume increase continuously with substitution, in spite ionic size compensation. This is due to addition of more and more oxygen. Initially this takes care of existing oxygen defects inherent in ZnO, which reduces defects and thereby reduce strain and Urbach energy. However, when such defects are compensated, extra oxygen adds as O-interstitials. This further creates Zn vacancies and thereafter structural distortions, causing strain and increase in Urbach energy. Also, Fe-3d electrons hybridize with O-2p electrons and forms intermediate states in between bands64,65 These defect states also contribute to PL spectrum and thereby have optoelectronic implications.
1, was intentionally chosen, so that the combination of bigger Ag+ and smaller Fe3+ ions can result in an equivalent crystal radii of Zn2+. This helped maintain solubility of dopant elements in the compositions. However, as the proportion of Fe3+ is more than Ag+ ions, effective added charge is positive. This extra charge helps attract more oxygen to the lattice. Note that the unit cell lattice parameters and volume increase continuously with substitution, in spite ionic size compensation. This is due to addition of more and more oxygen. Initially this takes care of existing oxygen defects inherent in ZnO, which reduces defects and thereby reduce strain and Urbach energy. However, when such defects are compensated, extra oxygen adds as O-interstitials. This further creates Zn vacancies and thereafter structural distortions, causing strain and increase in Urbach energy. Also, Fe-3d electrons hybridize with O-2p electrons and forms intermediate states in between bands64,65 These defect states also contribute to PL spectrum and thereby have optoelectronic implications.
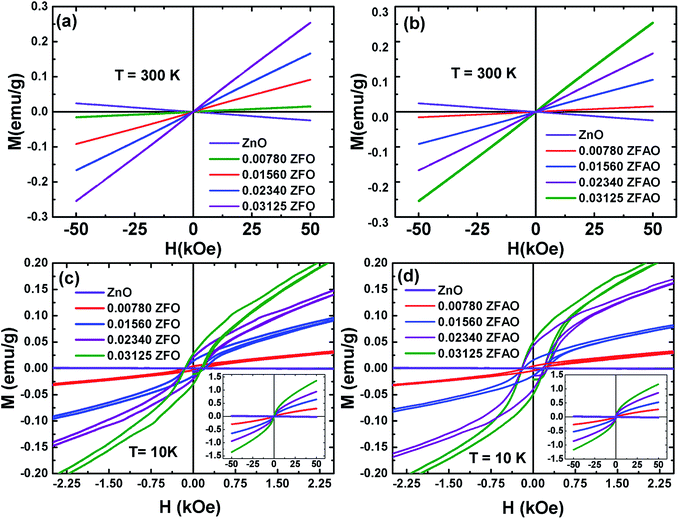 | ||
| Fig. 13 Hysteresis loops (M–H) of ZFO & ZFAO measured at 300 K and 10 K. The insets of (c) and (d) show the complete hysteresis loops measured between –50 kOe and 50 kOe. | ||
The hysteresis loops of the substituted samples measured at 10 K [shown in Fig. 13(c) and (d)] shows that the magnetization is not saturated even at 50 kOe for any of the samples. However, a close look at the low field regions of the loops show coercivity (Hc) and remanence magnetization (Mr) indicating the presence of weak ferromagnetic interactions in the compounds. The Hc linearly increase from ∼132 Oe (x = 0.0078) to ∼148 Oe (x = 0.03125) for ZFO and from ∼143 Oe (x = 0.0078) to ∼200 Oe (x = 0.03125) for ZFAO. Although Hc in both series are reasonably significant, the Mr for the samples are small. In case of ZFO, a maximum Mr of 0.028 emu g−1 is observed for x = 0.03125 and for the same concentration a maximum Mr of 0.05 emu g−1 is observed in ZFAO. The magnetization at 50 kOe range between 0.3 emu g−1 and 1.36 emu g−1 for ZFO and between 0.27 emu g−1 and 1.18 emu g−1 for ZFAO.
A ferromagnetic exchange interaction between Fe3+ and other ions may give rise to ferromagnetic properties observed in our samples. A longer ferromagnetic exchange can be mediated by polaronic percolation of bound magnetic polarons formed by point defects like oxygen vacancies.69,70 Ag incorporation in ZFAO increases the oxygen vacancies and therefore they exhibit relatively stronger ferromagnetism (as evident in their higher Hc and Mr) in comparison to ZFO. These observations suggest that although presence of ferromagnetism is evident in both ZFO and ZFAO at 10 K, superparamagnetism is dominant in the materials. Such coexistence of ferromagnetism and superparamagnetism has been observed by other researchers in Co-doped ZnO samples.67
Goktas et al. have reported RTF in Fe and Al co-doped ZnO nanostructured thin films.71 The RTF in their samples significantly depended on the annealing temperature. Goktas et al. also studied a series of Zn1−xFexO films and observed ferromagnetism at 5 K an 100 K in the film with x = 0.2.72 At higher temperatures the film showed diamagnetic behavior. For x ≤ 0.10 all their samples showed paramagnetic behavior at all temperatures. Zn0.95Co0.05O nanoparticles prepared by sol–gel method demonstrate paramagnetism at room temperature, while thin films of same composition deposited by pulsed laser deposition method showed superparamagnetic behavior at room temperature.67,68 These observations and proposed explanations mentioned in the literature suggest that the magnetic properties of substituted ZnO are extremely sensitive to defects that may vary with growth conditions. Even in absence of defects, a long-range ferromagnetic coupling may happen from interactions mediated by delocalized Zn-s states resulting in super- and double-exchange.73 As discussed earlier, Ag+ ions help to minimize zinc interstitial defects and stabilize structure. Better structural uniformity in ZFAO than ZFO may help in a better long range ferromagnetic coupling. Also, VO seems to be reduced due to extra charge of Fe3+. Hence, in these samples it seems a long range ferromagnetic coupling mediated through a hybridization involving Zn-s states may be instrumental to yield a very weak ferromagnetism in substituted samples which enhances upon better structural ordering.
Conclusion
Structural, optical and magnetic properties of sol–gel prepared hexagonal, wurtzite Zn(1−x)Fe(x) O and Zn(1−x)Fe(0.8x)Ag(0.2x)O nanoparticles, of size ∼48–80 nm have been studied. Substituting of Fe results in the decrease of lattice constants in ZFO while the lattice expands due to the co-doping of Fe and Ag in ZFAO. EXAFS studies confirm changes in local coordination of Zn atoms, which affects mechanical properties of these materials. While Fe-substitution reduces hardness of ZFO, Ag addition to the Fe-substituted lattice further strengthens the lattice. This may be related to excess oxygen addition to lattice being attracted by additional charge of Fe3+. For both systems, defects, strain and Urbach energy reduce with substitution up to x = 0.0156 probably due to reduction in inherent Zn-interstitials and O-vacancies. However, with further substitution and excess oxygen in lattice internal strain increases creating defects. Fe 3d–O 2p hybridization creates states inside bandgap which are further contributions to strain beyond x = 0.0156. Bandgap, photoluminescence follows same trend. XANES study clearly rules out presence of metallic Fe clusters, FeO and Fe2O3 phases in samples. However, it indicates that Fe gets incorporated in the ZnO lattice as mix charge state in Fe2+/Fe+3 causing reduction of oxygen vacancies. These observations corroborate to those of EXAFS study. Coercive field and remnant magnetization studies also hint at proper substitution. For such a homogeneous lattice solution, some ferromagnetic ordering is evident at very low temperature which is enhanced by Ag+ addition. This may be due to some Zn-s state facilitated long range exchange mechanism.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Authors thank Dr Vipul Singh at IIT, Indore, for providing Photoluminescence Spectroscopy. We also thank Sophisticated Instrumentation Center (SIC), IIT Indore for Scanning Electron Microscopy and IIT Indore for funding the project. Authors are grateful to Dr Kaushik for providing UV/vis facility in INST Mohali. We would like to thank Dr Anand Parey, Solid Mechanics lab, Department of Mechanical Engineering at IIT Indore. Authors wish to thank Mr Sandeep Patil for his help in performing Vickers micro-indentation measurements. One of the authors (Dr Sajal Biring) acknowledges financial support from the Ministry of Science and Technology (Grant No. MOST105-2218-E-131-003 and 106-2221-E-131-027).References
- U. Özgür, Y. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301 CrossRef.
- H. Zeng, W. Cai, P. Liu, X. Xu, H. Zhou, C. Klingshirn and H. Kalt, ACS Nano, 2008, 2, 1661–1670 CrossRef PubMed.
- H. Zeng, X. Xu, Y. Bando, U. K. Gautam, T. Zhai, X. Fang, B. Liu and D. Golberg, Adv. Funct. Mater., 2009, 19, 3165–3172 CrossRef.
- M. H. Huang, Science, 2001, 292, 1897–1899 CrossRef PubMed.
- P. Srivastava and Y. Sharma, Adv. Mater. Lett., 2011, 2, 290–293 CrossRef.
- D. A. Schwartz and D. R. Gamelin, Adv. Mater., 2004, 16, 2115–2119 CrossRef.
- H. Zhou, J. Fallert, J. Sartor, R. J. B. Dietz, C. Klingshirn, H. Kalt, D. Weissenberger, D. Gerthsen, H. Zeng and W. Cai, Appl. Phys. Lett., 2008, 92, 132112 CrossRef.
- B. Xiang, P. Wang, X. Zhang, S. A. Dayeh, D. P. R. Aplin, C. Soci, D. Yu and D. Wang, Nano Lett., 2007, 7, 323–328 CrossRef PubMed.
- G. D. Yuan, W. J. Zhang, J. S. Jie, X. Fan, J. A. Zapien, Y. H. Leung, L. B. Luo, P. F. Wang, C. S. Lee and S. T. Lee, Nano Lett., 2008, 8, 2591–2597 CrossRef PubMed.
- U. K. Gautam, L. S. Panchakarla, B. Dierre, X. Fang, Y. Bando, T. Sekiguchi, A. Govindaraj, D. Golberg and C. N. R. Rao, Adv. Funct. Mater., 2009, 19, 131–140 CrossRef.
- T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Science, 2000, 287, 1019–1022 CrossRef PubMed.
- K. Sato and H. Katayama-Yoshida, Jpn. J. Appl. Phys., 2001, 40, L555 CrossRef.
- T. Fukumura, Z. Jin, A. Ohtomo, H. Koinuma and M. Kawasaki, Appl. Phys. Lett., 1999, 75, 3366–3368 CrossRef.
- B. Panigrahy, M. Aslam and D. Bahadur, Nanotechnology, 2012, 23, 115601 CrossRef PubMed.
- M. V. Limaye, S. B. Singh, R. Das, P. Poddar and S. K. Kulkarni, J. Solid State Chem., 2011, 184, 391–400 CrossRef.
- G. Glaspell, P. Dutta and A. Manivannan, J. Cluster Sci., 2005, 16, 523–536 CrossRef.
- J. Iqbal, B. Wang, X. Liu, D. Yu, B. He and R. Yu, New J. Phys., 2009, 11, 063009 CrossRef.
- V. K. Sharma and G. D. Varma, Adv. Mater. Lett., 2012, 3, 126–129 CrossRef.
- A. Goktas, I. H. Mutlu, Y. Yamada and E. Celik, J. Alloys Compd., 2013, 553, 259–266 CrossRef.
- A. Goktas, I. H. Mutlu and Y. Yamada, Superlattices Microstruct., 2013, 57, 139–149 CrossRef.
- C. N. R. Rao and F. L. Deepak, J. Mater. Chem., 2005, 15, 573 RSC.
- J. Alaria, H. Bieber, S. Colis, G. Schmerber and A. Dinia, Appl. Phys. Lett., 2006, 88, 112503 CrossRef.
- S. Kolesnik and B. Dabrowski, J. Appl. Phys., 2004, 96, 5379–5381 CrossRef.
- M. A. Garcia, J. M. Merino, E. Fernandez Pinel, A. Quesada, J. De La Venta, M. L. Ruiz Gonzalez, G. R. Castro, P. Crespo, J. Liopis, J. M. Gonzalez-Calbet and A. Hernando, Nano Lett., 2007, 7, 1489 CrossRef PubMed.
- H. Li, Y. Huang, Q. Zhang, Y. Qiao, Y. Gu, J. Liu and Y. Zhang, Nanoscale, 2011, 3, 654–660 RSC.
- X. Qiu, L. Li, C. Tang and G. Li, J. Am. Chem. Soc., 2007, 38, 11908 CrossRef PubMed.
- B. S. Reddy, S. V. Reddy and R. P. V. Lakshmi, Optoelectron. Adv. Mater., Rapid Commun., 2012, 6, 953 Search PubMed.
- M. He, Y. F. Tian, D. Springer, I. A. Putra, G. Z. Xing, E. E. M. Chia, S. A. Cheong and T. Wu, Appl. Phys. Lett., 2011, 99, 222511 CrossRef.
- A. J. Chen, X. M. Wu, Z. D. Sha, L. J. Zhuge and Y. D. Meng, J. Phys. D: Appl. Phys., 2006, 39, 4762–4765 CrossRef.
- A. Singhal, S. Achary, A. Tyagi, P. Manna and S. Yusuf, Mater. Sci. Eng., B, 2008, 153, 47–52 CrossRef.
- A. H. Shah, M. B. Ahamed, E. Manikandan, R. Chandramohan and M. Iydroose, J. Mater. Sci.: Mater. Electron., 2013, 24, 2302–2308 CrossRef.
- M. Zarbali, A. Göktaş, I. H. Mutlu, S. Kazan, A. G. Şale and F. Mikailzade, J. Supercond. Novel Magn., 2012, 25, 2767–2770 CrossRef.
- A. Goktas, Appl. Surf. Sci., 2015, 340, 151–159 CrossRef.
- W. Zhang, J. Zhao, Z. Liu and Z. Liu, Appl. Surf. Sci., 2013, 284, 49–52 CrossRef.
- X. X. Wei, C. Song, K. W. Geng, F. Zeng, B. He and F. Pan, J. Phys.: Condens. Matter, 2006, 18, 7471–7479 CrossRef.
- V. Ghafouri, A. Ebrahimzad and M. Shariati, Sci. Iran., 2013, 20, 1039–1048 Search PubMed.
- H. S. Chin and L. S. Chao, J. Nanomater., 2013, 2013, 1–8 CrossRef.
- M. Saleem, L. Fang, A. Wakeel, M. Rashad and C. Y. Kong, World J. Condens. Matter Phys., 2012, 2, 10–15 CrossRef.
- J. Yang, Sensors, 2013, 13, 2719–2734 CrossRef PubMed.
- J. Yang, X. Liu, L. Yang, Y. Wang, Y. Zhang, J. Lang, M. Gao and B. Feng, J. Alloys Compd., 2009, 47, 632–635 CrossRef.
- S. Basu, C. Nayak, A. K. Yadav, A. Agrawal, A. K. Poswal, D. Bhattacharyya, S. N. Jha and N. K. Sahoo, J. Phys.: Conf. Ser., 2014, 493, 012032 CrossRef.
- A. K. Poswal, A. Agrawal, A. K. Yadav, C. Nayak, S. Basu, S. R. Kane, C. K. Garg, D. Bhattacharyya, S. N. Jha and N. K. Sahoo, AIP Conf. Proc., 2014, 1591, 649–651 CrossRef.
- B. S. Reddy, S. V. Reddy, N. K.Reddy and Y. P. Reddy, Adv. Mater. Lett., 2014, 5, 199–205 CrossRef.
- J. Wong, F. W. Lytle, R. P. Messmer and D. H. Maylotte, Phys. Rev. B, 1984, 30, 5596–5610 CrossRef.
- A. K. Rana, Y. Kumar, P. Rajput, S. N. Jha, D. Bhattacharyya and P. M. Shirage, ACS Appl. Mater. Interfaces, 2017, 9, 7691–7700 CrossRef PubMed.
- D. C. Konigsberger and R. Prince, X-Ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS and XANES, Edited book Wiley, New York, 1988 Search PubMed.
- S. D. Kelly, D. Hesterberg, B. Ravel, A. L. Ulery and L. R. Drees, SSSA Book Series Methods of Soil Analysis Part 5—Mineralogical Methods, 2008, vol. 5, pp. 387–464 Search PubMed.
- M. Newville, B. Ravel, D. Haskel, J. Rehr, E. Stern and Y. Yacoby, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 208, 154–156 CrossRef.
- E. H. Kisi and M. M. Elcombe, Acta Crystallogr., Sect. C: Struct. Chem., 1989, 45, 1867–1870 CrossRef.
- E. S. Jeong, H. J. Yu, Y. J. Kim, G. C. Yi, Y. D. Choi and S. W. Han, J. Nanosci. Nanotechnol., 2010, 10, 3562 CrossRef PubMed.
- S. Kumar, S. Basu, B. Rana, A. Barman, S. Chatterjee, S. N. Jha, D. Bhattacharyya, N. K. Sahoo and A. K. Ghosh, J. Mater. Chem. C, 2014, 2, 481–495 RSC.
- T. Chakraborty, C. Meneghini, G. Aquilanti and S. Ray, J. Phys.: Condens. Matter, 2013, 25, 236002 CrossRef PubMed.
- S. Kumar, N. Tiwari, S. N. Jha, S. Chatterjee, D. Bhattacharyya, N. K. Sahoo and A. K. Ghosh, RSC Adv., 2015, 5, 94658–94669 RSC.
- A. K. Yadav, R. Dey, R. Bhunia, S. Hussain, S. N. Jha, D. Bhattacharyya, R. Bhar and A. K. Pal, J. Polym. Res., 2016, 23, 265 CrossRef.
- E.-S. Jeong, H.-J. Yu, S.-W. Han, S. J. An, J. Yoo, Y.-J. Kim and G.-C. Yi, J. Korean Phys. Soc., 2008, 53, 461–465 CrossRef.
- Z. Wu, Y. Zhou, X. Zhang, S. Wei and D. Chen, Appl. Phys. Lett., 2004, 84, 4442–4444 CrossRef.
- A. Abdelkrim, S. Rahmane, O. Abdelouahab, A. Hafida and K. Nabila, Chin. Phys. B, 2016, 25, 046801 CrossRef.
- S. Benramache, B. Benhaoua and F. Chabane, J. Semicond., 2012, 33, 093001 CrossRef.
- N. Chahmat, A. Haddad, A. Ain-Souya, R. Ganfoudi, N. Attaf and M. Ghers, J. Mod. Phys., 2012, 03, 1781–1785 CrossRef.
- B. Cao, W. Cai and H. Zeng, Appl. Phys. Lett., 2006, 88, 161101 CrossRef.
- B. Lin, Z. Fu and Y. Jia, Appl. Phys. Lett., 2001, 79, 943–945 CrossRef.
- C. H. Ahn, Y. Y. Kim, D. C. Kim, S. K. Mohanta and H. K. Cho, J Appl. Phys., 2009, 105, 089902 CrossRef.
- S. Hosseini, I. A. Sarsari, P. Kameli and H. Salamati, J. Alloys Compd., 2015, 640, 408–415 CrossRef.
- J. Papierska, A. Ciechan, P. Bogusławski, M. Boshta, M. M. Gomaa, E. Chikoidze, Y. Dumont, A. Drabińska, H. Przybylińska, A. Gardias, J. Szczytko, A. Twardowski, M. Tokarczyk, G. Kowalski, B. Witkowski, K. Sawicki, W. Pacuski, M. Nawrocki and J. Suffczyński, Phys. Rev. B, 2016, 94, 224414 CrossRef.
- J. J. Beltrán, C. A. Barrero and A. Punnoose, Phys. Chem. Chem. Phys., 2015, 17, 15284–15296 RSC.
- J. Wang, J. Wan and K. Chen, Mater. Lett., 2010, 64, 2373 CrossRef.
- Q. Li, Y. Wang, L. Fan, J. Liu, W. Kong and B. Ye, Scr. Mater., 2013, 69, 694–697 CrossRef.
- A. Sivagamasundari, R. Pugaze, S. Chandrasekar, S. Rajagopan and R. Kannan, Appl. Nanosci., 2013, 3, 383 CrossRef.
- A. Kaminski and S. D. Sarma, Phys. Rev. Lett., 2002, 88, 247202 CrossRef PubMed.
- L. Bergqvist, O. Eriksson, J. Kudrnovský, V. Drchal, P. Korzhavyi and I. Turek, Phys. Rev. Lett., 2004, 93, 137202 CrossRef PubMed.
- A. Goktasa, F. Aslana, B. Yeşilatab and İ. Boza, Mater. Sci. Semicond. Process., 2018, 75, 221–233 CrossRef.
- A. Goktas, I. H. Mutlu and Y. Yamada, Superlattices Microstruct., 2013, 57, 139–149 CrossRef.
- L. Hedin and B. I. Lundqvist, J. Phys. C: Solid State Phys., 1971, 4, 2064–2083 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |