Open Access Article
Open Access ArticleMgTiO3:Mn4+ a multi-reading temperature nanoprobe†
Estelle Glais ab,
Vesna Đorđevićc,
Jelena Papanc,
Bruno Viana*b and
Miroslav D. Dramićanin*c
ab,
Vesna Đorđevićc,
Jelena Papanc,
Bruno Viana*b and
Miroslav D. Dramićanin*c
aSorbonne Université, CNRS UMR7574, Collège de France, Laboratoire de Chimie de la Matière Condensée de Paris, 4 Place Jussieu 75005 Paris, France
bPSL Research University, Institut de Recherche de Chimie Paris, Chimie Paristech-CNRS UMR 8247, 11 rue Pierre et Marie Curie, 75005 Paris, France. E-mail: bruno.viana@chimie-paristech.fr
cUniversity of Belgrade, Vinča Institute of Nuclear Sciences, P. O. Box 522, 11001 Belgrade, Serbia. E-mail: dramican@vinca.rs
First published on 18th May 2018
Abstract
MgTiO3 nanoparticles doped with Mn4+, with homogeneous size ranging about 63.1 ± 9.8 nm, were synthesized by a molten salt assisted sol gel method. These nanoparticles have been investigated as optical thermal sensors. The luminescence of tetravalent manganese ion in octahedral environment within the perovskite host presents drastic variations with temperature. Three different thermometry approaches have been proposed and characterized. Two luminescence intensity ratios are studied. Firstly between the two R-lines of Mn4+ emission at low temperature (−250 °C and −90 °C) with a maximal sensitivity of 0.9% °C−1, but also secondly between 2E → 4A2 (R-line) and the 4T2 → 4A2 transitions. This allows studying the temperature variation within a larger temperature range (−200 °C to 50 °C) with a sensitivity between 0.6% °C−1 and 1.2% °C−1 over this range. The last proposed method is the study of the lifetime variation versus temperature. The effective lifetime value corresponds to a combination of transitions from two excited energy levels of the tetravalent manganese (2E and 4T2) in thermal equilibrium toward the fundamental 4A2 state. Since the more energetic transition (4T2 → 4A2) is spin-allowed, contrary to the 2E → 4A2 one, the lifetime drastically decreases with the increase in temperature leading to an impressive high sensitivity value of 4.1% °C−1 at 4 °C and an exceptional temperature resolution of 0.025 °C. According to their optical features, MgTiO3:Mn4+ nanoparticles are indeed suitable candidates for the luminescence temperature probes at the nanoscale over several temperature ranges.
Introduction
Precise temperature measurement at the nanoscale based on the optical properties of a luminescent sensor presents many advantages since it provides a non-contact measurement on a wide range of temperatures including the biomedical region (30–50 °C). Many luminescent compounds have been studied in recent years, like organic species1–3 and polymers,4–6 but also nanomaterials doped with luminescent ions such as transition metal cations7–9 or lanthanides cations.10–12 Thermometry based on transition metals is particularly promising. Indeed, this family of compounds permits not only a self-referenced measurement but in addition a high thermal sensitivity thanks to their appropriate and tunable energy levels.13,14In previous work, we developed nanosized sensors for various applications.15–17 Here we investigate the MgTiO3 nanoparticles doped with Mn4+ ions elaborated from molten salt assisted sol–gel synthesis. The sol–gel method is often used for various types of inorganic material hosts synthesis.18 It provides a homogenous spread of ions in the liquid phase and relatively low final temperature treatments. Nevertheless, the final nanopowders are often agglomerated because of the temperature treatment, which is necessary for combusting the organic contents. In molten salt synthesis, salts are used in extent to the final product to facilitate an increase in the reaction rate and a lowering of the reaction temperature.19–21 The combination of these two synthetic routes presented here allows to obtain homogenous uniform nanosized MgTiO3:Mn4+nanoparticles.22–26
In this work we propose a multimodal optical approach for temperature determination and we compare the thermometry results. Due to their nanosizes, these sensors could allow a local temperature measurement. Such a measurement is very useful in many fields, for instance for temperature measurement in hazardous conditions (marine, aeronautic), when there is some difficulties to access (electronic devices), or for living cell temperature mapping (medicine).27
Materials and methods
The combination of two synthesis methods, the sol–gel and the molten salts methods, i.e. the so-called molten salt assisted sol–gel method was applied for the synthesis of Mn4+-doped MgTiO3 perovskite nanopowders. The sol mixture was prepared in the following way: titanium(IV) n-butoxide (Ti(OC4H9)4, 98%, Acros Organics) was dropwise added to stirring solution of acetic acid (CH3COOH, HPLC, Fisher) and ethanol (C2H5OH, Absol. HPLC, Fisher). Then, adequate amounts of magnesium nitrate (Mg(NO3)2·6H2O, 98%, Alfa Aesar) and manganese(II) nitrate (Mn(NO3)2·6H2O, 98+%, Alfa Aesar) were completely dissolved in the liquid to obtain a final molar ratio of 16(EtOH)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3(AA)
3(AA)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.995(Ti)
0.995(Ti)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005(Mn)
0.005(Mn)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1(Mg). Then the temperature was raised to 70 °C, and polymerization started, and excess solvents evaporated. The obtained yellow resin-like product was dried and powdered in a mortar. The dry gel was then mixed with the eutectic mixture of NaCl (99%, Alfa Aesar) and KCl (99%, Alfa Aesar) with 1
1(Mg). Then the temperature was raised to 70 °C, and polymerization started, and excess solvents evaporated. The obtained yellow resin-like product was dried and powdered in a mortar. The dry gel was then mixed with the eutectic mixture of NaCl (99%, Alfa Aesar) and KCl (99%, Alfa Aesar) with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 molar excess of the salts. After annealing of the mixture in an alumina crucible at 750 °C for 2 h, final powder was extracted from the salt by repeated washing with water. Such obtained powder was used for further characterization. X-ray diffraction (XRD) measurements were performed using a Rigaku SmartLab diffractometer using CuKα 1,2 radiation at 30 mA and 40 kV. Diffraction data were recorded in a 2θ range from 10° to 90° in 0.02° step. Transmission electron microscopy (TEM) samples were prepared by evaporating a drop of diluted suspension of nanoparticles in ethanol on a carbon-coated copper grid. The nanoparticles were studied using a TECNAI Spirit G2 apparatus. Excitation spectra were measured using a Varian Cary Eclipse Fluorescence Spectrophotometer in phosphorescence mode. Luminescence decay spectra are obtained after an excitation provided by an Optical Parametric Oscillator (OPO) YAG:Nd pulsed laser (EKSPLA 342B) at 550 nm and recorded by a photomultiplier coupled to an oscilloscope. Photoluminescence emission spectra were excited by the same device described above and recorded by an Intensified ICCD Roper Scientific camera coupled to a 1200 grooves per mm grating monochromator.
10 molar excess of the salts. After annealing of the mixture in an alumina crucible at 750 °C for 2 h, final powder was extracted from the salt by repeated washing with water. Such obtained powder was used for further characterization. X-ray diffraction (XRD) measurements were performed using a Rigaku SmartLab diffractometer using CuKα 1,2 radiation at 30 mA and 40 kV. Diffraction data were recorded in a 2θ range from 10° to 90° in 0.02° step. Transmission electron microscopy (TEM) samples were prepared by evaporating a drop of diluted suspension of nanoparticles in ethanol on a carbon-coated copper grid. The nanoparticles were studied using a TECNAI Spirit G2 apparatus. Excitation spectra were measured using a Varian Cary Eclipse Fluorescence Spectrophotometer in phosphorescence mode. Luminescence decay spectra are obtained after an excitation provided by an Optical Parametric Oscillator (OPO) YAG:Nd pulsed laser (EKSPLA 342B) at 550 nm and recorded by a photomultiplier coupled to an oscilloscope. Photoluminescence emission spectra were excited by the same device described above and recorded by an Intensified ICCD Roper Scientific camera coupled to a 1200 grooves per mm grating monochromator.
Results and discussion
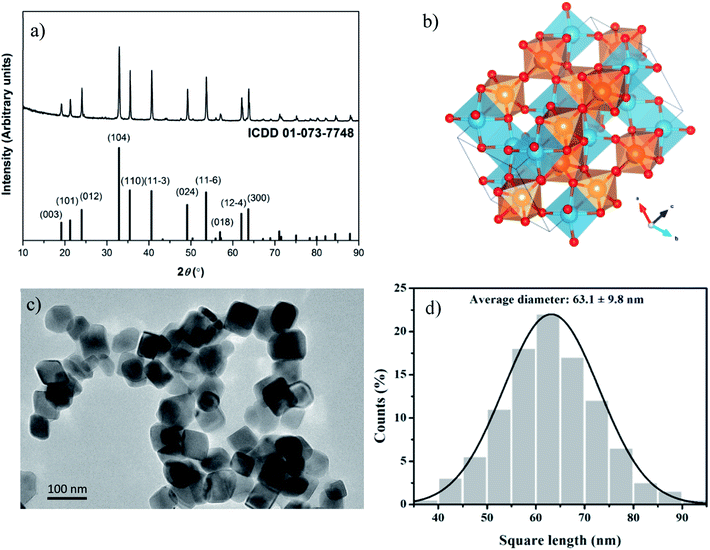
After synthesis, nanoparticles are first structurally characterized. MgTiO3:Mn4+ crystal structure has a rhombohedral symmetry R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (SG: 148) and XRD of sample, see Fig. 1a, can be indexed according to ICDD: 01-073-7748 (MgTiO3). In this structure, the local symmetry of Ti4+ (Mn4+) site is C3v,22 see Fig. 1b. TEM picture (Fig. 1c) highlights the shape and good dispersion of square nanoparticles. The associated size distribution diagram (Fig. 1d) is plotted for 200 randomly selected nanoparticles, and the average square length of particles is 63.1 ± 9.8 nm. The manganese ions introduced as dopant could easily substitute Ti4+ ions in the structure including no charge compensation and relatively close radii (0.39 Å and 0.42 Å for Mn4+ and Ti4+ respectively). Indeed, Mn4+ ions present a 3d3 configuration (isoelectronic with Cr3+). Since ligand field energy is highly stabilized in octahedral coordinated systems, Mn4+ ions almost exclusively occupy octahedral positions within the structure. Excitation spectrum of MgTiO3:Mn4+ nanoparticles is presented Fig. 2.
(SG: 148) and XRD of sample, see Fig. 1a, can be indexed according to ICDD: 01-073-7748 (MgTiO3). In this structure, the local symmetry of Ti4+ (Mn4+) site is C3v,22 see Fig. 1b. TEM picture (Fig. 1c) highlights the shape and good dispersion of square nanoparticles. The associated size distribution diagram (Fig. 1d) is plotted for 200 randomly selected nanoparticles, and the average square length of particles is 63.1 ± 9.8 nm. The manganese ions introduced as dopant could easily substitute Ti4+ ions in the structure including no charge compensation and relatively close radii (0.39 Å and 0.42 Å for Mn4+ and Ti4+ respectively). Indeed, Mn4+ ions present a 3d3 configuration (isoelectronic with Cr3+). Since ligand field energy is highly stabilized in octahedral coordinated systems, Mn4+ ions almost exclusively occupy octahedral positions within the structure. Excitation spectrum of MgTiO3:Mn4+ nanoparticles is presented Fig. 2.
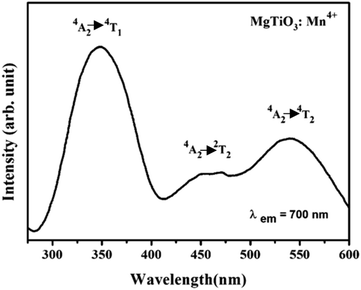 | ||
| Fig. 2 Excitation spectrum of MgTiO3:Mn4+ nanoparticles at room temperature (see details in Đorđević et al.22). | ||
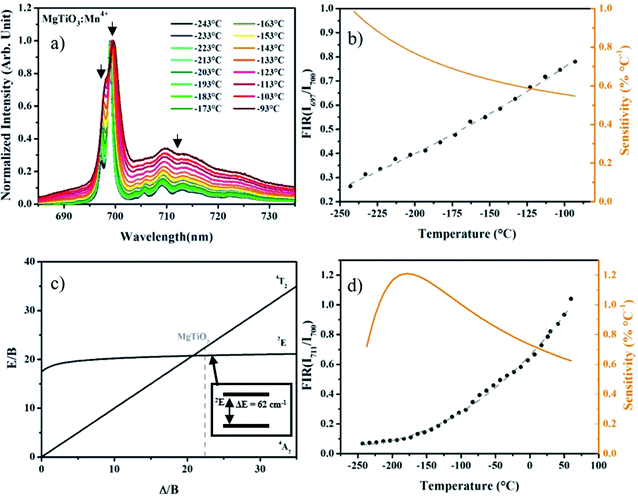
Crystal field parameters as well as experimental and calculated energy levels of Mn4+ have recently been considered experimentally and using crystal field calculations.22 At low temperature the 2E energy level splitting reaches 62 cm−1, which should correspond to a large variation of the intensity ratio between these two levels in the low temperatures range. On the excitation spectra presented in Fig. 2, two broad bands are obtained with a shoulder at about 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (455 nm) where 3 peaks can be distinguished, that may originated from the spin forbidden 2T2 state, even if the broadening seems quite important for this spin forbidden transition. This attribution is in agreement with the crystal field calculation presented in Đorđević et al. work.22 In the present study, nanoparticles are excited at 550 nm corresponding well to the 4A2 → 4T2 transition. Emission spectra are recorded between −250 °C and 50 °C with 10 °C step between each measurement (see Fig. 3a). Mn4+ ion in octahedral position presents a deep red emission centered at about 700 nm, mostly dominated by the spin forbidden 2E → 4A2 transition. All spectra are normalized to R1 line (at 700 nm). These two lines, separated by 62 cm−1, came from the lifting by the symmetry of the degeneracy of the doublet 2E manifold13 and better resolution is obtained with decrease in temperature.
000 cm−1 (455 nm) where 3 peaks can be distinguished, that may originated from the spin forbidden 2T2 state, even if the broadening seems quite important for this spin forbidden transition. This attribution is in agreement with the crystal field calculation presented in Đorđević et al. work.22 In the present study, nanoparticles are excited at 550 nm corresponding well to the 4A2 → 4T2 transition. Emission spectra are recorded between −250 °C and 50 °C with 10 °C step between each measurement (see Fig. 3a). Mn4+ ion in octahedral position presents a deep red emission centered at about 700 nm, mostly dominated by the spin forbidden 2E → 4A2 transition. All spectra are normalized to R1 line (at 700 nm). These two lines, separated by 62 cm−1, came from the lifting by the symmetry of the degeneracy of the doublet 2E manifold13 and better resolution is obtained with decrease in temperature.
Thus, the fluorescence intensity ratio method (FIR) can be applied between R1 (700 nm) and R2 (697 nm) peaks between −250 and −90 °C (Fig. 3b). One can estimate a relative sensitivity from the following formula:
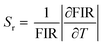 | (1) |
Using the R2/R1 ratio, the maximal sensitivity reaches about 1% °C−1 at −240 °C. Above −90 °C, signal broadening prevents accurate measurements and the resolution strongly decreases. Consequently only one sharp R line can be clearly identified.
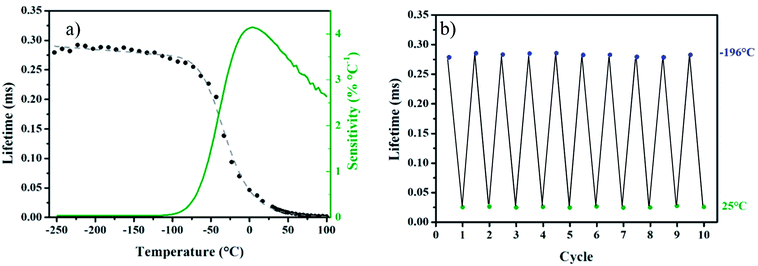
To go further, another intensity ratio can be used with Mn4+ since the crystal field value Δ/B is close to 22 (see Fig. 3c). Indeed, a strong intensity increase of the band centered at about 710 nm, corresponding to the overlap of the narrow peaks, coming from interaction between Mn4+ cations, superimposed to a broad band originating from the spin allowed 4T2 → 4A2 transition, can be observed with temperature rising. We proposed here to use the ratio of the 2E/4T2 emissions versus temperature for temperature sensing. Looking at this ratio, the investigated temperature range appears much larger, from −200 to 50 °C (see ESI-1†). Over 50 °C, as the signal intensity is quenched with temperature, as seen in the following (see the lifetime study), the signal over noise ratio in the same experimental conditions is very small. Of course, enlarging the slits of the monochromator or increasing the detector sensitivity could compensate the observed decrease but in order to get an accurate calibration, all the experimental parameters were kept constant. This also demonstrates that the simultaneous existence of both sharp R-lines emission from 2E excited state and the broadband emission from the 4T2 level corresponds well to the thermal equilibrium expected between these two states, according to the Tanabe–Sugano diagram reported Fig. 3c. The energy difference between 2E and 4T2 excited states is small enough to allow thermal equilibrium. Thus, with temperature increase, the probability to populate the 4T2 level strongly increase, but at the same time the phonon coupling is quite strong for the 4T2 → 4A2 transition. This also favors the non-radiative deexcitation toward the fundamental state, leading to the overall decrease of the intensity. The decrease of the quantum yield with temperature in the case of the Cr3+ (isoelectronic to the Mn4+) is fully documented in the literature28–43 and the same process occurs for the tetravalent manganese.44–46 The maximal relative sensitivity is around 1.2% °C−1 at −180 °C and remains above 0.6% °C−1 until 50 °C (Fig. 3d), which can give an accurate temperature measurement in the low-temperature range, but also matching well with the physiological temperature range for biophotonic applications. Following the photoluminescence variation at different temperatures, the lifetime and decay profiles should be strongly affected by the temperature variation. Photoluminescence decays are registered using a 550 nm pulsed laser (10 Hz) excitation. As expected, it appears that the PL lifetimes are strongly decreasing with an increase of temperature (see Fig. 4a). The experimental lifetimes, which present non-exponential decay profiles originate from thermal equilibrium of two deexcitations: the spin forbidden 2E → 4A2 transition, corresponding to longer lifetime component. But also the spin allowed 4T2 → 4A2 transition characterized by shorter lifetime values and electron/phonon coupling. As said before, in the case of tetravalent manganese in MgTiO3 matrix the 2E and the 4T2 levels are in thermal equilibrium. With thermal activation, the contribution of the spin allowed transition increases at the expense of 2E → 4A2 transition resulting in a decrease of the effective lifetime. The PL experimental lifetimes plotted in Fig. 4a can be deduced from the decay curves thanks to the following usual equation:
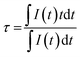 | (2) |
The lifetime variation is really significant between −75 °C and 50 °C. Once again, the relative sensitivity is calculated in order to compare the ability of the sensor as thermometer from the following formula:
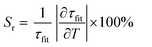 | (3) |
τfit corresponds to the lifetime adjustment determined with the following formula:12
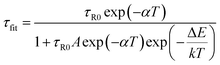 | (4) |
The maximal relative sensitivity value is 4.1% °C−1 at 4 °C. In addition to the relative sensitivity, the temperature resolution (uncertainty in temperature) δT is the other important figure of merit of the nanothermometer's performance.51 It describes the minimal change in the temperature that causes a noticeable variation in the studied parameter,12 and is estimated as:51
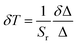 | (5) |
| Material | Thermometric parameter | Sensitivity (% °C−1) (temperature (°C)) | δT (°C) | Ref. |
|---|---|---|---|---|
| TiO2:Eu3+ | Emission intensity ratio | 2.43 (250) | 0.46 | 47 |
| TiO2:Eu3+ | Excited state lifetime | 2.43 (250) | 0.33 | 47 |
| GdVO4@SiO2:Tm3+,Yb3+ | Emission intensity ratio | 0.94 (50) | 0.40 | 48 |
| Gd2O3:Nd3+ | Emission intensity ratio | 1.75 (15) | 0.10 | 49 |
| CaF2:Gd3+,Nd3+ | Emission intensity ratio | 0.12 (25) | 1.80 | 50 |
| Bi2Ga4O9:Cr3+ | Emission intensity ratio | 0.7 (37) | 0.08 | 34 |
| LiLaP4O12:Cr3+,Nd3+ | Emission intensity ratio | 4.89 (50) | — | 7 |
| MgTiO3:Mn4+ | Excited state lifetime | 4.1 (4) | 0.025 | This work |
| MgTiO3:Mn4+ | Emission intensity ratio | 0.6 (−125) 1.2 (−180) | 0.42 (at −180 °C) 0.84 (at 50 °C) | This work |
The repeatability of measurements has also been investigated (see also ESI-2†). The experimental lifetime is registered by cycling between two arbitrary chosen temperatures (here between −196 °C and 25 °C) as represented in Fig. 4b. This result reveals the good repeatability of our system, but also a good stability of the sensor characteristics versus time.
Conclusions
In this work, we demonstrate the multimodal thermal reading of MgTiO3:Mn4+ luminescent nanosensors. The luminescence properties of the well crystallized and homogeneous nanoparticles with an average diameter of 63.1 ± 9.8 nm were studied. Two emission intensity ratio can be used to get precise temperature measurements on two different temperature ranges. The first between −250 °C and −90 °C coming from the two splitted R lines, displays a maximal sensitivity of 1% °C−1 and a thermal resolution of 0.42 °C. The second, corresponding to the ratio of the 2E → 4A2/4T2 → 4A2 transitions is relevant on the −200 °C to 50 °C temperature range with a maximal sensitivity of 1.2 °C at −180 °C and remains above the threshold value 0.6% °C−1 on all this temperature range. Finally, the lifetime study of these MgTiO3:Mn4+ nanoparticles allows to explore the −75 °C to 50 °C temperature range with a really high sensitivity of 4.1% °C−1 and an unique temperature resolution of 0.025 °C. The good stability and repeatability make this robust thermometer usable for many applications on a very large temperature range.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Authors from Serbia acknowledge support from the Ministry of Education, Science and Technological Development of the Republic of Serbia (Grant No. 171022). Authors from France acknowledge the Cluster of Excellence MATISSE, and DGA (Direction Générale de l’Armement, France). The authors thank the bilateral project between France and Serbia n°36214NE – Campus France.References
- R. K. P. Benninger, Y. Koç, O. Hofmann, J. Requejo-Isidro, M. A. A. Neil, P. M. W. French and A. J. deMello, Anal. Chem., 2006, 78, 2272–2278 CrossRef PubMed.
- Y. Shiraishi, R. Miyamoto, X. Zhang and T. Hirai, Org. Lett., 2007, 9, 3921–3924 CrossRef PubMed.
- F. H. C. Wong and C. Fradin, J. Fluoresc., 2011, 21, 299–312 CrossRef PubMed.
- X. Guan, X. Liu, Z. Su and P. Liu, React. Funct. Polym., 2006, 66, 1227–1239 CrossRef.
- F. Ye, C. Wu, Y. Jin, Y.-H. Chan, X. Zhang and D. T. Chiu, J. Am. Chem. Soc., 2011, 133, 8146–8149 CrossRef PubMed.
- D. Gong, T. Cao, S.-C. Han, X. Zhu, A. Iqbal, W. Liu, W. Qin and H. Guo, Sens. Actuators, B, 2017, 252, 577–583 CrossRef.
- L. Marciniak, A. Bednarkiewicz, D. Kowalska and W. Strek, J. Mater. Chem. C, 2016, 4, 5559–5563 RSC.
- S. K. Sharma, E. Glais, M. Pellerin, C. Chaneac and B. Viana, Proc. SPIE, 2016, 9749, 974922 CrossRef.
- L. Marciniak, A. Bednarkiewicz, J. Drabik, K. Trejgis and W. Strek, Phys. Chem. Chem. Phys., 2017, 19, 7343–7351 RSC.
- F. Vetrone, R. Naccache, A. Zamarrón, A. Juarranz de la Fuente, F. Sanz-Rodríguez, L. Martinez Maestro, E. Martín Rodriguez, D. Jaque, J. García Solé and J. A. Capobianco, ACS Nano, 2010, 4, 3254–3258 CrossRef PubMed.
- D. Wawrzynczyk, A. Bednarkiewicz, M. Nyk, W. Strek and M. Samoc, Nanoscale, 2012, 4, 6959 RSC.
- M. D. Dramićanin, Methods Appl. Fluoresc., 2016, 4, 042001 CrossRef PubMed.
- W. Mikenda and A. Preisinger, J. Lumin., 1981, 26, 53–66 CrossRef.
- W. Mikenda and A. Preisinger, J. Lumin., 1981, 26, 67–83 CrossRef.
- J. Planelles-Aragó, B. Julián-López, E. Cordoncillo, P. Escribano, F. Pellé, B. Viana and C. Sanchez, J. Mater. Chem., 2008, 18, 5193 RSC.
- D. Jaque, C. Richard, B. Viana, K. Soga, X. Liu and J. G. Solé, Adv. Opt. Photonics, 2016, 8, 1–103 CrossRef.
- L. Đačanin Far, S. R. Lukić-Petrović, V. Đorđević, K. Vuković, E. Glais, B. Viana and M. D. Dramićanin, Sens. Actuators, A, 2018, 270, 89–96 CrossRef.
- J. Livage and C. Sanchez, J. Non-Cryst. Solids, 1992, 145, 11–19 CrossRef.
- B. Milićević, V. Đorđević, K. Vuković, G. Dražić and M. D. Dramićanin, Opt. Mater., 2017, 72, 316–322 CrossRef.
- T. V. Gavrilović, D. J. Jovanović, L. V. Trandafilović and M. D. Dramićanin, Opt. Mater., 2015, 45, 76–81 CrossRef.
- T. V. Gavrilović, D. J. Jovanović, V. M. Lojpur, V. Đorđević and M. D. Dramićanin, J. Solid State Chem., 2014, 217, 92–98 CrossRef.
- V. Đorđević, M. G. Brik, A. M. Srivastava, M. Medić, P. Vulić, E. Glais, B. Viana and M. D. Dramićanin, Opt. Mater., 2017, 74, 46–51 CrossRef.
- H.-L. Li, Z.-N. Du, G.-L. Wang and Y.-C. Zhang, Mater. Lett., 2010, 64, 431–434 CrossRef.
- X. Liu, Mater. Lett., 2012, 80, 69–71 CrossRef.
- H. Lou and L. Wang, Mater. Lett., 2015, 155, 91–93 CrossRef.
- T. X. Wang, S. Z. Liu and J. Chen, Powder Technol., 2011, 205, 289–291 CrossRef.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301 RSC.
- B. A. Weinstein, Rev. Sci. Instrum., 1986, 57, 910–913 CrossRef.
- K. T. V. Grattan, R. K. Selli and A. W. Palmer, Rev. Sci. Instrum., 1987, 58, 1231–1234 CrossRef.
- J. P. Hehir, M. O. Henry, J. P. Larkin and G. F. Imbusch, J. Phys. C: Solid State Phys., 1974, 7, 2241 CrossRef.
- Z. Y. Zhang, K. T. V. Grattan, A. W. Palmer, V. Fernicola and L. Crovini, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 2656 CrossRef.
- A. Omrane, G. Juhlin, F. Ossler and M. Aldén, Appl. Opt., 2004, 43, 3523–3529 CrossRef PubMed.
- S. M. Borisov, K. Gatterer, B. Bitschnau and I. Klimant, J. Phys. Chem. C, 2010, 114, 9118–9124 Search PubMed.
- M. Back, E. Trave, J. Ueda and S. Tanabe, Chem. Mater., 2016, 28, 8347–8356 CrossRef.
- R. R. Sholes and J. G. Small, Rev. Sci. Instrum., 1980, 51, 882–884 CrossRef.
- H. Aizawa, N. Ohishi, S. Ogawa, T. Katsumata, S. Komuro, T. Morikawa and E. Toba, Rev. Sci. Instrum., 2002, 73, 3656–3658 CrossRef.
- W. H. Fonger and C. W. Struck, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 11, 3251 CrossRef.
- Z. Zhang, K. T. V. Grattan and A. W. Palmer, Rev. Sci. Instrum., 1992, 63, 3869–3873 CrossRef.
- Z. Y. Zhang and K. T. V. Grattan, J. Lumin., 1994, 62, 263–269 CrossRef.
- S. W. Allison, D. L. Beshears, M. R. Cates, M. Paranthaman and G. T. Gilles, International Society for Optics and Photonics, in Optical Diagnostics for Fluids, Solids, and Combustion, 2001, vol. 4448, pp. 28–36 Search PubMed.
- H. Uchiyama, H. Aizawa, T. Katsumata, S. Komuro, T. Morikawa and E. Toba, Rev. Sci. Instrum., 2003, 74, 3883–3885 CrossRef.
- N. Fuhrmann, T. Kissel, A. Dreizler and J. Brübach, Meas. Sci. Technol., 2011, 22, 045301 CrossRef.
- H. Aizawa, N. Ohishi, S. Ogawa, E. Watanabe, T. Katsumata, S. Komuro, T. Morikawa and E. Toba, Rev. Sci. Instrum., 2002, 73, 3089–3092 CrossRef.
- M. R. Cates, D. L. Beshears, S. W. Allison and C. M. Simmons, Rev. Sci. Instrum., 1997, 68, 2412–2417 CrossRef.
- N. Fuhrmann, E. Baum, J. Brübach and A. Dreizler, Rev. Sci. Instrum., 2011, 82, 104903 CrossRef PubMed.
- J. Brübach, T. Kissel, M. Frotscher, M. Euler, B. Albert and A. Dreizler, J. Lumin., 2011, 131, 559–564 CrossRef.
- M. G. Nikolić, Ž. Antić, S. Ćulubrk, J. M. Nedeljković and M. D. Dramićanin, Sens. Actuators, B, 2014, 201, 46–50 CrossRef.
- O. A. Savchuk, J. J. Carvajal, C. Cascales, M. Aguiló and F. Díaz, ACS Appl. Mater. Interfaces, 2016, 8, 7266–7273 Search PubMed.
- S. Balabhadra, M. L. Debasu, C. D. S. Brites, L. A. O. Nunes, O. L. Malta, J. Rocha, M. Bettinelli and L. D. Carlos, Nanoscale, 2015, 7, 17261–17267 RSC.
- P. Cortelletti, C. Facciotti, I. X. Cantarelli, P. Canton, M. Quintanilla, F. Vetrone, A. Speghini and M. Pedroni, Opt. Mater., 2017, 68, 29–34 CrossRef.
- C. D. S. Brites, A. Millán and L. D. Carlos, in Handbook on the Physics and Chemistry of Rare Earths, ed. B. Jean-Claude and P. K. Vitalij, Elsevier, 2016, vol. 49, pp. 339–427 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02482k |
| This journal is © The Royal Society of Chemistry 2018 |