Open Access Article
Open Access ArticleNon-isothermal TGA study on the combustion reaction kinetics and mechanism of low-rank coal char
Yingjie Hu ,
Zhiqiang Wang*,
Xingxing Cheng
,
Zhiqiang Wang*,
Xingxing Cheng and
Chunyuan Ma
and
Chunyuan Ma
National Engineering Laboratory for Coal-fired Pollutants Emission Reduction, Shandong University, 17923 Jingshi Road, Jinan 250061, PR China. E-mail: jackywzq@sdu.edu.cn
First published on 21st June 2018
Abstract
In this paper, the combustion reaction kinetics of pyrolysis char of low-rank coal is studied by thermal analysis technology. For the combustion process of the char at different heating rates, the reaction kinetic parameters were calculated by three common mode-free methods (FWO method, KAS method and Starink method); the reaction model was determined by Malek method and Popescu method. Research shows that activation energy Eα of char combustion calculated by the three methods was 110.66–70.31 kJ mol−1, 104.35–59.60 kJ mol−1 and 104.34–59.99 kJ mol−1, respectively, and the activation energy decreased with increasing conversion rates. There is a compensation effect between the activation energy and pre-exponential factor of char combustion. Results of the kinetic analysis by Malek method and Popescu method both indicated that the Avrami–Erofeev equation (n = 3/2) (f(α) = 3/2(1 − α)[−ln(1 − α)]1/3) controlled by nucleation and nuclei growth models is the most probable reaction model of char combustion.
1 Introduction
Coal is the most abundant fossil fuel in China, especially low-rank coal, and the proved reserves of low-rank coal in China account for more than half of the total.1 Pyrolysis is one of the most effective ways of low-rank coal grading for effective utilization technologies.2 However, a large amount of by-product, called char, is produced by this technology. The production of pyrolytic char accounts for about 50–70% of low-rank coal, and the energy contained in char accounts for up to 80% of low-rank coal.2 So using this char for combustion and power generation is emerging as a viable method for the grading utilization of low-rank coal. However, char is usually less volatile, and it has problems in terms of ignition, stable combustion and burnout.3 Many researchers have carried out a great deal of research on the combustion of char, but the previous research focuses on practical application.1–4 There is little work on the combustion mechanism of char from thermodynamics and kinetics.The thermal analysis technique is widely used in the laboratory to study the combustion characteristics and mechanism of solid fuel.5 Through the change of the weight loss curve, thermal analysis not only can yield the kinetic parameters and the mechanism function of the reaction, but also can be used study the physical and chemical properties of fuel.6 Sun7 investigated the combustion characteristics of bituminous coal and its pyrolytic char at different heating rates, and the kinetic parameters at different heating rates were calculated by distributed activation energy model methods. The results show that, compared with bituminous coal, the ignitability and comprehensive combustion characteristics of its pyrolytic char slightly decreased. With increasing conversion, the activation energy of bituminous coal increased firstly and then decreased, and the activation energy of char linearly decreased. Naktiyok8 used mode-free methods (FWO and KAS methods) and a model-fitting method (Coats–Redfern (C–R) method) to calculate the kinetic parameters of lignite, and the ideal reaction model was determined by the C–R method. Research suggests that the results of the two methods (FWO and KAS) are the same, and the most probable kinetic models used to describe lignite combustion are diffusion models (D4) with the C–R method. But Ren6 reported that there is an inaccuracy in determining the most probable kinetic models by the C–R method, because there is a compensation effect between activation energy and pre-exponential factor leading to the fitting lines of several mechanism functions all having good linearity. Wang9 calculated the activation energy of bituminous coal with different chlorine contents by the KAS method, and the optimal kinetic model for describing the combustion process of chlorine-containing bituminous coal was determined by the Malek method. The study found that the most probable kinetic models of the same sample at different heating rates are different. This is because the Malek method needs one to first obtain the activation energy at the different steps of the reaction and the time evolution equation of conversion. Different heating rates and the activation energy calculated by different methods have a great effect on the choice of the optimal kinetic model.10 In conclusion, there is an inaccuracy in obtaining the kinetic parameters of char combustion by model-fitting methods. And even if the kinetic parameters were calculated by single mode-free methods, there is still a great effect on the accuracy of the Malek method for determining the ideal reaction model of char combustion. So using several common mode-free methods to calculate the reaction kinetic parameters, and different methods to determine the ideal reaction model, will be more accurate and reliable.
In this paper, in order to obtain the accurate kinetic parameters and the ideal reaction model, the combustion reaction kinetics of pyrolytic char of low-rank coal was studied for different temperature programs. For the combustion process of char at different heating rates, the kinetic parameters were calculated by several common mode-free methods (FWO, KAS and Starink methods). The ideal reaction model was determined by two different methods (Malek method and Popescu method). Meanwhile, the effect of different mode-free methods and heating rate on the accuracy of the Malek method was discussed. This study aims to make up for gaps in knowledge of the combustion mechanism of char, and to provide a theoretical support for application.
2 Experimental
2.1 Sample preparation and analysis
Char used in this study was provided by Shaanxi Coal and Chemical Industry Group Co. Ltd, as a by-product in low-rank coal pyrolysis processes. In order to eliminate heat and mass transfer limitations, the sample was ground and sieved to particle sizes of less than 0.074 mm. The proximate and ultimate analyses of the samples were carried out and the results are given in Table 1.| Sample | Proximate analysis | Ultimate analysis | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mad | Vad | Aad | FCad | C | H | O | N | S | |
| Char | 2.18 | 4.51 | 19.54 | 73.77 | 81.47 | 0.37 | 7.13 | 0.85 | 0.59 |
The experiments were completed using a thermogravimetric analyzer (TGA/DSC1/1600HT, Mettler-Toledo). In each test, about (10 ± 0.2) mg samples were loaded into an Al2O3 crucible under an air atmosphere, with an air flow rate of 50 mL min−1. The furnace temperature was increased from 30 °C to 850 °C. All samples were tested at four different heating rates of 15, 20, 25, and 30 °C min−1, respectively.
2.2 Determination of apparent activation energy
Char combustion is a gas–solid heterogeneous oxidation reaction, and the non-isothermal kinetic equation for solid char sample decomposition can be described as follows:11
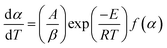 | (1) |
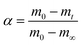 | (2) |
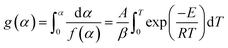 | (3) |
However, for the generally adopted constant heating rate program, eqn (1) transforms into eqn (3) that does not have an analytical solution.12 In order to resolve this problem, several integral iso-conversional methods that differ in approximations of the temperature integral in eqn (3) were proposed by many researchers. When using a crude temperature integral approximation by Doyle13 in eqn (3), it would lead to the popular equation that is generally called the Flynn–Wall–Ozawa (FWO) equation:14,15
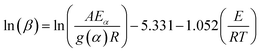 | (4) |
A more accurate approximation by Murray and White can be used in eqn (3) so that eqn (3) takes the form also known as the Kissinger–Akahira–Sunose (KAS) equation:16
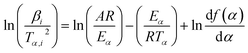 | (5) |
Starink studied the FWO and KAS equations, then presented a more accurate approximation of the temperature integral such that eqn (3) turned into:17,18
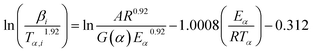 | (6) |
3 Results and discussion
3.1 Thermogravimetric analysis
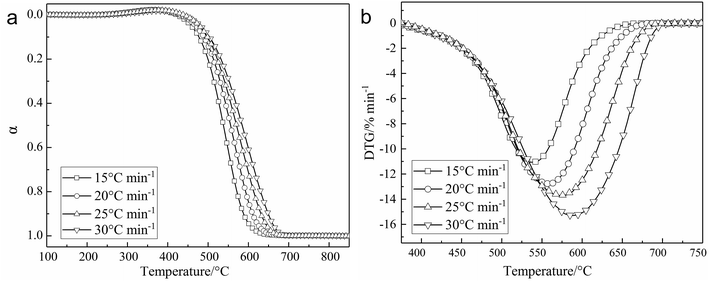
Fig. 1a and b shows the relationship of conversion versus temperature and the DTG curves of char at heating rates of 15, 20, 25, and 30 °C min−1 in air atmosphere. As shown in Table 1, the moisture and volatiles of char are very small, so the main weight loss process of char is as a result of the combustion of fixed carbon. As can be seen in Fig. 1a and b, the main weight loss process of char occurred in the temperature range of 400–700 °C. The ignition temperature of char is above 400 °C and higher than the ignition temperature of Shenhua coal (371 °C) from the literature.4 Meanwhile, these experimental results are close to those reported in the literature.7. This is principally because the volatile content (32.4%, mass) of bituminous coal (Shenhua coal in the literature4) is much higher than that of char in this study and the literature.7 So a lot of bridge and branch bonds of molecular structure that exist in bituminous coal are released as volatile matter during pyrolysis, and the burning of the volatile matter determines the ignition point of coal and char. The more volatile the content, the lower the ignition temperature.19 So the ignition temperature of char in this study is high.Besides, a moderate increase of the weight of char was observed in the range of 300–400 °C. This is because large specific surface area and pore structure emerged due to the release of volatiles, which improved the adsorption capacity of oxygen. And some of the groups of the coal structure could react with oxygen leading to the production of carboxyl.21 Wang found carboxyl (–COOH) and carbonyl (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) increased in the mass gain stage of the oxidation process, but remained unchanged in the pyrolysis process.21 So this phenomenon is considered as an oxygen-absorption mass-gain process of char and carboxyl and carbonyl were determined as the key functional groups for coal oxidation mass gain.20,21 As shown in Fig. 1, the curves of conversion versus temperature moved toward the right-hand side with an increase of heating rate. This is because the reaction time that samples stay at the same temperature range was reduced as the heating rate increased, and will lead to a higher temperature at which the samples are in same the combustion status.22 So the reaction moves toward the high-temperature zone. Besides, DTG curves moved toward the right-hand side, as well as downward, due to the shorter reaction time and the phenomenon of thermal hysteresis.22 So the corresponding rate of reaction also increases.
O) increased in the mass gain stage of the oxidation process, but remained unchanged in the pyrolysis process.21 So this phenomenon is considered as an oxygen-absorption mass-gain process of char and carboxyl and carbonyl were determined as the key functional groups for coal oxidation mass gain.20,21 As shown in Fig. 1, the curves of conversion versus temperature moved toward the right-hand side with an increase of heating rate. This is because the reaction time that samples stay at the same temperature range was reduced as the heating rate increased, and will lead to a higher temperature at which the samples are in same the combustion status.22 So the reaction moves toward the high-temperature zone. Besides, DTG curves moved toward the right-hand side, as well as downward, due to the shorter reaction time and the phenomenon of thermal hysteresis.22 So the corresponding rate of reaction also increases.
3.2 Kinetic analysis
In order to avoid the shortcomings of model-fitting methods, the activation energy of char was calculated by three common mode-free methods (FWO method, KAS method and Starink method). Thus one can avoid errors of selecting different kinetic model reduction f(α), and avoid the effect of the kinetic compensation effects.12,23 Fig. 2 illustrates the kinetic model fitting curves arising from three model-free kinetics methods. The value of Eα at each given α is determined from the slope of the fitting line. The results and their corresponding correlation coefficients r2 are listed in Table 2.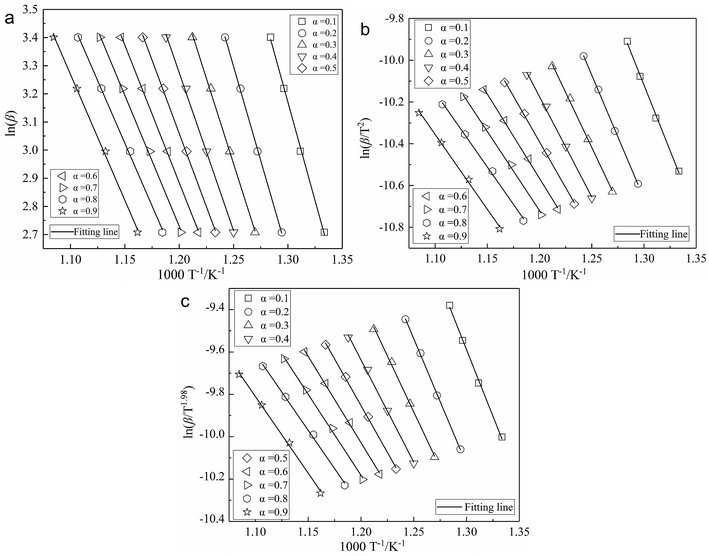 | ||
| Fig. 2 Curve fitting to kinetic model proposed by three model-free kinetics methods: (a) FWO method; (b) KAS method; (c) Starink method. | ||
| A | FWO method | KAS method | Starink method | |||
|---|---|---|---|---|---|---|
| Eα/kJ mol−1 | r2 | Eα/kJ mol−1 | r2 | Eα/kJ mol−1 | r2 | |
| 0.1 | 110.66 ± 2.72 | 0.999 | 104.35 ± 3.16 | 0.998 | 104.34 ± 2.92 | 0.998 |
| 0.2 | 105.75 ± 1.47 | 0.999 | 98.14 ± 1.53 | 0.999 | 98.59 ± 1.53 | 0.999 |
| 0.3 | 95.91 ± 2.37 | 0.999 | 87.50 ± 2.54 | 0.998 | 87.96 ± 2.54 | 0.998 |
| 0.4 | 88.77 ± 2.31 | 0.999 | 79.75 ± 2.49 | 0.998 | 80.23 ± 2.49 | 0.997 |
| 0.5 | 82.35 ± 1.54 | 0.999 | 72.78 ± 1.70 | 0.999 | 73.28 ± 1.69 | 0.998 |
| 0.6 | 77.23 ± 1.41 | 0.999 | 67.18 ± 1.57 | 0.999 | 67.69 ± 1.56 | 0.998 |
| 0.7 | 73.47 ± 1.82 | 0.999 | 63.01 ± 2.01 | 0.998 | 63.53 ± 2.00 | 0.997 |
| 0.8 | 70.31 ± 1.78 | 0.999 | 59.45 ± 1.97 | 0.998 | 59.99 ± 1.97 | 0.997 |
| 0.9 | 70.73 ± 1.85 | 0.999 | 59.60 ± 2.05 | 0.998 | 60.14 ± 2.04 | 0.998 |
| Average | 86.13 ± 1.92 | 0.999 | 76.86 ± 2.11 | 0.998 | 77.31 ± 2.08 | 0.998 |
As shown in Table 2, the change in trends of activation energy Eα according to the conversion α calculated by the three methods is consistent. The activation energy decreases with increasing conversion α. The activation energy calculated by the FWO, KAS and Starink methods was 110.66–70.31 kJ mol−1, 104.35–59.60 kJ mol−1 and 104.34–59.99 kJ mol−1, respectively. The average activation energy calculated by the FWO method is higher than that of the KAS and Starink methods by about 10 kJ mol−1, and the activation energy calculated by the KAS method was similar to the result of the Starink method. Besides, the correlation coefficients r2 of fitting lines proposed by the three model-free kinetics methods are all over 0.997, showing an acceptable accuracy of the results.20
As shown in Table 2, the activation energy at the early stage of reaction (α = 0.1–0.2) is high. It is considered that the char is difficult to ignite as a result of low volatility. The activation energy decreases quickly in the conversion range of 0.3–0.6, and reduces slowly between 0.6 and 0.8 conversion. It is determined that the char could burn rapidly after complete ignition, and less energy is needed to make stable combustion. Additionally, the activation energy increases slightly for α = 0.9. It is suggested that many pores in char are blocked by the ash particles covering the char particle surface, which increases the diffusion resistance of reactant gas, and has a great impact on the combustion reactivity and the burning-out of char. This result agreed with the results reported in previous research.
3.3 Determination of reaction model
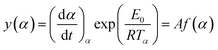 | (7) |
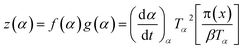 | (8) |
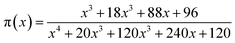 | (9) |
As seen from eqn (7) and (8), the shapes of the theoretical y(α) and/or z(α) master plots are entirely determined by the f(α) or g(α) functions because A is a constant. The experimental values of y(α) and/or z(α) can be determined for each value of α by the experimental values of Eα, dα/dt and Tα under different heating rates. So, for each value of α under different heating rates, one needs to determine experimental values of Eα, dα/dt and Tα related to this α and insert them into eqn (7) and (8). The resulting experimental values of y(α) and/or z(α) are plotted as a function of α and compared against theoretical y(α) and/or z(α) master plots to determine the most appropriate kinetic model. The most appropriate kinetic model is identified as the best match between the experimental and theoretical y(α) and/or z(α) master plots. Some differential and integral forms of kinetic models used in solid-state kinetics are listed in Table 3, and these kinetic models are frequently used in reaction mechanism investigations of a solid-state process, especially the coal or char combustion process.9,20 In this study, the difference between the theoretical and experimental values of y(α) is not obvious, so the z(α) master plots were used to determine the most appropriate kinetic model. The experimental and theoretical z(α) master plots for combustion of char under different heating rates are presented in Fig. 3.
| No. | Function name | Mechanisms | g(α) | f(α) |
|---|---|---|---|---|
| 1 | Jander equation | Diffusion, 3D (spherical symmetry) | [1 − (1 − α)1/3]1/2 | 3/2(1 − α)2/3[1 − (1 − α)1/3]−1 |
| 2 | G–B equation | Diffusion, 3D (column symmetry) | 1 − 2α/3 − (1 − α)2/3 | 3/2[(1 − α)−1/3 − 1]−1 |
| 3 | Anti–Jander equation | Diffusion, 3D | [(1 + α)1/3 − 1]2 | 3/2(1 + α)2/3[(1 + α)1/3 − 1]−1 |
| 4 | Z–L–T equation | Diffusion, 3D | [(1 − α)−1/3 − 1]2 | 3/2(1 − α)4/3[(1 − α)−1/3 − 1]−1 |
| 5 | Avrami–Erofeev equation | Random nucleation and nuclei growth, n = 3 | [−ln(1 − α)]1/3 | 3(1 − α)[−ln(1 − α)]2/3 |
| 6 | Avrami–Erofeev equation | Random nucleation and nuclei growth, n = 2 | [−ln(1 − α)]1/2 | 2(1 − α)[−ln(1 − α)]1/2 |
| 7 | Avrami–Erofeev equation | Random nucleation and nuclei growth, n = 3/2 | [−ln(1 − α)]2/3 | 3/2(1 − α)[−ln(1 − α)]1/3 |
| 8 | Avrami–Erofeev equation | Random nucleation and nuclei growth, n = 4/3 | [−ln(1 − α)]3/4 | 4/3(1 − α)[−ln(1 − α)]1/4 |
| 9 | Geometrical contraction | Shrinkage geometric shape (column symmetry) | 1 − (1 − α)1/3 | 3(1 − α)2/3 |
| 10 | Geometrical contraction | Shrinkage geometric shape (spherical symmetry) | 1 − (1 − α)1/2 | 2(1 − α)1/2 |
| 11 | Reaction order | Chemical reaction | (1 − α)−1 − 1 | (1 − α)2 |
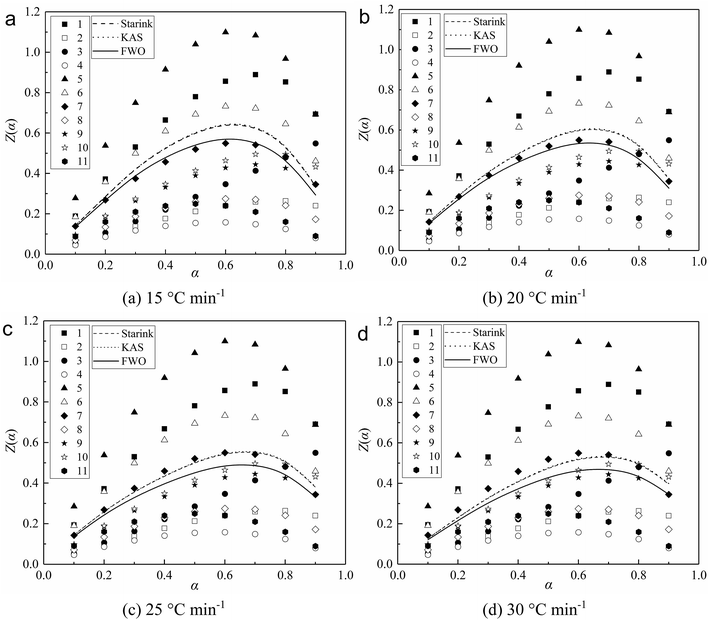 | ||
| Fig. 3 Experimental and theoretical z(α) master plots for combustion of char under different heating rates. | ||
As seen in Fig. 3, reaction model no. 7 is identified as the best match between the experimental and theoretical z(α) master plots. Especially when the heating rate is 15 and 25 °C min−1, the experimental z(α) master plots were basically identical with the no. 7 theoretical z(α) master plots. And the little differences between the experimental and the no. 7 theoretical z(α) master plots are considered to be the inaccuracy of the approximation of the temperature integral by Senum and Yang.10 It can be determined that reaction model no. 7 (f(α) = 3/2(1 − α)[−ln(1 − α)]1/3) is the most probable mechanism function that describes the reaction process of char combustion.
Under certain heating rates, the three different experimental values of z(α) were determined for each value of α by the experimental values of Eα calculated by the three mode-free methods. As seen from Table 2, the activation energy calculated by the KAS method was similar to the result of Starink method, so the corresponding shapes of the experimental z(α) master plots are similar. Besides, the experimental values of z(α) determined by the experimental values of Eα calculated by the FWO method were obviously less than the results obtained according to the KAS and Starink methods. It is determined that using single mode-free methods to calculate the activation energy will affect the validity of the Malek method. So in order to improve the reliability of the Malek method in determining the most appropriate kinetic model, we suggest that researchers should combine different mode-free methods with the Malek method to determine the most appropriate kinetic model.
It can be observed that the three different experimental values of z(α) all reduced with increasing heating rate. It is considered that the experimental values of Eα calculated by the same mode-free method are the same at different heating rates. And the experimental values of z(α) were determined by the experimental values of dα/dt and Tα at different heating rates. Generally, the char combustion still matches well using the Avrami–Erofeev equation controlled by nucleation and nuclei growth models. Especially when n equals 3/2, it can achieve the best match between the experimental and theoretical z(α) master plots.
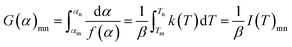 | (10) |
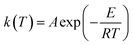 | (11) |
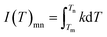 | (12) |
As seen from eqn (12), for the temperatures Tm and Tn being the same for all experiments, the value of I(T)mn is constant.25 So a plot of the values of G(α)mn versus 1/β will lead to a straight line with an intercept of zero if the differential conversion function of most appropriate kinetic model f(α) is chosen.25,26 Comparing with the Malek method, the main advantage of this method is that it does not require one to calculate the activation energy Eα in advance; furthermore, it is not based on any assumption concerning the temperature integral, thus imparting a higher degree of precision to the results.25
In order to avoid some error caused by the choice of Tm and Tn, their values in this experiment were considered such that they should be between the ignition temperature and burnout temperature of char combustion at various heating rates. And the corresponding parameter values could reflect well the relationship between α and T, β. So Tm and Tn were from 535 °C to 575 °C in this study. The correlation coefficient r and the absolute value of intercept I of various straight lines of G(α)mn versus 1/β are listed in Table 4. In practice, a better correlation coefficient r (r tending to 1) and a better intercept I (I tending to 0) can be used to choose the most probable mechanism function.27–29
| No. | Tm = 535 °C | Tn = 545 °C | Tm = 545 °C | Tn = 555 °C | Tm = 555 °C | Tn = 565 °C | Tm = 565 °C | Tn = 575 °C |
|---|---|---|---|---|---|---|---|---|
| r | I | r | I | r | I | r | I | |
| 1 | 0.99988 | 0.01223 | 0.99970 | 0.01244 | 0.98825 | 0.01563 | 0.99528 | 0.01425 |
| 2 | 0.99077 | 0.01206 | 0.99245 | 0.01620 | 0.99763 | 0.01825 | 0.99815 | 0.02151 |
| 3 | 0.99974 | 0.00295 | 0.99949 | 0.00249 | 0.98049 | 0.00087 | 0.95335 | 0.00066 |
| 4 | 0.97119 | 0.04224 | 0.96601 | 0.08169 | 0.96547 | 0.14799 | 0.95623 | 0.29972 |
| 5 | 0.99949 | 0.02236 | 0.99978 | 0.01934 | 0.99596 | 0.01980 | 0.99865 | 0.01193 |
| 6 | 0.99921 | 0.00907 | 0.99924 | 0.00362 | 0.99867 | 0.00348 | 0.99857 | 0.01030 |
| 7 | 0.99988 | 0.00413 | 0.99993 | 0.00470 | 0.99986 | 0.00047 | 0.99995 | 0.02959 |
| 8 | 0.99788 | 0.02684 | 0.99756 | 0.04080 | 0.99912 | 0.04752 | 0.99694 | 0.07783 |
| 9 | 0.99856 | 0.01243 | 0.99892 | 0.01510 | 0.99922 | 0.01382 | 0.99943 | 0.01747 |
| 10 | 0.99952 | 0.01183 | 0.99991 | 0.01225 | 0.99629 | 0.00671 | 0.99728 | 0.00598 |
| 11 | 0.99988 | 0.01223 | 0.9997 | 0.01244 | 0.98825 | 0.01563 | 0.99528 | 0.01425 |
As shown in Table 4, the best correlation coefficient (all the values of correlation coefficient for the different ranges of temperature exceed 0.999) is obtained for no. 7 straight line. And the values of the intercept are very low, being just higher than those of no. 3 straight line. However, the correlation coefficients of no. 3 straight line are significantly lower than those of the others at temperatures from 555 °C to 575 °C. Besides, the correlation coefficients r and intercept I of no. 6 straight line also were reliable. This is because the no. 6 and no. 7 straight lines depend on the nucleation and nuclei growth models. Generally, the Avrami–Erofeev equation (n = 3/2) (f(α) = 3/2(1 − α)[−ln(1 − α)]1/3) represents the most probable combustion mechanism of char. These results suggested that nucleation and nuclei growth were predominant during the main combustion process of char. The nucleation and nuclei growth models indicated char has fluctuating local energies from imperfections due to surfaces, edges, cracks, and dislocations caused by the release of volatiles.30 Such imperfections are sites for reaction nucleation, and are called nucleation sites. The reaction activation energy is minimized at these nucleation sites.30 So the ignition process of char first takes place in these nucleation sites. With the process of reaction, these nuclei gradually grow until the reaction is finished.
3.4 The kinetic compensation effects
By substituting the mechanism function f(α) values of kinetic model no. 7 and the activation energy Eα determined using the three model-free methods into eqn (4)–(6), the various pre-exponential factors Aα are obtained. Various linear curve fits were plotted for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Aα versus Eα. The results in Fig. 4 shown that Aα and Eα fit well to the equation of kinetic compensation effects (ln
Aα versus Eα. The results in Fig. 4 shown that Aα and Eα fit well to the equation of kinetic compensation effects (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = aE + b). Three fitting curves all have high correlation coefficient (r > 0.998). These results all demonstrate a strong correlation between the activation energy Eα and the pre-exponential factor Aα. This indicates that the kinetic compensation effect does occur in the char combustion process,9 which also proves the applicability of the kinetic model (f(α) = 3/2(1 − α)[−ln(1 − α)]1/3) for describing the reaction process of char combustion.
A = aE + b). Three fitting curves all have high correlation coefficient (r > 0.998). These results all demonstrate a strong correlation between the activation energy Eα and the pre-exponential factor Aα. This indicates that the kinetic compensation effect does occur in the char combustion process,9 which also proves the applicability of the kinetic model (f(α) = 3/2(1 − α)[−ln(1 − α)]1/3) for describing the reaction process of char combustion.
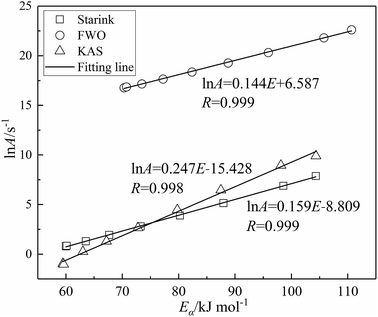 | ||
| Fig. 4 Compensation effect between activation energy and pre-exponential factor for combustion of char. | ||
4 Conclusions
In this paper, the combustion reaction kinetics of pyrolytic char of low-rank coal was investigated by using thermal analysis technology. The following conclusions have been drawn:(1) The activation energy Eα calculated by FWO, KAS and Starink methods was 110.66–70.31 kJ mol−1, 104.35–59.60 kJ mol−1 and 104.34–59.99 kJ mol−1, respectively. The activation energy Eα decreased with increasing conversion. An oxygen-absorption mass-gain process of char had been observed before the char combustion. At the early stage of reaction (α = 0.1–0.2), the activation energy was high. Then it decreased quickly in the conversion range of 0.3–0.6, and reduced slowly between 0.6 and 0.8 conversion. Finally, the activation energy increased slightly at α = 0.9. The average activation energy calculated by the KAS method was similar to the result of the Starink method, and was lower than that of the FWO method by about 10 kJ mol−1.
(2) Determination of reaction model was carried out by Malek method and Popescu method. Results of both methods indicated that the Avrami–Erofeev equation (n = 3/2) (f(α) = 3/2(1 − α)[−ln(1 − α)]1/3) controlled by nucleation and nuclei growth models is the most probable reaction model in describing the reaction process of char combustion. The accuracy of the Malek method is affected by the changing of Eα and β. So combining different mode-free methods with the Malek method to determine the most appropriate kinetic model is suggested, and it is more reliable. Besides, the Popescu method also has a higher degree of precision due to its not being based on any assumption concerning the temperature integral. So combining the Malek method and the Popescu method to determine the most probable reaction model is reliable and accurate.
(3) The activation energy Eα and the pre-exponential factor Aα fit well to the equation of kinetic compensation effects (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A = aE + b). The kinetic compensation effect does occur in the char combustion process.
A = aE + b). The kinetic compensation effect does occur in the char combustion process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the National Key R&D Program of China (no. 2017YFB0602002) for financial support.References
- Y. Yao, J. G. Zhu and Q. G. Lu, Energy Fuels, 2015, 29, 3985–3991 CrossRef.
- Y. Yao, J. G. Zhu, Q. G. Lu and Z. X. Zhou, J. Therm. Sci., 2015, 24, 370–377 CrossRef.
- Y. Yao, L. Qinggang, J. Zhu, Z. Ouyang and Z. Zhou, Proceeding of the CSEE, 2015, 35, 4417–4422 Search PubMed.
- C. Y. Chao, W. U. Keng, D. U. Rui-Ling, Z. Li, X. U. Da-An and C. E. Zhu, Chinese Journal of Engineering, 2016, 38, 1532–1538 Search PubMed.
- M. J. Liu, J. Z. Liu, R. K. Wang, J. H. Zhou and K. F. Cen, J. China Coal Soc., 2012, 37, 444–448 Search PubMed.
- N. Z. J. Ren, Prog. Chem., 2006, 18, 410–416 Search PubMed.
- M. Sun, X. Ning, J. Zhang, K. Li, Q. Tang, Z. Liu, G. Wang and H. Wang, J. Therm. Anal. Calorim., 2018, 131, 983–992 CrossRef.
- J. Naktiyok, H. Bayrakceken, A. K. Ozer and M. S. Gulaboglu, J. Therm. Anal. Calorim., 2017, 129, 531–539 CrossRef.
- C. Wang, J. L. Zhang, G. W. Wang, K. X. Jiao, Z. J. Liu and K. C. Chou, Int. J. Miner., Metall. Mater., 2017, 24, 745–755 CrossRef.
- J. Malek, Thermochim. Acta, 1992, 200, 257–269 CrossRef.
- H. J. Song, G. R. Liu, J. Z. Zhang and J. H. Wu, Fuel Process. Technol., 2017, 156, 454–460 CrossRef.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Perez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19 CrossRef.
- C. D. Doyle, J. Appl. Polym. Sci., 1962, 6, 639–642 CrossRef.
- J. H. Flynn and L. A. Wall, J. Polym. Sci., Part C: Polym. Lett., 1966, 4, 323–328 Search PubMed.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38, 1881–1886 CrossRef.
- R. L. Blaine and H. E. Kissinger, Thermochim. Acta, 2012, 540, 1–6 CrossRef.
- M. J. Starink, Thermochim. Acta, 1996, 288, 97–104 CrossRef.
- M. J. Starink, Thermochim. Acta, 2003, 404, 163–176 CrossRef.
- Y. Chen, S. Mori and W. P. Pan, Thermochim. Acta, 1996, 275, 149–158 CrossRef.
- C. Zou, J. X. Zhao, X. M. Li and R. M. Shi, J. Therm. Anal. Calorim., 2016, 126, 1469–1480 CrossRef.
- K. Wang, J. Deng, Y. N. Zhang and C. P. Wang, J. Therm. Anal. Calorim., 2018, 132, 591–598 CrossRef.
- H. P. Liu, M. Q. Lu, P. Xu and Q. Wang, J. Therm. Anal. Calorim., 2017, 130, 1191–1200 CrossRef.
- N. Sbirrazzuoli, L. Vincent, A. Mija and N. Guigo, Chemom. Intell. Lab. Syst., 2009, 96, 219–226 CrossRef.
- G. I. Senum and R. T. Yang, J. Therm. Anal., 1977, 11, 445–447 CrossRef.
- C. Popescu, Thermochim. Acta, 1996, 285, 309–323 CrossRef.
- C. Popescu and E. Segal, Int. J. Chem. Kinet., 1998, 30, 313–327 CrossRef.
- X. Wang, X. Wang, G. Qin, M. Chen and J. Wang, J. Therm. Anal. Calorim., 2018, 1–7 Search PubMed.
- A. Ortega, Int. J. Chem. Kinet., 2001, 33, 343–353 CrossRef.
- V. Mamleev, S. Bourbigot, M. Le Bras, S. Duquesne and J. Sestak, Phys. Chem. Chem. Phys., 2000, 2, 4708–4716 RSC.
- A. Khawam and D. R. Flanagan, J. Phys. Chem. B, 2006, 110, 17315–17328 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |