Open Access Article
Open Access ArticleDensity functional theory investigation on iridium(III) complexes for efficient blue electrophosphorescence
Jian-Po Zhanga,
Ying Wanga,
Jian-Bo Mab,
Li Jin*a,
Fang-Tong Liua and
Fu-Quan Bai *b
*b
aCollege of Chemical and Pharmaceutical Engineering, Jilin Institute of Chemical Technology, Jilin 132022, People's Republic of China. E-mail: lijin@jlict.edu.cn; Fax: +86 432 62185234; Tel: +86 432 62185223
bState Key Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun 130023, People's Republic of China. E-mail: baifq@jlu.edu.cn; Fax: +86-431-88923907; Tel: +86-431-88498961
First published on 25th May 2018
Abstract
The geometrical structures, electronic structures, optoelectronic properties and phosphorescence efficiencies of four blue-emitting phosphors [Ir(fpmi)2(pyim)] (1), [Ir(pyim)2(fpmi)] (2), [Ir(fpmi)2(fptz)] (3), [Ir(tfmppz)2(pyim)] (4), [fpmi = 1-(4-fluorophenyl)-3-methylimdazolin-2-ylidene-C,C2′; pyim = 2-(1H-imidazol-2-yl)pyridinato; fptz = 5-(trifluoromethyl-2H-1,2,4-triazol-3-yl)pyridine; tfmppz = 1-(4-trifluoromethylphenyl)pyrazolyl] were investigated by DFT and TDDFT methods. We first optimized geometrical structures in the ground and lowest triplet states, and computed the absorption and emission spectra of 1 and 5 [Ir(fpmi)2(pypz)] [pypz = 2-(1H-pyrazol-5-yl)pyridinato], which have been synthesized and characterized in a laboratory, using three functionals, B3LYP, CAM-B3LYP, and M062X. The calculation results were compared with relevant experimental data to assess the performance of the functionals. The suitable methods and functionals were then applied to study properties of the three other complexes. The HOMOs of 1–3 are composed of d(Ir) and π(cyclometalated ligands), however, the HOMO of 4 resides on the pyim ligand, while the LUMOs of all four complexes are dominantly localized on the chelating ligands. The calculated absorption results show that the corresponding absorption peaks for the four mainly studied complexes are almost at the same positions, however, the absorption intensities of the bands differ largely from each other. The lowest energy emissions of the four complexes are localized at 507, 512, 468, and 513 nm, respectively. In order to estimate their efficiencies, we carried out simplified radiative rate constant calculations. It turns out that complex 3, which possesses the shortest emission wavelength and the largest radiative rate constant (kr) value, can be considered as a highly efficient blue-emitting iridium(III) complex.
Introduction
Over the past decade, considerable attention has been paid to the development of organic light-emitting diodes (OLEDs), which are playing a vital role in future flat-panel display technologies and next generation solid-state energy-saving lighting sources.1,2 Phosphorescent emitters based on transition metal complexes have much higher efficiencies than their fluorescent counterparts and can achieve 100% internal quantum efficiency theoretically, because these complexes can harvest both singlet and triplet excitons.2–5 Therefore, a great deal of effort has been directed toward developing highly efficient phosphorescent transition metal complexes, especially iridium(III) complexes.6To attain a full-color display, phosphors that can emit three primary colors (red, green, and blue) are indispensable.7,8 Highly efficient green- and red-emitting Ir(III) complexes have been successfully synthesized.9–16 However, the challenge of synthesizing saturated blue phosphorescent materials with high efficiency still remains.17–19 The initially reported ‘blue’ phosphorescent complexes are bis[2-(2,4-difluorophenyl)pyridyl]iridium(acetylacetonate) [FIr(acac)] and bis[2-(2,4-difluorophenyl)pyridyl]iridium(picolinate) [FIrpic],20–23 and the device that utilizes FIrpic as the dopant emitter exhibited greenish-blue phosphorescence with Commission Internationale de l’Éclairage (x,y) coordinates (CIEx,y) of (0.16, 0.29),20 which cannot meet the requirement for true blue phosphors with an ideal CIEx,y of (0.14, 0.09).24 Subsequently, several corresponding blue-emitting complexes were reported, which were synthesized by varying the picolinate in FIrpic with other ancillary ligands, such as tetrakis(1-pyrazolyl)borate in FIr6,25 pyridyl triazolate ligand in FIrtaz,26,27 pyridyl tetrazolate in FIrN4 (ref. 26) and so on, all in the form of (dfppy)2Ir(L^X). Although the devices based on some of these complexes display excellent efficiency, the majority of these blue phosphors showed inferior color chromaticity which limits their practical applications in OLEDs.28 Further improvements were made by the adoption of N-heterocyclic carbene ligand and novel fluorine-substituted bipyridine based chelates.7,29 Recently, Chi and Chou et al. have made a significant contribution to the development of the blue-emitting phosphorescent OLEDs. Through bringing in a concept of non-π electron-conjugated cyclometalated ligand, they designed and synthesized a class of novel true-blue phosphors,29–33 especially the Ir(fppz)2(dfbdp)(fppzH): 5-(2-pyridyl)-3-trifluoromethylpyrazole, (dfbdpH: (2,4-difluorobenzyl)diphenylphosphine),32 on which the device based exhibits a true blue CIEx,y of (0.15, 0.11) and external quantum efficiency of ∼12%. More recently, they reported a series of Ir complexes applied tripodal, facially coordinated phosphite (or phosphonite), abbreviated as P^C2 chelate, as the ancillary ligand, which shows a lot of potential owing to its functionality of readily adjusting the electronic structures and of stabilizing the phosphors.24 The conclusion that we can draw from these researches is that the emission wavelength can be easily tuned through subtle changes in the ligands and a deep understanding of the structure–property relationships is quite significant in designing and synthesizing potentially highly efficient true-blue emitting complexes.34
The developments of computing equipment and methods make quantum calculation become an increasingly powerful tool for chemists and the quantum calculation shows significant advantages in many fields, in particular in elucidating the structure–property relationships. In a number of theoretical researches,35–39 the results of DFT calculations are comparable to the experimental data, such as bond length, emission wavelength, and spectroscopic properties and thus suggest their credibility.
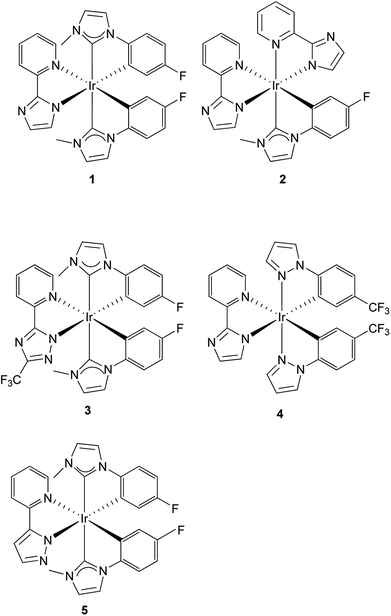
In this paper, we carried out a density functional theory (DFT) study on a novel complex, [Ir(fpmi)2(pyim)] (1),40 and its derivatives, [Ir(pyim)2(fpmi)] (2), [Ir(fpmi)2(fptz)] (3), [Ir(tfmppz)2(pyim)] (4), (fpmi = 1-(4-fluorophenyl-3-methylimdazolin)-2-ylidene-C,C2′; pyim = 2-(1H-imidazol-2-yl)pyridinato; fptz = 5-(trifluoromethyl-2H-1,2,4-triazol-3-yl)pyridine; tfmppz = 1-(4-trifluoromethylphenyl)pyrazolyl) (Scheme 1, Fig. 1).
Complex 1 has a high quantum yield with 30.7% and however, exhibits the sky-blue phosphorescence with vibronic peak wavelengths at 474 and 497 nm measured in toluene.40 According to what we know, the triazole has a larger HOMO–LUMO gap than that of imidazole,41 we thus anticipated that replacing the imidazole moiety with triazole group in complex 3 would lead to a blue-shifted emission wavelength.42
Moreover, we designed complexes 2, for which pyim ligand serves as the main ligand, and 4, for which tfmppz serves as the main ligand, and then studied electronic structures and phosphorescence properties of the four complexes, with the aim of finding suitable true-blue emitting complexes and of understanding their structure–property relationship. Finally, to study the phosphorescence efficiency of the four complexes, their radiative rate constant values were estimated.
Computational details
In all calculations, the “double-ζ” quality LANL2DZ basis set was employed for Ir atom,43 and 6-31G(d) basis set for non-metal atoms.44,45 A relativistic effective core potential (ECP) was used on Ir atom,43 which replaces the inner core electrons and accordingly leaves outer [(5s)2(5p)6] and (5d)6 as the valence electrons of Ir(III). Meanwhile, one f-type (αf = 0.14)46 polarization function was adopted for Ir atom.Considering that some experimental data, for example, the absorption and emission spectra, were measured in certain solutions, we thus used the polarized continuum model (PCM) approach to model the solvent effect.47–49
Recently, a large number of functionals have been developed to improve accuracy and save computational time. In this study, we examined the applicability of B3LYP (Becke's three parameter functional and the Lee–Yang–Parr functional),50,51 M062X,52 and CAM-B3LYP53 for our system. Because the crystal data of complex 1 lacks in the paper,40 for better comparing the reliability of the three functionals, geometry and excitation energies calculations were also performed on 5 (shown on Scheme 1 and Fig. 1). According to the ordinary process,54 the geometrical structures of 1 and 5 in the ground and lowest-lying triplet excited state were optimized using the DFT method with the above three functionals. To get accurate energies of reoptimizations, single-point calculations were performed with the dispersion-corrected functionals, but the computational accuracy is not increased immediately under the condition of increasing computational cost. Based on the respective optimized structures in the ground and excited states, TDDFT55–57 calculations utilizing these functionals associated with PCM model were carried out to acquire their vertical singlet–singlet and vertical singlet–triplet excitation energies. There is a newly developed method, the Spin-Flip TDDFT (SF-TDA), which performed better in computing phosphorescence energies of transition metal complexes than TDDFT.58 However, the TDDFT method was still used to calculate excitation energies in our work because it has been proven reliable and can implement PCM approach to stimulate the solvent effect.
The selected parameters of optimized geometrical structures of 1, 5 in the ground state and corresponding experimental data of 5 are presented in Table 1. The calculated geometries of 1 were also compared with experimental data of 5 as 1 is similar to 5 in terms of their chemical structures. From Table 1, the percent error indicates that the geometries optimized by CAM-B3LYP are in the best agreement with the measured values. However, with respect to absorption spectra, we can conclude from Fig. 2 and 3 that the absorption spectra computed by the B3LYP functional is more accurate than by other functionals comparing with experimental results.40 For example, the simulated absorption spectrum by B3LYP of 1 best reproduces the features, including band positions and separations, of its experimental spectrum. Meanwhile, for the simulated spectra of 5, it can be noticed that there is an absorption peak on the spectrum calculated by B3LYP appearing at approximately 356 nm that deviates from the corresponding experimental data (379 nm) by 23 nm,40 while there is almost no noticeable absorption peak around in the spectra simulated by CAM-B3LYP and M062X functionals. Because the geometries optimized by B3LYP are also comparable to experimental results (though not as good as CAM-B3LYP functional) and the absorption properties are quite important in our study, the B3LYP functional was used to optimize geometrical structures of three other complexes in the ground state and to calculate their absorption spectra. It should be indicated that the simulated absorption spectrum depends on the choice of half-width and it is set to 0.14 eV in this work.34
| Expta | 5 | 1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B3LYP | CAM-B3LYP | M062X | B3LYP | CAM-B3LYP | M062X | ||||||||
| Cal | δ | Cal | δ | Cal | δ | Cal | δ | Cal | δ | Cal | δ | ||
| Bond length (Å) | |||||||||||||
| a See ref. 40. | |||||||||||||
| Ir–C1 | 2.041 | 2.058 | 0.8 | 2.050 | 0.4 | 2.025 | 0.8 | 2.055 | 0.7 | 2.047 | 0.3 | 2.022 | 0.9 |
| Ir–C2 | 2.034 | 2.053 | 0.9 | 2.042 | 0.4 | 2.031 | 0.1 | 2.064 | 1.5 | 2.056 | 1.1 | 2.041 | 0.3 |
| Ir–C3 | 2.026 | 2.046 | 1.0 | 2.037 | 0.5 | 2.013 | 0.6 | 2.046 | 1.1 | 2.038 | 0.6 | 2.012 | 0.7 |
| Ir–C4 | 2.031 | 2.061 | 1.5 | 2.051 | 1.0 | 2.040 | 0.4 | 2.055 | 1.2 | 2.045 | 0.7 | 2.035 | 0.2 |
| Ir–N1 | 2.146 | 2.216 | 3.4 | 2.196 | 2.3 | 2.225 | 3.8 | 2.222 | 3.5 | 2.198 | 2.4 | 2.230 | 4.0 |
| Ir–N2 | 2.097 | 2.144 | 2.2 | 2.126 | 1.4 | 2.149 | 2.5 | 2.161 | 3.1 | 2.140 | 2.1 | 2.162 | 3.1 |
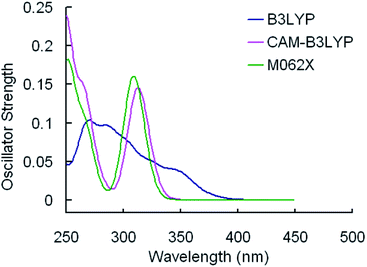 | ||
| Fig. 2 Simulated absorption spectra of 1 in CH2Cl2 media using TDDFT method with different functionals. | ||
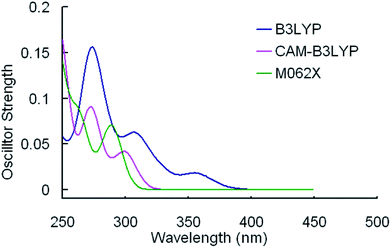 | ||
| Fig. 3 Simulated absorption spectra of 5 in CH2Cl2 media using TDDFT method with different functionals. | ||
The lowest emission wavelengths calculated by the three functionals on the basis of the excited state geometrical structures optimized by respective functionals are shown in Table 2. For 1, the result gained from M062X deviates from experimental data (497 nm) by 10 nm,40 while the emission wavelengths calculated by two other functions, B3LYP and CAM-B3LYP, lead to deviations of 43 nm and 81 nm, respectively. Meanwhile, it is obvious that the performance of M062X in calculating the emission wavelength of 5 is much better that other functionals. And previous work has proven that the M062X functional can be adopted to evaluate the singlet–triplet excitation energies of Ir complexes,54 and the non-local correlation effects and self-interaction error (delocalization SIE) have been systematically investigated by comparing the electron density distribution ρ(r) generated with a series of reference densities obtained by DFT that cover typical electron correlation effects. In this regard, the geometrical structures in the T1 state and the singlet–triplet excitation energies of three other complexes were calculated by TDDFT method with the M062X functional in this study. All the calculations were performed using the Gaussian 09 software package.59
Results and discussion
Molecular geometries structures in the ground and the excited states
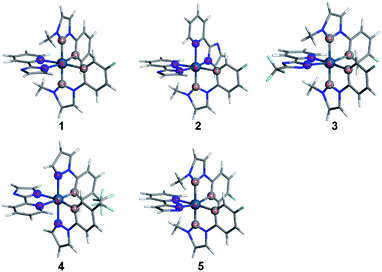
The optimized geometrical structures for 1–4 in the ground state are displayed in Fig. 1.Since Ir(III) has d6 configuration, all the complexes exhibit a pseudo-octahedral coordination geometry. Selected optimized geometrical parameters are listed in Table 3. In order to test if each of the optimized geometries is truly the global minimum of the potential energy surface, the vibrational frequencies calculation was performed for complexes 1–4. The results, in which there is no imaginary frequency, indicate that the optimized geometries are reasonable.
| 5 | 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Expta | S0 | T1 | S0 | T1 | S0 | T1 | S0 | T1 | |
| a See ref. 40. | |||||||||
| Bond length (Å) | |||||||||
| Ir–C1 | 2.041 | 2.055 | 2.015 | 2.041 | 2.015 | 2.053 | 2.020 | 2.042 | 2.001 |
| Ir–C2 | 2.034 | 2.064 | 2.051 | 2.000 | 1.967 | 2.056 | 2.035 | ||
| Ir–C3 | 2.026 | 2.046 | 2.019 | 2.043 | 2.017 | 2.028 | 2.004 | ||
| Ir–C4 | 2.031 | 2.055 | 2.033 | 2.063 | 2.042 | ||||
| Ir–N1 | 2.146 | 2.222 | 2.200 | 2.220 | 2.190 | 2.238 | 2.217 | 2.221 | 2.191 |
| Ir–N2 | 2.097 | 2.161 | 2.184 | 2.070 | 2.063 | 2.153 | 2.152 | 2.147 | 2.170 |
| Ir–N3 | 2.166 | 2.187 | 2.043 | 2.046 | |||||
| Ir–N4 | 2.064 | 2.044 | 2.147 | 2.044 | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Bond angle (°) | |||||||||
| C1–Ir–C2 | 79.11 | 78.84 | 79.33 | 79.29 | 79.65 | 78.90 | 79.27 | ||
| N1–Ir–N2 | 76.56 | 76.00 | 76.27 | 75.34 | 76.30 | 76.36 | 76.49 | ||
| C2–Ir–C4 | 168.54 | 169.90 | 169.55 | 169.92 | 169.10 | ||||
| N2–Ir–N4 | 168.35 | 168.49 | |||||||
| C1–Ir–N3 | 79.54 | 80.06 | |||||||
| N3–Ir–N4 | 77.79 | 77.81 | 174.16 | 174.08 | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Dihedral angle (°) | |||||||||
| C1–C2–Ir–C3 | 90.67 | 89.52 | 91.02 | 89.55 | |||||
| C1–Ir–C2–N1 | 95.96 | 95.07 | 95.35 | 95.07 | |||||
| N1–N2–Ir–N3 | 85.40 | 85.08 | |||||||
| N3–Ir–N4–C1 | 94.11 | 94.63 | |||||||
| C1–N3–Ir–C3 | 89.13 | 87.83 | |||||||
| C1–Ir–N3–N1 | 96.91 | 97.21 | |||||||
With respect to 1, two carbene fragments are at the trans position, whereas both of phenyl fragments are located in the cis position. As shown in Table 3, the dihedral angles of C1–C2–Ir–C3 (90.67) and C1–Ir–C2–N1 (95.96) are nearly 90 degree, suggesting that the three ligands are mutually perpendicular, which also can be observed in other complexes. It is worth noting that the bond distances of Ir–C2 and Ir–C4 are slightly longer than that of Ir–C1 and Ir–C3, respectively. The discrepancy can be traced back to the fact that the intense electron donation of the methyl group weakens the interaction between the carbene ligand and the metal center.39
It is notable that the bond distance of Ir–C (average = 2.055 Å) in 1 is significantly longer than that in complex 2 (2.020 Å). The different bond distances suggest that the bonds are not in the same electronic environment,8 though the two complexes have similar cyclometalated ligands. However, the average Ir–C distance (2.054 Å) in 3 is almost identical to that in 1, indicating that the replacement of imidazole moiety with triazole substituted by a CF3 group exerts no apparent effect on the Ir–C distances. Meanwhile, the lengths of Ir–C1 and Ir–C3 (average = 2.051 Å) in 1 are significantly longer than those in complex 4 (average = 2.035 Å), because the carbene is a stronger field ligand than the pyrazolyl.29 Moreover, for 1 and 3, since the π-accepting ability of the imidazole and triazole ring is bigger than that of the pyridine ring,54 the Ir–N1 bond lengths are longer than the Ir–N2.
The calculated geometrical parameters of 1–4 in the triplet excited states by M062X are also listed in Table 3. The selected dihedral angles in the two states are nearly identical, for example, the dihedral angles of C1–C2–Ir–C3 for complex 1 in ground and excited states are 90.67 and 89.52, respectively, meaning that there is only a slight distortion in geometry on going from the ground state to the T1 state.
The frontier molecular orbital properties
In order to investigate the effects of varying ligands on optoelectronic properties in nature, we would discuss comprehensively the ground state electronic structure in this part, particularly the HOMO and LUMO distributions, energy levels and energy gaps. Selected FMOs (frontier molecular orbitals) compositions of 1–4 are listed in Tables 4–7, and the HOMO and LUMO distributions and energy levels are illustrated in Fig. 4.| Orbital | Energy (eV) | MO composition (%) | Characteristics | |||
|---|---|---|---|---|---|---|
| Ir | fpmi-1 | fpmi-2 | pyim | |||
| L+4 | 0.09 | 6 | 23 | 63 | 7 | π*(fpmi) |
| L+3 | −0.17 | 8 | 63 | 26 | 2 | π*(fpmi) |
| L+2 | −0.29 | 10 | 25 | 57 | 8 | π*(fpmi) |
| L+1 | −0.58 | 2 | 5 | 4 | 89 | π*(pyim) |
| L | −1.04 | 7 | 3 | 2 | 88 | π*(pyim) |
| H | −4.96 | 18 | 8 | 5 | 69 | d(Ir) + π(pyim) |
| H−1 | −5.11 | 37 | 24 | 20 | 20 | d(Ir) + π(fpmi/pyim) |
| H−2 | −5.44 | 35 | 27 | 26 | 12 | d(Ir) + π(fpmi) |
| H−3 | −5.70 | 38 | 17 | 33 | 11 | d(Ir) + π(fpmi) |
| H−4 | −5.85 | 27 | 44 | 16 | 13 | d(Ir) + π(fpmi) |
| H−5 | −6.09 | 32 | 22 | 42 | 4 | d(Ir) + π(fpmi) |
| Orbital | Energy (eV) | MO composition (%) | Characteristics | |||
|---|---|---|---|---|---|---|
| Ir | pyim-1 | pyim-2 | fpmi | |||
| L+4 | −0.36 | 7 | 3 | 5 | 85 | π*(fpmi) |
| L+3 | −0.55 | 2 | 18 | 77 | 4 | π*(pyim) |
| L+2 | −0.78 | 2 | 76 | 16 | 6 | π*(pyim) |
| L+1 | −1.11 | 6 | 3 | 89 | 2 | π*(pyim) |
| L | −1.21 | 5 | 89 | 3 | 3 | π*(pyim) |
| H | −5.14 | 19 | 3 | 70 | 8 | d(Ir) + π(pyim) |
| H−1 | −5.25 | 11 | 78 | 7 | 5 | d(Ir) + π(pyim) |
| H−2 | −5.49 | 29 | 13 | 21 | 37 | d(Ir) + π(pyim/fpmi) |
| H−3 | −5.83 | 44 | 17 | 13 | 25 | d(Ir) + π(pyim/fpmi) |
| H−4 | −6.10 | 23 | 17 | 11 | 49 | d(Ir) + π(pyim/fpmi) |
| H−5 | −6.37 | 70 | 6 | 9 | 15 | d(Ir) + π(fpmi) |
| Orbital | Energy (eV) | MO composition (%) | Characteristics | |||
|---|---|---|---|---|---|---|
| Ir | fpmi-1 | fpmi-2 | fptz | |||
| L+5 | 0.34 | 7 | 77 | 13 | 4 | π*(fpmi) |
| L+4 | −0.01 | 7 | 14 | 72 | 8 | π*(fpmi) |
| L+3 | −0.18 | 9 | 80 | 9 | 3 | π*(fpmi) |
| L+2 | −0.39 | 11 | 9 | 5 | 74 | π*(fptz) |
| L+1 | −1.04 | 2 | 4 | 2 | 93 | π*(fptz) |
| L | −1.52 | 5 | 3 | 1 | 91 | π*(fptz) |
| H | −5.22 | 42 | 38 | 16 | 3 | d(Ir) + π(fpmi) |
| H−1 | −5.58 | 34 | 28 | 28 | 10 | d(Ir) + π(fpmi) |
| H−2 | −5.81 | 37 | 18 | 29 | 16 | d(Ir) + π(fpmi/pyim) |
| H−3 | −5.97 | 27 | 42 | 16 | 14 | d(Ir) + π(fpmi/pyim) |
| H−4 | −6.22 | 32 | 17 | 43 | 8 | d(Ir) + π(fpmi) |
| H−5 | −6.40 | 12 | 23 | 4 | 61 | d(Ir) + π(fpmi/pyim) |
| H−6 | −6.52 | 6 | 30 | 60 | 5 | π(fpmi) |
| H−7 | −6.94 | 4 | 16 | 14 | 66 | π(fpmi/fptz) |
| Orbital | Energy (eV) | MO composition (%) | Characteristics | |||
|---|---|---|---|---|---|---|
| Ir | tfmppz-1 | tfmppz-2 | pyim | |||
| L+4 | −0.19 | 6 | 23 | 63 | 8 | π*(ftmppz) |
| L+3 | −0.66 | 2 | 1 | 3 | 94 | π*(pyim) |
| L+2 | −1.16 | 5 | 32 | 3 | 61 | π*(tfmppz/pyim) |
| L+1 | −1.16 | 4 | 52 | 14 | 30 | π*(tfmppz/pyim) |
| L | −1.27 | 2 | 14 | 81 | 4 | π*(tfmppz) |
| H | −5.14 | 5 | 1 | 1 | 94 | π(pyim) |
| H−1 | −5.64 | 49 | 25 | 27 | 4 | d(Ir) + π(tfmppz) |
| H−2 | −5.92 | 52 | 10 | 7 | 30 | d(Ir) + π(tfmppz/pyim) |
| H−3 | −6.29 | 66 | 8 | 19 | 6 | d(Ir) + π(tfmppz) |
| H−4 | −6.38 | 2 | 45 | 41 | 13 | π(tfmppz/pyim) |
| H−5 | −6.65 | 3 | 5 | 21 | 72 | π(tfmppz/pyim) |
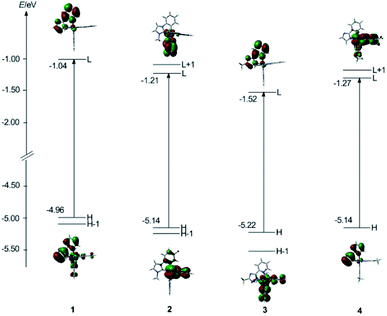 | ||
| Fig. 4 Presentation of the frontier molecular orbital energy levels and molecular orbital profiles of the HOMO and LUMO of four subject complexes calculated at DFT/B3LYP level. | ||
For complex 1, the HOMO is predominantly localized on the iridium metal center (18%) and the pyim ligand (69%), while the LUMO is principally composed of π*(pyim), indicating the ancillary ligand pyim is also involved in determining the emissive excited state of 1. Therefore, we anticipate that the emission color can be adjusted by grafting electron withdrawing groups or electron donating groups to the pyim ligand.2
With respect to 2, the HOMO is mainly composed of d(Ir) (19%) atom and π(pyim-2) (70%) and the LUMO is contributed principally by π*(pyim-1), almost identical to the compositions in 1. However, due to the large electronegativity of pyim ligand,8 the energy levels of HOMO (−5.14 eV) and LUMO (−1.21 eV) are lower than that of HOMO (−4.96 eV) and LUMO (−1.04 eV) in 1, respectively. We can see from Table 5 that the LUMO+1 is also contributed chiefly by one pyim ligand (89%), but not the one that mainly dominates the composition in the LUMO.
For 3, the HOMO is dominantly composed of d(Ir) and π(fpmi). Meanwhile, like that in 1, the LUMO resides primarily on the ancillary ligand (91%). Moreover, because triazole has a lower LUMO energy than that of imidazole and the LUMO is mainly composed of π(ancillary ligand) for 1, 3, the energy level of LUMO (−1.52 eV) of 3 is lower than that in 1 (−1.04 eV).
With respect to 4, unlike 1 and 3, for which the fpmi is the main ligand and the ancillary ligands contribute more to the LUMO, the LUMO is mainly contributed by the main ligand tfmppz, not the ancillary ligand pyim, verifying that the strong field of the fpmi ligand provides the LUMO level of the complexes principally located on the ancillary ligand.40 It is noteworthy that the HOMO resides mainly on pyim ligand, with less compositions from Ir atom (5%), which is different from most Ir complexes.
Absorptions in CH2Cl2 media
The calculated absorption spectra of the four complexes associated with their oscillator strengths, main configurations, and assignments with experimental wavelengths are shown in Table 8.| Complex | States | Oscillator | E/nm (eV) | Main configuration | Assignment | Expta/nm |
|---|---|---|---|---|---|---|
| a See ref. 40. | ||||||
| 1 | S1 | 0.017 | 368 (3.37) | H → L (88%) | MLCT/ILCT | |
| S2 | 0.0836 | 348 (3.57) | H−1 → L (79%) | MLCT/LLCT | 356 | |
| S3 | 0.0779 | 326 (3.80) | H−2 → L (91%) | MLCT/LLCT | ||
| S7 | 0.1317 | 303 (4.09) | H−3 → L (24%) | MLCT/LLCT | ||
| H−1 → L+1 (46%) | MLCT/LLCT/ILCT | |||||
| S10 | 0.0816 | 289 (4.28) | H−2 → L+1 (74%) | MLCT/LLCT | 292 | |
| S17 | 0.0744 | 272 (4.55) | H−5 → L (90%) | MLCT/LLCT | ||
| S19 | 0.1123 | 267 (4.65) | H−3 → L+2 (55%) | MLCT/LLCT/ILCT | ||
| 2 | S1 | 0.0255 | 367 (3.38) | H → L+1 (92%) | MLCT/ILCT | |
| S4 | 0.078 | 351 (3.53) | H−1 → L+1 (75) | MLCT/LLCT | ||
| S9 | 0.0826 | 312 (3.97) | H−3 → L+1 (77%) | MLCT/LLCT | ||
| S21 | 0.0716 | 275 (4.51) | H−2 → L+4 (69%) | MLCT/LLCT/ILCT | ||
| S22 | 0.2394 | 273 (4.54) | H−5 → L+1 (58%) | MLCT/LLCT | ||
| 3 | S1 | 0.0002 | 400 (3.10) | H → L (98%) | MLCT/LLCT | |
| S2 | 0.0481 | 360 (3.45) | H−1 → L (89%) | MLCT/LLCT | ||
| S5 | 0.0468 | 312 (3.98) | H−3 → L (90%) | MLCT/LLCT/ILCT | ||
| S12 | 0.121 | 281 (4.41) | H−5 → L (70%) | MLCT/LLCT/ILCT | ||
| S13 | 0.1015 | 277 (4.48) | H → L+4 (77%) | MLCT/LLCT/ILCT | ||
| S17 | 0.1067 | 269 (4.60) | H−2 → L+2 (71%) | MLCT/LLCT/ILCT | ||
| 4 | S1 | 0.0235 | 356 (3.49) | H → L (94%) | LLCT | |
| S2 | 0.1078 | 352 (3.53) | H → L+1 (91%) | LLCT/ILCT | ||
| S9 | 0.0719 | 303 (4.09) | H−2 → L+2 (33%) | MLCT/LLCT/ILCT | ||
| H → L+3 (25%) | ILCT | |||||
| S10 | 0.1237 | 302 (4.11) | H−2 → L+1 (32%) | MLCT/LLCT/ILCT | ||
| H−2 → L+2 (50%) | MLCT/LLCT/ILCT | |||||
| S14 | 0.1432 | 287 (4.33) | H−3 → L+1 (61%) | MLCT/LLCT | ||
| S18 | 0.1026 | 271 (4.58) | H−4 → L+2 (44%) | LLCT/ILCT | ||
| H−1 → L+4 (44%) | MLCT/LLCT/ILCT | |||||
| S20 | 0.1219 | 269 (4.61) | H−4 → L+2 (41%) | LLCT/ILCT | ||
| H−1 → L+4 (33%) | MLCT/LLCT/ILCT | |||||
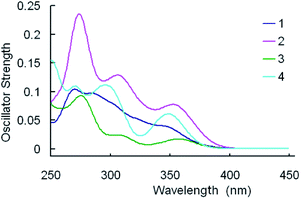
For clarity, merely the typical excited states possessing relatively larger oscillator strengths are listed. Meanwhile, the simulated Gaussian type absorption curves are displayed in Fig. 5.
As shown in Table 8, the lowest lying absorption bands of 1–4 are 368, 367, 400, 356 nm, respectively. The S0 → S1 transitions for the titled complexes are principally contributed by the HOMO → LUMO excitation, with the exception of 2, for which the HOMO → LUMO+1 excitation is the core configuration. According to above FMOs discussion, the HOMO of 1 is dominantly localized on the Ir atom and the pyim ligand, whereas the LUMO of 1 mainly resides on the pyim ligand, thus the lowest lying absorption can be characterized as [d(Ir) + π(pyim)] → [π*(pyim)] transition with mixing MLpyimCT/ILpyimCT characters. Correspondingly, for 2 and 3, the transitions can be described as characters of MLpyimCT/ILpyimCT, [d(Ir) + π(pyim)] → [π*(pyim)], and MLfptzCT/LfpmiLfptzCT, [d(Ir) + π(fpmi)] → [π*(fptz)], respectively. However, for complex 4, the HOMO is mainly localized on the pyim ligand, while the LUMO is primarily composed of π(tfmppz) (81%), therefore the lowest-lying absorption at 356 nm can be attributed to [π(pyim)] → [π*(pyim)] transition with ILpyimCT.
As shown in Table 8 and Fig. 5, the calculated values of the first distinguishable absorption bands are 348, 351, 360, and 352 nm for 1–4, respectively. The absorptions of 1 and 3 are contributed by the transition configuration of HOMO−1 → LUMO, while the HOMO–1 → LUMO+1 excitation is the main configuration for 2, and the HOMO → LUMO+1 for 4. As shown in Tables 4–7, for 1 and 3, LUMO resides primarily on the ancillary ligands, and HOMO is d(Ir) + π(chelate ligands), therefore, the MLCT/LLCT are the transition character for their absorptions around 350 nm. The absorption at 351 nm for 2 can be characterized as MLCT/LLCT, [d(Ir) + π(fpmi) → π*(fptz)]. For 4, the absorption at 352 nm can be ascribed to [π(pyim) → π*(pyim + tfmppz)] transition.
One can see from Fig. 5 that the calculated spectrum of complex 1 have two non-negligible higher energy absorption peaks at around 289, and 267 nm. However, in experiment, probably because they are too close to each other and are not well separated,60 or one of them is relatively weak and can't be detected experimentally, there is only one absorption peak localized at 292 nm in this region.40 In Fig. 5, the second apparent absorption bands of the four complexes are located at 285–315 nm. The absorption at 289 nm for 1 can be characterized as MLCT[d(Ir) → π*(pyim)] mixing with LLCT [π(fpmi) → π*(pyim)]. Likewise, with respect to 2, 3 and 4, the absorption at 312, 312 and 302 nm, respectively, can be classified as mixed character of MLCT/LLCT/ILCT.
Furthermore, the calculated highest-energy absorptions are 267, 273, 277, 271 nm for 1–4, respectively. The absorption at 267 nm for 1 is mainly contributed by the HOMO−3 → LUMO+2 configuration and can be characterized as MLCT/LLCT/ILCT, [d(Ir) + π(fpmi) → π* (fpmi)]. For 2 and 3, the absorptions are contributed by HOMO−5 [d(Ir) + π(fpmi)] → LUMO+2 [π*(fpmi)], and HOMO [d(Ir) + π(fpmi)] → LUMO+4 [π*(fpmi)], respectively. With respect to 4, the absorption at 271 nm is contributed by HOMO−4 → LUMO+2, [π(tfmppz) → π*(tfmppz + pyim)], and HOMO−1 → LUMO+4, [d(Ir) + π(tfmppz) → π*(tfmppz)].
It's notable that the corresponding absorption peak positions for the four complexes are practically identical to each other. Equally noteworthy is that the relative absorption intensities of the bands for the complexes are quite different, following the order: 2 > 4 > 1 > 3.
Phosphorescence spectra
On the basis of the optimized triplet excited-state geometries, TDDFT method was used to compute emission spectra of 1–4 in toluene solution with M062X functional, and the results are shown in Table 9. The FMOs concerning the lowest-lying emission transitions of the complexes are presented in Table 10 and Fig. 6.| MO composition (%) | Characteristics | |||||
|---|---|---|---|---|---|---|
| Ir | 1st ligand | 2nd ligand | 3rd ligand | |||
| 1 | fpmi-1 | fpmi-2 | pyim | |||
| L | −0.38 | 0.08 | 0.03 | 0.02 | 0.87 | π*(pyim) |
| H | −6.10 | 0.03 | 0.01 | 0.01 | 0.95 | π(pyim) |
| 2 | pyim-1 | pyim-2 | fpmi | |||
| L | −0.65 | 0.05 | 0.89 | 0.03 | 0.03 | π*(pyim) |
| H | −6.35 | 0.03 | 0.95 | 0.01 | 0.01 | π(pyim) |
| 3 | fpmi-1 | fpmi-2 | fptz | |||
| L | −0.97 | 0.04 | 0.03 | 0.02 | 0.92 | π*(fptz) |
| H−1 | −7.00 | 0.20 | 0.11 | 0.20 | 0.48 | d(Ir) + π(fpmi/fptz) |
| H−2 | −7.10 | 0.09 | 0.27 | 0.33 | 0.31 | π(fpmi/fptz) |
| 4 | tfmppz-1 | tfmppz-2 | pyim | |||
| L | −0.50 | 0.06 | 0.02 | 0.04 | 0.88 | π*(pyim) |
| H | −6.20 | 0.02 | 0.01 | 0.01 | 0.97 | π(pyim) |
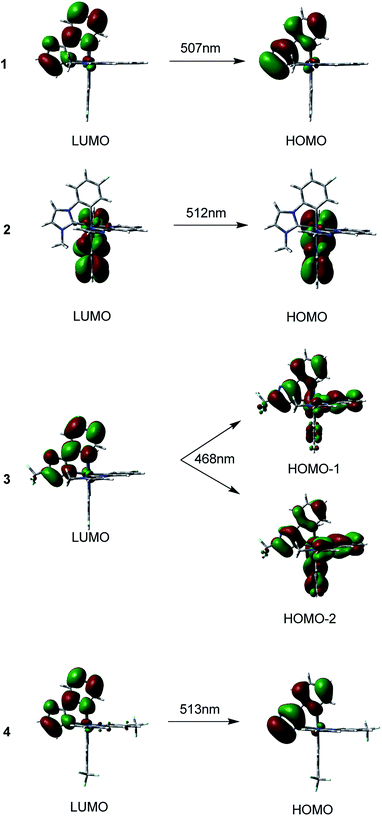
The maxima emission wavelengths of the four complexes under investigation are 507, 512, 468, 513 nm, respectively. The calculated emission wavelength of 1 is satisfactorily consistent with the experimental value of 497 nm,40 with a deviation of only 10 nm.
For 1, the 507 nm emission is principally contributed by HOMO → LUMO transition configuration. The HOMO for 1 is mainly localized on the pyim ligand, the LUMO is also primarily composed of π*(pyim). Thus, the calculated emission should be 3ILpyimCT character. Like 1, the emission of 2 at 512 nm is predominately contributed by transition of HOMO → LUMO. Since the HOMO of 2 has 89% π(pyim-1) and the LUMO is mainly localized on the pyim-1 moiety, the emission can be assigned to 3ILpyim-1CT character. With respect to 3, two transitions of HOMO−2 → LUMO and HOMO−1 → LUMO are responsible for the emission at 468 nm, which is blue-shifted compared with 1. Correspondingly, the calculated emission at 468 nm is contributed by the 3MLCT/3LLCT/3ILCT. As for 4, the calculated emission at 513 nm originates mainly from HOMO → LUMO. As the HOMO is contributed by π(pyim) with 97% compositions and the LUMO is composed of 88% π*(pyim), the phosphorescence at 513 nm can be assigned to 3ILpyimCT.36
The calculated emission wavelength of 3 at 468 nm is the shortest and is blue-shifted by almost 40 nm compared with 1. Thus, complex 3 can be considered as a potential pure-blue phosphorescent material.8
Prediction of the radiative rate constant for the complexes
It is meaningful to utilize our results of calculation to discuss the photoluminescence quantum yield, which is an important consideration when choosing which complex can be used as the dopant emitter for OLED device fabrication, in terms of the radiative rate constant kr.The radiative rate constant kr from the T1 state to the ground state (S0) can be theoretically calculated using the following formula:61–64
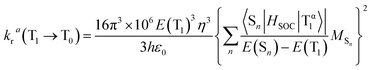 | (1) |
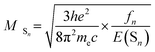 | (2) |
Therefore, by putting eqn (2) into (1), the kra can be depicted as
 | (3) |
In order to simplify the calculation, the spin–orbit integrals between two coupling states are reduced to that between two 5d atomic orbitals on iridium(III).61,62 It is important that the electronic spin–orbit coupling matrix element SOCMEs are often less sensitive to the level of electron correlation treatment than the energetic splittings.65,66 Hereupon, the matrix elements 〈Sn|HSOC|T1a〉 can be depicted as
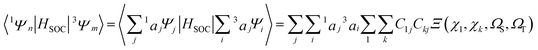 | (4) |
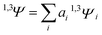 | (5) |
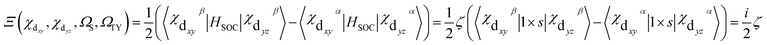 | (6) |
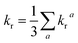 | (7) |
Thus, the calculation of radiative rate constant kr can be literally straightforward according to the above equations. Take the spin–orbit coupling between S2 and T1 of complex 1 for example, the T1 excited state is derived mainly from one transition: H → L (ai = 0.69), with H composed of Ir d orbital: 83% Ir(dyz), where the coefficient of natural atomic orbitals is obtained from NBO analysis.69 The S2 is derived dominately from the H−1 → L transition [ai = 0.47; 28% Ir(dxy)]. Thus, we could evaluate the 〈S2|HSOC|T1y〉 value, with theoretical values of ζ5d-Ir = 4430 cm−1 for the Ir(III) ion.70 The coefficients of natural atomic orbitals, and the use of eqn (4) and (6). Then, with E(S2), E(T1), f provided by TDDFT result, and η, the refractive index of the medium, the kr,2 can be obtained according to eqn (3). Further calculations for 1 and others can be done in the same way.
Presented in Table 11 are the t calculated radiative rate constants, kr. For 1, the number (kr = 3.90 × 104 s−1) is underestimated compared to the experimental radiative rate constant (kr,expt = 4.72 × 104) obtained from the phosphorescence lifetime and quantum yield: kr,expt = Φ/τ, however, the deviation, which can be due to the oversimplifications of spin–orbit interaction, is relatively small, and kr and kr,expt have the same magnitude. Thus, the present simplified analysis can be applicable in evaluating the kr values.
The calculated radiative decay rate constants kr are in the order: 3 (kr = 5.07 × 104 s−1) > 1 (kr = 3.90 × 104 s−1) > 2 (kr = 5.01 × 102 s−1) > 4 (kr = 76 s−1). It is obvious that the replacement of ligands leads to larger changes in kr values. The complex 4 has an extremely low kr value because the 1MLCT and 3MLCT transitions have almost no identical unoccupied ligand π* orbital, a requisite for the effective spin–orbit coupling between the triplet and singlet excited states. Meanwhile, complex 3 has the largest kr value and thus can be reasonably considered to be a highly efficient blue-emitting iridium(III) complex.
The gap between computational kr value and experimental radiative rate constant is still should not negligible, and first principle relativistic density functional theory may be only method for describing large and complex systems containing heavy elements very well. Meanwhile, it is of great value to extend it to the time-dependent domain in order to describe excited states and dynamical properties of heavy elements. Even though it is hard to treat the larger transition metal complexes throughout, but the exact two-component (X2C) Hamiltonian can be applied to construct the SOC operator to treat spin–orbit coupling as a perturbation for more accurate kr and kISC calculations.71 Our future work should be devoted to further improve the estimations of radiative and nonradiative rate constants and luminescence efficiencies in a quantitative basis.
Conclusions
The geometrical structures, electronic structures, optoelectronic properties and phosphorescence mechanism of four blue-emitting iridium(III) cyclometalated complexes were investigated in this study. Through the comparison of calculated results of 1, 5 with experimental data, we tested the applicability of three functionals and then applied the reasonable functionals to study three other complexes. The calculated results show that the HOMOs of 1–3 in the ground state were mainly localized on the metal center and the cyclometalated ligands. However, for 4, the HOMO mainly resides on pyim ligand, while the LUMOs of all these complexes are localized on the ligands. According to the frontier molecular orbital discussion, we can anticipate that the emission color can be adjusted by grafting electron withdrawing groups or electron donating groups to the pyim ligand in 1. Although the corresponding absorption peaks for the complexes are found at approximately the same positions, the absorption intensities of the bands differ largely from each other and follow the order: 2 > 4 > 1 > 3. As to phosphorescence behavior in toluene media, four complexes exhibit their emissions at 507, 512, 468 and 513 nm, respectively. Moreover, we evaluated the radiative rate constants and the results show 3 has the largest kr value and the complex 4 has the smallest kr value. That 1MLCT and 3MLCT transitions have almost no identical unoccupied ligand π* orbital probably explains the extremely low kr value of 4 (76 s−1). And 3 can be expected to be a highly efficient blue-emitting iridium(III) complex. In the end, we hope that our work in elucidating structure–property relationships and estimating the radiative rate constant kr values of the four complexes can provide experimenters with a guideline for the fabrication of more efficient blue phosphorescence-based OLED dyes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China (21405058) and the Young Scholar Training Program of Jilin University.Notes and references
- S.-C. Lo, R. E. Harding, C. P. Shipley, S. G. Stevenson, P. L. Burn and I. D. Samuel, J. Am. Chem. Soc., 2009, 131, 16681–16688 CrossRef PubMed.
- I. Avilov, P. Minoofar, J. Cornil and L. De Cola, J. Am. Chem. Soc., 2007, 129, 8247–8258 CrossRef PubMed.
- H.-W. Chen, J.-H. Lee, B.-Y. Lin, S. Chen and S.-T. Wu, Light: Sci. Appl., 2018, 7, 17168 CrossRef.
- M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef.
- F.-Q. Bai, J. Wang, B.-H. Xia, Q.-J. Pan and H.-X. Zhang, Dalton Trans., 2012, 41, 8841–8846 Search PubMed.
- T.-Y. Li, Y.-M. Jing, X. Liu, Y. Zhao, L. Shi, Z. Tang, Y.-X. Zheng and J.-L. Zuo, Sci. Rep., 2015, 5, 14912 CrossRef PubMed.
- S. J. Lee, K.-M. Park, K. Yang and Y. Kang, Inorg. Chem., 2008, 48, 1030–1037 CrossRef PubMed.
- L. Shi, B. Hong, W. Guan, Z. Wu and Z. Su, J. Phys. Chem. A, 2010, 114, 6559–6564 CrossRef PubMed.
- J. Markham, S.-C. Lo, S. Magennis, P. Burn and I. Samuel, Appl. Phys. Lett., 2002, 80, 2645–2647 CrossRef.
- S.-C. Lo, N. A. Male, J. P. Markham, S. W. Magennis, P. L. Burn, O. V. Salata and I. D. Samuel, Adv. Mater., 2002, 14, 975–979 CrossRef.
- T. D. Anthopoulos, J. P. Markham, E. B. Namdas, J. R. Lawrence, I. D. Samuel, S.-C. Lo and P. L. Burn, Org. Electron., 2003, 4, 71–76 CrossRef.
- T. D. Anthopoulos, M. J. Frampton, E. B. Namdas, P. L. Burn and I. D. Samuel, Adv. Mater., 2004, 16, 557–560 CrossRef.
- S. C. Lo, G. J. Richards, J. P. Markham, E. B. Namdas, S. Sharma, P. L. Burn and I. D. Samuel, Adv. Funct. Mater., 2005, 15, 1451–1458 CrossRef.
- C. Adachi, M. A. Baldo, S. R. Forrest and M. E. Thompson, Appl. Phys. Lett., 2000, 77, 904–906 CrossRef.
- F. Hua, S. Kinayyigit, J. R. Cable and F. N. Castellano, Inorg. Chem., 2005, 44, 471–473 CrossRef PubMed.
- J. Kavitha, S. Y. Chang, Y. Chi, J. K. Yu, Y. H. Hu, P. T. Chou, S. M. Peng, G. H. Lee, Y. T. Tao and C. H. Chien, Adv. Funct. Mater., 2005, 15, 223–229 CrossRef.
- D. J. Stufkens and A. Vlček Jr, Coord. Chem. Rev., 1998, 177, 127–179 CrossRef.
- S. Ranjan, S.-Y. Lin, K.-C. Hwang, Y. Chi, W.-L. Ching, C.-S. Liu, Y.-T. Tao, C.-H. Chien, S.-M. Peng and G.-H. Lee, Inorg. Chem., 2003, 42, 1248–1255 CrossRef PubMed.
- S.-C. Lo, C. P. Shipley, R. N. Bera, R. E. Harding, A. R. Cowley, P. L. Burn and I. D. Samuel, Chem. Mater., 2006, 18, 5119–5129 CrossRef.
- C. Adachi, R. C. Kwong, P. Djurovich, V. Adamovich, M. A. Baldo, M. E. Thompson and S. R. Forrest, Appl. Phys. Lett., 2001, 79, 2082–2084 CrossRef.
- R. Holmes, S. Forrest, Y.-J. Tung, R. Kwong, J. Brown, S. Garon and M. Thompson, Appl. Phys. Lett., 2003, 82, 2422–2424 CrossRef.
- S. Tokito, T. Iijima, Y. Suzuri, H. Kita, T. Tsuzuki and F. Sato, Appl. Phys. Lett., 2003, 83, 569–571 CrossRef.
- Y. You, S. H. Kim, H. K. Jung and S. Y. Park, Macromolecules, 2006, 39, 349–356 CrossRef.
- C. H. Lin, Y. Y. Chang, J. Y. Hung, C. Y. Lin, Y. Chi, M. W. Chung, C. L. Lin, P. T. Chou, G. H. Lee and C. H. Chang, Angew. Chem., 2011, 123, 3240–3244 CrossRef.
- X. Ren, J. Li, R. J. Holmes, P. I. Djurovich, S. R. Forrest and M. E. Thompson, Chem. Mater., 2004, 16, 4743–4747 CrossRef.
- S. J. Yeh, M. F. Wu, C. T. Chen, Y. H. Song, Y. Chi, M. H. Ho, S. F. Hsu and C. H. Chen, Adv. Mater., 2005, 17, 285–289 CrossRef.
- P. T. Chou and Y. Chi, Chem.–Eur. J., 2007, 13, 380–395 CrossRef PubMed.
- Y.-C. Chiu, Y. Chi, J.-Y. Hung, Y.-M. Cheng, Y.-C. Yu, M.-W. Chung, G.-H. Lee, P.-T. Chou, C.-C. Chen and C.-C. Wu, ACS Appl. Mater. Interfaces, 2009, 1, 433–442 Search PubMed.
- T. Sajoto, P. I. Djurovich, A. Tamayo, M. Yousufuddin, R. Bau, M. E. Thompson, R. J. Holmes and S. R. Forrest, Inorg. Chem., 2005, 44, 7992–8003 CrossRef PubMed.
- Y. H. Song, Y. C. Chiu, Y. Chi, Y. M. Cheng, C. H. Lai, P. T. Chou, K. T. Wong, M. H. Tsai and C. C. Wu, Chem.–Eur. J., 2008, 14, 5423–5434 CrossRef PubMed.
- C. Chang, Y. Cheng, Y. Chi, Y. Chiu, C. Lin, G. Lee, P. Chou, C. Chen, C. Chang and C. Wu, Angew. Chem., Int. Ed., 2008, 120, 4618–4621 CrossRef.
- Y. C. Chiu, J. Y. Hung, Y. Chi, C. C. Chen, C. H. Chang, C. C. Wu, Y. M. Cheng, Y. C. Yu, G. H. Lee and P. T. Chou, Adv. Mater., 2009, 21, 2221–2225 CrossRef.
- J.-Y. Hung, Y. Chi, I.-H. Pai, Y.-C. Yu, G.-H. Lee, P.-T. Chou, K.-T. Wong, C.-C. Chen and C.-C. Wu, Dalton Trans., 2009, 33, 6472–6475 RSC.
- X. Li, B. Minaev, H. Ågren and H. Tian, J. Phys. Chem. C, 2011, 115, 20724–20731 Search PubMed.
- Q. Peng, Q. Shi, Y. Niu, Y. Yi, S. Sun, W. Li and Z. Shuai, J. Mater. Chem. C, 2016, 4, 6829–6838 RSC.
- F. Q. Bai, X. Zhou, B. H. Xia, T. Liu, J. P. Zhang and H. X. Zhang, J. Organomet. Chem., 2009, 694, 1848–1860 CrossRef.
- H.-W. Fan, F.-Q. Bai, Z.-X. Zhang, Y. Wang, Z.-X. Qu, R.-L. Zhong and H.-X. Zhang, RSC Adv., 2017, 7, 17368–17376 RSC.
- M.-X. Song, Y. Li, D. Xu, R.-P. Deng, F.-Q. Bai and Z.-K. Qin, RSC Adv., 2016, 6, 68960–68963 RSC.
- L.-M. Xie, F.-Q. Bai, W. Li, Z.-X. Zhang and H.-X. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 10014–10021 RSC.
- C. H. Hsieh, F. I. Wu, C. H. Fan, M. J. Huang, K. Y. Lu, P. Y. Chou, Y. H. O. Yang, S. H. Wu, I. Chen and S. H. Chou, Chem.–Eur. J., 2011, 17, 9180–9187 CrossRef PubMed.
- K. Tamao, M. Uchida, T. Izumizawa, K. Furukawa and S. Yamaguchi, J. Am. Chem. Soc., 1996, 118, 11974–11975 CrossRef.
- E. Orselli, G. S. Kottas, A. E. Konradsson, P. Coppo, R. Fröhlich, L. De Cola, A. van Dijken, M. Büchel and H. Börner, Inorg. Chem., 2007, 46, 11082–11093 CrossRef PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef.
- A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef.
- G. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef.
- A. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 5121–5129 CrossRef PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- J. Wang, F.-Q. Bai, B.-H. Xia and H.-X. Zhang, J. Phys. Chem. A, 2011, 115, 11689–11695 CrossRef PubMed.
- J. Autschbach, T. Ziegler, S. J. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 116, 6930–6940 CrossRef.
- T. Helgaker and P. Jorgensen, J. Chem. Phys., 1991, 95, 2595–2601 CrossRef.
- K. L. Bak, P. Jorgensen, T. Helgaker, K. Ruud and H. J. r. A. Jensen, J. Chem. Phys., 1993, 98, 8873–8887 CrossRef.
- M. Kühn and F. Weigend, ChemPhysChem, 2011, 12, 3331–3336 CrossRef PubMed.
- M. J. Frish, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- I. Omae, Coord. Chem. Rev., 2016, 310, 154–169 CrossRef.
- Z. A. Siddique, Y. Yamamoto, T. Ohno and K. Nozaki, Inorg. Chem., 2003, 42, 6366–6378 CrossRef PubMed.
- K. Nozaki, J. Chin. Chem. Soc., 2006, 53, 101–112 CrossRef.
- S. Haneder, E. Da Como, J. Feldmann, J. M. Lupton, C. Lennartz, P. Erk, E. Fuchs, O. Molt, I. Münster and C. Schildknecht, Adv. Mater., 2008, 20, 3325–3330 CrossRef.
- S. Obara, M. Itabashi, F. Okuda, S. Tamaki, Y. Tanabe, Y. Ishii, K. Nozaki and M.-a. Haga, Inorg. Chem., 2006, 45, 8907–8921 CrossRef PubMed.
- Z. Cao, F. Wang and M. Yang, J. Chem. Phys., 2017, 146, 134108 CrossRef PubMed.
- F. Dinkelbach, M. Kleinschmidt and C. M. Marian, J. Chem. Theory Comput., 2017, 13, 749–766 CrossRef PubMed.
- G. S. M. Tong and C. M. Che, Chem.–Eur. J., 2009, 15, 7225–7237 CrossRef PubMed.
- Y. Komada, S. Yamauchi and N. Hirota, J. Phys. Chem., 1986, 90, 6425–6430 CrossRef.
- F. Weinhold and C. R. Landis, Chem. Educ. Res. Pract., 2001, 2, 91–104 RSC.
- S. Fraga, J. Karwowski and K. M. S. Saxena, Handbook of Atomic Data, Physical Science Data, Elsevier, Amsterdam, 1976 Search PubMed.
- X. Zhang, D. Jacquemin, Q. Peng, Z. Shuai and D. Escudero, J. Phys. Chem. C, 2018, 122, 6340–6347 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |