Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discovery of zirconium dioxides for the design of better oxygen-ion conductors using efficient algorithms beyond data mining†
Joohwi Lee *,
Nobuko Ohba
*,
Nobuko Ohba and
Ryoji Asahi
and
Ryoji Asahi
Toyota Central R&D Laboratories, Inc., Nagakute, Aichi 480-1192, Japan. E-mail: j-lee@mosk.tytlabs.co.jp
First published on 16th July 2018
Abstract
It is important to find crystal structures with low formation (Ev) and migration-barrier (Em) energies for oxygen vacancies for the development of fast oxygen-ion conductors. To identify crystal structures with lower Ev and Em than those of ground-state ZrO2, we first reoptimize the crystal structures of various oxides reported in the database, and then directly construct them using an evolutionary algorithm. For efficient searching, we employ the linearized ridge regression model for Ev using descriptors obtained from density functional theory calculations of the unit cells and apply the predicted Ev as a fitness value in the evolutionary algorithm. We also find a correlation between the Ev and Em for the crystal structures of ZrO2. On the basis of this correlation, we confirm that the newly constructed crystal structures, as well as certain reoptimized structures from the database, that possess low Ev also have Em lower than that of ground-state ZrO2. Our successful strategy consisting of a combination of the evolutionary algorithm, first-principles calculations, and machine-learning techniques may be applicable to other oxide systems in finding crystal structures with low Ev and Em.
1. Introduction
A high oxygen ion conductivity (σO) is an important property for applications1,2 such as the electrolytes of solid-oxide fuel cells (SOFC), oxygen separation membranes, and gas sensors. Low vacancy formation (Ev) and migration-barrier (Em) energies of oxygen vacancies VO are favorable for achieving a higher σO.3 Currently, Y-doped ZrO2 (YSZ) is widely used because of its advantages such as abundance, chemical stability, non-toxicity, and low cost. This material shows the σO of ∼10−2 S cm−1 at the high temperature of 1000 K.4 For useful industrial applications, it is necessary to have similar σO values at lower temperatures or a higher σO at a similar temperature. Indeed, several oxides such as Gd-doped CeO2 (GDC),5 pure or Er-doped δ-phase Bi2O3,6,7 and Sr- and Mg-doped LaGaO3 (LSGM)8,9 have been reported to show higher σO than YSZ at the same temperature. However, the need for the development of new oxygen-ion conductors remains.The type of crystal structure strongly affects the σO as well as Ev and Em. The monoclinic ground-state structure of ZrO2 (space group P21/c) is known to have a low σO. However, the σO can be significantly increased through phase transformation into either the tetragonal (space group P42/nmc) or cubic fluorite structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) upon doping with Y.5 The δ-phase Bi2O3 in the defective fluorite structure (its high-temperature phase) is known to have a high σO, whereas its α-phase counterpart is a low-temperature phase with a low σO.6 Reported crystal structures with high σO are mainly fluorites, perovskites,5 and their derivatives, such as the defective fluorite and melilite10 structures. However, we expect that other undiscovered crystal structures may have high σO values.
m) upon doping with Y.5 The δ-phase Bi2O3 in the defective fluorite structure (its high-temperature phase) is known to have a high σO, whereas its α-phase counterpart is a low-temperature phase with a low σO.6 Reported crystal structures with high σO are mainly fluorites, perovskites,5 and their derivatives, such as the defective fluorite and melilite10 structures. However, we expect that other undiscovered crystal structures may have high σO values.
The evolutionary algorithm is useful for the construction and search of crystal structures.11 This has been applied in combination with first-principles calculations for determining crystal structures with maximized or minimized functional properties (fitness values) such as enthalpy at high pressure,12–14 hardness,15 and dielectric constant.16 This algorithm is especially powerful for easily obtained fitness values, because it requires many individual crystal structures. From this perspective, the direct usage of the Ev or Em as a fitness value may be inefficient because these properties should be obtained from supercell calculations.17 In this case, one useful method is machine-learning techniques.
A regression analysis, one of the machine-learning techniques, is used to predict a target variable on the basis of already accumulated data, which can be used for descriptors (also called “predictor variables” or “representations”). If the descriptors are composed of “density functional theory (DFT)-unit-cell descriptors” that contain information regarding the unit-cells obtained only from DFT calculations,18,19 the prediction model can be constructed with the advantage of computational efficiency. Some regression models have employed descriptors obtained from DFT calculations of the unit-cells to predict target variables such as the melting temperatures of binary metals,20 GW-level band gaps for inorganic compounds,21 and interatomic potentials.22 In addition, Deml et al.23 constructed a prediction equation for Ev using ordinary least-square regression (OLSR) with four unit-cell descriptors and 45 oxides. However, it is not yet guaranteed whether this prediction model maintains accuracy in predicting Ev for various types of crystal structures.
The purpose of the present study is to propose an efficient method to find various crystal structures with lower Ev and Em values than those of ground-state ZrO2. To this end, we reoptimized the reported crystal structures of various oxides in the Materials Project Database (MPD),24 one of the inorganic materials databases based on first-principles calculations, and reconsidered their Ev and Em. We constructed a prediction model for Ev based on linearized regression analyses using DFT-unit-cell descriptors and subsequently constructed crystal structures based on the predicted Ev using the evolutionary algorithm. We also investigated the relationship between Ev and Em for the crystal structures of ZrO2. Finally, we found crystal structures having Ev and Em values lower than those of ground-state ZrO2.
2. Methodology
2.1. Overview
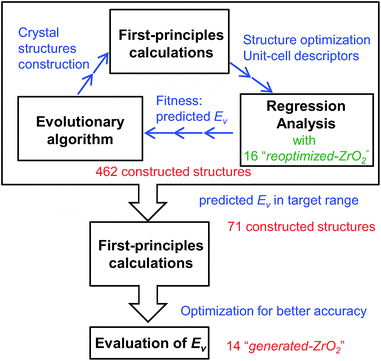
First, we reoptimized the crystal structures of several oxides from the MPD24 for ZrO2. The computed Ev and other properties of the unit-cells are used as the target variable and descriptors, respectively, for the regression analyses.Fig. 1 shows the workflow for the construction of the crystal structures and prediction of the Ev. New structures were constructed using the evolutionary algorithm. First-principles calculations were performed to optimize the constructed crystal structures and extract the DFT-unit-cell descriptors. The regression analyses were then applied to obtain the predicted Ev. In total, 462 crystal structures were constructed through the repetition of cycles comprising the construction of crystal structures, calculation of DFT-unit-cell descriptors from the constructed structures, and application of regression analysis to predict Ev.
We identified crystal structures with predicted Ev in the target range and performed structural optimization again under tighter conditions. The accurate Ev of the remaining crystal structures were computed from their supercells. Finally, we obtained 14 newly constructed crystal structures that have both the predicted and computed Ev.
More details regarding each method are found in the next subsection.
2.2. Crystal structures for the training set in regression analysis
As mentioned in the previous subsection, we collected various crystal structures of oxides with cation-to-O ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in the MPD24 for use as training data in regression analysis and for considering their Ev and Em. We set the number of atoms in the unit-cells to ≤30. We performed first-principles calculations for structural optimization and computation of the Ev. To identify crystal structures with reliable Ev, we adopted several filters. Firstly, the crystal structures must satisfy the convergence of electronic and ionic relaxations. Secondly, they should be non-metallic. Thirdly, they should maintain a displacement of the center of the VO site of 0.1 Å at most after structural relaxations; this is for avoiding the convergence of crystal structures into other crystal structures. On the basis of these filters, we collected 16 crystal structures of ZrO2 with the computed Ev, as summarized in Table 1. Henceforth, this set of 16 crystal structures is called “reoptimized-ZrO2” and each structure in the set is called by its space group type. Excluded crystal structures are summarized in Table S1 in ESI.† All the crystal structures in this study are displayed using the VESTA program.25
2 in the MPD24 for use as training data in regression analysis and for considering their Ev and Em. We set the number of atoms in the unit-cells to ≤30. We performed first-principles calculations for structural optimization and computation of the Ev. To identify crystal structures with reliable Ev, we adopted several filters. Firstly, the crystal structures must satisfy the convergence of electronic and ionic relaxations. Secondly, they should be non-metallic. Thirdly, they should maintain a displacement of the center of the VO site of 0.1 Å at most after structural relaxations; this is for avoiding the convergence of crystal structures into other crystal structures. On the basis of these filters, we collected 16 crystal structures of ZrO2 with the computed Ev, as summarized in Table 1. Henceforth, this set of 16 crystal structures is called “reoptimized-ZrO2” and each structure in the set is called by its space group type. Excluded crystal structures are summarized in Table S1 in ESI.† All the crystal structures in this study are displayed using the VESTA program.25
| Space group type | Oxide reported in MPD24 | E − E(ground-state) (eV per atom) | EgGGA+U (eV) | Computed Ev (eV)a |
|---|---|---|---|---|
| a Values in the parentheses are the minimum and the maximum values in sequence, which depend on the kinds of O sites. | ||||
| P21/c | ZrO2 | 0.000 | 3.53 | 6.15 (6.13, 6.16) |
| Pbca | ZrO2 | 0.007 | 3.52 | 6.15 (6.14, 6.15) |
| I41/amd | ZrO2 | 0.013 | 3.89 | 6.40 |
| P21/m | TiO2 | 0.017 | 3.85 | 6.40 (6.38, 6.41) |
| C2/c | TiO2 | 0.018 | 3.85 | 6.38 |
| Pca21 | ZrO2 | 0.019 | 3.78 | 5.93 (5.93, 5.93) |
| P41212 | SiO2 | 0.021 | 3.51 | 6.71 |
| P42/mnm | ZrO2 | 0.026 | 3.55 | 6.68 |
| Pnma | TiO2 | 0.028 | 4.11 | 6.06 (6.01, 6.10) |
| P42/nmc | ZrO2 | 0.029 | 3.89 | 5.81 |
| Pbcn | ZrO2 | 0.032 | 3.85 | 5.82 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
ZrO2 | 0.037 | 3.38 | 5.84 |
| P4/n | ZrO2 | 0.054 | 3.34 | 5.71 (5.35, 5.80) |
| Pna21 | SiO2 | 0.116 | 2.80 | 5.14 (4.97, 5.30) |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
SiO2 | 0.126 | 3.75 | 5.93 (5.87, 6.00) |
| P63mc | TiO2 | 0.179 | 3.75 | 6.51 (6.19, 6.76) |
2.3. Regression analysis
The linearized ridge regression (RR)26 model uses a minimization function of the OLSR with a L2-norm penalty term that is given by
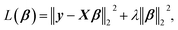 | (1) |
Table 2 shows the list of the DFT-unit-cell descriptors. To predict Ev of the crystal structures of ZrO2, RR was employed with all 11 descriptors. The OLSR with three descriptors (x01–x03), suggested by Deml et al.,23 was also used for comparison. Henceforth, the former and latter prediction models are referred to as RR-11-descriptors and OLSR-3-descriptors, respectively.
| Name | Unit-cell-descriptor | Note |
|---|---|---|
| x01 | Formation energy (ΔEf) | Relative energy from the Zr metal and the half-energy of O2 gas molecule |
| x02 | Band-gap (EgGGA+U) | From the electronic DOS |
| x03 | Center of O 2p-band (EO2p) | From the minimum energy of the electronic DOS to the VBM |
| x04 | Volume per atom | |
| x05 | Average bond length (rZr–O) | Cutoff radius of 2.4 Å |
| x06 | Coordination number of O (CNO) | Cutoff radius of 2.4 Å |
| x07 | Mean of |x02 − x02(ground-state)| | |
| x08 | Mean of |x03 − x03(ground-state)| | |
| x09 | Mean of |x04 − x04(ground-state)| | |
| x10 | Mean of |x05 − x05(ground-state)| | |
| x11 | Mean of |x06 − x06(ground-state)| |
The training and test data were randomly divided in the ratio of 75% to 25%. To avoid overfitting, three-fold cross-validation (CV) was also used. The prediction errors were defined as root-mean-square-errors (RMSE) that were averaged for 30 different random samplings of the training set.
2.4. Structure construction using an evolutionary algorithm
We used the USPEX11,27,28 code to generate crystal structures based on an evolutionary algorithm. Here, the predicted Ev was used as a fitness value for minimizing the quantity |predicted Ev − 5 eV|. This form was applied to focus on the search for crystal structures with Ev values moderately lower than that (6.15 eV) of the ground-state P21/c structure.Each newly constructed unit-cell of ZrO2 was set to have four Zr and eight O atoms. Sixty first-generation crystal structures were produced using randomly selected space group types. The fitness value was obtained after structural relaxation based on the first-principles calculations. From the second generation onwards, new crystal structures were produced by genetic operators, namely, heredity (30%), random symmetric algorithm (30%), and mutation (40%). Each generation consisted of 40 crystal structures. The evolutionary algorithm was terminated if the best-ranked crystal structure was not changed over eight generations or after the number of generations reached 30.
2.5. First-principles calculations
All first-principles calculations were performed using the projector augmented-wave (PAW)29,30 method implemented in the Vienna Ab-initio Simulation Package (VASP)31,32 within the framework of the Generalized Gradient Approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) form,33 including on-site Coulomb interaction34 with an effective U − J of 3 eV (ref. 35) (GGA+U) for the d-orbitals of Zr. Here, we employed the GGA+U rather than the GGA to decrease the number of metallic crystal structures constructed by the evolutionary algorithm (See Fig. S1 in ESI†). The valence electrons occupied the 4s, 4p, 5s, and 4d orbitals for Zr, and the 2s and 2p orbitals for O.During the construction of crystal structures by the evolutionary algorithm, structural relaxations of the unit-cells (with the associated changes in lattice constants and atomic coordinates) were modeled until the interatomic force on each atom was reduced to within 0.01 eV Å−1. To avoid bad convergence, we constrained the number of ionic iteration cycles to the maximum of 120. The cutoff energy was set to 400 eV. The Brillouin zone was sampled by Γ-centered meshes with the density of 2π × 0.12 Å−1 for structural optimization such as fast screening. The calculations for the total energy and electronic density of states (DOS) of the optimized unit-cells were performed with a finer sampling of 2π × 0.08 Å−1 of the Brillouin zone. Subsequently, structural optimizations were performed for the survivors of the evolutionary algorithm again, but in tighter computational conditions: the cutoff energy was increased to 500 eV, and the Brillouin zone was sampled using Γ-centered 8 × 8 × 8 meshes.
The computed Ev were obtained using the supercell method17 as follows,
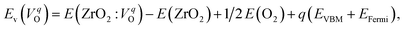 | (2) |
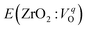 is the energy of a supercell including a VO, E(ZrO2) is the energy of a supercell of pure ZrO2, 1/2E(O2) is the half-energy of an O2 gas molecule (used as the chemical potential of O for the O-rich condition), q is the unit charge, EVBM is the energy of the valence band maximum (VBM), and EFermi is the Fermi level, that is a variable changes between the VBM and the conduction band minimum (CBM). The chemical potential of O depends on the processing condition, but it provides a constant shift to the Ev of all of the crystal structures of ZrO2 and the general consequence related to the ranks of the Ev are unchanged. Therefore, we only considered the O-rich condition in this study (See other O-rich conditions in Table S2 in ESI†). We calculated both of the Ev for a neutral oxygen vacancy
is the energy of a supercell including a VO, E(ZrO2) is the energy of a supercell of pure ZrO2, 1/2E(O2) is the half-energy of an O2 gas molecule (used as the chemical potential of O for the O-rich condition), q is the unit charge, EVBM is the energy of the valence band maximum (VBM), and EFermi is the Fermi level, that is a variable changes between the VBM and the conduction band minimum (CBM). The chemical potential of O depends on the processing condition, but it provides a constant shift to the Ev of all of the crystal structures of ZrO2 and the general consequence related to the ranks of the Ev are unchanged. Therefore, we only considered the O-rich condition in this study (See other O-rich conditions in Table S2 in ESI†). We calculated both of the Ev for a neutral oxygen vacancy 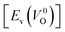 and a doubly charged oxygen vacancy
and a doubly charged oxygen vacancy 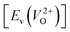 . For a prediction model based on the evolutionary algorithm and regression analysis,
. For a prediction model based on the evolutionary algorithm and regression analysis, 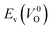 was used as the computed Ev. The calculations for the supercell with a VO were performed until the interatomic forces on each atom were reduced to within 0.02 eV Å−1 with fixed lattice constants. The sizes of the supercells were set such that the lengths of the three lattice constants were ∼10 Å. Γ-centered 2 × 2 × 2 meshes were used to describe the k-space. The types of O sites were confirmed by SPGLIB implemented in PHONOPY.36,37 For a crystal structure containing more than two types of O sites, the computed Ev values were averaged.
was used as the computed Ev. The calculations for the supercell with a VO were performed until the interatomic forces on each atom were reduced to within 0.02 eV Å−1 with fixed lattice constants. The sizes of the supercells were set such that the lengths of the three lattice constants were ∼10 Å. Γ-centered 2 × 2 × 2 meshes were used to describe the k-space. The types of O sites were confirmed by SPGLIB implemented in PHONOPY.36,37 For a crystal structure containing more than two types of O sites, the computed Ev values were averaged.
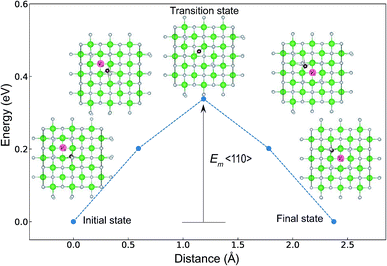
The minimum energy path (MEP) for a VO migration was obtained by the climbing-images nudged-elastic-band (CI-NEB) method.38,39 The Em of a VO can be defined as the energy difference between the transition state and the initial or final state from the obtained MEP, as shown in Fig. 2. The CI-NEB calculations were performed with three intermediate images (states) until the forces decreased below 0.03 eV Å−1 with a spring constant of 5 eV Å−2 between images. Here, the climbing images with even numbers were used to increase the probability of finding the transition state. We employed a 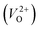 for Em, assuming that VO were formed by the reduction of cation valency upon doping. The supercells with a
for Em, assuming that VO were formed by the reduction of cation valency upon doping. The supercells with a 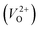 were described by decreasing two electrons of the background charge for compensation. The internal coordinates for the supercells with a
were described by decreasing two electrons of the background charge for compensation. The internal coordinates for the supercells with a 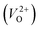 were relaxed in the same computational conditions as those for
were relaxed in the same computational conditions as those for 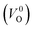 .
.
3. Results and discussion
3.1. Construction of a prediction model for Ev using DFT-unit-cell descriptors
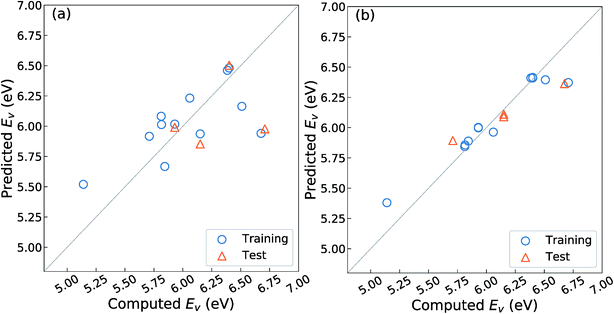
As mentioned in the Introduction, Deml et al.23 constructed a linear prediction model for the Ev with four unit-cell descriptors, namely, the formation energy of oxides (ΔEf) obtained as the fitted elemental-phase reference energy (FERE),35 the computed band-gaps obtained by GGA+U (EgGGA+U) or GW40 calculations, the O 2p band center (EO2p), and the differences in electronegativity between the cations and O, for 45 different oxides in six crystal structures. Their prediction error was reported as ∼0.20 eV as the mean absolute error (MAE). To evaluate whether this model is well-fitted for the different crystal structures upon fixing the substituted chemical elements and composition ratio as listed in Table 1, we employed the OLSR-3-descriptors model with the descriptors x1–x3 listed in Table 2. For the RR-11 descriptor, the average difference in electronegativity between the cations and O is not used because it does not vary among the different types of crystal structures. The 16 crystal structures of the reoptimized-ZrO2 in Table 1 were used to construct the prediction model.Fig. 3(a) shows the relationship between the predicted and computed Ev obtained by using the OLSR-3-descriptors model. The distribution of data is largely scattered from the diagonal line that indicates equality between the predicted and computed Ev. As arranged in Table 3, the CV-score and RMSE of the test set are 0.76 and 0.51 eV, respectively, which are much larger errors than the MAE of 0.20 eV for the 45 oxides.23 The large difference between the CV-score and RMSE of the test set also indicates that the prediction model has a large dependence on the type of training set. Therefore, it implies that the prediction model using the OLSR-3-descriptors is not good enough to predict the Ev of the various crystal structures of ZrO2.
| Prediction Model | Data divided into training (75%) and test (25%) set | Whole data | |||
|---|---|---|---|---|---|
| RMSE of training set | CV-score | RMSE of test set | RMSE of training set | CV-score | |
| OLSR-3-descriptors | 0.27 (0.05) | 0.76 (0.36) | 0.51 (0.22) | 0.31 | 0.60 (0.19) |
| RR-11-descriptors | 0.04 (0.04) | 0.17 (0.06) | 0.16 (0.16) | 0.02 (0.01) | 0.14 (0.07) |
To improve the prediction accuracy, we constructed RR-11-descriptors by adding more DFT-unit-cell descriptors on top of the three descriptors; these DFT descriptors are intuitively thought to be related to the forming and breaking of chemical bonds. We employed the RR model, which can control the coefficients of various descriptors through a penalty term and thereby minimize overfitting. Fig. 3(b) shows the relationship between the predicted and computed Ev obtained by using the RR-11-descriptors model. The scattering of points from the diagonal line is significantly decreased. The CV-score and RMSE of the test sets are 0.17 and 0.16 eV, respectively, which are much smaller than those obtained from the OLSR-3-descriptors model. The similarity in the two values suggests the absence of any serious overfitting.
Furthermore, we applied the RR-11-descriptor model with a training set consisting of all 16 crystal structures of reoptimized-ZrO2. In the results, the CV-score slightly decreased to 0.14 eV. This improvement can be attributed to the increased number of training data points. This value is also only 0.02 eV different from that of the RMSE of the test set of the prediction model with a 75% training set, which suggests the absence of any serious overfitting. Finally, we identified the coefficients for a linear fitting function applied as the fitness value in the evolutionary algorithm by using the RR-11-descriptors model with all 16 crystal structures of the reoptimized-ZrO2.
3.2. Crystal structures with low Ev
As Fig. 1 shows, we generated 462 crystal structures through combinations of the regression analysis for the Ev and evolutionary algorithm, and screened out 71 crystal structures based on the criterion |predicted Ev − 5| < 0.5 eV. After crystal relaxation once again under tighter conditions, we obtained 14 remaining crystal structures with the predicted and computed Ev, excluding those that were metallic or could not satisfy the criteria for structural optimization. The detailed properties of the 14 crystal structures are listed in Table 4. Henceforth, this set of crystal structures is referred to as “generated-ZrO2”, and the name of each such structure is prefixed with “Gen-” (“generated or constructed”); these structures are numbered in the order of the computed Ev. These crystal structures have very low symmetry; most of them are P1. To identify similar crystal structures with higher symmetry, a looser tolerance for finding the space group was also applied.| Name of constructed crystal structure | Space group typea | E − E(ground-state) (eV per atom) | EgGGA+U (eV) | Predicted Ev (eV) | Computed Ev (eV)b |
|---|---|---|---|---|---|
| a The space group in parentheses is identified using looser tolerance in SPGLIB in PHONOPY code36,37 to determine similar higher-symmetry crystal structures.b Values in the parentheses are the minimum and the maximum values in sequence, which depend on the kinds of O sites. | |||||
| Gen-01 | P1 (Pnma) | 0.113 | 2.77 | 5.11 | 5.11 (4.94, 5.30) |
| Gen-02 | Pnma (Pnma) | 0.110 | 2.82 | 5.18 | 5.21 (5.11, 5.30) |
| Gen-03 | P1 (Pnma) | 0.110 | 2.83 | 5.18 | 5.21 (5.11, 5.30) |
| Gen-04 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (Pnma) (Pnma) |
0.110 | 2.83 | 5.18 | 5.21 (5.11, 5.30) |
| Gen-05 | P1 (Pnma) | 0.110 | 2.83 | 5.18 | 5.21 (5.11, 5.31) |
| Gen-06 | P212121 (Pnma) | 0.110 | 2.83 | 5.18 | 5.21 (5.11, 5.30) |
| Gen-07 | Pca21 (P63mc) | 0.223 | 2.86 | 5.80 | 5.69 (5.56, 5.83) |
| Gen-08 | P1 (P42/nmc) | 0.024 | 3.79 | 5.80 | 5.79 (5.79, 5.79) |
| Gen-09 | P1 (P42/nmc) | 0.023 | 3.97 | 5.75 | 5.85 (5.85, 5.85) |
| Gen-10 | P1 (P21/m) | 0.021 | 4.20 | 5.85 | 6.03 (5.90, 6.16) |
| Gen-11 | P1 (P21/m) | 0.021 | 4.20 | 5.86 | 6.03 (5.90, 6.17) |
| Gen-12 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (P21/m) (P21/m) |
0.021 | 4.18 | 5.86 | 6.03 (5.90, 6.17) |
| Gen-13 | P1 (Fdd2) | 0.030 | 3.44 | 6.00 | 6.20 (6.07, 6.33) |
| Gen-14 | P1 (P21/m) | 0.113 | 3.70 | 6.53 | 6.39 (6.33, 6.53) |
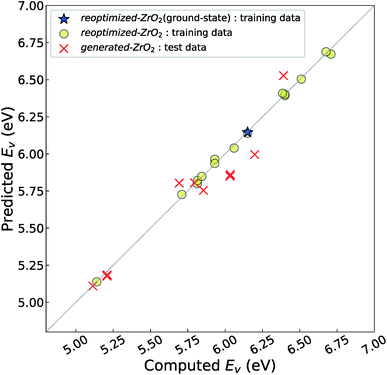
Fig. 4 shows the relationship between the computed and predicted Ev of the crystal structures of reoptimized-ZrO2 and generated-ZrO2, which are used as the training and test data, respectively. The Ev of the ground-state P21/c structure is emphasized with a star-shaped mark for easier viewing. Note that the distribution of the predicted Ev for the 14 test-data crystal structures is in the range 5.11–6.53 eV, which is wider than the screening criteria. This is because some crystal structures are relaxed into more stable structures, with changes in the predicted Ev.
The distribution of the test data is close to the diagonal line. The prediction error is only 0.11 eV, which is almost the same as the CV-score of the RR-11-descriptors model with the 16 training data (0.14 eV). This means that the Ev of the 14 crystal structures of generated-ZrO2 have been successfully predicted using only DFT-unit-cell descriptors. Note that the distribution of the 16 training data points is very close to the diagonal line in Fig. 3(b), because their predicted Ev are obtained as the training data, and not as the test data.
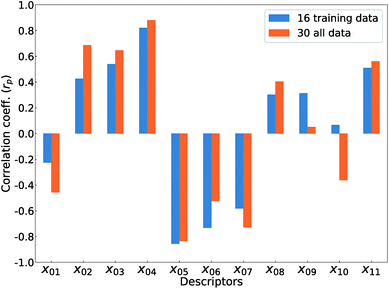
Fig. 5 shows Pearson's linear correlation coefficient (rp) for each DFT-unit-cell descriptor with respect to the computed Ev. The absolute value of rp is larger than 0.7, which indicates a strong correlation between the two properties for a given data point.41 For the 16 crystal structures of reoptimized-ZrO2, the |rp| for the volume per atom, average bond lengths (rZr–O), and O coordination number (CNO) are 0.82, 0.85, and 0.73 (high), respectively, while the |rp| for the formation energy (ΔEf) and EgGGA+U are 0.22 and 0.42 (low), respectively. This observation differs from that of Deml's model23 for 45 various oxides, which showed strong correlations between the FERE and Ev, and between the EgGGA+U and Ev, with |rp| values of 0.84 and 0.89, respectively. The different accuracies of the prediction models between this study and ref. 23 can arise from several factors. Firstly, the 45 training-data oxides used in ref. 23 included six types of crystal structures with high symmetries, namely, anti-fluorite, fluorite, rocksalt, rutile, perovskite, and spinel. Most of these oxides are energetically stable for various combinations of constituent elements. However, the crystal structures of ZrO2 in this study all have different types of metastable lower-symmetry crystal structures. The contribution of each descriptor in the regression analysis may differ. Secondly, the range of training data can also affect the accuracy of prediction model. The Ev of the 45 training-data structures in ref. 23 are widely distributed between 2.6 and 7.0 eV, whereas the Ev of ZrO2 in this study are distributed between only 5.1 and 6.7 eV.
The rp changes for all 30 crystal structures of the reoptimized-ZrO2 and generated-ZrO2. The values of |rp| for the volume per atom and rZr–O are similarly large as 0.88 and 0.82 respectively, while |rp| for CNO decreases to 0.49. The |rp| for ΔEf and EgGGA+U changed to 0.51 and 0.69, respectively. When the RR-11-descriptors model is applied to all 30 crystal structures, the prediction accuracy is improved, with the RMSE of the test data of 0.08 eV compared with that of the same prediction model (0.16 eV) with the 16 training data crystal structures. Because the descriptors also maintain their correlations with each other in the regression analysis, the important unit-cell descriptors for the prediction of Ev can be changed according to the target materials and training data. Therefore, we suggest employing more types of unit-cell descriptors but with regression analysis using a penalty term; this is a useful way to construct the prediction model of the Ev.
We identify many crystal structures having Ev lower than that of the ground-state P21/c structure. As shown in Table 1 and Fig. 4, eight crystal structures, including the P42/nmc and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures that are well-known high-temperature structures of ZrO2 and that can be stabilized by extrinsic doping,5 reveal lower Ev than that of the ground-state P21/c structure. In particular, the Pna21 structure, which is obtained from the structural data of SiO2, shows the lowest Ev of 5.14 eV, which is almost 1 eV less than that of the ground-state P21/c structure. This implies that exchanging the substituting elements in the crystal structures of other oxides can be an efficient way to reconsider a functional property. Additionally, we obtain 14 crystal structures based on the evolutionary algorithm that have lower Ev than that of the ground-state P21/c structure. This suggests that the discovery of a crystal structure with a special functional property can be accelerated by a combination of the machine-learning technique and the direct construction of crystal structures based on the evolutionary algorithm.
m structures that are well-known high-temperature structures of ZrO2 and that can be stabilized by extrinsic doping,5 reveal lower Ev than that of the ground-state P21/c structure. In particular, the Pna21 structure, which is obtained from the structural data of SiO2, shows the lowest Ev of 5.14 eV, which is almost 1 eV less than that of the ground-state P21/c structure. This implies that exchanging the substituting elements in the crystal structures of other oxides can be an efficient way to reconsider a functional property. Additionally, we obtain 14 crystal structures based on the evolutionary algorithm that have lower Ev than that of the ground-state P21/c structure. This suggests that the discovery of a crystal structure with a special functional property can be accelerated by a combination of the machine-learning technique and the direct construction of crystal structures based on the evolutionary algorithm.
Meanwhile, we reveal why the neutral oxygen vacancy 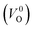 is mainly employed in the calculations of the Ev for the prediction model. The VO in the crystal structures of ZrO2 has been widely investigated. The P21/c and P42/nmc structures are known to form a deep level inside the Eg based on the GGA42–44 and HSE06 (ref. 45 and 46) calculations. Additionally, the Ev of the
is mainly employed in the calculations of the Ev for the prediction model. The VO in the crystal structures of ZrO2 has been widely investigated. The P21/c and P42/nmc structures are known to form a deep level inside the Eg based on the GGA42–44 and HSE06 (ref. 45 and 46) calculations. Additionally, the Ev of the 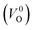 in the dilute limit is physically well defined regardless of the doping level of the cation sites, and quickly converged with respect to the supercell size.
in the dilute limit is physically well defined regardless of the doping level of the cation sites, and quickly converged with respect to the supercell size.
However, it is also worth investigating the relationship between 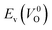 and
and 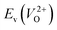 considering the cases of extrinsic doping by aliovalent ions. Here, for
considering the cases of extrinsic doping by aliovalent ions. Here, for 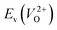 , we fixed the EFermi at the center of the Eg because the crystal structures of reoptimized-ZrO2 are all insulators (EgGGA+U > ∼3 eV). Among the 16 crystal structures of the reoptimized-ZrO2 in Table 1, the Pnma and the P63mc structures were excluded from the computation of
, we fixed the EFermi at the center of the Eg because the crystal structures of reoptimized-ZrO2 are all insulators (EgGGA+U > ∼3 eV). Among the 16 crystal structures of the reoptimized-ZrO2 in Table 1, the Pnma and the P63mc structures were excluded from the computation of 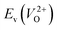 because crystal structures with a
because crystal structures with a 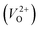 are considered too unstable for convergence. Fig. 6 shows the relationship between the computed
are considered too unstable for convergence. Fig. 6 shows the relationship between the computed 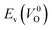 and
and 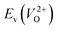 of the 14 crystal structures of the reoptimized-ZrO2. It is noticeable that the
of the 14 crystal structures of the reoptimized-ZrO2. It is noticeable that the 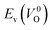 and
and 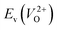 have a very strong correlation with the rp of 0.86. This suggests that the crystal structures with low
have a very strong correlation with the rp of 0.86. This suggests that the crystal structures with low 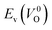 also have low
also have low 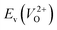 , which implies that extrinsic doping with aliovalent ions may also more easily generate VO for these crystal structures (numerical values are summarized in Table S3 in ESI†).
, which implies that extrinsic doping with aliovalent ions may also more easily generate VO for these crystal structures (numerical values are summarized in Table S3 in ESI†).
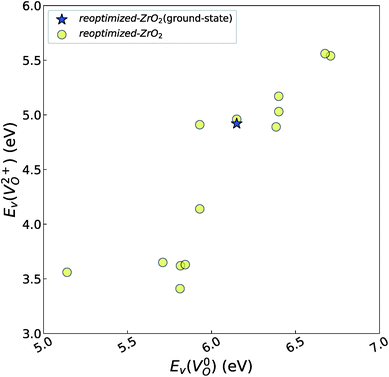 | ||
Fig. 6 Relationship of the computed 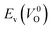 and and 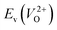 of the 14 crystal structures of reoptimized-ZrO2. The rp between the of the 14 crystal structures of reoptimized-ZrO2. The rp between the 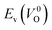 and and 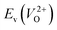 is 0.86, which implies a very strong correlation between the two properties. is 0.86, which implies a very strong correlation between the two properties. | ||
Before proceeding, it is worthwhile to discuss the comparison of the computed values (Eg and Ev shown in Fig. S1 in ESI†) between the GGA+U and GGA methods. It is noticeable that the Eg obtained by the GGA+U are larger than those by the GGA, which implies that the GGA+U is useful to reduce the underestimation of the Eg. For the computed Ev, it is found that the Ev obtained by the GGA are slightly smaller or almost the same as those obtained by the GGA+U. This suggests that the GGA+U does not lose its reliability compared with the GGA, despite including the empirical U parameter.
3.3. Crystal structures with low Em
We summarize the Em values of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and the P42/nmc structures obtained herein and in former computational studies42,47–50 in Table 5. Former computational studies have mainly used the GGA, rather than the GGA+U. To compare the results, we also employ the GGA with the PBE form.33 The Em values obtained herein using the GGA are almost the same as those mentioned in previous computational reports. The Em values obtained using the GGA+U are larger than those obtained using the GGA for both the Fm
m and the P42/nmc structures obtained herein and in former computational studies42,47–50 in Table 5. Former computational studies have mainly used the GGA, rather than the GGA+U. To compare the results, we also employ the GGA with the PBE form.33 The Em values obtained herein using the GGA are almost the same as those mentioned in previous computational reports. The Em values obtained using the GGA+U are larger than those obtained using the GGA for both the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and P42/nmc structures.
m and P42/nmc structures.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and the P42/nmc structures
m and the P42/nmc structures
| Crystal structure | Em (eV)a | Reference | Method | GGA parameterization | |
|---|---|---|---|---|---|
| From GGA | From GGA+U | ||||
a Values outside and in the parentheses are obtained using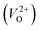 and and 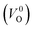 , respectively.b (110) direction in a tetragonal cell.c (001) direction in a tetragonal cell.d Ultrasoft pseudopotentials.66 , respectively.b (110) direction in a tetragonal cell.c (001) direction in a tetragonal cell.d Ultrasoft pseudopotentials.66 |
|||||
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0.26 (0.54) | 0.39 (1.80) | This study | PAW (VASP code) | Perdew et al. (PBE)33 |
| 0.25 (0.45) | 47 | Atomic orbital (SIESTA code)63 | Perdew et al. (PBE)33 | ||
| 0.24 | 48 | PAW (VASP code) | Perdew et al. (PBE)33 | ||
| 0.26 (0.54) | 49 | PAW (VASP code) | Perdew et al. (PBE)33 | ||
| 0.28 | 50 | Plane-wave with US-PPd (Quantum-espresso code)64 | Perdew et al. (PBE)33 | ||
| P42/nmc | 0.26 (1.44)b, 0.63 (1.57)c | 0.34 (1.74)b, 0.64 (1.66)c | This study | PAW (VASP code) | Perdew et al. (PBE)33 |
| 0.22 (1.35)b, 0.61 (1.43)c | 42 | PAW (VASP code) with cutoff energy of 250 eV | Perdew et al.65 | ||
We also compare the Em values of 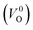 and
and 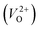 . Table 5 shows that the Em values of
. Table 5 shows that the Em values of 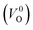 are much larger than those of
are much larger than those of 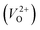 , independent of the crystal structure and the exchange-correlation functional. Larger Em values for
, independent of the crystal structure and the exchange-correlation functional. Larger Em values for 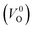 than for
than for 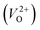 have been reported in other oxides like MgO51 and ZnO.52 When a VO jumps into its nearest-neighboring O site, the O atom at the nearest-neighboring site migrates in the opposite direction. For
have been reported in other oxides like MgO51 and ZnO.52 When a VO jumps into its nearest-neighboring O site, the O atom at the nearest-neighboring site migrates in the opposite direction. For 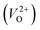 , no occupied levels are present inside Eg. On the other hand, for
, no occupied levels are present inside Eg. On the other hand, for 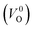 , the two electrons occupying the deep level have transition into the conduction band when the moving O atom is in the transition state (center of the hopping path),47 which may need more energy for VO hopping. Considering the abovementioned reasons, we employed
, the two electrons occupying the deep level have transition into the conduction band when the moving O atom is in the transition state (center of the hopping path),47 which may need more energy for VO hopping. Considering the abovementioned reasons, we employed 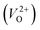 for the Em in this study.
for the Em in this study.
Hereafter, we will refer to the Em obtained by the GGA+U calculations.
In the case of the initial-state structure for the CI-NEB method, we employed the relaxed supercell possessing a 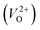 having the lowest energy among the different O sites. For the 14 crystal structures of reoptimized-ZrO2 that have well-converged structures with a
having the lowest energy among the different O sites. For the 14 crystal structures of reoptimized-ZrO2 that have well-converged structures with a 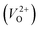 , we considered various final-state structures that have the VO at the nearest-neighboring O site with the cutoff distance of 3.5 Å for the CI-NEB method (see Fig. S2 in ESI†). Among the Em values of different migration paths, the lowest value was extracted; we then checked whether the VO could migrate to the original site in the nearest-neighboring supercell via the one type of migration path with the lowest Em, because the migration of the VO through the bulk system is practically meaningful. In 12 of the 14 crystal structures, VO could migrate to the original site in the nearest-neighboring supercell via the migration path with the lowest Em. However, for the P4/n and R
, we considered various final-state structures that have the VO at the nearest-neighboring O site with the cutoff distance of 3.5 Å for the CI-NEB method (see Fig. S2 in ESI†). Among the Em values of different migration paths, the lowest value was extracted; we then checked whether the VO could migrate to the original site in the nearest-neighboring supercell via the one type of migration path with the lowest Em, because the migration of the VO through the bulk system is practically meaningful. In 12 of the 14 crystal structures, VO could migrate to the original site in the nearest-neighboring supercell via the migration path with the lowest Em. However, for the P4/n and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) structures, a VO needs different paths with different Em values to migrate to the original site in the nearest-neighboring supercell. We define the Em for these structures as the minimum barrier energy required for migration from the original site to that in the nearest-neighboring supercell with several kinds of CI-NEB calculations. The energy diagrams for the migration of a VO are shown in Fig. S3 and Table S4 in ESI.†
structures, a VO needs different paths with different Em values to migrate to the original site in the nearest-neighboring supercell. We define the Em for these structures as the minimum barrier energy required for migration from the original site to that in the nearest-neighboring supercell with several kinds of CI-NEB calculations. The energy diagrams for the migration of a VO are shown in Fig. S3 and Table S4 in ESI.†
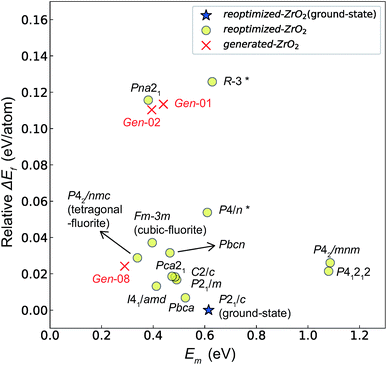
Fig. 7 and 8 show the relationships between the computed Ev and Em values, and between the relative ΔEf (compared with that of the ground-state P21/c structure) and Em values of various ZrO2 crystal structures, respectively. Firstly, we compare the Em of the 14 crystal structures of the reoptimized-ZrO2. The Em values (0.39 and 0.34 eV, respectively) of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and P42/nmc structures are lower than that (0.61 eV) of the ground-state P21/c structure. Ten crystal structures, including the Fm
m and P42/nmc structures are lower than that (0.61 eV) of the ground-state P21/c structure. Ten crystal structures, including the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and the P42/nmc structures, show lower Em than that of the ground-state P21/c structure.
m and the P42/nmc structures, show lower Em than that of the ground-state P21/c structure.
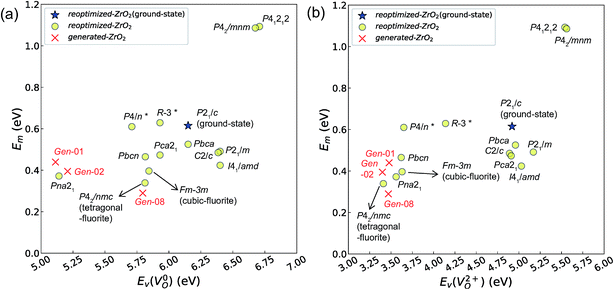 | ||
Fig. 7 Relationship between the computed Ev [(a) 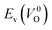 and (b) and (b) 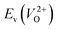 , respectively] and Em of various crystal structures of ZrO2. The rp between the Em and , respectively] and Em of various crystal structures of ZrO2. The rp between the Em and 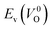 and between the Em and and between the Em and 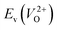 of the 14 crystal structures from reoptimized-ZrO2 are 0.64 and 0.62, respectively, which implies that the correlation in a reasonable level is found. The crystal structures with asterisks (*) need several different types of migration for a VO to move to the same site in the nearest-neighboring computational cell (see Fig. S3 in ESI†). On the basis of this information, the Em of three crystal structures from generated-ZrO2 are obtained (red × marks). of the 14 crystal structures from reoptimized-ZrO2 are 0.64 and 0.62, respectively, which implies that the correlation in a reasonable level is found. The crystal structures with asterisks (*) need several different types of migration for a VO to move to the same site in the nearest-neighboring computational cell (see Fig. S3 in ESI†). On the basis of this information, the Em of three crystal structures from generated-ZrO2 are obtained (red × marks). | ||
Among these ten, eight crystal structures have only 0.05 eV per atom higher ΔEf than the ground-state P21/c structure (Table 1 and Fig. 8). This suggests that high σO can be realized for these structures with stabilizing methods such as extrinsic doping and the formation of epitaxial heterostructures. The P42/nmc and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures are confirmed to have both relatively low Em and ΔEf. The Pbcn structure, which also shows relatively low ΔEf, is reportedly produced by biaxial tensile strain53 on fluorite-structured CeO2, which forms the (100) interface. This structure, obtained by 7% tensile strain, is also reported to show a higher O diffusivity than that of YSZ based on first-principles molecular dynamics calculations.54 The I41/amd, Pbca, Pca21, C2/c, and P21/m structures also have the potential for stabilization, although they have somewhat larger Em than the P42/nmc and Fm
m structures are confirmed to have both relatively low Em and ΔEf. The Pbcn structure, which also shows relatively low ΔEf, is reportedly produced by biaxial tensile strain53 on fluorite-structured CeO2, which forms the (100) interface. This structure, obtained by 7% tensile strain, is also reported to show a higher O diffusivity than that of YSZ based on first-principles molecular dynamics calculations.54 The I41/amd, Pbca, Pca21, C2/c, and P21/m structures also have the potential for stabilization, although they have somewhat larger Em than the P42/nmc and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures do. These crystal structures have not been investigated as oxygen-ion conductors to the best of the authors' knowledge; however, some of them have been reported as metastable structures. The Pbca structure was experimentally synthesized at 600 °C and 6 GPa.55 This structure was also confirmed by first-principles calculations to be stabilized by hydrostatic pressure over 4.1 GPa.56 Mg-doped tetragonal ZrO2 cooled to ∼30 K reportedly transforms to the orthorhombic structure with the space group of Pbc21 (Pca21).57
m structures do. These crystal structures have not been investigated as oxygen-ion conductors to the best of the authors' knowledge; however, some of them have been reported as metastable structures. The Pbca structure was experimentally synthesized at 600 °C and 6 GPa.55 This structure was also confirmed by first-principles calculations to be stabilized by hydrostatic pressure over 4.1 GPa.56 Mg-doped tetragonal ZrO2 cooled to ∼30 K reportedly transforms to the orthorhombic structure with the space group of Pbc21 (Pca21).57
The Em values for the 14 crystal structures of the reoptimized-ZrO2 have similarly large rp of 0.64 and 0.62 with the computed 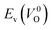 and
and 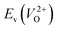 , respectively. The Ev is the energy required for breaking all the chemical bonds to separate an O atom from an oxide, and the Em is the energy required for breaking some of the chemical bonds locally in an oxide, as shown in Fig. 2. Therefore, this correlation may be reasonable in terms of chemical bond cleavage. Correlations between Ev and Em have also been reported for other oxides, like perovskite oxides58 with various kinds of constituent elements and a multinary oxide of Ba1−xSrxCo1−yFeyO3−δ.59 On the other hand, the relative ΔEf and Em do not show any correlation, having an |rp| of only 0.10, which implies that the relative ΔEf is not a good single descriptor for the Em. To realize crystal structures with low values for both relative ΔEf and Em, special challenges in processing may be necessary.
, respectively. The Ev is the energy required for breaking all the chemical bonds to separate an O atom from an oxide, and the Em is the energy required for breaking some of the chemical bonds locally in an oxide, as shown in Fig. 2. Therefore, this correlation may be reasonable in terms of chemical bond cleavage. Correlations between Ev and Em have also been reported for other oxides, like perovskite oxides58 with various kinds of constituent elements and a multinary oxide of Ba1−xSrxCo1−yFeyO3−δ.59 On the other hand, the relative ΔEf and Em do not show any correlation, having an |rp| of only 0.10, which implies that the relative ΔEf is not a good single descriptor for the Em. To realize crystal structures with low values for both relative ΔEf and Em, special challenges in processing may be necessary.
The above information suggests that we are likely to identify a low-Em crystal structure when we initially investigate crystal structures with low Ev. Therefore, for Em calculations, we choose the four crystal structures (Gen-01, Gen-02, Gen-07, and Gen-08) of the generated-ZrO2 that possess the lowest Ev values in ascending order. The crystal structures between Gen-03 and Gen-06 are not chosen because we expect these structures to have properties similar to Gen-02 (see Fig. S4 in ESI†). The crystal structures from Gen-09 to Gen-14 are also not considered for the Em because they may have relatively high Em values.
The Em values of these crystal structures from the generated-ZrO2 are also shown in Fig. 7 and 8. The Em values of Gen-01, Gen-02, and Gen-08 are 0.42, 0.39, and 0.28 eV, respectively. Therefore, we succeed in constructing crystal structures with lower Em as well as lower Ev than those of the ground-state P21/c structure.
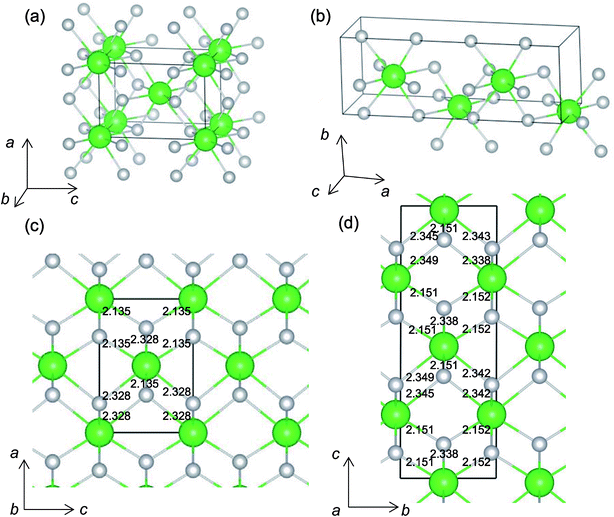
It is worth analyzing the Gen-08 structure further because it is very similar in crystal structure and energetic properties to P42/nmc, despite its space group being P1. Fig. 9 shows the crystal structures of the P42/nmc and Gen-08 structures. We confirm that Gen-08 and P42/nmc do not become the same by structural optimizations with denser k-space sampling. However, the space group defined by using looser tolerance and structural properties, such as the radial distribution function and the bond lengths (see Fig. S4 in ESI†), imply that these crystal structures are quite similar; the Gen-08 structure is slightly distorted in terms of its bond lengths and lattice parameters (see Table S5 in ESI†). In the macroscopic view, these crystal structures may be difficult to distinguish from each other. For the construction of the Gen-08 structure, we only prepared the prediction model of Ev by the regression analysis and evolutionary algorithm that requires the initial structure-related input of only the number of constituting atoms of Zr and O in empty space. Therefore, the construction of Gen-08, which has a similar crystal structure to P42/nmc, implies a successful result of a combination of evolutionary algorithm and regression analysis.
The Gen-07 structure, possessing an energy of 0.2 eV per atom higher than that of the ground-state P21/c structure, is too unstable to contain a 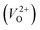 . This suggests that the energetic stability and the low Ev of the crystal structures should be considered in choosing candidates for low Em. The Gen-01–Gen-07 crystal structures have energies more than 0.1 eV per atom higher than that of ground-state P21/c structure, despite having Ev lower than 5.7 eV. On the other hand, the crystal structures Gen-08–Gen-13 have less than 0.03 eV per atom higher energy than the ground-state P21/c structure, although they have higher Ev values. The latter group may have higher stabilization potential than the former.
. This suggests that the energetic stability and the low Ev of the crystal structures should be considered in choosing candidates for low Em. The Gen-01–Gen-07 crystal structures have energies more than 0.1 eV per atom higher than that of ground-state P21/c structure, despite having Ev lower than 5.7 eV. On the other hand, the crystal structures Gen-08–Gen-13 have less than 0.03 eV per atom higher energy than the ground-state P21/c structure, although they have higher Ev values. The latter group may have higher stabilization potential than the former.
Before concluding, we note our exclusion of dynamical stabilities based on the phonon calculations with harmonic approximations36,37 from this study. The P42/nmc and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures are known to be stabilized at temperatures exceeding ∼1173 °C and ∼2370 °C, respectively. However, as Fig. S5 in ESI† shows, the P42/nmc structure includes no imaginary phonon frequencies, whereas the Fm
m structures are known to be stabilized at temperatures exceeding ∼1173 °C and ∼2370 °C, respectively. However, as Fig. S5 in ESI† shows, the P42/nmc structure includes no imaginary phonon frequencies, whereas the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure includes imaginary phonon frequencies despite its capacity for high-temperature stabilization, which is consistent with the phonon calculations by Wang et al.60 Therefore, anharmonic phonon effects,61,62 which are particularly significant at high temperatures, must be considered for these materials.
m structure includes imaginary phonon frequencies despite its capacity for high-temperature stabilization, which is consistent with the phonon calculations by Wang et al.60 Therefore, anharmonic phonon effects,61,62 which are particularly significant at high temperatures, must be considered for these materials.
4. Conclusion
We have constructed a prediction model for the Ev values of various crystal structures of ZrO2 using a linearized RR with 11 unit-cell descriptors. The predicted Ev was used as the fitness value for crystal structure constructions based on the evolutionary algorithm in order to mainly construct crystal structures having Ev lower than that of the ground-state P21/c structure. Our prediction model guarantees prediction errors of less than ∼0.15 eV for various crystal structures of ZrO2.We also obtained the Em values of various crystal structures of ZrO2, and found that this property is correlated with Ev. On the basis of this correlation, we calculated the Em values of several newly constructed crystal structures having low Ev, and confirmed that these Em values are also lower than those of the ground-state P21/c structure and lower than or similar to those of the P42/nmc and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structures.
m structures.
We have successfully discovered various crystal structures with low Ev and Em values for ZrO2 by the direct construction of crystal structures based on a combination of evolutionary algorithm and regression analysis and by reconsidering the crystal structures present in other oxides. Our DFT-unit-cell descriptors are constructed on the basis of the properties related to the chemical bonds between cations and O. Therefore, the good accuracy of the prediction model for Ev and the correlation between the Ev and Em may be reasonable because these properties are all related to the chemical bond cleavage. We expect that the method employed in this study can be applied to determine unknown low-Ev and -Em crystal structures of other material systems, which have not been investigated closely. In addition, the strategy described herein can be also applied to search for crystal structures with other functional properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr N. Nagasako in TCRDL for fruitful discussions.References
- P. Knauth and H. L. Tuller, J. Am. Ceram. Soc., 2002, 85, 1654–1680 CrossRef.
- S. J. Skinner and J. A. Kilner, Mater. Today, 2003, 6, 30–37 CrossRef.
- S. C. Singhal and K. Kendall, High-temperature solid oxide fuel cells: fundamentals, design and applications, Elsevier, 2003 Search PubMed.
- P. J. Gellings and H. Bouwmeester, Handbook of solid state electrochemistry, CRC Press, 1997 Search PubMed.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63–94 CrossRef.
- N. Sammes, G. Tompsett, H. Näfe and F. Aldinger, J. Eur. Ceram. Soc., 1999, 19, 1801–1826 CrossRef.
- K. Shitara, T. Moriasa, A. Sumitani, A. Seko, H. Hayashi, Y. Koyama, R. Huang, D. Han, H. Moriwake and I. Tanaka, Chem. Mater., 2017, 29, 3763–3768 CrossRef.
- K. Huang and J. B. Goodenough, J. Alloys Compd., 2000, 303, 454–464 CrossRef.
- T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801–3803 CrossRef.
- X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Nat. Mater., 2008, 7, 498–504 CrossRef PubMed.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. R. Oganov, C. W. Glass and S. Ono, Earth Planet. Sci. Lett., 2006, 241, 95–103 CrossRef.
- A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867 CrossRef PubMed.
- Y. Shen, A. R. Oganov, G. Qian, J. Zhang, H. Dong, Q. Zhu and Z. Zhou, Sci. Rep., 2015, 5, 14204 CrossRef PubMed.
- A. R. Oganov and A. O. Lyakhov, J. Superhard Mater., 2010, 32, 143–147 CrossRef.
- Q. Zeng, A. R. Oganov, A. O. Lyakhov, C. Xie, X. Zhang, J. Zhang, Q. Zhu, B. Wei, I. Grigorenko and L. Zhang, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 76–84 CrossRef PubMed.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- A. Seko, T. Maekawa, K. Tsuda and I. Tanaka, Phys. Rev. B, 2014, 89, 054303 CrossRef.
- J. Lee, A. Seko, K. Shitara, K. Nakayama and I. Tanaka, Phys. Rev. B, 2016, 93, 115104 CrossRef.
- A. Seko, A. Takahashi and I. Tanaka, Phys. Rev. B, 2014, 90, 024101 CrossRef.
- A. M. Deml, A. M. Holder, R. P. O'Hayre, C. B. Musgrave and V. Stevanović, J. Phys. Chem. Lett., 2015, 6, 1948–1953 CrossRef PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Appl. Phys. Lett. Mater., 2013, 1, 011002 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef.
- A. E. Hoerl and R. W. Kennard, Technometrics, 1970, 12, 55–67 CrossRef.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505–1509 CrossRef.
- V. Stevanović, S. Lany, X. Zhang and A. Zunger, Phys. Rev. B, 2012, 85, 115104 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B, 2008, 78, 134106 CrossRef.
- A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B, 2010, 81, 174301 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef.
- M. Shishkin and G. Kresse, Phys. Rev. B, 2007, 75, 235102 CrossRef.
- J. D. Evans, Straightforward statistics for the behavioral sciences, Brooks/Cole, 1996 Search PubMed.
- A. Eichler, Phys. Rev. B, 2001, 64, 174103 CrossRef.
- J. Zheng, G. Ceder, T. Maxisch, W. Chim and W. Choi, Phys. Rev. B, 2007, 75, 104112 CrossRef.
- A. S. Foster, V. Sulimov, F. L. Gejo, A. Shluger and R. M. Nieminen, Phys. Rev. B, 2001, 64, 224108 CrossRef.
- J.-H. Hur, S. Park and U.-I. Chung, J. Appl. Phys., 2012, 112, 113719 CrossRef.
- W.-J. Yin, S.-H. Wei, M. M. Al-Jassim and Y. Yan, Appl. Phys. Lett., 2011, 99, 142109 CrossRef.
- S. Kasamatsu, T. Tada and S. Watanabe, Appl. Phys. Express, 2009, 2, 061402 CrossRef.
- J. Hirschfeld and H. Lustfeld, Phys. Rev. B, 2011, 84, 224308 CrossRef.
- B. Liu, H. Xiao, Y. Zhang, D. S. Aidhy and W. J. Weber, Comput. Mater. Sci., 2014, 92, 22–27 CrossRef.
- O. I. Malyi, P. Wu, V. V. Kulish, K. Bai and Z. Chen, Solid State Ionics, 2012, 212, 117–122 CrossRef.
- J. Mulroue and D. Duffy, Proc. R. Soc. A, 2011, 467, 2054–2065 CrossRef.
- P. Erhart and K. Albe, Phys. Rev. B, 2006, 73, 115207 CrossRef.
- D. S. Aidhy, B. Liu, Y. Zhang and W. J. Weber, J. Phys. Chem. C, 2014, 118, 30139–30144 CrossRef.
- M. Oka, H. Kamisaka, T. Fukumura and T. Hasegawa, Phys. Chem. Chem. Phys., 2015, 17, 29057–29063 RSC.
- O. Ohtaka, T. Yamanaka, S. Kume, N. Hara, H. Asano and F. Izumi, Proc. Jpn. Acad., Ser. B, 1990, 66, 193–196 CrossRef.
- J. Dewhurst and J. Lowther, Phys. Rev. B, 1998, 57, 741 CrossRef.
- E. H. Kisi, C. J. Howard and R. J. Hill, J. Am. Ceram. Soc., 1989, 72, 1757–1760 CrossRef.
- T. T. Mayeshiba and D. D. Morgan, Solid State Ionics, 2016, 296, 71–77 CrossRef.
- R. Merkle, Y. A. Mastrikov, E. A. Kotomin, M. M. Kuklja and J. Maier, J. Electrochem. Soc., 2011, 159, B219–B226 CrossRef.
- G. Wang, G. Luo, Y. L. Soo, R. F. Sabirianov, H.-J. Lin, W.-N. Mei, F. Namavar and C. L. Cheung, Phys. Chem. Chem. Phys., 2011, 13, 19517–19525 RSC.
- O. Hellman, I. A. Abrikosov and S. I. Simak, Phys. Rev. B, 2011, 84, 180301 CrossRef.
- P. Souvatzis, O. Eriksson, M. I. Katsnelson and S. P. Rudin, Phys. Rev. Lett., 2008, 100, 095901 CrossRef PubMed.
- E. Artacho, E. Anglada, O. Diéguez, J. D. Gale, A. García, J. Junquera, R. M. Martin, P. Ordejón, J. M. Pruneda and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2008, 20, 064208 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B, 1992, 46, 6671–6687 CrossRef.
- D. Vanderbilt, Phys. Rev. B, 1990, 41, 7892–7895 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02958j |
| This journal is © The Royal Society of Chemistry 2018 |