Open Access Article
Open Access ArticleA modelling approach to assess the long-term stability of a novel microbial/electrochemical system for the treatment of acid mine drainage†
Emma Thompson Brewster‡
 ,
Guillermo Pozo§
,
Damien J. Batstone,
Stefano Freguia and
Pablo Ledezma
,
Guillermo Pozo§
,
Damien J. Batstone,
Stefano Freguia and
Pablo Ledezma *
*
Advanced Water Management Centre, The University of Queensland, St Lucia, QLD 4072, Australia. E-mail: p.ledezma@awmc.uq.edu.au; Fax: +61 7 3365 4726; Tel: +61 7 3346 3228
First published on 22nd May 2018
Abstract
Microbial electrochemical processes have potential to remediate acid mine drainage (AMD) wastewaters which are highly acidic and rich in sulfate and heavy metals, without the need for extensive chemical dosing. In this manuscript, a novel hybrid microbial/electrochemical remediation process which uses a 3-reactor system – a precipitation vessel, an electrochemical reactor and a microbial electrochemical reactor with a sulfate-reducing biocathode – was modelled. To evaluate the long-term operability of this system, a dynamic model for the fluxes of 140 different ionic species was developed and calibrated using laboratory-scale experimental data. The model identified that when the reactors are operating in the desired state, the coulombic efficiency of sulfate removal from AMD is high (91%). Modelling also identified that a periodic electrolyte purge is required to prevent the build-up of Cl− ions in the microbial electrochemical reactor. The model furthermore studied the fate of sulfate and carbon in the system. For sulfate, it was found that only 29% can be converted into elemental sulfur, with the rest complexating with metals in the precipitation vessel. Finally, the model shows that the flux of inorganic carbon under the current operational strategy is insufficient to maintain the autotrophic sulfate-reducing biomass. The modelling approach demonstrates that a change in system operational strategies plus close monitoring of overlooked ionic species (such as Cl− and HCO3−) are key towards the scaling-up of this technology.
Introduction
Production of acid and metalliferous mine drainage (AMD) is the result of atmosphere-exposed mining and processing of metal sulfide deposits for the extraction of numerous metals and minerals of commercial interest.1 Safe management and disposal of AMD is a global environmental issue due to its highly-acidic nature, richness in heavy metals, strong chemical stability and lack of organics (that could facilitate its biological treatment).2 Given these issues, the most common practice for AMD management worldwide is storage in dams plus evaporation, with significant environmental risks in the event of heavy rain/flooding, inadequate/insufficient storage dam capacity and soil/tectonic movements.2 However, other options exist for both the prevention of AMD and its treatment. Other common treatment options include additional of alkaline chemicals to precipitate metals, ion exchange, adsorption and membrane technology.3 Novel forms of AMD treatment offer opportunities for resource recovery. These include water recovery of sufficient quality for discharge or onsite reuse, as well as secondary minerals and/or metals of commercial interest.4,5 Recently, our group has developed a hybrid autotrophic-microbial/electrochemical AMD treatment system that requires no chemical dosing and that is able to concomitantly produce a pH-neutral water effluent, recover elemental sulfur (S0), produce a metal-sludge with superior settleability and that includes rare Earth elements and yttrium (REY) with numerous current and emerging industrial applications.4Microbial electrochemical AMD remediation is nevertheless a relatively new proposed alternative to other conventional management/remediation methods6 – such as neutralisation and precipitation by chemical dosing (of, for example, lime)2 – meaning that questions remain open with regards to long-term system stability. For this purpose, and as complement to pilot-scale studies, the electrochemical model hereby presented evaluates the non-biological fluxes of 140 different ionic species and reveals potential issues with regards to the long-term operability and stability of the system we have proposed.6
Recently, modelling methods for electrochemical systems using wastewater (anaerobic digester liquor and source-separated urine7,9) as electrolyte have been developed. However, AMD contains lower concentrations of organics and nutrients, and higher concentrations of heavy metals and sulfate compared to these other streams, and has not been modelled in electrochemical systems before. There is, however, a strong background of equilibrium-based thermodynamic speciation models for geochemistry applications, which have been used to study AMD for decades.10,11 MINTEQ,12 PHREEQC13 and other models are commonly employed for environmental risk assessments.14 In particular, PHREEQC has been used to understand sulfate and pH remediation of AMD with coal fly ash,15 and it has been combined with hydrologic models to study the ecological impacts of AMD releases.16 The latest electrochemical models utilise speciation plus activity corrections to more accurately model the governing mechanisms of the processes, with speciation modelling methods detailed Flores-Alsina et al.17 These methods have commonly been applied to domestic wastewater, but the solution principles are similar to MINTEQ and PHREEQC and should yield similarly valid outcomes to AMD related applications.8
In particular, while we have methodically studied the microbial and electrochemical transformation of sulfur, and flux of sulfur species in the laboratory,6,18–20 the modelling approach hereby presented calculates the fluxes of up to 140 different ionic species present in the AMD. This is technically feasible but extremely complex to achieve experimentally. The results demonstrated provide valuable lessons for upcoming pilot-scale trials, including the accumulation of previously overlooked problematic ions in the system, such as carbonate species, Cl− and NO3−. Microbial electrochemical technologies are a promising alternative for the treatment of mining wastewater with concomitant resource recovery, but their long-term stability and scalability is challenging. As a complement to pilot-scale trials, in this paper we present a mechanistic modelling approach to investigate these issues.
Materials and methods
Model configuration
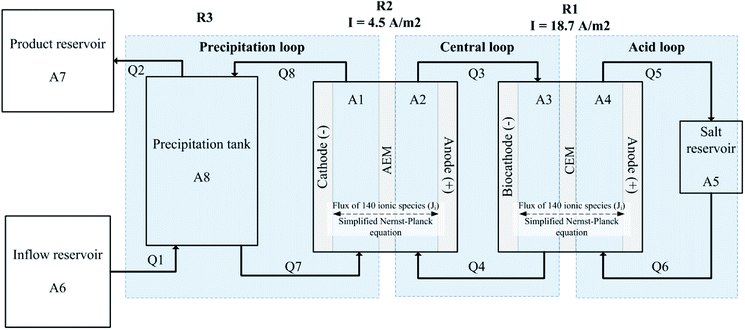
The modelled system shown in Fig. 1 reflects the physical dimensions and operation of the hybrid microbial/electrochemical AMD treatment system developed by our group.6 The treatment system (and its model accordingly) utilises three reactors (R1, R2 and R3) and three main recirculation loops that link these reactors hydraulically. The system operation can be summarised as follows (see Pozo et al.6 for further details, and a detailed process configuration from Pozo et al.6 is provided in Fig. S1† in the ESI†).Raw AMD is fed into the precipitation tank (see R3 in Fig. 1), which is recirculated at a relatively high-flow-rate between the cathodic chamber of R2, a two-chamber electrochemical cell with an anion exchange membrane (AEM). The precipitation tank (R3) and the cathodic chamber of R2 are linked hydraulically and form what is referred to as the precipitation loop. In the experiments, a power source applied a fixed 1.7 V to R2, causing anions to migrate across the AEM. At this potential the expected electrode reactions in R2 at the anode is sulfide oxidation and at the cathode is water reduction. See further description of the electrode reactions below in the Electrode reactions section. Because most of the anions in the AMD feed are sulfate, migration mainly removes sulfate from the AMD and increases the pH in the precipitation tank (R3) from its acidic pH to a neutral controlled set point of 7.3. This neutral pH enables further removal of sulfate and heavy metals through precipitation of metal hydroxides and sulfides in R3. This is the main operational objective: treating the AMD for safe environmental discharge by removing sulfate and heavy metals and neutralising pH. Concomitantly, the system is able to recover elemental sulfur (S0) through microbial and electrochemical reactions. The solution from the anode in R2 (which contains the migrated sulfate) is circulated to the biocathode of a microbial electrochemical cell (R1). The anodic chamber of R2 and the cathode chamber of R1 are called the central loop. The biocathodic reaction in R1 reduces sulfate to sulfide utilising the metabolism of autotrophic sulfate reducing bacteria (SRBs), and the anode of R2 electrochemically oxidises the sulfide produced by SRBs to elemental sulfur. The solution in the anodic chamber of R1 is looped onto an external reservoir (A5), which is called the acid loop. The pH of the acid loop is approximately pH 3, with migration in R1 mainly transporting protons across a cation exchange membrane (CEM) to help regulate the pH in the biocathode chamber A3.
The model (Fig. 1) has 8 spatial domains including: constant-volume catholytes and anolytes of R1 and R2 (A1 200 cm3, A2 86 cm3, A3 184.5 cm3, A4 70.9 cm3), a constant-volume precipitation vessel (A8 1800 cm3), a constant-volume acidic recirculation reservoir (A5 29 cm3), as well as varying volume feed and product reservoirs (A6, A7). In the laboratory experiments, A2 and A3 were packed with graphite granules with 43% porosity (El Carb 100, Graphite Sales Inc., USA), which is taken into account by modelled working volumes.20,21 The modelled convective flow rates Q1 and Q2 were 0.03 L h−1 matching the average conditions of the laboratory experiments,6 while the electrolytes in the precipitation loop (Q7, Q8), the central loop (Q3, Q4) and acid loop (Q5, Q6) are recirculated at a relatively fast speed (15 L h−1). This fast speed is to model ideal mixing in the loops. The hydraulic retention time (HRT) for A8 is 60 h, while the HRT for A1, A2, A3, A4 and A5 are all less than 1 min. R1 had an effective membrane area of 121.85 cm2 and R2 had an effective membrane area of 100 cm2. Full MATLAB codes for this model (including instructions for use) can be found in the ESI 3.†
Initial conditions
There are three initial compositions used in the model, with the following compartments set equal to each other: feed initial composition, which is the same as the real AMD used in Pozo et al.6 (A1, A6–A8), the initial concentrations in the central loop buffer solution prior to the start of the experiments (A2 and A3), and an initial salt solution (A4 and A5). The feed composition and initial concentrations in the model are provided in Table 1. The model simulates the later stages of the continuous experiments in Pozo et al.6 However, the central loop buffer solution composition is only known for the conditions at the start of the experiments. Therefore the dynamic model requires a 15 d simulation start-up period for the model to reflect the conditions of the experimental data. The ionic strength of the feed solution is ∼0.2 M. This ionic strength is not sufficiently high to be limiting in electro-concentration processes.22,23| Component [mM] | Real AMD feed (A1, A6–A8) | Central loop buffer solution (A2, A3) | Salt solution (A4, A5) |
|---|---|---|---|
| Total sodium | 63 | 130 | 0.62 |
| Total potassium | 1.0 | 22 | 0.18 |
| Total ammonium | 2.9 | 1.9 | 0 |
| Total chloride | 2.0 | 11 | 0 |
| Total calcium | 14 | 0.14 | 0 |
| Total magnesium | 24 | 0 | 0 |
| Total carbonate | 0.030 | 6.0 | 0 |
| Total sulfate | 110 | 16 | 0 |
| Total phosphate | 0.10 | 64 | 0.49 |
| Total aluminium | 18 | 0 | 0 |
| Iron(II) | 7.9 | 0 | 0 |
| Iron(III) | 2.3 | 0 | 0 |
| Total nitrate | 2.7 | 0 | 0 |
Precipitation reactions
In the experimental work, precipitation was observed both in the precipitation vessel (R3), as well as scaling on the cathode in A1 (R2). Undesired scaling/precipitation in A3 or A4 (R1) was not observed experimentally and is consequently not studied here. Instead of modelling scaling as several different terms, precipitation occurring on the cathode in A1 and in the precipitation reactor (R3) is included within a single sink term representing the overall precipitation. For practical purposes and considering the objective is to study the concentrations/fluxes in the aqueous phase, the model assumes all precipitation occurs in the precipitation tank (R3, A8). In A8, pH neutralisation removes nearly all the Al, Fe2+, Fe3+, Mg and Na, and some of the SO42− from the liquid through continuous switch functions (eqn (1)). The residual threshold concentration parameter (Ki) was estimated for each component listed above through parameter estimation against experimental effluent concentrations (see Table 2).
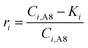 | (1) |
| Component | Average measured experimental value [mM] | Modelled value at 15 d simulation [mM] |
|---|---|---|
| Effluent values | ||
| Total sulfur | 16.8 ± 1.6 | 16.7 |
| Total sodium | 21.3 ± 2.5 | 21.3 |
| Total calcium | 3.3 ± 0.4 | 3.3 |
| Total magnesium | 2.1 ± 0.2 | 2.0 |
| Total iron | 0.09 ± 0.03 | 0.02 (Fe2+ and Fe3+) |
| Total aluminium | 0.001 ± 0.002 | 0.02 |
| pH | 7.2 ± 0.002 | 7.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| A2/A3 loop values | ||
| Total sulfate | 19.2 ± 3.2 | 19.0 |
| Total sulfide | 8.4 ± 3.3 | 8.4 |
| Total chloride | 40.3 ± 2.2 | 41.4 |
| pH | ∼7.3 | 6.3 |
Ionic mass transport and speciation
Based on the ionic flux, pH and speciation methods developed in Thompson Brewster et al.,7 the electrochemical (R2) and microbial electrochemical (R1) reactors were modelled using a Nernst–Planck equation, accounting for the speciation of different ionic species17 and using a current proportioning method to describe membrane transport. Diffusion and migratory fluxes occurring across the anion exchange membrane (AEM) and cation exchange membrane (CEM) were represented by the Nernst–Planck equation and taking into account the components sodium, potassium, ammonium, chloride, acetate, calcium, magnesium, carbonate, sulfate, phosphate, aluminium, iron (2+), iron (3+), sulfide and nitrate, as well as acid–base pairing and ionic pairing. In this paper, components are referred to by the name of the component and species are referred to by the elemental symbol. The use of AMD compared to previously studied wastewaters8,9 required the speciation code applied to electrochemical systems to be expanded to include aluminium, iron 2+ and iron 3+. Copper and nickel were not included as their concentrations in the AMD feed were 2 orders of magnitude lower than iron, aluminium, calcium and magnesium, and that they are not included in the speciation code from Flores-Alsina et al.17 Copper and nickel would likely precipitate in the precipitation vessel (R3) to even lower aqueous concentrations, and their inclusion in the model would not influence the key findings.The experimental current densities for both reactors were stable with the current density in R1 (I1) being 18.7 ± 0.001 A m−2 and R2 (I2) being 4.5 ± 0.005 A m−2, with uncertainty expressed here as the 95% confidence interval. Due to the high stability, the average values for current density were used in the model. No diffusion boundary layers (DBLs) were taken into account in the modelling as at the large chamber widths utilised, these were unlikely to be a limiting mechanism.7
Electrode reactions
Implicit water splitting reactions were included at the R2 cathode and R1 anode based on the ionic fluxes of major ionic species (i.e. species not H+ or OH−), to evaluate the pH effect from these electrode reactions (eqn (2) and (3), respectively). Explicit electrochemical oxidation of HS− to S0 was included for the R2 anode (eqn (4)), as well as the implicit cathodic water splitting and explicit biofilm reaction of sulfate to HS− at the R1 biocathode (eqn (5) and (6), respectively).| 2H2O + 2e− → H2(g) + 2OH− | (2) |
| 4H2O → 8H+ + 8e− + 2O2 | (3) |
| HS− → S0(s) + H+ + 2e− | (4) |
| 8H+ + 8e− → 4H2 | (5) |
| 4H2 + SO42− + H+ → HS− + 4H2O | (6) |
The experiments and model were run such that the current density of R1 (relating to the biocathodic sulphur reduction reactions in eqn (5) and (6)) is 4.1 times that of R2 (relating to the oxidation to form elemental sulphur in eqn (4)). This accounts for the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of electrons required for eqn (5) and (6), and eqn (4), respectively. When modelling the system, it became evident that the reagents of the key explicit reactions (eqn (4) and (6)) are limiting, and the reactions do not occur at 100% coulombic efficiency (CE). Practically, this means there are additional electrode reactions occurring. In particular, at the R2 anode at least one of the following reactions necessarily occurs: (i) elemental sulfur oxidation to sulfate, (ii) water oxidation to O2, and/or (iii) H2 oxidation to water. The effects of these additional reactions are modelled as implicit water splitting (eqn (2) and (3)). A continuous switch function was used to regulate the source or sink rates for the explicit electrode reactions based on the reactive species and a constant, K1 or K2, representing the residual threshold concentration of the reactant required for the reaction to proceed. Eqn (7)–(10) show how the rates of explicit reactions were calculated for the R1 biocathode (eqn (7) and (8)) and the R2 anode (eqn (9) and (10)).
2 ratio of electrons required for eqn (5) and (6), and eqn (4), respectively. When modelling the system, it became evident that the reagents of the key explicit reactions (eqn (4) and (6)) are limiting, and the reactions do not occur at 100% coulombic efficiency (CE). Practically, this means there are additional electrode reactions occurring. In particular, at the R2 anode at least one of the following reactions necessarily occurs: (i) elemental sulfur oxidation to sulfate, (ii) water oxidation to O2, and/or (iii) H2 oxidation to water. The effects of these additional reactions are modelled as implicit water splitting (eqn (2) and (3)). A continuous switch function was used to regulate the source or sink rates for the explicit electrode reactions based on the reactive species and a constant, K1 or K2, representing the residual threshold concentration of the reactant required for the reaction to proceed. Eqn (7)–(10) show how the rates of explicit reactions were calculated for the R1 biocathode (eqn (7) and (8)) and the R2 anode (eqn (9) and (10)).
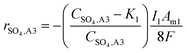 | (7) |
| rHS,A3 = −rSO4,A3 | (8) |
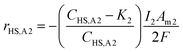 | (9) |
| rS0,A2 = −rHS,A2 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1).
485 C mol−1).
H2O2 production at the cathode in the presence of oxygen is a topic discussed in the electrochemical remediation literature.25 The cathode water splitting reaction in eqn (2) may complete with the reaction in eqn (11), producing H2O2.
| 2H2O + O2 + 2e− → H2O2 + 2OH− | (11) |
These two reactions (eqn (2) and (11)) remove the same charge, producing the same net effect on pH and hence reaction (11) can be implicitly included as for reaction (2) (since H2 and O2 are not considered as states). This study focuses on OH− formation. Therefore, the presence of oxygen at the cathode is assumed to not affect the estimation of OH− formation. If H2O2 and HO2− are not involved with speciation or ion pairing, the pH model output is unaffected. It is possible, but extremely unlikely, to have H2O2 production in the cathode of the electrochemical reactor R2 (A1), since R2 is operated at a fixed 1.7 V, resulting in a low cathode potential that would produce H2 and convert H2O2 to H2O immediately. In addition, dissolved oxygen would need to be present in the AMD feed solution to produce H2O2.
Results and discussion
Model output and validation
Fig. 2 displays some key model outputs for a 30 d simulation. The model was run using the fitted parameters of K1 = 3.7 mol m−3 and K2 = 0.55 mol m−3 for the explicit electrode reactions by comparing the model results with the experimental data shown in Table 2. For each of the precipitation sinks, the following parameters were fitted: KAl = 0.005, KCa = 1.9, KFe2 = 0.01, KFe3 = 0.01, KMg = 0.17, KNa = 17.7, KPO4 = 0.01 and KSO4 = 12.45.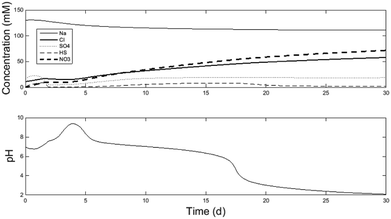 | ||
| Fig. 2 30 d model simulation demonstrating of anion accumulation in the central loop (A2/A3) and the resulting decrease in pH. See further details of species concentration and pH evolution per reactor chamber in the ESI.† | ||
Fig. 2 demonstrates 30 d of simulation. At which point the system becomes unstable. The key outcome of the paper is demonstrating that long-term system operation is unstable. Followed by discussion on why it is so, and suggestions for long-term operability. As can be observed in Fig. 2, the model did not reach steady-state within the 30 d period. Running the model for a longer duration would not provide additional information as after 17 d the model no-longer reflected appropriate operation of the system, as discussed further below. The desired operation state of the system occurs between 10–16 days of simulation time. For this section of the discussion, the model operation at 15 d simulation time will be discussed. Afterwards, operational strategies to maintain steady state will be described.
The model was calibrated against a period of relatively steady data collected in the laboratory, when the experimental system successfully and continuously neutralised the AMD to pH = 7.3 and removed sulfate at a rate of 0.946 ± 18 kg SO4-S m−3 d−1 (referred to as Period IV of the experiments in Pozo et al.6). Due to limited experimental data for the initial conditions and no long-term steady-state experimental data, the goal of the model validation is to demonstrate there is representative similarity between the simulation and the observations. The model therefore can be used to better understand the fluxes of major ions and the relationships between ionic composition and pH in the microbial/electrochemical system.
The calibration data was averaged from the experimental data shown in the ESI-2† spreadsheet from Pozo et al.6 While the measured concentrations were relatively constant, measurements were not taken of all ionic species in solution (for example, chloride and nitrate were not measured). In addition, the measured data did not demonstrate long-term steady-state conditions for all species, even if the stability of the electrical performance appeared to indicate so (see above, current densities with 95% confidence intervals ≤ ± 0.005 A m−2). The laboratory experimental data set includes effluent concentrations of iron, magnesium, manganese, sodium, nickel, lead, sulfur, zinc and pH from R3 (A8) and the sulfate, sulfite and chloride concentrations in the central loop. To demonstrate the representative similarity between the model and experiments, model conditions at the end of 15 d simulation time were compared with the average values in the experimental data, as shown in Table 2. See Fig. S2–S5 in the ESI† for raw model output. At 15 d simulation time, the model demonstrates conditions within the 95% confidence intervals of most of the experimental observations. The exception is the pH of the A2/A3 central loop in which the pH is low (6.4, compared to the desired value of 7.3). However, it is worth noting that this pH discrepancy reflects a difference of approximately 1 mM of concentration imbalance from the major ions, which is within reasonable variance of the experimental observations shown below.
Coulombic efficiencies (CE) of the explicit electrode reactions
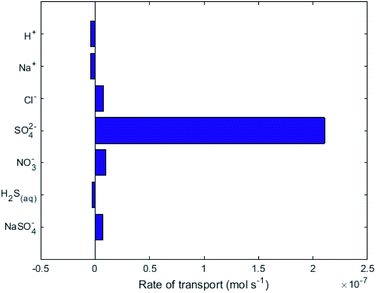
The following results describe the conditions at 15 d simulation time, which reflects the desired operational conditions. The CE of the sulfate removal equation (eqn (6)) in A3 is 81% and elemental sulfur production (eqn (4)) in A2 is 93%. The model reflects the experimental observations with targeted explicit reactions having a high CE (>80%) as estimated experimentally (85 ± 2%).6 While the modelled equations used for these reactions are simplified compared the complexity of the real life conditions, particularly for the biocathodic reaction in R1, the modelled CEs (based on a mass balance independent of the reaction pathway complexity) illustrate similarity to the data.Ion transport across the AEM in reactor 2
While no biological carbon consumption was modelled here, looking at the fluxes of the carbon containing species can give some insight. Fig. 4 shows the rates of ionic transport of carbon-containing species at 15 d of simulation time; note that the x-axis scale in Fig. 4 is 3 orders of magnitude smaller than in Fig. 3. The results indicate that at 15 d operation time, H2CO3(aq) is transporting carbon out of the central loop (i.e. away from the biocathode) due to diffusion at a rate higher than HCO3− is migrating towards the biocathode. This is largely due to the relatively-higher concentrations of H2CO3(aq) in the central loop compared to the precipitation loop.
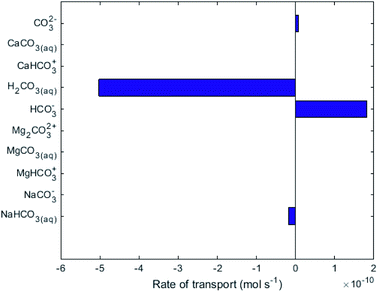 | ||
| Fig. 4 Rate of transport of the species containing carbon across the AEM in R2. Positive values indicate the intended direction (from cathode to anode). | ||
Fig. 4 shows that some HCO3− (2 × 10−10 mol s−1) does migrate from the AMD into the central loop. While the conditions set in the model do not support that there can be a net flux of carbon into the central loop (Q3, Q4, A2 and A3 in Fig. 1). To provide the biomass with this essential nutrient, different operational conditions could promote a net flux of carbon-containing species in the desired direction based on the Nernst–Planck equation discussed in Thompson Brewster et al.7 If the central loop carbonate concentrations were lower than seen here, because either the buffer solution contained less carbonate initially, or the biological activity consumed a sufficient amount of carbonate, this would reduce the back-diffusive driving force, allowing migration of HCO3− and CO32− towards the biocathode to be the dominant form of carbon flux (to sustain the biomass). The model shows that attention is needed to ensure that C is not limiting for the maintenance of the autotrophic SRB biomass when up-scaling the proposed technology. This should be done in consideration of the known metabolic flexibility of SRBs,28 either by controlling the carbonate transport as discussed above or (less-ideally) by chemical addition of, for example, bicarbonate salts.
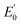 = +1.36 V and the inherent overpotential of the carbon electrodes hereby utilised,31 this would require a significantly higher applied voltage than the 1.7 V used for R2 for chlorine evolution to occur. If chlorine evolution did happen it would be deleterious for the linked biocathode of R1, but it is unlikely to occur under the existing operational conditions.
= +1.36 V and the inherent overpotential of the carbon electrodes hereby utilised,31 this would require a significantly higher applied voltage than the 1.7 V used for R2 for chlorine evolution to occur. If chlorine evolution did happen it would be deleterious for the linked biocathode of R1, but it is unlikely to occur under the existing operational conditions.Fig. 3 shows that the net flux of anions (primarily Cl− and NO3−) will eventually cause a decrease of pH in the central loop to below biological limits (<4), due to unintended anode reactions at A2 (i.e. reactions which are not eqn (4)). These unintended reactions were modelled here as oxygen evolution, but in reality they could also be reformation of sulfate from elemental sulfur. Accumulation of anions, Cl− and NO3− in the central loop will result in a drop in pH, due to the charge balance relating to speciation modelling.17 These results indicate that a constant or periodical purge of the electrolyte from the central loop would be necessary as part of the operational strategy to remove the build-up of Cl− beyond physiological pH limitations. A constant electro-osmotic flux of water will occur into the central loop due to the migration of hydrated ions.32,33 If this small flux of water was matched in volume by a purge this would result in Cl− concentrations reaching a steady value, therefore preventing the pH crash. The electroosmotic flux should be determined experimentally in order to implement and validate a water flux model as in Pronk et al.32 For a pilot-scale system, a level control loop could be installed in an external recirculation reservoir for the central loop, with the reservoir level maintained constant via a feedback control loop.
Another application consideration is variation in influent composition. Feed composition would be different at different treatment sites, but also at the same site over time due to geochemical weathering and rainfall events. Chemical pH neutralisation is a commonly used treatment across many AMD sites, and electrochemical pH neutralisation should work similarly. However, ensuring the biocathode has stable conditions would be of importance.
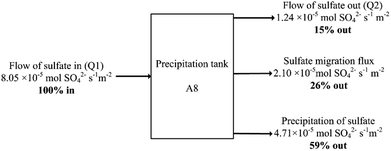 | ||
| Fig. 5 Sulfate balance over the precipitation reactor normalised per membrane areas of the R2 anion exchange membrane (0.01 m2) at 15 d simulation time. | ||
The case for S0 recovery would not become more favourable even at 100% CE efficiency for SO42− transport, as this would only remove 2.33 × 10−5 mol SO42− s−1 m−2 through the AEM (see Fig. 1), which would mean 26% of the total SO42− entering the system. Precipitation of sulfate in the R3 does not appear to be detrimental to process operation, and it lowers the load on the microbial and electrochemical cells R1/R2, which would mean reduced reactor sizes and thus lower AMD remediation costs when compared to a 100% sulfate-to-sulfur conversion.
Conclusions
The model hereby presented studied the fluxes of 140 ionic species in a novel 3-reactor microbial/electrochemical reactor configuration designed to treat AMD without chemical additions. The results confirm that the proposed treatment system can achieve relatively high (≥80%) coulombic efficiencies for its explicit electrochemical reactions. However, some key limitations and valuable lessons towards pilot-scale trials were also discovered. Firstly, in order to achieve steady-state operation with stable pH, a regular liquid purge of the central loop is required to prevent the pH from dropping due to Cl− ion accumulation. Secondly, a mass balance analysis showed that the majority (59%) of the removed sulfate would precipitate in R3 (the precipitation reactor) and only 26% would be converted to S0 in R2. This decreases system loading and therefore sizing and costs, but means S0 recovery cannot not be a significant focus of the process. The recovery should therefore probably focus on valuable REY elements rather than S0. A final limitation is that the mass flux of carbon from the AMD to the central loop as HCO3− is insufficient to maintain the autotrophic biofilms over time. A small carbon source from the AMD (approximately 2 × 10−8 mol C s−1 m−2) was observed. However, the operational conditions have to be changed in order to reduce undesirable H2CO3 diffusion to process areas away from the biomass. The total C migration should be monitored through longer term studies to ensure carbon supply for the microbes can be met. Long-term operation considerations relating from membrane and electrode scaling were not covered in this paper, but are an important avenue of future work and will be included in the pilot-scale study.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank the Australian Research Council for funding support through Discovery Project DP120104415. G. Pozo acknowledges a Chilean Scholarship (Becas Chile) from the National Commission for Science Research and Technology (CONICYT) of Chile. P. Ledezma acknowledges an ECR Development Fellowship from The University of Queensland.References
- J. Phillips, Applied Geography, 2016, 74, 95–108 CrossRef.
- D. B. Johnson and K. B. Hallberg, Sci. Total Environ., 2005, 338, 3–14 CrossRef PubMed.
- K. K. Kefeni, T. A. M. Msagati and B. B. Mamba, J. Cleaner Prod., 2017, 151, 475–493 CrossRef.
- O. Modin and F. Aulenta, Environ. Sci.: Water Res. Technol., 2017, 3, 391–402 Search PubMed.
- Y. Feng, L. Yang, J. Liu and B. E. Logan, Environ. Sci.: Water Res. Technol., 2016, 2, 800–831 Search PubMed.
- G. Pozo, S. Pongy, J. Keller, P. Ledezma and S. Freguia, Water Res., 2017, 126, 411–420 CrossRef PubMed.
- E. Thompson Brewster, C. M. Mehta, J. Radjenovic and D. J. Batstone, Water Res., 2016, 94, 176–186 CrossRef PubMed.
- E. Thompson Brewster, J. Jermakka, S. Freguia and D. J. Batstone, Water Res., 2017, 124, 210–218 CrossRef PubMed.
- E. Thompson Brewster, A. J. Ward, C. M. Mehta, J. Radjenovic and D. J. Batstone, Water Res., 2017, 110, 202–210 CrossRef PubMed.
- E. H. Perkins, H. W. Nesbitt, W. D. Gunter, L. C. St-Arnaud and J. R. Mycroft, Critical Review of Geochemical Processes and Geochemical Models Adaptable for Prediction of Acidic Drainage from Waste Rock, Energy, Mines and Resources Canada, Centre for Mineral and Energy Technology, 1995 Search PubMed.
- B. S. Caruso, T. J. Cox, R. L. Runkel, M. L. Velleux, K. E. Bencala, D. K. Nordstrom, P. Y. Julien, B. A. Butler, C. N. Alpers, A. Marion and K. S. Smith, Hydrol. Processes, 2008, 22, 4011–4021 CrossRef.
- J. D. Allison, D. S. Brown and K. J. Novo-Gradac, MINTEQA2/PRODEFA2, a geochemical assessment model for environmental systems: version 3.0 user's manual, Environmental Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency, Athens, GA. 1991 Search PubMed.
- D. L. Parkhurst and C. A. J. Appelo, User's guide to PHREEQC (Version 2): a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations, Report 99–4259, 1999 Search PubMed.
- G. D. Betrie, R. Sadiq, C. Nichol, K. A. Morin and S. Tesfamariam, J. Hazard. Mater., 2016, 301, 187–196 CrossRef PubMed.
- G. Madzivire, W. M. Gitari, V. R. K. Vadapalli, T. V. Ojumu and L. F. Petrik, Miner. Eng., 2011, 24, 1467–1477 CrossRef.
- N. Papassiopi, C. Zaharia, A. Xenidis, K. Adam, A. Liakopoulos and I. Romaidis, Miner. Eng., 2014, 64, 78–91 CrossRef.
- X. Flores-Alsina, C. Kazadi Mbamba, K. Solon, D. Vrecko, S. Tait, D. J. Batstone, U. Jeppsson and K. V. Gernaey, Water Res., 2015, 85, 255–265 CrossRef PubMed.
- G. Pozo, L. Jourdin, Y. Lu, P. Ledezma, J. Keller and S. Freguia, RSC Adv., 2015, 5, 89368–89374 RSC.
- G. Pozo, L. Jourdin, Y. Lu, J. Keller, P. Ledezma and S. Freguia, Electrochim. Acta, 2016, 213, 66–74 CrossRef.
- G. Pozo, Y. Lu, S. Pongy, J. Keller, P. Ledezma and S. Freguia, Bioelectrochemistry, 2017, 118, 62–69 CrossRef PubMed.
- S. Freguia, K. Rabaey, Z. Yuan and J. Keller, Electrochim. Acta, 2007, 53, 598–603 CrossRef.
- A. J. Ward, K. Arola, E. Thompson Brewster, C. M. Mehta and D. J. Batstone, Water Res., 2018, 135, 57–65 CrossRef PubMed.
- J. Jermakka, E. Thompson Brewster, P. Ledezma and S. Freguia, Sep. Purif. Technol., 2018, 203, 48–55 CrossRef.
- C. Kazadi Mbamba, S. Tait, X. Flores-Alsina and D. J. Batstone, Water Res., 2015, 85, 359–370 CrossRef PubMed.
- H. H. Yang and R. L. McCreery, J. Electrochem. Soc., 2000, 147, 3420–3428 CrossRef.
- K. Jansen, R. K. Thauer, F. Widdel and G. Fuchs, Arch. Microbiol., 1984, 138, 257–262 CrossRef.
- K. Brysch, C. Schneider, G. Fuchs and F. Widdel, Arch. Microbiol., 1987, 148, 264–274 CrossRef.
- C. M. Plugge, W. Zhang, J. C. M. Scholten and A. J. M. Stams, Frontiers in Microbiology, 2011, 2, 81 CrossRef PubMed.
- B. Virdis, K. Rabaey, R. A. Rozendal, Z. Yuan and J. Keller, Water Res., 2010, 44, 2970–2980 CrossRef PubMed.
- B. Virdis, K. Rabaey, Z. Yuan and J. Keller, Water Res., 2008, 42, 3013–3024 CrossRef PubMed.
- K. S. Exner, J. Anton, T. Jacob and H. Over, Angew. Chem., Int. Ed., 2016, 55, 7501–7504 CrossRef PubMed.
- W. Pronk, M. Biebow and M. Boller, Environ. Sci. Technol., 2006, 40, 2414–2420 CrossRef PubMed.
- P. Ledezma, J. Jermakka, J. Keller and S. Freguia, Environ. Sci. Technol. Lett., 2017, 4, 119–124 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: ESI1: System schematic and modelling results; ESI 2: experimental data for model fitting; ESI 3: MATLAB codes. See DOI: 10.1039/c8ra03153c |
| ‡ Present address: Centre for Mined Land Rehabilitation, Sustainable Minerals Institute, The University of Queensland, St Lucia, QLD 4072, Australia |
| § Present address: Separation and Conversion Technologies, VITO-Flemish Institute for Technological Research, Boeretang 200, 2400, Mol, Belgium |
| This journal is © The Royal Society of Chemistry 2018 |