Open Access Article
Open Access ArticleElectrorheological behavior of iron(II) oxalate micro-rods
E. Kutalkova,
T. Plachy,
J. Osicka,
M. Cvek,
M. Mrlik and
M. Sedlacik *
*
Centre of Polymer Systems, University Institute, Tomas Bata University in Zlín, tr. T. Bati 5678, 760 01 Zlín, Czech Republic. E-mail: msedlacik@utb.cz
First published on 10th July 2018
Abstract
Electrorheological (ER) fluids represent smart materials with extensive application potential due to their rheological properties which can be readily changed under an external electric field. In this study, the iron(II) oxalate particles with rod-like morphology were successfully synthesized by the co-precipitation method using sulphate heptahydrate and oxalic acid dihydrate. The characterization of particles was performed via X-ray diffractometry and scanning electron microscopy. Subsequently, the ER fluids were prepared by dispersing the synthesized particles in silicone oil. The optical microscopy demonstrated the formation of chain-like particle structures upon the application of an electric field. Rheological properties were determined by means of rotational rheometry including creep-recovery experiments. The viscoelastic behavior of systems under investigation in the presence of the electric field was confirmed by the presence of recoverable strain of the system.
Introduction
Electrorheological (ER) fluids are well-known intelligent systems whose rheological parameters can be controlled by application of an external electric field. They are typically two-phase systems consisting of electrically-polarizable particles dispersed in a non-conducting liquid medium. After application of the electric field, the particles start to join themselves into chain-like structures spanning the electrodes due to dipole–dipole interactions.1 This behaviour is accompanied by a significant change in rheological parameters and is called the ER effect. The intensity of the ER effect depends on the electric field strength,2 E, the volume fraction of the particles,3,4 ϕ, their morphology, size,5–7 and conductivity,8,9 σ. Moreover, dielectric properties such as dielectric permittivity of the particles, dielectric relaxation strength, Δε, and relaxation time, τrel, of the ER fluids,10 and temperature,11,12 T, play a significant role in achieving a high ER effect. Depending on these parameters the ER fluids thus undergo transitions from liquid to viscoelastic systems exhibiting a portion of elastic (recoverable) deformation.1,13–15One of the important parameters of the ER fluids is the yield stress, τy, representing the value of stress that the ER fluids can withstand before they start to flow. It has been shown that rod-like particle-based ER fluids exhibit higher ER effects (higher τy) than those containing the equivalent amount of spherical particles not only due to stronger friction forces but also stronger dipole moments developed in the built-up chains of polarized particles after switching on the electric field.6,7,16,17 On the other hand, another important feature of the ER fluids is their efficiency, e. In the case of the ER fluids containing the rod-like particles their η0 is often higher since the rod-like particles possess higher viscous drag forces.18 The higher viscosity of the systems containing the rod-like particles can then be explained as a higher energy required for the orientation of such particles in the direction of the flow when compared to spherical ones.18
The co-precipitation method is a synthetic route that supports crystal growth in a certain direction, thus a material with unique properties resulting from the shape anisotropy can be obtained. The molar ratio of the precursors and the conditions during the co-precipitation determine morphology and size of the particles which can be thus optimized in order to obtain material with preferable ER effects.19 Moreover, this method is facile, cost effective and enables large-scale production.19
Iron(II) oxalate dihydrate (FeC2O4·2H2O) is an inorganic compound often employed in solid-state chemistry as precursor for thermally-induced syntheses of various nanocrystalline metal oxides.20 A wider potential of this material recently appeared when Plachy et al.21 successfully employed the iron oxalate as a stabilizing agent in magnetorheological applications. In this study, rod-like iron(II) oxalate dihydrate particles prepared via co-precipitation method were introduced to electrorheology as a novel dispersed phase to fabricate the ER fluids. A dependence of the ER effects on the particles concentration was investigated and viscoelastic properties of the ER fluids were further studied through creep-recovery test confirming their transition from a liquid state to a viscoelastic solid in the presence of the electric field.
Experimental
Particle synthesis
Iron(II) oxalate particles were synthesized via the co-precipitation method using iron(II) sulphate heptahydrate (Sigma Aldrich; USA) and oxalic acid dihydrate (Lach-Ner; Czech Republic).21,22 Briefly, iron(II) sulphate heptahydrate (FeSO4·7H2O, ≥99%) and oxalic acid dihydrate (C2H2O4·2H2O, p.a.) were used in an equivalent amount (20 mmoL) and were separately dissolved in a 28 mL mixture of ethyleneglycol (Penta; Czech Republic) and demineralized water 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v). The oxalic acid solution served as a precipitating agent, which was slowly added into the iron sulphate solution under stirring using a magnetic stirrer. While the solution was further treated in a pressurized reactor in the previous study,22 in this case the stirring proceeded until yellow precipitate was developed. Subsequently, the product was thoroughly filtered-off with a distilled water and dried overnight at the temperature of 70 °C.
1 (v/v). The oxalic acid solution served as a precipitating agent, which was slowly added into the iron sulphate solution under stirring using a magnetic stirrer. While the solution was further treated in a pressurized reactor in the previous study,22 in this case the stirring proceeded until yellow precipitate was developed. Subsequently, the product was thoroughly filtered-off with a distilled water and dried overnight at the temperature of 70 °C.
Particle characterization
The prepared iron(II) oxalate particles were investigated using an X-ray diffractometry (XRD) to confirm their successful preparation. The XRD data was collected monitoring the diffraction pattern appearing in the 2θ angle range of 10–95° (scan speed of 1° min−1) with Co Kα1 radiation using an X-ray diffractometer Miniflex 600 (Rigaku, Japan). The conductivity of the particles (1.5 × 10−8 S m−1) was measured by the two-point method at ambient temperature using an electrometer (Keithley 6517B, USA). A scanning electron microscope (SEM; Nova NanoSEM 450, FEI, USA) was used to observe size, morphology, and uniformity of the prepared particles. Density of the prepared particles was determined with the help of a gas pycnometer (UltraFoam 1200e, Quantachrome Instruments, Germany) using a nitrogen as a gaseous medium. The density of synthesized particles was 2.35 ± 0.05 g cm−3. The obtained density is further expressed as a mean value and standard deviation of 10 independent measurements. The ER fluids were obtained by mixing the dried particles with silicone oil (Lukosiol M200, Chemical Works Kolín, Czech Republic, dynamic viscosity ηc = 194 mPa s at the temperature of 25 °C) at various volume concentrations of the particles (1, 5, and 10 vol%). Before each measurement, the prepared ER fluids were manually stirred for 5 min with a glass stick.Optical microscopy
Optical microscopy was used in order to evaluate the formation of internal chain-like structures in the prepared ER fluid. The representative sample of concentration 0.5 vol% was placed on the glass plate between two copper electrodes while the external electric field strength of 0.5 kV mm−1 was supplied by the DC high-voltage source (Keithley 2400, USA). The chain-like structures were observed using an optical microscope (Leica DVM2500; Leica Microsystems, UK).Rheological measurements
Electrorheological measurements were performed using a rotational rheometer Bohlin Gemini (Malvern Instruments, UK) with a plate–plate geometry (diameter of 20 mm with a gap of 0.5 mm) at 25 °C. The external electric field strengths of 0.3–1.5 kV mm−1 were induced by the high-voltage source DC TREK (TREK 668B, USA). In the case of the on-state characterization, the electric field was applied for 1 min before starting the shearing in order to provide time enough for the particles to create equilibrium chain-like structures. After each on-state test run, the constant shear rate of 20 s−1 was applied for 1 min to disrupt the residual structures.Creep and creep-recovery experiments were performed in order to investigate the viscoelastic properties of prepared ER fluids containing the iron(II) oxalate particles. In the presence of the external electric field, recoverable strains, γREC, of the ER fluids were observed, while during the measurements in its absence, zero recoverable strain was found. The recoverable strain can be calculated as (eqn 1):
| γREC = (γi − γf)/γi × 100 (%) | (1) |
Results and discussion
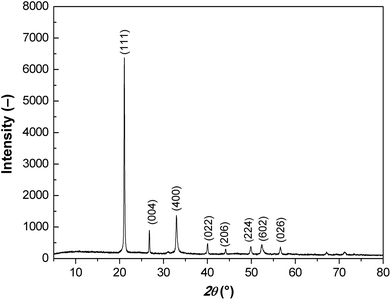
X-ray diffraction patterns of the prepared particles possess all the characteristic peaks confirming dominant presence of the FeC2O4 phase (Fig. 1).21,22 In the X-ray spectrum the diffraction peak is dominant at approximately 21° 2θ indexed for material as the (111) peak.The prepared particles possess rod-like morphology with relatively high aspect ratio. The length of the particles was ranging from 15 to 30 μm and their thickness was ranging from 1 to 2 μm (Fig. 2).
As can be seen, in the absence of the electric field the investigated ER fluids exhibited random distribution of dispersed particles (Fig. 3a). However, after its application the particles start to span the gap between the electrodes creating oriented chain-like structures (Fig. 3b). This particle alignment is associated with a significant increase in the viscosity of the system as will be described further in detail.
 | ||
| Fig. 3 Optical microscopy images of silicone-oil suspensions containing the iron(II) oxalate particles (0.5 vol%) at 0 kV mm−1 (a) and 1 kV mm−1 (b) of the external electric field. | ||
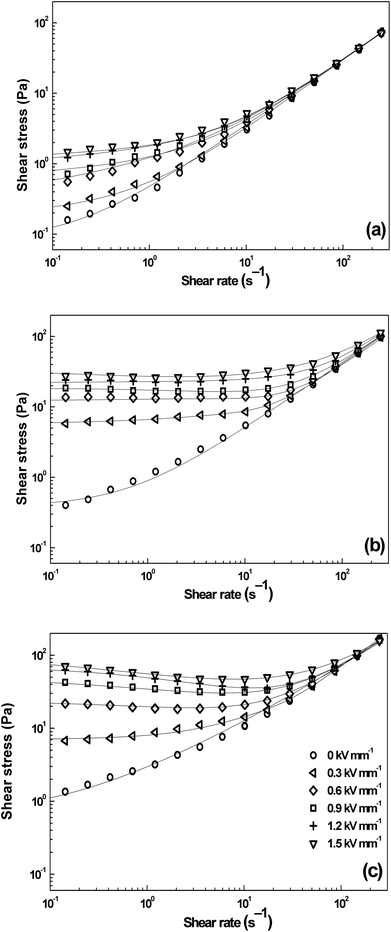
Fig. 4 demonstrates rheological properties of silicone-oil suspensions containing the iron(II) oxalate particles at the concentrations of 1, 5, and 10 vol% in the absence as well as in the presence of the external electric field strengths of 0.3; 0.6; 0.9; 1.2, and 1.5 kV mm−1. A substantial increase of shear stress, τ, can be observed upon the application of the external electric field, when the particles in silicon-oil suspensions start to develop internal chain-like structures along the direction of electric field applied. This effect also leads to the increase in viscosity of the system. As can be seen in Fig. 4, in the absence of the electric field, the shear stress of prepared ER fluids is almost linearly dependent on the shear rate illustrating nearly newtonian behavior. In the presence of the electric field, however, the ER fluids start to exhibit τy as a rule the higher electric field the higher value of τy due to polarization forces between the particles. With increasing particles concentration in the system τy values further increase due to enhanced electrostatic interactions acting between dispersed particles. The ER fluid with particle loading of 10 vol.% possesses the shear stress values substantially higher (about more than 1.5 order of a magnitude) at low shear rate values than the ER fluids with lower particles loading (Fig. 4c). Upon the application of the external electric field strength of 1.5 kV mm−1 in the case concentration of the particles 10 vol%, the yield stress values are around 80 Pa. The observed ER performance is thus comparable with that of recently-developed ER fluids containing the particles prepared via multi-step syntheses.23,24 Hence, the presented material in this study can be characterized by two benefits, the sufficient ER performance and its facile synthesis not requiring any special or toxic chemicals.
In the case of ER fluids, Cho-Choi-Jhon (CCJ) model has been proposed very well for fitting the flow curves of ER fluids (eqn (2)):25
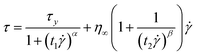 | (2) |
| Parameters | 0 kV mm−1 | 0.3 kV mm−1 | 0.6 kV mm−1 | 0.9 kV mm−1 | 1.2 kV mm−1 | 1.5 kV mm−1 |
|---|---|---|---|---|---|---|
| τy | 0.4 | 5.1 | 12.1 | 18.1 | 22.2 | 26.5 |
| t1 | 0.05 | 0.08 | 0.06 | 0.03 | 0.01 | 3.40 |
| α | 0.41 | 1.75 | 1.20 | 0.68 | 0.93 | 0.46 |
| η∞ | 0.28 | 0.38 | 0.34 | 0.39 | 0.39 | 0.32 |
| t2 | 0.59 | 0.25 | 0.29 | 0.90 | 0.23 | 0.01 |
| β | 0.16 | 0.84 | 0.65 | 0.99 | 0.76 | 0.90 |
Another important rheological property for the description of the ER fluids behavior is ER efficiency, e (eqn (3)). This factor shows the behavior changes in the viscosity of the ER fluids in the absence and in the presence of external electric field. It can be calculated as:
| e = (ηE − η0)/η0 | (3) |
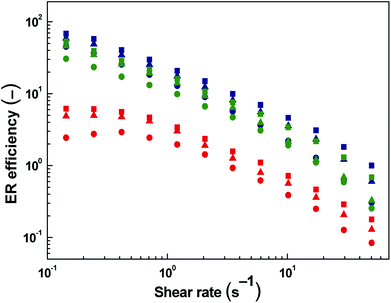
Fig. 5 shows the dependence of the ER efficiency on the shear rate. The ER efficiency of ER fluids under investigation is enhanced with increasing intensity of electric field at each concentration.
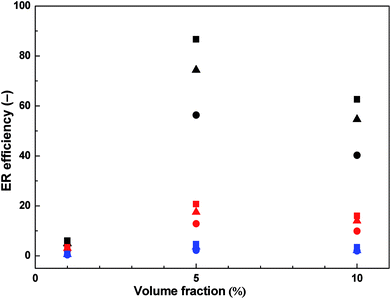
The ER efficiency is significantly higher at low shear rates compared to high shear rates as the electrostatic forces are dominating over hydrodynamic ones. However, the latter forces increase with increasing shear rate and the domination of electrostatic forces is disappearing since the rupturing of formed internal structures is starting to continuously predominate over the self-healing ability of the chain-like structure given just by the polarization of particles. The highest ER efficiency (Fig. 6) is determined at the concentration of 5 vol% and the electric field strength of 1.5 kV mm−1. It is evident that with further increase in particle concentration the efficiency is not increasing anymore due to the effect of increased field-off viscosity. Similar phenomenon with optimum concentration of the particles on the ER performance of ER fluids has been already introduced.4 The effect of competition between electrostatic forces and hydrodynamic ones described above can be also observed in this case.
The τy values obtained applying eqn (2) on experimental data for all investigated ER fluids was further used to show the increasing rigidity of created internal structures within the ER fluids after the application of the external electric field in Fig. 7. The dependence of the τy of ER fluids on the electric field strength, Ec, applied obeys mostly the power law dependence (eqn (4)):26
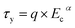 | (4) |
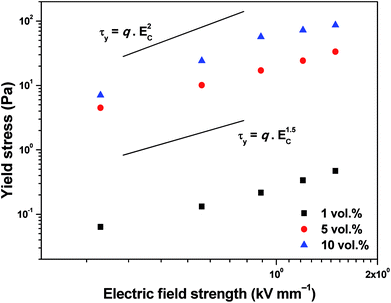 | ||
| Fig. 7 Dependence of the dynamic yield stress on the applied electric field strength for ER fluids iron(II) oxalate particles of various concentrations. | ||
A creep test involves two distinct phases, the creep phase and the recovery phase. In the former one, a constant stress is applied to the sample for a fixed time period. After removal of the τ some deformation may be recoverable (the recovery phase). For a viscoelastic material, recoverable strain, γREC, is expressed as in eqn (1).
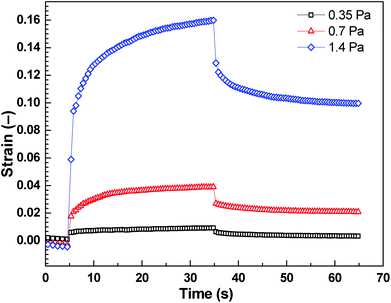
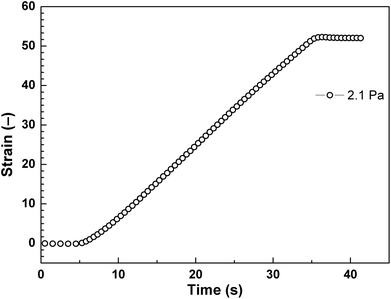
The strain of viscoelastic material increases with time under the application of constant τ to the samples for 30 s. After the removal of applied τ, the deformation in the case of viscoelastic materials is partly recoverable. Shear stress values were taken below the elastic stress, τ′, evolved from storage modulus, G′, of the ER fluid by the relation expression of τ′ = G′γ, where γ represents deformation strain, since τ′ represents the maximum value to support complete recovery when τ is eliminated.24 These τ values (0.35 Pa, 0.7 Pa, 1.4 Pa) were applied to the ER fluid (5 vol%) under investigation in the presence of the electric field strength of 0.9 kV mm−1 (Fig. 8). After application of the external electric field, the ER fluid changes its solely viscous behaviour to viscoelastic one and exhibits a certain level of the γREC depending on the intensity of the applied τ (Fig. 8). The γREC was evaluated according to eqn (1) (Table 2). These observations confirmed the transition of the investigated ER systems from liquid to viscoelastic solids upon the application of the electric field. As can be seen in Fig. 9, the applied τ value above the τ′ caused continuous flow resulting in almost no γREC.
| Shear stress, τ (Pa) | Recoverable strain, γREC (%) |
|---|---|
| 0.35 | ∼64 |
| 0.7 | ∼46 |
| 1.4 | ∼38 |
| 2.1 | ∼0 |
Electrorheological reproducibility (Fig. 10) of the system after the switching on and off an external electric field has been confirmed by means of the time course of shear stress at the shear rate 1 s−1. In the absence of field, polarization of the particles disappears and viscosity is relatively quickly returned to its original value. Since the ER performance of ER fluids based on iron(II) oxalate particles is driven by conduction model and these particles have rod-like structure at the same time, their orientation along the electric field is a little bit slower when compared with globular nanoparticles ER systems.28 However, when the rigid structure along the field direction is formed, this is stable within the wide shear rate region as illustrated in Fig. 4 and Table 1 just probably due to the conduction model and friction between oriented rod-like particles in the particulate chains.
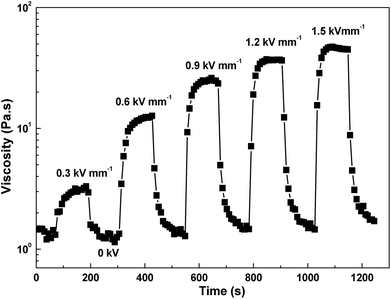 | ||
| Fig. 10 Time dependence of the shear stress alternating between 0 and 1.5 kV mm−1 at the shear rate of 1 s−1 for 10 vol% ER fluid. | ||
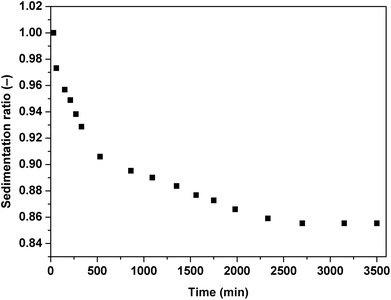
The important issue of contemporary ER fluids is their sedimentation stability. The particles are generally dispersed in a liquid medium which possess lower density than the dispersed particles. This leads to undesirable effects and consequently possible problems in their potential applications. As can be seen in Fig. 11, the ER fluid based on 5 vol% of iron(II) oxalate particles keeps stable for a long time probably because of the particles' rod-like structure hindering their sedimentation.29 containing the iron(II) oxalate particles in the presence of the electric field strength of 0.9 kV mm−1 under the applied shear stresses of 0.35 Pa (black squares), 0.7 Pa (red triangles) and 1.4 Pa (blue diamonds).
Conclusions
Iron(II) oxalate particles were synthesized via co-precipitation method using iron(II) sulphate heptahydrate and oxalic acid dihydrate as precursors. These particles with rod-like morphology were subsequently mixed with silicone oil at concentrations of 1, 5, and 10 vol% in order to create novel ER fluids. Utilization of particles with rod-like morphology led to significant ER effects. Furthermore, the highest ER efficiency was found for the system containing 5 vol% of synthesized particles. The viscoelastic behavior investigation of the ER fluids was conducted through creep-recovery test. At levels of shear stress where electrostatic forces dominated over hydrodynamic ones the systems exhibited certain elastic portion of deformation. In the case of utilizing shear stress values of 0.35 Pa, 0.7 Pa, and 1.4 Pa the recoverable strain was 64%, 46%, and 38%, respectively. The creep-recovery test confirmed the transition of the ER fluids from a liquid state to viscoelastic solid.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the Internal Grant Agency of Tomas Bata University in Zlín (projects nos. IGA/CPS/2017/004 and IGA/CPS/2018/004) for the financial support. This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic – Program NPU I (LO1504). This research was also carried out with support of the Operational Program Research and Development for Innovations co-funded by the European Regional Development Fund (ERDF) and national budget of the Czech Republic, within the framework of the Centre of Polymer Systems project (CZ.1.05/2.1.00/19.0409).References
- J. Stejskal, M. Mrlik, T. Plachy, M. Trchova, J. Kovarova and Y. Li, React. Funct. Polym., 2017, 120, 30–37 CrossRef.
- M. Mrlik, M. Ilcikova, T. Plachy, R. Moucka, V. Pavlinek and J. Mosnacek, J. Ind. Eng. Chem., 2018, 57, 104–122 CrossRef.
- Y. D. Liu and H. J. Choi, Electrorheological fluids: smart soft matter and characteristics, Soft Matter, 2012, 8, 11961–11978 RSC.
- A. Lengalova, V. Pavlinek, P. Saha, O. Quadrat, T. Kitano and J. Steiskal, Eur. Polym. J., 2003, 39, 641–645 CrossRef.
- A. Lengalova, V. Pavlinek, P. Saha, O. Quadrat and J. Steiskal, Colloids Surf., A, 2003, 227, 1–8 CrossRef.
- M. Sedlacik, M. Mrlik, Z. Kozakova, V. Pavlinek and I. Kuritka, Colloid Polym. Sci., 2013, 291, 1105–1111 CrossRef.
- J. B. Yin, X. X. Wang, R. T. Chang and X. P. Zhao, Soft Matter, 2012, 8, 294–297 RSC.
- M. Stenicka, V. Pavlinek, P. Saha, N. V. Blinova, J. Stejskal and O. Quadrat, Colloid Polym. Sci., 2009, 287, 403–412 CrossRef.
- T. Plachy, M. Sedlacik, V. Pavlinek and J. Stejskal, J. Mater. Chem. C, 2015, 3, 9973–9980 RSC.
- L. C. Davis, J. Appl. Phys., 1992, 72, 1334–1340 CrossRef.
- T. Plachy, M. Sedlacik, V. Pavlinek, J. Stejskal, M. P. Graca and L. C. Costa, J. Intell. Mater. Syst. Struct., 2016, 27, 880–886 CrossRef.
- J. B. Yin, X. A. Xia, L. Q. Xiang and X. P. Zhao, Smart Mater. Struct., 2011, 20, 015002 CrossRef.
- O. Erol, H. I. Unal and B. Sari, Polym. Compos., 2010, 31, 471–481 Search PubMed.
- K. Oz, M. Yavuz, H. Yilmaz, H. I. Unal and B. Sari, J. Mater. Sci., 2008, 43, 1451–1459 CrossRef.
- B. Sari, N. Yavas, M. Makulogullari, O. Erol and H. I. Unal, React. Funct. Polym., 2009, 69, 808–815 CrossRef.
- X. A. Xia, J. B. Yin, P. F. Qiang and X. P. Zhao, Polymer, 2011, 52, 786–792 CrossRef.
- J. B. Yin, X. P. Zhao, X. Xia, L. Q. Xiang and Y. P. Qiao, Polymer, 2008, 49, 4413–4419 CrossRef.
- D. Vincenzi, J. Fluid Mech., 2013, 719, 465–487 CrossRef.
- Z. G. Jia, D. P. Ren, L. X. Xu and R. S. Zhu, Mater. Sci. Semicond. Process., 2012, 15, 270–276 CrossRef.
- M. Hermanek, R. Zboril, M. Mashlan, L. Machala and O. Schneeweiss, J. Mater. Chem., 2006, 16, 1273–1280 RSC.
- T. Plachy, M. Cvek, Z. Kozakova, M. Sedlacik and R. Moucka, Smart Mater. Struct., 2017, 26, 025026 CrossRef.
- Z. Kozakova, I. Kuritka, P. Bazant, M. Pastorek and V. Babayan, Mater. Lett., 2015, 138, 116–119 CrossRef.
- X. Q. Ji, W. L. Zhang, W. P. Jia, X. X. Wang, Y. Tian, L. Deng and J. Q. Liu, J. Ind. Eng. Chem., 2017, 56, 203–211 CrossRef.
- C. S. Jun, S. H. Kwon, H. J. Choi and Y. Seo, ACS Appl. Mater. Interfaces, 2017, 9, 44811–44819 CrossRef PubMed.
- M. S. Cho, H. J. Choi and M. S. Jhon, Polymer, 2005, 46, 11484–11488 CrossRef.
- S. G. Kim, J. Y. Lim, J. H. Sung, H. J. Choi and Y. Seo, Polymer, 2007, 48, 6622–6631 CrossRef.
- K. Zhang, Y. D. Liu, M. S. Jhon and H. J. Choi, J. Colloid Interface Sci., 2013, 409, 259–263 CrossRef PubMed.
- S. H. Piao, C. Y. Gao and H. J. Choi, Polymer, 2017, 127, 174–181 CrossRef.
- C. G. Niu, X. F. Dong, H. Zhao and M. Qi, Smart Mater. Struct., 2014, 23, 075018 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |