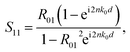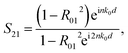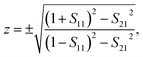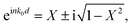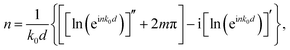DOI:
10.1039/C8RA03758B
(Paper)
RSC Adv., 2018,
8, 22361-22369
Numerical investigation of terahertz polarization-independent multiband ultrahigh refractive index metamaterial by bilayer metallic rectangular ring structure
Received
2nd May 2018
, Accepted 1st June 2018
First published on 19th June 2018
Abstract
Multiband high index of refraction can be realized by thin ring-type terahertz metamaterials composed of multilayer coupled unit cells. We have focused on the numerical investigation of this type of a metamaterial. By drastically decreasing the diamagnetic effect with a thin metallic structure in the unit cell and by increasing the effective permittivity through strong capacitive coupling, a bandwidth of 1.5 THz with an index of more than 24 can be achieved using a single-layer thin brick-type metamaterial. The refractive index peak is 35. Then, we design a ring-type metamaterial structure, achieving a refractive index of 91 at about 0.45 THz, which is due to a decrease in the diamagnetic effect with smaller area surrounded by toroidal currents. Based on the coupling effects of double layer ring-type metamaterials or single-layer double ring-type structures, the refractive index peaks reach 43.2 and 18.68 at 0.43 THz and 0.92 THz, respectively. A three-layer ring-type metamaterial structure is proposed to obtain three band high index metamaterials.
1. Introduction
An arbitrary control of the electromagnetic properties of materials has been achieved by using metamaterials.1–11 Recently, the discovery of artificial materials with unusual and effective electromagnetic responses has become the key to metamaterial technology. Previous studies have focused on high-impedance surfaces, which have been used as an antenna substrate,6 negative refractive index metamaterials,7,8 effective surface plasmons9,10 on perfect metal surfaces with gratings,11 and effective bulk plasmons in thin-wire structures.1 On the contrary, it is found that a high-refractive index metamaterial attracts far less attention. It is important to prepare a metamaterial with ultrahigh effective refractive index for providing more flexible designs in transformation optics for applications such as clocking.4,5 Also, a metamaterial with an unnaturally high refractive index can be applied in imaging and lithography industries, where high resolutions can be achieved by exploiting the high refractive index of the material.3
Recently, Shin et al. numerically demonstrated the mechanisms of a broadband high-refractive index metamaterial, which could be realized by appropriate structure with cubic components.12 Choi et al. designed an “I”-shaped terahertz metamaterial with an unnaturally high refractive index.4 However, the “I”-shaped high-refractive index metamaterial was polarization-dependent, which did not benefit the application in polarization-independent devices.
In this study, we numerically designed a polarization-independent multiband ultrahigh-refractive index metamaterial based on brick structure and ring-type structure in the terahertz region. In addition, a thin rectangular ring structure was used to avoid the diamagnetic effect arising from induced current loops in the metallic structure.13 By strong capacitive coupling from a smaller gap width between unit cells, the effective permittivity could be drastically increased. By decreasing the area enclosed by induced surface currents, the diamagnetic response of the metamaterials was reduced, resulting in the increase in the effective permeability. The single-layer double ring-type metamaterial structure, the double-layer ring-type metamaterial structure, and the three-layer ring-type metamaterial structure were proposed to realize a multiband high-index metamaterial. By optimizing the geometric parameters of the designed metamaterials, the characteristics of the multiband high index, including peak and bandwidth, could be easily manipulated.
2. Extraction method of effective refractive index of metamaterial
Recently, Smith et al. proposed a general method of extracting equivalent basic parameters using the reflection and transmission coefficients (S-parameters).14–16 The comparison between theoretical and experimental extractions proved that this method is accurate.4 We characterized the metamaterial structure as an effective homogenous slab under the condition of a long wavelength. A plane wave was incident normally on the slab of metamaterials. The S parameters are represented as17,18| |
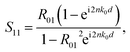 | (1) |
| |
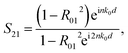 | (2) |
where R01 = (z − 1)/(z + 1) is the half space reflection coefficient, z is the impedance, n is the refractive index, and d is the thickness of the slab. By transforming the above two formulas, the impedance z and refractive index n can be expressed as| |
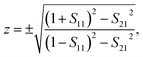 | (3) |
| |
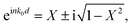 | (4) |
where X = (1 − S112 + S212). From the above two formulas, the effective refractive index can be determined by| |
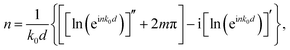 | (5) |
where m refers to an integer related to the branch index of n′. For the above-mentioned retrieval process, eqn (3) and (4) can be directly used to calculate the effective refractive index and the impedance of the designed metamaterials. Then, the permittivity ε and permeability μ of the metamaterials are immediately calculated by ε = n/z and μ = nz, respectively.17
According to the Maxwell's macro description, the effective refractive index of materials can be determined by the effective permittivity and effective permeability, and this remains valid for the synthetic material.4 The effective relative permittivity can be described by ε = 1 + (P/ε0E), and the effective relative permeability can be defined as μ = 1 + (M/H), where E, H, P and M represent electric field, magnetizing field, polarization and magnetization, respectively. To obtain high effective refractive index, the effective permittivity or effective permeability should be increased.
3. Design of high-refractive index metamaterials
A. The thin brick-type metallic structure
The brick-type metallic structure of the proposed high-refractive index metamaterial is shown in Fig. 1(a). The electric field vector of an incident terahertz wave is along the y direction (TE polarization). We used the three-dimensional full-wave electromagnetic field finite integral method (CST Microwave Studio software) to accurately calculate S-parameters and near-field distribution of metamaterials.19–21 The metal layer (copper) was embedded in the substrate; the substrate was made from a dielectric polyimide material, and it had a refractive index of n = 1.8 + 0.04i.4 Polyimide material is basically transparent in terahertz range, and its absorption is low. The polyimide material with the index of 1.8 + 0.04i is important in terahertz devices. The polyimide layers have good mechanical elongation and tensile strength, which helps the adhesion between the polyimide layers or between polyimide layers and metal layers. The minimum interaction between the metal film and polyimide film coupled with high-temperature stability of the polyimide film results in a system that provides reliable insulation when subjected to various types of environmental stresses. Thus, it is a rational design choice for designing a high-refractive index metamaterial. In this structure, the length of the unit cell was a = 60 μm, the length of the metal structure was pa = 59.5 μm, and the metal gap between bricks was g = a − pa = 0.5 μm. The thin brick-type metallic structure with thickness of t = 0.2 μm was embedded symmetrically in the substrate with thickness d = 2 μm.
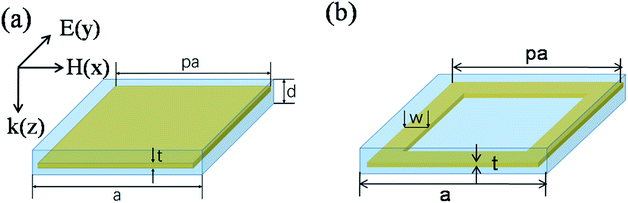 |
| | Fig. 1 (a) Schematic diagram of unit cell structure of the thin brick structure embedded in the substrate. (b) The rectangular ring-type metallic high-index metamaterial embedded in the substrate. | |
Careful attention must be paid to the estimation of the effective thickness while extracting effective basic parameters for the designed metamaterial, such as effective refractive index and effective permittivity and permeability, especially when there is no specific physical boundary. The effective thickness can be defined as the distance between the virtual boundaries. The transmitted and reflected waves are plane waves in the virtual boundaries. To extract the exact values of the metamaterial parameters, we used a multi-layer metamaterial to achieve more accurate calculations. As the number of layers of the metamaterial increased, the convergent refractive index at the quasi-static limit was obtained.4 The effective refractive index is a basic property of the metamaterial block structure. Thus, the effective thickness can be defined as a single layer of metamaterial with virtual thickness that has the same volume refractive index at the quasi-static limit as the multilayer metamaterial.4 In the process of extracting parameters, we compared the effective refractive index and impedance of the quasi-static limit of the multilayer metamaterial with those of the monolayer metamaterial. Therefore, the exact equivalent parameters of metamaterials could be obtained, as shown in Fig. 2, for thin brick metamaterials. The effective permittivity ε, the permeability μ and the effective refractive index n are shown. This metamaterial structure provided Re (ε) with a value of 2700 at the resonant frequency of 1.15 THz. The value of the permeability μ was 0.16, leading to the strong suppression of the diamagnetic effect. A bandwidth of 1.5 THz with an index of more than 24 could be observed with the refractive index peaking at 35.
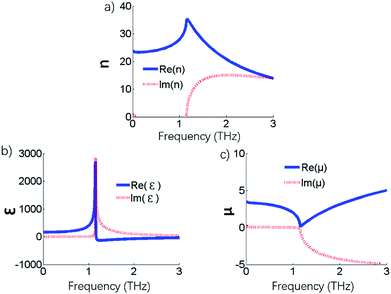 |
| | Fig. 2 The extracted (a) effective refractive index, (b) the effective permittivity and (c) permeability for the brick metallic patches with the polarization of the incident electric field along the y direction. | |
To investigate the physical effects of the brick structure, we impinged an external TE wave on the brick structure. The electric field was concentrated intensely in the gap between the adjacent brick unit cell structures, as shown in Fig. 3(a). A large amount of surface charge built up, and the opposite side of the gap formed a parallel plate capacitor, resulting in a dipole moment and higher permittivity. In addition, Fig. 3(b) and (c) show the formation of a large area current and magnetic field distribution when an electric field is applied; these surface currents were generated by magnetic moments opposite to the applied magnetic field components.17 A thin brick means that the structure exhibits large suppression of the diamagnetic effect, resulting in high effective permeability. Since the refractive index of the metamaterial is directly related to the effective permeability, high permeability caused an increase in the refractive index.
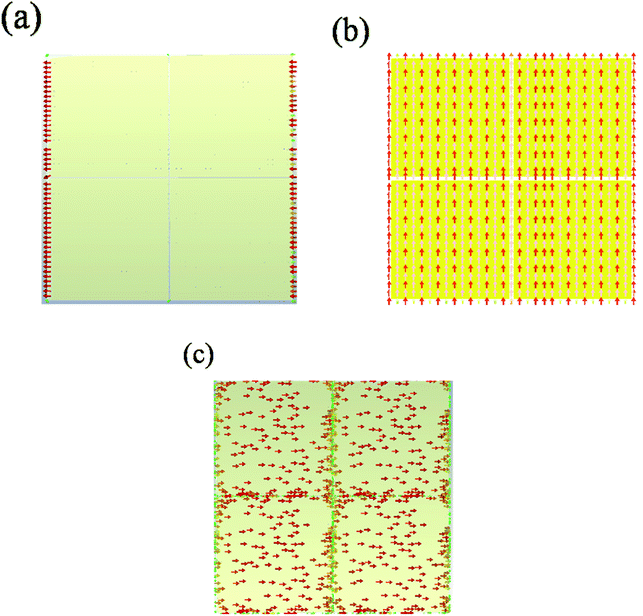 |
| | Fig. 3 (a) Saturated electric field distribution at 1 THz for the single layer brick structure metamaterial in four unit cells; the red region shows strong electric field. (b) The vector plot of the magnetic field distribution at 1 THz in four unit cells. (c) Saturated surface current distribution at 1 THz. | |
B. The rectangular ring-type metallic structure
To further decrease the diamagnetic effect of the metamaterial, a polarization-independent rectangular ring structure was proposed with smaller metallic area enclosed by the current loop. A ring structure of a = 60 μm, pa = 59.5 μm, and t = 0.2 μm was designed, and the width of the ring structure was w = 3 μm, as shown in Fig. 1(b). The metal ring was symmetrically embedded in the substrate with a substrate thickness d = 2 μm. In addition, the substrate was made of a dielectric material having a refractive index of n = 1.8 + 0.04i. The effective refractive index and permeability could be extracted by the S-parameter method. As shown in Fig. 4(a) and (b), the refractive index of the ring-type structure was significantly greater compared with that of the brick structure. The diamagnetic response in the ring-type structure was weaker. Fig. 4(a) confirms that the observed electrical resonance had a peak relative permittivity of 2623 at 0.438 THz, and the peak of the refractive index could reach 91.3, as seen in Fig. 4(b).
 |
| | Fig. 4 (a) Extracted effective permittivity. (b) Refractive index for the rectangular ring structure high-index metamaterial by the S-parameter retrieval method. | |
To explore the physical effects of the ring structure, we numerically simulated the electromagnetic effect. As shown in Fig. 5(a), the electric field was strongly concentrated in the gap between the cells. The gap width plays a decisive role in enhancing effective permittivity. A large amount of surface charge accumulated on the edge of the parallel plate capacitor because charges on each edge of the unit cell interacted with the opposite charges on the adjacent edge of the cell. This charge accumulation could form a significant dipole moment in the unit cell. Due to the large charge accumulation in the unit cell, high dipole moment eventually resulted in enhanced effective permittivity.4,12 Therefore, we inferred that reducing the gap width can increase the effective permittivity. Although the effective permittivity can be increased by reducing the gap width, it is still necessary to suppress the diamagnetic effect to achieve high refractive index. The ring metal structure could effectively reduce the diamagnetic effect because it provided a smaller area surrounded by surface currents. Fig. 5(b) and (c) show the surface-induced current and the magnetic field around the metal patch in the monolayer metamaterial cell at a frequency of 0.45 THz. Besides, the influence of structure parameters on the refractive index is demonstrated in Fig. 6.
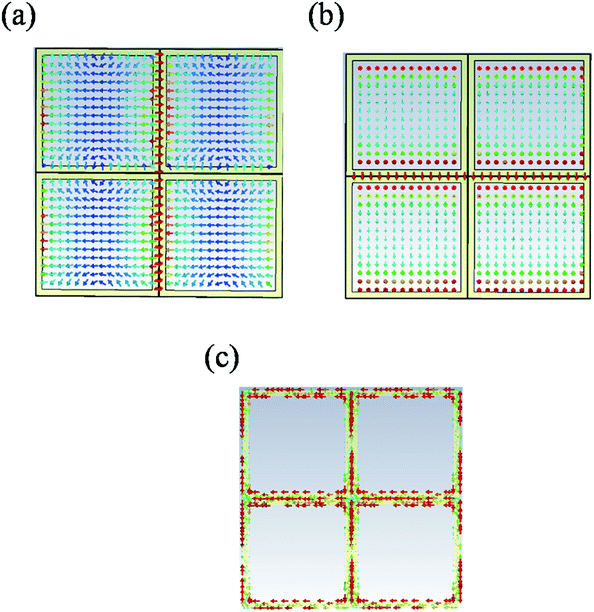 |
| | Fig. 5 (a) Saturated electric field distribution at 0.45 THz for the single layer ring structure metamaterial; the red region shows strong electric field. (b) The vector plot of the magnetic field distribution at 0.45 THz in four unit cells. (c) Surface current distribution. | |
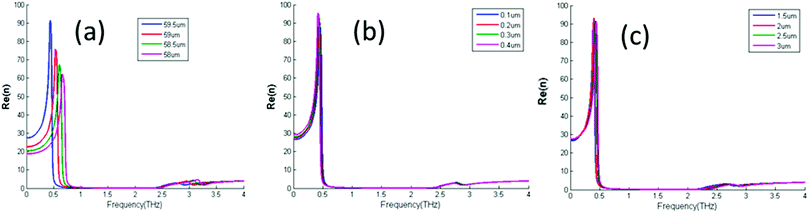 |
| | Fig. 6 Extracted real part of refractive index with different (a) lengths of the metal structure pa, (b) metal thickness t, and (c) metal structure width w. | |
To clearly indicate the influence of gap width on the effective constitutive parameters of the metamaterials, the refractive index, permittivity and magnetic permeability with a gap width of g = 7 μm between the adjacent ring-type metal structures are shown in Fig. 7. The other parameters are unchanged. It is found that the resonance frequency is 1.13 THz, which is different from that of the gap width of g = 0.5 μm, as shown in Fig. 4. When the gap width becomes larger, the dipole moment between the adjacent metal pieces becomes smaller. The charge accumulation between the adjacent metal surfaces is decreased and thus, the permittivity is decreased, resulting in a decrease in the refractive index.
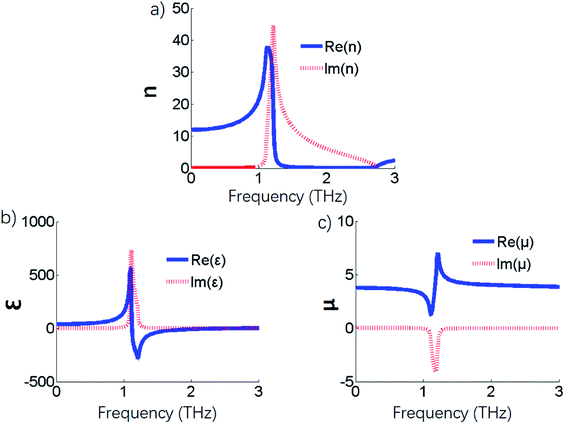 |
| | Fig. 7 Extracted (a) effective refractive index, (b) effective permittivity, and (c) permeability for ring structure high-index metamaterial. | |
C. Double-layer rectangular ring-type metamaterial
To further increase the bandwidth of the high refractive index, we constructed a double-layer ring-type metamaterial, as shown in Fig. 8. The geometrical parameters were a = 60 μm, pa = 59.5 μm, and s = 0.5 μm, and the width was w = 3 μm. The metallic thickness was set at t = 0.2 μm. Each layer of the substrate had thickness of d = 2 μm, and each layer of metal structure was symmetrically embedded in the substrate. We observed that the structure had two resonance frequencies at 0.435 THz and 0.923 THz, and the refractive index peaks reached 43.2 and 18.68, respectively, as shown in Fig. 9(b). To quantify the effects of our proposed dual-band metamaterials, the effective permittivity, effective permeability and effective refractive index were extracted, as shown in Fig. 9. A strong electric resonance with a peak permittivity of 1319 was observed at a frequency close to 0.43 THz, and a relatively weak electrical resonance occurred at about 0.922 THz with peak permittivity of about 252, as shown in Fig. 9(a). Although the reduction in the gap width can increase the effective permittivity, it is still necessary to strongly suppress the diamagnetic response of the designed metamaterials to achieve high effective refractive index of the dual band. The ring metal structure can effectively reduce the diamagnetic response because the ring structure has a small area surrounded by currents. At the two frequencies of electrical resonance, two weakly diamagnetic resonances were observed with high refractive index.
 |
| | Fig. 8 (a) The structure with two metallic rings embedded in two dielectric layers. (b) Top view of the double-layer ring-type metamaterial structures. | |
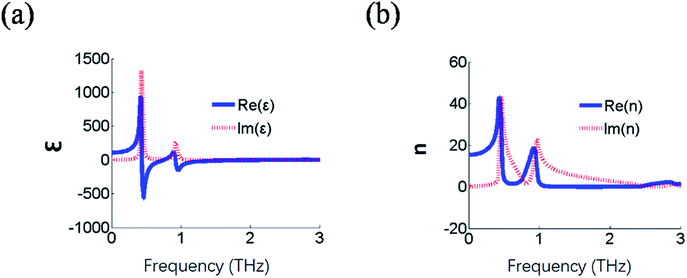 |
| | Fig. 9 Extracted (a) effective permittivity and (b) refractive index of double-layer single-ring-type structure of metamaterial. | |
The effective constitutive parameters of both metamaterial structures were calculated (Fig. 11) to distinguish the effective characteristics of single-layer double ring-type structure and double-layer ring-type structure, as shown in Fig. 10. The refractive indices of the single-layer double ring-type metamaterial structure increased to around 59 and 33 at both resonance frequencies. The resonance frequencies of the two structures were the same. It was observed that the permittivities of the two structures were almost the same, and the permeability of the single-layer structure was higher than that of the double-layer structure. Also, for the double layer structure, the substrate thickness and the length of the metal structure pa of one metal ring to the refractive index are demonstrated in Fig. 12. For double-layer rectangular loop metamaterials, increasing the distance between metal structures affected the distribution of the metamaterial's magnetic and electric fields. Therefore, we increased the substrate thickness without changing the metal thickness, as shown in Fig. 12(a). It can be seen that when the distance between metal structures reached 6 μm, a second refraction peak appeared, and its value was higher than that of the first peak.
 |
| | Fig. 10 (a) Single-layer double ring-type structure. (b) Double-layer ring-type structure. | |
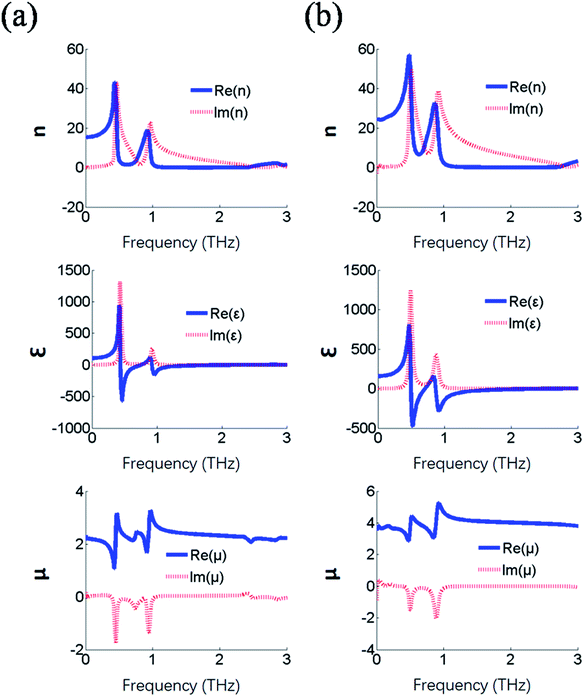 |
| | Fig. 11 (a) Effective constitutive parameters of the double-layer ring-type structure (left column). (b) Effective constitutive parameters of the single-layer double ring-type structure (right column). | |
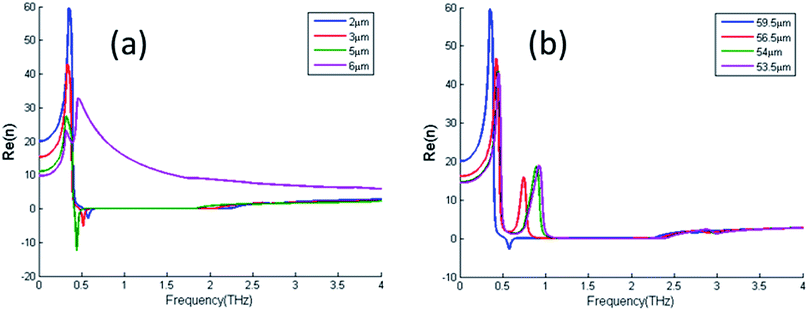 |
| | Fig. 12 Extracted real part of effective index as a function of (a) substrate thickness and (b) the length of the metal structure pa of one metal ring. | |
D. Three-layer rectangular ring-type metamaterial
Based on the above-mentioned analysis and design, it was found that the number of high refractive index bands is related to the number of layers or rectangular rings in a single layer. We designed a three band high-refractive index metamaterial having a three-layer structure. The effective constitutive parameters were extracted and are shown in Fig. 13. It was found that the three-layer ring structure metamaterial generated three resonance frequency bands. The value of the first resonance frequency and the value of the refractive index were almost the same as those of the two-layer structure. Therefore, it was expected that each layer of the metamaterial with a single ring or a single ring in single layer can exhibit a high-refractive index band. The geometric parameters of a single rectangle could manipulate the amplitude of effective refractive index and resonance frequency. Thus, by carefully designing the metamaterial structure, a multiband high refractive index could be realized for use in broadband responsive elements. Also, for the three layer structure, the effects of substrate thickness and length of the metal structure pa of middle metal ring on the refractive index are demonstrated in Fig. 14.
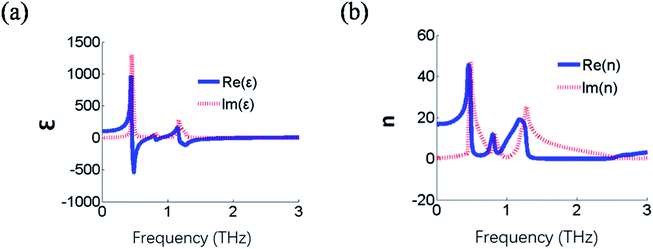 |
| | Fig. 13 Extracted (a) effective permittivity and (b) refractive index of three-layer ring-type structure of metamaterial. | |
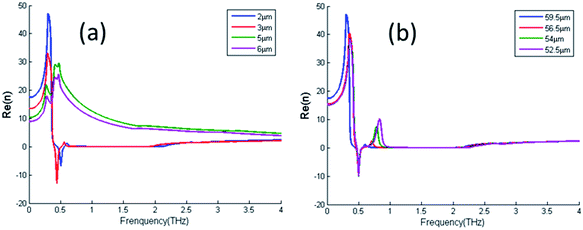 |
| | Fig. 14 Extracted real part of effective index for three layer structure: (a) variation of substrate thickness with same three metal rings and (b) variation of the length of the metal structure pa for middle layer metal ring. | |
4. Conclusions
We have numerically shown that an artificial multiband high-refractive index metamaterial can be designed to extend the spectrum of indices in the THz region. Due to relatively strong diamagnetic response in the brick-type metallic structure, the refractive index is relatively lower than that for the ring-type structure metamaterials. It is possible to obtain an even higher index of refraction by further decreasing the gap width. To obtain the dual band effective refractive index, we have designed a two-ring structure embedded in the substrate. Our findings concerning multiband high-index metamaterials may lead to many interesting applications of subwavelength-scale functional devices such as broadband slow light devices, invisibility devices of transformation optics, and compact cavity resonators.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported in part by the National Key Research and Development Plan (Grant No. 2016YFF0100505), Natural Science Foundation of Zhejiang Province (LY17F050009), National Program on Key Basic Research Project of China (973 Program) (2014CB339806), Shanghai Leading Talent (2016–2019), and Young Yangtse River Scholar.
References
- D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer and J. B. Pendry, Science, 2006, 314, 977–980 CrossRef PubMed.
- D. Sun, M. Wang, Y. Huang, Y. Zhou, M. Qi, M. Jiang and Z. Ren, Chin. Opt. Lett., 2017, 15, 051603 CrossRef.
- Z. Bai, G. Tao, Y. Li, J. He, K. Wang, G. Wang, X. Jiang, J. Wang, W. Blau and L. Zhang, Photonics Res., 2017, 5, 280–286 CrossRef.
- M. Choi, S. H. Lee, Y. Kim, S. B. Kang, J. Shin, M. H. Kwak, K. Y. Kang, Y. H. Lee, N. Park and B. Min, Nature, 2011, 470, 369–373 CrossRef PubMed.
- A. Karalis, E. Lidorikis, M. Ibanescu, J. D. Joannopoulos and M. Soljacić, Phys. Rev. Lett., 2005, 95, 063901 CrossRef PubMed.
- X. Wei, H. Shi, X. Dong, Y. Lu and C. Du, Appl. Phys. Lett., 2011, 97, 011904 CrossRef.
- R. Liu, C. Ji, J. J. Mock, J. Y. Chin, T. J. Cui and D. R. Smith, Science, 2009, 323, 366–369 CrossRef PubMed.
- W. Zhu, M. Jiang, H. Guan, J. Yu, H. Lu, J. Zhang and Z. Chen, Photonics Res., 2017, 5, 684–688 CrossRef.
- L. Chen, N. Xu, L. Singh, T. Cui and R. Singh, Adv. Opt. Mater., 2017, 5, 1600960 CrossRef.
- L. R. Chen, Chin. Opt. Lett., 2017, 15, 010004 CrossRef.
- L. Chen, Y. Wei, X. Zang, Y. Zhu and S. Zhuang, Sci. Rep., 2016, 6, 22027 CrossRef PubMed.
- J. Shin, J. T. Shen and S. Fan, Phys. Rev. Lett., 2009, 102, 093903 CrossRef PubMed.
- B. Wood and J. B. Pendry, J. Phys.: Condens. Matter, 2007, 19, 076208 CrossRef PubMed.
- D. R. Smith, S. Schultz, P. Marko and C. M. Soukoulis, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 195104 CrossRef.
- B. I. Popa and S. A. Cummer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165102 CrossRef.
- R. Marqués, F. Medina and R. Rafii-El-Idrissi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 4440 Search PubMed.
- D. R. Smith, D. C. Vier, T. Koschny and C. M. Soukoulis, Phys. Rev. E, 2005, 71, 036617 CrossRef PubMed.
- T. Koschny, P. Marko, E. N. Economou, D. R. Smith, D. C. Vier and C. M. Soukoulis, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 71, 245105 CrossRef.
- Z. Meng, L. Ke, L. L. Hui and L. Y. Qiu, Chin. Opt. Lett., 2017, 15, 101203 CrossRef.
- W. Wang, F. Yan, S. Tan, H. Zhou and Y. Hou, Photonics Res., 2017, 5, 571–577 CrossRef.
- H. J. Hua, L. X. Hong, Z. J. Jun and Z. Jun, Chin. Opt. Lett., 2017, 15, 030502 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Xue Lib
b and
Xue Lib