Open Access Article
Open Access ArticlePreparation of macroporous scaffolds with holes in pore walls and pressure driven flows through them†
Soumyajyoti Chatterjee‡
 a,
Aditi Potdar‡
a,
Aditi Potdar‡ b,
Simon Kuhn
b,
Simon Kuhn *b and
Guruswamy Kumaraswamy
*b and
Guruswamy Kumaraswamy *a
*a
aJ-101, Polymers and Advanced Materials Laboratory, Complex Fluids and Polymer Engineering, Polymer Science and Engineering Division, CSIR-National Chemical Laboratory, Pune-411008, Maharashtra, India. E-mail: g.kumaraswamy@ncl.res.in; Fax: +91-20-2590-2618; Tel: +91-20-2590-2182
bKU Leuven, Department of Chemical Engineering, Celestijnenlaan 200F, Leuven 3001, Belgium. E-mail: simon.kuhn@kuleuven.be
First published on 9th July 2018
Abstract
Controlling the pore architecture in macroporous scaffolds has important implications for their use as reactor packings and as catalyst supports. We report the preparation of a macroporous structure, where the pore walls are perforated by holes. These materials are prepared by modification of the ice-templating protocol developed in our group. We freeze a dispersion of colloidal silica, polymer and cross-linker in a water/acetonitrile medium and allow crosslinking to proceed in the frozen state. The presence of a small fraction of acetonitrile (varying between 1.6% to 6.4%) results in the formation of holes in the pore walls. Increasing the acetonitrile concentration changes the pore size distribution, and produces smaller pores on average. This also results in an increasing fraction of the wall area being covered by small pores, of the order of a few microns in size. Perforation of the walls by pores does not change the overall porosity or modulus of the scaffolds. However, the introduction of pores leads to a drastic reduction in the pressure drop required to pump liquid through the scaffolds. The observed residence time distribution (RTD) in the scaffolds is represented by two plug flow reactors (PFRs) in parallel. The RTD results indicate that increasing the hole fraction in the pore walls results in increased channelling which explains the aforementioned decreased pressure drop during pressure driven flow.
1. Introduction
The flow of liquids through porous beds is of relevance to a variety of applications. For example, porous materials are often used as supports in catalysis. Mounting a catalytic moiety on a porous support allows us to heterogenize the catalyst while providing a large specific surface area for the substrate reactants to access the catalyst. The specific surface area is inversely proportional to the pore size of the support. Thus, a smaller pore size corresponds to a larger specific surface area. However, there is a significant increase in pumping costs when reactants are pumped through small pore size supports in continuous flow synthesis. Therefore, it is necessary to optimize the pore size distribution when designing porous catalyst supports for flow reactors. Similarly, column packings for chromatography also need to balance the separation achieved with the pressure drop required to pump liquid through the column. Here too, optimizing the pore architecture and pore size distribution is critical. One strategy that has been described in the past is to use hierarchically porous structures that combine macroporous scaffolds, associated with low pressure drops for flow, with microporous structures that afford a high specific surface area (for example, for catalyst immobilization1–6). It has been demonstrated that bimodal pore structure decreases the scaffold weight while increasing the specific surface area without compromising the scaffold strength.7,8 Researchers have reported a variety of techniques, including templating of emulsions and liquid crystalline mesophases, to prepare structures with bimodal pore architecture.2,7–9 However, detailed studies of the residence time distribution for flow through such hierarchically micro/macroporous structures have not been reported. The residence time distribution also reflects the level of spatial homogeneity in macropore distribution, that determines the mass transport efficiencies in a reactor.10 As the residence time distribution decides the time available for reaction on a catalyst immobilized on a porous support, it is important to determine how the pore architecture influences this.Several strategies have been described for the preparation of macroporous materials. Of these, the most widely adopted routes are emulsion templating and templating of sacrificial templates such as colloidal crystals. Recently, researchers have reported several other porogen-based methods including dynamic surfactant templating,11–14 foaming by generation of gas bubbles15–18 and breath figure19–22 techniques to synthesize 3-D macroporous structures and 2-D porous films. With these techniques, researchers have demonstrated control over pore size and over overall porosity. However, these routes to macroporous materials are either characterized by processing complexity and/or require the use of solvents for template removal.
Recently, we have described an elegant method for the preparation of macroporous materials.23–26 This method employs a green solvent, water as the porogen, to prepare a macroporous structure. We employ ice-templating, where an aqueous dispersion of colloidal particles, cross-linkable polymer and cross-linker is frozen. The ice crystals that form on freezing expel the colloids, polymer and cross-linker to form walls around ice crystals. We allow the polymer to cross-link in the frozen state such that the resultant structure has the colloids entrapped in the cross-linked polymer mesh. After cross-linking, the sample is simply thawed to obtain the scaffold. Thus, expensive lyophilisation is avoided since the hybrid walls of the scaffold, comprising colloids and cross-linked polymer have sufficient mechanical strength to prevent collapse of the macropore walls during drying. We have demonstrated that this strategy is versatile and can be applied to a wide variety of colloids, polymers and cross-linking chemistries. This allows us access to a wide range of scaffolds with different functional colloids and with variation in the organic content. Hybrid scaffolds once prepared can also be calcined to burn off the organic content while retaining the pore structure.26
Researchers have demonstrated that the structure of the macroporous scaffold obtained by ice templating can be manipulated by varying the conditions for ice templating. For example, directional ice templating has been employed to produce oriented pore morphologies.27–36 Ice templating of suspensions of microporous particles has been used to prepare monoliths that combine micro and macroporosity.37,38 Ice templating has also been performed from suspensions in solvent mixtures. For example, particle suspensions in miscible systems such as water/acetone; water/alcohol; water/dioxan have been ice templated to yield materials with bimodal pore size distribution and defined morphology.27,39–42 In these reports, researchers have exploited the systematic addition of secondary liquid to increase the viscosity of the aqueous slurry and increase the degree of undercooling, leading to a decrease in average pore size. In these examples, the solvents were removed by lyophilisation to yield macroporous structures where the pore size distribution is strongly influenced by the addition of secondary solvent.
Here, we demonstrate a simple route to the preparation of dual macroporous polymer/particle hybrid scaffolds that affords mechanically resilient 3D structure. We show that pore walls perforated with holes can be formed by ice-templating process from water/acetonitrile mixtures. We demonstrate that these holes form through the cooling-induced phase separation of acetonitrile from the mixture. These holes are distinct from the pores and are clearly visible using microscopy. Thus, an unusual pore architecture is obtained in the scaffold, with perforated pore walls.
2. Experimental section
2.1 Materials and chemicals
Polyethylenimine (PEI, branched polymer with supplier specified molecular weight Mw = 750 kDa); 1,4-butanediol diglycidyl ether, acetonitrile (HPLC grade), chloroform d6 (CDCl3) were obtained from Sigma Aldrich and were used as received. Distilled deionized water (resistivity ∼ 18.2 MΩ cm) from a Millipore MilliQ unit was used as solvent to prepare scaffolds. Glass tubes (inner diameter 3.4 mm; length 40 mm) were cleaned using an acidic piranha etch before use.2.2 Fabrication of hybrid scaffolds with different acetonitrile concentration
Scaffolds were prepared in glass tubes, using a modification of previously reported protocols, as follows.43 Piranha etched glass tubes were dipped in an aqueous solution of PEI, to allow the polymer to adsorb on the walls of the tube. Subsequently, the tubes were removed and one end of the tube was blocked using Teflon tape. Ice templating is performed in this tube. In a typical synthesis, 120 mg of silica particles was taken in a plastic container and dispersed in 1064 μl water by sonication for 15 min. To this aqueous particle dispersion, 10 mg PEI (100 μl of 100 mg ml−1 stock solution), 16 mg 1,4-butanediol diglycidyl ether as cross-linker and 20 μl acetonitrile (corresponding to 1.6% v/v) was thoroughly mixed. This dispersion is then transferred to a glass tube, prepared as described earlier. The dispersion is then frozen by keeping the glass tube at −10 °C for 24 h.When water freezes to form ice, the silica particles and organic molecules in the dispersion are concentrated in the regions between ice crystals. We have demonstrated that this enhancement in concentration results in cross-linking of the PEI, and a composite structure forms with silica particles held together in a cross-linked PEI mesh.44 Here, the composite scaffold forms in the glass tube surface adsorbed with PEI. PEI adsorbed on the walls of the glass tube is cross-linked with that in the porous structure, resulting in strong adhesion of the scaffold with the tube. After cross-linking proceeds for 24 h, the scaffold formed is thoroughly washed with copious amounts of water.
Scaffolds prepared with 1.6% acetonitrile added to the ice-templated aqueous dispersion are termed S1.6. Similarly, we also prepare hybrid scaffolds with the same quantity of particle, polymer and cross-linker as earlier but with varying acetonitrile (ACN) concentration (3.2 and 6.4%). These scaffolds are termed S3.2 and S6.4, respectively. Hybrid scaffolds prepared without the addition of ACN are termed S0. Scaffolds synthesized in the glass tubes were used for pressure drop and residence time distribution (RTD) measurements, while identical scaffolds are prepared in plastic vials for structural and mechanical characterization.
2.3 Pressure drop and RTD study
We use a home-built experimental set up to examine the pressure drop to pump water through the scaffolds. Initially, we manually fill the glass tube containing the scaffold with water. In all our experiments, we used scaffolds of length = 4 cm. The glass tube is then connected to a syringe pump (Harvard Apparatus PHD 2000) through a soft silicone connector tube. A digital manometer (HTC PM 6205) was used to record the pressure drop across the length of the scaffold as water is pumped through it using the syringe pump. The manometer was connected across the scaffold through T-joints in the silicone tubes (Scheme 1).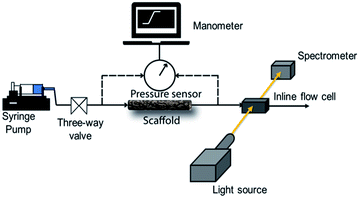 | ||
| Scheme 1 Schematic representation of the experimental setup for the measurement of pressure drop and residence time distribution. | ||
RTD measurements were performed with an aqueous solution of the tracer dye Rhodamine B (concentration: 312 μM). A step inlet pulse was generated for the RTD experiments with the help of a three-way valve. However, as this technique does not result in an ideal concentration step change as input signal, the concentration pulse was measured at both inlet and outlet using an inline UV-Vis spectrometer (Avaspec 2048L, Avantes) connected to a deuterium-halogen light source (Avalight DH-S-BAL, Avantes). Experiments were performed at different flow rates (0.25, 0.5 and 1 ml min−1) which were adjusted by a syringe pump (PHD Ultra, Harvard Apparatus). Each experiment was repeated three times to ensure reproducibility. Moreover, before the start of each measurement, the scaffold was filled with deionized water and special care was taken to ensure removal of any trapped bubbles. Scheme 1 depicts the schematic representation of the experimental setup for RTD measurements.
To obtain the RTD of the scaffold, we applied the deconvolution of the measured inlet signal from the outlet signal.45 This post-processing step was performed using fast Fourier transformation (FFT) with an in-house Matlab code. The so obtained response of the scaffold was further evaluated by fitting (using a nonlinear least-squares solver in Matlab) it to various known RTD models, i.e. the axial dispersion model,46 two plug flow reactors (PFRs) in parallel model,47 and a model combining axial dispersion and exchange with stagnant zones.48 It was observed that the two PFRs in parallel model describes the response of the scaffold most accurately.
The two PFRs in parallel model implies that there is compartmentation inside the scaffold where each compartment behaves like an independent PFR. If ‘F’ represents the total flow rate and ‘V’ is the total void volume of the scaffold, then ‘α’ represents the fraction of the total flow rate ‘F’ that is flowing through an independent PFR of the scaffold which has a void volume fraction of ‘β’. The overall response of the scaffold can be represented as the sum of the responses from each compartment as given by eqn (1).
| E(t) = αE1(t) + (1 − α)E2(t) | (1) |
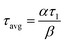 | (2) |
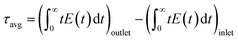 | (3) |
The likelihood of each compartment to behave like a plug flow reactor was determined by fitting each compartment response to the axial dispersion model (eqn (4)).
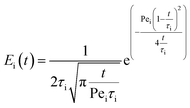 | (4) |
2.4 Instruments and characterization
The microstructure of the scaffolds was characterized using a Quanta 200 3D scanning electron microscope (SEM) and Xradia Versa 510-Carl Zeiss X-ray Micro-computed Tomography (Pleasanton, California). Image data from the X-ray μ-tomography was analysed using Dragon software, supplied with the instrument. Proton NMR measurements were carried out on a Bruker instrument at 400 MHz frequency using CDCl3 as reference. Thermogravimetric analysis (TGA) was performed using a TA Instruments SDT Q6000 analyzer between 120 and 700 °C at a heating rate of 10 °C min−1 in N2 atmosphere. Mechanical properties of the scaffolds were characterized using a strain controlled rheometer, TA-ARES G2, equipped with a normal force transducer.3. Results and discussion
3.1 Characterization of ice-templated scaffolds
Ice-templating results in the formation of macroporous scaffolds, with hybrid walls templating the shape of the ice crystals. The walls of the scaffold are comprised of silica particles held in a mesh of cross-linked polymer. We obtain centimetre-sized macroporous scaffolds following the preparation protocol outlined in Scheme 2. Addition of small quantities of ACN, a water-miscible organic solvent, has a significant effect on the microstructure of the ice-templated scaffolds.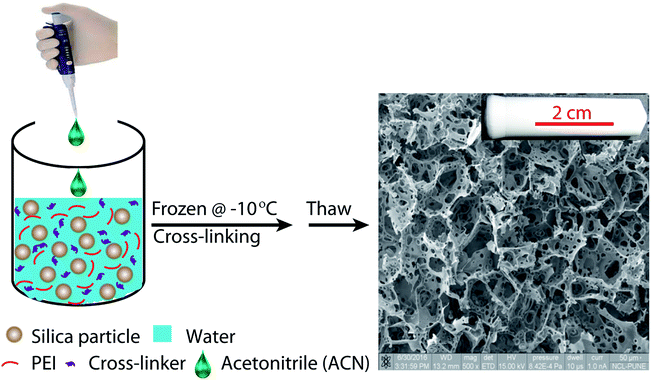 | ||
| Scheme 2 Schematic representation of the preparation protocol for hierarchically porous ice-templated hybrid scaffolds. | ||
SEM images reveal that ice-templating results in the formation of an interconnected network structure in all scaffolds (Fig. 1, ESI Fig. S1†). The particles/cross-linked polymer hybrid structure form walls that enclose the pores formed by ice crystals, that act as porogens. Qualitatively, addition of acetonitrile to the dispersion that undergoes ice templating results in the appearance of holes that perforate the walls formed by the particle/cross-linked polymer hybrid. Additionally, we observe a decrease in pore size. This decrease in pore size with addition of organic solvent is consistent with previous reports.27,39–42 We characterize the pore size distribution by analysing a large number of SEM images (at least 500 pores for each sample). SEM indicates that the pores are not strictly spherical and are anisotropic. We analyse the SEM images using ImageJ and use edge-detection to identify the pores and obtain their size as the largest length scale of the pore. For S0, we have performed X-ray microcomputed tomography (X-ray μ-CT) to quantitatively obtain the pore size distribution and have reported this previously.25 When we compare the pore size distribution from SEM image analysis with that from μ-CT measurements (ESI Fig. S2†), we observe that these are reasonably well matched. Therefore, it appears that despite the problems associated with using SEM image analysis to resolve the pore size (due to the anisotropy and tilt of the pores), the pore size distribution from averaging over a large number of pores reasonably well approximates that from μ-CT measurements. This gives us confidence in the estimate of pore sizes obtained from image analysis. We define “pores” as the large voids created by cross-linking the particle/polymer hybrid around the ice crystal porogens, and “holes” as the perforations in the hybrid walls. From the SEM micrographs, it is evident that pores are characterized by larger length scales (>10 μm), compared with holes (3–10 μm). We also performed X-ray μ-CT to characterize S6.4. Image data was analysed using software supplied with the instrument to obtain the size distribution of voids. Voids with a size less than 10 μm are considered holes, while larger voids are considered to be pores (ESI Fig. S3†). Here, too we obtain a reasonable agreement between the SEM image analysis and the μ-CT measurements. μ-CT measurements are very time consuming, and necessitate the deposition of a thin coating of a metal salt on the pore walls to get sufficient contrast to resolve the holes. Therefore, here we resort to analysis of a large number of SEM images to characterize the distribution of pore and hole sizes. For each material, we use multiple SEM micrographs taken at different locations of the sample and measure at least 500 pores and 2000 holes to obtain their size distribution (Fig. 2). Comparison between SEM and X-ray μ-CT data suggests that the “apparent” size distribution of pores and holes from SEM analysis is a reasonably accurate estimate of the real size distribution. Finally, we note that these scaffolds are soft compressible materials – thus, it is not possible to perform mercury porosimetry on them.
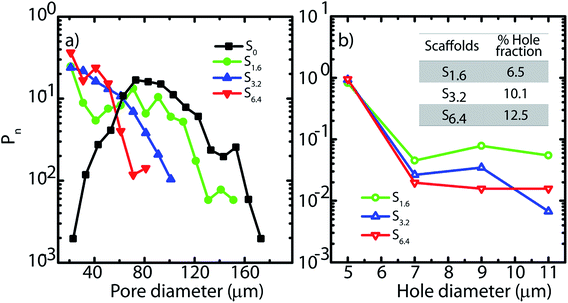 | ||
| Fig. 2 (a) Pore and (b) hole size distributions obtained from SEM micrographs. Inset (b) indicates the fraction of the wall surface area that is covered by holes in the scaffolds. | ||
In Fig. 2, we plot the normalized size distribution for pores and holes, obtained by binning the size data from image analysis. We estimate number fraction (Pn) of pore size by normalizing the binned frequency of a pore size with the sum of all frequencies above 10 μm. Similarly we report hole fraction number (Pn) by normalizing the binned frequency of a hole size with the sum of all frequencies between 3–10 μm. We observe that S0 has a peak in the pore size distribution, indicating a most probable pore size of 65 μm (Fig. 2a), consistent with our previous analysis.25 Interestingly, on addition of ACN, there is no longer a clear maximum in the pore size distribution. Rather, there is a qualitative change in the shape of the pore size distribution due to a dramatic increase in the frequency of small size pores (Fig. 2a). Increase in ACN concentration leads to a decrease in the average pore size.
The ACN–water binary solvent system is extensively used in chromatography and is therefore well studied.49–51 At the concentrations used in this work, water and ACN remain miscible.52 Addition of miscible organic solvents such as ACN, results in a decrease in the freezing point of the mixture. There is greater decrease in freezing point for higher ACN concentrations – however, even at 6.4%, the decrease in freezing point is reported to be only about 3 °C.53 The size of the ice crystals formed by freezing of water–organic solvent mixtures is governed by a wide variety of factors including solvent-induced changes in nucleation and growth rates, temperature equilibration in the sample (that depends on sample size and cooling rate), Ostwald ripening, etc. While models have been described54 that predict ice crystal size obtained by freezing water-solvent mixtures, these models still require significant inputs from experimental measurements and therefore cannot be used in a predictive manner. In our experiments, the aqueous dispersion has silica particles, polymer and diepoxy cross-linker, in addition to ACN. Therefore, rationalization of our experimental observations on the effect of ACN on the pore size distribution is challenging. We simply note that we observe a decrease in average pore size, and a qualitative change in the shape of the pore size distribution on ice templating dispersions with increasing ACN concentration.
SEM reveals another interesting consequence of the addition of ACN. We observe that ice-templated samples from water–ACN mixtures are characterized by walls that are perforated, with small holes that are 3–10 μm in size (Fig. 2b). With increase in ACN concentration, there is an increase in the apparent fraction of the wall area with holes (obtained from SEM image analysis) from 6.5% to 10.1% to 12.5% for 1.6%, 3.2% and 6.4% ACN, respectively. In all scaffolds, the frequency of holes decreases with increasing hole size (Fig. 2b). The data also suggests that increasing ACN concentration strongly increases the fraction of small (3 to 5 μm) holes at the expense of the larger (5 to 12 μm) holes.
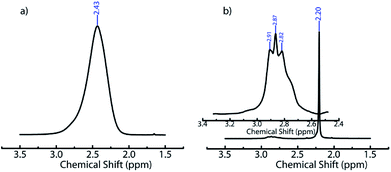
We believe that ACN plays a key role in hole formation. ACN and water are miscible. However, they can separate into ACN rich and water rich phases on addition of small molecule electrolytes such as NaCl49,55 or non-ionic small molecules such as glucose.56 This phase separation is promoted on cooling.49 There are also reports of phase separation of mixtures of partially miscible liquids at the surface of dispersed colloidal particles.57 In our ice-templating experiments, the water/ACN mixtures contain silica particles, polymer (PEI) and cross-linker. We hypothesized that PEI induced a phase separation of our system into water rich and ACN rich phases on cooling. To verify this, we cooled water/6.4% ACN mixtures containing PEI and performed liquid state 1H NMR on these samples in the frozen state. We focus on the signal from the methyl protons in ACN. At room temperature, we observe a sharp peak for the ACN protons at about 2.2 ppm for water/ACN mixtures and for water/ACN mixtures containing 1% PEI (ESI, Fig. S4†). We use a Peltier stage to cool the water/ACN mixtures to −10 °C in situ in the NMR and investigate this sample in the frozen state. We observe that there is a significant broadening of the ACN proton peak (full width at half maximum = 0.15 ppm, compare with 0.003 ppm for the sample at room temperature, Fig. 3). Broadening of NMR peaks is indicative of slowing down of molecular motions in the frozen samples. Therefore, this data indicates that cooling a water/6.4% ACN sample to −10 °C results in the sample freezing. In contrast, NMR data from water/6.4% ACN samples containing 1% PEI frozen to −10 °C yield a narrow peak for the ACN protons. This strongly suggests that the ACN remains liquid, with high molecular mobility even on freezing the sample. When water and ACN phase separate on cooling, colloids, polymer and cross-linker partition between these phases. PEI and the diepoxy cross-linker used here are highly water soluble – however, they are only sparingly soluble in pure ACN. Therefore, it is likely that they do not partition into the ACN rich domains. Since the ACN rich phase does not freeze and since polymer and cross-linker do partition into this phase, there is no cross-linking. Therefore, after the sample is thawed, the regions where the phase separated ACN droplets are located remain uncross-linked and form holes in the composite walls. While the details of hole formation during ice templating require further investigation, the NMR data provides strong support to the suggested mechanism, viz. water/ACN phase separation leading to hole formation. This mechanism is significantly different from those reported earlier for alcohol/water, acetone/water or dioxan/water mixtures. There, it has been hypothesized that depression in the freezing point of the mixture due to addition of the secondary solvent to water results in the formation of bimodal pore size distributions. Microscopy data on those systems do not show evidence for the hole in wall morphologies that we obtain in our experiments. Therefore, it is possible that this mechanism, viz. cooling induced phase separation in water/ACN systems gives rise to a hole in wall morphology that is qualitatively different from those obtained previously.
The addition of ACN does not significantly vary the organic content viz. fraction of polymer and cross-linker, relative to the silica across the scaffolds during ice-templating, as evidenced by TGA data (Fig. S5†). Thus, TGA data reveals that the unusual perforated wall morphology observed in SEM is not a consequence of ACN-induced changes in polymer coating and/or cross-linking. Rather, it is a consequence of the influence of ACN on the freezing of the suspension and subsequent consolidation of the hybrid walls as the polymer cross-links around the silica particles.
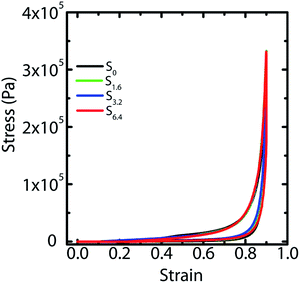
We have previously demonstrated25 that fluid transport through macroporous scaffolds during uptake of a wetting liquid is strongly dependent on the overall volume porosity of the scaffold. We estimate the porosity, as before, by taking a known volume of the scaffold and swelling it with water. Weighing the swollen scaffold yields the weight of the water absorbed (and therefore, the volume of the water can be calculated). The scaffold porosity is estimated as the volume of water absorbed normalized by the scaffold volume. We observe a small increase in the scaffold porosity from S0 to the scaffolds prepared by ice-templating dispersions with water–ACN as solvent (Table 1). However, we observe no systematic variation in the porosity from S1.6 to S3.2 to S6.4. We also subject water saturated scaffolds to compressive strain in a rheometer and measure the stress generated on imposition of strain. We observe that ice-templated scaffolds formed by freezing colloidal dispersions and cross-linking the polymer in the frozen state are elastic and recover completely from compressive strains as large as 85% (Fig. 4). The stress–strain data from compression/expansion measurements are similar for S0, S1.6, S3.2 and S6.4. All scaffolds show a slow initial linear increase in stress on compression, followed by a rapid increase at higher strain and exhibit hysteresis during expansion from the compressed state. We measure the modulus of the scaffolds as the slope of the linear stress–strain relationship, at low strains during the unloading cycle (Table 1). We observe that the compression modulus is not significantly affected by the presence of ACN in the ice-templated suspension and that ACN concentration has no systematic effect on E*. We have previously shown43 that when the scaffold is compressed, the mechanical response arises not from bending of the walls; rather, it arises from an increase in the average wall thickness. Therefore, the modulus is determined largely by the density of the scaffold (or, equivalently by the porosity, see Table 1). Therefore, the modulus of the scaffold is largely unaffected by addition of ACN during ice templating.
| Scaffolds | % Porosity | Density (kg m−3) | E* (kPa) |
|---|---|---|---|
| S0 | 90 ± 2 | 88 ± 5 | 26 ± 0.8 |
| S1.6 | 93 ± 3 | 90 ± 4 | 25 ± 0.6 |
| S3.2 | 94 ± 1 | 92 ± 2 | 27 ± 0.7 |
| S6.4 | 93 ± 3 | 91 ± 4 | 23 ± 0.6 |
3.2 Pressure drop and residence time distribution study
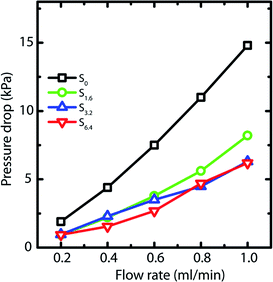
Capillary pressure measurements are performed in a home-built experimental setup. This setup is described in Experimental section (Section 2.3) and is shown in Scheme 1. We measure pressure drop across scaffolds when water is pumped through them at different flow rates viz. 0.2, 0.4, 0.6, 0.8 and 1.0 ml min−1 (Fig. S6†). At higher flow rates, the scaffolds debond from the walls of the glass capillary. Scaffolds are bonded to the glass tube through cross-linking between the PEI in the scaffold walls to that adsorbed on the walls of the glass tube. These bonds fail at the high stresses associated with flow rates in excess of 1 ml min−1. When flow is initiated by pumping water, we observe an initial build-up of pressure after which flow proceeds at a steady state value of the pressure drop across the scaffold (Scheme 1). Here we report the steady state pressure drop as a function of the flow rate. In all scaffolds, the steady state pressure drop increases monotonically with flow rate, as expected. We observe at remarkable decrease in the steady state pressure drop required to sustain a flow rate from S0 to the scaffolds prepared using ACN (Fig. 5). The decrease in pressure drop is already very significant from S0 to S1.6, and we observe a further drop in pressure drop for S6.4 (Fig. 5).Next, we investigate the residence time distribution of water when it undergoes pressure driven flow through the scaffold. The results obtained from RTD parameter fitting are summarized in Table 2. The ‘α’ values indicate that fluid primarily flows through a first compartment which has slightly higher fraction of void volume compared to a second compartment for each scaffold at all the flow rates. Fig. 6 visualizes the response of the individual compartments at different flow rates. As mentioned earlier, a narrower profile indicates that the character of the flow is closer to plug flow. It can be observed that at a flow rate of 0.5 and 1 ml min−1, the response of the first compartment of S0 and S1.6 show more PFR like behavior compared to S3.2 and S6.4 (ESI, Table S1†). The same can be observed for the second compartment, where the response for S3.2 and S6.4 is broader than S0 and S1.6. This can be attributed to the structure of these scaffolds. The increased number of holes in the pore walls for S3.2 and S6.4 compared to S0 and S1.6 cause flow channelling and thus deviation from the primary tortuous flow path, resulting in a broader response and deviation from plug flow. However, this trend is not visible at the lowest flow rate of 0.25 ml min−1, where all scaffolds show similar behavior. This suggests that at this low flow rate the local fluid pressure is not sufficient to penetrate and flow through the small holes in the pore walls.
| Flow rate (ml min−1) | Scaffolds | |||||||
|---|---|---|---|---|---|---|---|---|
| S0 | S1.6 | S3.2 | S6.4 | |||||
| α | β | α | β | α | β | α | β | |
| 0.25 | 0.850 | 0.646 | 0.801 | 0.591 | 0.831 | 0.642 | 0.794 | 0.620 |
| 0.5 | 0.924 | 0.680 | 0.842 | 0.567 | 0.968 | 0.685 | 0.925 | 0.637 |
| 1 | 0.897 | 0.751 | 0.860 | 0.675 | 0.924 | 0.729 | 0.914 | 0.649 |
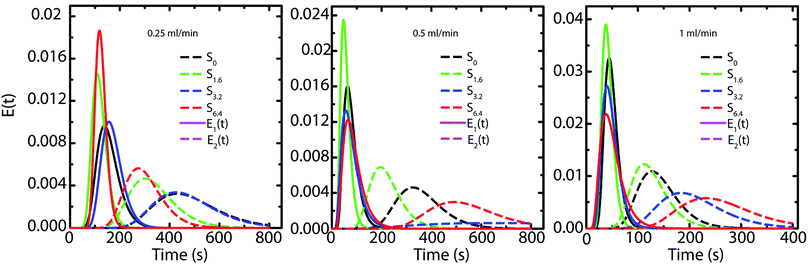 | ||
| Fig. 6 Representation of the RTD response of each compartment based on the fitting with the two PFRs in parallel model. | ||
The influence of channelling is also observed in the pressure drop measurements, where the scaffolds S6.4 and S3.2 exhibit a lower pressure drop compared to scaffold S0 (Fig. 5). This observation of lower pressure drop upon channelling is consistent with an earlier experimental study investigating the hydrodynamics of various structured porous reactors.58 The reduced pressure drop of the scaffold S1.6 can be attributed to the combined effect of higher porosity together with a lower pore wall surface area covered by holes (Fig. 2b), which indicates that the major contribution to porosity is aligned with the flow direction. This observation is additionally supported by the RTD measurements, where a plug flow behavior is observed for the scaffold S1.6.
4. Conclusions
We have demonstrated that holes can be introduced in the pore walls of ice-templated scaffolds using a very simple preparation protocol. Ice-templating dispersions containing small concentrations of acetonitrile introduces perforation in the pore walls. We demonstrate that perforation of the composite wall is significantly influenced by ACN concentration. We observe a decrease in average pore size with increasing ACN content, and an increase in the fraction of the wall surface containing holes. Addition of the miscible organic solvent does not affect the overall porosity and mechanical response of the ice-templated porous structure. We also demonstrate that perforated walls significantly reduce the pressure drop for flow of water through the scaffolds. Pressure driven flow through these scaffolds can be accurately described using a model comprising two PFRs in parallel. Especially at high flow rates, S3.2 and S6.4 show a broader response in the second PFR relative to S0 and S1.6. This is suggestive of channelling in S3.2 and S6.4, with the increased hole fraction in the pore walls. At the lowest flow rate, however, all scaffolds behave similarly due to lack of sufficient fluid pressure to penetrate through the holes. Our results have implications for controlling the pressure drop and mixing in macroporous scaffolds used as mixing elements or as catalyst supports.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially funded by a BRNS Grant Number 37(3)/14/03/2015. S. K. acknowledges funding from FWO-Odysseus II. We acknowledge helpful discussions with Dr T. G. Ajithkumar from the NMR group at CSIR-NCL during the design of the NMR experiments. We also acknowledge help from the NMR group in carrying out these experiments.References
- D. Enke, R. Gläser and U. Tallarek, Chem. Ing. Tech., 2016, 88, 1561–1585 CrossRef.
- A. K. Ganai, S. Kumari, K. P. Sharma, C. Panda, G. Kumaraswamy and S. Sen Gupta, Chem. Commun., 2012, 48, 5292 RSC.
- Q. Tan, X. Bao, T. Song, Y. Fan, G. Shi, B. Shen, C. Liu and X. Gao, J. Catal., 2007, 251, 69–79 CrossRef.
- Z.-Y. Yuan and B.-L. Su, J. Mater. Chem., 2006, 16, 663–677 RSC.
- J. G. Yu, Y. R. Su and B. Cheng, Adv. Funct. Mater., 2007, 17, 1984–1990 CrossRef.
- K. H. Rhodes, S. A. Davis, F. Caruso, B. Zhang and S. Mann, Chem. Mater., 2000, 12, 2832–2834 CrossRef.
- L. L. C. Wong, V. O. Ikem, A. Menner and A. Bismarck, Macromol. Rapid Commun., 2011, 32, 1563–1568 CrossRef PubMed.
- A. Quell, T. Sottmann and C. Stubenrauch, Langmuir, 2017, 33, 537–542 CrossRef PubMed.
- J. Elsing, T. Stefanov, M. D. Gilchrist and C. Stubenrauch, Phys. Chem. Chem. Phys., 2017, 19, 5477–5485 RSC.
- T. Müllner, A. Zankel, A. Höltzel, F. Svec and U. Tallarek, Langmuir, 2017, 33, 2205–2214 CrossRef PubMed.
- G. S. Attard, J. C. Glyde and C. G. Göltner, Nature, 1995, 378, 366–368 CrossRef.
- C. G. Goltner and M. Antonietti, Adv. Mater., 1997, 9, 431–436 CrossRef.
- F. Schüth, Angew. Chem., Int. Ed., 2003, 42, 3604–3622 CrossRef PubMed.
- B. Smarsly and M. Antonietti, Eur. J. Inorg. Chem., 2006, 2006, 1111–1119 CrossRef.
- Y. S. Nam, J. J. Yoon and T. G. Park, J. Biomed. Mater. Res., 2000, 53, 1–7 CrossRef PubMed.
- J. J. Yoon, J. H. Kim and T. G. Park, Biomaterials, 2003, 24, 2323–2329 CrossRef PubMed.
- S. Şenel and S. J. McClure, Adv. Drug Delivery Rev., 2004, 56, 1467–1480 CrossRef PubMed.
- M. O. Montjovent, L. Mathieu, B. Hinz, L. L. Applegate, P. E. Bourban, P. Y. Zambelli, J. A. Månson and D. P. Pioletti, Tissue Eng., 2005, 11, 1640–1649 CrossRef PubMed.
- A. Monnier, F. Schuth, Q. Huo, D. Kumar, D. Margolese, R. S. Maxwell, G. D. Stucky, M. Krishnamurty, P. Petroff, A. Firouzi, M. Janicke and B. F. Chmelka, Science, 1993, 261, 1299–1303 CrossRef PubMed.
- L. Song, R. K. Bly, J. N. Wilson, S. Bakbak, J. O. Park, M. Srinivasarao and U. H. F. Bunz, Adv. Mater., 2004, 16, 115–118 CrossRef.
- A. Böker, Y. Lin, K. Chiapperini, R. Horowitz, M. Thompson, V. Carreon, T. Xu, C. Abetz, H. Skaff, A. D. Dinsmore, T. Emrick and T. P. Russell, Nat. Mater., 2004, 3, 302–306 CrossRef PubMed.
- L. A. Connal, P. A. Gurr, G. G. Qiao and D. H. Solomon, J. Mater. Chem., 2005, 15, 1286–1292 Search PubMed.
- S. Chatterjee, S. Sen Gupta and G. Kumaraswamy, Chem. Mater., 2016, 28, 1823–1831 CrossRef.
- C. Das, S. Chatterjee, G. Kumaraswamy and K. Krishnamoorthy, J. Phys. Chem. C, 2017, 121, 3270–3278 CrossRef.
- S. Chatterjee, P. Doshi and G. Kumaraswamy, Soft Matter, 2017, 13, 5731–5740 RSC.
- S. Chatterjee, K. Shanmuganathan and G. Kumaraswamy, ACS Appl. Mater. Interfaces, 2017, 9, 44864–44872 CrossRef PubMed.
- E. Munch, E. Saiz, A. P. Tomsia and S. Deville, J. Am. Ceram. Soc., 2009, 92, 1534–1539 CrossRef.
- M. Fukushima and Y. Yoshizawa, Mater. Lett., 2015, 153, 99–101 CrossRef.
- A. Ouyang, C. Wang, S. Wu, E. Shi, W. Zhao, A. Cao and D. Wu, ACS Appl. Mater. Interfaces, 2015, 7, 14439–14445 CrossRef PubMed.
- A. Ouyang and J. Liang, RSC Adv., 2014, 4, 25835–25842 RSC.
- J. Wang, Q. Gong, D. Zhuang and J. Liang, RSC Adv., 2015, 5, 24749 RSC.
- H. Zhang, I. Hussain, M. Brust, M. F. Butler, S. P. Rannard and A. I. Cooper, Nat. Mater., 2005, 4, 787–793 CrossRef PubMed.
- T. Fukasawa, M. Ando, T. Ohji and S. Kanzaki, J. Am. Ceram. Soc., 2001, 84, 230–232 CrossRef.
- T. Fukasawa, Z.-Y. Deng, M. Ando, T. Ohji and S. Kanzaki, J. Am. Ceram. Soc., 2002, 85, 2151–2155 CrossRef.
- S. R. Mukai, H. Nishihara and H. Tamon, Chem. Commun., 2004, 0, 874 RSC.
- S. Deville, Adv. Eng. Mater., 2008, 10, 155–169 CrossRef.
- J.-W. Kim, K. Tazumi, R. Okaji and M. Ohshima, Chem. Mater., 2009, 21, 3476–3478 CrossRef.
- H. Zhang, P. D'Angelo Nunes, M. Wilhelm and K. Rezwan, J. Eur. Ceram. Soc., 2016, 36, 51–58 CrossRef.
- H. Kirsebom, D. Topgaard, I. Y. Galaev and B. Mattiasson, Langmuir, 2010, 26, 16129–16133 CrossRef PubMed.
- J. Zeng, Y. Zhang, K. Zhou and D. Zhang, Trans. Nonferrous Met. Soc. China, 2014, 24, 718–722 CrossRef.
- C. Guizard, J. Leloup and S. Deville, J. Am. Ceram. Soc., 2014, 97, 2020–2023 CrossRef.
- Y. Tang, S. Qiu, C. Wu, Q. Miao and K. Zhao, J. Eur. Ceram. Soc., 2016, 36, 1513–1518 CrossRef.
- R. Rajamanickam, S. Kumari, D. Kumar, S. Ghosh, J. C. Kim, G. Tae, S. Sen Gupta and G. Kumaraswamy, Chem. Mater., 2014, 26, 5161–5168 CrossRef.
- K. Suresh, S. Patil, P. Ramanpillai Rajamohanan and G. Kumaraswamy, Langmuir, 2016, 32, 11623–11630 CrossRef PubMed.
- C. Hutter, A. Zenklusen, R. Lang and P. Rudolf von Rohr, Chem. Eng. Sci., 2011, 66, 1132–1141 CrossRef.
- O. Levenspiel, Ind. Eng. Chem., 1958, 50, 343–346 CrossRef.
- J. B. Joshi, V. V. Ranade, S. D. Gharat and S. S. Lele, Can. J. Chem. Eng., 1990, 68, 705–741 CrossRef.
- J. Villermaux and W. P. M. Van Swaaij, Chem. Eng. Sci., 1969, 24, 1097–1111 CrossRef.
- T. Gu, Y. Gu, Y. Zheng, P. E. Wiehl and J. J. Kopchick, Sep. Technol., 1994, 4, 258–260 CrossRef.
- G. P. Cunningham, G. A. Vidulich and R. L. Kay, J. Chem. Eng. Data, 1967, 12, 336–337 CrossRef.
- Y. Gu and P.-H. Shih, Enzyme Microb. Technol., 2004, 35, 592–597 CrossRef.
- D. N. Oence and T. Gu, Sep. Technol., 1996, 6, 261–264 CrossRef.
- P. K. Zarzkycki, E. Wlodarczyk, D.-W. Lou and K. Jinno, Anal. Sci., 2006, 22, 453–456 CrossRef.
- A. Arsiccio, A. A. Barresi and R. Pisano, Cryst. Growth Des., 2017, 17, 4573–4581 CrossRef.
- T. Takamuku, A. Yamaguchi, D. Matsuo, M. Tabata, M. Kumamoto, J. Nishimoto, K. Yoshida, T. Yamaguchi, M. Nagao, T. Otomo and T. Adachi, J. Phys. Chem. B, 2001, 26, 6236–6245 CrossRef.
- P. B. Dhamole, P. Mahajan and H. Feng, J. Chem. Eng. Data, 2010, 55, 3803–3806 CrossRef.
- Y. Jayalakshmi and E. W. Kaler, Phys. Rev. Lett., 1997, 78, 1379–1382 CrossRef.
- A. Potdar, L. N. Protasova, L. Thomassen and S. Kuhn, React. Chem. Eng., 2017, 2, 137–148 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra03867h |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2018 |