Cooperative effects between π-hole triel and π-hole chalcogen bonds

Abstract

MP2/aug-cc-pVTZ calculations have been performed on π-hole triel- and chalcogen-bonded complexes involving a heteroaromatic compound. These complexes are very stable with large interaction energy up to −47 kcal mol⁻¹. The sp²-hybridized nitrogen atom engages in a stronger π-hole bond than the sp-hybridized species although the former has smaller negative electrostatic potential. The sp²-hybridized oxygen atom in 1,4-benzoquinone is a weaker electron donor in the π-hole bond than the sp²-hybridized nitrogen atom. The π-hole triel bond is stronger than the π-hole chalcogen bond. A clear structural deformation is found for the triel or chalcogen donor molecule in these π-hole-bonded complexes. The triel bond exhibits partially covalent interaction, whereas the chalcogen bond exhibits covalent interaction in the SO₃ complexes of pyrazine and pyridine derivatives with a sp²-hybridized nitrogen atom. Intermolecular charge transfer (>0.2e) occurs to a considerable extent in these complexes. In ternary complexes involving an aromatic compound, wherein a triel bond and a chalcogen bond coexist, both the interactions are weakened or strengthened when the central aromatic molecule acts as a double Lewis base or plays a dual role of both a base and an acid. Both electrostatic and charge transfer effects have important contributions toward changes in the strength of both interactions.

---

1. Introduction

Intermolecular interactions play a crucial role in chemistry, biology, and materials science;^1–3 they can lower the activation free energy of a reaction,⁴ govern the conformational stability and biological activity of proteins and other biological macromolecules,⁵ and modulate the functions and properties of materials.⁶ Other than the most important and prevalent intermolecular interaction, i.e., the H-bond, more types of intermolecular interactions have caused considerable interest.^7–10 Herein, we focus on chalcogen and triel bonding interactions, wherein the group V and III atoms act as a Lewis acid center to bind with a base.^11,12 For most of the cases, the origin of the acidic center of a chalcogen atom can be traced back to the presence of a region with positive electrostatic potentials (σ-hole) in the outer regions of a Ch–R bond.¹³ For a triel atom, this region is often vertical to the planar molecule or a planar portion of a molecular framework (π-hole).¹⁴ Some group V molecules, such as SO₃, also have such π-holes.¹⁵ It should be pointed out that the π-hole triel bond has a completely different nature from the π-hole in chalcogen bond since in the literature, a triel bond is referred as a dative bond.¹⁶

Due to their importance in crystalline materials and biological systems, many studies have been conducted on chalcogen bonds by means of experimental and theoretical methods.^17–27 Chalcogen-bonded complexes of SOF₂, SOFCl, and SOCl₂ with a series of N bases are stabilized by coulombic attractions of N to the σ-hole opposite the S atom as well as by the Lp_N→σ* (S–Z) electron transfer (Z = O, F, Cl).¹⁷ Tetravalent SF₄ also has one σ-hole along the extension of the S–F bond, and the strength of chalcogen bonding between tetravalent SF₄ and amines is similar to that with divalent SF₂.¹⁸ In realizing its functions in crystalline materials and biological systems, chalcogen bonding often coexists with more than one interaction including that with itself, exhibiting cooperative effects. For instance, bidentate chalcogen bonding increases the association constant by an order of magnitude in binding of perfluoroaryl-substituted tellurophenes with an anion.¹⁹ Thus, substantial theoretical attention has been paid to the cooperative effect of chalcogen bonding with itself and other types of interactions,^26–33 showing some interesting results. For instance, although SO₃⋯NH₃⋯NH₃ is more stable than NH₃–SO₃⋯NH₃, the latter is identified in argon matrixes, where the two N–S bonds are nonequivalent.³³

A trivalent triel atom in TrR₃, owing to its electron deficiency, is usually used to bind with Lewis bases such as HCN, CH₃CN, and NH₃.^34–41 Upon complexation, the geometric structure of TrR₃ exhibits substantial deviation from the planar one, and it becomes more prominent for a stronger triel bond. There is clear difference between the solid- and gas-phase structures of HCN⋯BF₃, which is mainly caused by the cooperative effect in the solid.⁴² Thus, there is growing interest regarding the cooperative effect of a triel bond with itself and other interactions.^43–48 In BF₃⋯NCH⋯NCH, where a triel bond and a hydrogen bond coexist, both B⋯N and H⋯N distances are shortened, but the shortening of the B⋯N distance in the stronger triel bond is larger than that of the H⋯N distance in the weaker hydrogen bond.⁴³ This abnormal result is also found in similar complexes composed of a triel bond and a halogen bond⁴⁷ or a pnicogen bond.⁴⁷

In this paper, we study the interplay between the triel bond and chalcogen bond in the complexes of pyrazine, 1,4-dicyanobenzene, and 1,4-benzoquinone as well as their derivatives. These three molecules are often used in studying the cooperative effects between an anion–π interaction and other interactions including hydrogen bonding,⁴⁹ halogen bonding,⁵⁰ chalcogen bonding,⁵¹ pnicogen bonding,⁵² tetrel bonding,⁵³ triel bonding,⁵⁴ and metal–Lp interactions.⁵⁵ It should be noted that there are two important reviews on cooperative effects.^56,57 Their derivatives contain 4-BH₂-pyrazine, 4-BF₂-pyrazine, 1-CN-4-BH₂-benzene, and 1-CN-4-BF₂-benzene although these molecules are not found in the Cambridge Structural Database. We focus on the comparison of the strengths of triel bonding among these molecules, comparison of the strengths of chalcogen bonding among these molecules, and interplay between triel bonding and chalcogen bonding. The results are estimated by means of binding distances, interaction energies, and electron densities. To reveal the mechanism for the cooperative effects in these systems, charge transfer and molecular electrostatic potentials are analyzed for these complexes.

2. Theoretical methods

All the calculations were performed using the Gaussian 09 program.⁵⁸ All the complexes were first optimized using the second-order Møller–Plesset perturbation theory (MP2) level with the aug-cc-pVDZ basis set. Frequency analysis at the same computational level was then applied to confirm that the optimized geometries corresponded to stationary points with no imaginary frequencies. Finally, the complexes with MP2/aug-cc-pVDZ geometries were again optimized at the MP2/aug-cc-pVTZ level. The interaction energy (ΔE_int) in the binary system was obtained by subtracting the energies of the monomers frozen in the complex from the energy of the complex. If the energies of the optimized monomers are used as the reference, the binding energy (ΔE_b) can be calculated. The difference between ΔE_b and ΔE_int is denoted as the deformation energy (DE). Both ΔE_b and ΔE_int were corrected from the basis set superposition error (BSSE) by the counterpoise procedure suggested by Boys and Bernardi.⁵⁹ The total interaction energy (ΔE_total) in the ternary systems and the interaction energy between the molecule pair were calculated with a similar supramolecular method using the following formulas: ΔE_total = E_ABC − E_A − E_B − E_C, ΔE_A–BC = E_A–BC − E_A−E_BC, and ΔE_AB–C = E_AB–C − E_AB − E_C, where the energies of the monomers and dyads are from the ternary complex. The interplay between the two interactions in the ternary system was estimated with cooperative energy (E_coop), which was obtained by E_coop = ΔE_total − ΔE_A–B − ΔE_B–C − ΔE_A–C; here, ΔE_A–B and ΔE_B–C are the interaction energies of the optimized binary systems, and ΔE_A–C is the interaction energy between the two unbonded molecules in the ternary system.

Molecular electrostatic potentials (MEPs) were computed on the 0.001 au electron density contour at the MP2-aug-cc-pVTZ level with the Wave Function Analysis-Surface Analysis-Suite (WFA-SAS) program.⁶⁰ The topological analysis of all the complexes was carried out using Bader's theory of atoms in molecules (AIM) with the help of the AIM2000 software.⁶¹ The contour of the Laplacian of the electron density was plotted by the Multiwfn software.⁶² Natural bond orbital (NBO) analysis was performed at the HF/aug-cc-pVTZ level via the NBO 3.1 procedure included in Gaussian 09 to analyze charge transfer.⁶³

3. Results and discussion

3.1. MEPs of monomers

Fig. 1 shows the MEP maps of the studied monomers. For BH₃ (2), BF₃ (3), and SO₃ (4), there are two π-holes (red region) along the vertical direction of the molecular plane. The most positive MEP on the π-hole is larger in BF₃ than that in BH₃, which is consistent with previously reported results.¹⁴ The most positive MEP on the π-hole is almost equal for BF₃ and SO₃. The π-holes in BH₃/BF₃ and SO₃ thus can form a triel bond and a chalcogen bond with a base, respectively. A blue region with negative MEPs is found around the N/O atom for NH₃ (1), pyrazine (5), 1,4-dicyanobenzene (6), and 1,4-benzoquinone (7). Due to sp³ hybridization, the N atom of 1 has larger negative MEP than those for 5 and 6. It is thus not difficult to understand the fact that NH₃ often acts as the Lewis base in intermolecular interactions. The N atom of 5 has smaller negative MEP than that for 6 due to greater delocalization in the former. In 8–11, a red region (π-hole) and a blue area are found on the B and N atoms, respectively. The π-hole on the B atom in 8–11 has smaller positive MEP than those in 2 and 3, indicating that the aromatic ring is electron-donating. The stronger electron-withdrawing ability of CN in 9/11 results in larger positive MEP on the B atom relative to that in 8/10. The negative MEP on the N atom in 10/11 is smaller than that in 8/9 due to stronger electron-withdrawing ability of BF₂.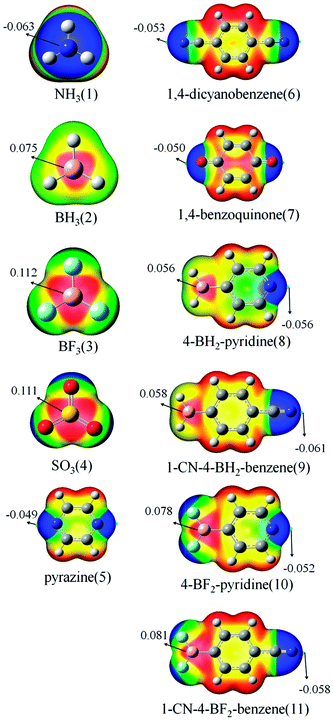

Fig. 1 MEP maps of the monomers. Color ranges, in eV, are as follows: red, greater than 0.0210; yellow, between 0.0210 and −0.0028; green, between −0.0028 and −0.0150; and blue, less than −0.0150.

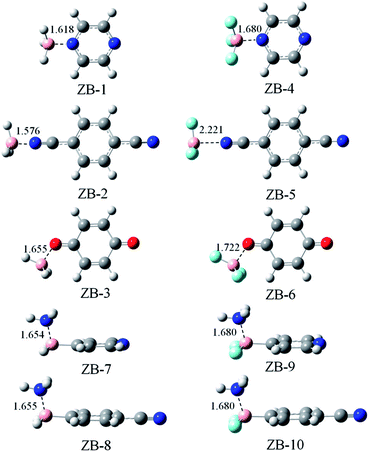
3.2. Triel-bonded dyads

Fig. 2 shows the optimized structures of ten triel-bonded dyads. These structures have approximate C_s symmetry. The plane of symmetry is along the aromatic ring in ZB-2, ZB-3, ZB-5, and ZB-6, whereas it is vertical to the aromatic ring along the B–N–N or B–C–N axis in the other dyads. A clear change in geometry is that the B-containing molecule deviates from the planar structure, and this phenomenon is often observed in triel-bonded complexes.¹⁴ The B–C bond exhibits smaller deviation than the B–H/F bond in ZB-8, ZB-9, ZB-10, and ZB-11 due to the stronger B–C bond. To estimate the deformation of the B-containing molecule, we list the average of the three N⋯B–H/F angles in ZB-1 to ZB-6 except the average of the two N⋯B–H/F angles and one N⋯B–C angle in the other dyads (Table 1). The deformation is larger if this average value has larger deviation from 90°; this value is larger than 90° for all the complexes. Thus, the B-containing molecule exhibits deformation. The largest deformation is found in ZB-1, whereas the smallest one is found in ZB-5. It is noted that such an indicator is only an approximate estimation of deformation.

Fig. 2 Optimized structures of the triel-bonded binary complexes. Distances are given in Å.

Table 1 Interaction energy (ΔE_int, kcal mol⁻¹), binding energy (ΔE_b, kcal mol⁻¹), deformation energy (DE, kcal mol⁻¹), relative Gibbs free energy (ΔG, kcal mol⁻¹), and angle (α, deg) in the triel-bonded binary systems^a

Dyads	ΔEint	ΔEb	DE	ΔE^ZPEb	ΔG	α
a ΔE^ZPEb is the binding energy corrected for zero-point vibrational energy (ZPE). α is the average of the three N⋯B–H/F angles in the former six dyads but the average of the two N⋯B–H/F angles and one N⋯B–C angle in the latter four dyads.
2 + 5(ZB-1)	−46.81	−34.42	14.03	−30.51	−20.67	104.8
2 + 6(ZB-2)	−33.03	−21.60	12.70	−18.30	−7.69	104.4
2 + 7(ZB-3)	−27.44	−17.79	11.15	−13.99	−3.20	103.1
3 + 5(ZB-4)	−44.52	−23.08	24.47	−21.24	−14.28	104.2
3 + 6(ZB-5)	−8.79	−7.04	3.10	−6.35	−0.07	95.4
3 + 7(ZB-6)	−25.40	−10.82	17.28	−9.40	−0.51	102.0
1 + 8(ZB-7)	−42.06	−29.50	14.17	−24.86	−15.29	104.4
1 + 9(ZB-8)	−41.70	−29.04	14.29	−24.46	−14.83	104.5
1 + 10(ZB-9)	−37.38	−19.28	20.33	−15.81	−9.11	103.7
1 + 11(ZB-10)	−37.53	−19.22	20.53	−15.77	−9.00	103.8

---

The binding distance is also shown in Fig. 2. The B⋯N distance is in the range of 1.576–2.221 Å, whereas the B⋯O distance varies from 1.655 Å in ZB-3 to 1.722 Å in ZB-6. These distances are much shorter than the sum of the van der Waals (vdW) radii of the corresponding atoms (3.68 Å for B⋯N and 3.66 Å for B⋯O), which indicates that the triel bond is very strong. ZB-2 has shorter distance than ZB-1, whereas ZB-5 has longer distance than ZB-4; the former is consistent with negative MEPs on the N atoms of 5 and 6, whereas the latter shows an inconsistent change. The F-substitution lengthens the binding distance, which is inconsistent with the changes in the positive MEP on the B atom. This implies that electrostatic interaction is not the sole dominant factor in stabilizing the triel-bonded complexes.

Table 1 presents interaction energy and binding energy; their difference is denoted as the deformation energy, which can be used to measure the deformation of both the subsystems in the complex. The deformation energy is relatively large, i.e., from 3.10 kcal mol⁻¹ in ZB-5 to 24.47 kcal mol⁻¹ in ZB-4. The deformation energy amounts to 30–68% of the interaction energy; thus, its contribution is very important. Larger deformation energy corresponds to larger interaction energy although they do not have a linear relationship. In the following discussion, the interaction energy is utilized to estimate the stability of the triel-bonded complex.

The interaction energy varies from −8.79 kcal mol⁻¹ in ZB-5 to −46.81 kcal mol⁻¹ in ZB-1. When BH₃ and BF₃ are considered, the interaction energy is more negative in the order of ZB-3 < ZB-2 < ZB-1 and ZB-5 < ZB-6 < ZB-4, respectively. Both orders are inconsistent with the negative MEP on the N/O atom; this shows that the N atom of pyrazine has strong affinity toward the B atom, which is similar to that observed for the tetrel atom in tetrel bonds.⁶³ ZB-7 has slightly larger interaction energy than ZB-8, which is inconsistent with the positive MEP on the B atom. However, the interaction energy and deformation energy in ZB-9 are almost equal to those in ZB-10 although the positive MEP on the B atom is larger in 11 than that in 10. The B–F system has smaller interaction energy than the B–H analogue. Interestingly, the interaction energy reduces by 24.24 kcal mol⁻¹ in ZB-5 when compared with that for ZB-2. Although the values of the interaction energy and binding energy have large difference in most systems, their variations are similar, and both are thus appropriate for estimating the relative stability of the complex. The binding energy is reduced by 7–18% if it is corrected for zero-point vibrational energy (ZPE). Nonetheless, its variation tendency remains unchanged. For the triel-bonded complexes, the binding processes are exergonic (ΔG < 0) at 298 K. The entropy change (ΔS) is negative in the formation of complexes; thus, the ΔH term is dominant over the unfavorable TΔS term. Generally, more negative ΔG results in stronger triel bond.

There are some studies on triel bonds between BH₃/BF₃ and some small compounds containing N. Herein, we compare our results with those of the previous studies. The interaction energies were calculated to be −44.8, −6.7 and −1.8 kcal mol⁻¹ in the BF₃ complexes with NH₃, HCN, and N₂, respectively.⁶⁴ Thus, the N atoms of pyrazine and NH₃ indicated similar affinities toward the B atom of BF₃ although the latter exhibited more negative MEP due to sp³ hybridization; moreover, it exhibited stronger affinity toward the B atom of BH₃ than the N atom of NH₃ since the interaction energy was about −30 kcal mol⁻¹ in the latter.³⁵ For the BF₃⋯CH₃CN complex, two configurations were found with the interaction energies of −7.7 and −8.7 kcal mol⁻¹.^65,66 Clearly, its interaction energy was comparable with that of ZB-5. This comparison indicated that pyrazine and 1,4-dicyanobenzene are good electron donors in triel bonds.

A strong triel bond results in substantial charge transfer from the electron acceptor to the triel donor (Table 2). The charge transfer is larger than 0.2e in most complexes except that for ZB-5. The large charge transfer is chiefly due to the deformation of monomers; Grabowski stated that the deformation energy is strongly related to the above-mentioned charge transfer.⁶⁷ Although no linear relationship is found between charge transfer and interaction energy, they exhibit a consistent change.

Table 2 Electron density (ρ_BCP, au), Laplacian (∇²ρ_BCP, au), and total electron energy density (H_BCP, au) at the bond critical point as well as charge transfer (CT, e) in the triel-bonded binary systems^a

Dyads	ρBCP	∇^2ρBCP	HBCP	CT
a CT is the sum of the NBO charge on all the atoms of the electron donor molecule.
ZB-1	0.109	0.315	−0.074	0.3223
ZB-2	0.098	0.064	−0.005	0.3133
ZB-3	0.072	0.564	−0.018	0.2578
ZB-4	0.106	0.315	−0.074	0.2917
ZB-5	0.026	0.064	−0.005	0.0488
ZB-6	0.073	0.317	−0.038	0.2129
ZB-7	0.103	0.503	−0.061	0.3662
ZB-8	0.103	0.502	−0.061	0.3659
ZB-9	0.104	0.351	−0.070	0.3324
ZB-10	0.104	0.349	−0.070	0.3324

---

The presence of a B⋯N/O bond critical point (BCP) is used to characterize the triel bond (not shown), and its electron density (ρ_BCP), Laplacian (∇²ρ_BCP), and total electron energy density (H_BCP) are shown in Table 2. The electron density is in the range of 0.026–0.109 au, and this value is large in most complexes. For all the complexes, ∇²ρ_BCP is positive and H_BCP is negative. Therefore, the triel bond belongs to a partially covalent interaction based on the classification of the interaction suggested by Arnold and Oldfield.⁶⁸ The contour plots of ∇²ρ_BCP for the triel-bonded complexes are shown in Fig. S1.† Green solid lines represent the region of ∇²ρ_BCP > 0, and purple dashed lines highlight the area of ∇²ρ_BCP < 0. For the cases where ∇²ρ_BCP is positive and H_BCP is highly negative, we get a region where electron density is accumulated between the two centers; BCP lies just outside this region in most cases. This phenomenon was reported in the XeBeCN₂ cluster⁶⁹ and B₃Ng₃⁺ (Ng = Ar–Rn) complexes.⁷⁰ Previously, the sign of H_BCP was used to characterize the covalent properties of a bond.⁷¹ It should be noted that ∇²ρ_BCP is not sufficient to describe a covalent bond including covalent bonds exhibited by elements other than the first row elements.^72–74 In addition, in some cases, H_BCP gives a highly negative value even for ionic bonds.^75–78

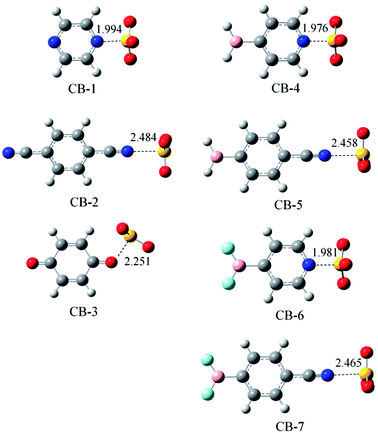
3.3. Chalcogen-bonded dyads

Fig. 3 shows the optimized structures of seven chalcogen-bonded complexes represented from CB-1 to CB-7. These structures also exhibit C_s symmetry similar to the triel-bonded complexes, as shown in Fig. 2. In CB-1, 3, 4, and 6, there are two weak H⋯O interactions other than the chalcogen bond. The geometry of SO₃ also deviates from a planar structure, and its deviation is estimated with the average of the three N/O⋯S–O angles (Table 3) since these angles are larger than 90° in chalcogen-bonded complexes. The deformation of SO₃ in chalcogen-bonded complexes is smaller than that in a B-containing molecule in triel-bonded complexes due to the smaller N/O⋯S–O angle. The deformation of both the molecules is consistent with the deformation energy (Table 3). This value is larger than 8 kcal mol⁻¹ in the complexes with the sp²-hybridized N atom as the electron donor, whereas it is smaller when the sp-hybridized N atom acts as the electron donor. The deformation energy in the chalcogen-bonded complexes is smaller than that in the triel-bonded complex, that is, the geometrical deformation of the subsystems in the former is smaller than that in the latter.

Fig. 3 Optimized structures of the chalcogen-bonded binary complexes. Distances are given in Å.

Table 3 Interaction energy (ΔE_int, kcal mol⁻¹), binding energy (ΔE_b, kcal mol⁻¹), deformation energy (DE, kcal mol⁻¹), relative Gibbs free energy (ΔG, kcal mol⁻¹), and angle (α, deg) in the chalcogen-bonded binary systems^a

Dyads	ΔEint	ΔEb	DE	ΔE^ZPEb	ΔG	α
a α is the average of the three N/O⋯S–O angles.
4 + 5(CB-1)	−29.93	−21.81	8.12	−19.96	−8.04	97.4
4 + 6(CB-2)	−8.67	−8.11	0.56	−7.31	−0.28	92.1
4 + 7(CB-3)	−12.25	−10.04	2.21	−8.91	0.28	93.8
4 + 8(CB-4)	−33.48	−24.47	9.01	−22.55	−10.39	97.8
4 + 9(CB-5)	−9.26	−8.57	0.69	−7.74	−0.33	92.3
4 + 10(CB-6)	−32.61	−23.77	8.84	−21.90	−9.71	97.7
4 + 10(CB-7)	−9.12	−8.47	0.65	−7.65	−0.27	92.2

---

Since the sp²-hybridized N atom can lose electrons more easily than the sp-hybridized N atom, the chalcogen bond is stronger in CB-1 than that in CB-2, as evidenced by the shorter N⋯S distance and larger interaction energy. Similarly, the sp²-hybridized N atom in CB-4/6 forms a stronger chalcogen bond than the sp-hybridized N atom in CB-5/7. Similar to that in the triel bond, the oxygen atom of 1,4-benzoquinone engages in a weaker chalcogen bond than the nitrogen atom of pyrazine. The BF₂ substituent decreases the chalcogen bond relative to the BH₂ substituent. Although the π-hole of SO₃ has more negative MEP than that of BH₃, the chalcogen bond is weaker than the corresponding triel bond; the main reason is the larger deformation energy in the latter. For the chalcogen bond, the binding energy also has a consistent change with the interaction energy, and the reduction caused by ZPE (7–11%) is smaller than that in the triel bond. At 298 K, ΔG is negative in most chalcogen-bonded complexes excluding CB-3. The positive ΔG value of CB-3 indicates that the formation of this complex is an endergonic process.

The chalcogen bond leads to smaller charge transfer than the corresponding triel bond. However, the charge transfer in the chalcogen bond has a linear relationship with the interaction energy (Fig. S2†). The electron density at S⋯N/O BCO supports change in the interaction energy (Table 4) since they have a linear relationship (Fig. S3†). H_BCP is negative in all chalcogen-bonded complexes, whereas the values of ∇²ρ_BCP are positive in CB-2, 3, 5, and 7, but they are negative in CB-1, 4, and 6. Therefore, the chalcogen bond exhibits partially covalent interaction in the former and covalent interaction in the latter.

Table 4 Electron density (ρ_BCP, au), Laplacian (∇²ρ_BCP, au), and total electron energy density (H_BCP, au) at the bond critical point as well as charge transfer (CT, e) in the chalcogen-bonded binary systems^a

Dyads	ρBCP	∇^2ρBCP	HBCP	CT
a CT is the sum of the NBO charge on all the atoms of the electron donor molecule.
CB-1	0.1173	−0.1305	−0.0810	0.2535
CB-2	0.0311	0.0875	−0.0011	0.0227
CB-3	0.0506	0.1020	−0.0086	0.0719
CB-4	0.1240	−0.1656	−0.0905	0.2781
CB-5	0.0331	0.0889	−0.0016	0.0268
CB-6	0.1223	−0.1563	−0.0880	0.2715
CB-7	0.0326	0.0887	−0.0016	0.0258

---

The charge transfer values were calculated to be 0.0019, 0.010, 0.015, 0.21, and 0.26e in the SO₃ complexes with N₂, HCN, CH₃CN, NH₃, and NMe₃, respectively.¹⁶ The larger charge transfer corresponded to a stronger chalcogen bond; thus, we can infer that NMe₃ engages in a stronger chalcogen bond than the other four nitrogenated bases. The charge transfer in CB-1, 4, and 6 is almost equal to that in SO₃⋯NMe₃; thus, we can infer that the sp²-hybridized N atom in pyrazine, 4-BH₂-pyridine, and 4-BF₂-pyridine is a good electron donor in the chalcogen bond. The interaction energy is larger than −30 kcal mol⁻¹ in CB-1, 4, and 6. It should be noted that the magnitude of charge transfer is related to the calculation methods used.⁷⁹

3.4. Interplay between triel bond and chalcogen bond

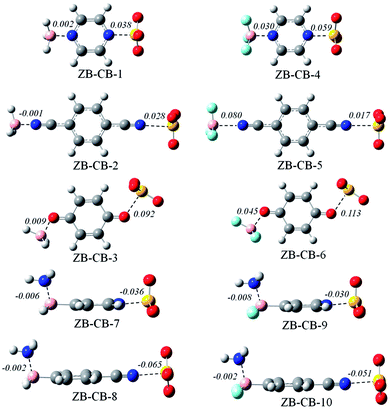
Fig. 4 shows the optimized structures of ten ternary complexes, where a triel bond and a chalcogen bond coexist. The conformation of the triad is similar to that in a dyad. In the former six triads, the binding distances of both the triel bond and chalcogen bond are elongated relative to that in the corresponding dyad. Interestingly, the B⋯N distance is reduced in ZB-CB-2. Moreover, the lengthening of the S⋯N/O distance is much larger than that of the B⋯N/O distance in ZB-CB-1, 3, 4, and 6; in the latter four triads, the binding distances of both the triel bond and chalcogen bond are shortened, and the shortening is much larger for the chalcogen bond.

Fig. 4 Optimized structures of the ternary complexes. Distances are given in Å.

Table 5 presents the total interaction energy and the interaction energies of both the triel bond and chalcogen bond. The total interaction energy is dependent on the strength of both the interactions. The change (ΔΔE) in the interaction energies of both the triel bond and chalcogen bond is also listed in Table 5. ΔΔE is positive for both the interactions in the former six triads, but it is negative for both the interactions in the latter four triads. This indicates that both the interactions weaken from ZB-CB-1 to 6, but they are strengthened from ZB-CB-7 to 10. Generally, the interaction energies exhibit larger change when both types of interactions have comparable strengths. From ZB-CB-1 to 6, both N/O atoms in the central molecule are taken as a double Lewis base to form a triel bond and a chalcogen bond simultaneously; thus, they weaken each other. However, from ZB-CB-7 to 10, the central molecule plays the dual role of a Lewis acid and base to engage in the triel and chalcogen bonding interactions, respectively; thus, they are enhanced. The interaction energy between the two distant molecules is positive in ZB-CB-1 to 6, but it is negative in ZB-CB-7 to 10. Nonetheless, it is small in all the ternary systems.

Table 5 Total interaction energy (ΔE_total), interaction energies (ΔE) of triel bond (ZB) and chalcogen bond (CB), and cooperative energy (E_coop) in the ternary systems. All are in kcal mol^−1a

Triads	ΔEtotal	ΔEZB	ΔECB	ΔEfar	ΔΔEZB	ΔΔECB	Ecoop
a ΔΔE is the difference of ΔE in the triad relative to the corresponding dyad. ΔEfar is the interaction energy between two unbonded molecules in the ternary system. Data in parentheses denote the percentage of Ecoop to ΔEtotal.
ZB-CB-1	−71.56	−42.05	−24.56	0.25	4.76	5.37	4.93(6.9)
ZB-CB-2	−40.93	−32.36	−8.05	0.01	0.67	0.62	0.76(1.9)
ZB-CB-3	−35.58	−25.28	−9.77	0.01	2.16	2.48	4.10(11.5)
ZB-CB-4	−63.16	−35.97	−22.61	0.43	8.55	7.32	10.86(17.2)
ZB-CB-5	−17.24	−7.53	−8.28	0.01	1.26	0.39	0.21(1.2)
ZB-CB-6	−31.97	−20.93	−9.32	0.02	4.47	2.93	5.66(17.7)
ZB-CB-7	−82.60	−47.52	−39.69	−0.20	−5.46	−6.21	−6.86(8.3)
ZB-CB-8	−52.77	−43.21	−10.49	−0.03	−1.51	−1.23	−1.78(3.3)
ZB-CB-9	−76.32	−42.30	−37.70	−0.21	−4.92	−5.09	−6.12(8.0)
ZB-CB-10	−48.13	−38.79	−10.29	−0.03	−1.26	−1.17	−1.45(3.0)

---

The interplay between both the interactions can be further estimated with cooperative energy. This term is positive in ZB-CB-1 to 6, but it is negative in ZB-CB-7 to 10, which indicates that there is negative synergistic effect in the former, but positive synergistic effect in the latter. In most cases, this effect is relatively prominent when the strength is sufficiently large for both the interactions. For instance, the cooperative energy amounts to 10.86 kcal mol⁻¹ in ZB-CB-4, where the interaction energies of both the interactions are larger than −20 kcal mol⁻¹. The cooperative energy corresponds to 1.2–17.7% of the total interaction energy, and it varies in a large range depending on the strength of both the interactions. This percentage in ZB-CB-1 to 10 is smaller than 17–55% in F₃B⋯NCX⋯NCM (X, M = halogen), where a triel bond and a halogen bond coexist.⁴⁷

The cooperative effect between both the interactions can also be evidenced by the change in the electron density at the intermolecular BCP in the ternary complex relative to that in the corresponding dyad (Table 6). The electron density decreases for both the types of BCPs in ZB-CB-1 to 6, but a reverse result is found in ZB-CB-7 to 10. The change in the electron density supports change in the strength of the corresponding interaction since electron density can be used to estimate the interaction strength. Moreover, the electron density exhibits larger change for the chalcogen bond.

Table 6 Electron densities (ρ, au) at the triel bond (ZB) and chalcogen bond (CB) BCPs in the triads and their changes (Δρ, au) relative to the corresponding dyads

Triads	ρZB	ΔρZB	ρCB	ΔρCB
ZB-CB-1	0.1064	−0.0028	0.1060	−0.0113
ZB-CB-2	0.1040	−0.0001	0.0290	−0.0021
ZB-CB-3	0.0746	−0.0027	0.0401	−0.0105
ZB-CB-4	0.0959	−0.0097	0.1004	−0.0169
ZB-CB-5	0.0221	−0.0041	0.0298	−0.0013
ZB-CB-6	0.0651	−0.0084	0.0381	−0.0126
ZB-CB-7	0.1054	0.0026	0.1356	0.0116
ZB-CB-8	0.1035	0.0007	0.0388	0.0057
ZB-CB-9	0.1070	0.0032	0.1320	0.0098
ZB-CB-10	0.1046	0.0008	0.0369	0.0043

---

Although deformation energy is very important in the triel bond and chalcogen bond, it was demonstrated that electrostatic interaction is still the main driving force in the formation of both the interactions.^13,14 To explain the interplay between both the interactions, MEPs in the dyads are shown in Table 7. The most negative MEP on the free N/O atom decreases in ZB-1 to 6, but it increases in ZB-7 to 10 and thus, the former is a weaker Lewis base, and the latter is a stronger base; the former forms a weaker chalcogen bond in ZB-CB-1 to 6, whereas the latter engages in a stronger chalcogen bond in ZB-CB-7 to 10. The most negative MEP on the free N/O atom also decreases in CB-1 to 3, corresponding to a weaker base, and it forms a weaker triel bond in ZB-CB-1 to 6. The more positive MEP on the B atom increases in CB-4 to 7; thus, it is a stronger acid and forms a stronger triel bond.

Table 7 The most negative MEP (V_min) on the free N/O atom in the dyads and the most positive MEP (V_max) on the free B atom in the dyads as well as their change (ΔV) relative to the corresponding monomers; all values are in eV

Dyads	Vmin	ΔVmin	Dyads	Vmax	ΔVmax
ZB-1	−0.031	0.018	CB-4	0.0917	0.0352
ZB-2	−0.045	0.008	CB-5	0.0680	0.0097
ZB-3	−0.036	0.014	CB-6	0.1091	0.0313
ZB-4	−0.024	0.025	CB-7	0.0892	0.0086
ZB-5	−0.048	0.005
ZB-6	−0.032	0.018
ZB-7	−0.071	−0.015
ZB-8	−0.072	−0.011
ZB-9	−0.065	−0.013
ZB-10	−0.068	−0.010
CB-1	−0.020	0.029
CB-2	−0.048	0.005
CB-3	−0.038	0.012

---

The interplay between both the interactions can also be understood with a change in the charge transfer (Table 8). The charge transfer is reduced for both the interactions in ZB-CB-1 to 6, where it moves from the central molecule to BH₃/BF₃/SO₃. In ZB-CB-1 to 6, the direction of charge transfer is reverse for both the interactions. On the other hand, the charge transfer increases for both the interactions in ZB-CB-7 to 10, where the direction of charge transfer is from left to right for both the interactions. ΔΔE has a linear relationship with ΔCT for both the interactions, but a better relationship is found for the chalcogen bond (Fig. S4†).

Table 8 Charge transfer (CT, e) of the triel bond (ZB) and chalcogen bond (CB) in the triads as well as its change (ΔCT, e) relative to the corresponding dyads

Triads	CTZB	ΔCTZB	CTCB	ΔCTCB
ZB-CB-1	0.2995	−0.0228	0.2150	−0.0385
ZB-CB-2	0.3095	−0.0038	0.0187	−0.0040
ZB-CB-3	0.2492	−0.0086	0.0451	−0.0268
ZB-CB-4	0.2640	−0.0277	0.1976	−0.0559
ZB-CB-5	0.0343	−0.0145	0.0202	−0.0025
ZB-CB-6	0.1882	−0.0247	0.0405	−0.0314
ZB-CB-7	0.3797	0.0135	0.3161	0.0380
ZB-CB-8	0.3695	0.0036	0.0391	0.0123
ZB-CB-9	0.3454	0.0130	0.3044	0.0329
ZB-CB-10	0.3356	0.0032	0.0348	0.0090

---

4. Conclusions

Ab initio calculations have been performed for ternary complexes, where both a π-hole triel bond and a π-hole chalcogen bond coexist, along with the respective binary complexes. These π-hole bonds are very strong, possessing numerous characteristics of at least partially covalent interactions. The stability of these complexes is mainly due to charge transfer from the electron donor to the triel or chalcogen donor, caused by electrostatic, polarization, and deformation effects. H_BCP is negative for all the complexes; furthermore, ∇²ρ_BCP is also negative for the chalcogen-bonded complexes of pyrazine and pyridine derivatives. A comparison of the different hybridized nitrogen atoms indicates that the sp²-hybridized nitrogen atom is favorable to bind with the π-hole at the triel or chalcogen center. The triel molecule is more easily deformed to bind with the electron donor than the chalcogen molecule, thus forming a stronger π-hole bond.

Both triel and chalcogen bonds can coexist in the same ternary complex where a heteroaromatic compound is located in the central position. If the central molecule acts as a double Lewis base to bind with another two molecules, both the interactions are weakened, and a larger weakening effect is found for the chalcogen bond. If the central molecule plays a dual role of both a base in the triel bond and an acid in the chalcogen bond, both interactions are strengthened, and larger strengthening effect is found for the chalcogen bond. The cooperative mechanism of both the interactions is mainly governed by electrostatic and charge transfer effects.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21573188).

References

1. S. Scheiner, Hydrogen Bonding: A Theoretical Perspective, Oxford University Press, Oxford, 1997.
2. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, 1997.
3. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond, Oxford University Press, Oxford, United Kingdom, 1999.
4. M. Breugst, E. Detmar and D. v. d. Heiden, ACS Catal., 2016, 6, 3203–3212.
5. M. Iwaoka, S. Takemoto and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 10613–10620.
6. M. Bai, S. P. Thomas, R. Kottokkaran, S. K. Nayak, P. C. Ramamurthy and T. N. G. Row, Cryst. Growth Des., 2014, 14, 459–466.
7. M. X. Liu, Q. Z. Li and S. Scheiner, Phys. Chem. Chem. Phys., 2017, 19, 5550–5559.
8. S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem.–Eur. J., 2011, 17, 6034–6038.
9. A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321.
10. Q. Z. Li, R. Li, X. F. Liu, W. Z. Li and J. B. Cheng, ChemPhysChem, 2012, 13, 1205–1212.
11. S. J. Grabowski, ChemPhysChem, 2015, 16, 1470–1479.
12. W. Z. Wang, B. M. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135.
13. J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038.
14. S. J. Grabowski, ChemPhysChem, 2014, 15, 2985–2993.
15. M. D. Esrafili and R. Nurazar, Mol. Phys., 2016, 114, 276–282.
16. D. L. Fiacco, Y. Mo, S. W. Hunt, M. E. Ott, A. Roberts and K. R. Leopold, J. Phys. Chem. A, 2001, 105, 484–493.
17. L. M. Azofra, I. Alkorta and S. Scheiner, J. Phys. Chem. A, 2015, 119, 535–541.
18. V. d. P. N. Nziko and S. Scheiner, J. Phys. Chem. A, 2014, 118, 10849–10856.
19. G. E. Garrett, E. I. Carrera, D. S. Seferos and M. S. Taylor, Chem. Commun., 2016, 52, 9881–9884.
20. Q. Z. Li, H. Qi, R. Li, X. F. Liu, W. Z. Li and J. B. Cheng, Phys. Chem. Chem. Phys., 2012, 14, 3025–3030.
21. M. D. Esrafili and F. Mohammadian-Sabet, Chem. Phys. Lett., 2015, 628, 71–75.
22. W. A. Burns, J. A. Phillips, M. Canagaratna, H. Goodfriend and K. R. Leopold, J. Phys. Chem. A, 1999, 103, 7445–7453.
23. M. Pyziak, J. Pyziak, M. Hoffmann and M. Kubicki, Cryst. Growth Des., 2015, 15, 5223–5232.
24. H. T. Huynh, O. Jeannin and M. Fourmigué, Chem. Commun., 2017, 53, 8467–8469.
25. K. T. Mahmudov, M. N. Kopylovich, M. F. C. G. d. Silva and A. J. L. Pombeiro, Dalton Trans., 2017, 46, 10121–10138.
26. T. T. Wang, W. Z. Li, Q. Z. Li and J. B. Cheng, Russ. J. Phys. Chem. A, 2015, 89, 812–817.
27. X. Guo, X. L. An and Q. Z. Li, J. Phys. Chem. A, 2015, 119, 3518–3527.
28. M. D. Esrafili, F. Mohammadian-Sabet and M. Solimannejad, Struct. Chem., 2014, 25, 1197–1205.
29. M. D. Esrafili and M. Vakili, Mol. Phys., 2014, 112, 2746–2752.
30. J. George, V. L. Deringer and R. Dronskowski, J. Phys. Chem. A, 2014, 118, 3193–3200.
31. M. D. Esrafili and F. Mohammadian-Sabet, Struct. Chem., 2015, 26, 199–206.
32. M. D. Esrafili and M. Vakili, J. Mol. Model., 2014, 20, 2291.
33. K. Haupa, A. Bil and Z. Mielke, J. Phys. Chem. A, 2015, 119, 10724–10734.
34. I. R. Beattie and P. J. Jones, Angew. Chem., Int. Ed., 1996, 35, 1527–1529.
35. V. Jonas, G. Frenking and M. T. Reetz, J. Am. Chem. Soc., 1994, 116, 8741–8753.
36. W. A. Burns and K. R. Leopold, J. Am. Chem. Soc., 1993, 115, 11622–11623.
37. H. J. Jiao and P. v. R. Schleyer, J. Am. Chem. Soc., 1994, 116, 7429–7430.
38. S. W. Reeve, W. A. Burns, F. J. Lovas, R. D. Suenram and K. R. Leopold, J. Phys. Chem., 1993, 97, 10630–10637.
39. G. Venter and J. Dillen, J. Phys. Chem. A, 2004, 108, 8378–8384.
40. J. A. Phillips, D. J. Giesen, N. P. Wells, J. A. Halfen, C. C. Knutson and J. P. Wrass, J. Phys. Chem. A, 2005, 109, 8199–8208.
41. H. Hirao, K. Omoto and H. Fujimoto, J. Phys. Chem. A, 1999, 103, 5807–5811.
42. E. Iglesias, T. L. Sordo and J. A. Sordo, Chem. Phys. Lett., 1996, 248, 179–181.
43. D. L. Fiacco and K. R. Leopold, J. Phys. Chem. A, 2003, 107, 2808–2814.
44. S. Yourdkhani, T. Korona and N. L. Hadipour, J. Comput. Chem., 2015, 36, 2412–2428.
45. M. D. Esrafili and P. Mousavian, Mol. Phys., 2017, 115, 2999–3010.
46. M. X. Liu, H. Y. Zhuo, Q. Z. Li, W. Z. Li and J. B. Cheng, J. Mol. Model., 2016, 22, 10.
47. Q. J. Tang and Q. Z. Li, Mol. Phys., 2015, 113, 3809–3814.
48. M. D. Esrafili and P. Mousavian, Chem. Phys. Lett., 2017, 678, 275–282.
49. D. Escudero, A. Frontera, D. Quiñonero and P. M. Deyà, J. Comput. Chem., 2009, 30, 75–82.
50. C. Estarellas, A. Frontera, D. Quiñonero and P. M. Deyà, ChemPhysChem, 2011, 12, 2742–2750.
51. H. A. Samimi, M. D. Esrafili, F. Mohammadian-Sabet and H. Haddadi, Mol. Phys., 2015, 113, 1442–1450.
52. M. D. Esrafili, F. Mohammadian-Sabet and M. Solimannejad, J. Mol. Graphics Modell., 2015, 57, 99–105.
53. H. L. Xu, J. B. Cheng, X. Yang, Z. B. Liu, W. Z. Li and Q. Z. Li, ChemPhysChem, 2017, 18, 2442–2450.
54. M. D. Esrafili and P. Mousavian, Mol. Phys., 2018, 116, 388–398.
55. M. Gao, G. Q. Gao, Q. Z. Li, X. Yang, W. Z. Li and J. B. Cheng, RSC Adv., 2015, 5, 76912–76918.
56. A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825.
57. I. Alkorta, F. Blanco, P. M. Deya, J. Elguero, C. Estarellas, A. Frontera and D. Quiñonero, Theor. Chem. Acc., 2010, 126, 1–14.
58. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision A02. Gaussian Inc., Wallingford, 2009.
59. S. B. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
60. F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691.
61. R. F. W. Bader, AIM2000 program, version 2.0, McMasterUniversity, Hamilton, Canada, 2000.
62. T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592.
63. A. E. Reed, L. A. Curtiss and F. A. Weinhold, Chem. Rev., 1988, 88, 899–926.
64. S. J. Grabowski, J. Comput. Chem., 2018, 39, 472–480.
65. D. J. Giesen and J. A. Phillips, J. Phys. Chem. A, 2003, 107, 4009–4018.
66. J. A. Phillips and C. J. Cramer, J. Phys. Chem. B, 2007, 111, 1408–1415.
67. S. J. Grabowski, Phys. Chem. Chem. Phys., 2017, 19, 29742–29759.
68. W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841.
69. S. Pan, D. Moreno, J. L. Cabellos, J. Romero, A. Reyes, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2014, 118, 487–494.
70. R. Saha, S. Pan, S. Mandal, M. Orozco, G. Merino and P. K. Chattaraj, RSC Adv., 2016, 6, 78611–78620.
71. D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628.
72. I. V. Novozhilova, A. V. Volkov and P. Coppens, J. Am. Chem. Soc., 2003, 125, 1079–1087.
73. P. Macchi, L. S. Garlaschelli, S. Martinengo and A. Sironi, J. Am. Chem. Soc., 1999, 121, 10428–10429.
74. P. Macchi, D. M. Proserpio and A. Sironi, J. Am. Chem. Soc., 1998, 120, 13429–13435.
75. S. Pan, A. Gupta, S. Mandal, D. Moreno, G. Merino and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2015, 17, 972–982.
76. S. Pan, R. Saha, S. Mandal and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2016, 18, 11661–11676.
77. G. Jana, S. Pan, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2017, 121, 6491–6499.
78. S. Pan, A. Gupta, R. Saha, G. Merino and P. K. Chattaraj, J. Comput. Chem., 2015, 36, 2168–2176.
79. B. Szefczyk, W. A. Sokalski and J. Leszczynski, J. Chem. Phys., 2002, 117, 6952–6958.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04106g

---