Open Access Article
Open Access ArticleInvestigation on cure kinetics of epoxy resin containing carbon nanotubes modified with hyper-branched polyester
Li Luabc,
Liao Xia *a,
Hao Zengheng*bc,
Sheng Xingyueb,
Zhang Yib and
Liu Panb
*a,
Hao Zengheng*bc,
Sheng Xingyueb,
Zhang Yib and
Liu Panb
aCollege of Polymer Science and Engineering, Sichuan University, Chengdu, 610065, China. E-mail: xliao@scu.edu.cn
bChongqing Zhixiang Paving Technology Engineering Co., Ltd., Chongqing, 401336, China. E-mail: haozengheng@cmhk.com
cChina Merchants Chongqing Communications Research & Design Institute Co., Ltd., Chongqing 400067, China
First published on 23rd August 2018
Abstract
The cure kinetics of epoxy resin cured by diethyltoluene diamine (D-EP), D-EP/multi-walled carbon nanotube (D-EP/CNT) composites and D-EP/hyper branched polyester functionalized CNTs (D-EP/CNTs-H20) were investigated by non-isothermal differential scanning calorimetry (DSC). Results revealed that the presence of CNTs shifted the cure temperature to a lower temperature and accelerated the curing of D-EP, and the addition of CNTs-H20 exhibited a stronger effect in accelerating the cure of D-EP. Activation energies were calculated based on the Kissinger approach and Ozawa approach respectively. Lowered activation energy was observed after the addition of CNTs or CNTs-H20 at low degrees of cure, indicating that the CNTs had a large effect on the curing reaction. The presence of CNTs facilitated the curing reaction, especially the initial epoxyamine reaction. Moreover, CNTs-H20 exhibited better performance. The autocatalytic model was used to describe the cure kinetics phenomena of the studied systems. When CNTs or CNTs-H20 were added, the Sesták–Berggren model still can describe the cure kinetics of the D-EP composites because the results, calculated by the model, agreed with the experimental data well. Moreover, the kinetics parameters as well as the equation describing the cure process were proposed.
1. Introduction
Being one of the most important classes of thermosetting polymers, epoxy resins (EP) are widely applied in many important areas such as coatings, adhesives, molding compounds and polymer composites.1–3 However, epoxy resins are restricted by their poor toughness in many cases. Therefore, it is very important to improve the toughness and to enhance the impact resistance, fatigue behavior and damage tolerance of the material.3–5In recent years, great efforts have been made to improve the toughness of epoxy thermosets. Toughness implies energy absorption and is achieved through various deformation mechanisms before failure occurs. One effective mechanisms to increase toughness is the addition of a second phase (elastomers).6,7 However, the introduction of elastomers usually receives desirable enhancement of toughness at the expense of other performance such as thermal resistance and strength.
Recently, the introduction of inorganic fillers is found to be an efficient way to improve the toughness of epoxy resin without sacrificing other properties.8–13 The multi-walled carbon nanotubes (CNTs) are ideal fillers for polymer composites due to their high Young's modulus as well as good electrical and thermal conductivity.9,14–17 The addition of a small amount of CNTs can strongly improve the electrical, thermal and mechanical properties of the polymer matrix, resulting in the composites with good processability, balanced stiffness and toughness as well as other functional properties.18–21 However, the main problem is that, the CNTs are insoluble and difficult to be evenly dispersed in the matrix due to its inorganic nature and lack of functional groups on the surface. To improve its compatibility with epoxy resin, the surface modification is proved to be an effective way.11,22–24
Hyperbranched polymers have a lower branching efficiency than dendrimers while possessing many useful properties.25–27 The highly branched architecture minimizes chain–chain ability and low melt viscosity to these polymers, which is compatible with epoxy thermosets. The presence of plenty of functional groups (–OH) provides high reaction activity with inorganic filler, providing us a possibility to be desirable macromolecular surface modifier for CNTs, to further enhance the compatibility and dispersion in epoxy resin. In the previous study,8 we successfully prepared hyperbranched polyester grafted CNTs, and applied it in the toughening of epoxy resin cured by diethyltoluene diamine (D-EP). Results revealed that the hyperbranched polyester grafted CNTs received a better dispersion in the epoxy prepolymer compared with the raw CNTs, which further decreased the glass transition temperature of the D-EP/CNTs composites and exhibited better performance in the enhancement in toughening D-EP.
The previous study provides novel method to prepare high performance D-EP/CNTs composites. However, the surface modification of CNTs using hyperbranched polyester might influence the curing kinetics, which is very important in understanding the impact of modified CNTs on the performance of D-EP/CNTs composites. The aim of this study is to comparatively investigate the role of hyperbranched polyester surface modification of CNTs in the cure kinetics of the D-EP/CNTs resin. From the curing kinetics analysis, the better understanding of the impact of CNTs and CNTs-H20 in the curing behavior, morphology and performances of the composites can be obtained.
2. Experimental
2.1 Materials
The epoxy resin used (Epon® 825) was purchased from Shell (Houston, TX, USA); the carboxylic multi-walled carbon nanotube (denoted as CNTs in this paper) was purchased from Chengdu Organic Chemicals Co., LTD., Chinese Academy of Science, China. The diameter of the raw CNTs ranged from 10 to 20 nm and their length was about 5–15 μm.Hyperbranched polymer Boltorn H20 (Mw = 1350 g mol−1, hydroxyl number = 320 mg KOH per g polymer, names as Hyper H20 in this study) was purchased from Shanghai Seebio Biotech, Inc (China), and was used as received; diglycidyl ether of bisphenol A (DGEBA, Araldite GY 240, Huntsman) (182 g mol−1) was dried under vacuum at 80 °C for 8 h before use; diethyltoluene diamine (DETDA) and N,N-dimethylformamide (DMF) were purchased from Sinopharm Chemical Reagent Beijing Co., Ltd, China, and were used as received.
The chemical structures of the epoxy, DGEBA, DETDA, CNTs and Hyper H20 are shown in Scheme 1.8
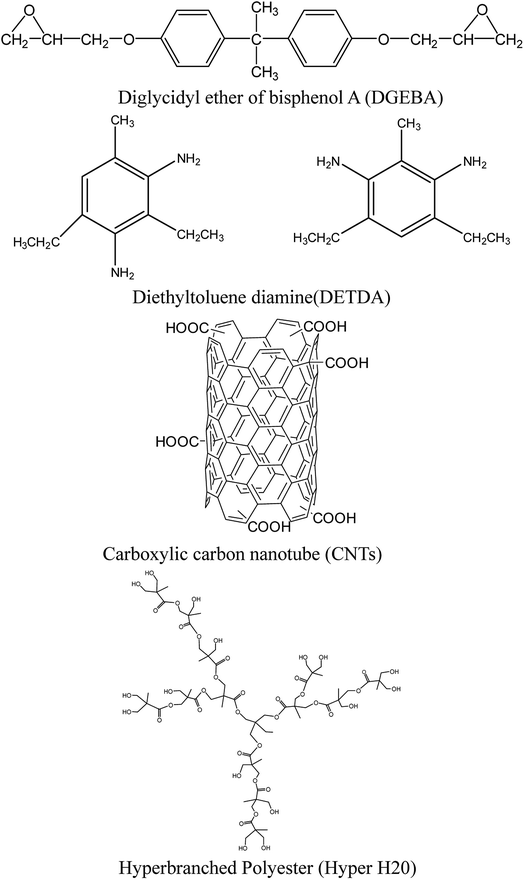 | ||
| Scheme 1 Structure of epoxy resin, curing agent, carbon nanotube and hyperbranched polyester.8 | ||
2.2 Preparation of CNTs-H20
The hyperbranched polyester Hyper H20 and CNTs were dissolved in DMF in room temperature, and then irradiated using ultrasound for 1 h. After that, they were heated up to 120 °C and react under magnetic stirring for 24 h. After that, they were cooled to room temperature slowly and filtered using PVDF filtration membrane with the average pore diameter of 0.22 μm. The product was firstly washed by acetone and filtered for several times to eliminate the unreacted Hyper H20 and extra solvent. Each time, the washed acetone was taken for FT-IR analysis, and the washing is finished until the washed acetone has the same FT-IR spectra compared with pure acetone. The collected material was then heated under vacuum drier at 80 °C for 24 h, and the final product, CNTs grafted with Hyper H20 (named as CNTs-H20), was obtained. The reaction principle between Hyper H20 and CNTs was shown in Scheme 2.8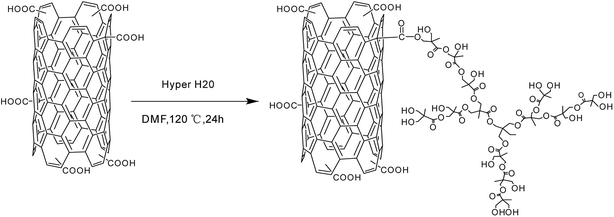 | ||
| Scheme 2 Reaction principle of hyperbranched polyester modified carbon nanotubes.8 | ||
2.3 Preparation of D-EP/CNTs and D-EP/CNTs-H20 composites
To prepare D-EP/CNTs composites for the DSC measurement, the epoxy prepolymer and CNTs (CNTs or CNTs-H20) were firstly mixed in the weight ratio of 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, then, they were irradiated for 1 h to ensure a finely dispersion of CNTs in epoxy prepolymer. After that, 20 wt% DETDA were added, and the mixture was used for thermal analysis. Three samples used in this study were named as D-EP, D-EP/CNTs and D-EP/CNTs-H20, respectively.
1, then, they were irradiated for 1 h to ensure a finely dispersion of CNTs in epoxy prepolymer. After that, 20 wt% DETDA were added, and the mixture was used for thermal analysis. Three samples used in this study were named as D-EP, D-EP/CNTs and D-EP/CNTs-H20, respectively.
2.4 Characterization
3. Results and discussion
3.1 Characterization of the CNTs and CNTs-H20
The microstructure of CNTs and CNTs-H20 have been characterized in detail in the previous study.8 A brief description is given here. The FT-IR spectra of CNTs, CNTs-H20 and Hyper H20 are shown in Fig. 1.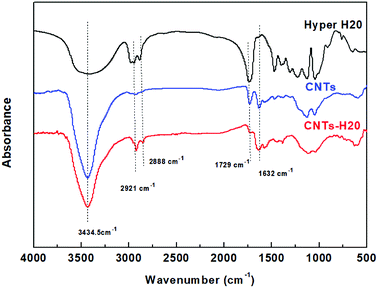 | ||
| Fig. 1 FT-IR spectra of Hyper H20, CNTs and CNTs-H20.8 | ||
Fig. 1 shows that for Hyper H20, the peak at 3420 cm−1 represents the vibration of –OH group, while signals at the wavenumbers of 2921 cm−1 and 2888 cm−1 represent the asymmetric and symmetric vibrations of –CH3 and –CH2, respectively. The peaks at the wavenumber of 1734 cm−1 is the stretching vibration peak of carbonyl; for CNTs, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O of carbonyl is in the form of carboxylic acid, the corresponding absorption peak (1734 cm−1) is usually big due to the formation of hydrogen bond; for CNTs-H20, the new peaks at 2921 cm−1 and 2888 cm−1 can be seen, corresponding to the asymmetric and symmetric vibrations of –CH3 and –CH2, respectively, suggesting that the Hyper H20 is successfully grafted onto CNTs. Moreover, it can also be observed that in the FT-IR spectra of CNTs-H20, the intensity of the peak at 1729 cm−1 representing the stretching vibration peak of carbonyl decreases significantly, indicating that the –COOH groups on the surface of CNTs have reacted with the terminal hydroxyl groups on hyperbranched polyester (Hyper H20), resulting in the significant decrease of carbonyl absorption peak at 1734 cm−1. Since the un-grafted H20 has already been washed away before the FT-IR test, therefore, the results above suggest that the reaction between H20 and CNTs takes place, and the reaction mechanism between CNTs and Hyper H20 should be the occurrence of esterification reaction between the carboxyl groups on the surface of CNTs and the hydroxyl groups of Hyper H20.
O of carbonyl is in the form of carboxylic acid, the corresponding absorption peak (1734 cm−1) is usually big due to the formation of hydrogen bond; for CNTs-H20, the new peaks at 2921 cm−1 and 2888 cm−1 can be seen, corresponding to the asymmetric and symmetric vibrations of –CH3 and –CH2, respectively, suggesting that the Hyper H20 is successfully grafted onto CNTs. Moreover, it can also be observed that in the FT-IR spectra of CNTs-H20, the intensity of the peak at 1729 cm−1 representing the stretching vibration peak of carbonyl decreases significantly, indicating that the –COOH groups on the surface of CNTs have reacted with the terminal hydroxyl groups on hyperbranched polyester (Hyper H20), resulting in the significant decrease of carbonyl absorption peak at 1734 cm−1. Since the un-grafted H20 has already been washed away before the FT-IR test, therefore, the results above suggest that the reaction between H20 and CNTs takes place, and the reaction mechanism between CNTs and Hyper H20 should be the occurrence of esterification reaction between the carboxyl groups on the surface of CNTs and the hydroxyl groups of Hyper H20.
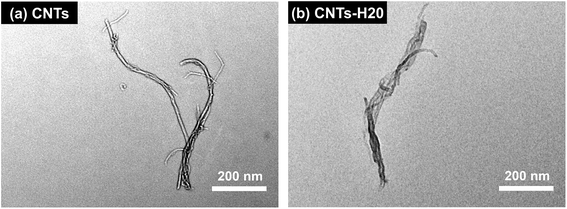
The TEM images of CNTs and CNTs-H20 are shown in Fig. 2. It can be seen from Fig. 2 that, the morphologies of CNTs and CNTs-H20 are quite different from each other. For CNTs, the shape of typical “nanotube”10 can be clearly seen, while for CNTs-H20, uniform dark-colored morphology can be observed, indicating that the CNTs is covered with Hyper-H20.
3.2 Basic assumptions of curing kinetics analyzed by DSC
Using DSC, the curing kinetics of the samples can be characterized by measuring heat signal generated during the curing reaction as a function of temperature and time.22 The area under the curves is proportional to the conversion, which could be defined as eqn (1). The heat evolution recorded by DSC is assumed to be proportional to the extent of consumption of the reactive groups. The curing rate during the curing process can be described as the following eqn (2):
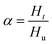 | (1) |
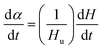 | (2) |
Most curing kinetics can be described by eqn (3):
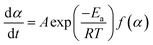 | (3) |
The non-isothermal kinetic model can identify two types of reaction: n-th order or autocatalytic model. Autocatalytic model (Sesták–Berggren equation) assumes that the reaction obeys the eqn (4):32
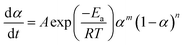 | (4) |
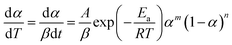 | (5) |
3.3 Curing characteristics for the D-EP, D-EP/CNTs and D-EP/CNTs-H20
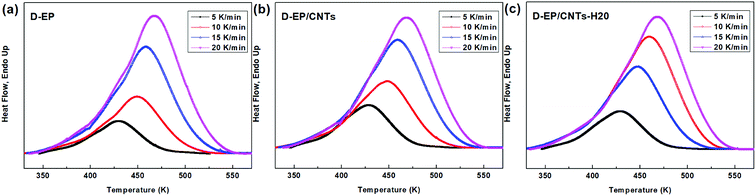
DSC curves of the D-EP, D-EP/CNTs and D-EP/CNTs-H20 at different heating rates are shown in Fig. 3. The curing parameters are listed in Table 1. The conversion α(T) can be calculated by eqn (1). Fig. 3 shows α(T) with respect to T for D-EP, D-EP/CNTs and D-EP/CNTs-H20 in different heating rates. These curves can be used as basic data for the kinetic calculation.| Cooling rate | Toa (K) | Tpb (K) | Tec (K) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (K min−1) | D-EP | D-EP/CNTs | D-EP/CNTs-H20 | D-EP | D-EP/CNTs | D-EP/CNTs-H20 | D-EP | D-EP/CNTs | D-EP/CNTs-H20 |
| a To (Temperature that the reaction starts).b Tp (Peak temperature).c Te (Terminal temperature). | |||||||||
| 5 | 335.7 | 333.9 | 331.9 | 428.1 | 426.9 | 423.6 | 527.1 | 524.1 | 521.2 |
| 10 | 341.8 | 340.2 | 339.2 | 448.3 | 447.4 | 445.1 | 543.1 | 539.1 | 536 |
| 15 | 343.8 | 342.9 | 341.8 | 458.8 | 457.1 | 455.3 | 552.6 | 550.5 | 547.2 |
| 20 | 347.6 | 346.1 | 345.1 | 467.9 | 466.2 | 464.1 | 558.5 | 555.2 | 553.9 |
The polymerization of thermosets is a complex mechanism that may include several chemical reactions. Aromatic primary amines are commonly used as curing agents. These active hydrogen compounds undergo an addition reaction with epoxy ring. The polyaddition occurs between epoxy and primary amine, followed by secondary amine addition, and at latter stages of the reaction or at higher temperature, side reactions such as etherification or homopolymerization. It can be seen from the results above that, the presence of CNTs or CNTs-H20 has strong impact on the curing process as reflected by the difference in the DSC curves of the epoxy and its nanocomposites. The presence of CNTs shifts the To, Te and Tp to lower temperature, indicating that the addition of CNTs accelerates the curing of EP, which might be attributed to an increase in the efficiency of collisions, and can be explained by catalytic effect of CNTs on the epoxy ring opening. In other words, the amine groups on the surface of CNTs can play the role of curing agents and promote the primary amine–epoxide reaction.10,11 In addition, a change of the shape of thermo analytical curves suggests possible modifications of the kinetic parameters and of the cure mechanism in the presence of CNTs (Fig. 4).
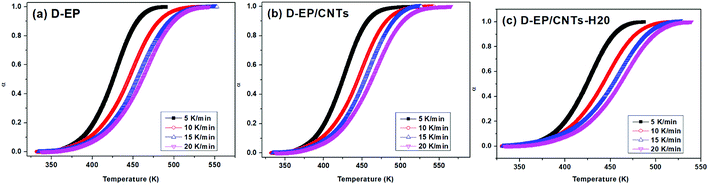 | ||
| Fig. 4 Conversion α as a function of temperatures for the system of D-EP, D-EP/CNTs and D-EP/CNTs-H20 at different heating rates. | ||
On the other hand, compared with CNTs, it can be observed that after the addition of CNTs-H20, the parameters of Tp, To and Te shift to lower temperature range, indicating that the functionalization of CNTs further accelerates the curing of EP.
3.4 Calculation of the activation energy of curing
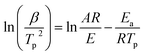 | (6) |
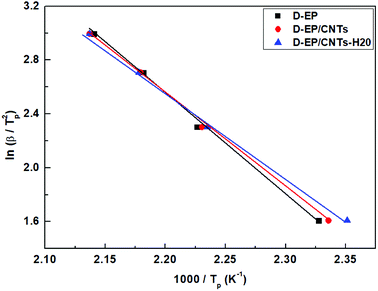
Fig. 5 shows the relationship between ln(β/Tp2) and 1000/Tp for both the D-EP system and its nanocomposite. The four points correspond to the four heating rates of 5, 10, 15, and 20 K min−1. Fig. 5 suggests that there is an excellent linear fit in all the cases, indicating that the experimental data fits the Kissinger model quite well. From the slopes of these three plots the overall activation energy for D-EP, D-EP/CNTs and D-EP/CNTs-H20 were found to be 60.6, 50.8 and 47.4 kJ mol−1, respectively, indicating that addition of CNTs or CNTs-H20 decreases the activation energy barrier of EP during curing process, making the occurrence of cure easier. The addition of CNTs-H20 further decreases the activation energy compared with CNTs, which might be attributed to the positive effect of the organic intercalant to promote the chemical reaction of CNTs-H20.11,26,32,33
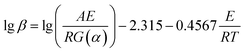 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs. T−1 for a chosen degree of conversion, the activation energy corresponding to that degree of conversion can be obtained.
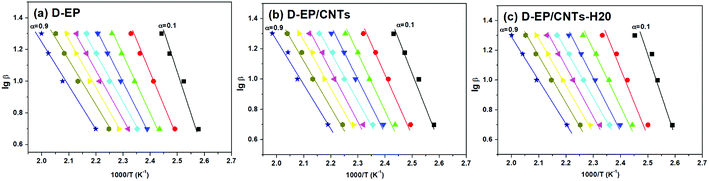
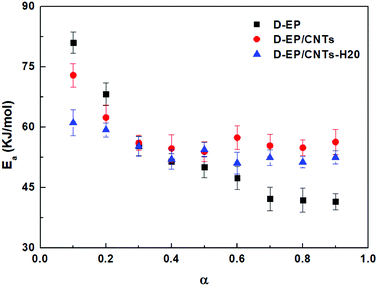
β vs. T−1 for a chosen degree of conversion, the activation energy corresponding to that degree of conversion can be obtained.Fig. 6 shows the relationship between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs. T−1 for nine different degrees of conversion ranging from 0.1 to 0.95. The linear relationship observed in all cases indicates that the approach is applicable for this case. The activation energies Ea calculated for the systems are given in Fig. 7.
β vs. T−1 for nine different degrees of conversion ranging from 0.1 to 0.95. The linear relationship observed in all cases indicates that the approach is applicable for this case. The activation energies Ea calculated for the systems are given in Fig. 7.
As can be seen from Fig. 6 and 7, there is a significant difference in behavior between D-EP, D-EP/CNTs and D-EP/CNTs-H20: for the D-EP, the apparent Ea keeps more or less steadily as a function of the degree of cure, from 81.0 ± 2.6 kJ mol−1 at 0.1 to 41.5 ± 2.0 kJ mol−1 at 0.9. For the D-EP/CNTs system, at a low degree of cure (α < 0.3) the apparent Ea is obviously lower than the D-EP system, but as the degree of cure increases, Ea decreases slightly, reaching 56.1 ± 1.9 kJ mol−1 at α = 0.3 and then keeps almost constant to α = 0.9. For D-EP/CNTs-H20 system, the Ea is 61.1 ± 3.2 kJ mol−1 at low degree of cure (α < 0.3), which is obviously lower than that of D-EP and D-EP/CNTs; which gradually decreases to 52–55 kJ mol−1 and keeps almost constant to the finish of cure. The variation of the Ea during the cure process of the samples can be explained as following:
In the early stages of the cure, the temperature is lower, the dominant reaction is expected to be that between epoxy and amine groups. In the later stages of cure, at higher temperatures, other reactions (mainly epoxy etherification, but possibly others like hydroxyl hydroxyl) are expected to become more important.33,35 The unusual low activation energy observed for the nanocomposite at lower degrees of cure indicates that the addition of CNTs or CNTs-H20 facilitates the curing reaction, especially the initial epoxy-amine reaction.
The first stage of the dependency of D-EP is characteristic of epoxy-amine reactions. At the end of the reaction, the decrease of Ea is due to the transition from chemical control of the crosslinking to a diffusion control that becomes detectable in this system already at gelation. In the case of D-EP/CNTs and D-EP/CNTs-H20 systems, the characteristic decrease of Ea observed is lower, leading to the hypothesis that diffusion contribution is less pronounced in this case. Side reactions (etherifications/homopolymerizations) are known to occur at elevated temperatures, so it can also be postulated that these reactions become significant in the case of D-EP/CNTs-H20.
Moreover, the activation energies obtained by the Kissinger approach (60.6 kJ mol−1 for D-EP, 50.8 kJ mol−1 and 47.4 kJ mol−1 for D-EP/CNTs and D-EP/CNTs-H20 respectively) are lower than those obtained by the Ozawa approach (63.2, 58.2 and 54.3 kJ mol−1 for D-EP, D-EP/CNTs and D-EP/CNTs-H20, respectively). This can be explained by the differences in assumptions and mathematical approach. However, for the two methods, similar results that the apparent slight increase in Ea are observed for the nanocomposites. Thus, both the two approaches can be used to detect the activation energy.
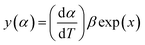 | (8) |
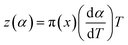 | (9) |
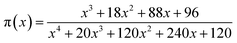 | (10) |
The values of both y(α) and z(α) functions normalized within (0, 1) intervals are given by the following equations:
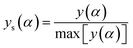 | (11) |
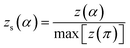 | (12) |
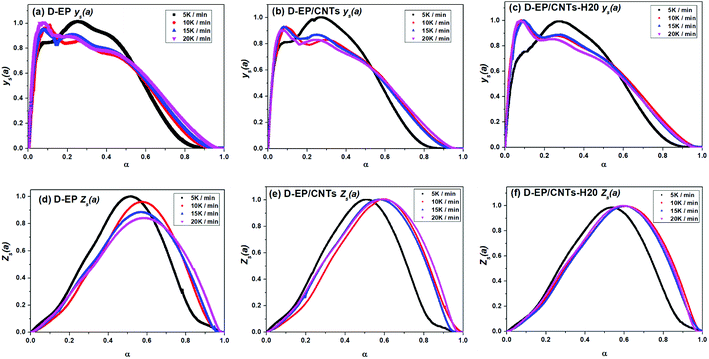
According the shape and the maximum of both ys(α) and zs(α) functions, the most suitable kinetic model can be determined among several models and subsequently the kinetic parameters such as n and m can be calculated. Fig. 8 shows the variation of ys(α) and zs(α) values with conversion α.
The curves of ys(α) and zs(α) exhibit maxima at αM and α∞p, respectively. The values of αM and α∞p are shown in Table 2. The results in Fig. 8 and Table 2 indicate the curing process can be described by the two-parameter autocatalytic kinetic model Sesták–Berggren (eqn (5)).13 The mean value of αM was used to calculate the kinetic parameters. In eqn (5), the ratio of reaction order, p = m/n as pointed out by Málek, can be replaced by:
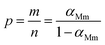 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex] vs. ln[αp(1 − α)] (from eqn (4), (5) and (13)) as well as the kinetic parameter m can be calculated from eqn (13).
ex] vs. ln[αp(1 − α)] (from eqn (4), (5) and (13)) as well as the kinetic parameter m can be calculated from eqn (13).
| β | D-EP | D-EP/CNTs | D-EP/CNTs-H20 | |||
|---|---|---|---|---|---|---|
| (K min−1) | αM | α∞p | αM | α∞p | αM | α∞p |
| 5 | 0.2526 | 0.5155 | 0.2714 | 0.5071 | 0.2772 | 0.5373 |
| 10 | 0.0762 | 0.5729 | 0.0924 | 0.5678 | 0.0792 | 0.5953 |
| 15 | 0.0748 | 0.5658 | 0.0792 | 0.5860 | 0.0951 | 0.6009 |
| 20 | 0.1111 | 0.5846 | 0.0850 | 0.5895 | 0.0835 | 0.5938 |
| Mean | 0.1287 | 0.5597 | 0.1320 | 0.5626 | 0.1338 | 0.5818 |
All of kinetic parameters, E, n and m are listed in Table 3. The validity of Málek method is evaluated by comparison of the curves of dα/dT versus T plotted with the calculated data in Table 3 and experimental data. Compared results for D-EP, D-EP/CNTs and D-EP/CNTs-H20 are shown in Fig. 9.
| Samples | Ea (kJ mol−1) | m | n | f(α) |
|---|---|---|---|---|
| D-EP | 60.6 ± 0.99 | 0.44 ± 0.02 | 2.98 ± 0.02 | α0.44(1 − α)2.98 |
| D-EP/CNTs | 50.8 ± 1.13 | 0.43 ± 0.02 | 2.81 ± 0.02 | α0.43(1 − α)2.81 |
| D-EP/CNTs-H20 | 47.4 ± 0.87 | 0.35 ± 0.02 | 2.25 ± 0.02 | α0.35(1 − α)2.25 |
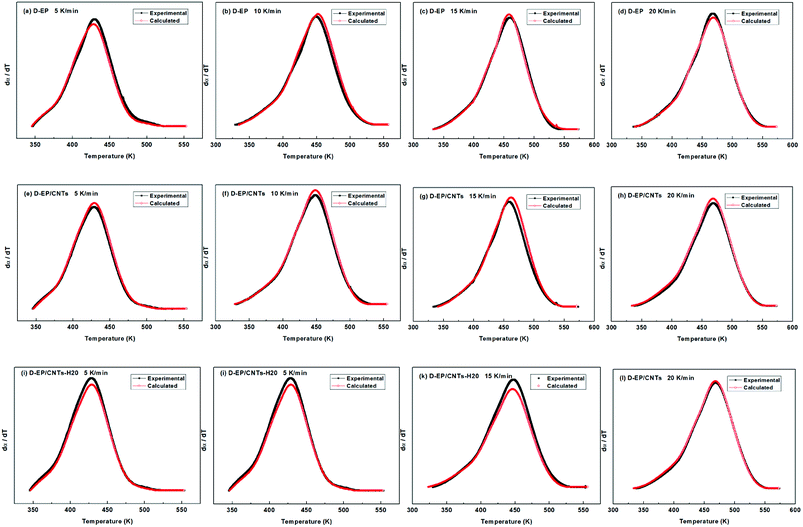 | ||
| Fig. 9 Comparison of experimental values and calculated values at different heating rates for the D-EP, D-EP/CNTs and D-EP/CNTs-H20 systems. | ||
The results in Fig. 9 show that calculated data coincides with experimental data, indicating that the Sesták–Berggren model deduced by Málek method could describe the entire curing reaction process. On the other hand, the results in Table 3 reveal that after the addition of CNTs, the reaction order parameters m and n changes evidently, reflecting the significant influence of CNTs and the modification of CNTs on the curing behavior of the epoxy resin. Moreover, the parameters obtained above can be used to describe the curing kinetics (to calculate the degree of cure at certain time certain temperature, to calculate the time or temperature needed to achieve certain degree of cure) according to following equation:
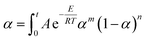 | (14) |
Therefore, the results of this study is of great importance from the practical point.
4. Conclusions
The cure kinetics of D-EP before and after the addition of CNTs or CNTs-H20 were investigated by non-isothermal DSC. It was found that the presence of CNTs shifted the cure temperature to lower temperature and accelerates the curing of D-EP. The addition of CNTs-H20 exhibited a stronger effect in accelerating the cure of D-EP.Activation energy was calculated based on Kissinger approach and Ozawa approach. The lowered activation energy was observed after the addition of CNTs or CNTs-H20 at low degrees of cure, which indicated that the CNTs has a large effect on the curing reaction. The presence of CNTs facilitated the curing reaction, especially the initial epoxyamine reaction. Moreover, functionalized CNTs (CNTs-H20) exhibited better performance.
Autocatalytic model was used to describe the cure kinetic phenomena of studied systems. When the CNTs or CNTs-H20 was added, Sesták–Berggren model still can describe the cure kinetic of D-EP composites because the results, calculated by the model, agree with the experimental data well. Moreover, the kinetics parameters as well as the equation describing the cure process were proposed based on the Sesták–Berggren model. In general, the functionalized CNTs (CNTs-H20) exhibited obviously better performance in accelerating the cure of D-EP.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support from the National Natural Science Foundation of China (51702282), and the Foundation of Distinguished Young Scholars of Chongqing (CSTC2014JCYJJQ0019).References
- A. Boukerrou, J. Duchet, S. Fellahi and H. Sautereau, Processing of mica/epoxy nanocomposites by ultrasound mixing, J. Appl. Polym. Sci., 2007, 105(3), 1420–1425 CrossRef.
- X. Luo, X. Yu, Y. Ma, K. Naito and Q. Zhang, Preparation and cure kinetics of epoxy with nanodiamond modified with liquid crystalline epoxy, Thermochim. Acta, 2018, 663, 1–8 CrossRef.
- T. Na, H. Jiang, L. Zhao and C. Zhao, Preparation and characterization of novel naphthyl epoxy resin containing 4-fluorobenzoyl side chains for low-k dielectrics application, RSC Adv., 2017, 7(85), 53970–53976 RSC.
- M. Qi, Y.-J. Xu, W.-H. Rao, X. Luo, L. Chen and Y.-Z. Wang, Epoxidized soybean oil cured with tannic acid for fully bio-based epoxy resin, RSC Adv., 2018, 8(47), 26948–26958 RSC.
- W. Li, D. Xiang, L. Wang, E. Harkin-Jones, C. Zhao, B. Wang and Y. Li, Simultaneous enhancement of electrical conductivity and interlaminar fracture toughness of carbon fiber/epoxy composites using plasma-treated conductive thermoplastic film interleaves, RSC Adv., 2018, 8(47), 26910–26921 RSC.
- A. Reghunadhan, J. Datta, N. Kalarikkal, J. T. Haponiuk and S. Thomas, Toughness augmentation by fibrillation and yielding in nanostructured blends with recycled polyurethane as a modifier, Appl. Surf. Sci., 2018, 442, 403–411 CrossRef.
- S. Fatemeh, A. Laura, P. Paola, C. Cosimo, B. Thatiane, C. M. O. Hilário, P. Concetto, S. Filippo and A. Veronica, A novel hybrid linear–hyperbranched poly(butylene adipate) copolymer as an epoxy resin modifier with toughening effect, Polym. Int., 2016, 65(3), 308–319 CrossRef.
- Z. Hao, L. Li, X. Liao, X. Sheng and Y. Zhang, Preparation and toughening performance investigation of epoxy resins containing carbon nanotubes modified with hyperbranched polyester, Polym. Bull., 2018, 75(3), 1013–1026 CrossRef.
- S. Jung-Hoon, P. B. Gangadhara and C. Alan, Effect of the addition of multi-walled carbon nanotubes on the thermomechanical properties of epoxy resin, Polym. Compos., 2017, 38(9), 1873–1880 CrossRef.
- T. Tsafack, J. M. Alred, K. E. Wise, B. Jensen, E. Siochi and B. I. Yakobson, Exploring the interface between single-walled carbon nanotubes and epoxy resin, Carbon, 2016, 105, 600–606 CrossRef.
- W. Jianqiao, G. Jian, Z. Qingjie, G. Liang, L. Hao, D. Huoying, J. Wenge, S. Gang and Y. Xiaoping, Effect of different amino functionalized carbon nanotubes on curing behavior and mechanical properties of carbon fiber/epoxy composites, Polym. Compos., 2016, 24142 Search PubMed.
- A. M. Visco, A. Pistone, V. Brancato, D. Iannazzo and M. Fazio, Mechanical and physical properties of epoxy resin based nanocomposites reinforced with polyamine functionalized carbon nanotubes, Polym. Compos., 2016, 37(4), 1007–1015 CrossRef.
- Y. Chen, S. Zhou, H. Zou and M. Liang, Investigation of cure kinetics of epoxy resin/organic montmorillonite system by differential scanning calorimetry, Polym. Sci., Ser. B, 2014, 56(5), 623–631 CrossRef.
- J. Wu, J. Guo, Q. Zhang, L. Gao, H. Li, H. Deng, W. Jiang, G. Sui and X. Yang, Effect of different amino functionalized carbon nanotubes on curing behavior and mechanical properties of carbon fiber/epoxy composites, Polym. Compos., 2018, 39(S2), E733–E744 CrossRef.
- A. Dettlaff, M. Sawczak, E. Klugmann-Radziemska, D. Czylkowski, R. Miotk and M. Wilamowska-Zawłocka, High-performance method of carbon nanotubes modification by microwave plasma for thin composite films preparation, RSC Adv., 2017, 7(51), 31940–31949 RSC.
- M. Rajabi, K. Mahanpoor and O. Moradi, Removal of dye molecules from aqueous solution by carbon nanotubes and carbon nanotube functional groups: critical review, RSC Adv., 2017, 7(74), 47083–47090 RSC.
- W. Han, X. Liao, Q. Yang, G. Li, B. He, W. Zhu and Z. Hao, Crystallization and morphological transition of poly(l-lactide)–poly(ε-caprolactone) diblock copolymers with different block length ratios, RSC Adv., 2017, 7(36), 22515–22523 RSC.
- J. Kang, J. He, Z. Chen, F. Yang, J. Chen, Y. Cao and M. Xiang, Effects of β-nucleating agent and crystallization conditions on the crystallization behavior and polymorphic composition of isotactic polypropylene/multi-walled carbon nanotubes composites, Polym. Adv. Technol., 2015, 26(1), 32–40 CrossRef.
- J. Kang, J. H. He, Z. Chen, H. Yu, J. Chen, F. Yang, Y. Cao and M. Xiang, Investigation on the crystallization behavior and polymorphic composition of isotactic polypropylene/multi-walled carbon nanotubes composites nucleated with β-nucleating agent - the role of melt structures, J. Therm. Anal. Calorim., 2015, 119(3), 1769–1780 CrossRef.
- H. Jiang, C. Li, T. Sun and J. Ma, A green and high energy density asymmetric supercapacitor based on ultrathin MnO2 nanostructures and functional mesoporous carbon nanotube electrodes, Nanoscale, 2012, 4(3), 807–812 RSC.
- Z. Hao, Y. Tan, X. Zhang and F. Zhang, Epithermal ageing mechanism of gussasphalt, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2009, 24(3), 466–470 CrossRef.
- M. R. Saeb, E. Bakhshandeh, H. A. Khonakdar, E. Mader, C. Scheffler and G. Heinrich, Cure kinetics of epoxy nanocomposites affected by MWCNTs functionalization: a review, TheScientificWorldJournal, 2013, 2013, 703708 Search PubMed.
- W. Ye, W. Li, Q. Sun, J. Yu and Q. Gao, Microwave absorption properties of lightweight and flexible carbon fiber/magnetic particle composites, RSC Adv., 2018, 8(44), 24780–24786 RSC.
- C. Yu, W. Gong, J. Zhang, W. Lv, W. Tian, X. Fan and Y. Yao, Hot pressing-induced alignment of hexagonal boron nitride in SEBS elastomer for superior thermally conductive composites, RSC Adv., 2018, 8(45), 25835–25845 RSC.
- M. Al Samman and W. Radke, Two-dimensional chromatographic separation of branched polyesters according to degree of branching and molar mass, Polymer, 2016, 99, 734–740 CrossRef.
- R. d'Arcy, J. Burke and N. Tirelli, Branched polyesters: Preparative strategies and applications, Adv. Drug Delivery Rev., 2016, 107, 60–81 CrossRef PubMed.
- J. Zhang and C. P. Hu, Synthesis, characterization and mechanical properties of polyester-based aliphatic polyurethane elastomers containing hyperbranched polyester segments, Eur. Polym. J., 2008, 44(11), 3708–3714 CrossRef.
- J. Wang, R. Xu, F. Yang, J. Kang, Y. Cao and M. Xiang, Probing influences of support layer on the morphology of polyamide selective layer of thin film composite membrane, J. Membr. Sci., 2018, 556, 374–383 CrossRef.
- R. Xu, G. Xu, J. Wang, J. Chen, F. Yang, J. Kang and M. Xiang, Influence of l-lysine on the permeation and antifouling performance of polyamide thin film composite reverse osmosis membranes, RSC Adv., 2018, 8(44), 25236–25247 RSC.
- B. Xiong, R. Chen, F. Zeng, J. Kang and Y. Men, Thermal shrinkage and microscopic shutdown mechanism of polypropylene separator for lithium-ion battery: In-situ ultra-small angle X-ray scattering study, J. Membr. Sci., 2018, 545, 213–220 CrossRef.
- B. Xiong, J. Kang, R. Chen and Y. Men, Initiation of cavitation upon drawing of pre-oriented polypropylene film: in situ SAXS and WAXD studies, Polymer, 2017, 128, 57–64 CrossRef.
- W. J. Choi, R. L. Powell and D. S. Kim, Curing behavior and properties of epoxy nanocomposites with amine functionalized multiwall carbon nanotubes, Polym. Compos., 2009, 30(4), 415–421 CrossRef.
- K. Yang, M. Gu and Y. Jin, Cure behavior and thermal stability analysis of multiwalled carbon nanotube/epoxy resin nanocomposites, J. Appl. Polym. Sci., 2008, 110(5), 2980–2988 CrossRef.
- S. Kumar, S. K. Samal, S. Mohanty and S. K. Nayak, Study of curing kinetics of anhydride cured petroleum-based (DGEBA) epoxy resin and renewable resource based epoxidized soybean oil (ESO) systems catalyzed by 2-methylimidazole, Thermochim. Acta, 2017, 654, 112–120 CrossRef.
- A. Moroni, J. Mijovic, E. M. Pearce and C. C. Foun, Cure kinetics of epoxy resins and aromatic diamines, J. Appl. Polym. Sci., 1986, 32(2), 3761–3773 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |