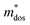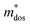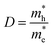DOI:
10.1039/C8RA04569K
(Paper)
RSC Adv., 2018,
8, 32317-32324
Group-IVA element-doped SrIn2O4 as potential materials for hydrogen production from water splitting with solar energy
Received
29th May 2018
, Accepted 4th September 2018
First published on 18th September 2018
Abstract
Band gap engineering can efficiently improve the photocatalytic activity of semiconductors for hydrogen generation from water splitting. Herein, we present a comprehensive investigation on the geometrical structures, electronic, optical, and potential photocatalytic properties and charge carrier mobility of pristine and group-IVA element-doped SrIn2O4 using first-principles density functional theory with the meta-GGA+MBJ potential. The calculated formation energies are moderate, indicating that the synthesis of the doped structures is experimentally feasible. In addition, the energy band gaps of the group-IVA element-doped SrIn2O4 range from 1.67 to 3.07 eV, which satisfy the requirements for photocatalytic water splitting, except for that of the Si mono-doped structure. Based on the deformation potential theory, a high charge carrier mobility of 2093 cm2 V−1 s−1 is obtained for the pristine SrIn2O4 and those of the doped-structures are also large, although a decrease in the values of some are observed. The optical absorption coefficient of the doped structures in the near ultraviolet (UV) and visible light range significantly increases. Therefore, group-IVA element-doped SrIn2O4 are potential candidates as photocatalysts for hydrogen generation from water splitting driven by visible light.
1. Introduction
Hydrogen is considered as one of the future fuels, and thus has attracted increasing attention as renewable and clean energy.1–4 The conversion of solar energy into hydrogen by a photocatalyst via water splitting is an attractive technology, which can efficiently reduce the severe environment and energy issues.5–7 Photocatalytic water splitting is regarded as artificial photosynthesis, which involves three main steps: (i) absorption of photons with equivalent or greater energy than the band gap of the semiconductor photocatalyst, where electrons are excited from the valence band to the conduction band, leading to the generation of electron–hole pairs. (ii) The photoexcited carriers migrate to the surface of the photocatalyst. (iii) The separated photoexcited carriers reduce H+ to produce H2 and oxidize H2O to produce O2.8 Generally, only water, solar energy, and photocatalyst are needed for photocatalytic water splitting, where solar energy is inexhaustible and water is one of the most abundant resources on earth. Therefore, the key factor to achieve efficient photocatalytic water splitting is the development of suitable photocatalysts. Since the photocatalytic production of hydrogen from water splitting by TiO2 was reported in 1972,9 much effort has been dedicated to improving the hydrogen production efficiency.10 In recent years, the integration of atomic dopants has been confirmed to be an important approach for improving the efficiency of photocatalytic water splitting.11 Doping can efficiently enhance the photocatalytic performance by extending the absorption edge of semiconductors to a lower energy range. For example, Mg-doped anatase TiO2 had been synthesized successfully by Gao et al.12 They found that the absorption coefficient of TiO2 increased with an increase in the Mg doping concentration. Highly efficient photocatalytic water splitting was achieved on Pt-embellished 0.5% Mg–TiO2, and the hydrogen evolution reached as high as 850 μmol g−1 h−1. Also, metal ion (Nb, Cr, Cu, and Ni) and nitrogen (N) co-doped TiO2 photocatalysts were synthesized by Lin et al.,13 and they found that the significant photocatalytic enhancement of the Cu, N co-doped TiO2 was attributed to the enhanced visible light absorption. Similarly, Cu-doped ZnS microspheres were prepared via microwave hydrothermal method by Lee et al.14 They reported that the absorption coefficient of ZnS in the visible light range was significantly enhanced with the introduction of Cu dopant, and the hydrogen evolution rate reached as high as 973.1 μmol g−1 h−1 under ZnS with 2 mol% Cu dopant.
Two groups of elements can act as active components in photocatalytic water splitting.15 Photocatalysts with a d0 or d10 electronic configuration generally present a better photo-response than that with partially filled d orbitals. As one of the p-block metal oxides with a d10 electronic configuration, SrIn2O4 has been reported to exhibit stable and high photocatalytic activity for water splitting.16 However, its energy band gap is 3.6 eV,17 indicating that it only responds to ultraviolet (UV) light, which is only about 7% of solar energy.18 Therefore, SrIn2O4 photocatalytic water splitting cannot efficiently utilize solar energy. Also, its rate of hydrogen formation is only about 7 μmol g−1 h−1, which is much smaller than that of TiO2 (106 μmol g−1 h−1).19,20 Considering that band gap engineering is an effective method to extend the absorption edge of photocatalysts to the visible light range, there are several reports on cation/anion doped SrIn2O4 to efficiently use solar energy.21–24 For example, Dy3+/Pr3+/Tb3+-doped SrIn2O4 was successfully prepared by Liu et al.25 They found that SrIn2O4:Dy3+/Pr3+/Tb3+ exhibited stronger near white, red and green luminescence, which results from the efficient energy transfer from the host lattice to the dopants. Additionally, Eu3+, Sm3+-doped SrIn2O4 was successfully synthesized by Li et al.26 through a combustion method. They found that Sm3+-doped SrIn2O4 effectively extended and strengthened the absorption range from 400 to 405 nm.
However, to the best of our knowledge, there are no experimental or theoretical investigations on group-IVA element-doped SrIn2O4. Therefore, we comprehensively investigate the electronic, optical, and potential photocatalytic properties and carrier mobility (μ) for pristine and IVA-doped SrIn2O4 to understand the influence of the dopants on the photocatalytic properties of SrIn2O4 for water splitting. A high μ is observed for the pristine SrIn2O4, which implies that the carriers can transfer to its surface efficiently in the process of photocatalytic water splitting. The absorption coefficient of SrIn2O4 in the visible light range is significantly enhanced with the introduction of the dopants, and the mechanism is explored in accordance with the total density of states (TDOS) and partial density of states (PDOS). The results obtained are beneficial for the design of new photocatalytic materials driven by visible light.
2. Computational details
In this study, a 2 × 2 × 2 supercell of SrIn2O4 with the space group Pnam belonging to orthorhombic symmetry, containing 8 Sr atoms, 16 In atoms and 32 O atoms, was constructed. The IVA-doped structures were built by substituting the Sr atom with IVA atoms, which correspond to a doping molar concentration of 1.5%. Hereafter, the doped structures are denoted as C@Sr, Si@Sr, Ge@Sr, Sn@Sr, and Pb@Sr. In the present study, all the density functional theory (DFT) simulations were carried out using the Vienna Ab initio simulation package (VASP).27 The projector augmented wave (PAW) potential28 was used to describe the ion–electron interactions, which means that 2s22p4 for O, 4d105s2 for Sr, 5s25p1 for In, 2s22p2 for C, 3s23p2 for Si, 4s24p2 for Ge, 5s25p2 for Sn and 6s26p2 for Pb were treated as valence electrons. The electron exchange-correlation functional was treated as the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) parametrization for structural optimization.29 All the atomic positions were fully relaxed until the residual forces and energy convergence were less than 0.01 eV Å−1 and 10−6 eV, respectively. The plane-wave cutoff kinetic energy was set as 450 eV throughout the calculation. For the geometry optimization and electronic properties calculation, Monkhorst–Pack k-point grids of 3 × 3 × 5 and 5 × 5 × 7 were used. The meta-GGA+MBJ potential30 was used to obtain credible calculations for the energy gap and optical absorption coefficient.
To confirm the validity of the present calculational results, we performed additional calculations for CaIn2O4/GaN/GaAs/ZnS and C/Pb-doped ZnS, which were synthesized experimentally. For the pristine structures, we investigated the geometrical structures and energy band gaps of CaIn2O4, GaN, and GaAs, as listed in Table 1. The results from Table 1 show that the lattice parameters of CaIn2O4 are a = 9.735, b = 11.389 and c = 3.249 Å, which are slightly larger than the experimental values.31 The calculated energy band gap of CaIn2O4 is 3.67 eV, which is also close to the experimental value31 and that of GaN and GaAs,32–35 indicating that the present theoretical level is rational for the pristine structure. For the doped structure, we investigated the energy band gap of C, Pb-doped ZnS. The results from Table 2 show that the parameters and energy band gaps of the pristine ZnS are almost close to that obtained in the previous works,36,37 whereas, the calculated energy band gaps of C, Pb-doped ZnS are 0.3 eV smaller than the experimental value.38,39 However, it is still acceptable for us. In addition, the carrier mobility of GaAs was also investigated. The results in Table 3 demostrate that the calculated carrier mobility of the pristine GaAs is 0.594 m2 V−1 s−1, which is in good agreement with the experimental values.40 All of these results indicate that the present theoretical level is rational and that the results for SrIn2O4 herein are credible.
Table 1 Calculated lattice parameters a, b, and c (Å), and energy band gaps, Eg (eV), for the experimentally synthesized semiconductors
Table 2 Calculated lattice parameters a, b, and c (Å), and energy band gaps, Eg (eV), for the pristine and C/Pb doped ZnS
| |
a = b = c |
Eg |
| Pristine |
5.436 |
3.57 eV |
| 5.412 (ref. 36) |
3.70 eV (ref. 37) |
| C@ZnS |
5.422 |
2.25 eV |
| — |
1.95 eV (ref. 38) |
| Pb@ZnS |
5.480 |
2.59 eV |
| — |
2.30 eV (ref. 39) |
Table 3 Calculated carrier mobility, μ (m2 V−1 s−1), for GaAs
| |
Type |
Cβ |
Eβ |
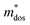
|
μ |
| Pristine |
Electron |
0.65 |
16.68 |
0.11 |
0.594 |
| — |
— |
— |
0.700 (ref. 40) |
3. Results and discussion
3.1 Geometrical structures and energy stability of SrIn2O4
The optimized structure of Sn@Sr in Fig. 1 is used to represent the IVA-doped SrIn2O4 structures and the others are omitted for brevity. The optimized lattice parameters of the pristine and doped SrIn2O4 are presented in Table 4. The calculated lattice parameters of the pristine SrIn2O4 are a = 9.906, b = 11.602 and c = 3.305 Å, which are in great agreement with the previous works.26,41 For the doped structures, all the changes in the lattice parameters are less than 0.1 Å compared to that of the pristine structure, which means that the dopants did not lead to significant deformation of the lattice.
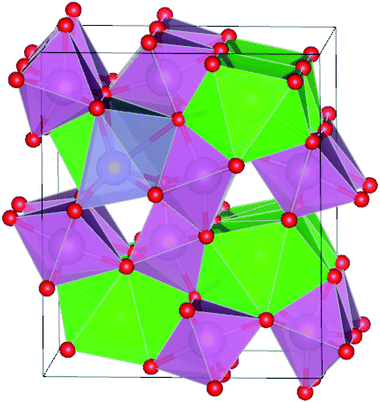 |
| | Fig. 1 Optimized structure of Sn@Sr. The green, purple, red and gray spheres represent the Sr, In, O, and Sn elements, respectively. | |
Table 4 Calculated lattice parameters a, b, and c (Å), energy band gaps Eg (eV), formation energies Eform (eV) and electronegativity χ (eV) for SrIn2O4
| |
Lattice parameters |
Eg |
Eform |
χ |
| a |
b |
c |
| Pristine |
9.906 |
11.602 |
3.305 |
3.61 eV |
— |
4.84 |
| 9.830 (ref. 24) |
11.496 (ref. 24) |
3.269 (ref. 24) |
3.60 eV (ref. 17) |
| 9.809 (ref. 29) |
11.449 (ref. 29) |
3.265 (ref. 29) |
|
| C@Sr |
10.006 |
11.578 |
3.306 |
1.67 eV |
4.92 |
4.94 |
| Si@Sr |
9.994 |
11.586 |
3.303 |
1.32 eV |
4.40 |
4.91 |
| Ge@Sr |
9.954 |
11.586 |
3.297 |
2.64 eV |
6.14 |
4.91 |
| Sn@Sr |
9.926 |
11.616 |
3.302 |
2.31 eV |
6.62 |
4.91 |
| Pb@Sr |
9.920 |
11.620 |
3.305 |
3.07 eV |
6.74 |
4.90 |
To evaluate the feasibility of the synthesis of the doped SrIn2O4, the formation energy (Eform) was calculated as follows:42
| | |
Eform = E(doped) − E(pristine) − nμX + nμSr
| (1) |
where,
E(doped) and
E(pristine) are the total energy of the doped and pristine SrIn
2O
4, respectively.
μX and
μSr represent the chemical potential of the dopants and Sr atom, respectively. The calculated
Eform of the doped structures are collected in
Table 4. The results demonstrate that the
Eform of the doped structures are in the range of 4.40 to 6.74 eV, which is acceptable for their general synthesis.
3.2 Photocatalytic water splitting and band engineering
The calculated energy band gaps (Eg) of all the structures are listed in Table 4. The Eg of 3.61 eV for the pristine SrIn2O4 is close to the experimental value,17 which signifies that the present theoretical level is credible. However, it is too large to respond to visible light. Thus, band gap engineering of the electronic properties of SrIn2O4 is necessary. Fortunately, the results in Table 4 demonstrate that the Eg of SrIn2O4 significantly decreased with the introduction of IVA elements, especially for C@Sr and Si@Sr. However, one can find from Table 4 that the change tendency of the energy band gaps for the doped structures is not singlet, which is similar to the case of IVA-doped ZnS.43 The change tendency of the ionization energy of IVA elements is responsible for the characteristic of the energy band gaps. For examples, the ionization energy of Si is smallest and that of Pb is the largest, which results in the smallest Eg of Si@Sr and the largest Eg of Pb@Sr among the doped structures, respectively. The Egs of the doped structures are in the range from 1.32 eV to 3.07 eV, implied that all the doped structures can respond to the visible light. The Eg for photocatalytic water splitting should be higher than 1.23 eV considering the minimum potential for water splitting is 1.23 eV, while an Eg smaller than 3.0 eV means that the photocatalytic water splitting reaction can be efficiently driven by visible light.44 Moreover, the suitable band edge position of a semiconductor is also indispensable for photocatalytic water splitting. The valence band maximum (VBM) of a photocatalyst must be lower than the oxidation potential (VO2/H2O = −5.67 eV) so that it can be used for oxygen production, while its conduction band minimum (CBM) must be higher than the reduction potential (VH2/H+ = −4.44 eV) for hydrogen production.45 The VBMs and CBMs of the present structures can be calculated from the following equations:46| |
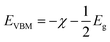 | (2) |
| |
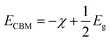 | (3) |
where, χ is the Mulliken electronegativity value of the compound and Eg is the energy band gap of the structure. The electronegativity can be determined using the following equation:47| |
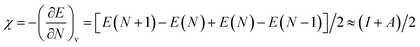 | (4) |
where, I is the ionization energy and A is the electron affinity of the atom. Using eqn (4), the electronegativities of Sr, In, O, C, Si, Ge, Sn, and Pb were calculated. The Mulliken electronegativity of a compound can be considered as the electronegativity of its constituent atoms, which corresponds to the following equation:48| | |
χ(compound) = χa1χb2…χcn
| (5) |
where, χ1, χ2 and χn represent the electronegativities of the atoms in the compound, and a, b, and c are the molar fractions of the atoms. The electronegativities of the pristine and doped SrIn2O4 were calculated based on eqn (5), and the results are listed in Table 4. The results reveal that the electronegativities of the doped structures are larger than that of the pristine structure, which can be understood from the fact that the electronegativities of IVA elements are larger than that of the Sr atom. As a result, the reductive ability of the doped structures is stronger than that of the pristine structure. Base on eqn (2)–(5), the calculated absolute CBMs and VBMs of the pristine and doped SrIn2O4 are shown in Fig. 2. This figure shows that the CBM of the pristine SrIn2O4 is −3.04 eV, which is more positive than the reduction potential VH2/H+, and the VBM is more negative than the oxidation potential VO2/H2O, indicating that it can be used for hydrogen production from water splitting. It can also be observed that the CBMs and VBMs of the IVA-doped structures shift toward the potential of the water oxidation and reduction reactions in Fig. 2. Fortunately, all the CBMs and VBMs except that of Si@Sr satisfy the requirements for the water splitting reaction. Therefore, the pristine SrIn2O4 and the C@Sr, Ge@Sr, Sn@Sr and Pb@Sr structures are favorable for photocatalytic water splitting.
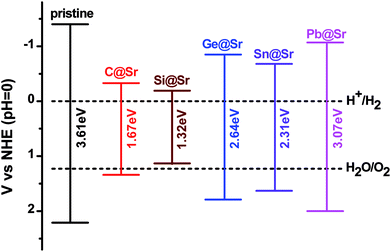 |
| | Fig. 2 Absolute VBM and CBM energy levels relative to the NHE potential for the pristine and doped SrIn2O4. | |
3.3 Enhancement of absorption coefficient of IVA-doped SrIn2O4
Enhancement of the absorption coefficient of SrIn2O4 in the visible light range can promote the full use of solar energy to produce hydrogen from photocatalytic water splitting. Thus, to evaluate the absorption coefficient of SrIn2O4, its complex dielectric function was first calculated. The details of the calculation of the complex dielectric function can be found in the previous literature49 and is thus omitted here for brevity. The results are plotted in Fig. 3, which shows that the imaginary part ε2(ω) of the dielectric function of the pristine SrIn2O4 is close to zero in the visible and infrared light range. Nevertheless, a significant red-shift of ε2(ω) was observed when SrIn2O4 is doped with IVA elements, especially for C@Sr and Si@Sr.
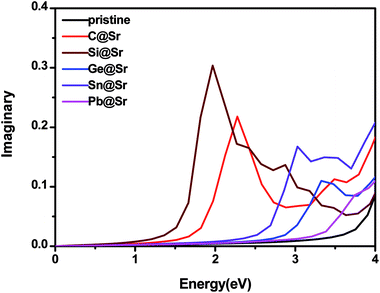 |
| | Fig. 3 Imaginary part of the dielectric function of the pristine and doped SrIn2O4. | |
The optical absorption properties can be deduced from the complex dielectric function according to the following expression:50
| |
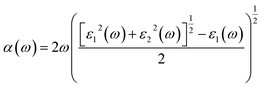 | (6) |
where,
α is the optical absorption coefficient.
Fig. 4 shows the absorption coefficient of the pristine and doped SrIn
2O
4. The results reveal that the pristine SrIn
2O
4 shows no significant absorption in the visible light range, which is in agreement with the previous works.
51 Therefore, the pristine SrIn
2O
4 does not respond to visible light, and as a result, its photocatalytic efficiency using solar energy is low. Nevertheless, significant red-shifts due to absorption are identified for the IVA-doped structures, especially for C@Sr, Si@Sr, and Ge@Sr, where a significant enhancement in absorption in the visible light range is observed. This indicates that these structures are preferable to the pristine structure to capture solar energy in the photocatalytic water splitting reaction.
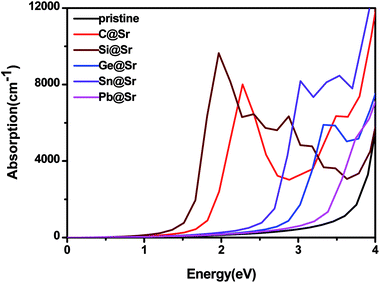 |
| | Fig. 4 Absorption coefficient of the pristine and doped SrIn2O4. | |
3.4 Density of states and partial density of states
To understand the origin of the visible light absorption of the IVA-doped structures, their TDOS and PDOS were calculated, as shown in Fig. 5 and 6, respectively. Fig. 5 shows new energy levels resulting from the doped IVA elements in the band gap of the pristine structure, which are responsible for the reduction in the energy band gap of the doped structures. The effect of the dopants on PDOS of SrIn2O4 is demonstrated in Fig. 6. Fig. 6a shows that VBM of the pristine SrIn2O4 is mainly dominated by O 2p states with a small number of 4p, 4d and 5s states of Sr as well as 4d states of In, while its CBM is mainly dominated by 5s states of In with a small number of 5s states of Sr, as well as 2s and 2p states of O. However, a new additional donor energy level mainly comprising of p states from the dopant is observed in the band gap of SrIn2O4 after the IVA doping. Specifically, the electron transfer from the p states of the dopants to the 5s states of In is responsible for the significant enhancement in the absorption of the doped SrIn2O4 in the visible light range. Moreover, the energy of the CBM for the doped structures remained unchanged although the components are changed compared to that of the pristine structure.
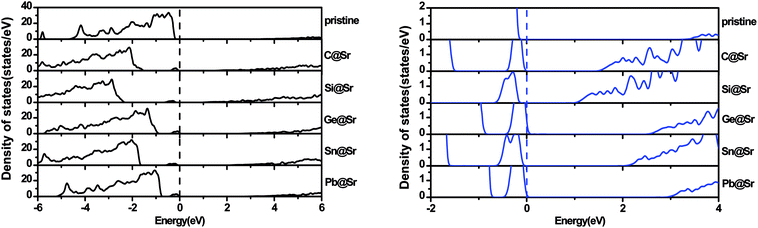 |
| | Fig. 5 Total density of states for the pristine and doped SrIn2O4. | |
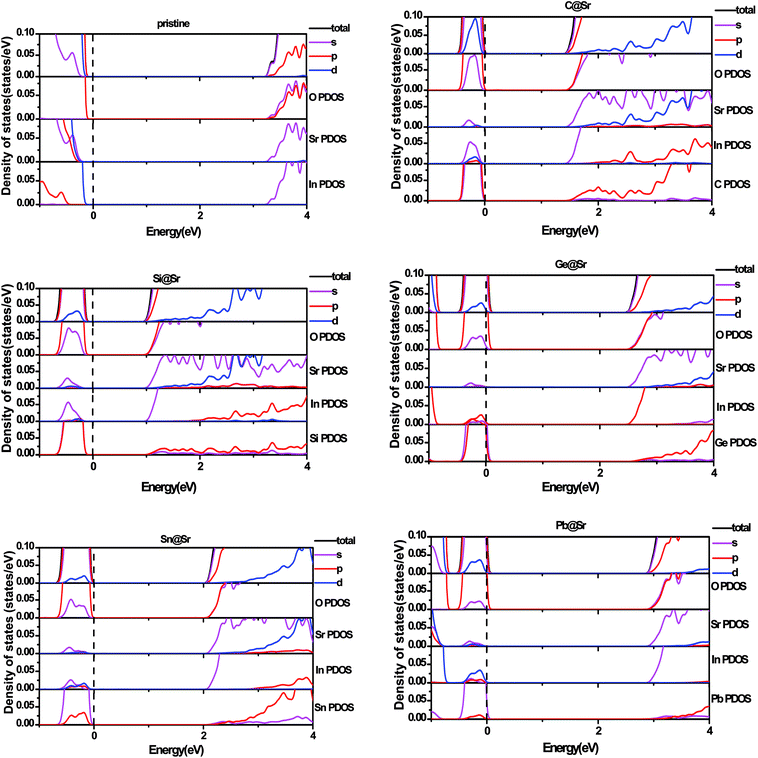 |
| | Fig. 6 Partial density of states for pristine and doped SrIn2O4. | |
3.5 Effective mass and carrier mobility
The efficient separation of charge carriers and high mobility μ significantly impact the efficiency of photocatalytic water splitting. Thus, μ and relative ratio (D) between the effective mass of electrons 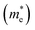 and holes
and holes 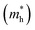 for the pristine and doped SrIn2O4 were calculated considering the relaxation time (τ) as follows:52
for the pristine and doped SrIn2O4 were calculated considering the relaxation time (τ) as follows:52| |
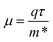 | (7) |
where, q is the carrier charge and m* is the effective mass of the charge carriers. τ can be calculated depending on the detailed scattering mechanisms. For a three-dimensional system, τ along the β-direction at temperature T can be expressed as follows:53| |
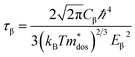 | (8) |
where, ℏ represents the reduced Planck constant and kB stands for the Boltzmann constant. Cβ is the elastic constant, which can be calculated as 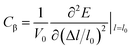 , where, E is the total energy of the structure, l0 is the lattice constant along the β-direction, Δl = l − l0 is the corresponding lattice distortion, and V0 is the equilibrium volume of the unit cell. The deformation potential constant Eβ is calculated by
, where, E is the total energy of the structure, l0 is the lattice constant along the β-direction, Δl = l − l0 is the corresponding lattice distortion, and V0 is the equilibrium volume of the unit cell. The deformation potential constant Eβ is calculated by 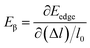 , where, Eedge is the energy level of the electrons in the CBM and holes in the VBM. The density-of-states effective mass
, where, Eedge is the energy level of the electrons in the CBM and holes in the VBM. The density-of-states effective mass 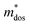 is given by
is given by 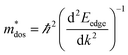 . The calculated Cβs, Eβs,
. The calculated Cβs, Eβs, 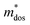 and μs of the pristine and doped SrIn2O4 are summarized in Table 5. A larger μ represents a higher migration rate of photogenerated charge carriers, which leads to charge carriers quickly reaching the surface of the materials to drive the redox reaction for hydrogen and oxygen production. The results in Table 5 reveal that the calculated μ of the electrons in the pristine SrIn2O4 is 2093.00 cm2 V−1 s−1, while that of the holes is only about 0.97 cm2 V−1 s−1, indicating that the separation of electrons and the holes is significant. Therefore, the pristine SrIn2O4 is beneficial for water splitting. Moreover, the μ of the electrons in the doped structures is higher than that of other effective photocatalytic materials, such as MoS2 (200 cm2 V−1 s−1),54 although it significantly decreases compared with that of the pristine structure. As a result, IVA-doped SrIn2O4 also exhibits efficient photocatalytic behavior theoretically.
and μs of the pristine and doped SrIn2O4 are summarized in Table 5. A larger μ represents a higher migration rate of photogenerated charge carriers, which leads to charge carriers quickly reaching the surface of the materials to drive the redox reaction for hydrogen and oxygen production. The results in Table 5 reveal that the calculated μ of the electrons in the pristine SrIn2O4 is 2093.00 cm2 V−1 s−1, while that of the holes is only about 0.97 cm2 V−1 s−1, indicating that the separation of electrons and the holes is significant. Therefore, the pristine SrIn2O4 is beneficial for water splitting. Moreover, the μ of the electrons in the doped structures is higher than that of other effective photocatalytic materials, such as MoS2 (200 cm2 V−1 s−1),54 although it significantly decreases compared with that of the pristine structure. As a result, IVA-doped SrIn2O4 also exhibits efficient photocatalytic behavior theoretically.
Table 5 Calculated elastic constant Cβ (N m−1), deformation potential constant Eβ (eV), density-of-states effective mass 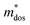 , relaxation time τ (fs) and carrier mobility μ (cm2 V−1 s−1) for SrIn2O4
, relaxation time τ (fs) and carrier mobility μ (cm2 V−1 s−1) for SrIn2O4
| |
Type |
Cβ |
Eβ |
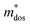
|
μ |
D |
| Pristine |
Electron |
1.55 |
16.15 |
0.24 |
2093.00 |
27.83 |
| Hole |
|
11.61 |
6.68 |
0.97 |
|
| C@Sr |
Electron |
1.53 |
14.80 |
0.59 |
250.98 |
19.34 |
| Hole |
|
13.08 |
11.41 |
0.20 |
|
| Si@Sr |
Electron |
1.51 |
15.56 |
0.90 |
79.37 |
8.16 |
| Hole |
|
13.82 |
7.34 |
0.53 |
|
| Ge@Sr |
Electron |
1.54 |
16.12 |
0.29 |
1214.70 |
17.28 |
| Hole |
|
13.19 |
5.01 |
1.54 |
|
| Sn@Sr |
Electron |
1.52 |
16.49 |
0.47 |
353.02 |
5.68 |
| Hole |
|
14.11 |
2.67 |
6.43 |
|
| Pb@Sr |
Electron |
1.53 |
16.35 |
0.37 |
674.00 |
7.62 |
| Hole |
|
13.17 |
2.82 |
6.49 |
|
The recombination of electrons and holes is one of the factors that limits the photoactivity of a semiconductor. Thus, to further analyze the recombination rate of electrons and holes, the relative ratio (D) between the effective mass of electrons 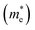 and holes
and holes 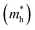 was calculated according to the following expression:55
was calculated according to the following expression:55
A high value of D is related to a great distinction between the mobility of electrons and holes, which reduces the probability of their recombination. The absolute D values of the pristine and doped SrIn2O4 are listed in Table 5. Evidently, the D value of 27.83 for the pristine SrIn2O4 implies the efficient separation of photogenerated charge carriers. The D values of the doped structures show a slight decrease; however, they are still several times higher than that of many typical photocatalytic materials, such as TiO2 (0.97),56 BiVO4 (1.42),57 and WS2 (1.36).57 Therefore, both the pristine and IVA-doped SrIn2O4 are efficient photocatalysts with satisfactory photogenerated charge carrier recombination rates.
4. Conclusion
The feasibility and properties of IVA-doped SrIn2O4 as photocatalysts for hydrogen production from water splitting were investigated. The geometrical, electronic and optical properties and carrier mobilities of all the considered structures were calculated using first-principles DFT with the meta-GGA+MBJ potential. The energy levels of the CBM and VBM for all the structures except for Si@Sr satisfy the requirements of photocatalytic water splitting, although the Eg of the doped structures decreased by 1.94, 2.29, 0.97, 1.30 and 0.54 eV in comparison with that of the pristine structure. Moreover, the absorption coefficients in the visible light range are significantly enhanced, especially for the C@Sr, Si@Sr and Ge@Sr structures, which indicates that the photocatalytic water splitting by C@Sr and Ge@Sr can be efficiently driven by solar energy. The TDOS and PDOS of these structures demonstrate that the new additional donor energy levels mainly comprising of the p states of the dopants are responsible for the reduction in energy band gap and enhancement of absorption coefficient in the visible light range. In addition, a high carrier mobility and efficient separation of photogenerated charge carriers are observed for both the pristine and doped structures, which lead to efficient photocatalytic performances. Therefore, we predict that C@Sr and Ge@Sr are the most promising candidates as photocatalysts for hydrogen production from water splitting driven by visible light.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. NSFC-11374132 and NSFC-11574125, as well as the Taishan Scholars Project of Shandong Province (ts201511055).
References
- F. J. López-Tenlladoa, J. Hidalgo-Carrilloa, V. Montesa, A. Marinasa, F. J. Urbanoa, J. M. Marinasa, L. Ilievab, T. Tabakovab and F. Reida, Catal. Today, 2017, 280, 58–64 CrossRef.
- K. N. Li, C. L. Yang, Y. X. Han, M. S. Wang and L. Z. Wang, Energy, 2016, 106, 131–136 CrossRef.
- B. C. Qiu, Q. H. Zhu, M. M. Du, L. G. Fan, M. Y. Xing and J. L. Zhang, Angew. Chem., 2017, 129, 2728–2732 CrossRef.
- H. C. Huang, C. L. Yang, M. S. Wang and X. G. Ma, Int. J. Hydrog. Energy, 2017, 42, 15464–15470 CrossRef.
- B. H. Wu, D. Y. Liu, S. Mubeen, T. T. Chuong, M. Moskovits and G. D. Stucky, J. Am. Chem. Soc., 2016, 138, 1114–1117 CrossRef PubMed.
- Z. K. He, J. W. Fu, B. Cheng, J. G. Yu and S. W. Cao, Appl. Catal. B., 2017, 205, 104–111 CrossRef.
- A. Carrero, A. J. Vizcaíno, J. A. Calles and L. García-Moreno, J. Energy Chem., 2017, 26, 42–48 CrossRef.
- K. Maeda, J. Photochem. Photobiol., C, 2011, 12, 237–268 CrossRef.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef PubMed.
- K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef.
- B. C. Zhu, J. F. Zhang, C. J. Jiang, B. Cheng and J. G. Yu, Appl. Catal. B., 2017, 207, 27–34 CrossRef.
- L. J. Gao, Y. G. Li, J. B. Ren, S. F. Wang, R. N. Wang, G. S. Fu and Y. Hu, Appl. Catal. B., 2017, 202, 127–133 CrossRef.
- H. Lin and C. Shih, J. Mol. Catal. A: Chem., 2016, 411, 128–137 CrossRef.
- G. J. Lee, S. Anandan, S. J. Masten and J. J. Wu, Renewable Energy, 2016, 89, 18–26 CrossRef.
- K. Maeda, J. Photochem. Photobiol., C, 2011, 12, 237–268 CrossRef.
- J. Sato, N. Saito, H. Nishiyama and Y. Inoue, Chem. Lett., 2001, 30, 868–869 CrossRef.
- A. Baszczuk, M. Jasiorski, M. Nyk, J. Hanuza, M. Mączka and W. Stręka, J. Alloys Compd., 2005, 394, 88–92 CrossRef.
- X. Li, Z. Li and J. Yang, Phys. Rev. Lett., 2014, 112, 018301 CrossRef PubMed.
- S. Tabata, N. Nishida, Y. Masaki and K. Tabata, Catal. Lett., 1995, 34, 245 CrossRef.
- J. Sato, N. Saito, H. Nishiyama and Y. Inoue, J. Phys. Chem. B, 2001, 105, 6061 CrossRef.
- M. Guan, H. Zheng, L. F. Mei, M. S. Molokeev, J. Xie, T. Yang, X. W. Wu, S. F. Huang and Z. H. Huang, J. Am. Ceram. Soc., 2015, 98, 1182–1187 CrossRef.
- F. S. Kao, Mater. Chem. Phys., 2002, 76, 295–298 CrossRef.
- Y. P. Kang, B. Thuy, Y. Shimokawa, T. Hayakawa, S. Sakaida, L. Miao, S. Tanemura, S. Honda and Y. Iwamoto, J. Lumin., 2016, 169, 78–85 CrossRef.
- M. Guan, H. Zheng, L. F. Mei, Z. H. Huang, T. Yang, M. H. Fang and Y. G. Liu, Infrared Phys. Technol., 2014, 67, 107–110 CrossRef.
- X. M. Liu, C. K. Lin, Y. Luo and J. Lin, J. Electrochem. Soc., 2007, 154, J21–J27 CrossRef.
- P. Li, Z. J. Wang, Z. P. Yang and Q. L. Guo, J. Electrochem. Soc., 2011, 158, H1201–H1205 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- J. A. Camargo-Martínez and R. Baquero, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195106 CrossRef.
- S. E. Dali, V. S. Sundar, M. Jayachandran, M. Jayachandran and M. J. Chockalingam, J. Mater. Sci. Lett., 1998, 17, 619–623 CrossRef.
- J. H. Edgar, Properties of Group III Nitrides, Institution of Electrical Engineers, 1994 Search PubMed.
- N. Fu, E. Li, Z. Cui, D. Ma, W. Wang, Y. L. Zhang, S. Song and J. Lin, J. Alloys Compd., 2014, 596, 92–97 CrossRef.
- J. Black and P. Lublin, J. Appl. Phys., 1964, 35, 2462–2467 CrossRef.
- D. C. Kim, D. L. Dheeraj, B. O. Fimland and H. Weman, Appl. Phys. Lett., 2013, 102, 142107 CrossRef.
- S. Ves, U. Schwarz, N. E. Christensen, K. Syassen and M. Cardona, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9113 CrossRef.
- D. Denzler, M. Olschewski and K. Sattler, J. Appl. Phys., 1998, 84, 2841–2845 CrossRef.
- M. Muruganandham and Y. Kusumoto, J. Phys. Chem. C, 2009, 113, 16144–16150 CrossRef.
- I. Tsuji and A. Kudo, J. Photochem. Photobiol., A, 2003, 156, 249–252 CrossRef.
- H. J. Joyce, C. J. Docherty, Q. Gao, H. H. Tan, C. Jagadish, J. Lloyd-Hughes, L. M. Herz and M. B. Johnston, Nanotechnology, 2013, 24, 214006 CrossRef PubMed.
- V. R. Von Schenck and H. Muller-Buschbaum, Z. Anorg. Allg. Chem., 1973, 398, 24–30 CrossRef.
- X. Y. Jiang, C. L. Yang, Y. X. Han, M. S. Wang and X. G. Ma, Mater. Chem. Phys., 2016, 183, 349–355 CrossRef.
- H. C. Huang, C. L. Yang, M. S. Wang and X. G. Ma, Renewable Energy, 2018, 117, 22–27 CrossRef.
- F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, ChemistrySelect, 2017, 2, 6304–6316 CrossRef.
- J. Liu, X. B. Li, D. Wang, H. Liu, P. Peng and L. M. Liu, J. Mater. Chem. A, 2014, 2, 6755–6761 RSC.
- Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543–556 CrossRef.
- M. V. Putz, N. Russo and E. Sicilia, Theor. Chem. Acc., 2005, 114, 38–45 Search PubMed.
- Y. Xu and M. A. A. Schoonen, Am. Mineral., 2000, 85, 543–556 CrossRef.
- H. C. Huang, C. L. Yang, M. S. Wang and X. G. Ma, Sol. Energy Mater. Sol. Cells, 2017, 170, 233–238 CrossRef.
- Y. M. Lin, Z. Y. Jiang, C. Y. Zhu, X. Y. Hu, H. Y. Zhu, X. D. Zhang, J. Fan and S. H. Lin, Int. J. Hydrog. Energy, 2013, 38, 5209–5214 CrossRef.
- S. B. Kokane, S. D. Sartale, C. A. Betty and R. Sasikala, RSC Adv., 2014, 4, 55539–55547 RSC.
- M. Nolan and S. D. Elliott, Phys. Chem. Chem. Phys., 2006, 8, 5350–5358 RSC.
- Q. Y. Xue, H. J. Liu, D. D. Fan, L. Cheng, B. Y. Zhao and J. Shi, Phys. Chem. Chem. Phys., 2016, 18, 17912–17916 RSC.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef PubMed.
- H. Zhang, L. Liu and Z. Zhou, RSC Adv., 2012, 2, 9224–9229 RSC.
- F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, Int. J. Quantum Chem., 2018, 118, e25505 CrossRef.
- F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, New J. Chem., 2017, 41, 11701–11713 RSC.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Mei-Shan Wanga,
Xiao-Guang Maa and
You-Gen Yib
*a,
Mei-Shan Wanga,
Xiao-Guang Maa and
You-Gen Yib

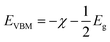
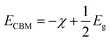
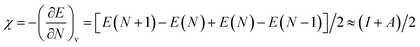

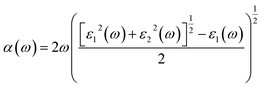
 and holes
and holes 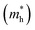 for the pristine and doped SrIn2O4 were calculated considering the relaxation time (τ) as follows:52
for the pristine and doped SrIn2O4 were calculated considering the relaxation time (τ) as follows:52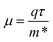
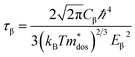
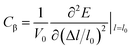 , where, E is the total energy of the structure, l0 is the lattice constant along the β-direction, Δl = l − l0 is the corresponding lattice distortion, and V0 is the equilibrium volume of the unit cell. The deformation potential constant Eβ is calculated by
, where, E is the total energy of the structure, l0 is the lattice constant along the β-direction, Δl = l − l0 is the corresponding lattice distortion, and V0 is the equilibrium volume of the unit cell. The deformation potential constant Eβ is calculated by 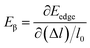 , where, Eedge is the energy level of the electrons in the CBM and holes in the VBM. The density-of-states effective mass
, where, Eedge is the energy level of the electrons in the CBM and holes in the VBM. The density-of-states effective mass 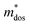 is given by
is given by 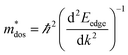 . The calculated Cβs, Eβs,
. The calculated Cβs, Eβs, 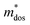 and μs of the pristine and doped SrIn2O4 are summarized in Table 5. A larger μ represents a higher migration rate of photogenerated charge carriers, which leads to charge carriers quickly reaching the surface of the materials to drive the redox reaction for hydrogen and oxygen production. The results in Table 5 reveal that the calculated μ of the electrons in the pristine SrIn2O4 is 2093.00 cm2 V−1 s−1, while that of the holes is only about 0.97 cm2 V−1 s−1, indicating that the separation of electrons and the holes is significant. Therefore, the pristine SrIn2O4 is beneficial for water splitting. Moreover, the μ of the electrons in the doped structures is higher than that of other effective photocatalytic materials, such as MoS2 (200 cm2 V−1 s−1),54 although it significantly decreases compared with that of the pristine structure. As a result, IVA-doped SrIn2O4 also exhibits efficient photocatalytic behavior theoretically.
and μs of the pristine and doped SrIn2O4 are summarized in Table 5. A larger μ represents a higher migration rate of photogenerated charge carriers, which leads to charge carriers quickly reaching the surface of the materials to drive the redox reaction for hydrogen and oxygen production. The results in Table 5 reveal that the calculated μ of the electrons in the pristine SrIn2O4 is 2093.00 cm2 V−1 s−1, while that of the holes is only about 0.97 cm2 V−1 s−1, indicating that the separation of electrons and the holes is significant. Therefore, the pristine SrIn2O4 is beneficial for water splitting. Moreover, the μ of the electrons in the doped structures is higher than that of other effective photocatalytic materials, such as MoS2 (200 cm2 V−1 s−1),54 although it significantly decreases compared with that of the pristine structure. As a result, IVA-doped SrIn2O4 also exhibits efficient photocatalytic behavior theoretically.
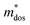 , relaxation time τ (fs) and carrier mobility μ (cm2 V−1 s−1) for SrIn2O4
, relaxation time τ (fs) and carrier mobility μ (cm2 V−1 s−1) for SrIn2O4
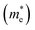 and holes
and holes 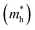 was calculated according to the following expression:55
was calculated according to the following expression:55