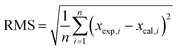Prediction of ¹H NMR chemical shifts for ionic liquids: strategy and application of a relative reference standard

Abstract

The computational predictions of ¹H NMR chemical shifts for ionic liquids were investigated. To calculate the chemical shifts more accurately, the approach of relative reference standard (RRS) was proposed. This straightforward computational technique uses organic compounds and ionic liquids that are similar to the studied ionic liquids as standards. The calculated chemical shifts of single ion pairs were strongly influenced by the anion type and the local environment. Using the RRS methodology, the calculated results agreed well with the experimental chemical shifts due to the cancellation of errors caused by the anion. Ionic clusters consisting of 4 ion pairs were also employed to model the ionic liquids with strongly coordinating anions. Large clusters slightly improve the accuracy by reducing systematic errors. Although the experimental ¹H NMR data of the reference ionic liquid should be used, the RRS methodology has been shown to predict ¹H NMR chemical shifts efficiently at different levels of theory.

---

Introduction

In the last decade, ionic liquids (ILs) were widely used in chemical reactions, extraction, and catalysis processes.¹ As a type of molten salt, ionic liquids have many favourable properties, including good chemical and physical stability, low vapour pressure, non-flammability, and tuneable properties.^2–4 A typical ionic liquid usually consists of organic-type cations and inorganic-type anions. However, it is believed that the ionic liquid is a complicated system.⁵ Nuclear magnetic resonance (NMR) is one of the most powerful tools to investigate the ionic liquid. The interaction between anion and cation can be detected by means of ¹H NMR chemical shifts.⁶ For example, the proton chemical shift of H2 in the [C₄mim]⁺-based IL is very sensitive to the change of the local environment. A downfield H2 chemical shift can be attributed to hydrogen bond formation,⁷ and the position of the NMR peaks corresponding to the H2 proton heavily depended on the anion type.⁸ Therefore, the ¹H NMR chemical shifts can help us understand the effects of the local environment and the transport properties of ILs. However, the chemical factors that influence proton chemical shifts of the ILs are still not very clear due to the complication of interionic interactions.^9,10

Recently, several studies have shown that quantum chemical methods are successful in the prediction of NMR chemical shifts. The ¹H and ¹³C NMR chemical shifts can be predicted reasonably well with quantum chemical calculations for various organic compounds.⁸ However, in the cases of ILs, large deviations were observed for the computing proton NMR chemical shifts when compared with the experimental values. For imidazolium-based ILs, the absolute errors between the predicted and experimental shift of H2 were usually greater than 1 ppm. The backbone H4 and H5 protons of the imidazolium ring also gave large deviations in the cases of [C₄mim]Cl and [C₄mim][OAc].⁹ It is believed that the predicted ¹H NMR chemical shifts strongly depended on the geometry of the IL. In addition, hydrogen bond and the type of anion significantly influence the accuracy of the predicted values.^11,12

Many efforts have been made to improve the accuracy of the predicted ¹H NMR chemical shifts. Using empirical scaling corrections to remove systematic errors can obtain well predicted chemical shifts.¹³ This method requires a large number of experimental data to obtain scaling factors. However, the experimental values of ionic liquids seem not enough to support this procedure so far. A multi-standard approach (MSTD) for the calculation of ¹H NMR chemical shifts of organic molecules also can give relatively accurate results.¹⁴ Instead of employing the most common standard tetramethysilane (TMS), the MSTD method uses methanol and benzene as the corresponding reference compounds for sp³ and sp²–sp hybridized carbon atoms, respectively.¹⁵ Although this simple modification could obtain much better calculation results for many organic molecules, large deviations exist in the calculations for ionic liquids. Chen et al. suggested that large cluster calculations can improve the accuracy of the prediction of proton chemical shifts. When an IL cluster consisting of 8 ion pairs (IP), it can predict proton chemical shifts with relatively high accuracy. If the computational cost were not a problem, a large IL cluster might give good predicted results: mean absolute errors of ¹H chemical shifts in the range of 0.2 to 0.8 ppm.^16,17

Ionic liquid is composed of cation and anion pairs, which is very different from the ordinary organic compounds. For computing the ¹H NMR chemical shifts of ILs, more effort should be made to obtain much better accuracy at lower computational cost. The following strategy maybe helps us to further improve the accuracy of calculations. First, besides the sp³ and sp²–sp hybridized carbon atoms, the structure of cation also markedly affects the calculation of the proton chemical shifts. If the structure of a reference compound were similar to that of the IL cation, the quantum chemical methods might produce little error with respect to experiment. Therefore, apart from TMS, benzene, and methanol, other organic compounds that similar to the cations of ILs (e.g., 1-methyl-imidazole) should be used as the reference compounds to calculate the proton chemical shifts. Secondly, the high quality prediction of ¹H NMR chemical shifts should take into account the impact of anions, and then the IL that similar to the structure of the studied IL should also be employed as a reference standard. Because this reference IL is analogous to the studied IL, the effect of anion on both ILs should be very similar. Using this approach, the calculations for the particular chemical shifts of those hydrogens contacted with oxygen or nitrogen atom (–OH or –NH group) might give more confident results than those computed with TMS standard. In consequence, an approach of relative reference standard (RRS) is proposed to achieve accurate predictions of ¹H NMR parameters at any level of theory. The only apparent trade-off is the slight increase in complexity when processing data utilizing relative reference compounds. Thirdly, some studies have revealed that a single ion pair was not considered a reliable model for studying particular chemical shifts.^5,18 If more ion pairs were given consideration in the calculation with RRS approach, it might produce good agreement with experiment.

In this paper, we did a systematic study on the prediction of ¹H NMR chemical shifts of a number of ILs. We have calculated chemical shifts by the RRS methodology with the above-mentioned strategy: (1) using single ion pairs as far as possible to calculate the chemical shifts of ILs. (2) ¹H NMR chemical shifts are calculated by using the organic compound that is similar to the cation of the studied IL as a reference standard. (3) When the studied IL containing stronger coordinating anions such as chloride and acetate, the IL that similar to the studied IL is employed as the reference compound. (4) An ionic cluster approach is also adopted to study changes in the chemical shifts. Finally, the results of the performance of RRS at different levels of theory have been compared with those of TMS standard.

Theoretical methods

All calculations were performed with the Gaussian 09 package.¹⁹ Recently, Zahn²⁰ and Li¹⁸ have performed an assessment of density functional theory and Møller–Plesset perturbation theory for ILs. Li et al. recommended that the density functional of the Minnesota family of the M0X type with a diffusion function basis set (aug-cc-pvdz or 6-31++g**) would give reliable results for IL calculations. In addition, Grimme et al. noted that dispersion-corrected density functionals, such as B3LYP/6-31++G**-gd3bj (DFT-D3), could also lead to reliable results.²¹ Therefore, the m06-2x/aug-cc-pvdz (or B3LYP/6-31++G**-gd3bj) level of theory was used to optimize all ionic liquids under study. This level is known to afford good geometry at low computational cost, particularly appropriate to be used for the calculation of weak interaction (e.g., hydrogen bonding).²² The ¹H absolute magnetic shielding values were computed using the following levels of theory: (1) B3LYP with DFT-D3 dispersion correction,²³ (2) mPW1PW91,²⁴ GGA-based functional which was found to provide best results within the MSTD approach for ¹H NMR, (3) WP04,²⁵ similar to B3LYP but parameterized to reproduce NMR chemical shifts in chloroform. (4) B972,²⁶ functional augmented with the empirical dispersion correction, (5) m06-2x,²⁷ a meta-GGA functional, (6) Hartree–Fock (HF), and (7) a second-order Mǿller–Plesset (MP2) theory was also considered, which might obtain reasonable results.

In order to investigate the effect of basis sets on the accuracy of the predicted ¹H chemical shifts, both Pople and Dunning-type double- and triple-ζ basis sets including 6-31++G(d,p), 6-311++G(d,p), 6-311+(3df,2p), cc-PVTZ, and aug-cc-PVDZ were investigated. Due to the “gauge including atomic orbitals approach” (GIAO) success in accurate calculations of NMR chemical shifts,²⁸ the magnetic shielding constants were computed using this method. The NMR calculations were carried out in solution, using chloroform, acetonitrile, or DMSO-d₆ as the solvent. The effect of solvent plays an important role on the geometry optimization of ionic liquids. The SMD solvation model that proposed by Truhlar et al. has been used for the IL calculation very well.^29,30 Therefore, the density functional theory (m06-2x and B3LYP with dispersion-corrected) combined with the SMD model was employed to investigate the IL optimization and their proton NMR chemical shifts.

When the ¹H NMR chemical shifts of [C₄mim]Cl are under studied, the RRS approach should be carried out as the following steps:

(1) The organic molecule similar to the cation of the studied IL was used as the reference compound. In this case, 1-methlyimidozle was employed as a corresponding reference compound.

(2) The ¹H absolute magnetic shielding values of H2′, H3′, and H4′ protons in 1-methylimidazole ring were calculated at the certain level of theory.

(3) The shielding constants of [C₄mim]Cl with a single ion pair were calculated at the same level as the 1-methylimidazole calculations.

(4) Once the shielding constants were computed, the ¹H NMR chemical shifts can be calculated in accordance with the following equation:

δ^x_calc = σ_ref,x − σ_x + δ_ref,x

(5) Where σ_ref,x and σ_x are the NMR isotropic magnetic shielding values. Generally, the x hydrogen atoms for the given molecule and for the reference compound have similar structure. And δ_ref,x is the certain proton chemical shift of the reference compound in deuterated chloroform, which was taken from the Spectral Data Base for Organic Compounds (SDBS).³¹ For instance, the δ^H2_calc of [C₄mim]Cl would include the calculated values of σ_{1-methylimidazole,H2′} and σ[C₄mim]Cl,H2, and the experimental data of δ_{1-methylimidazole,H2′}.

(6) H3 and H4 calculations of [C₄mim]Cl have the similar procedure of H2, but x in the equation should be replaced by H3 and H4, respectively. The –CH₂– or –CH₃ hydrogens (H5–H8) in the [C₄mim]⁺ cation were calculated by using TMS (δ = 0.00 ppm) as the reference compound.

In addition, clusters consisting of 4 ion pairs (4 IP) were also modelled for ILs. The clusters of [C₄mim]OH, ethanolamine acetate and [C₄mim][BF₄] were constructed by combining energetically preferable ion pair configurations, while ensuring the resulting cluster occupied the minimal volume. All ionic clusters studied were confirmed as minima on the potential energy surface by the absence of imaginary vibrational frequencies. We used the mean absolute errors (MAE, defined as Σ|δ_calc,x − δ_exp,x|/n) to analyse the results of the calculations, and compare the performances of the methods under study. Root mean square deviations (RMS) were also used to investigate the differences between values predicted by a model and the values actually observed. The RMS being defined as follows:

where x_exp,i represents the experimental value of the ¹H NMR chemical shift, x_cal,i is the calculated shift of this hydrogen, and n is the number of hydrogens in the studied ionic liquid.

Results and discussion

RRS performance for single ion pairs

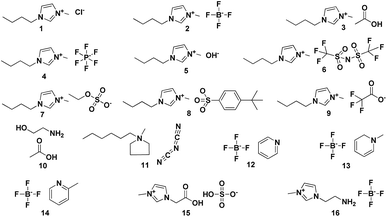
To carry out this study, we have worked with a test set of 16 ionic liquids shown in Fig. 1 and S1.† Single ion pair (1 IP) of the studied IL were adopted to investigate the accuracy of theory levels at reasonable computational cost. Table 1 lists the results obtained after carrying out the ¹H NMR calculations using TMS and RRS methodology. In the cases of [C₄mim]Cl and [C₄mim][BF₄], it is found that RMSs and MAEs of the calculating results are great even using the “expensive” method mp2/aug-cc-pvdz to optimize and to predict (entries 1 and 2). But a better result could be obtained when using m06-2x/aug-cc-pvdz level of theory for the IL [C₄mim][BF₄] (entry 3). When an IL with weekly coordinating anions (e.g., [BF₄]⁻) is under the NMR calculation, it is believed that the accuracy of chemical shifts displays a high dependence on the level of theory employed.^11,17 Recent studies also show that the calculated ¹H NMR chemical shifts for IL systems using either the global minima or all significant configurations might be very similar.^8,14 We analysed the performance of TMS and RRS methods for [C₄mim][BF₄] and [C₄mim][NTf₂], which could adopt more preferred configurations. However, it is found that no improvement on the RMSs was obtained when using Boltzmann weighted values (entries 4 and 9, respectively). So only the global minimum was considered in all cases of this work. More details of Boltzmann distribution please see the ESI† (Fig. 2 and 3).

Fig. 1 Test set.

Table 1 Mean absolute errors (MAE) and root mean square deviations (RMS) of calculated proton chemical shifts

Entry	Ionic liquid	Reference compound	Solvent	Level of theory	MAE		RMS
					RRS	TMS	RRS	TMS
1	[C4mim]Cl	1-Methyl-imidazole	Chloroform	mp2/aug-cc-pvdz	0.764	0.747	1.197	1.417
2	[C4mim][BF4]^9,32		Chloroform	mp2/aug-cc-pvdz	0.354	0.441	0.371	0.558
3	[C4mim][BF4] global minimum		Chloroform	m06-2x/aug-cc-pvdz	0.369	0.114	0.450	0.155
4	[C4mim][BF4] Boltzmann average		Chloroform	m06-2x/aug-cc-pvdz	0.393	0.140	0.467	0.180
5	[C4mim][OAc]^33		Chloroform	m06-2x/aug-cc-pvdz	0.750	0.649	1.221	1.318
6	[C4mim][PF6]^9		Chloroform	m06-2x/aug-cc-pvdz	0.372	0.240	0.425	0.285
7	[C4mim]OH^34		Chloroform	m06-2x/aug-cc-pvdz	0.459	0.289	0.573	0.511
8	[C4mim][Tf2N]^9,35 global minimum		Chloroform	m06-2x/aug-cc-pvdz	0.612	0.632	0.977	1.134
9	[C4mim][Tf2N] Boltzmann average		Chloroform	m06-2x/aug-cc-pvdz	0.525	0.633	0.952	1.135
10	[C4mim][MeSO4]^36		Chloroform	m06-2x/aug-cc-pvdz	0.479	0.411	0.529	0.559
11	[C4mim][OTS]^32		Water	b3lyp/6-31++g(d,p)-d3	0.555	0.385	0.748	0.424
12	[C4mim][TFA]^32		Water	b3lyp/6-31++g(d,p)-d3	0.817	0.610	1.291	1.370
13	[P16][DCA]^37	Pyrrole	DMSO-d6	m06-2x/aug-cc-pvdz	0.360	0.330	0.387	0.350
14	[Py][BF4]^38	Pyridine	Acetonitrile	hf-6-31g(d)	0.854	1.159	1.295	1.439
15	[1-me-Py][BF4]^38	Pyridine	Acetonitrile	b3lyp/6-31++g(d,p)-d3	0.328	0.105	0.365	0.122

---

Fig. 2 Configuration of [C₄mim]Cl optimized by mp2/aug-cc-pvdz.

Fig. 3 Configuration of [C₄mim][BF₄] optimized by mp2/aug-cc-pvdz.

On the other hands, it is also found that almost all RMSs of those ILs containing strongly coordinating anions (e.g., Cl⁻, OH⁻, OAc⁻) are relatively large. No matter which level of theory was employed for calculating the proton chemical shifts of [C₄mim][OAc], the values of MAE are always greater than 1.0 ppm, as Fig. 4 illustrated. These results should be attributed to the influence of the anion to the cation. Ionic liquids are different from the ordinary organic compounds. Due to the complicated relationships of ions, the anion would significantly affect the ¹H NMR chemical shifts. When the ionic liquids have strongly coordinating anions, the interionic interactions of these ILs are difficult to model. In the cases of C_nmim-based ILs, the predicted proton NMR chemical shifts of H2 were found to be sensitive to the effect of the anion. If we did not take into consideration the effects of the anions, it is not surprising that the theoretical calculation of a C_nmim-based IL would give a poor result. Particularly, the level of theory is insensitive to the prediction of the IL with strongly coordinating anion and therefore, those methods with high computational cost have no contribution to the improvement of the predicted chemical shifts (Scheme 1).

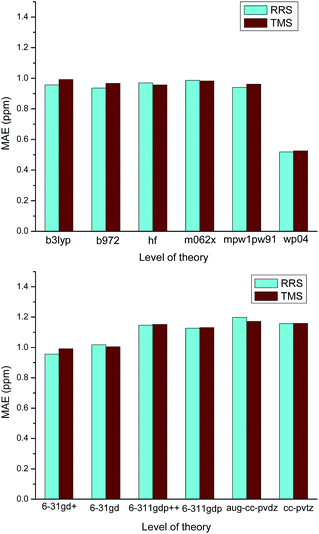Fig. 4 Effect of the method and the basis set used in the calculation of [C₄mim][OAC] ¹H NMR chemical shifts.

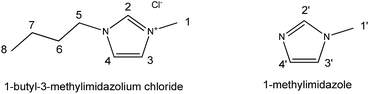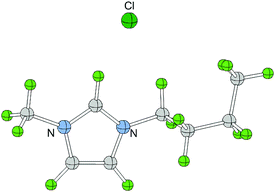
Scheme 1 Structure of 1-butyl-3-methylimidazolium chloride and 1-methylimidazole with hydrogen atoms numbered.

Modification of RRS approach

Using the reference compound that similar to the cation of the studied IL, the effects of anion are not completely reflected in the RRS calculation. It is necessary to employ an IL that similar to the studied IL as a reference standard to predict the chemical shifts. This modification should be considered as an upgrade of the RRS approach. The data collected in Table 2 show that the modification of RRS can give more accurate and precise ¹H NMR chemical shifts than those obtained with the ordinary RRS standard. Whether pyridinium-based or imidazolium-based ILs, most RMSs are less than 0.3 ppm. The detailed calculations for the cases of [C_nmim]⁺-based ILs are listed in Table 3. The main improvement in those imidazolium-based ILs came for the H2 proton, whose chemical shift deviation from experiment reduced to 0.2 ppm on average. These results might be explained in terms of error cancellation in isotropic magnetic shielding constants when using relative reference standards that more resemble different types of hydrogens within the studied IL. The RRS approach affords better results than those obtained using TMS, implying that RRS decrease the predicted errors caused by the interaction of anions.

Table 2 Mean absolute errors (MAE) and root mean square deviations (RMS) of the IL chemical shifts using the modification of RRS approach

Ionic liquid	Reference compound	Level of theory	MAE		RMS
			RRS	TMS	RRS	TMS
[1-me-Py][BF4]	[Py][BF4]	b3lyp/6-31++g(d,p)-d3	0.226	0.105	0.254	0.122
		wp04/6-31+g(d)	0.113	0.229	0.124	0.241
[2-me-Py][BF4]^38	[Py][BF4]	b3lyp/6-31++g(d,p)-d3	0.103	0.370	0.125	0.536
		wp04/6-31+g(d)	0.073	0.493	0.105	0.739
P16-DCA	P12-DCA^37	b3lyp/6-31++g(d,p)-d3	0.081	0.151	0.107	0.192
[CMI][HSO4]^32	[Emim][HSO4]^32	b3lyp/6-31++g(d,p)-d3	0.295	0.470	0.352	0.500
		m06-2x/aug-cc-pvdz	0.265	0.539	0.296	0.579
		wp04/6-31+g(d)	0.193	0.346	0.215	0.368
[C4mim][MeSO4]	[C2mim][EtSO4]^36	b3lyp/6-31++g(d,p)-d3	0.118	0.471	0.162	0.790
		m06-2x/aug-cc-pvdz	0.200	0.383	0.261	0.534
		wp04/6-31+g(d)	0.222	0.423	0.236	0.567
[NH2Emim][BF4]^39	[C2mim][BF4]^17	m06-2x/aug-cc-pvdz	0.225	0.457	0.274	0.495
[C4mim][BF4]	[C2mim][BF4]	b3lyp/6-31++g(d,p)-d3	0.170	0.290	0.192	0.402
		m06-2x/aug-cc-pvdz	0.134	0.204	0.167	0.214
		wp04/6-31+g(d)	0.338	0.446	0.377	0.712
[C4mim][PF6]	[C2mim][PF6]^17	b3lyp/6-31++g(d,p)-d3	0.190	0.192	0.252	0.247
		m06-2x/aug-cc-pvdz	0.270	0.240	0.351	0.285
		wp04/6-31+g(d)	0.262	0.301	0.266	0.356
[C4mim][OAc]	[C2mim][OAc]^33	b3lyp/6-31++g(d,p)-d3	0.142	1.098	0.171	1.761
		m06-2x/aug-cc-pvdz	0.088	0.649	0.113	1.318
[C4mim][OTS]	[C2mim][OTS]^32	b3lyp/6-31++g(d,p)-d3	0.117	0.385	0.131	0.424
[C4mim][Tf2N]	[C2mim][Tf2N]^35	b3lyp/6-31++g(d,p)-d3	0.099	0.354	0.157	0.707
		m06-2x/aug-cc-pvdz	0.188	0.330	0.224	0.483
		wp04/6-31+g(d)	0.222	0.423	0.236	0.567
[C4mim][TFA]	[C2mim][TFA]^32	b3lyp/6-31++g(d,p)-d3	0.103	0.610	0.122	1.370

---

Table 3 Calculated ¹H NMR chemical shifts of the [C₄mim]⁺-based ILs^a

Ionic liquid	δ cal	Chemical shifts (ppm)								MAE	RMS
		H2	H3	H4	H1	H5	H6	H7	H8
a The detailed calculation data of Table 2. b Using b3lyp/6-31++g(d,p) with gd3bj correction for optimization and calculation. c Using m06-2x/aug-cc-pvdz for optimization and calculation.
[C4mim][PF6]	RRS^b	9.10	7.37	7.22	4.30	4.00	1.83	1.21	1.10	0.190	0.252
	TMS^b	9.05	7.52	7.53	4.02	4.20	1.76	1.13	1.03	0.192	0.247
	RRS^c	7.88	7.47	7.16	4.49	4.16	1.83	0.80	0.97	0.270	0.351
	TMS^c	9.54	7.88	7.82	4.12	4.36	1.95	0.92	1.09	0.240	0.285
	δ exp	8.52	7.49	7.52	4.25	3.97	1.93	1.38	0.94
[C4mim][MeSO4]	RRS^b	9.15	7.59	7.57	4.25	3.60	1.60	1.37	0.84	0.118	0.162
	TMS^b	10.04	7.40	7.50	3.87	5.45	1.76	1.53	1.00	0.471	0.790
	RRS^c	9.15	7.53	7.54	4.35	3.62	1.29	1.16	0.87	0.200	0.261
	TMS^c	10.51	7.67	7.82	4.02	4.27	1.51	1.39	1.09	0.383	0.534
	δ exp	9.42	7.63	7.58	4.26	3.37	1.88	1.35	0.94
	RRS^b	8.54	7.38	7.43	4.14	4.04	1.81	1.46	0.97	0.170	0.192
[C4mim][BF4]	TMS^b	9.56	7.44	7.51	3.89	5.06	1.84	1.50	1.01	0.290	0.402
	RRS^c	8.89	7.42	7.68	3.95	4.06	1.64	1.39	0.86	0.134	0.167
	TMS^c	9.03	7.76	7.89	3.84	3.98	1.78	1.53	1.14	0.204	0.214
	δ exp	8.77	7.63	7.69	4.04	4.32	1.93	1.38	0.94
[C4mim][OAc]	RRS^b	9.90	7.91	7.85	4.22	3.83	1.76	1.47	1.05	0.142	0.171
	TMS^b	14.16	7.36	7.43	3.88	6.75	1.74	1.44	1.03	1.098	1.761
	RRS^c	9.95	7.85	7.82	4.22	3.82	1.50	1.21	0.96	0.088	0.113
	TMS^c	13.82	7.74	7.85	4.26	4.60	1.67	1.38	1.13	0.649	1.318
	δ exp	10.18	7.88	7.96	4.2	3.89	1.6	1.21	0.84
[C4mim][Tf2N]	RRS^b	9.02	7.73	7.42	4.22	3.87	1.87	1.41	0.98	0.099	0.157
	TMS^b	10.59	7.26	7.27	4.07	3.85	1.92	1.46	1.02	0.354	0.707
	RRS^c	8.93	7.80	7.76	4.22	3.87	1.69	1.10	0.97	0.188	0.224
	TMS^c	9.79	7.81	7.95	4.17	4.09	1.91	1.32	1.40	0.330	0.483
	δ exp	8.63	7.54	7.46	4.24	3.96	1.92	1.4	0.97
[C4mim][OTS]	RRS^b	8.52	7.74	7.37	4.23	3.65	1.88	1.37	0.97	0.117	0.131
	TMS^b	7.89	7.28	7.53	3.33	3.91	2.08	1.56	1.16	0.385	0.424
	δ exp	8.53	7.66	7.29	4.02	3.78	1.71	1.22	0.87
[C4mim][TFA]	RRS^b	8.87	7.56	7.49	4.17	3.73	1.60	1.29	0.89	0.103	0.122
	TMS^b	12.51	7.30	7.40	3.71	4.00	1.70	1.39	0.96	0.610	1.370
	δ exp	8.67	7.43	7.39	4.14	3.85	1.79	1.26	0.86

---

The modified RRS approach can provide a high quality prediction of ¹H NMR chemical shifts regardless the level of theory employed, as can be observed in Fig. 5. Further observations can be drawn from the data collected in Table S23 of the ESI.† In general, m06-2x and B3LYP with DFT-D3 corrections were found to provide good results for the RRS approach. Although the results would be better when triple-ζ basis sets such as aug-cc-pvdz and 6-31++G(d,p) were used, the low cost basis sets such as wp04/6-31+G(d) can give good results as well (Fig. 6).

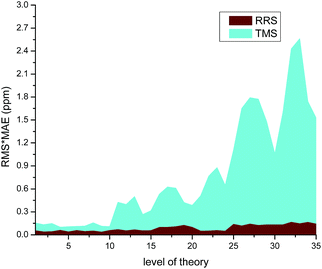Fig. 5 Effect of the level of theory used in the calculation of ¹H NMR chemical shifts for various ILs.

Fig. 6 IL cluster of [C₄mim][BF₄] (4 IP).

However, an apparent limitation of the RRS method is that the experimental ¹H NMR shifts of a relatively simple ionic liquid must be used. The purpose of using experimental ¹H NMR data is mainly to cancel the errors from the anion influence. On the other hand, for those ionic liquids with long alkyl chains, the alkyl–alkyl chain interactions maybe dominate the bulk. Although it is generally considered that the proton chemical shifts were relatively insensitive to increasing alkyl chain length,⁴⁰ the effects of long alkyl chain on the prediction of the calculated proton chemical shifts is still ambiguous. Therefore, we set out to calculate ¹H NMR chemical shifts of a series of 1-alkyl-3-methylimdazolium ([C_nmim][BF₄] with n = 6, 8, and 12) ILs by means of RRS method. The results show that the length of alkyl chains in the imidazolium ring has little impact on the accuracy of calculated chemical shifts. The RMS of [C₁₂mim][BF₄] ionic liquid is less than 0.25 ppm. The details see Tables S32–S34 of the ESI.†

IL cluster and RRS for ILs with weakly coordinating anions

Those ILs with strongly coordinating anions, such as 1-butyl-3-methylimidazolium hydroxide and ethanolamine acetate, maybe require a cluster model to improve the accuracy of the prediction. Moreover, some studies have suggested that the cluster should consist of at least 4 ion pairs to do the calculation.¹⁷ The predicted chemical shifts of IL clusters together with MAE and RMS were collected in Table 4. However, when TMS was used as the reference standard, the cluster model is clearly not sufficient to predict ¹H NMR chemical shifts for the ILs with some particular anions (e.g., OH⁻ and [OAc]⁻). The 4 ion-paired (4 IP) clusters of [C₄mim]OH and ethanolamine acetate did not produce better results when compared to those using single ion pair (1 IP). Their RMSs exceeding 0.6 and even 5.0 ppm on average, respectively. By contrast, good accuracy for these ILs could be obtained when the RRS approach with 1 IP model was used.

Table 4 Mean absolute errors (MAE) and root mean square deviations (RMS) of the IL clusters

Ionic liquid	Size	Level of theory	Reference compound	MAE	RMS
Ethanolamine acetate	1 IP	m06-2x/aug-cc-pvdz	Ethanolamine formate (RRS)	0.111	0.126
	1 IP	m06-2x/aug-cc-pvdz	TMS	4.069	5.668
	4 IP	m06-2x/aug-cc-pvdz	TMS	3.457	5.182
[C4mim]OH	1 IP	m06-2x/aug-cc-pvdz	[C2mim]OH (RRS)	0.086	0.125
	1 IP	m06-2x/aug-cc-pvdz	TMS	0.406	0.839
	4 IP	m06-2x/aug-cc-pvdz	TMS	0.411	0.610
[C4mim][BF4]	1 IP	mp2/aug-cc-pvdz	TMS	0.441	0.558
	4 IP	mp2/aug-cc-pvdz	TMS	0.308	0.390

---

In the case of [C₄mim][BF₄], the cluster with 4 ion pairs worked slightly better than that in the single ion pair. It is worth noting that the isotropic magnetic shielding constants tend to have more equal values when the cluster was used (Tables S25–S29†). Therefore, more ion pairs might decrease the influence of anions or the local arrangement of surrounding ions on the ¹H NMR chemical shifts. However, it is found that the cluster model was more likely to influence the prediction accuracy of those ILs with weakly coordinating anions. The calculated chemical shifts are not nearly accurate for the ILs containing strongly coordinating anions, which is obviously due to the fact that the large cluster models could not reduce the effects of anion on the ¹H NMR calculations (4 IP [C₄mim]OH and ethanolamine acetate).

In addition, a generalised standard might be proposed when the ILs have the weakly coordinating anions. As Table 5 shown, if the IL [C₂mim][BF₄] were used as a reference standard, the proton NMR chemical shifts of ILs with weakly interacting anions could be well predicted. For example, the RMSs of [C₄mim][PF₆] and [C₂mim][PF₆] are 0.242 and 0.284, respectively. Moreover, an order that representing the intensity of anion interactions might also be obtained by means of RMS analysis. That is, larger RMS usually indicates stronger interaction between the cation and the anion. According to the RMS results, the intensity order of the anion interaction is: [C₄mim][PF₆] ≈ [C₂mim][PF₆] < [C₄mim][NTf₂] < [C₄mim][OTS] ≈ [C₄mim][MeSO₄] < [C₄mim][TFA] < [C₄mim][OAc]. The details see Tables S35–S41 of the ESI.†

Table 5 Root mean square deviations (RMS) of ILs using [C₂mim][BF₄] as a generalised reference standard

Reference standard	Ionic liquids	RMS
[C2mim][BF4]	[C4mim][PF6]	0.242
	[C2mim][PF6]	0.284
	[C4mim][NTf2]	0.374
	[C4mim][OTS]	0.477
	[C4mim][MeSO4]	0.495
	[C4mim][TFA]	1.064
	[C4mim][OAc]	1.272

---

Case study

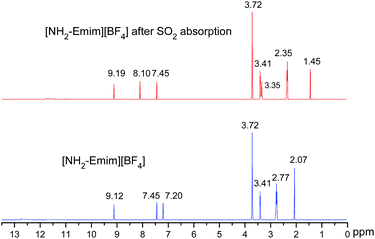
We present a case study from our laboratory to give a further example on the utility of RRS methodology to solve the real life problem.⁴¹ As a functional IL, [NH₂-Emim][BF₄]can be used for SO₂ removal.⁴² However, the ¹H NMR spectroscopic data of unsaturated C–H in the imidazolium ring was easy to be confused with the values of N–CH₂–CH₂–NH₂ after SO₂ absorption. Consequently, the relationship of [NH₂-Emim][BF₄] and SO₂ was not very clear.⁴³ The quantum chemical calculation gives us an opportunity to investigate the reaction between [NH₂-Emim][BF₄] and SO₂. We have optimized [NH₂-Emim][BF₄] and SO₂–[NH₂-Emim]BF₄ compounds, and computed the ¹H chemical shifts using RRS approach. Fig. 7 presents the experimental values in deuterated chloroform for neat and SO₂-absorbed [NH₂-Emim][BF₄], together with calculated chemical shifts at the m06-2x/aug-cc-pvdz level of theory in the same solution. The calculated results show a good agreement with experimental data. The predicted spectral data reveal that the proton chemical shifts of –NH₂ group were significantly changed after the SO₂ absorption: from 2.07 to 1.45 and to 3.35 ppm, respectively. The experimental ¹H NMR spectrum of the SO₂-treated and untreated [NH₂-Emim][BF₄] IL is represented in Fig. 8. The resonance peaks of H (unsaturated C–H in the imidazole ring, with N–CH₂–CH₂–NH₂ connected to the right) moved downfield from 7.20 to 8.10 ppm due to the impact of [BF₄]⁻ and SO₂ group, which is basically in line with the predicted chemical shifts. These results suggest that the proposed reaction between [NH₂-Emim][BF₄] and SO₂ had occurred (Fig. 7). For details, please see the ESI.†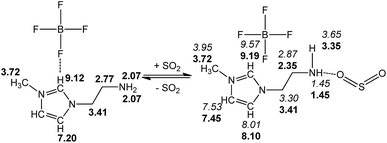

Fig. 7 Experimental (in bold) and calculated (in italics) ¹H NMR chemical shifts of [NH₂-Emim][BF₄] before and after SO₂ absorption.

Fig. 8 ¹H NMR spectra of [NH₂-Emim][BF₄] before and after SO₂ absorption.

Conclusions

We have investigated the application of the RRS approach for computing ¹H NMR chemical shifts of ILs. The results were compared with those obtained with the use of the typical TMS standard to assess the performance of the RRS methodology. To decrease the errors caused by the anion and the local environment, the ILs that similar to the structure of the studied ILs were used as reference standards in the calculations. m06-2x/aug-cc-pvdz DFT functional can give good prediction results with lower computational cost, which should be as the preferred DFT functional for the prediction. Besides using relative reference standards, ionic clusters consisting of 4 ion pairs were also employed for computing the proton chemical shifts. For the ILs with strongly coordinating anions, the effect of anions was shown to be the main factor contributing to a more reliable prediction of the proton chemical shifts. Single ion pair with the RRS approach is sufficient to produce more accurate and precise ¹H NMR chemical shifts for most of the studied ILs. An additional advantage of the RRS method is that the computational results do not depend much on the level of theory used in the calculations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for the financial support from the National Natural Science Foundation of China (21766021 and 21266015).

References

1. A. S. Amarasekara, Chem. Rev., 2016, 116, 6133–6183.
2. B. Wang, L. Qin, T. Mu, Z. Xue and G. Gao, Chem. Rev., 2017, 117, 7113–7131.
3. Y. Cao and T. Mu, Ind. Eng. Chem. Res., 2014, 53, 8651–8664.
4. J. Dupont, R. F. de Souza and P. A. Z. Suarez, Chem. Rev., 2002, 102, 3667–3691.
5. E. I. Izgorodina, Phys. Chem. Chem. Phys., 2011, 13, 4189–4207.
6. D. Bankmann and R. Giernoth, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 51, 63–90.
7. S.-T. Lin, M.-F. Ding, C.-W. Chang and S.-S. Lue, Tetrahedron, 2004, 60, 9441–9446.
8. E. I. Izgorodina, Z. L. Seeger, D. L. A. Scarborough and S. Y. S. Tan, Chem. Rev., 2017, 117, 6696–6754.
9. A. Bagno, F. D'Amico and G. Saielli, J. Phys. Chem. B, 2006, 110, 23004–23006.
10. A. Dejaegere, R. A. Bryce and D. A. Case, ACS Symposium Series, American Chemical Society, Washington, DC, 1999, pp. 194–206.
11. S. Chen, R. Vijayaraghavan, D. R. MacFarlane and E. I. Izgorodina, J. Phys. Chem. B, 2013, 117, 3186–3197.
12. Y. Chen, Y. Cao, X. Sun and T. Mu, J. Mol. Liq., 2014, 190, 151–158.
13. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862.
14. A. M. Sarotti and S. C. Pellegrinet, J. Org. Chem., 2012, 77, 6059–6065.
15. A. M. Sarotti and S. C. Pellegrinet, J. Org. Chem., 2009, 74, 7254–7260.
16. E. I. Izgorodina, J. Rigby and D. R. MacFarlane, Chem. Commun., 2012, 48, 1493–1495.
17. S. Chen and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2017, 19, 17411–17425.
18. H. P. Li, Y. H. Chang, W. S. Zhu, W. Jiang, M. Zhang, J. X. Xia, S. Yin and H. M. Li, J. Phys. Chem. B, 2015, 119, 5995–6009.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision E.01), Gaussian, Inc., Wallingford, CT, 2013.
20. S. Zahn, D. R. MacFarlane and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 13664–13675.
21. S. Grimme, W. Hujo and B. Kirchner, Phys. Chem. Chem. Phys., 2012, 14, 4875–4883.
22. T. M. Simeon, M. A. Ratner and G. C. Schatz, J. Phys. Chem. A, 2013, 117, 7918–7927.
23. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
24. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
25. K. W. Wiitala, T. R. Hoye and C. J. Cramer, J. Chem. Theory Comput., 2006, 2, 1085–1092.
26. A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560.
27. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118.
28. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
29. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
30. V. S. Bernales, A. V Marenich, R. Contreras, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2012, 116, 9122–9129.
31. Spectral Database for Organic Compounds, https://www.aist.go.jp/RIODB/SDBS/cgi-bin.
32. W. Li, S. Dai, D. Li, Q. Zhang, H. Fan, T. Zhang and Z. Zhang, Synthesis, 2016, 49, 1065–1072.
33. B. Banerjee, D. Kundu, G. Pugazhenthi and T. Banerjee, RSC Adv., 2015, 5, 85280–85290.
34. B. C. Ranu and S. Banerjee, Org. Lett., 2005, 7, 3049–3052.
35. L. Sun, G. K. Ramesha, P. V. Kamat and J. F. Brennecke, Langmuir, 2014, 30, 6302–6308.
36. J. D. Holbrey, W. M. Reichert, R. P. Swatloski, G. A. Broker, W. R. Pitner, K. R. Seddon and R. D. Rogers, Green Chem., 2002, 4, 407–413.
37. D. R. MacFarlane, S. A. Forsyth, J. Golding and G. B. Deacon, Green Chem., 2002, 4, 444–448.
38. B. D. McCarthy and J. L. Dempsey, Inorg. Chem., 2017, 56, 1225–1231.
39. K. A. Kurnia, M. I. A. Mutalib and B. Ariwahjoedi, J. Chem. Eng. Data, 2011, 56, 2557–2562.
40. J. D. Holbrey and K. R. Seddon, J. Chem. Soc., Dalton Trans., 1999, 2133–2139.
41. W. Li, Y. Liu, L. Wang and G. Gao, Energy Fuels, 2017, 31, 1771–1777.
42. Z. Lei, J. Yuan and J. Zhu, J. Chem. Eng. Data, 2010, 55, 4190–4194.
43. M. Wang, L. Q. Zhang, L. X. Gao, K. W. Pi, J. Y. Zhang and C. G. Zheng, Energy Fuels, 2013, 27, 461–466.

---

Footnote

† Electronic supplementary information (ESI) available: Examples of the RRS approach, Boltzmann averaging and calculation data of ILs. Cartesian coordinates of optimized ionic liquids and details on case study. See DOI: 10.1039/c8ra04822c

---