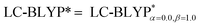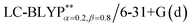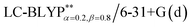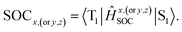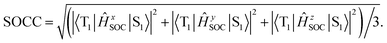Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermally activated delayed fluorescence processes for Cu(I) complexes in solid-state: a computational study using quantitative prediction†
Lingling Lv *a,
Kui Liua,
Kun Yuana,
Yuancheng Zhua and
Yongcheng Wangb
*a,
Kui Liua,
Kun Yuana,
Yuancheng Zhua and
Yongcheng Wangb
aCollege of Chemical Engineering and Technology, Tianshui Normal University, TianShui, GanSu 741001, China. E-mail: lvling100@163.com
bCollege of Chemistry and Chemical Engineering, Northwest Normal University, LanZhou, GanSu 730070, China. E-mail: ycwang02@163.com
First published on 9th August 2018
Abstract
The photophysical properties of four representative Cu(I) complex crystals have been investigated using the combination of an optimally tuned one- and two-dimensional range-separated hybrid functional 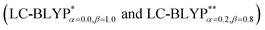 with the polarizable continuum model, and the thermal vibration correlation function (TVCF) approach. The calculated excited singlet–triplet energy gap, radiative rates and lifetimes match the experimentally available data perfectly. At 300 K, the reverse intersystem crossing (RISC) proceeds at a rate of kdir.RISC ≈ 106–8 s−1, which is 4–5 orders of magnitude larger than the mean phosphorescence rate, kP ≈ 102–3 s−1. At the same time, the ISC rate kdir.ISC ≈ 109 s−1 is again 2 orders of magnitude larger than the fluorescence rate kF ≈ 107 s−1. In the case of kdir.RISC ≫ kF and kdir.RISC ≫ kP, thermally activated delayed fluorescence should occur. Vibronic spin–orbit coupling can remarkably enhance the ISC rates by the vital “promoting” modes, which can provide crucial pathways to decay. This can be helpful for designing novel excellent TADF Cu(I) complex materials.
with the polarizable continuum model, and the thermal vibration correlation function (TVCF) approach. The calculated excited singlet–triplet energy gap, radiative rates and lifetimes match the experimentally available data perfectly. At 300 K, the reverse intersystem crossing (RISC) proceeds at a rate of kdir.RISC ≈ 106–8 s−1, which is 4–5 orders of magnitude larger than the mean phosphorescence rate, kP ≈ 102–3 s−1. At the same time, the ISC rate kdir.ISC ≈ 109 s−1 is again 2 orders of magnitude larger than the fluorescence rate kF ≈ 107 s−1. In the case of kdir.RISC ≫ kF and kdir.RISC ≫ kP, thermally activated delayed fluorescence should occur. Vibronic spin–orbit coupling can remarkably enhance the ISC rates by the vital “promoting” modes, which can provide crucial pathways to decay. This can be helpful for designing novel excellent TADF Cu(I) complex materials.
1. Introduction
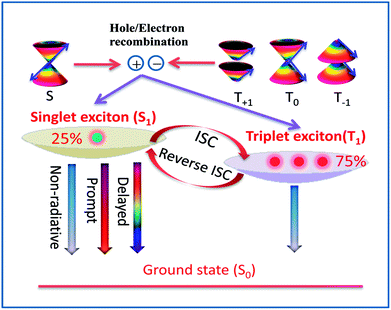
Recently, the thermally activated delayed fluorescence (TADF) materials displayed by organo-transition metal complexes and organic molecules have attracted great attention because of the remarkable variability in their emission properties for organic light-emitting diodes (OLED).1–4 Under electrical excitation, the singlet–triplet counter pairs of electrons and holes are equally weighted to recombine and yield excitons, resulting in 25% singlet excitons and 75% triplet excitons in the electroluminescence device according to spin statistics.5–7 However, the energies of all triplet excitons (75%) are dissipated as heat in the conventional fluorescent materials, which leads to a theoretical upper limit of 25% for the internal quantum efficiency (Fig. 1).6,7 To obtain high-efficiency OLED materials, recent studies have found that TADF emitters can rely on efficient thermal upconversion from the triplet state T1 into an emissive singlet state S1 through reverse intersystem crossing (RISC), which in principle, causes the efficiency of exciton utilization to reach 100%.8–10It is well known that efficient TADF must satisfy the vital condition of a small energy gap, ΔE(S1–T1), between the T1 and S1 states involved in the RISC process. One effective strategy to decrease the ΔE(S1–T1) involves using covalently linked electron donor and acceptor units and consequently, such molecules have become the focus of molecular designs adopted for TADF.11 Using this strategy, one obtains the T1 and S1 states with strong charge transfer (CT) character from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) transitions. These states are characterized by a small spatial overlap between the HOMO and LUMO, which decreases the electron exchange energy and the energy gap, ΔE(S1–T1).11,12 However, in this simple model, one negative effect is inevitably generated: the small spatial 〈HOMO|LUMO〉 overlap for S1 with CT causes the slow radiative decay rate of the S1 → S0 transition and low luminescence efficiency. Therefore, it is an essential challenge to obtain a reasonable balance between a small ΔE(S1–T1) and the oscillator strength of the S1 → S0 transition in the TADF molecular design. An accurate evaluation of ΔE(S1–T1) with a reasonable oscillator strength is necessary to guide the TADF molecular design and expand the range of TADF materials.
Moreover, it is well established that the optical properties of TADF materials can have a considerable impact as a function of their environment. In other words, TADF materials are usually mixed into appropriate host matrixes to remit the concentration quenching and exciton annihilation processes, which restrain the efficiency enhancement of OLEDs. The study reported by Yersin et al.13 has shown that the same TADF complex can have a much larger photoluminescence quantum yield in the solid state than that in solution. Therefore, it is also a challenge to be able to accurately describe the solid phase excited-state properties of TADF emitters. However, the theoretical studies of TADF materials, taking into account a solid-state environment, have great limitations so far.
From a theoretical standpoint, a reliable and computationally efficient method for the prediction of the excited state properties for the solid state would thus be highly beneficial since it would allow one to possibly help in determining the origin of the variation in experimental results. The time-dependent density functional theory (TD-DFT) is a useful and reliable tool to compute the excited states of relatively larger systems and is considerably more computationally efficient.14 Unfortunately, the conventional (semi)local exchange–correlation (XC) functionals may fail completely in predicting the electronic structure in donor–acceptor CT systems.15 In addition, for molecular crystals, the surrounding environment is substantially different from that of single molecules, ascribed to polarization effects, which is essentially a phenomenon related to nonlocal correlation. These systematic errors are mainly attributed to the inappropriate XC introduction and the potential and density can be incorrect at asymptotically large distances.16–18 Recently, the range-separated exchange (RS) density functional comprising a suitable fixed amount of exact-exchange (eX) has overcome the incorrect asymptotic behavior in the long-range limit, and provides an improved description of the excited-state properties.16–21 Abramson et al.22 reported the dielectric constant (ε) in a “screened” RS functional by replacing the 1/R asymptotic behavior with the more general asymptotic 1/(ε × R), which is required when the calculations are performed on the periodic crystals. Very recently, a more computationally efficient method was proposed by Sun et al.23 for the quantitative characterization of the excited-state properties in molecular crystals. This calculation method is to combine the polarizable continuum model (PCM) and optimally tuned RS functionals, whose advantage comes from the optimal tuning of the range-separation parameter ω for a long-range corrected (LC) functional in the PCM environment. For the simulation of a solid-state environment, the molecules in the crystal phase were “dissolved” in a solvent with the same kind of molecules as the crystal.
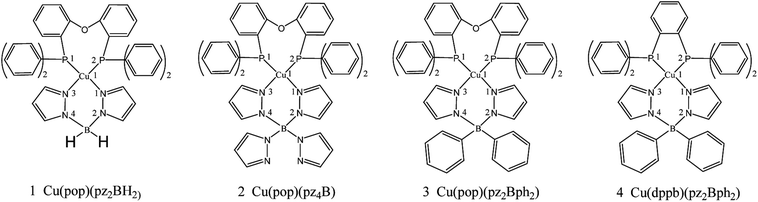
Potential candidates for Cu(I) complexes in the fields of OLEDs have attracted a lot of attention from the academic and commercial communities. A much deeper investigation of the photophysical and chemical properties of the Cu(I) compounds will lead to the development of new materials and material design strategies. In this study, we chose four representative TADF emitters that are Cu(I) complexes, namely, Cu(pop)(NN) (pop = bis(2-(diphenylphosphanyl)-phenyl)ether and NN = bis(pyrazol-1-yl)borohydrate(pz2BH2), tetrakis(pyrazol-1-yl) borate (pz4B), bis(pyrazol-1-yl)-diphenyl-borate (pz2Bph2) and dppb = 1,2-bis(diphenylphosphino)-benzene; Fig. 2), as our research objects because their extensive experimental data are available.13 Herein, the kr radiative decay rates are determined via the Einstein relationship and the kISC decay rates are quantitatively calculated using the thermal vibration correlation function (TVCF) rate theory in combination with the PCM-tuned LC-BLYP method in the solid-state.24–29 In addition, vibronic spin–orbit coupling (SOC) has been taken into account from the promoted vibration modes.
2. Computation details
2.1 Optimization of geometries
The optimal tuning method was performed according to the RS functionals. In the expression of RS hybrid functionals, the two-electron repulsion operator 1/R12 was divided into a short-range domain and a long-range domain by means of the Ewald-style partition based on the error function (erf) as follows:30
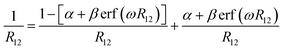 | (1) |
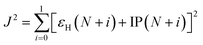 | (2) |
In addition, there have been recent studies31,32 showing that some amount of short-range HF exchange (i.e. setting α to a nonzero value) can lead to improved electronic properties and excitation energies. We used two different parameterizations: a long-range corrected LC-BLYP functional without any short-range exchange (i.e., α = 0.0, β = 1.0) as well as an LC-BLYP functional containing 20% exchange over the entire range (i.e., α = 0.2, β = 0.8) in conjunction with tuning ω via the non-empirical procedure,33 which are denoted as 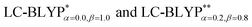 .
.
The optimization of the parameter ω was performed by tuning the optDFTw procedure,34 as described in Fig. 3, and all the ground geometries were optimized using the 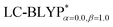 functional and 6-31+G(d) basis set as shown in Fig. 5. The geometries of the excited states were optimized using the corresponding time-dependent
functional and 6-31+G(d) basis set as shown in Fig. 5. The geometries of the excited states were optimized using the corresponding time-dependent 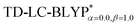 functionals. As for the simulation of the environmental solid polarization effects, the default PCM model using the integral equation formalism variant was employed, where the molecule in the crystal phase was “dissolved” in the solvent with the same kind of crystal molecules. These were performed by adding the “SCRF (PCM, solvent = generic, read)” keyword in the Gaussian 09 package.35 The settings for the PCM parameters have been explicitly described in ref. 23b.
functionals. As for the simulation of the environmental solid polarization effects, the default PCM model using the integral equation formalism variant was employed, where the molecule in the crystal phase was “dissolved” in the solvent with the same kind of crystal molecules. These were performed by adding the “SCRF (PCM, solvent = generic, read)” keyword in the Gaussian 09 package.35 The settings for the PCM parameters have been explicitly described in ref. 23b.
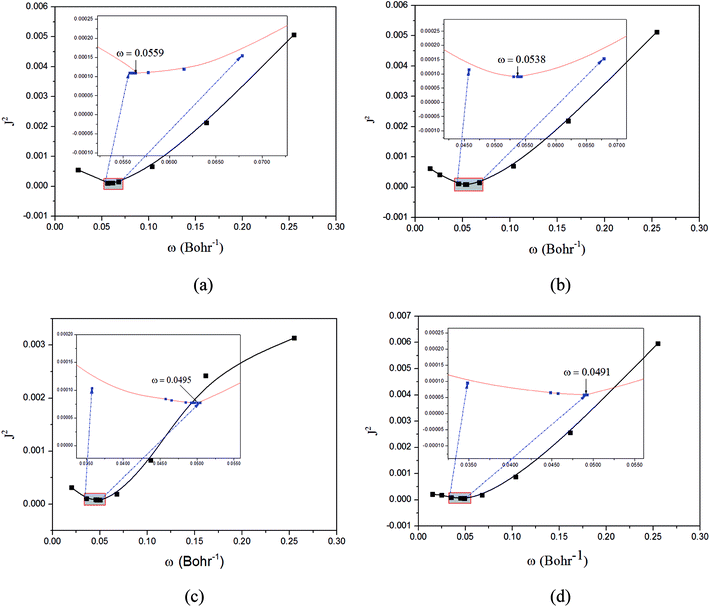 | ||
Fig. 3 Functions defined in eqn (2) used for determining of the optimally-tuned range-separation parameter ω (bohr−1) at the 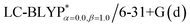 level in the solid state. (a) Cu(pop)(pz2BH2); (b) Cu(pop)(pz4B); (c) Cu(pop)(pz2Bph2); (d) Cu(dppb)(pz2Bph2). level in the solid state. (a) Cu(pop)(pz2BH2); (b) Cu(pop)(pz4B); (c) Cu(pop)(pz2Bph2); (d) Cu(dppb)(pz2Bph2). | ||
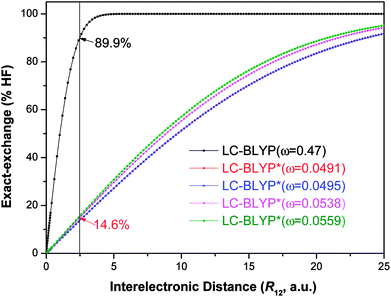 | ||
Fig. 4 Diagram of the percentage of exact-exchange (%HF) versus the interelectronic distance (R12) for the 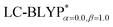 functional in the four Cu(I) complexes. functional in the four Cu(I) complexes. | ||
2.2 Calculations of the electronic-structure and energy gap ΔE(S1–T1)
High level of accuracy of calculations is crucial for the quantitative theoretical prediction of TADF molecules. As described in previous studies, the vertical excitation energies of the S0 → S1, EV(S1) and S0 → T1, EV(T1) and the energy gap ΔE(S1–T1) = EV(S1) − EV(T1) were calculated by applying the PCM-tuned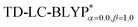 and PCM-tuned
and PCM-tuned 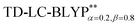 functionals, combined with the 6-31+G(d) basis set within the Tamm–Dancoff approximation (TDA).36 For comparison, two exchange–correlation functionals, namely, B3LYP (α = 0.2) and M062X (α = 0.54), and two RS hybrid functions, CAM-B3LYP (ω = 0.33, α = 0.19, α + β = 0.65) and ωB97XD (ω = 0.20, α = 0.22, α + β = 1.0), were used.23b,25 To give a quantitative characterization of the excited states, we also calculated the distance between the centroid of the hole and electron, ΔRH–L, hole–electron overlap integral SH–L, and CT excitation energy ECT corresponding to the S0 → S1 transition. These calculations were conducted at the theoretical level of PCM(ε)-tuned
functionals, combined with the 6-31+G(d) basis set within the Tamm–Dancoff approximation (TDA).36 For comparison, two exchange–correlation functionals, namely, B3LYP (α = 0.2) and M062X (α = 0.54), and two RS hybrid functions, CAM-B3LYP (ω = 0.33, α = 0.19, α + β = 0.65) and ωB97XD (ω = 0.20, α = 0.22, α + β = 1.0), were used.23b,25 To give a quantitative characterization of the excited states, we also calculated the distance between the centroid of the hole and electron, ΔRH–L, hole–electron overlap integral SH–L, and CT excitation energy ECT corresponding to the S0 → S1 transition. These calculations were conducted at the theoretical level of PCM(ε)-tuned 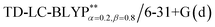 using the Multiwfn program.37
using the Multiwfn program.37
2.3 Calculations of fluorescence and phosphorescence rates
The phosphorescence transitions (T1 → S0) are strictly forbidden in the regime of non-relativistic treatment. If the SOC is considered, the pure singlet or triplet becomes a mixed state. In this case, the forbidden emission can borrow dipole activity from spin-allowed transitions (S0 ↔ Sn and T1,ζ ↔ Tm,ζ; see eqn (3)) through the perturbation SOC interactions, resulting in the non-zero intensity of transitions.38 These calculations were performed using the parallel version of the combined PCM-tuned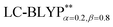 functional and restricted open-shell configuration interaction with the single excitation (DFT/ROCIS) method by the ORCA 4.0 package.39 DFT/ROCIS calculations with the parameters40 c1 = 0.21, c2 = 0.49, and c3 = 0.29 were performed using the converged restricted Kohn–Sham functions at the PCM-tuned
functional and restricted open-shell configuration interaction with the single excitation (DFT/ROCIS) method by the ORCA 4.0 package.39 DFT/ROCIS calculations with the parameters40 c1 = 0.21, c2 = 0.49, and c3 = 0.29 were performed using the converged restricted Kohn–Sham functions at the PCM-tuned 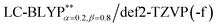 level, together with the auxiliary basis set def2/J in order to accelerate the calculations in the framework of the RI approximation. The electric dipole transition,
level, together with the auxiliary basis set def2/J in order to accelerate the calculations in the framework of the RI approximation. The electric dipole transition, 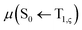 , between T1 and S0 becomes allowed and
, between T1 and S0 becomes allowed and 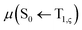 can be expressed as follows:41,42
can be expressed as follows:41,42
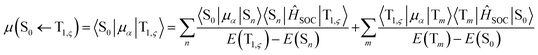 | (3) |
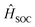 represent the electric dipole and SOC Hamiltonian, respectively. At ambient temperature, the emission rates can be calculated by eqn (4):41,42
represent the electric dipole and SOC Hamiltonian, respectively. At ambient temperature, the emission rates can be calculated by eqn (4):41,42
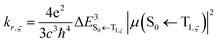 | (4) |
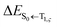 indicates a vertical emission energy.
indicates a vertical emission energy.
2.4 Calculations of ISC rates
ISC rates of the T1 ↔ S1 mainly depend on the energy gap (ΔE(S1–T1)) as well as on the strength of the SOC between T1 and S1 states. However, in TADF Cu(I) complexes, their SOC interaction is strictly forbidden due to the same CT electronic structures. Therefore, the vibronic SOC contribution to the ISC and RISC rates should be considered,43 and these calculations were conducted based on the TVCF theory using the MOMAP suite of programs.24–29 The potential energy surface of S1 was considered by using QS1 = SQT1 + D, relative to that of T1. The vector D is the displacement between S1 and T1 geometries and S is the Duschinsky rotation matrix representing the mixing of normal modes in the S1 and T1 states; Q represents the nuclear normal mode coordinates. In the Franck–Condon approximation, the ISC rate constant at temperature T is then given by eqn (5).26,44
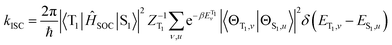 | (5) |
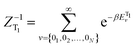 is the canonical partition function; v and u are the vibrational quantum numbers of T1 and S1 states. Further details of the formula can be found in ref. 26.
is the canonical partition function; v and u are the vibrational quantum numbers of T1 and S1 states. Further details of the formula can be found in ref. 26.
3. Results and discussion
3.1 Parameter ω optimization and the geometric structures
The optimally tuned derived ω values are given in Fig. 3 for the four Cu(I) molecular systems in the solid states; i.e., using the PCM model with the respective screening effects of the dielectric constant of the molecular crystal during the tuning process. Under the environment of the larger dielectric constants, the optimal ω values were greatly reduced to the range of 0.0491–0.0559 bohr−1 for the solid phase system, which is compared with the default ω = 0.47 bohr−1 for LC-BLYP. As discussed in detail elsewhere, since ω reflects the global delocalization degree, there is an inverse relationship between the tuned ω value and the spatial extension of the delocalization. The smaller ω values demonstrate that the electron density in the simulated crystal environment is more delocalized than that for the isolated molecule in the gas phase.In addition, from the perspective of the equation of RS functionals as shown in eqn (1), a smaller ω value corresponds to a larger interelectronic distance, R12, where the description of exchange switches from the short-range DFT-type to the long-range exact-exchange (HF-type) or, in other words, an effective electron delocalization length; the previously optimal ω values were found to decrease with increasing system size and conjugation length. However, in some instances, this correlation was not monotonous and varied strongly for systems with different electronic structures. Here, the Cu(I) complexes have different sizes, being smallest for Cu(pop)(pz2BH2) (ω = 0.0559 bohr−1) and largest for Cu(pop)(pz2Bph2) (ω = 0.0495 bohr−1) and Cu(dppb)(pz2Bph2) (ω = 0.0491 bohr−1), which has a strong dependence of ω on the size of ligands around the central Cu(I) atom.
To illustrate the above behavior, the dependence of the percentage (%HF) of eX in LC-BLYP and 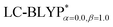 versus the R12 for four Cu(I) complexes is displayed in Fig. 4. We take the tuned ω value of the
versus the R12 for four Cu(I) complexes is displayed in Fig. 4. We take the tuned ω value of the 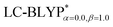 functional for the Cu(dppb)(pz2Bph2) system as an example. At R12 = 2.5 a.u. for the solid state, the HF exchange of the optimally tuned functional is 14.6% (ω = 0.0491 bohr−1), whereas the default LC-BLYP (ω = 0.47 bohr−1) gives more than 89.9% HF exchange. This indicates that the precise description of the solid phase requires the functionals to include less “localized” HF exchange and more “delocalized” DFT-BLYP exchange for the Cu(I) complexes. The eX percentage functional of the other three complexes is similar to that of Cu(dppb)(pz2Bph2).
functional for the Cu(dppb)(pz2Bph2) system as an example. At R12 = 2.5 a.u. for the solid state, the HF exchange of the optimally tuned functional is 14.6% (ω = 0.0491 bohr−1), whereas the default LC-BLYP (ω = 0.47 bohr−1) gives more than 89.9% HF exchange. This indicates that the precise description of the solid phase requires the functionals to include less “localized” HF exchange and more “delocalized” DFT-BLYP exchange for the Cu(I) complexes. The eX percentage functional of the other three complexes is similar to that of Cu(dppb)(pz2Bph2).
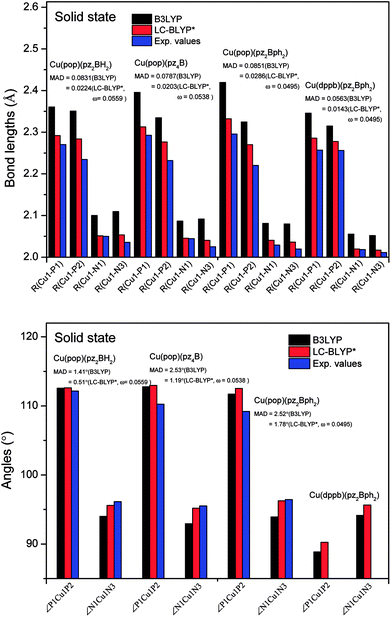
The ground state (S0) geometries of the solid state molecules were optimized using the optimally tuned functional 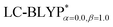 and conventional functional B3LYP. These structural parameters are illustrated in Fig. 5 and Table S1 in the ESI.† It is easily noted that the optimal tuning of functionals is very important for the geometric optimization of S0. For the B3LYP, deviations in the optimized results are much larger. For example, the mean absolute deviations (MADs) in variation between the lower and the upper deviations are 0.0563 Å and 0.0851 Å, respectively, for the bond lengths in the four Cu(I) complexes and between 1.41° and 2.53° for the bond angles, as compared with the crystal data. For the PCM-tuned (ω = 0.0559 bohr−1)
and conventional functional B3LYP. These structural parameters are illustrated in Fig. 5 and Table S1 in the ESI.† It is easily noted that the optimal tuning of functionals is very important for the geometric optimization of S0. For the B3LYP, deviations in the optimized results are much larger. For example, the mean absolute deviations (MADs) in variation between the lower and the upper deviations are 0.0563 Å and 0.0851 Å, respectively, for the bond lengths in the four Cu(I) complexes and between 1.41° and 2.53° for the bond angles, as compared with the crystal data. For the PCM-tuned (ω = 0.0559 bohr−1) 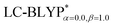 functional, the MADs were merely 0.0224 Å for the bond lengths and 0.51° for the bond angles in the Cu(pop)(pz2BH2) complexes; these estimated geometric parameters are in good agreement with experimental crystal data. In this study, we ultimately chose the PCM-tuned (TD-)
functional, the MADs were merely 0.0224 Å for the bond lengths and 0.51° for the bond angles in the Cu(pop)(pz2BH2) complexes; these estimated geometric parameters are in good agreement with experimental crystal data. In this study, we ultimately chose the PCM-tuned (TD-) 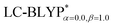 level, unless otherwise stated, to optimize the geometry structures (including the S0, S1 and T1 states) of the Cu(I) molecular crystals.
level, unless otherwise stated, to optimize the geometry structures (including the S0, S1 and T1 states) of the Cu(I) molecular crystals.
3.2 Energy gap ΔE(S1–T1) and transition properties
A concise summary of all four Cu(I) molecule excited energies obtained by TD-DFT (B3LYP, M062X, ωB97XD, CAM-B3LYP,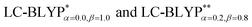 ) is given in Table 1. Overall, the two RS functionals provide significantly better predictions for the excited state energies and properties than the conventional hybrid functionals. Compared to the experimental ΔE(S1–T1) values, the energy gaps of Cu(I) molecules are most accurately calculated by
) is given in Table 1. Overall, the two RS functionals provide significantly better predictions for the excited state energies and properties than the conventional hybrid functionals. Compared to the experimental ΔE(S1–T1) values, the energy gaps of Cu(I) molecules are most accurately calculated by 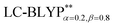 , including some short-range exchange, and least accurately predicted by B3LYP (this can be attributed to the large electron self-interaction error of the B3LYP functional, which spuriously favors the CT character of the excitations). We also found that
, including some short-range exchange, and least accurately predicted by B3LYP (this can be attributed to the large electron self-interaction error of the B3LYP functional, which spuriously favors the CT character of the excitations). We also found that 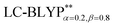 significantly improves the accuracy of these excitations in comparison to the
significantly improves the accuracy of these excitations in comparison to the 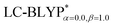 results. The calculated values of ΔE(S1–T1), 1129, 1048, 887, and 565 cm−1 for the four Cu(I) molecules, namely, Cu(pop)(pz2BH2), Cu(pop)(pz4B), Cu(pop)(pz2Bph2), and Cu(dppb)(pz2Bph2), are in very good agreement with the measured values of 1300, 1000, 800, and 370 cm−1, respectively in the powder.14 In the following investigations,
results. The calculated values of ΔE(S1–T1), 1129, 1048, 887, and 565 cm−1 for the four Cu(I) molecules, namely, Cu(pop)(pz2BH2), Cu(pop)(pz4B), Cu(pop)(pz2Bph2), and Cu(dppb)(pz2Bph2), are in very good agreement with the measured values of 1300, 1000, 800, and 370 cm−1, respectively in the powder.14 In the following investigations, 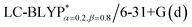 was selected to predict the excited state properties, corresponding to optimal ω values listed in Table 2.
was selected to predict the excited state properties, corresponding to optimal ω values listed in Table 2.
| Methods | Cu(pop)(pz2BH2) | Cu(pop)(pz4B) | Cu(pop)(pz2Bph2) | Cu(dppb)(pz2Bph2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ev(S1) | Ev(T1) | ΔE(S1–T1) | Ev(S1) | Ev(T1) | ΔE(S1–T1) | Ev(S1) | Ev(T1) | ΔE(S1–T1) | Ev(S1) | Ev(T1) | ΔE(S1–T1) | |
| a The experimental values of ΔE(S1–T1): 1300, 1000, 800, and 370 cm−1 for Cu(pop)(pz2BH2), Cu(pop)(pz4B), Cu(pop)(pz2Bph2), and Cu(dppb)(pz2Bph2), respectively; vertical excited energies between about 3.35 and 3.99 eV. | ||||||||||||
| B3LYP | 3.34 | 3.20 | 0.14(1129) | 3.34 | 3.22 | 0.12(968) | 3.27 | 3.16 | 0.11(887) | 3.03 | 2.96 | 0.07(565) |
| M062X | 4.42 | 4.10 | 0.32(2581) | 4.43 | 4.03 | 0.40(3226) | 4.39 | 4.09 | 0.30(2420) | 3.83 | 3.54 | 0.29(2339) |
| ωB97XD | 4.29 | 3.89 | 0.40(3226) | 4.30 | 3.89 | 0.41(3307) | 4.26 | 3.88 | 0.38(3065) | 3.83 | 3.51 | 0.32(2580) |
| CAM-B3LYP | 4.28 | 3.81 | 0.47(3791) | 4.29 | 3.80 | 0.49(3952) | 4.25 | 3.80 | 0.45(3629) | 3.81 | 3.50 | 0.31(2500) |
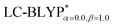 |
2.51 | 2.45 | 0.06(484) | 2.52 | 2.47 | 0.05(403) | 2.42 | 2.35 | 0.07(565) | 2.28 | 2.23 | 0.05(403) |
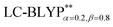 |
3.34 | 3.20 | 0.14(1129) | 3.35 | 3.22 | 0.13(1048) | 3.27 | 3.16 | 0.11(887) | 3.03 | 2.96 | 0.07(565) |
| Species | PCM(ε)-tuned | |||||
|---|---|---|---|---|---|---|
| ε | ω | IP(-εH) | EA(-εL) | Eg | ECTa | |
| a The CT excitation energy: ECT = IP − EA − 1/R; εH = HOMO energy, εL = LUMO energy. | ||||||
| Cu(pop)(pz2BH2) | 3.19 | 0.0169 | 5.01 | 0.59 | 4.42 | 0.38 |
| Cu(pop)(pz4B) | 3.23 | 0.0172 | 5.10 | 0.68 | 4.42 | 0.30 |
| Cu(pop)(pz2Bph2) | 3.49 | 0.0144 | 4.93 | 0.65 | 4.28 | 0.14 |
| Cu(dppb)(pz2Bph2) | 3.66 | 0.0131 | 4.84 | 0.78 | 4.06 | −0.63 |
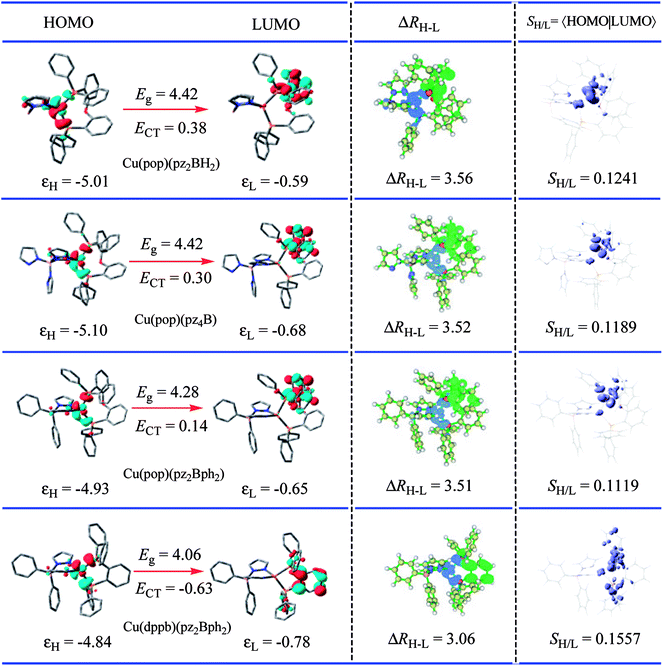
For the studied complexes, their first S1 and T1 excited states mainly come from the electronic transitions from HOMO to LUMO, and they possess obvious CT character and have the same configurations, 1CT and 3CT (see Fig. 6). Based on the quantum theory, the S1 and T1 states are separated by twice the electron exchange energy J, as illustrated in eqn (6) and (7) with ϕL and ϕH corresponding to the electron (LUMO) and hole (HOMO) orbitals involved in the transitions, respectively. The J value is determined by the spatial separation and overlap integral of ϕL and ϕH, the higher overlap of HOMO and LUMO and smaller spatial separation lead to higher J and ΔE(S1–T1).12
| ΔE(S1–T1) = E(S1) − E(T1) = 2J | (6) |
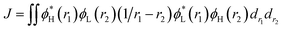 | (7) |
Thus, to gain a quantitative understanding, parameters such as the extent of hole–electron overlap (SH/L) and mean separation distance (ΔRH–L) of HOMO and LUMO associated with the S1 transitions were calculated using the Multiwfn program,37 and the calculated results are given in Fig. 6. As expected, a correlation between the ΔE(S1–T1) and SH/L was observed for the solid state Cu(I) complexes, except for Cu(dppb)(pz2Bph2) and those with a smaller overlap SH/L and therefore a smaller ΔE(S1–T1). The SH/L overlap gradually decreases, 0.1241 > 0.1189 > 0.1119 for Cu(pop)(pz2BH2), Cu(pop)(pz4B), and Cu(pop)(pz2Bph2), respectively, and the corresponding ΔE(S1–T1) values also have a decreasing trend with 1129 > 1048 > 887 cm−1. For the S1 state of Cu(dppb)(pz2Bph2) in the solid state (ε = 3.66), the calculated SH/L and ΔRH–L values are 0.1557 and 3.06 Å, respectively, which indicate that it should have a larger ΔE(S1–T1); however, contrary to the theoretical analysis, it had a smaller ΔE(S1–T1) of 565 cm−1. One key factor is that this does not consider the localisation and spatial confinement of the HOMO–LUMO. This degree of spatial confinement is very crucial, which will alter the coulombic and exchange energies. Indeed, since the S1 state of Cu(dppb)(pz2Bph2) is more delocalised than the three other S1 excited states, it will exhibit the smallest ΔE(S1–T1). This is not addressed by the relation ΔE(S1–T1) ∝ SH/L.
An understanding of the degree of spatial confinement can be gained from the energetic gap (Eg) between the HOMO and the LUMO and the CT excitation energy (ECT), which becomes larger with increasing localisation. According to the description, we would consequently expect that the larger Eg and ECT would lead to the larger ΔE(S1–T1) as confinement increases for the Cu(I) complexes and this trend is reflected in Table 2. Here, a clear trend is found and those with a larger Eg and a larger ΔE(S1–T1) are observed.
3.3 Phosphorescence and fluorescence
For excited T1 states, if their phosphorescence and non-radiative decay are slow and the energy gap ΔE(S1–T1) is small enough, then after vibration thermalisation, a reverse of ISC back to the S1 can occur followed by delayed fluorescence; therefore, a detailed study of the T1 states is very important. We know that the degeneracy of the three spin sublevels (T1,I, T1,II, and T1,III) can be lifted due to the presence of zero-field splitting (ZFS) due to the SOC interaction, which can lead to quite different radiative and non-radiative properties. Yersin et al.13,45 have reported the experimental ZFS values in the range of 1 to 10 cm−1 for Cu(I) complex crystals. The results of the calculated ZFS parameters show that the D values are in the range of 0.1 to 4.7 cm−1 at the PCM-tuned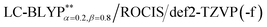 levels, consistent with the experimental values (see Table 3).
levels, consistent with the experimental values (see Table 3).
Taking into account ZFS, kP (phosphorescence) and kF (fluorescence) rates or (τ) lifetimes, have been obtained by the PCM-tuned 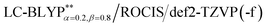 calculation at the T1 geometry, including SOC interactions, which are listed in Table 4. At room temperature, due to the usually small ZFS for the four Cu(I) complexes, an average emission decay time τav of the three sub-states can be calculated by the three individual decay times according to τav = 3(τI−1 + τII−1+ τIII−1)−1 (where τI, τII, and τIII represent the emission decay times of the TI, TII, and TIII substates, respectively).43 The phosphorescence of the four Cu(I) complexes started from T1 and all the average radiative decay rate constants kP are relatively slow (less than 103 s−1), particularly for Cu(dppb)(pz2Bph2), for which the kP was calculated to be 9.01 × 102 s−1 because the decreased rigidity of the dppb ligand leads to a smaller kP in comparison with the three Cu(I) molecules, including the pop ligand. The calculated means for the three phosphorescence rates are kP,av = 7.69 × 103 (τav = 130 μs), 1.53 × 103 (τav = 654 μs), 2.02 × 102 (τav = 495 μs), and 9.01 × 102 s−1 (τav = 1109 μs) for Cu(pop)(pz2BH2), Cu(pop)(pz4B), Cu(pop)(pz2Bph2) and Cu(dppb)(pz2Bph2), respectively, and the corresponding fluorescence rates kF (see Table 4) are in good agreement with the experimentally observed values.
calculation at the T1 geometry, including SOC interactions, which are listed in Table 4. At room temperature, due to the usually small ZFS for the four Cu(I) complexes, an average emission decay time τav of the three sub-states can be calculated by the three individual decay times according to τav = 3(τI−1 + τII−1+ τIII−1)−1 (where τI, τII, and τIII represent the emission decay times of the TI, TII, and TIII substates, respectively).43 The phosphorescence of the four Cu(I) complexes started from T1 and all the average radiative decay rate constants kP are relatively slow (less than 103 s−1), particularly for Cu(dppb)(pz2Bph2), for which the kP was calculated to be 9.01 × 102 s−1 because the decreased rigidity of the dppb ligand leads to a smaller kP in comparison with the three Cu(I) molecules, including the pop ligand. The calculated means for the three phosphorescence rates are kP,av = 7.69 × 103 (τav = 130 μs), 1.53 × 103 (τav = 654 μs), 2.02 × 102 (τav = 495 μs), and 9.01 × 102 s−1 (τav = 1109 μs) for Cu(pop)(pz2BH2), Cu(pop)(pz4B), Cu(pop)(pz2Bph2) and Cu(dppb)(pz2Bph2), respectively, and the corresponding fluorescence rates kF (see Table 4) are in good agreement with the experimentally observed values.
| State | ΔE (cm−1) | f | kr (s−1) | τ (μs) |
|---|---|---|---|---|
| a ref. 13a.b ref. 13b. | ||||
| Cu(pop)(pz2BH2) | ||||
| T1,I | 22343.9 | 1.68 × 10−6 | 5.59 × 102 | 1789 |
| T1,II | 22344.0 | 9.80 × 10−8 | 3.26 × 101 | 30670 |
| T1,III | 22348.7 | 6.76 × 10−5 | 2.25 × 104 | 44 |
| Average | kP = 7.69 × 103 | τav (T1) = 130 (610)a | ||
| S1 | 22993.3 | 5.47 × 10−2 | kF = 2.89 × 107 | τ (S1) = 0.035 (0.03)a |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Cu(pop)(pz4B) | ||||
| T1,I | 22728.3 | 1.45 × 10−6 | 5.28 × 102 | 1894 |
| T1,II | 22728.5 | 8.28 × 10−7 | 2.85 × 102 | 3509 |
| T1,III | 22729.9 | 1.09 × 10−5 | 3.75 × 103 | 267 |
| Average | kP = 1.53 × 103 | τav (T1) = 654 (450)a | ||
| S1 | 23200.0 | 1.06 × 10−2 | kF = 3.80 × 106 | τ (S1) = 0.263 (0.2)a |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Cu(pop)(pz2Bph2) | ||||
| T1,I | 20643.3 | 4.07 × 10−6 | 1.16 × 103 | 862 |
| T1,II | 20643.7 | 1.58 × 10−5 | 4.49 × 103 | 223 |
| T1,III | 20646.3 | 1.40 × 10−6 | 3.98 × 102 | 2513 |
| Average | kP = 2.02 × 103 | τav (T1) = 495 (480)a | ||
| S1 | 21380.5 | 3.44 × 10−2 | kF = 1.05 × 107 | τ (S1) = 0.095 (0.12)a |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Cu(dppb)(pz2Bph2) | ||||
| T1,I | 22576.1 | 2.43 × 10−7 | 8.26 × 101 | 12106 |
| T1,II | 22576.1 | 1.73 × 10−6 | 5.88 × 102 | 1701 |
| T1,III | 22576.2 | 5.96 × 10−6 | 2.03 × 103 | 493 |
| Average | kP = 9.01 × 102 | τav (T1) = 1109(1200)b | ||
| S1 | 22948.66 | 2.28 × 10−2 | kF = 8.06 × 106 | τ (S1) = 0.124 (0.18)b |
3.4 ISC and RISC
As discussed previously, owing to the small energy gap ΔE(S1–T1) between the S1 and T1, TADF should, in principle, be possible. However, to actually take place effectively, S1 has to be repopulated, which indicates that the RISC rate should be larger than the rates of radiative and nonradiative decay of the T1 state to the S0 state. In fact, the S1 and T1 states have the same electronic configurations and almost equivalent weights, and their direct SOC interaction is almost forbidden. In this case, vibronic spin–orbit coupling effects should be considered.Intersystem crossing rate constants were calculated by considering the direct spin–orbit coupling, (kdir.ISC/RISC) and the vibronic spin–orbit coupling, (kvib.ISC/RISC) between the T1 and S1 states, as shown in Table 5. As can be seen from Tables 4 and 5, for the four Cu(I) complexes, RISC rates are approximately kdir.RISC ≈ 106–8 s−1 at 300 K, which is 4–5 orders of magnitude larger than the mean phosphorescence rate, kP ≈ 102–3 s−1. This indicates that the S1 state can be redistributed from the T1 state by the RISC process. At the same time, the ISC rate kdir.ISC ≈ 109 s−1 is again 2 orders of magnitude larger than the fluorescence rate kF ≈ 107 s−1. Based on the kinetic analysis of a three-level system proposed by Kirchhoff et al.,46 in the case of kdir.ISC > kF + kIC0 and kdir.RISC > kP + kISC0, the S1 and T1 state populations rapidly equilibrate before decaying radiatively at room temperature, and TADF should be observable. Here, the rate constants of the internal conversion of S1 to S0 (kIC0) and of ISC from T1 to S0 were not calculated owing to the larger energy difference between S1 (or T1) and S0, assuming that these processes are much slower than the radiative rates and will be omitted in the following discussion.
| T = 300 K | kdir.ISC | kdir.RISC | kvib.ISC | kvib.RISC |
|---|---|---|---|---|
| Cu(pop)(pz2BH2) | 4.72 × 109 | 6.97 × 106 | 1.39 × 1011 | 1.97 × 108 |
| Cu(pop)(pz4B) | 5.68 × 109 | 1.23 × 107 | 1.74 × 1010 | 3.79 × 107 |
| Cu(pop)(pz2Bph2) | 6.14 × 109 | 2.93 × 107 | 7.94 × 1011 | 3.78 × 109 |
| Cu(dppb)(pz2Bph2) | 1.57 × 109 | 1.04 × 108 | 4.85 × 1011 | 1.08 × 1010 |
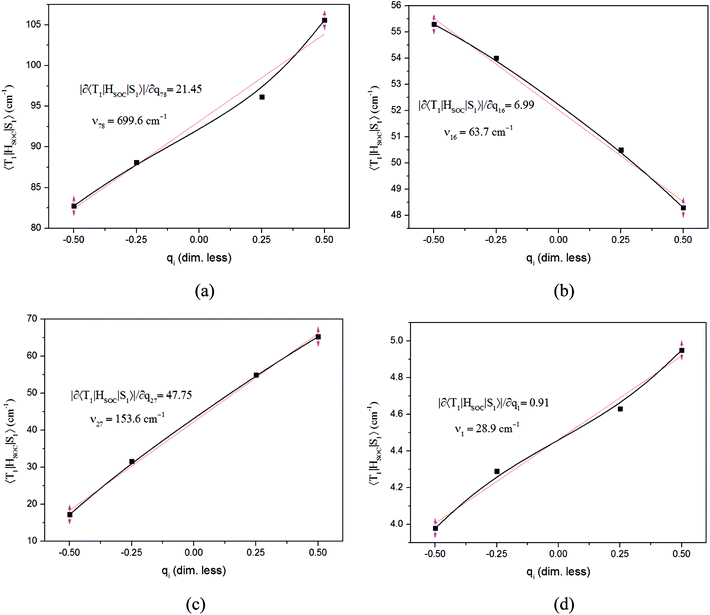
The first equilibrium condition, kdir.ISC ≫ kF is easily satisfied at all temperatures, while the second condition, namely kdir.RISC ≫ kP, because of the strong dependence on temperature, is not. A spin-forbidden T1 ↔ S1 transition requires the effect of SOC that provides a major mechanism for RISC. SOC induces a different spin-multiplicity mixing that allows the wave function to break spin symmetry, but direct SOC between S1 and T1 states tends to zero; thus, a kind of geometrical alteration must exist, which either leads to the increase in the spin–orbit interaction or causes direct T1–S1 intersection. For the T1 state, among many vibration modes, only a few vibration modes play a significant role in altering the geometric structure, inducing stronger SOC interaction. In the present study, these favorite modes are called “promoting” modes, which are determined by Huang-Rhys factors and related reorganization energies of the normal modes, i (see Table S2 in ESI†). Their relationship can be expressed as follows:47
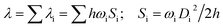 | (8) |
The values of component-averaged 〈T1|HSOC|S1〉 SOCs calculated along the displacement of the vital “promoting” modes with respect to the coordinates at the equilibrium geometry are illustrated in Fig. 8. For Cu(pop)(pz2BH2), Cu(pop)(pz4B), Cu(pop)(pz2Bph2) and Cu(dppb)(pz2Bph2), the promoting modes ν78, ν16, ν27, and ν1 with frequencies of 699.6, 63.7, 153.6 and 28.9 cm−1, corresponding to Huang-Rhys factors Si = 2.07, 1.07, 4.27, and 2.42 (see Table S2 in ESI†), respectively, lead to the remarkable increase in the 〈T1|HSOC|S1〉 SOCs in the ranges of 82.5–105.2, 48.5–55.3, 16.2–65.3, and 4.0–4.9 cm−1, respectively. Recalling that we calculated the direct SOC to be several orders of magnitude lower, the vibronic SOC may thus be suspected to be the dominant coupling interaction here. The results show that vibronic SOC can remarkably enhance the ISC rates between T1 and S1. The largest ISC rates, kvib.ISC, including vibronic SOC, were actually obtained for the non-radiative transition T1 ↔ S1 and were of the order of ≈1010–11 s−1, which is about 2 orders of magnitude larger than kdir.ISC. Moreover, the RISC rates from T1 to S1 are affected by the same intensity. Therefore, considering the case of the vibronic SOC, TADF should be obviously observable.
4. Conclusions
The accuracy of the calculation level is crucial for the quantitative theoretical prediction of the photophysical properties of TADF molecules. In this study, the geometries and photophysical properties of a series of TADF Cu(I) crystal complexes have been quantitatively investigated using a methodology proposed by Sun et al. This method uses the combination of an optimally tuned one- and two-dimensional range-separated hybrid functional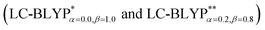 with the polarizable continuum model, in which the solid-state screening effects are achieved via the introduction of the solid-state dielectric constant, ε. When using an optimal tuning ω value, we find that the LC technique gives an outstanding description of the charge-transfer excited state properties. The calculated results have demonstrated that the two-dimensional tuning of the
with the polarizable continuum model, in which the solid-state screening effects are achieved via the introduction of the solid-state dielectric constant, ε. When using an optimal tuning ω value, we find that the LC technique gives an outstanding description of the charge-transfer excited state properties. The calculated results have demonstrated that the two-dimensional tuning of the 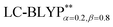 functional provides excellent agreement with experimental data. In contrast, we find that reoptimizing the fraction of the Hartree Fock exchange in conventional hybrid functionals still yields an inconsistent description of excitation energies. For geometries, the one-dimensional tuning of the range-separated hybrid functional
functional provides excellent agreement with experimental data. In contrast, we find that reoptimizing the fraction of the Hartree Fock exchange in conventional hybrid functionals still yields an inconsistent description of excitation energies. For geometries, the one-dimensional tuning of the range-separated hybrid functional 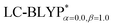 performs slightly better than both the B3LYP and
performs slightly better than both the B3LYP and 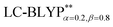 functionals.
functionals.
Photophysical radiation and non-radiation processes by combining an optimal tuning ω value of LC functional methods and TVCF rate theory have been comprehensively investigated for four Cu(I) complexes. At 300 K, the RISC rate was kdir.RISC ≈ 106–8 s−1, which is 4–5 orders of magnitude larger than the mean phosphorescence rate, kP ≈ 102–3 s−1. This indicates that the S1 state can be redistributed from the T1 state by the RISC process. At the same time, the ISC rate kdir.ISC ≈ 109 s−1 was again 2 orders of magnitude larger than the fluorescence rate kF ≈ 107 s−1. In the case of kdir.ISC ≫ kF and kdir.RISC ≫ kP, the TADF phenomenon should be observable. Hence, the electronic-vibrational coupling activated by temperature is responsible for the occurrence of delayed fluorescence in Cu(I) complexes. It is worth noting that vibronic spin–orbit coupling can remarkably enhance the ISC rates between T1 and S1 by the vital “promoting” modes with the larger Huang-Rhys factor. These “promoting” modes correspond to the distortion motion of the phenylene ring of the pop or dppb ligands, which can provide an important pathway to decay between T1 and S1, and would be helpful for designing excellent novel TADF Cu(I) complex materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The study was supported by the National Natural Science Foundation of China (Grant No. 21263022, 21663025, 21663024). We gratefully thank Dr Haitao Sun (East China Normal Universty) for providing the help in using the PCM-tuned LC-BLYP* approach.References
- H. Xu, R. F. Chen, Q. Sun, W. Lai, Q. Q. Su, W. Huang and X. G. Liu, Chem. Soc. Rev., 2014, 43, 3259–3302 RSC.
- Z. Y. Yang, Z. Mao, Z. L. Xie, Y. Zhang, S. W. Liu, J. Zhao, J. R. Xu, Z. G. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. H. Li, R. F. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 47, 7931–7956 CrossRef PubMed.
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2011, 225, 2622–2652 CrossRef.
- T. Ogiwara, Y. Wakikawa and T. Ikoma, J. Phys. Chem. A, 2015, 119, 3415–3418 CrossRef PubMed.
- M. A. Baldo, D. O'brien, Y. You, A. Shoustikov, S. Sibley, M. Thompson and S. Forrest, Nature, 1998, 395, 151–154 CrossRef.
- F. B. Dias, K. B. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef PubMed.
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5505 CrossRef.
- B. Zhao, T. Zhang, B. Chu, W. Li, Z. Su, Y. Luo, R. Li, X. Yan, F. Jin and Y. Gao, Org. Electron., 2015, 17, 15–21 CrossRef.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef PubMed.
- M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed.
- T. Chen, L. Zheng, J. Yuan, Z. F. An, R. F. Chen, Y. Tao, H. H. Li, X. J. Xie and W. Huang, Sci. Rep., 2015, 5, 10923 CrossRef PubMed.
- (a) R. Czerwieniec, J. Yu and H. Yersin, Inorg. Chem., 2011, 50, 8293–8301 CrossRef PubMed; (b) R. Czerwieniec and H. Yersin, Inorg. Chem., 2015, 54, 4322–4327 CrossRef PubMed.
- J. Föller, M. Kleinschmidt and C. M. Marian, Inorg. Chem., 2016, 55, 7506–7516 CrossRef PubMed.
- H. T. Sun, C. Zhong and J.-L. Brédas, J. Chem. Theory Comput., 2015, 11, 3851–3858 CrossRef PubMed.
- J. Autschbach and M. Srebro, Acc. Chem. Res., 2014, 47, 2592–25602 CrossRef PubMed.
- D. J. Tozer, J. Chem. Phys., 2003, 119, 12697–12699 CrossRef.
- T. Körzdörfer and J. L. Brédas, Acc. Chem. Res., 2014, 47, 3284–3291 CrossRef PubMed.
- S. P. Huang, Q. S. Zhang, Y. Shiota, T. Nakagawa, K. Kuwabara, K. Yoshizawa and C. Adach, J. Chem.Theory. Comput., 2013, 9, 3872–3877 CrossRef PubMed.
- U. Salzner and A. Aydin, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef PubMed.
- T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820 CrossRef PubMed.
- S. Refaely-Abramson, S. Sharifzadeh, M. Jain, R. Baer, J. B. Neaton and L. Kronik, Phys. Rev. B, 2013, 88, 081204 CrossRef.
- (a) H. T. Sun, S. Ryno, C. Zhong, M. K. Ravva, Z. R. Sun, T. Körzdörfer and J.-L. Brédas, J. Chem. Theory Comput., 2016, 12, 2906–2916 CrossRef PubMed; (b) Z. Hu, B. Zhou, Z. R. Sun and H. T. Sun, J. Comput. Chem., 2017, 38, 569–575 CrossRef PubMed.
- Q. Peng, Y. P. Yi, Z. G. Shuai and J. S. Shao, J. Chem.Phys., 2007, 126, 114302 CrossRef PubMed.
- Y. L. Niu, Q. Peng, C. M. Deng, X. Gao and Z. G. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef PubMed.
- Q. Peng, Y. L. Niu, Q. Shi, X. Gao and Z. G. Shuai, J. Chem. Theory Comput., 2013, 9, 1132–1143 CrossRef PubMed.
- Y. L. Niu, W. Q. Li, Q. Peng, H. Geng, Y. P. Yi, L. J. Wang, G. J. Nan, D. Wang and Z. G. Shuai, Mol. Phys., 2018, 116, 1078–1090 CrossRef.
- L. L. Lv, K. Yuan and Y. C. Wang, Org. Electron., 2017, 51, 207–219 CrossRef.
- L. L. Lv, K. Yuan and Y. C. Wang, Phys. Chem. Chem. Phys., 2018, 20, 6548–6561 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- A. E. Raeber and B. M. Wong, J. Chem. Theory Comput., 2015, 11, 2199–2209 CrossRef PubMed.
- M. A. Rohrdanz, K. M. Martins and J. M. Herber, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- D. A. Egger, S. Weismann, S. Refaely-Abramson, S. Sharifzadeh, M. Dauth, R. Baer, S. Kummel, J. B. Neaton, E. Zojer and L. Kronik, J. Chem. Theory Comput., 2014, 10, 1934–1952 CrossRef PubMed.
- T. Lu, optDFTw and scanDFTw program v1.0, https://sobereva.com/346, (2017-3-8) Search PubMed.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision-D.01, Gaussian Inc, Wallingford, CT, 2009 Search PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef PubMed.
- K. Sugisaki, K. Toyota, K. Sato, D. Shiomi and T. Takui, J. Phys. Chem. A, 2016, 120, 9857–9866 CrossRef PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 Search PubMed.
- M. Roemelt and F. Neese, J. Phys. Chem. A, 2013, 117, 3069–3083 CrossRef PubMed.
- B. Minaev, G. Baryshnikov and H. Agren, Phys. Chem. Chem. Phys., 2016, 16, 1719–1758 RSC.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537 CrossRef PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018 DOI:10.1021/acs.chemrev.7b00617.
- Q. Peng, D. Fan, R. H. Duan, Y. P. Yi, Y. L. Niu, D. Wong and Z. G. Shuai, J. Phys. Chem. C, 2017, 121, 13448–13456 CrossRef.
- R. Czerwieniec, M. J. Leitl, H. H. H. Homeier and H. Yersin, Coord. Chem. Rev., 2016, 325, 2–28 CrossRef.
- J. R. Kirchhoff, R. E. Gamache Jr, M. W. Blaskie, A. A. Del Paggio, R. K. Lengel and D. R. McMillin, Inorg. Chem., 1983, 22, 2380–2384 CrossRef.
- P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04978e |
| This journal is © The Royal Society of Chemistry 2018 |