Open Access Article
Open Access ArticleA hybrid micromixer with planar mixing units†
Sajad Razavi Bazazab,
Ali Abouei Mehrizi*b,
Sadegh Ghorbanic,
Steven Vasilescud,
Mohsen Asadnia e and
Majid Ebrahimi Warkiani
e and
Majid Ebrahimi Warkiani *af
*af
aSchool of Biomedical Engineering, University of Technology Sydney, New South Wales 2007, Australia. E-mail: majid.Warkiani@uts.edu.au
bBiomedical Engineering Division, Department of Life Science Engineering, Faculty of New Sciences and Technologies, University of Tehran, Tehran, Iran. E-mail: abouei@ut.ac.ir
cDepartment of Anatomical Sciences, Faculty of Medicine, Tarbiat Modares University, Tehran, Iran
dFaculty of Science, University of Technology Sydney, New South Wales 2007, Australia
eDepartment of Engineering, Faculty of Science and Engineering, Macquarie University, Sydney, NSW 2109, Australia
fInstitute of Molecular Medicine, Sechenov University, Moscow 119991, Russia
First published on 25th September 2018
Abstract
The application of microfluidic systems in chemical and biological assays has progressed dramatically in recent years. One of the fundamental operations that microfluidic devices must achieve is a high mixing index. Of particular importance is the role of planar mixing units with repetitive obstacles (MURO) in the formation of micromixers. To date, a myriad of planar passive micromixers has been proposed. However, a strategy for the combination of these units to find an efficient planar mixer has not been investigated. As such, five different MURO have been selected to form a “hybrid micromixer,” and their combination was evaluated via numerical and experimental methods. These mixing units include ellipse-like, Tesla, nozzle and pillar, teardrop, and obstruction in a curved mixing unit. Since these units have distinctive dimensions, dynamic and geometric similarities were used to scale and connect them. Afterwards, six slots were designated to house each mixing unit. Since the evaluation of all possible unit configurations is not feasible, the design of experiment method is applied to reduce the total number of experiments from 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 to 25. Following this procedure, the “hybrid” micromixer proposed here, comprising Tesla, nozzle and pillar, and obstruction units, shows improved performance for a wide range of Re (i.e., mixing index of >90% for Re 0.001–0.1, 22–45) over existing designs. The use of velocity profiles, concentration diagrams, vorticity and circulation plots assist in the analysis of each unit. Comparison of the proposed “hybrid” micromixer with other obstacle-based planar micromixers demonstrates improved performance, indicating the combination of planar mixing units is a useful strategy for building high-performance micromixers.
625 to 25. Following this procedure, the “hybrid” micromixer proposed here, comprising Tesla, nozzle and pillar, and obstruction units, shows improved performance for a wide range of Re (i.e., mixing index of >90% for Re 0.001–0.1, 22–45) over existing designs. The use of velocity profiles, concentration diagrams, vorticity and circulation plots assist in the analysis of each unit. Comparison of the proposed “hybrid” micromixer with other obstacle-based planar micromixers demonstrates improved performance, indicating the combination of planar mixing units is a useful strategy for building high-performance micromixers.
1 Introduction
There have been many studies recently investigating the implementation of microfluidic systems in biological and chemical assays. Microfluidic systems offer several advantages over lab scale operations stemming from elevated heat and mass transfer; a result of high surface area to volume ratios. Higher levels of sensitivity, fast and straightforward fabrication as well as the practicability of in situ operation make them ideal.1 The future of biological research could greatly benefit from microfluidic devices, among which micromixers—exhibiting precise and controllable features—have manifold practical applications.2 Micromixer applications are not limited to chemical synthesis; they can also contribute to DNA purification, synthesis of nucleic acids, cell lysis, drug delivery, biological analysis, and polymerase chain reaction (PCR).3,4 For example, Kim et al. reported the use of micromixers to enhance the mixing of glucose and glucose oxidase in chemical synthesis. Their results indicated a mixing index of 81 to 91% within a range of 0.08 to 16 Reynolds numbers (Re).5 In another study, Kim et al. makes use of rapid micromixers to conduct an investigation in organic synthesis; the reported mixing index and resulting product yield were 80% and 91%, respectively.6 Micromixers are also critical in microreactors. Ko and colleagues utilized a micromixer with different nozzle and pillar units for DNA ligation where the maximum mixing efficiency was reported to be 87.7% in Re of 66.5.7 Tobias et al. used an active micromixer to investigate the relation between metastasizing of tumors and the formation of thrombosis.8 Nason et al. used a zigzag micromixer for biological analysis, specifically drug screening, where the mixing index was reported as 79.4%.9 Micromixers continue to be applied to a diverse range of applications from biological analysis to chemical synthesis.Micromixers typically fall in the two categories of active and passive.10 Active micromixers rely on external forces such as thermal, acoustic, magnetic, and electro-kinetic to improve the mixing efficiency while passive micromixers do not need an external power source.11 Although active micromixers have high mixing efficiency, their power requirements and added complexity make them a less viable option. In contrast, passive micromixers rely on chaotic advection by way of their geometry to stretch, fold, split, or break the flow of fluids. Furthermore, they also rely on molecular diffusion by lamination of the flow and an increase the surface area between fluid layers. These effects afford more versatility in this regard.12 They can be easily integrated with other microfluidic components such as micropumps and microvalves in order to make a lab-on-a-chip device, “a device which integrates several distinct experimental functions into a single integrated circuit.13,14” Furthermore, they are easily fabricated and do not require an external power/force to manipulate the fluid. Passive micromixers do not always require low Re or a fixed flow rate for operation.15 Hence, an adaptable micromixer with an appropriate mixing index for a range of different Re should be proposed.
Based on the channel geometry, passive micromixers are divided into two groups. The first group consists of devices with either simple or complicated geometries with no repetitive design patterns. In this group, the geometry is manipulated to create either Dean forces or chaotic advection to increase molecular diffusion and in turn the mixing efficiency. The second group has two or more mixing units that repeat along the length of the microchannel. Generally, passive micromixers with mixing units can be categorized into three separate classes: planar mixing units with repetitive obstacles (MURO), planar mixing units with repetitive units (MURU), and mixing units with repetitive 3D units (MUR3DU). Generally, micromixers whose height changes with length are defined as 3D micromixers.16 In these types of micromixers, the Z-direction plays a significant role in mixing efficiency as it impacts chaotic advection and Dean forces. On the other hand, micromixers which have the same height are referred to as planar micromixers. The salient feature of mixing units with 3D units is their high mixing index. However, the complicated fabrication process of these units as well as the time-consuming process for integration with other components (in a lab-on-a-chip device) are considerable issues. In MURU, stream flow varies with the geometry of the channel while no additional obstacles are being used. These kinds of mixing units chiefly use split and recombine (SAR) techniques in which the flow patterns separate into sub-channels, and later re-combine. Since the geometry manipulation is the only variable of these mixing units, it is often difficult to reach the desired mixing efficiency. Furthermore, in some cases, an increase in geometric complexity may complicate the fabrication processes. Micromixers with MURO have a specific patterned obstacle which is repeated along the length of the microchannel. Based on their shape, obstacles can break the flow pattern of the stream and create additional vortices and enhance chaotic advection. Therefore, the mixing index of MURO is significantly higher than MURU, making them the favorable choice for planar mixing units.
A review of relevant publications reveals that numerous mixing units have been proposed. Elliptical units,17 Tesla units,18 E-shaped mixing units,19 F-shaped mixing units,20 and J-shaped mixing units21 are just a few mixing units with obstacles that have been named. In some cases, a unit is proposed, and then, several groups work to improve its efficiency regarding their mixing units, pressure drop, mixing time, and so forth. For example, rhombic mixing units, which fall into the MURU category, were initially proposed by C. K. Chung et al.22 inspired from a zigzag microchannel. This lead to the publication of more than six papers working with this type of mixing unit. Among those papers, one of them added obstacles in the microchannel,23 while another one appended an extra sub-branch.24 Shakhawat Hossain et al. utilized three-split rhombic sub-channels to increase the mixing efficiency.25 Although numerous mixing units are offered, a combination of these units together is not investigated, to date. Since there are myriad ways to unite certain nominated MURO together, a solution has to be implemented to address this issue. As a result, the design of experiment (DOE) method is employed to organize the combination of mixing units and reduce the total number of experiments (please refer to ESI† for a detailed history of DOE).
The primary aim of this study is to investigate the combination of different MURO to form a “hybrid” micromixer for a wide range of applications. At first, nominated planar mixing units were delineated. Then, the appropriate method of DOE was employed to investigate the combination of these units. In order to connect these units together efficiently and correctly, dynamic and geometric similarities were utilized. Since obtaining experimental results for a large number of experiments is time consuming, labour intensive, and costly, a validation process has been performed in order to be confident in the CFD codes. A number of combined micromixers were fabricated, tested, and investigated during the entire process. Ensuing analysis using the S/N ratio diagrams allowed us to determine the optimum results of the MURO. After selecting the optimized micromixer with MURO, as the “hybrid” micromixer, the impact of each mixing unit on the total performance of the micromixer was carefully investigated. This investigation yielded a variety of results that have been depicted. Following these processes, the function of the “hybrid” micromixer over a wide range of applications was carefully evaluated.
2 Modeling assumptions and fabrication process
Firstly, the theoretical background behind the micromixer designs, including the governing equations, will be presented. This is followed by the description of DOE and the selected geometries of the MURO, as well as the fabrication process used in this study.2.1 Theoretical aspect of the “hybrid” micromixer
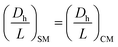 | (1a) |
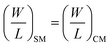 | (1b) |
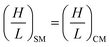 | (1c) |
Due to the effects of mass advection and mass diffusion during mixing, the velocity and concentration are two vital parameters in the mixing process. As a result, two dimensionless numbers (either of which is responsible for one vital parameter) are applied to evaluate the dynamic similarity. The first one is Re which indicates the ratio of inertia to viscous forces and is defined by eqn (2).
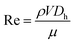 | (2) |
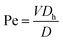 | (3) |
Re in the SM and CM must be similar in order to confirm identical fluid characteristics. By using fluids in the SM and CM with the exact same physical properties, eqn (4) will be obtained.
| (Re)SM = (Re)CM → (VDh)SM = (VDh)CM | (4) |
Pe will be achieved if the diffusion coefficient is divided in both sides. Thus, if Re is the same in both the SM and CM, Pe will be maintained, and the dynamic similarity can be confirmed.
| ∇·V = 0 | (5) |
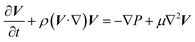 | (6) |
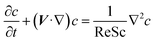 | (7) |
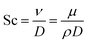 | (8) |
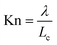 | (9) |
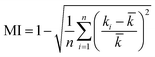 | (10) |
In eqn (10), MI is the mixing index, n is the total numbers of sample points, ki is the mole fraction over the outlet cross-section, and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) is the average mole fraction. The value of MI varies between 0 and 1 where MI = 0 (0% mixing) indicates no mixing, while MI = 1 represents complete mixing (100% mixing). The transverse diffusion time can be calculated by eqn (11).
is the average mole fraction. The value of MI varies between 0 and 1 where MI = 0 (0% mixing) indicates no mixing, while MI = 1 represents complete mixing (100% mixing). The transverse diffusion time can be calculated by eqn (11).
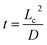 | (11) |
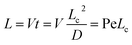 | (12) |
Since Pe is directly related to V, by increasing Pe, V will be increased, and as a result, so will Re. Eqn (12) illustrates that a higher Pe is related to mixing as a result of diffusion for a limited range of L. This condition is true if the value of Re is less than the critical point in which the turbulent flow occurs or if it is unable to generate additional vortices and chaotic advection. Higher values for Re contribute to a higher Pe and as a result, the MI is decreased. The critical value of Re is contingent on the geometry of the mixer and the velocity of the flow. After the critical point, when streams reach planted obstacles, the laminar flow breaks up thereby inducing the formation of a secondary flow field, detaching the boundary layer, and generating the vortices. The vortices generated a curling action in which the stream broke up into layers and the diffusion distance between the molecules of liquids decreased. During this process, mass advection was dominant and the passive method for mixing proved advantageous for chaotic advection.
2.2 Design of experiment and the geometry of selected mixing units with obstacles
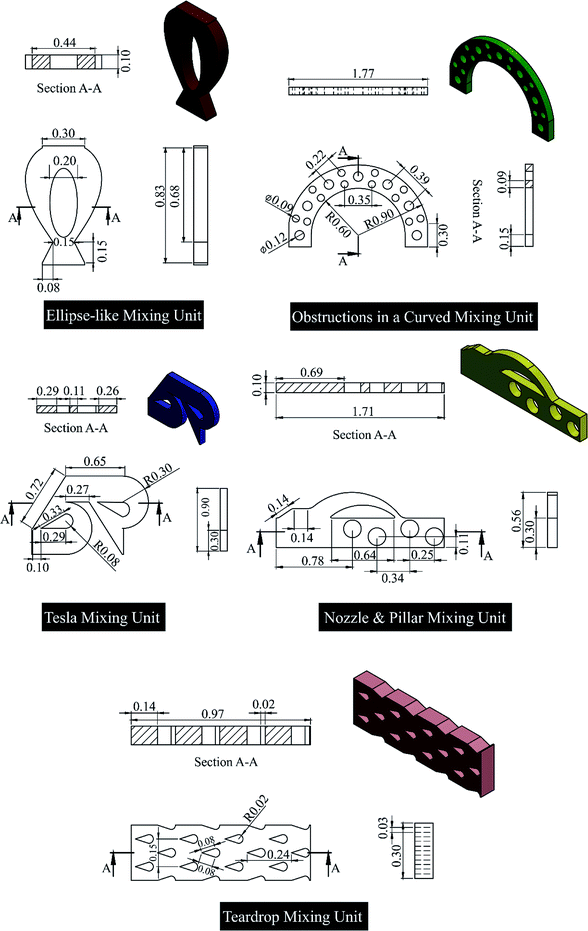
For the aim of forming a “hybrid” micromixer, five MURO were selected, each of which had a unique feature. It is of significant importance to mention that these units have to approximately carry the same volume of samples; otherwise, outliers in the result of DOE as a statistical approach occur. In addition, if a unit from a famous family had been selected, meticulous attention had to be paid to whether the latest generation of this unit had been selected or not. Furthermore, inherent features of units must remain intact. For instance, in some cases, when the flow passed the first mixing unit, the flow changed 90 degrees counterclockwise or clockwise, or the direction of the mixing unit changed from upward to downward, or vice versa. In all cases, this feature for the “hybrid” micromixer had to be maintained. Following an investigation into MURO, five units, each of which is illustrated in Fig. 1, were selected. The first selected MURO was an ellipse-like mixing unit.17 In the original study, Nhut Tran-Minh used ten mixing units which were connected together with a link to build a micromixer. The cross-section of the outlet of each unit was smaller than that of the inlet of each unit, and this led to an increase in the outlet velocity. Therefore, at the outlet of each unit, two flows were recombined with high velocity, so that the mixing index increased. The second MURO chosen was circular in shape with obstructions in a curved microchannel. The microchannel connected seven units together in which the first one was orientated upward, the second one was downward, and others followed the same pattern.27 As we aimed to have a combined micromixer with minimal length, the selection of one unit informed the selection of the following unit. When considering mixing units, two categories exist. The first is non-directional, whereas the second may be orientated upwards or downwards about the center axis. If a directional unit with an upward pattern is selected, the following directional unit must be orientated downwards, and vice versa. Therefore, in order to minimize the length of the micromixer, directional units were not immediately repeated.The third unit was Tesla mixing unit. Tesla structure had formerly been utilized in in-plane microvalves and micropumps.28,29 In 2003, Chien-Chong Hong et al. proposed a micromixer in which a Tesla structure was used.18 Then, Ali Asgar S. Bhagat used this structure to enhance particle dispersion in his designed micromixer.30 Shakhwat Hossain showed by a parametric study that the pressure drop and the mixing index in the Tesla structure strictly depended on geometrical parameters. He opted for a specific method where he optimized the parameters of Tesla structure,31 obtaining the scaled Tesla structure illustrated in Fig. 1. The fourth mixing unit was a mixture of nozzle and pillar mixing units which was proposed by Yong-Jun Ko et al.7 The device had been mainly applied for DNA ligation. In the mentioned study, three micromixers with separate mixing units were tested and the appointed one showed a meaningful mixing index in high Re numbers, which was employed for this study. Similar to the second selected unit, this unit arrangement was also upward–downward. Therefore, its direction changed when flow passed through it. The last selected unit was a unit with teardrop obstruction elements. Kristina J. Cook et al. in her study employed uneven interdigital inlets to investigate her proposed micromixer for the Re ranging between 1 and 100.32 A series of obstacles in the shape of a teardrop were used to increase the mixing efficiency. Fig. 1 demonstrates the nominated mixing units after scaling from their centroid with two extra views and an isometric 3D view.
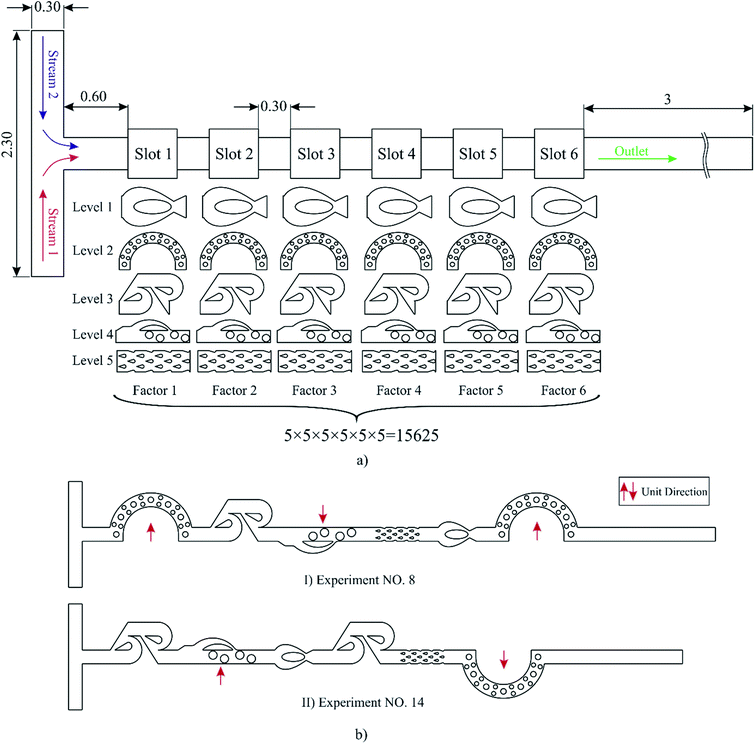
Although increasing the number of mixing units leads to an increase in the mixing index, the total length of micromixer is important as it has to be integrated with other parts of a lab-on-a-chip device. Six design slots were selected for potential mixing units and all these units were linked together with a connecting channel. Since we scaled units about their centroid to successfully assemble them, the height of units differed from each other. Assembling units with different heights could cause such unpredictable and uncontrollable effects as accelerated or decelerated flows to create additional vortices and undesirable pressure drops. These devices referred to as planar micromixers, owing to the fact that the Z direction was the same in each unit, experienced no transverse effect. The Z direction had the least effect on the total function of each unit. Thus, a specific height of 100 μm prevalent in planar MURO7,12,27,33 was proposed for the height of all units and “hybrid” micromixer to obviate all the mentioned detrimental effects. The schematic design of the “hybrid” micromixers with MURO with all possible number of experiments is elucidated in Fig. 2a.
Fig. 2a shows that so as to find the best combination of MURO, six factors, all of which have 5 levels, exist. Therefore, a total number 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 experiments and simulations had to be carried out which was not feasible in the real world. Since our data is categorical, Taguchi method has been employed as a DOE. As the order of levels in Taguchi method was not important, the arrangement of factors and levels are similar to Fig. 2a. For the six factors and five levels, Taguchi offered the orthogonal array of L25 (56 which 5 denotes number of factors and 6 represents number of levels for each factor) which reduced the total number of experiments from 15
625 experiments and simulations had to be carried out which was not feasible in the real world. Since our data is categorical, Taguchi method has been employed as a DOE. As the order of levels in Taguchi method was not important, the arrangement of factors and levels are similar to Fig. 2a. For the six factors and five levels, Taguchi offered the orthogonal array of L25 (56 which 5 denotes number of factors and 6 represents number of levels for each factor) which reduced the total number of experiments from 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 to 25 with its specific combination. The detailed table of Taguchi is indicated in Table 1 where the numbers indicate the level (mixer type) based on Fig. 2. (Please refer to ESI† for a comprehensive description of Taguchi method)
625 to 25 with its specific combination. The detailed table of Taguchi is indicated in Table 1 where the numbers indicate the level (mixer type) based on Fig. 2. (Please refer to ESI† for a comprehensive description of Taguchi method)
| Experiments | Slots | |||||
|---|---|---|---|---|---|---|
| Slot 1 | Slot 2 | Slot 3 | Slot 4 | Slot 5 | Slot 6 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 |
| 4 | 1 | 4 | 4 | 4 | 4 | 4 |
| 5 | 1 | 5 | 5 | 5 | 5 | 5 |
| 6 | 2 | 1 | 2 | 3 | 4 | 5 |
| 7 | 2 | 2 | 3 | 4 | 5 | 1 |
| 8 | 2 | 3 | 4 | 5 | 1 | 2 |
| 9 | 2 | 4 | 5 | 1 | 2 | 3 |
| 10 | 2 | 5 | 1 | 2 | 3 | 4 |
| 11 | 3 | 1 | 3 | 5 | 2 | 4 |
| 12 | 3 | 2 | 4 | 1 | 3 | 5 |
| 13 | 3 | 3 | 5 | 2 | 4 | 1 |
| 14 | 3 | 4 | 1 | 3 | 5 | 2 |
| 15 | 3 | 5 | 2 | 4 | 1 | 3 |
| 16 | 4 | 1 | 4 | 2 | 5 | 3 |
| 17 | 4 | 2 | 5 | 3 | 1 | 4 |
| 18 | 4 | 3 | 1 | 4 | 2 | 5 |
| 19 | 4 | 4 | 2 | 5 | 3 | 1 |
| 20 | 4 | 5 | 3 | 1 | 4 | 2 |
| 21 | 5 | 1 | 5 | 4 | 3 | 2 |
| 22 | 5 | 2 | 1 | 5 | 4 | 3 |
| 23 | 5 | 3 | 2 | 1 | 5 | 4 |
| 24 | 5 | 4 | 3 | 2 | 1 | 5 |
| 25 | 5 | 5 | 4 | 3 | 2 | 1 |
Drawing of all mixing units as well as assembly was undertaken in SolidWorks 2016, commercial CAD/CAE software. Special care was taken when assembling these units so that units 2 and 4 have the sequence of upward–downward, and their direction changes when flow passed through them. The first direction of both of them was upward. To better illustrate, two models among the 25 models are shown in Fig. 2b, and the others follow this protocol.
2.3 Fabrication process and mixing experiments
Observing the accuracy of the numerical results led us to perform experiments on specific devices. The fabrication of the micromixers was done in accordance with the identified geometric dimensions with standard photolithography technique. Afterwards, the developed PDMS and the glass were bonded together by oxygen plasma treatment. The microchips were monitored through a CCD camera mounted on an optical microscope (Olympus, Japan). Two samples were simultaneously introduced from inlets at the same Re using a syringe pump (Harvard Co., USA). Then, the images and the related video files were separately captured along the length of the micromixers to evaluate the mixing quality of the devices. (Please refer to the ESI and Fig. S1† for experimental setup and fabricated microchips)3 Results and discussion
3.1 Analysis of Taguchi table
Fig. 3 shows a multi-panel graph depicting 25 experimental results which were proposed by Taguchi. Since most lab-on-a-chip devices work with low Re, the optimization process was performed for a Re of 5, and later extended to a wide range of Re. (Please refer to the ESI† for the grid study of the numerical results). Fig. 3(a–f) represent the mixing index of each experiment versus each unit in the combined micromixer. It also shows the specific number for each experiment in its legend in accordance with the Taguchi table. As can be concluded from Fig. 3, the total number of experiments were normally distributed among all factors and levels. Indeed, each level in a unit contributed to 5 experiments, and this number was the same for all units and their levels. It is seen in Fig. 3a that experiments 2, 3, and 4, as shown in dark blue color, have the best mixing index in unit 1 and level 1. The combined micromixer of 2, 3, and 4 in the DOE table show that level 1 in this unit is not an effective unit, but the 2nd, 3rd, and 4th level are dominant. Therefore, for unit 1, levels 2, 3, and 4 are suitable candidates. A trenchant analysis of these six figures reveals that the mixing index is smallest in the experiments where unit 1 and unit 5 play the major role as marked by a green circle. Thus, it can be approximated that the 1st and 5th levels of all factors can be neglected for the final selection. (Please refer to the ESI and Fig. S2† for detailed results of simulation no. 7 in the DOE table)3.2 Experimental results
To justify the credibility of the numerical simulations, experimental results for certain simulations were carried out. Five different micromixers from Table 1 were randomly chosen; their simulation numbers were 7, 12, 16, 21, and 25. To enhance the accuracy of experimental results, exact dimensions of the microchannel were extracted using a profilometer (Bruker, USA). Fig. 4 illustrates the images obtained from the profilometer for simulation numbers 7 and 21. (Please refer to ESI and Fig. S3† for profilometer of experimental numbers 12, 16, 25, and the “hybrid” micromixer.)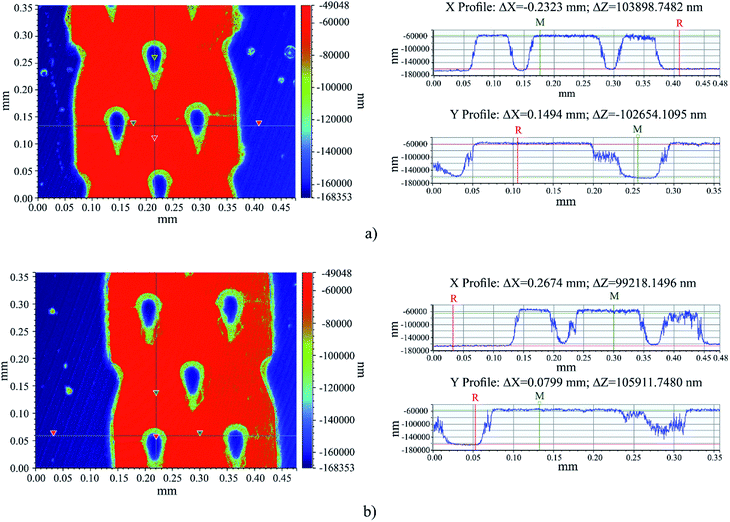 | ||
| Fig. 4 Image extracted via profilometer to measuring the exact dimensions of the (a) design number 7 (b) design number 21. | ||
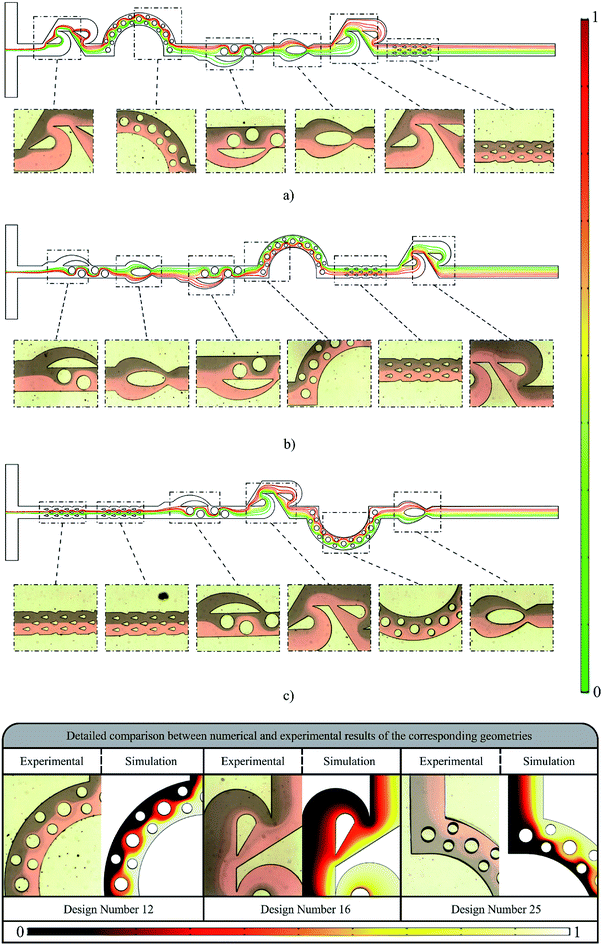
By using the parameters analyzed from the profilometer, exact dimensions of the microchip were identified, followed by the calculation of the hydraulic diameter. Therefore, the calculation of the input flow rate of the syringe pump was made as accurate as possible. Initially, in numerical simulations, original sample concentrations are displayed by solid color bands. These color bands gradually integrate as they interact with mixing units. In such cases, when the obstacles impede the path of the fluids, different layers of streams represented by different colors are discernible. It is of significant importance that the numerical simulations reflect the experimental test results. In other words, the simulations are able to predict the fluid behavior so they may be a reliable reference for future scrutiny. Accordingly, Fig. 5 shows a comparison between the experimental results and the numerical simulations in different cross-sectional areas for design numbers of 12, 16 and 25. (Please refer to the ESI and Fig. S5† for other comparisons)
In Fig. 5, contour plots of concentration distribution extracted from numerical simulations are depicted. Then, the experimental results are illustrated in each section to compare them with the numerical ones. This analogy establishes a quantitative framework for detecting and analyzing these two kinds of results. Prior to this, it was difficult to make predictions about the reliability of the numerical results. Since Re is set at 5, the flow regime is diffusive, and there is no trace of turbulence. In design number 12, when the streams reach the first mixing unit, they pass either side of the obstacle, splitting the fluid before recombining. As a result, the intensity of the light decreases as shown in Fig. 5. To better evaluate the CFD code, a magnified version of the experimental and numerical result is displayed. Upon comparison, a reliable correlation between simulation results and experimental data was observed; simulation models were able to accurately predict the flow behavior for experimental tests. Comparing the design numbers of 16 and 25 reveals that the flow prediction from the numerical results of design number 12 is not accidental, the proof of which can clearly be identified in Fig. 5. Taken together, the accuracy of numerical results was proved through comparison, demonstrating that these findings will be of interest to the researchers working in this field (the video of these experimental results are provided in ESI†).
3.3 The “hybrid” micromixer with MURO
An analysis was performed on the signal to noise (S/N) ratio diagram (Fig. 6) to find the best-nominated design from the proposed six factors and five levels. There are three classes of quality in the analysis of S/N ratio which categorically states that the-lower-the-better, the-nominal-the-better, and the-higher-the-better. The criterion for this study was set as the-higher-the-better, since the higher value of the mixing index increased the desirability of the “hybrid” micromixer. Eqn (13) shows the corresponding formula.34
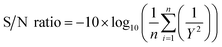 | (13) |
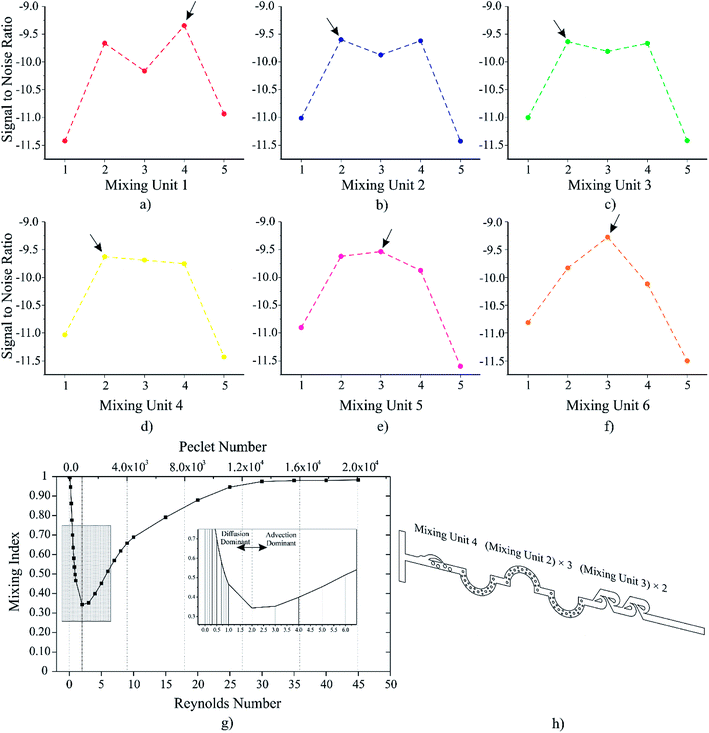
| Hybrid micromixer: mixing unit 3 + (mixing unit 2) × 3 + (mixing unit 3) × 2 |
As can be concluded from Fig. 6(a–f), unit 1 and unit 6 are more sensitive to the change of mixing units in comparison to other units. The sensitivity of six mixing units can be ranked as below:
| unit 1 ≈ unit 6 > unit 2 ≈ unit 3 ≈ unit 5 > unit 4 |
Therefore, there are more variations in units 1 and 6 compared with other units. The “hybrid” micromixer with MURO design as well as its mixing efficiency across a range of Re is clarified in Fig. 6(g and h). Various mixing tactics exist in the “hybrid micromixer”. The first unit in the “hybrid micromixer” is the nozzle and pillar mixing unit which contains an asymmetric sequence of obstacles (offering more effective mixing when compared to linearly arranged obstacles35) to enhance the mixing efficiency and a micronozzle to minimize the diffusion length. The second, third, and fourth mixing units are curved mixing units with in-built obstructions which involve embedded barriers in a curved microchannel to increase the mixing efficiency. In the curved channels, fluids experience a unique application of inertial and viscous forces for the generation of a transverse flow field (Dean flows). Dean flows enhance diffusive transport and increase mixing quickly over short lengths. The mixing index can also be improved with embedded barriers. Obstacles in microchannels can agitate the fluids which leads to the generation of lateral mass transport to further increase the mixing efficiency. The fifth and the sixth mixing units are Tesla units which make use of the “Coanda effect”. (Please refer to ESI† for the detailed description of Coanda effect in Tesla unit) Due to these effects, the “hybrid micromixer” is able to increase the mixing efficiency considerably.
Based on eqn (12), locating the critical point in the mixing index diagram is essential to investigating the effects of Re on the mixing index. The simulations were performed with Re 0.001, 0.01, 0.1, 0.2, (with increment of 0.1), 1, 2, (with increment of 1), 9, 10, 15 to 45 (with increment of 5). As noted above, the mixing process is divided into two separate parts. These two parts are separated at the critical point: the point where the minimum mixing index takes place. The location of the critical point depends on the velocity profile and geometry design of the microchannel and signals the mixing mechanism has changed from diffusion to mass advection. Before the critical point, the mixing process mainly relies on the diffusion where the velocity inverse varies with the mixing index. For a value of Re less than 0.1, the velocity is small enough for the two fluids to mix together completely. As the velocity increases, Pe increases, and according to eqn (12), which associates the mixing process with a specific length, the mixing procedure becomes harder. This trend continues until it reaches the critical point, where the mixing mechanism changes. As Fig. 6g demonstrates, the critical point is at Re = 2. After the critical point, the mechanism of mixing changes to mass advection, where the velocity varies proportionally with the mixing index. After a specific value for Re, which tends to be 35 in this case, complete mixing takes place.
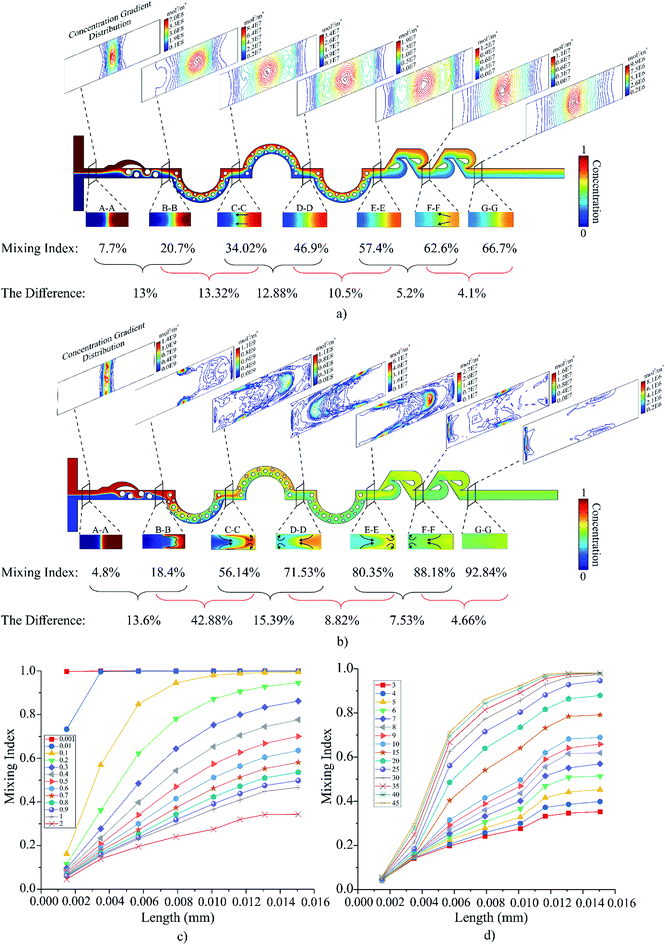
Fig. 7(a and b) represent a detailed diagram of the mixing processes for the two Re of 0.5 and 25, before and after the critical point, respectively. However, mere study of concentration is not enough to evaluate and entirely comprehend the mixing process. The concentration gradient is exploited to evaluate diffusion trends within the fluids, and the contours of concentration gradient distribution can denote the occurrence of diffusion; as reported by Fick's second law which is ∂C/∂t = D∇2C.36 Accordingly, if the distribution of the concentration gradient is adequate and homogenous on the transverse section, the diffusion path is shorter; therefore, it assists in the mixture of the fluids.
Fig. 7a depicts the mixing process based on the diffusion for Re 0.5 (please refer to the ESI† for the experimental results). The mixing scheme does not contain any chaotic advection, and it is solely based on molecular diffusion. As the concentration gradient distribution illustrates, this “hybrid” micromixer induces a more homogeneous gradient after each mixing unit in order to improve the quality of the mixing process. In the absence of mixing units, the mixing index of the micromixer will be significantly inadequate as the homogeneity of the concentration gradient will remain largely constant. As specified by Fig. 7(a and b), the 1st, 2nd, and 3rd units play a major role in the mixing process compared to the others, with the most effective unit being the 2nd. Fig. 7b illustrates the mixing process of the mass advection dominant combined micromixer with Re 25. The cross-sections of C–C and D–D represent the phenomenon of “disarray” in the concentration and concentration gradient contours. From the cross-section of C–C to F–F, the interface rotates 180 degrees clockwise, and at each cross-section, in a specific region, the interface of the two fluids swings. This leads to a heightened level of chaotic advection and a decrease in the diffusion path, enhancing the mixing index. Moreover, the “saddle-shaped” pattern demonstrated in the concentration gradient distribution leads to exponential growth in the contact surface, shortening the diffusion path.37 These mentioned phenomena significantly improve the mixing index, allowing it to reach a value of 94.6% by the end of unit 6. Fig. 7b clarifies that the second mixing unit has the most impact on the output compared with other units. (Please refer to ESI,† for video of experiments of this nominated device) To better understand the effect of each unit, Fig. 7(c and d) show the mixing index of the nominated design versus the length of micromixer.
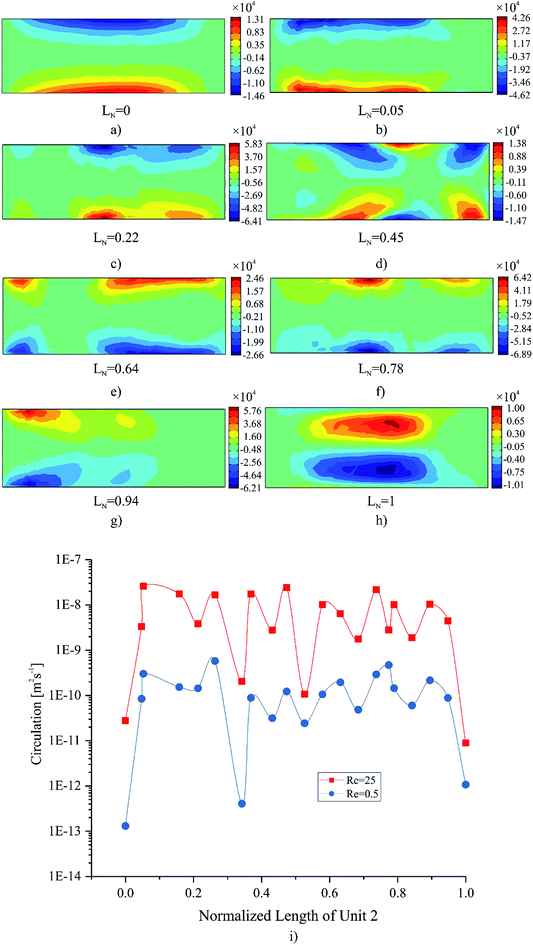
Fig. 7(c and d) are divided into two parts. The first is accountable for the diffusion dominant mixing process and the second is representative of the advection-based mixing process. The range of Re values in Fig. 7c correspond to mass diffusion, producing an increasingly negative mixing index. Whereas the range of Re values in Fig. 7d correspond to the presence of mass advection resulting in an increasing mixing index. This is due to the increase in the velocity, which enhances the tendency of fluids to become entirely mixed. An extensive analysis on Fig. 7(c and d) shows that unit 2 has the most effect on the mixing index, while the last unit has the least effect. Furthermore, by increasing the velocity, complete mixing is achieved before the fluids reach the end. In other words, the mixing length will be decreased. There is no doubt that beyond Re 50, the role of the last unit is negligible and unit 2 plays a significant role in the mixing process. Further investigating unit 2, Fig. 8(a–h) represent the contour plot diagram of the stream-wise vorticity in the YZ-plane for Re 25. For better illustration, a normalized length of unit 2 (LN) was used. The vorticity in the direction of X(ωx) can be calculated from eqn (14).
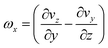 | (14) |
The circulation of the sections in the Y–Z plane as illustrated in Fig. 8a–h, for Re 0.5 and 25 are depicted in Fig. 8i as a semi-logarithmic diagram. The circulation in the Y–Z plane can be defined by eqn (15).
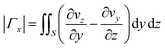 | (15) |
At the inlet, the circulation is low but increases rapidly as the length increases. Chaotic advection, which is induced by obstacles in the curved microchannel of unit 2, is related to the increased value of the circulation. Re is directly proportional to the intensity of the circulation. The fluctuation in the diagram can be attributed to the change in the direction of the peak vorticity which occurs near the middle of unit 2. After the flow reaches the end of unit 2, the value of circulation drops to its lowest point since no obstacles are present to disrupt the flow.
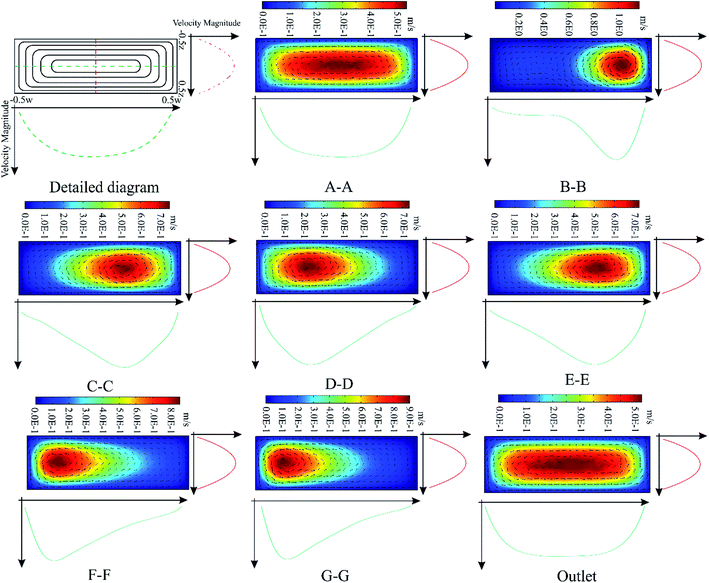
For further evaluation of the overall function of the “hybrid” micromixer Fig. 9 portrays the velocity diagram of each cross-section, before and after each mixing unit. (Please refer to the ESI† for evaluation of Tesla units in the “hybrid” micromixer). The velocity field in a rectangular channel for Poiseuille flow is described by eqn (16), while contour plots of the velocity field along symmetrical axes are depicted in Fig. 9a.
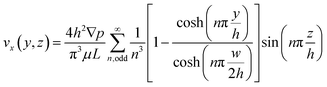 | (16) |
As expected, at cross-section of A–A, the velocity diagram resembles microscale flow in a rectangular channel. After the fluids pass the first mixing unit, the peak velocity changes and relocates to the outer wall of the microchannel which is around 0.5 W. From here on, the peak velocity continually varies between the C–C and F–F cross-sections. The corresponding circumstances are mainly related to the sequential upward/downward orientation of mixing units. This phenomenon induces further chaos and vortices at the transverse section and decreases the diffusional path, increasing the mixing index. As Fig. 9 reveals, after the cross-section of E–E, due to the fact that no mixing unit exists, the flow pattern adopted a rectangular flow pattern like that in A–A. The direction of the vorticity field confirms the above situations. The main feature of the “hybrid” design is the combination of three different mixing units, each of which has unique features that when combined provide maximum mixing efficiency.
In order to evaluate the function of the “hybrid” micromixer in terms of its bio-applications, Table 2 compares the mixing efficiencies and Re for previously reported micromixers against the current “hybrid” micromixer for certain applications.
| Category | Examples | Features of the device | Comparison with the Corresponding Study |
|---|---|---|---|
| Chemical synthesis | Identification of glucose-catalyst reactions5 | Mixing efficiency of 81 to 92% for Re of 0.08 to 16 | As the “hybrid” micromixer has an efficiency of 100%, it can facilitate the process of detection in low and high Re (0.001–0.1 and 22–45 respectively) |
| Active mixer for loading of drug on TiO2 (ref. 39) | Mixing efficiency about 90% at Re of 0.006. The device also had low mixing index in high Re | The proposed micromixer has the mixing efficiency of 100% in Re of 0.001–0.1. Furthermore, it has a favorable function on high Re where the mixing efficiency in about 100% | |
| Synthesis of organic samples6 | Mixing efficiency for a specific flow rate was reported as 80% where yield efficiency was 91% | Using the “hybrid” micromixer can be effective in enhancing the mixing index, and by doing so, yield efficiency will be improved | |
| Chemical reactors | A micromixer with nozzle and pillar mixing units for DNA ligation7 | Mixing efficiency of 88.2% for Re of 66.5 | The “hybrid” micromixer proposes a mixing efficiency of 100% in high Re, with significant function in low Re which can improve the efficiency of the device for the proposed application |
| Polymerization | Polymerization of vinyl ethers40 | The effect of mixing was investigated with different parameters where mixing index changes from 55 to 99% in different cases | The “hybrid” micromixer which employs different mixing tactics can have a mixing efficiency of 100% in high and low Re |
| Sample concentration | Using unbalanced split and recombine mixing units for sample preparation proteins41 | Mixing index was reported as 35% in low Re while it reached the 85% in high Re | The minimum efficiency of the “hybrid” micromixer is more than this study. Therefore, it can easily be used for wide ranges of Re, and in low and high Re, the mixing efficiency is 100% |
| Square-wave mixing units for blood plasma mixing42 | The mixing index was reported as 76% for the optimized one | The “hybrid” micromixer can perform this experiment in low Re where the mixing index is 100% | |
| Biological analysis | Formation of thrombosis8 | Using an active micromixer | Since the active forces might be hazardous to biological samples, “hybrid” micromixer can readily be adapted to this aim |
| Drug screening with a zig-zag shaped micromixer9 | Maximum mixing efficiency of 79.4% in the experimental test was reported | The proposed micromixer can produce results with a mixing index of 100% in low and high Re | |
| Wide ranges of applications | “Hybrid” micromixer | Based on the comparison of mixing index of different devices, the “hybrid micromixer” offers complete mixing in Re 0.001–0.1, 40–45 and more than 90% mixing index in Re 22–40 which can be used for various bio-applications in either low or high ranges of Re | |
Table 3 details the properties of various named micromixers and provides a comparative analysis against the “hybrid” micromixer, in terms of Re range and mixing index.
| Unit design | Range of Re | Maximum mixing Index | Comparison with the corresponding study |
|---|---|---|---|
| a a, b, c, d, e – these studies are account for mixing units 1, 2, 3, 4, and 5. | |||
| Ellipse-likea,17 | 0.2381–2.381 | (Re = 0.2381) 90% | Not applicable for wide ranges of Re, low mixing index at low range of Re |
| Obstruction in curved unitb,27 | 0.1–60 | (Re = 0.1) 88% | Lower mixing index in low and high Re, high pressure drop due to the numerous obstacles |
| Modified Teslac,31 | 0.05–40 | (Re = 40) 88% | Lower mixing index, especially in Re = 0.1–20 |
| Nozzle & pillard,7 | 6.65–66.5 | (Re = 66.5) 88.2% | Not effective in low Re, lower MI in comparison to this study |
| Teardrope,32 | 1–100 | (Re = 1) 68.5% | Lower mixing index in all ranges of Re, relative high region for diffusion dominant mechanism |
| J-shaped baffle21 | 5–350 | (Re = 350) 70.6% | Low mixing index in high Re |
| S-shaped43 | 2.5–30 | (Re = 5) 80% | Limited range of application, not applicable in low range of Re, lower mixing index in comparison with this study |
| Diamond-shaped obstacles44 | 0.02–10 | (Re = 0.1) 90% | Not applicable in high range of Re |
| Triangle-shaped45 | 0.1–20 | (Re = 0.1, 20) 90% | Not applicable in all ranges of Re, lower mixing index compared to this study |
| This study | 0.001–45 | (Re = 0.001–0.1, 40–45) ≈ 100% | Wide range of Re, employs several different mixing tactics including the use of embedded barriers, micronozzle, coanda effect and asymmetric layout of obstacles to generate Dean flows and chaotic advection, leading to a reduction in the diffusion path and increase the mixing efficiency, complete mixing in Re = 0.001–0.1, 40–45 and more than 90% mixing index in Re = 22–40 |
These comparisons reveal that the proposed “hybrid” micromixer can not only be employed in a wide variety of bio-applications at different Re, but also exerts different mixing methods due to the combination of different mixing units. Furthermore, it becomes clear that instead of using the complex 3D structures of micromixers, the proposed planar micromixer can be used for a range of 0.001–0.1 and 40–45 Re with a maximum mixing efficiency of 100%. In addition, in other ranges of Re, the proposed micromixer indicated better or comparable results for application in comparison with other MURO. Altogether, the superior function of the “hybrid” micromixer composed of nominated MURO is apparent in both the detailed investigation regarding vortex, circulation, velocity profile, concentration and concentration distribution, and in comparison with other micromixers. As the micromixers are ubiquitous for all microfluidic devices, we are of the opinion that the corresponding geometry can render the experiments of researchers more accurate and convenient especially when considering integrated systems, such as lab-on-a-chip devices.
4 Conclusion
The primary aim of this study was to form a “hybrid” micromixer with MURO for wide ranges of applications. After the investigation on MURO, five units of elliptical, Tesla, nozzle and pillar, and teardrop mixing units, as well as a curved mixing unit with in-built obstructions were selected. Then, six slots were designated to put the mixing units in. As the combination of all these units leads to a total of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 experiments, Taguchi method as an appropriate DOE method was applied for the optimization process and reduced the total number of experiments to 25. As these units are not alike in terms of dimensions, the methods of dynamic similarity (an investigation about the dimensionless number) and geometric similarity (an investigation about mere dimensions of the units) were performed. The comparison illustrated that the numerical results could efficiently predict the experimental ones, and the flow behavior is the same in two cases. The optimized micromixer, termed the “hybrid micromixer” had six mixing units in which one was a nozzle and pillar mixing unit, three were obstacles in a curved unit, and two were modified Tesla units. The “hybrid” micromixer was tested for Re ranging between 0.001 and 45, and the results indicated that the mixing index first decreased as it approached the critical point, but later increased. This critical point divided this diagram into two separate parts. For the mentioned micromixer, Re 2 was related to the critical point, where the mixing mechanism changed from diffusion to advection process. The function of the “hybrid” micromixer in terms of mixing efficiency was considerable as the mixing index in the range of 0.001–0.1 and 40–45 Re is approximately 100% and in the range of 22–40 is greater than 90%. For further investigation of the micromixer, the precise function of each unit was investigated by the velocity profiles, concentration and concentration distribution diagrams, and mixing index, before and after each unit. The results demonstrated that the second unit has the highest impact on the mixing index, especially where advection is dominant in the mixing process. For better understanding, contour plots of vorticity and circulation along the length of the second unit have been displayed, and its function was evaluated. Since micromixers have various applications in microfluidic devices, a comparison of the “hybrid” micromixer with other micromixers in terms of mixing efficiency reveals that this micromixer can be applied for wide ranges of bio-applications. Since the suggested micromixer contains different mixing units which lead to a combination of mixing techniques, it would be an appropriate choice for future studies.
625 experiments, Taguchi method as an appropriate DOE method was applied for the optimization process and reduced the total number of experiments to 25. As these units are not alike in terms of dimensions, the methods of dynamic similarity (an investigation about the dimensionless number) and geometric similarity (an investigation about mere dimensions of the units) were performed. The comparison illustrated that the numerical results could efficiently predict the experimental ones, and the flow behavior is the same in two cases. The optimized micromixer, termed the “hybrid micromixer” had six mixing units in which one was a nozzle and pillar mixing unit, three were obstacles in a curved unit, and two were modified Tesla units. The “hybrid” micromixer was tested for Re ranging between 0.001 and 45, and the results indicated that the mixing index first decreased as it approached the critical point, but later increased. This critical point divided this diagram into two separate parts. For the mentioned micromixer, Re 2 was related to the critical point, where the mixing mechanism changed from diffusion to advection process. The function of the “hybrid” micromixer in terms of mixing efficiency was considerable as the mixing index in the range of 0.001–0.1 and 40–45 Re is approximately 100% and in the range of 22–40 is greater than 90%. For further investigation of the micromixer, the precise function of each unit was investigated by the velocity profiles, concentration and concentration distribution diagrams, and mixing index, before and after each unit. The results demonstrated that the second unit has the highest impact on the mixing index, especially where advection is dominant in the mixing process. For better understanding, contour plots of vorticity and circulation along the length of the second unit have been displayed, and its function was evaluated. Since micromixers have various applications in microfluidic devices, a comparison of the “hybrid” micromixer with other micromixers in terms of mixing efficiency reveals that this micromixer can be applied for wide ranges of bio-applications. Since the suggested micromixer contains different mixing units which lead to a combination of mixing techniques, it would be an appropriate choice for future studies.
Conflicts of interest
There are no conflicts to declare.References
- A. Lashkaripour, R. Silva and D. Densmore, Desktop micromilled microfluidics, Microfluid. Nanofluid., 2018, 22(3), 31 CrossRef.
- F. A. Gomez, Biological applications of microfluidics, John Wiley & Sons, 2008 Search PubMed.
- N.-T. Nguyen and Z. Wu, Micromixers—a review, J. Micromech. Microeng., 2004, 15(2), R1 CrossRef.
- C.-Y. Lee and L.-M. Fu, Recent advances and applications of micromixers, J. Micromech. Microeng., 2018, 259, 677–702 Search PubMed.
- D. Kim, et al., An easily integrative and efficient micromixer and its application to the spectroscopic detection of glucose-catalyst reactions, Analyst, 2005, 130(3), 293–298 RSC.
- H. Kim, et al., Submillisecond organic synthesis: outpacing fries rearrangement through microfluidic rapid mixing, Science, 2016, 352(6286), 691–694 CrossRef PubMed.
- Y.-J. Ko, et al., DNA ligation using a disposable microfluidic device combined with a micromixer and microchannel reactor, J. Micromech. Microeng., 2011, 157(2), 735–741 Search PubMed.
- T. Goerge, et al., Microfluidic reveals generation of platelet-strings on tumoractivated endothelium, Thromb. Haemostasis, 2007, 98(02), 283–286 Search PubMed.
- F. Nason, et al., Design of microfluidic devices for drug screening on in vitro cells for osteoporosis therapies, Microelectron. Eng., 2011, 88(8), 1801–1806 CrossRef.
- X. Chen and T. Li, A novel passive micromixer designed by applying an optimization algorithm to the zigzag microchannel, Chem. Eng. J., 2017, 313, 1406–1414 CrossRef.
- S. Yu, T.-J. Jeon and S. M. Kim, Active micromixer using electrokinetic effects in the micro/nanochannel junction, Chem. Eng. J., 2012, 197, 289–294 CrossRef.
- C.-Y. Lee, et al., Passive mixers in microfluidic systems: a review, Chem. Eng. J., 2016, 288, 146–160 CrossRef.
- J. Zhang, et al., Fundamentals and applications of inertial microfluidics: a review, Lab Chip, 2016, 16(1), 10–34 RSC.
- M. Mollajan, S. R. Bazaz and A. A. Mehrizi, A Thoroughgoing Design of a Rapid-cycle Microfluidic Droplet-based PCR Device to Amplify Rare DNA Strands, J. Appl. Fluid Mech., 2018, 11(1), 21–29 Search PubMed.
- M. Rafeie, et al., An easily fabricated three-dimensional threaded lemniscate-shaped micromixer for a wide range of flow rates, Biomicrofluidics, 2017, 11(1), 014108 CrossRef PubMed.
- S.-J. Park, et al., Rapid three-dimensional passive rotation micromixer using the breakup process, J. Micromech. Microeng., 2003, 14(1), 6 CrossRef.
- N. Tran-Minh, T. Dong and F. Karlsen, An efficient passive planar micromixer with ellipse-like micropillars for continuous mixing of human blood, Comput. Methods Programs Biomed., 2014, 117(1), 20–29 CrossRef PubMed.
- C.-C. Hong, J.-W. Choi and C. H. Ahn, A novel in-plane passive microfluidic mixer with modified Tesla structures, Lab Chip, 2004, 4(2), 109–113 RSC.
- X. Chen and J. Shen, Numerical and experimental investigation on splitting-and-recombination micromixer with E-shape mixing units. Microsystem Technologies, 2016: pp. 1–7 Search PubMed.
- X. Chen and J. Shen, Simulation and experimental analysis of a SAR micromixer with F-shape mixing units, Anal. Methods, 2017, 9(12), 1885–1890 RSC.
- Y.-C. Lin, Y.-C. Chung and C.-Y. Wu, Mixing enhancement of the passive microfluidic mixer with J-shaped baffles in the tee channel, Biomed. Microdevices, 2007, 9(2), 215–221 CrossRef PubMed.
- C.-K. Chung and T. Shih, Effect of geometry on fluid mixing of the rhombic micromixers, Microfluid. Nanofluid., 2008, 4(5), 419–425 CrossRef.
- C.-K. Chung and T. Shih, A rhombic micromixer with asymmetrical flow for enhancing mixing, J. Micromech. Microeng., 2007, 17(12), 2495 CrossRef.
- C. Chung, C. Chang and C. Lai, Simulation and fabrication of a branch-channel rhombic micromixer for low pressure drop and short mixing length, Microsyst. Technol., 2014, 20(10–11), 1981–1986 CrossRef.
- S. Hossain and K.-Y. Kim, Mixing analysis of passive micromixer with unbalanced three-split rhombic sub-channels, Micromachines, 2014, 5(4), 913–928 CrossRef.
- A. Nejat, et al., Unsteady pulsating characteristics of the fluid flow through a sudden expansion microvalve, Microfluid. Nanofluid., 2014, 17(4), 623–637 CrossRef.
- A. Alam, A. Afzal and K.-Y. Kim, Mixing performance of a planar micromixer with circular obstructions in a curved microchannel, Chem. Eng. Res. Des., 2014, 92(3), 423–434 CrossRef.
- L.-S. Jang, et al., Transport of particle-laden fluids through fixed-valve micropumps, Microelectromechanical Systems, ASME MEMS, 1999, vol. 1, p. 503–509 Search PubMed.
- D. C. Duffy, et al., Rapid prototyping of microfluidic switches in poly(dimethyl siloxane) and their actuation by electro-osmotic flow, J. Micromech. Microeng., 1999, 9(3), 211 CrossRef.
- A. A. S. Bhagat and I. Papautsky, Enhancing particle dispersion in a passive planar micromixer using rectangular obstacles, J. Micromech. Microeng., 2008, 18(8), 085005 CrossRef.
- S. Hossain, et al., Analysis and optimization of a micromixer with a modified Tesla structure, Chem. Eng. J., 2010, 158(2), 305–314 CrossRef.
- K. J. Cook, Y. Fan and I. Hassan, Experimental investigation of a scaled-up passive micromixer with uneven interdigital inlet and teardrop obstruction elements, Exp. Fluids, 2012, 52(5), 1261–1275 CrossRef.
- S. B. Islami and M. Khezerloo, Enhancement of Mixing Performance of Non-Newtonian Fluids using Curving and Grooving of Microchannels, J. Appl. Fluid Mech., 2017, 10(1), 127–141 CrossRef.
- N. Solehati, J. Bae and A. P. Sasmito, Optimization of Wavy-Channel Micromixer Geometry Using Taguchi Method, Micromachines, 2018, 9(2), 70 CrossRef.
- H. Wang, et al., Optimizing layout of obstacles for enhanced mixing in microchannels, Smart Mater. Struct., 2002, 11(5), 662 CrossRef.
- X. Feng, Y. Ren and H. Jiang, An effective splitting-and-recombination micromixer with self-rotated contact surface for wide Reynolds number range applications, Biomicrofluidics, 2013, 7(5), 054121 CrossRef PubMed.
- H. Xia, et al., Chaotic micromixers using two-layer crossing channels to exhibit fast mixing at low Reynolds numbers, Lab Chip, 2005, 5(7), 748–755 RSC.
- M. A. Ansari, Parametric study on mixing of two fluids in a three-dimensional serpentine microchannel, Chem. Eng. J., 2009, 146(3), 439–448 CrossRef.
- N. Veldurthi, et al., Computational fluid dynamic analysis of poly (dimethyl siloxane) magnetic actuator based micromixer, J. Micromech. Microeng., 2015, 212, 419–424 Search PubMed.
- A. Nagaki, et al., Polymerization of vinyl ethers initiated by dendritic cations using flow microreactors, Tetrahedron, 2015, 71(35), 5973–5978 CrossRef.
- K. Anwar, et al., Integrated micro/nano-fluidic system for mixing and preconcentration of dissolved proteins, Microchim. Acta, 2011, 173(3–4), 331–335 CrossRef.
- J.-N. Kuo, H.-S. Liao and X.-M. Li, Design optimization of capillary-driven micromixer with square-wave microchannel for blood plasma mixing, Microsyst. Technol., 2017, 23(3), 721–730 CrossRef.
- P. Li, J. Cogswell and M. Faghri, Design and test of a passive planar labyrinth micromixer for rapid fluid mixing, J. Micromech. Microeng., 2012, 174, 126–132 Search PubMed.
- A. A. S. Bhagat, E. T. Peterson and I. Papautsky, A passive planar micromixer with obstructions for mixing at low Reynolds numbers, J. Micromech. Microeng., 2007, 17(5), 1017 CrossRef.
- K. Conlisk and G. M. O'Connor, Analysis of passive microfluidic mixers incorporating 2D and 3D baffle geometries fabricated using an excimer laser, Microfluid. Nanofluid., 2012, 12(6), 941–951 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra05763j |
| This journal is © The Royal Society of Chemistry 2018 |