Open Access Article
Open Access ArticleA simple capillary viscometer based on the ideal gas law
Le Hoang Phu Pham,
Luis Bautista,
Deyvid C. Vargas and
Xiaolong Luo *
*
Department of Mechanical Engineering, The Catholic University of America, Washington, D.C. 20064, USA. E-mail: luox@cua.edu; Fax: +1 202 319 5173; Tel: +1 202 319 6952
First published on 29th August 2018
Abstract
We report a simple, inexpensive and user-friendly capillary viscometer based on the measurement of pressure drop in capillary tubing using the principle of ideal gas law. Viscosity is an important physical property of a fluid that provides molecular information of the fluid's behavior under flow conditions. Measuring viscosity, however, generally requires relatively large fluid volume samples and is expensive with commercial viscometers. Microfluidic viscometers at different levels of complexity can measure fluids at different flow rates with a small sample volume but the cost of commercially available microfluidic viscometers is still high. The reported capillary viscometer is cost-effective, uses small amounts of sample fluid and can measure viscosity under various shear rates. According to the Hagen–Poiseuille equation, the pressure drop of laminar flows in a capillary at a given flow rate is proportional to the viscosity of the fluid. When an enclosed air volume is connected to the upstream of the capillary, the pressure drop can be calculated with the change of the connected air volume, which is reflected by the displacement change of the air–liquid interface in the connecting capillary to the enclosed air volume. Based on these principles, the viscometer was assembled with readily accessible materials, and required no internal sensors or extensive programming. Measurements were successfully performed for five liquids including water, acetone, 2% fat milk, glycerin 30% and glycerin 40%. Except for acetone, the difference between measured and known viscosity was within 4% and highly consistent, well within the 13% uncertainty errors of readily accessible laboratory materials. Overall, the simple viscometer was easily assembled with low cost materials, was portable and accurate, and provided an alternative to expensive commercial viscometers. Finally, the simple capillary viscometer was a good outreach project for K-12 students to understand fluid behavior.
Introduction
Viscosity is an important physical property of a fluid that provides information about molecular interactions of the fluid's behavior under flow conditions. For any application requiring a fluid to perform a task, it is imperative to know the viscosity of the fluid. Technically, viscosity is a measure of its resistance to gradual deformation by shear stress which is colloquially called the “thickness” of a substance. The resistance of fluids in response to the increase of shear stress is constant for Newtonian fluids such as water or is shear thickening or thinning for non-Newtonian fluids such as whole blood. Viscosity measurement of Newtonian fluids is less complex compared to non-Newtonian fluids for which viscosity should be measured under various shear rates.Conventional viscosity measurements are generally performed with well-established viscometers including:1–4 (1) tube-type capillary or orifice viscometers that measure the time to discharge the sample fluid through a section of capillary or orifice structure, (2) falling-body viscometers that measure the time for a sphere ball or a needle to fall through a sample fluid, (3) oscillating or vibrational viscometers that measure the movement of a oscillator or damping of a resonator immersed in sample fluid, and (4) rotational viscometers that measure the drag torque of a rotating cylinder or cone disk spinning in sample fluid at a variable speed. The first two types of viscometers measure the timing of the fluid or a falling object generally driven by gravity and sometimes by external force, therefore often measure viscosity under one flow condition. The latter two types of viscometers generally can measure the viscosity proportional to driving forces at various shear rate conditions. A decent tube-type or falling body viscometer costs hundreds of dollars and takes at least 5 mL of sample fluids, while the rotational viscometer costs more but can use less sample volume. Modern viscometers are digital and able to measure viscosity at different shear rates, which often cost more.
With the advancement of microfluidics, sample volume consumption can be substantially lower by using rheology-on-a-chip (ROC) technologies for viscosity measurement, which has other advantages over conventional viscometers such as minimizing inertial effects and measurement time, providing direct visualization and the potential for portability.5,6 One example is the viscometer/rheometer-on-a-chip (VROC®) developed by RheoSense, which embeds sensors within a microchannel that reads the pressure drop as a test liquid flows through.7 The VROC device measures sample as low as 20 μL with 2% accuracy, but its cost is above ten thousand US dollars. Other microfluidic viscometers in literature provide cheaper solutions and generally use some form of comparator to measure viscosity of an unknown fluid with a reference fluid of known properties by observing their interactions within the comparator. The difference in devices comes from the complexity of the comparators, which can be a single microchannel comparator,8 a comparator with a flexible membrane in a microchannel,9 a comparator composed of 100 microchannels,10 or the comparison of flow distance between sample and reference liquid in microchannels activated by a degassed poly(dimethylsiloxane) space. A more sophisticated device used at oil sites is a vibrating wire viscometer built for high pressure and high temperature conditions that would be experienced deep in earth.11 Thorough reviews of microfluidic viscometers are provided in recent literatures,12 which summarizes different types of microfluidic viscometer based on the sensing and measurement of pressure drop,7,13,14 flow rate,15 surface tension including but not limited to droplets,16,17 co-flowing steam,8 diffusion,18 particle image velocimetry (PIV)19 and viscosity indexer.20 Overall, microfluidic viscometers at different level of complexities can measure fluids at different flow rates with a small to medium sample volume. For commercially available microfluidic viscometer such as VROC®, sample consumption is minimum, but the cost is still high.
Here, we report a simple capillary viscometer based on the pressure drop of laminar flow inside capillary tubing measured with the ideal gas law principle. It is the first that, to the best of our knowledge, ideal gas law was applied for viscosity measurement. The simple capillary viscometer was assembled with readily accessible materials including simple syringe pumps, capillary tubing and laboratory syringes, and required no internal sensors or extensive programming. Less than 1 mL of each sample fluid was required to measure its viscosity. Except for the case of volatile acetone, the difference between the measured and known viscosities was within 4% and highly consistent. The simple capillary viscometer has served as a good outreach project for K-12 students to understand and measure fluid behaviors.
Theory
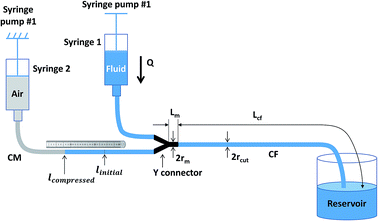
The schematic setup of the capillary viscometer is shown in Fig. 1. Syringe #1 containing the sample fluid was mounted on a syringe pump that pumped the sample fluid at various flow rates, while syringe #2 containing the enclosed air was fixed on a syringe pump that did not move during measurement. Three segments of capillary tubing of known radius, r, were connected with a Y-connector. Sample fluid in syringe #1 was connected with the first segment of capillary tubing to the Y-connector, and pumped through the second segment of capillary with flow (CF) of know distance, L, while the third segment of capillary under measurement (CM) was connected to an enclosed volume of air in syringe #2 fixed on a syringe pump that did not move during measurement. Before the test started, syringe #2 was adjusted on the pump and then fixed so that an air–liquid interface in CM was maintained and recorded within the range of the measuring ruler, and the air volume was recorded. When pump #1 was started, the pressure drop in CF was reflected by the displacement change of the air–liquid interface in CM.The viscosity measurement is based on two well-known principles: (1) the ideal gas law principle to measure the pressure drop through capillary by measuring the change of air volume, and (2) the Hagen–Poiseuille flow equation to calculate the liquid viscosity based on the pressure drop in capillary at a fixed flowrate. The ideal gas law principle is described as:
| PV = nRT | (1) |
Assuming nRT remains constant for the enclosed air volume at a constant room temperature, eqn (1) follows the Boyle's equation where the product of pressure and volume is equal at both the initial and final states:
| PV = (P0 + ΔP) (V0 − ΔV) = P0V0 | (2) |
Therefore, pressure drop can now be written:
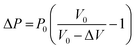 | (3) |
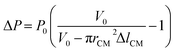 | (4) |
Pressure drop of fluid flow in CF is related to viscosity with the following Hagen–Poiseuille flow equation:
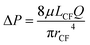 | (5) |
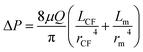 | (6) |
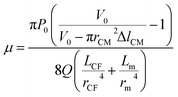 | (7) |
Eqn (7) can also be simplified as
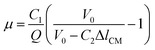 | (8) |
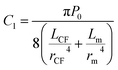 , and C2 = πrCM2. By measuring the air–fluid interface displacement Δlcum under a set flow rate Q, the viscosity of the sample fluid can be simply calculated using eqn (8).
, and C2 = πrCM2. By measuring the air–fluid interface displacement Δlcum under a set flow rate Q, the viscosity of the sample fluid can be simply calculated using eqn (8).
The relative error in the viscosity determined by eqn (8) arises from the measurement uncertainties of the variables involved in this equation. The uncertainty of the flow rate, Q, is given by the syringe pump manufacturer as 1%. The reading error of the air–liquid interface displacement, Δlcum, is estimated to be about 0.5%. The uncertainty in the determination of atmospheric pressure P0 is 0.5%. The rest of the measurement uncertainty mainly comes from the errors of the readily accessible materials including the inner diameters of the capillary tube, rcum and rcut, and the metal Y connector, rm. While accuracy of these inner diameters was not provided from manufactures, caliper gauge was used in the lab and the variations were measured to be about 0.8%. The uncertainty in length is about 0.5%. The uncertainty in the determination of the initial gas volume V0 is about 1%. Using the familiar error propagation formula,
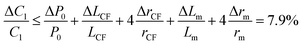 | (9) |
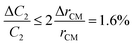 | (10) |
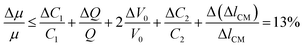 | (11) |
Materials and methods
Materials
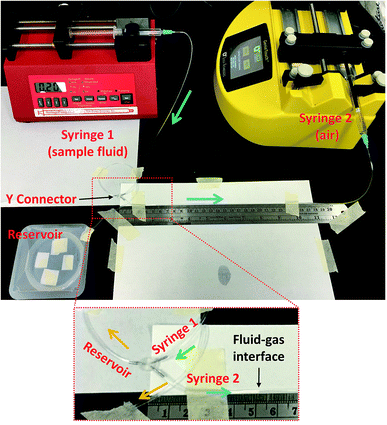
Standard BD syringes (Becton, Dickinson and Company) of 1 mL were used to hold the fixed volume of air and the sample fluid, respectively, as syringe #1 and syringe #2 in Fig. 2. One Genie Touch syringe pump (Lucca Technologies) and a NE-300 Just Infusion™ Syringe Pump (New Era Pump Systems Inc.) were used to hold both syringes, which were capped with Luer couplers (L22, Instech Labs), connected with Tygon microbore tubing (0.020′′ ID or the radius rc is 0.254 mm, Cole Parmer), and joined with a metal Y connector (22ga, Instech Labs) with a fixed length, Lm, for the metal branch. The length of the CM between syringe 2 and the original air–liquid interface mark is recorded as lintital, and the length of the CF connecting the output of the metal Y connector and the waste reservoir is Lc. A relatively large (3 15/16′′ width SEOH Plastic) square weight dish was used as the waste reservoir. The water in the reservoir barely covered the end of CF, so that the change of hydrostatic pressure because of liquid level variation was minimized, and the surface tension of potential liquid drop forming at the end of CF was eliminated. The length from syringe 1 to the metal Y connector did not affect the overall displacement of the air–liquid interface. Different length Lc were used for the different fluids. Finally, a measuring tape was used in place of the ruler. Acetone, glycerin and 2% fat milk were purchase from grocery store. All Tygon tubing were disposed after use, and the Y connector were thoroughly rinsed with bleach then DI water for re-use.Experimental process
The general experiment started with filling the capillary connecting the sample syringe #1 and the Y connector, the Y connector and the CF by starting the pump #1 while blocking with finger or tape the branch of Y connector to be connected to the CM. When the sample fluid was observed coming out to the waste reservoir, the filling was completed and pump #1 was stop. Next, one end of the CM was connected to the Y connector branch that was previously blocked, and a measuring tape was placed along the CM. By pumping the fluid in syringe #1 slowly, the air–liquid interface in CM was gently positioned in accordance with the ruler until a satisfied air–liquid interface was reached. Pump #1 was then stop and the CM was connected to syringe #2, and the initial position of the air–fluid interface was recorded. To test that there was no air leakage in the experimental setup, the sample fluid was pumped at a random flow rate for a few seconds to notice the displacement of the air–liquid interface and then stop. If the air–liquid interface returned to within a few mm of the original position, no air leakage was assumed. The difference of a few mm between the new and previous positions of the air–liquid interface was constantly observed presumably due to surface tension in the tubing. The setup with displacement observation was set for experiment.To prove the versatility of this measurement strategy, different Newtonian fluids were measured: tap water, acetone (Semiconductor grade, Alliance Chemical), milk 2% fat (Garelick Farms® Dairy Pure®, CVS), glycerin 30% and glycerin 40% diluted from natural pure vegetable glycerin (Earth's Care, CVS). The experiments were performed at different time with various initial conditions such as room temperature and length of CF. The initial values and fluid information were summarized in Table 1. For viscosity measurements, the sample fluid was pumped at a set of flow rates ramping from 0.1 to 1 mL min−1, step of 0.1 mL min−1. At each flow rate, the air–liquid interface was dislocated then stop at a new equilibrium position within tens of seconds to a few minutes. The higher the flow rate, the bigger change of volume and the longer time it took to reach the new equilibrium position. It was also found that the bigger the initial air volume, the more distance the air–liquid interface moved and the longer the equilibrium time. Displacement was recorded if the air–liquid interface went back to the original position after pump #1 was stop. For better accuracy, each flowrate was run five times and the displacement was recorded to provide an average.
Results
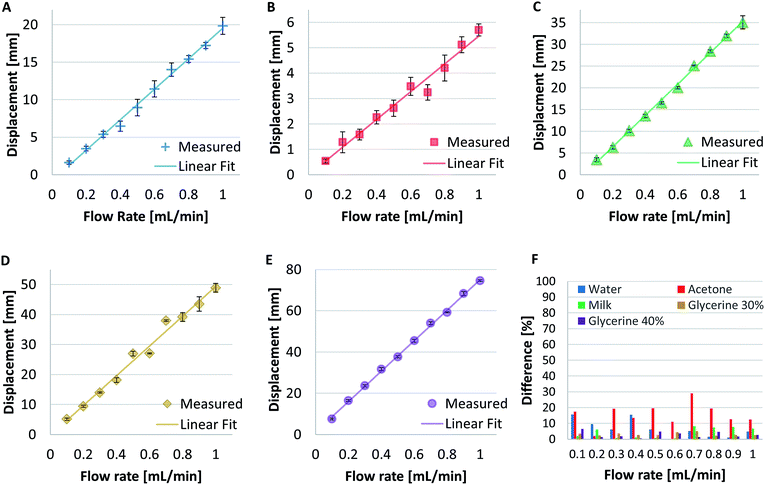
The measured displacement Δl vs. flow rate for five sample fluids is shown in Fig. 3A–E. Each data point with its error bar (standard deviations) was an average of five measurements. The measurement results clearly show that the displacement increased almost linearly with the increase of flow rate. It is worth to note that the maximum displacement at 1 mL min−1 flow rate vary from less than 6 mm for least viscous sample fluid acetone to about 75 mm for most viscous sample fluid 40% glycerin. Linear fit was then imposed to the data. The linear trend lines fit the measured displacement points well except for a few points for the cases of acetone and glycerin 30% in Fig. 3B and D, correspondingly. The error bars for acetone are larger than those for other fluids. The data points for glycerin 30% fluctuated especially within the flow rate range from 0.4 to 0.8 mL min−1 presumably due to experimental errors.The comparison between the experimentally measured and theoretically calculated displacements based on known viscosities of the sample fluids is shown in Fig. 3F, which also shows the fluctuation of the displacements at various flow rates. To do this, the ideal gas law principle was used to calculate the theoretical displacements based on known viscosities. The theoretical displacements were calculated by rearranging eqn (8) to:
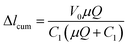 | (12) |
As shown in Fig. 3F, the difference between measured and theoretical displacements normalized to the theoretical values of the case of acetone was generally higher than 10%, it reaches its peak of near 30% at 0.7 mL min−1 and its lowest is lower than 5% at 0.2 mL min−1. While the difference percentage of water also fluctuated during the first 4 flow rates, it dropped to around 5% at later flow rates. For other fluids, it remained below 7.5% throughout all the flow rates.
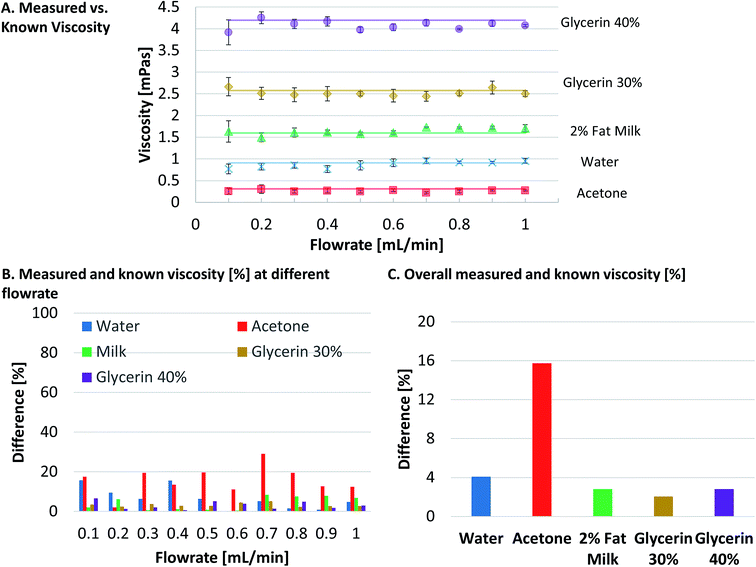
Next, the viscosities of sample fluids were calculated using eqn (7) for each of the five measured displacements at each flow rate and plotted in Fig. 4A. Each data point in Fig. 4A was the average of five measurements and the error bars shows the standard deviations of the five measurements. Known viscosities of the sample fluids were plotted as the straight lines in Fig. 4A since the viscosities of the Newtonian sample fluids stay the same under different shear rates, in this case the flow rates. The results (Fig. 4A) show that the measured viscosities were relatively consistent and close to the known viscosities for all sample fluids. To further quantify the accuracy of our measurements, the difference between measured and calculated viscosities for each flow rate were normalized to known viscosities and plotted in Fig. 4B. The comparison in Fig. 4B shows similar discrepancy of viscosities with those of displacements in Fig. 3F, which shows less than 7.5% of difference between measured and known viscosity for the measured data except for some data points of water and most data points of acetone where bigger discrepancy was noted.
The final measured viscosity for each sample fluids was calculated by taking the average of the calculated viscosities at different flow rates in Fig. 4A. For water, the final measured viscosity was 0.901 × 10−3 Pa s, 4.09% different from known value of 0.9107 × 10−3 Pa s at 24 °C. This measurement result is similar to the accuracy of commercially available viscometers and demonstrates that the capillary viscometer is reliable. For acetone, the final measured viscosity is 0.261 × 10−3 Pa s, 15.73% different from the known value of 0.31 at 25 °C. The big difference is presumably due to the facts that, although the PTFE Tygon tubing has excellent compatibility with acetone,21 acetone is a volatile fluid and it is hard to measure over time while maintaining its original properties. For 2% fat milk, the measured viscosity is 1.645 × 10−3 Pa s, 2.79% different from known value of 1.6 at 20 °C. For 30% glycerin and 40% glycerin, the measured viscosities are 2.522 × 10−3 Pa s and 4.079 × 10−3 Pa s, respectively, which are 2.04% and 2.82% different from known values of 2.575 × 10−3 Pa s and 4.197 × 10−3 Pa s, respectively. Fig. 4C shows the normalized difference of the measured to known viscosities of all five sample fluids. These measurement results fall within the 13% uncertainty as analyzed in the Theory section except for the case of the volatile solvent acetone.
Based on the results in Fig. 4, it is concluded that the capillary viscometer based on ideal gas law can be used to approximate viscosities of Newtonian liquids with relative high accuracy (equal or less than 4% error) except for the volatile solvent acetone. Approximately 5 mL of each sample fluids was consumed for measurements over the 10 flow rates with 5 measurements at each flow rate to calculate the final viscosity. With the current setup described in the Materials section, measurements of a sample liquid at one flow rate in the range of 0.5–1 mL min−1 could be used to estimate liquid viscosity of within 10% accuracy, which would consume less than 1 mL of sample liquid. The accuracy could be improved to be within 4% if measurements were to perform at multiple flow rates, which would consume up to 5 mL of the sample fluid.
Discussion
It is worthwhile to mention that the volume consumption of sample fluid could potentially be further decreased if capillary of smaller diameter is used. The ideal gas law principle for pressure measurement was found to able to measure pressure drop of 500–5000 Pa within 2% accuracy, which corresponds to about 0.5–5% change of the enclosed air volume. According to the Hagen–Poiseuille flow eqn (5), 1/16 of the original flow rate is needed to generate the same amount of pressure drop if the capillary diameter is half of the original size. Therefore, only 1/16 of the original sample liquid volume would be needed. Tygon microbore capillary tubing with ID size 0.010′′ is commercially available (Cole Parmer) to replace the capillary with ID size 0.020′′ used in the current study, which could potentially decrease 10 times the sample consumption of current study. The viscosity measurement method can be extended to measure non-Newtonian fluids as well by varying the flow rate with a syringe pump and referring to the Hagen–Poiseuille velocity profile of non-Newtonian fluids available in literature.22–24There are a few considerations for future usage of this capillary viscometer. First, attention should be given to set the size of the initial air volume. To minimize the travel time of the air–liquid interface before the new equilibrium to within tens of seconds or a minute, the displacement distance in capillary tubing should be ideally within 50 mm, which corresponds to around 10 μL of air volume change for capillary tubing with ID of 0.020′′, and 5% change of air volume for initial air volume of 0.2 mL. Second, liquid viscosity is sensitive to temperature, most commercial viscometers have an accurate temperature control as a built-in part of the viscometer. The current measurements were limited to the room temperature using the simple capillary setup. Temperature control could be added by using temperature bath or modulating the room temperature to increase measurement accuracy.
Furthermore, syringe #2 and syringe pump #2 can also be simply replaced with one long segment of capillary tubing with a metal plug. For example, for the 0.020′′ ID Tygon tubing (Cole Parmer), a 22ga stainless steel catheter plug (SP22/12, Instech Labs) can be used. This simple replacement of syringe and Luer coupler with metal plug could further minimize the potential air leakage within the syringe and between the Luer coupler and syringe. To observe 50 mm of air–liquid interface displacement, a segment of capillary tubing of 1 m is sufficient to accommodate 5% change of the air volume. The cost to assemble the simple capillary viscometer is only a few hundred dollars, which includes one NE-300 Just Infusion™ Syringe Pump, a Y-connector, a metal plug, two syringes with Luer couplers and a roll of capillary tubing.
Finally, this simple capillary viscometer and the pressure measurement with ideal gas law has served as a good outreach project for three sophomore high school students, two from the Thomas Jefferson High School of Science and Technology and one from the Dematha Catholic High School around the Washington DC area. The students worked in the lab as summer interns, and performed pressure or viscosity measurement of biopolymer solutions (results not shown). The students were most excited in directly connecting the ideal gas law they learned in high school classrooms with the understanding and measurement of fluid behaviors using an apparatus assembled with simple lab materials.
Conclusions
We demonstrated a capillary viscometer that simply calculates liquid viscosity with the Hagen–Poiseuille flow equation by measuring the pressure drop inside capillary tubing using the ideal gas law principle. Except for the case of volatile acetone, the viscometer was verified with sample fluids (water, acetone, milk, glycerin 30% and 40%) within 4% accuracy, well within the uncertainty errors of readily accessible laboratory materials. Measurement can also be explored for non-Newtonian fluids as it is easy to vary flow rate.24 The capillary viscometer is a simple alternative to expensive viscometer in that it can be simply configured with simple lab materials, requires a small liquid sample, is cost effective, and is able to measure viscosity at various shear rates. Finally, the simple capillary viscometer was a good outreach project for K-12 students in connecting the ideal gas law the students learned in class with the measurement of fluid behaviors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the National Science Foundation CAREER award (#1553330) and the School of Engineering at the Catholic University of America.References
- R. Rosencranz and S. A. Bogen, Am. J. Clin. Pathol., 2006, 125, S78–S86 Search PubMed.
- R. Jethra, ISA Trans., 1994, 33, 307–312 CrossRef.
- D. S. Viswanath, Viscosity of liquids: theory, estimation, experiment, and data, Springer, Dordrecht, 2007 Search PubMed.
- M. C. Bourne, Food Texture and Viscosity – Concept and Measurement, Elsevier, 2nd edn, 2002 Search PubMed.
- A. Lindner and P. E. Arratia, Biomicrofluidics, 2016, 10, 043301 CrossRef PubMed.
- H. Zuoyan, T. Xiaoju and Z. Bo, J. Micromech. Microeng., 2007, 17, 1828 CrossRef.
- C. J. Pipe, T. S. Majmudar and G. H. McKinley, Rheol. Acta, 2008, 47, 621–642 CrossRef.
- S. Goel, P. S. Venkateswaran, R. Prajesh and A. Agarwal, Fuel, 2015, 139, 213–219 CrossRef.
- X. Tang and B. Zheng, Analyst, 2011, 136, 1222–1226 RSC.
- Y. J. Kang, S. Y. Yoon, K. H. Lee and S. Yang, Artif. Organs, 2010, 34, 944–949 CrossRef PubMed.
- G. Dehestru, M. Leman, J. Jundt, P. Dryden, M. Sullivan and C. Harrison, Rev. Sci. Instrum., 2011, 82, 035113 CrossRef PubMed.
- S. Gupta, W. S. Wang and S. A. Vanapalli, Biomicrofluidics, 2016, 10, 043402 CrossRef PubMed.
- M. Taha and M. D. Rafael, Eur. J. Phys., 2015, 36, 065045 CrossRef.
- J. Nowak and S. Odenbach, J. Magn. Magn. Mater., 2016, 411, 49–54 CrossRef.
- S. D. Hudson, P. Sarangapani, J. A. Pathak and K. B. Migler, J. Pharm. Sci., 2015, 104, 678–685 CrossRef PubMed.
- M. F. DeLaMarre, A. Keyzer and S. A. Shippy, Anal. Chem., 2015, 87, 4649–4657 CrossRef PubMed.
- Y. Li, K. R. Ward and M. A. Burns, Anal. Chem., 2017, 89, 3996–4006 CrossRef PubMed.
- P. Arosio, K. Hu, F. A. Aprile, T. Müller and T. P. J. Knowles, Anal. Chem., 2016, 88, 3488–3493 CrossRef PubMed.
- G. Degré, P. Joseph, P. Tabeling, S. Lerouge, M. Cloitre and A. Ajdari, Appl. Phys. Lett., 2006, 89, 024104 CrossRef.
- E. Livak-Dahl, J. Lee and M. A. Burns, Lab Chip, 2013, 13, 297–301 RSC.
- PTFE Chemical Resistance Chart, http://www.componentsupplycompany.com/ptfe-chemical-resistance-data.php, accessed 19 August 2018 Search PubMed.
- T.-A. Lee, W.-H. Liao, Y.-F. Wu, Y.-L. Chen and Y.-C. Tung, Anal. Chem., 2018, 90, 2317–2325 CrossRef PubMed.
- N. Srivastava and M. A. Burns, Anal. Chem., 2006, 78, 1690–1696 CrossRef PubMed.
- B. C. Eu, Am. J. Phys., 1990, 58, 83–87 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |

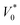
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1325
1325