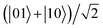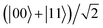DOI:
10.1039/C8RA06342G
(Paper)
RSC Adv., 2018,
8, 35928-35935
EPR steering of polar molecules in pendular states and their dynamics under intrinsic decoherence
Received
27th July 2018
, Accepted 11th October 2018
First published on 23rd October 2018
Abstract
Einstein–Podolsky–Rosen (EPR) steering gives evidence for the phenomenon called “spooky action at a distance” in quantum mechanics, and provides a useful resource for the implementation of quantum information tasks. In this paper, we consider a pair of ultracold polar molecules trapped in an external electric field as a promising quantum information carrier, and analyze the evolution behavior of EPR steering for the two coupled polar molecules in pendular states. Our results show that the steering of the two linear dipoles is remarkably reliant upon the Stark effect and dipole–dipole interaction. To be specific, the steerability degree is inversely associated with the intensity of the electric field while it is positively correlated with the coupling strength between the two polar molecules. Moreover, it is found that high ambient temperature can lead to a rapid loss of the steerable resource in thermal equilibrium. Further, we put forward an effective strategy to enhance the steerability using the technique of weak measurement reversal (WMR). By taking into account the influence of intrinsic decoherence on the steering dynamics, we found that robust EPR steering preservation can be realized for the initial state being in the Bell state 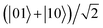 . Our findings may shed some new light on molecular quantum information processing with pendular states.
. Our findings may shed some new light on molecular quantum information processing with pendular states.
1 Introduction
EPR steering as a form of quantum nonlocality was originally introduced by Schrödinger1 in 1935 to explain the EPR paradox,2 which is described as the ability to steer or manipulate a quantum state remotely from one observer to another observer by local measurement. In 2007, Wiseman et al.3,4 provided an operational definition for EPR steering as a quantum information task and proved that the steering is a type of quantum correlation which lies in between nonseparability and Bell nonlocality. Since then, many investigations about the classification of quantum nonlocality5–8 and quantification of EPR steering9–14 have been carried out. Recently, based on the experimental criteria proposed by Cavalcanti, Jones, Wiseman, and Reid (CJWR),15 Costa et al.10,11 derived an analytical formula for the steering in a two- or three-measurement scenario, which can be applied for the evaluation of the steerability degree of arbitrary two-qubit states. Moreover, as a kind of special quantum correlation, EPR steering has been proven to be advantageous for verifying some basic principles of quantum mechanics, subchannel discrimination, and one-sided quantum security communication.16–20 It is notable that EPR steering has been achieved experimentally with both photon systems21–25 and an ultracold atomic system.26
On the other hand, rapid progress has been made in a number of methods and technologies for the cooling, trapping and controlling of cold polar molecules in the past several decades.27–29 As a consequence, the electric dipole moments of ultracold polar molecules, trapped in a 1D optical lattice and coupled by a dipole–dipole interaction, can be chosen as a candidate carrier for quantum computation.30,31 We note that Wei et al.32,34 evaluated the entanglement of the pendular qubit states for coupled polar molecules, Zhu et al.35 put forward an approach to realize basic quantum logic gates using polar molecules in pendular states, and others have undertaken some research on the physical characteristics of the polar molecules in various external fields.36–41 However, to our knowledge, until now studies have seldom involved the EPR steering of polar molecules in pendular states. In this paper, we attempt to investigate the steering of a two-dipole system consisting of polar molecules trapped in an external electric field. We found that the EPR steering of the two coupled polar molecules can be manipulated by adjusting the electric field strength, the dipole–dipole interaction, and the ambient temperature. Moreover, with the application of quantum WMR, the enhancement of the steerability was studied. Besides, we also found that EPR steering can achieve the preservation of the nonzero steady value under intrinsic decoherence if the polar molecular system is initially in the Bell state 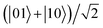 , whereas it almost disappears after a long evolution time for the initial states
, whereas it almost disappears after a long evolution time for the initial states 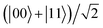 and |01〉. Our results could be useful for the implementation of quantum information tasks based on molecular pendular states for bipartite systems.
and |01〉. Our results could be useful for the implementation of quantum information tasks based on molecular pendular states for bipartite systems.
2 Theory
2.1 Polar molecules in pendular states
The Hamiltonian of a trapped polar diatomic or linear molecule interacting with an external electric field can be expressed as32,37| |
H = BJ2 − με![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ,
| (1) |
where B is the molecular rotational constant, J is the angular momentum operator, and θ is the angle between the molecular permanent dipole moment μ and the electric field ε. The effective dipole moment of the polar molecule is defined as μeff = μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, which can be regarded as the projection of the dipole moment on the direction of the electric field.33 The polar molecules in low rotational states can be superposed and regarded as “pendular states” due to the anisotropy of the Stark effect.42,43 The pendular states of the polar molecules are described by the Dirac symbol |
θ, which can be regarded as the projection of the dipole moment on the direction of the electric field.33 The polar molecules in low rotational states can be superposed and regarded as “pendular states” due to the anisotropy of the Stark effect.42,43 The pendular states of the polar molecules are described by the Dirac symbol |![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) ,M〉, here
,M〉, here ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) is not a good quantum number any more, whereas M (the projection of J on the direction of electric field ε) remains good. In 2002, DeMille30 chose the two lowest energy states at M = 0 with
is not a good quantum number any more, whereas M (the projection of J on the direction of electric field ε) remains good. In 2002, DeMille30 chose the two lowest energy states at M = 0 with ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) = 0 and 1 as the qubits |0〉 and |1〉, respectively. The qubits of ref. 30 can be written as
= 0 and 1 as the qubits |0〉 and |1〉, respectively. The qubits of ref. 30 can be written as| |
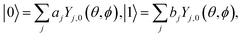 | (2) |
where Yj,0(θ, ϕ) are the spherical harmonics, ϕ represents the azimuth and is assumed to be 0 ≤ ϕ ≤ 2π, and aj and bj are the coefficients of the sum of the spherical harmonics for the pendular states |0〉 and |1〉 respectively. In this situation, the effective dipole moments of the polar molecules are characterized by C0 = 〈0|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|0〉 and C1 = 〈1|cos
θ|0〉 and C1 = 〈1|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|1〉, while the transition dipole moment between the two pendular states |0〉 and |1〉 is characterized by Ct = 〈0|cos
θ|1〉, while the transition dipole moment between the two pendular states |0〉 and |1〉 is characterized by Ct = 〈0|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|1〉.
θ|1〉.
If there is another identical polar molecule in the static electric field, the two trapped polar molecules can be coupled by a dipole–dipole interaction. After averaging the azimuthal angle, the dipole–dipole interaction for M = 0 can be reduced to32,44
| |
Vd–d = Ω(1 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)cos α)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 θ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, θ2,
| (3) |
where
Ω =
μ2/
r123 (with
r12 = |
r1 −
r2| being the distance between the two molecules),
θ1 and
θ2 are the angles between the directions of the dipole moments and the external field, and
α is the angle between
r12 and the electric field direction. Thus the total Hamiltonian of the two polar molecules in the external electric field can be given by
Under the basis of the pendular qubits {|00〉,|01〉,|10〉,|11〉}, the total Hamiltonian H′ can be expanded as
| |
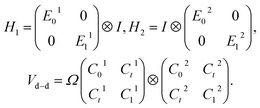 | (5) |
Here,
E0x and
E1x (
x = 1, 2) are the eigenenergies of the pendular states |0〉 and |1〉, respectively,
I is an identity matrix of 2 × 2 dimensions,
C0x and
C1x are the expected values of cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ with regard to the qubits |0〉 and |1〉 of each dipole, and
Ctx denotes the transition dipole moment between the pendular states.
To examine the EPR steering of the polar molecules in thermal states, we considered the two-dipole system initially in thermal equilibrium at the temperature T, whose density matrix can be given by
| |
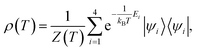 | (6) |
where |
ψi〉 is the
ith eigenstate corresponding to the
ith eigenvalue
Ei of the Hamiltonian
H′,
kB is the Boltzmann constant, and
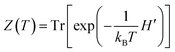
is the partition function.
2.2 EPR steering
In 2009, Cavalcanti, Jones, Wiseman, and Reid set up a criterion to diagnose the steering:15| |
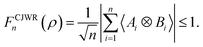 | (7) |
Here Ai = ûi·![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) and Bi =
and Bi = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) i·
i·![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) with ûi and
with ûi and ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) i being the measurement directions, and n denoting the allowed number of the observables which can be measured per site. Generally, the bipartite quantum state ρ satisfying the inequality is unsteerable, otherwise it is steerable.
i being the measurement directions, and n denoting the allowed number of the observables which can be measured per site. Generally, the bipartite quantum state ρ satisfying the inequality is unsteerable, otherwise it is steerable.
Based on the CJWR inequality, in 2016 Costa and Angelo quantified the steering by the amount that the inequality is violated maximally and derived a closed formula in the two- and three-measurement scenarios as follows10
| |
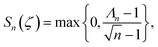 | (8) |
here,
n = 2 or 3 measurements per site,
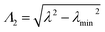
,
Λ3 =
λ,
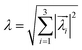
,
λmin = min{|
λ1|,|
λ2|,|
λ3|}, and
λi is the parameter of the following state
| |
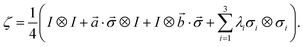 | (9) |
As was proved by Luo,45 the form of the state ζ can always be simplified from any of the states of two qubits by local unitary equivalence. In our study, formula (8) with three observables is employed to quantify the steering of the two-particle system.
3 The EPR steering of polar molecules in pendular states
In the following, we analyze the influences of the electric field intensity, the dipole–dipole interaction, and the ambient temperature on the EPR steering of the two coupled polar molecules when the pendular two-qubit states are initially in the ground and thermal states.
In Fig. 1, we plot the variations of the EPR steering depending on με/B and Ω/B for the ground state at zero temperature. From Fig. 1(a), we can find that the steering of the coupled polar molecules decays gradually with the growing strength of electric field when the dipole–dipole interaction is fixed. If με/B is large, the steering is approximately 0, which may be due to the strong Stark effect between the external electric field and the polar molecules which weakens the interactions among the pendular states. Moreover, for the fixed με/B, it is found that the larger Ω/B is, the stronger the steering will be. To describe more clearly the relationship between the EPR steering and the dipole–dipole interaction, in Fig. 1(b) we depict the behaviors of the steering versus Ω/B for the different values of με/B. From the subfigure, we can observe that the steering enhances monotonously with the increase of Ω/B, which means that the quantum nonlocality of the coupled polar molecules has an inverse correlation with the intermolecular distance r12. For the limit of Ω/B → 0, the polar molecular system is unsteerable, since the quantum states consisting of the two dipoles are nearly separable without the dipole–dipole coupling.
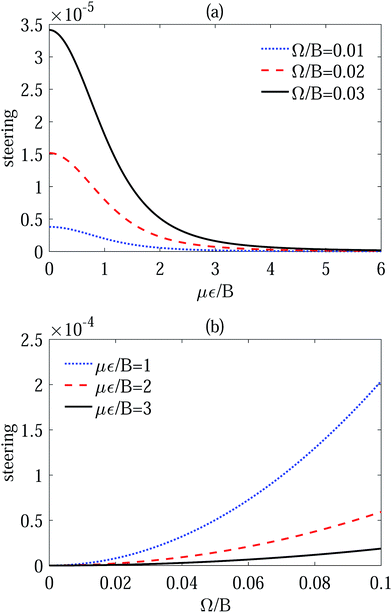 |
| | Fig. 1 The EPR steering for the ground state of the Hamiltonian H′ as a function of με/B with different Ω/B (a) and a function of Ω/B with different με/B (b). | |
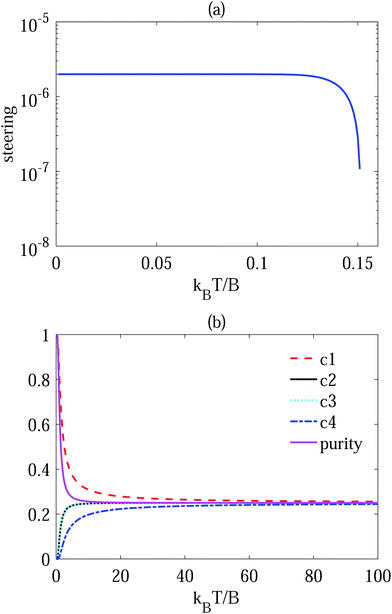
Experimentally, the rovibrational states of polar molecules are very difficult to cool to the ground states with 100% probability.27,46–48 According to eqn (6), herein we explore the EPR steering of the two dipoles in thermal equilibrium, which is related to the thermal excitations resulting from the ambient temperature. As shown in Fig. 2(a), the steering remains almost invariant when the value of kBT/B is relatively small. However, a rapid reduction of the steering occurs if kBT/B exceeds a critical value. To explain the loss of the steerable resource due to the high temperature, in Fig. 2(b) we plot the variance trends for the systemic purity of the two dipoles and the coefficients cj of the eigenstates constituting the density matrix ρ(T) as a function of kBT/B. Here the purity of the thermal state is given by Tr[ρ(T)2] and the coefficients cj are defined as 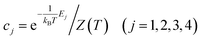 . From Fig. 2(b) we can see that as kBT/B increases, the proportion of the ground state decreases quickly, whereas the three excited states become more populated, and in the meantime the systemic purity decreases since the rovibrational states of the molecules are excited to higher energy levels with greater probability. At the high temperature limit, the proportions of the different energy levels tend to achieve a balance, and the systemic purity decays to 0.25 synchronously. This means that the reduction of the nonlocality results from the decrease of the systemic purity. Moreover, it can be seen that the coefficients c2 and c3 approximately coincide with each other at different kBT/B values, this is because the energy levels of the two intermediate states are almost degenerate when the dipole–dipole interaction is very weak.
. From Fig. 2(b) we can see that as kBT/B increases, the proportion of the ground state decreases quickly, whereas the three excited states become more populated, and in the meantime the systemic purity decreases since the rovibrational states of the molecules are excited to higher energy levels with greater probability. At the high temperature limit, the proportions of the different energy levels tend to achieve a balance, and the systemic purity decays to 0.25 synchronously. This means that the reduction of the nonlocality results from the decrease of the systemic purity. Moreover, it can be seen that the coefficients c2 and c3 approximately coincide with each other at different kBT/B values, this is because the energy levels of the two intermediate states are almost degenerate when the dipole–dipole interaction is very weak.
 |
| | Fig. 2 EPR steering (a), coefficients ci and systemic purity of the two dipoles in thermal equilibrium state (b) as a function of kBT/B with με/B = 1 and Ω/B = 0.01. | |
Generally, the quantum nonlocality is fragile due to the presence of the thermal excitations (see Fig. 2), thereby how to preserve EPR steering in a thermal state is an interesting problem that needs to be explored. As we know, a systemic quantum state suffering from damping noise can be recovered to its initial state with a certain probability by using WMR, which is beneficial for the suppression of the decoherence of a quantum system from the external environment.49–52 WMR has exhibited some potential applications in various fields, such as enhancing quantum entanglement,53 reducing entropic uncertainty,54 and implementing biomolecule sensors.55 In the following, we examine whether the reversal operation is helpful for the protection of the EPR steering of the polar molecules from the thermal excitations or not. For a qubit particle, the WMR can be expressed as a non-unitary quantum operation56,57
| |
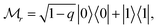 | (10) |
where
q is the strength of the reversing measurement. For simplicity, the WMR is assumed to be performed only on the first pendular qubit of the two dipoles, then the post-measurement state can be obtained as
| |
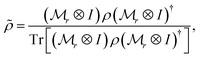 | (11) |
where
ρ is the density matrix of the two-dipole system shown in
eqn (6). In
Fig. 3, we plot the EPR steering in thermal equilibrium as a function of the measurement strength
q for fixed
με/
B and
Ω/
B. It is not hard to find an apparent enhancement of the steering with the increase of
q, and the steering for the different ambient temperatures will converge to the same value asymptotically as
q → 1. In
Fig. 4 the thermal EPR steering of the polar molecules with varying
με/
B (and
Ω/
B) for different values of
q is depicted. Compared with the situation of no reversal operation (
q = 0), we can observe that the WMR does not change the evolution trends of EPR steering with respect to the electric field strength and the dipole–dipole interaction, but the value of the steering with WMR introduced is always larger than the one without WMR, which implies that the reversal operation does indeed contribute to the protection of the quantum nonlocality of the coupled polar molecules in pendular states.
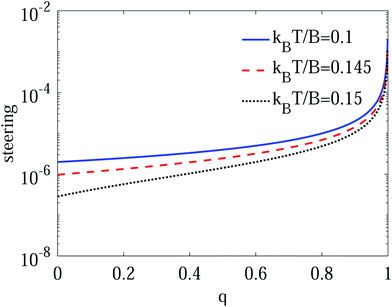 |
| | Fig. 3 The EPR steering of the two dipoles in thermal state as a function of WMR parameter q with με/B = 1 and Ω/B = 0.01 for different kBT/B values. | |
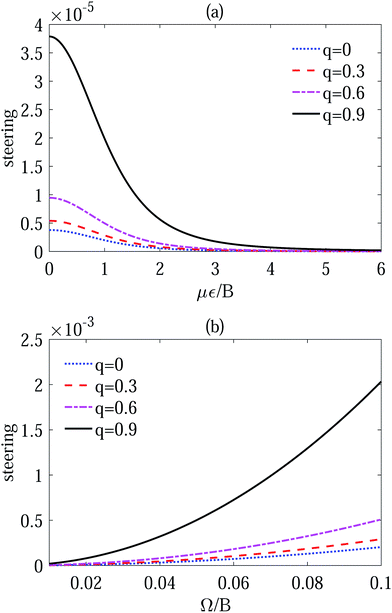 |
| | Fig. 4 For several given values of q, the EPR steering of the two dipoles in thermal state versus με/B with Ω/B = 0.01 (a) and versus Ω/B with με/B = 1 (b). | |
4 The EPR steering of polar molecules under intrinsic decoherence
As we know, an actual physical system cannot avoid interactions with its external environment, which will lead to the loss of quantum coherence. In 1991, Milburn58 assumed that the evolution of a quantum system is not a continuous unitary transformation in a very short time period, and then established the Milburn model describing the phase decoherence in a Markov environment. The density matrix of a quantum system evolving with time in the Milburn model can be given by| |
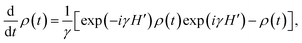 | (12) |
where γ is the phase decoherence rate and H′ is the Hamiltonian of the system. Under Markovian approximation, the master equation of the system can be written as the following form:| |
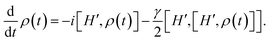 | (13) |
The solution of eqn (13) is expressed as58–60
| |
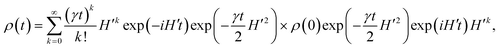 | (14) |
where
ρ(0) is the density operator of the initial system. If the eigenvalues and the corresponding eigenstates of the Hamiltonian
H′ are denoted by
Em,n and |
ψm,n〉 respectively,
eqn (14) can be expanded as
61,62| |
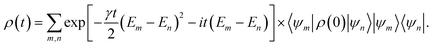 | (15) |
According to the above equation, next we analyzed the temporal evolutions of EPR steering with decoherence factor and electric field intensity for the cases of the two-dipole system being in the three different initial states 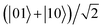 ,
, 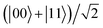 , and |01〉.
, and |01〉.
In Fig. 5, we plot the dynamics of the EPR steering if the two dipoles are initially in the Bell state 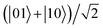 . The first thing to notice from this figure is that the steering hardly decays with time for the different intensities of the decoherence and the different electric fields in the whole evolution process, which indicates that the quantum nonlocality of the polar molecular system in this initial state is very robust against the intrinsic noise. Fig. 5(a) shows that the steering is kept at the value of 1 when t = 0, this is because the initial Bell state has not yet begun to evolve and maintains maximal entanglement, as we expect. If γ = 0, i.e., no interactions exist between the system and its external environment, the steering only oscillates without decay. If γ ≠ 0, the steering undergoes slightly damped oscillations and tends to a constant value eventually. Moreover, it can be seen that the larger γ is, the more quickly the steering attenuates. However, γ has no effect on the oscillation frequency of the steering evolutions. This can be explained qualitatively from the term
. The first thing to notice from this figure is that the steering hardly decays with time for the different intensities of the decoherence and the different electric fields in the whole evolution process, which indicates that the quantum nonlocality of the polar molecular system in this initial state is very robust against the intrinsic noise. Fig. 5(a) shows that the steering is kept at the value of 1 when t = 0, this is because the initial Bell state has not yet begun to evolve and maintains maximal entanglement, as we expect. If γ = 0, i.e., no interactions exist between the system and its external environment, the steering only oscillates without decay. If γ ≠ 0, the steering undergoes slightly damped oscillations and tends to a constant value eventually. Moreover, it can be seen that the larger γ is, the more quickly the steering attenuates. However, γ has no effect on the oscillation frequency of the steering evolutions. This can be explained qualitatively from the term 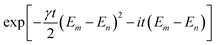 of the time-dependent density matrix of the system described by eqn (15). The term
of the time-dependent density matrix of the system described by eqn (15). The term 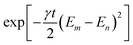 can be regarded as the modulation factor of the amplitude term exp[−it(Em − En)]. Obviously, the modulation factor is an exponential attenuation function depending on γ, here γ is proportional to the decay rate. But, the oscillation frequency is dependent on the invariant Em − En in the amplitude term. This is why γ decides the decay rate instead of the oscillation frequency. In addition, from Fig. 5(b) we can see that the EPR steering first decreases and then increases versus με/B for a given nonzero time. At με/B ≈ 1.2, there exists a minimum value for the steering. Thus, the strong quantum nonlocality of the coupled polar molecules under intrinsic decoherence can be obtained by properly adjusting the strength of the electric field.
can be regarded as the modulation factor of the amplitude term exp[−it(Em − En)]. Obviously, the modulation factor is an exponential attenuation function depending on γ, here γ is proportional to the decay rate. But, the oscillation frequency is dependent on the invariant Em − En in the amplitude term. This is why γ decides the decay rate instead of the oscillation frequency. In addition, from Fig. 5(b) we can see that the EPR steering first decreases and then increases versus με/B for a given nonzero time. At με/B ≈ 1.2, there exists a minimum value for the steering. Thus, the strong quantum nonlocality of the coupled polar molecules under intrinsic decoherence can be obtained by properly adjusting the strength of the electric field.
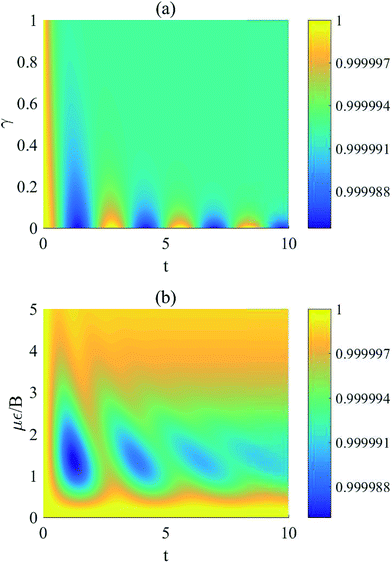 |
| | Fig. 5 Evolution of the EPR steering of the two dipoles under intrinsic decoherence for the initial state 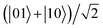 . (a) Steering as functions of γ and t , with με/B = 1 and Ω/B = 0.01, and (b) steering as functions of με/B and t , with Ω/B = 0.01 and γ = 0.1. . (a) Steering as functions of γ and t , with με/B = 1 and Ω/B = 0.01, and (b) steering as functions of με/B and t , with Ω/B = 0.01 and γ = 0.1. | |
In Fig. 6, we plot the time evolution of the EPR steering for the case of the two dipoles being in the initial state 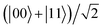 . From this figure, we can find that the evolution trends of the steering are very different from the initial state
. From this figure, we can find that the evolution trends of the steering are very different from the initial state 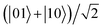 (see Fig. 5), although the two Bell states are both maximally steerable at the initial stage. Fig. 6(a) shows that for γ = 0, the steering is always equal to 1 and does not exhibit oscillations at all compared to Fig. 5(a). In other words, it can be regarded as a kind of special oscillation where the variance amplitude is equal to 0. Moreover, we can observe that, if γ ≠ 0, the steering decreases to 0 monotonously and rapidly with the time evolution, whereas the steering of the initial state
(see Fig. 5), although the two Bell states are both maximally steerable at the initial stage. Fig. 6(a) shows that for γ = 0, the steering is always equal to 1 and does not exhibit oscillations at all compared to Fig. 5(a). In other words, it can be regarded as a kind of special oscillation where the variance amplitude is equal to 0. Moreover, we can observe that, if γ ≠ 0, the steering decreases to 0 monotonously and rapidly with the time evolution, whereas the steering of the initial state 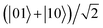 shown in Fig. 5(a) evolves into a large constant eventually after oscillating. Fig. 6(b) shows that the stronger the electric field is, the shorter the duration of steering will be, which means that the strong Stark effect is not good for the existence of quantum nonlocality when the initial state of the two-dipole system is
shown in Fig. 5(a) evolves into a large constant eventually after oscillating. Fig. 6(b) shows that the stronger the electric field is, the shorter the duration of steering will be, which means that the strong Stark effect is not good for the existence of quantum nonlocality when the initial state of the two-dipole system is 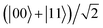 .
.
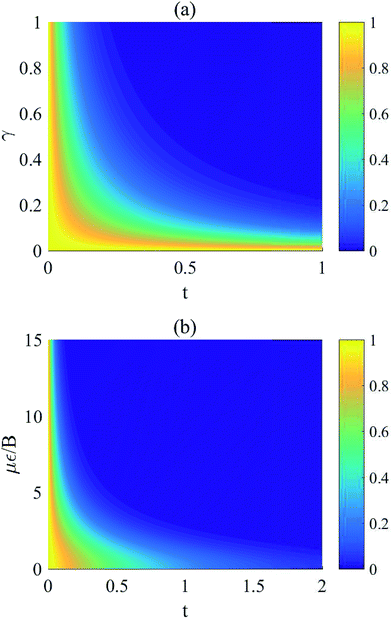 |
| | Fig. 6 Evolutions of the EPR steering of the two dipoles under intrinsic decoherence for the initial state 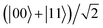 . (a) Steering as functions of γ and t, with με/B = 1 and Ω/B = 0.01, (b) steering as functions of με/B and t, with Ω/B = 0.01 and γ = 0.1. . (a) Steering as functions of γ and t, with με/B = 1 and Ω/B = 0.01, (b) steering as functions of με/B and t, with Ω/B = 0.01 and γ = 0.1. | |
In Fig. 7, we depict the evolution behaviors of the EPR steering for the initial state of the system being |01〉. From the figure, we find that the steering does not exist when t = 0 due to the separability of the initial state. Fig. 7(a) shows that if γ = 0, the EPR steering exhibits periodic oscillation between the values of 0 and 1 as time increases. If γ ≠ 0, the steering oscillates with a damping of the amplitude and attenuates to 0 after a long time. Moreover, Fig. 7(b) indicates that the electric field intensity is helpful for the enhancement of the duration of the steering, which is opposite to the case of Fig. 6(b) for the same decoherence factor γ. Although the steering of the separable state |01〉 evolves to 0 eventually, it takes more time to become steady compared with the situation of the initial Bell state 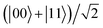 . Therefore, if people want to study the dynamics of the steering experimentally, taking the separable state as the initial state may be a better choice due to the longer duration of nonlocality.
. Therefore, if people want to study the dynamics of the steering experimentally, taking the separable state as the initial state may be a better choice due to the longer duration of nonlocality.
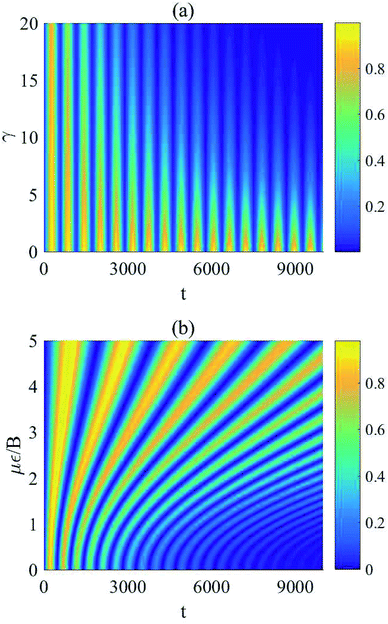 |
| | Fig. 7 Evolutions of the EPR steering of the two dipoles under intrinsic decoherence for the initial state |01〉. (a) Steering as functions of γ and t, with με/B = 1 and Ω/B = 0.01, (b) steering as functions of με/B and t, with Ω/B = 0.01 and γ = 10. | |
5 Conclusions
In summary, we have studied the evolution features of the EPR steering for two coupled polar molecules in pendular states, depending on the external electric field intensity, the dipole–dipole interaction, and the ambient temperature. Then, we have also examined the influences of the intrinsic decoherence on the EPR steering of the two dipoles for three different initial states. Our results show that for the ground and thermal states, the EPR steering is proportional to the dipole–dipole interaction and inversely proportional to the electric field strength. In particular, we find that a high temperature can result in a lower systemic purity, and further leads to the reduction of the steering in the thermal equilibrium. This is because more molecules populate the rovibrational excited states when the ambient temperature is relatively high, which weakens the intercoupling among the pendular qubit states. Fortunately, it is found that the WMR can be used to protect the EPR steering of the polar molecules in the thermal state, and the steering can be effectively enhanced by increasing the reversing measurement strength.
Last but not least, we have found that when the two dipoles suffer from the intrinsic decoherence, the decoherence factor has no effect on the oscillation frequency but plays a significant role in the decay rate. Moreover, the Stark effect accelerates the decay of the EPR steering for the initial entangled state 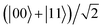 , whereas it suppresses the decoherence for the initial separable state |01〉. In addition, for the Bell state
, whereas it suppresses the decoherence for the initial separable state |01〉. In addition, for the Bell state 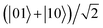 , the steering always evolves into large steady values over a long time limit, but for the initial states
, the steering always evolves into large steady values over a long time limit, but for the initial states 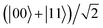 and |01〉, it almost vanishes after enough evolution time. The reason may be because the state
and |01〉, it almost vanishes after enough evolution time. The reason may be because the state 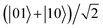 contributes to resist phase decoherence and can be coded into decoherence-free subspace,63,64 but the state
contributes to resist phase decoherence and can be coded into decoherence-free subspace,63,64 but the state 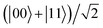 is sensitive to phase decoherence. Thus in the case of intrinsic decoherence, the two dipoles being initially in the
is sensitive to phase decoherence. Thus in the case of intrinsic decoherence, the two dipoles being initially in the 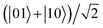 state are more suitable to accomplish the storage of quantum information to some extent. We expect that our results might deepen the understanding of the quantum nonlocality in a molecular system, and could stimulate further studies on multi-particle quantum correlations of polar molecules in pendular states.
state are more suitable to accomplish the storage of quantum information to some extent. We expect that our results might deepen the understanding of the quantum nonlocality in a molecular system, and could stimulate further studies on multi-particle quantum correlations of polar molecules in pendular states.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Key Research and Development Program of China under Grant No. 2016YFB0501601, the National Natural Science Foundation of China under Grant No. 11174081 and 11774093, and the Natural Science Foundation of Shanghai under Grant No. 16ZR1448300.
Notes and references
- E. Schrödinger, Naturwissenschaften, 1935, 23, 807 CrossRef.
- A. Einstein, B. Podolsky and N. Rosen, Phys. Rev., 1935, 47, 777 CrossRef CAS.
- H. M. Wiseman, S. J. Jones and A. C. Doherty, Phys. Rev. Lett., 2007, 98, 140402 CrossRef CAS PubMed.
- S. J. Jones, H. M. Wiseman and A. C. Doherty, Phys. Rev. A, 2007, 76, 052116 CrossRef.
- M. T. Quintino, T. Vértesi, D. Cavalcanti, R. Augusiak, M. Demianowicz, A. Acín and N. Brunner, Phys. Rev. A, 2015, 92, 032107 CrossRef.
- Q. Y. He, Q. H. Gong and M. D. Reid, Phys. Rev. Lett., 2015, 114, 060402 CrossRef CAS PubMed.
- J.-L. Chen, C. Ren, C. Chen, X.-J. Ye and A. K. Pati, Sci. Rep., 2016, 6, 39063 CrossRef CAS PubMed.
- W.-Y. Sun, D. Wang, J.-D. Shi and L. Ye, Sci. Rep., 2017, 7, 39651 CrossRef CAS PubMed.
- P. Skrzypczyk, M. Navascués and D. Cavalcanti, Phys. Rev. Lett., 2014, 112, 180404 CrossRef PubMed.
- A. C. S. Costa and R. M. Angelo, Phys. Rev. A, 2016, 93, 020103 CrossRef.
- A. C. S. Costa, M. W. Beims and R. M. Angelo, Phys. A, 2016, 461, 469 CrossRef.
- K. Sun, X.-J. Ye, J.-S. Xu, X.-Y. Xu, J.-S. Tang, Y.-C. Wu, J.-L. Chen, C.-F. Li and G.-C. Guo, Phys. Rev. Lett., 2016, 116, 160404 CrossRef PubMed.
- H.-Y. Ku, S.-L. Chen, C. Budroni, A. Miranowicz, Y.-N. Chen and F. Nori, Phys. Rev. A, 2018, 97, 022338 CrossRef.
- X. Deng, C. Tian, M. Wang, Z. Qin and X. Su, Opt. Commun., 2018, 421, 14 CrossRef CAS.
- E. G. Cavalcanti, S. J. Jones, H. M. Wiseman and M. D. Reid, Phys. Rev. A, 2009, 80, 032112 CrossRef.
- M. Hillery, V. Bužek and A. Berthiaume, Phys. Rev. A, 1999, 59, 1829 CrossRef CAS.
- C. Branciard, E. G. Cavalcanti, S. P. Walborn, V. Scarani and H. M. Wiseman, Phys. Rev. A, 2012, 85, 010301 CrossRef.
- S. Armstrong, M. Wang, R. Y. Teh, Q. Gong, Q. He, J. Janousek, H.-A. Bachor, M. D. Reid and P. K. Lam, Nat. Phys., 2015, 11, 167 Search PubMed.
- Q. He, L. Rosales-Zárate, G. Adesso and M. D. Reid, Phys. Rev. Lett., 2015, 115, 180502 CrossRef PubMed.
- S. Nagy and T. Vértesi, Sci. Rep., 2016, 6, 21634 CrossRef CAS PubMed.
- J. C. Howell, R. S. Bennink, S. J. Bentley and R. W. Boyd, Phys. Rev. Lett., 2004, 92, 210403 CrossRef PubMed.
- D. J. Saunders, S. J. Jones, H. M. Wiseman and G. J. Pryde, Nat. Phys., 2010, 6, 845 Search PubMed.
- A. J. Bennet, D. A. Evans, D. J. Saunders, C. Branciard, E. G. Cavalcanti, H. M. Wiseman and G. J. Pryde, Phys. Rev. X, 2012, 2, 031003 Search PubMed.
- D. H. Smith, G. Gillett, M. P. de Almeida, C. Branciard, A. Fedrizzi, T. J. Weinhold, A. Lita, B. Calkins, T. Gerrits, H. M. Wiseman, S. W. Nam and A. G. White, Nat. Commun., 2012, 3, 625 Search PubMed.
- S.-J. Xiong, Y. Zhang, Z. Sun, L. Yu, Q. Su, X.-Q. Xu, J.-S. Jin, Q. Xu, J.-M. Liu, K. Chen and C.-P. Yang, Optica, 2017, 4, 1065 Search PubMed.
- P. Kunkel, M. Prüfer, H. Strobel, D. Linnemann, A. Frölian, T. Gasenzer, M. Gärttner and M. K. Oberthaler, Science, 2018, 360, 413 CrossRef CAS PubMed.
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, New J. Phys., 2009, 11, 055049 CrossRef.
- O. Dulieu and C. Gabbanini, Rep. Prog. Phys., 2009, 72, 086401 CrossRef.
- G. Quéméner and P. S. Julienne, Chem. Rev., 2012, 112, 4949 CrossRef PubMed.
- D. DeMille, Phys. Rev. Lett., 2002, 88, 067901 CrossRef CAS PubMed.
- E. Kuznetsova, R. Côté, K. Kirby and S. F. Yelin, Phys. Rev. A, 2008, 78, 012313 CrossRef.
- Q. Wei, S. Kais, B. Friedrich and D. Herschbach, J. Chem. Phys., 2011, 134, 124107 CrossRef PubMed.
- Q. Wei, S. Kais, B. Friedrich and D. Herschbach, J. Chem. Phys., 2011, 135, 154102 CrossRef PubMed.
- Q. Wei, Y. Cao, S. Kais, B. Friedrich and D. Herschbach, ChemPhysChem, 2016, 17, 3714 CrossRef PubMed.
- J. Zhu, S. Kais, Q. Wei, D. Herschbach and B. Friedrich, J. Chem. Phys., 2013, 138, 024104 CrossRef PubMed.
- M. Härtelt and B. Friedricha, J. Chem. Phys., 2008, 128, 224313 CrossRef PubMed.
- Y.-J. Li and J.-M. Liu, Acta Phys. Sin., 2014, 63, 200302 Search PubMed.
- K. Sharma and B. Friedrich, New J. Phys., 2015, 17, 045017 CrossRef.
- K. Sharma and B. Friedrich, Phys. Chem. Chem. Phys., 2016, 18, 13467 RSC.
- J.-X. Han, Y. Hu, Y. Jin and G.-F. Zhang, J. Chem. Phys., 2016, 144, 134308 CrossRef PubMed.
- Z.-Y. Zhang and J.-M. Liu, Sci. Rep., 2017, 7, 17822 CrossRef PubMed.
- B. Friedrich and D. R. Herschbach, Nature, 1991, 353, 412 CrossRef CAS.
- J. M. Rost, J. C. Griffin, B. Friedrich and D. R. Herschbach, Phys. Rev. Lett., 1992, 68, 1299 CrossRef CAS PubMed.
- A. J. Stone, The Theory of Intermolecular Forces, Clarendon, Oxford, 2nd edn, 2002 Search PubMed.
- S. Luo, Phys. Rev. A, 2008, 77, 042303 CrossRef.
- M. Schnell and G. Meijer, Angew. Chem., Int. Ed., 2009, 48, 6010 CrossRef CAS PubMed.
- D. J. McCarron, M. H. Steinecker, Y. Zhu and D. DeMille, Phys. Rev. Lett., 2018, 121, 013202 CrossRef CAS PubMed.
- L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle and J. M. Doyle, Nat. Phys., 2018, 14, 890 Search PubMed.
- Y. Aharonov, D. Z. Albert and L. Vaidman, Phys. Rev. Lett., 1988, 60, 1351 CrossRef PubMed.
- A. N. Korotkov and K. Keane, Phys. Rev. A, 2010, 81, 040103(R) CrossRef.
- Y. W. Cheong and S. W. Lee, Phys. Rev. Lett., 2012, 109, 150402 CrossRef PubMed.
- R.-Y. Yang and J.-M. Liu, Quantum Inf. Process., 2017, 16, 125 CrossRef.
- J. C. Lee, Y. C. Yeong, Y. S. Kim and Y. H. Kim, Opt. Express, 2011, 19, 16309 CrossRef PubMed.
- L. Li, Q.-W. Wang, S.-Q. Shen and M. Li, Quantum Inf. Process., 2017, 16, 188 CrossRef.
- Y. Zhang, D. Li, Y. He, Z. Shen and Q. He, Opt. Lett., 2016, 41, 5409 CrossRef CAS PubMed.
- T. Pramanik and A. S. Majumdar, Phys. Lett. A, 2013, 377, 3209 CrossRef CAS.
- Y. S. Kim, J. C. Lee, O. Kwon and Y. H. Kim, Nat. Phys., 2012, 8, 117 Search PubMed.
- G. J. Milburn, Phys. Rev. A, 1991, 44, 5401 CrossRef CAS.
- P. F. Yu, J. G. Cai, J. M. Liu and G. T. Shen, Eur. Phys. J. D, 2007, 44, 151 CrossRef CAS.
- Z.-Y. Zhang, D. X. Wei and J.-M. Liu, Laser Phys. Lett., 2018, 15, 065207 CrossRef.
- K.-M. Fan and G.-F. Zhang, Eur. Phys. J. D, 2014, 68, 163 CrossRef.
- L. Zheng and G.-F. Zhang, Eur. Phys. J. D, 2017, 71, 288 CrossRef.
- G. M. Palma, K.-A. Suominen and A. K. Ekert, Proc. R. Soc. London, Ser. A, 1996, 452, 567 CrossRef.
- D. A. Lidar, I. L. Chuang and K. B. Whaley, Phys. Rev. Lett., 1998, 81, 2594 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
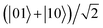 . Our findings may shed some new light on molecular quantum information processing with pendular states.
. Our findings may shed some new light on molecular quantum information processing with pendular states.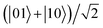 , whereas it almost disappears after a long evolution time for the initial states
, whereas it almost disappears after a long evolution time for the initial states 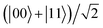 and |01〉. Our results could be useful for the implementation of quantum information tasks based on molecular pendular states for bipartite systems.
and |01〉. Our results could be useful for the implementation of quantum information tasks based on molecular pendular states for bipartite systems.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, which can be regarded as the projection of the dipole moment on the direction of the electric field.33 The polar molecules in low rotational states can be superposed and regarded as “pendular states” due to the anisotropy of the Stark effect.42,43 The pendular states of the polar molecules are described by the Dirac symbol |
θ, which can be regarded as the projection of the dipole moment on the direction of the electric field.33 The polar molecules in low rotational states can be superposed and regarded as “pendular states” due to the anisotropy of the Stark effect.42,43 The pendular states of the polar molecules are described by the Dirac symbol |![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) ,M〉, here
,M〉, here ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) is not a good quantum number any more, whereas M (the projection of J on the direction of electric field ε) remains good. In 2002, DeMille30 chose the two lowest energy states at M = 0 with
is not a good quantum number any more, whereas M (the projection of J on the direction of electric field ε) remains good. In 2002, DeMille30 chose the two lowest energy states at M = 0 with ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) = 0 and 1 as the qubits |0〉 and |1〉, respectively. The qubits of ref. 30 can be written as
= 0 and 1 as the qubits |0〉 and |1〉, respectively. The qubits of ref. 30 can be written as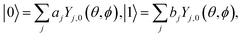
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|0〉 and C1 = 〈1|cos
θ|0〉 and C1 = 〈1|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|1〉, while the transition dipole moment between the two pendular states |0〉 and |1〉 is characterized by Ct = 〈0|cos
θ|1〉, while the transition dipole moment between the two pendular states |0〉 and |1〉 is characterized by Ct = 〈0|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|1〉.
θ|1〉.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α)cos
α)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1
θ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2,
θ2,
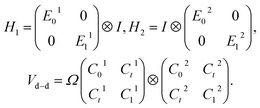
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ with regard to the qubits |0〉 and |1〉 of each dipole, and Ctx denotes the transition dipole moment between the pendular states.
θ with regard to the qubits |0〉 and |1〉 of each dipole, and Ctx denotes the transition dipole moment between the pendular states.
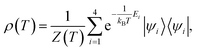
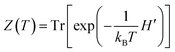 is the partition function.
is the partition function.
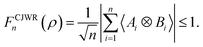
![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) and Bi =
and Bi = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) i·
i·![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) with ûi and
with ûi and ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) i being the measurement directions, and n denoting the allowed number of the observables which can be measured per site. Generally, the bipartite quantum state ρ satisfying the inequality is unsteerable, otherwise it is steerable.
i being the measurement directions, and n denoting the allowed number of the observables which can be measured per site. Generally, the bipartite quantum state ρ satisfying the inequality is unsteerable, otherwise it is steerable.
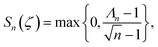
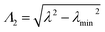 , Λ3 = λ,
, Λ3 = λ, 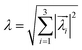 , λmin = min{|λ1|,|λ2|,|λ3|}, and λi is the parameter of the following state
, λmin = min{|λ1|,|λ2|,|λ3|}, and λi is the parameter of the following state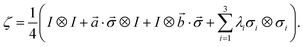

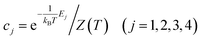 . From Fig. 2(b) we can see that as kBT/B increases, the proportion of the ground state decreases quickly, whereas the three excited states become more populated, and in the meantime the systemic purity decreases since the rovibrational states of the molecules are excited to higher energy levels with greater probability. At the high temperature limit, the proportions of the different energy levels tend to achieve a balance, and the systemic purity decays to 0.25 synchronously. This means that the reduction of the nonlocality results from the decrease of the systemic purity. Moreover, it can be seen that the coefficients c2 and c3 approximately coincide with each other at different kBT/B values, this is because the energy levels of the two intermediate states are almost degenerate when the dipole–dipole interaction is very weak.
. From Fig. 2(b) we can see that as kBT/B increases, the proportion of the ground state decreases quickly, whereas the three excited states become more populated, and in the meantime the systemic purity decreases since the rovibrational states of the molecules are excited to higher energy levels with greater probability. At the high temperature limit, the proportions of the different energy levels tend to achieve a balance, and the systemic purity decays to 0.25 synchronously. This means that the reduction of the nonlocality results from the decrease of the systemic purity. Moreover, it can be seen that the coefficients c2 and c3 approximately coincide with each other at different kBT/B values, this is because the energy levels of the two intermediate states are almost degenerate when the dipole–dipole interaction is very weak.
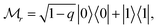
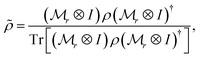


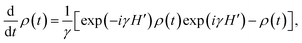
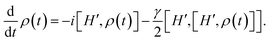
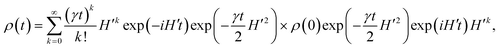
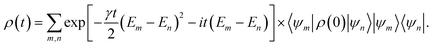
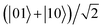 ,
, 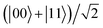 , and |01〉.
, and |01〉.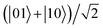 . The first thing to notice from this figure is that the steering hardly decays with time for the different intensities of the decoherence and the different electric fields in the whole evolution process, which indicates that the quantum nonlocality of the polar molecular system in this initial state is very robust against the intrinsic noise. Fig. 5(a) shows that the steering is kept at the value of 1 when t = 0, this is because the initial Bell state has not yet begun to evolve and maintains maximal entanglement, as we expect. If γ = 0, i.e., no interactions exist between the system and its external environment, the steering only oscillates without decay. If γ ≠ 0, the steering undergoes slightly damped oscillations and tends to a constant value eventually. Moreover, it can be seen that the larger γ is, the more quickly the steering attenuates. However, γ has no effect on the oscillation frequency of the steering evolutions. This can be explained qualitatively from the term
. The first thing to notice from this figure is that the steering hardly decays with time for the different intensities of the decoherence and the different electric fields in the whole evolution process, which indicates that the quantum nonlocality of the polar molecular system in this initial state is very robust against the intrinsic noise. Fig. 5(a) shows that the steering is kept at the value of 1 when t = 0, this is because the initial Bell state has not yet begun to evolve and maintains maximal entanglement, as we expect. If γ = 0, i.e., no interactions exist between the system and its external environment, the steering only oscillates without decay. If γ ≠ 0, the steering undergoes slightly damped oscillations and tends to a constant value eventually. Moreover, it can be seen that the larger γ is, the more quickly the steering attenuates. However, γ has no effect on the oscillation frequency of the steering evolutions. This can be explained qualitatively from the term 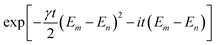 of the time-dependent density matrix of the system described by eqn (15). The term
of the time-dependent density matrix of the system described by eqn (15). The term 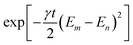 can be regarded as the modulation factor of the amplitude term exp[−it(Em − En)]. Obviously, the modulation factor is an exponential attenuation function depending on γ, here γ is proportional to the decay rate. But, the oscillation frequency is dependent on the invariant Em − En in the amplitude term. This is why γ decides the decay rate instead of the oscillation frequency. In addition, from Fig. 5(b) we can see that the EPR steering first decreases and then increases versus με/B for a given nonzero time. At με/B ≈ 1.2, there exists a minimum value for the steering. Thus, the strong quantum nonlocality of the coupled polar molecules under intrinsic decoherence can be obtained by properly adjusting the strength of the electric field.
can be regarded as the modulation factor of the amplitude term exp[−it(Em − En)]. Obviously, the modulation factor is an exponential attenuation function depending on γ, here γ is proportional to the decay rate. But, the oscillation frequency is dependent on the invariant Em − En in the amplitude term. This is why γ decides the decay rate instead of the oscillation frequency. In addition, from Fig. 5(b) we can see that the EPR steering first decreases and then increases versus με/B for a given nonzero time. At με/B ≈ 1.2, there exists a minimum value for the steering. Thus, the strong quantum nonlocality of the coupled polar molecules under intrinsic decoherence can be obtained by properly adjusting the strength of the electric field.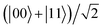 . From this figure, we can find that the evolution trends of the steering are very different from the initial state
. From this figure, we can find that the evolution trends of the steering are very different from the initial state 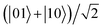 (see Fig. 5), although the two Bell states are both maximally steerable at the initial stage. Fig. 6(a) shows that for γ = 0, the steering is always equal to 1 and does not exhibit oscillations at all compared to Fig. 5(a). In other words, it can be regarded as a kind of special oscillation where the variance amplitude is equal to 0. Moreover, we can observe that, if γ ≠ 0, the steering decreases to 0 monotonously and rapidly with the time evolution, whereas the steering of the initial state
(see Fig. 5), although the two Bell states are both maximally steerable at the initial stage. Fig. 6(a) shows that for γ = 0, the steering is always equal to 1 and does not exhibit oscillations at all compared to Fig. 5(a). In other words, it can be regarded as a kind of special oscillation where the variance amplitude is equal to 0. Moreover, we can observe that, if γ ≠ 0, the steering decreases to 0 monotonously and rapidly with the time evolution, whereas the steering of the initial state 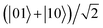 shown in Fig. 5(a) evolves into a large constant eventually after oscillating. Fig. 6(b) shows that the stronger the electric field is, the shorter the duration of steering will be, which means that the strong Stark effect is not good for the existence of quantum nonlocality when the initial state of the two-dipole system is
shown in Fig. 5(a) evolves into a large constant eventually after oscillating. Fig. 6(b) shows that the stronger the electric field is, the shorter the duration of steering will be, which means that the strong Stark effect is not good for the existence of quantum nonlocality when the initial state of the two-dipole system is 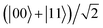 .
.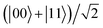 . Therefore, if people want to study the dynamics of the steering experimentally, taking the separable state as the initial state may be a better choice due to the longer duration of nonlocality.
. Therefore, if people want to study the dynamics of the steering experimentally, taking the separable state as the initial state may be a better choice due to the longer duration of nonlocality.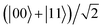 , whereas it suppresses the decoherence for the initial separable state |01〉. In addition, for the Bell state
, whereas it suppresses the decoherence for the initial separable state |01〉. In addition, for the Bell state 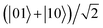 , the steering always evolves into large steady values over a long time limit, but for the initial states
, the steering always evolves into large steady values over a long time limit, but for the initial states 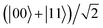 and |01〉, it almost vanishes after enough evolution time. The reason may be because the state
and |01〉, it almost vanishes after enough evolution time. The reason may be because the state 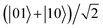 contributes to resist phase decoherence and can be coded into decoherence-free subspace,63,64 but the state
contributes to resist phase decoherence and can be coded into decoherence-free subspace,63,64 but the state 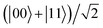 is sensitive to phase decoherence. Thus in the case of intrinsic decoherence, the two dipoles being initially in the
is sensitive to phase decoherence. Thus in the case of intrinsic decoherence, the two dipoles being initially in the 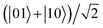 state are more suitable to accomplish the storage of quantum information to some extent. We expect that our results might deepen the understanding of the quantum nonlocality in a molecular system, and could stimulate further studies on multi-particle quantum correlations of polar molecules in pendular states.
state are more suitable to accomplish the storage of quantum information to some extent. We expect that our results might deepen the understanding of the quantum nonlocality in a molecular system, and could stimulate further studies on multi-particle quantum correlations of polar molecules in pendular states.