Open Access Article
Open Access ArticleAnalysis of nanofiber-based La0.2Sr0.8TiO3–Gd0.2Ce0.8O1.9 electrode kinetics
Yuwei Wanga,
Erqing Zhaob,
Liquan Fan *a,
Qianjun Huc,
Xijun Liua,
Yufeng Lia and
Yueping Xiong*c
*a,
Qianjun Huc,
Xijun Liua,
Yufeng Lia and
Yueping Xiong*c
aCollege of Materials Science and Engineering, Heilongjiang Provincial Key Laboratory of Polymeric Composite Materials, Qiqihar University, No. 42, Wenhua Street, Qiqihar 161006, China. E-mail: Liquan_Fan@163.com
bSchool of Chemistry and Chemical Engineering, Henan Institute of Science and Technology, Xinxiang, 453003, China
cMIIT Key Laboratory of Critical Materials Technology for New Energy Conversion and Storage, School of Chemistry and Chemical Engineering, Harbin Institute of Technology, 92 West Dazhi Street, Mailbox 1247, Harbin 150001, China. E-mail: ypxiong@hit.edu.cn
First published on 18th October 2018
Abstract
For the sake of comparison, a single cell with nanofiber-based LST–GDC composite anode (Cell-1) and a single cell with nanoparticle-based LST–GDC composite anode (Cell-2) are fabricated, respectively. The electrolyte ohmic resistances of the LST–GDC composite anode side half-cells are determined by an AC resistance measurement. Current interrupt is applied to measure the ohmic resistance of the half-cells. Combined with V–I characteristics, the influences of the potential drops caused by electrolyte ohmic resistance, electrode ohmic resistance and electrode electrochemical reaction on the cell kinetics are investigated. Under a current density of 0.6 A cm−2 at 850 °C, for the nanofiber-based LST–GDC composite anode (NF-LST–GDC), the electrode ohmic potential drop is 0.007 V and the potential drop caused by the electrode electrochemical reaction is 0.080 V. While for the nanoparticle-based LST–GDC composite anode (NP-LST–GDC), the corresponding potential drops are 0.159 V and 0.246 V, respectively. Both the potential drops of the former are lower than those of the latter. The kinetics of Cell-1 is greater than Cell-2, i.e., the kinetics of NF-LST–GDC is greater than that of NP-LST–GDC.
1. Introduction
As one of the most important major fuel cell components, an anode for solid oxide fuel cells (SOFCs) has to possess many properties including catalytic activity and electrical conductivity. The improvement in anode performance and microstructure is very conducive to the development of highly robust solid oxide fuel cells operated over a wide range of fuels.1 Over the past twenty years, lanthanum doped strontium titanate (LST) anodes have received wide attention due to their greater tolerance to sulfur poisoning, higher resistance to carbon deposition when using carbon-based fuels, and improved dimensional and chemical stability when subjected to redox cycling comparing to conventional Ni-based anodes.2–5 However as a single electronic conductor, LST alone is not suitable for use as an anode for SOFCs.6 An efficient method to get a promising LST-based composite anode is by adding or infiltrating doped ceria based materials with good oxygen ionic conductivity into LST.7–11From previous studies on performance of Gd0.2Ce0.8O1.9 (GDC) infiltrated La0.2Sr0.8TiO3 (LST) nanofiber scaffolds as anodes for solid oxide fuel cells,12,13 it was shown that nanofiber-based LST–GDC composite anodes with the optimal mass ratio range of LST to GDC show good electrochemical performance and microstructure stability when subjected to thermal and redox cycling due to the porous LST nanofiber scaffold in the composite anode buffers the volume change. Compared with YSZ and ScSZ, the LST–GDC composite anode with LSGM as the electrolyte shows the best electrochemical performance due to the electrolyte high O2− conductivity. As a follow-up study, the purpose of our study was to further investigate which factors affect the kinetics of the single cells with the nanofiber-based LST–GDC composite anode.
The transient measurement method provides an effective way to observe the total ohmic potential of the electrochemical systems.14 Current interruption (CI) technique can be successfully applied to estimate the internal resistance of fuel cells. By interrupting briefly the current flowing to the electrochemical system of a fuel cell, the instantaneous change in voltage and current of the cell just prior to the interrupt event are accurately recorded. The resultant quotient of the instantaneous change is considered as the total ohmic resistance of the fuel cell because the cell voltage increases instantaneously by the amount of the ohmic potential drop.15,16 For SOFCs, the total ohmic resistance consists of the electrode ohmic resistance and the electrolyte ohmic resistance. The electrolyte ohmic resistance can be obtained from electrochemical impedance spectra study which corresponds to the high frequency intercept at real axis.17 So the electrode ohmic resistance here is the total ohmic resistance obtained from CI measurement minus the electrolyte ohmic resistance determined by electrochemical impedance spectra (EIS). This paper mainly focuses on the influence of electrode ohmic resistance on kinetics property of the SOFCs with different nanostructured anodes.
2 Experimental
2.1 Preparation of LSGMC electrolytes
La0.8Sr0.2Ga0.8Mg0.15Co0.05O3−δ (LSGMC) electrolyte pellets with 19 mm in diameter and 600–630 μm in thickness were prepared by uniaxially pressing a commercially available LSGMC powder (Seimi Chemical Co., Ltd., Japan), followed by cold isostatic pressing at 400 MPa for 8 min and sintering at 1450 °C for 8 h.2.2 Preparation of single cells
Sm0.5Sr0.5CoO3−δ (SSC) nanofibers and La0.2Sr0.8TiO3 (LST) nanofibers or nanoparticles obtained from electrospinning were symmetrically sintered onto the two sides of the LSGMC pellet at 1000 °C for 1 h. The apparent area of the two circular electrodes was 0.785 cm2 (i.e. the diameter of the electrodes was 1 cm). Composite electrodes were produced by infiltration of Gd0.2Ce0.8O1.9 (GDC) precursor solution into the electrode scaffolds and followed by calcination process. The optimal GDC amount achieved by multiple infiltration cycles was carried out. Details on the fabrication procedures of the composite electrodes and the determination of the optimum GDC loading amount can be found in literature18 for nanofiber-based SSC–GDC composite cathode (denoted as NF-SSC–GDC),12 for nanofiber-based LST–GDC composite anode (denoted as NF-LST–GDC), and19 for nanoparticle-based LST–GDC composite anode (denoted as NP-LST–GDC). Here, the composite electrodes with optimum composition were used for making single cells. The single cells were consisted of NF-SSC–GDC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7–0.8) as air electrode, NF-LST–GDC (1
0.7–0.8) as air electrode, NF-LST–GDC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.1–1.2) or NP-LST–GDC (1
1.1–1.2) or NP-LST–GDC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5) as fuel electrode, and LSGMC electrolyte. Pt pastes were painted and fired at 1000 °C for 1 h as a reference electrode on the rim of the LSGMC disk. Au mesh and Pt mesh were used as current collector for the anode and the cathode, respectively. The humidified hydrogen (97% H2 + 3% H2O) was used as fuel gas on the anode side.
0.5) as fuel electrode, and LSGMC electrolyte. Pt pastes were painted and fired at 1000 °C for 1 h as a reference electrode on the rim of the LSGMC disk. Au mesh and Pt mesh were used as current collector for the anode and the cathode, respectively. The humidified hydrogen (97% H2 + 3% H2O) was used as fuel gas on the anode side.
For comparison, two kinds of three-electrode systems were prepared in the current work. The three-electrode system consisting of NF-LST–GDC as a working electrode, NF-SSC–GDC as a counter electrode, Pt on the rim of the LSGMC disk (thickness: 610 μm) as a reference electrode was denoted as Cell-1. The three-electrode system consisting of NP-LST–GDC as a working electrode, NF-SSC–GDC as a counter electrode, Pt on the rim of the LSGMC disk (thickness: 623 μm) as a reference electrode was denoted as Cell-2.
2.3 Characterizations and measurements
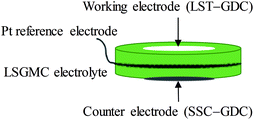
Microstructures of all samples were studied by a ZEISS SUPRA55 SAPPHIRE scanning electron microscope (SEM). Three-electrode systems consisting of NF-LST–GDC or NP-LST–GDC as a working electrode, NF-SSC–GDC as a counter electrode, Pt on the rim of the LSGMC disk as a reference electrode were denoted as anode side half-cells in the current work. The schematic diagram of three-electrode system used for the half-cell testing is shown in Fig. 1. Pylex glass (0.5–0.7 mm thick) was used as sealing material for the anode side. At 700 °C, the Pylex glass begun to soften, and then humidified Ar was introduced. Further heating up to 850 °C and keeping the temperature constant, when the measured open circuit voltage (OCV) value was less than −0.20 V (about −0.25 V), the anode atmosphere was changed from humidified Ar gas to 3% H2O + 97% H2 mixture gas. If the switch didn't lead to the increase in the temperature of test furnace, the sealing was preliminarily affirmed to be fine. Then keeping at the temperature of 850 °C for 4 h, the reduction process of the anode was accomplished. Then, if the OCV difference between the measurement value and the theoretical one was less than 20 mV, sealing was believed to be well done. The test can be started. All electrochemical measurements were performed with an electrochemical workstation (CHI 650D, Shanghai CH Instruments Co., China). Impedance measurements of the electrodes were carried out under open circuit conditions over a frequency range from 0.1 Hz to 100 kHz with a 10 mV perturbation at 700°, 750°, 800° and 850 °C, respectively. Current interrupt (CI) testing was performed on the three-electrode systems at 700°, 750°, 800° and 850 °C, respectively. After 50 s galvanostatic polarization of 10–50 mA, the cell current was very rapidly interrupted. The variations of voltage and current with time were recorded shortly after current interruption, with a sample period of 1 ms. And then, the cell ohmic resistances can be calculated. The current–voltage (I–V) characteristics of three electrode systems were measured at 700°, 750°, 800° and 850 °C, respectively.3 Results and discussion
Fig. 2a shows the low-magnification scanning electron microscopy (SEM) overview micrograph of a typical single cell with the configuration of NF-SSC–GDC|LSGMC|NF-LST–GDC. The LSGMC electrolyte appeared as a dense and thick layer. The thickness was about 600 μm. Fig. 2b and c show the high-magnification SEM images of the nanofiber-based composite electrodes prepared by infiltration of GDC into nanofiber electrode scaffolds. As observed, NF-LST–GDC (Fig. 2b) and NF-SSC–GDC (Fig. 2c) had high porosity which effectively facilitated gas transport in the electrodes and played an important role in enlarging three-phase boundary (TPB).12,18 | ||
| Fig. 2 SEM results showing (a) an overview of a typical single cell with the configuration of NF-SSC–GDC|LSGMC|NF-LST–GDC, (b) NF-LST–GDC and (c) NF-SSC–GDC. | ||
In order to compare the microstructures of the two different anodes, the SEM images of NF-LST–GDC in Cell-1 and NP-LST–GDC in Cell-2 are showed in Fig. 3a and Fig. 3b, respectively. As observed, there is high porosity for gas transport in the electrode due to the randomly distributed LST nanofibers (shown in Fig. 3a). Apparently, for NP-LST–GDC produced by infiltration of GDC into the LST nanoparticle scaffold, several particles get together which lead to the invisible grain boundaries, and the size of the conglutinated particles is ranged from about 100 nm to several hundred nm, as can be seen in Fig. 3b. In contrast, NP-LST–GDC has much denser structure, which results in lower electrode porosity than NF-LST–GDC. That is to say, NF-LST–GDC has larger TPB region than NP-LST–GDC.
Electrochemical impedance spectra (EIS) measurements were conducted on the single cell of NF-SSC–GDC|LSGMC|NF-LST–GDC at 700°, 750°, 800° and 850 °C. In order to clearly compare the difference in interfacial polarization resistance (Rp) between the anode and the cathode, all electrolyte ohmic resistances were removed from the impedance data. As presented in Fig. 4a, the impedance spectra obtained with NF-LST–GDC appeared as two depressed capacitive arcs, which can be fitted by the equivalent circuit of LR0(R1Q)(R2Q). Here L is an inductance and Q a constant phase element. R0 represents ohmic resistance, R1 high frequency region resistance and R2 low frequency region resistance. R1 and R2 constitute the interfacial polarization resistance (Rp). The Rp values of NF-LST–GDC were 0.578, 0.372, 0.261 and 0.222 Ω cm2 at 700°, 750°, 800° and 850 °C, respectively. As shown in Fig. 4b, the Rp values of NF-SSC–GDC were 0.155, 0.083, 0.044 and 0.032 Ω cm2 at 700°, 750°, 800° and 850 °C, respectively. Obviously, the Rp values of NF-LST–GDC were much larger than those of NF-SSC–GDC. The Rp values of the cathode are small enough to ignore the effect on cell performance relative to the anode. Thus, we only focus on the performance of anode side half-cells.
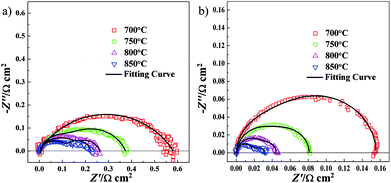
For comparison, two kinds of three-electrode systems were prepared in the current work. The three-electrode system consisting of NF-LST–GDC as a working electrode, NF-SSC–GDC as a counter electrode, Pt on the rim of the LSGMC disk (thickness: 610 μm) as a reference electrode was denoted as Cell-1. Impedance spectra of Cell-1 obtained at 700°, 750°, 800° and 850 °C are presented in Fig. 5a. The three-electrode system consisting of NP-LST–GDC as a working electrode, NF-SSC–GDC as a counter electrode, Pt on the rim of the LSGMC disk (thickness: 623 μm) as a reference electrode was denoted as Cell-2. Impedance spectra of Cell-2 obtained at 700°, 750°, 800° and 850 °C are shown in Fig. 5b. From these spectra we can calculate the LSGMC electrolyte ohmic resistance (Re) as the high frequency intercept with abscissa. The Rp of the LST–GDC electrode was derived from the difference between the low and high-frequency intercepts at the real impedance axis. For the sake of comparison, the Re and Rp values for Cell-1 and Cell-2 are summarized in Table 1. It was observed that the Re values of Cell-1 were lower than Cell-2, which related to the different thickness of the LSGMC electrolytes. The electrolyte ohmic resistance can be reduced by lowering the thickness of the electrolyte. The resulting lower potential drop of the electrolyte ohmic resistance increases the cell current density, i.e. enhances the cell kinetics. Besides electrolyte resistance, the factors influencing the cell kinetics are the potential drops caused by electrode ohmic resistance and electrode electrochemical reaction. Seen from Table 1, the Rp values of Cell-1 were also lower than Cell-2. It can be concluded that the electrochemical performance of Cell-1 was greater than Cell-2. The Rp values of NF-LST–GDC were smaller than Re in Cell-1. The electrolyte ohmic resistance dominates the potential drop for Cell-1, comparing with Rp. While the Rp values of NP-LST–GDC were larger than Re in Cell-2. By contrast, the anode resistance was the main factor of the potential drop for Cell-2, and the influence increased with the reducing temperature.
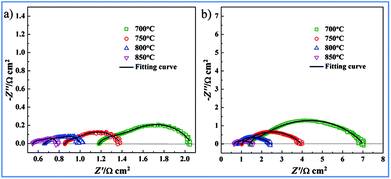 | ||
| Fig. 5 Impedance spectra of LST–GDC anode side half-cells: (a) Cell-1 and (b) Cell-2 obtained at 700°, 750°, 800° and 850 °C. | ||
| Temperature | Cell-1 | Cell-2 | ||
|---|---|---|---|---|
| Re (Ω cm2) | Rp (Ω cm2) | Re (Ω cm2) | Rp (Ω cm2) | |
| 700 °C | 1.182 | 0.856 | 1.418 | 5.445 |
| 750 °C | 0.855 | 0.529 | 1.022 | 2.905 |
| 800 °C | 0.661 | 0.331 | 0.795 | 1.594 |
| 850 °C | 0.548 | 0.236 | 0.643 | 0.920 |
CI testing was performed on Cell-1 and Cell-2 to obtain the cell ohmic resistance. After 50 s galvanostatic polarization of 10–50 mA, the cell current was very rapidly interrupted. The voltage and current variations with time for Cell-1 measured at 700°, 750°, 800° and 850 °C are shown in Fig. 6. The resulting variations of voltage and current with time for Cell-1 recorded at the times ranging from 50.001 s to 50.006 s shortly after current interruption are shown in Fig. 7. As expected, voltage scaled linearly with current under the galvanostatic polarization of 10–50 mA and these lines were parallel. The slope of each line was the cell ohmic resistance (Ro) at a certain temperature. Here, Ro obtained by CI was a combination of Re and anode ohmic resistance (Ra). The Ro values under the galvanostatic polarization of 10–50 mA and the calculated average of Ro value for Cell-1 are summarized in Table 2. By subtracting electrolyte contribution from the total ohmic resistance, the ohmic resistance attributed to the anode can be estimated. Ra of NF-LST–GDC in Cell-1 equals the average Ro (shown in the last column of Table 2) minus Re (shown in the second column of Table 1). The calculated Ra values of NF-LST–GDC in Cell-1 were 0.103 Ω cm2, 0.051 Ω cm2, 0.017 Ω cm2 and 0.011 Ω cm2 at 700°, 750°, 800° and 850 °C, respectively. The Ro values under the galvanostatic polarization of 10–50 mA and the calculated average of Ro value for Cell-2 are summarized in Table 3. By the same way, the obtained Ra values of NP-LST–GDC in Cell-2 were 1.398 Ω cm2, 0.930 Ω cm2, 0.393 Ω cm2 and 0.266 Ω cm2 at 700°, 750°, 800° and 850 °C, respectively. By comparison, the former was lower than the latter. Ra is closely associated with characteristics and microstructure of an electrode material. The LST nanofiber electrode scaffold with three-dimensional structure forms continuous electronic conduction path,12 which is the main reason why ohmic resistance of NF-LST–GDC is lower than that of NP-LST–GDC.
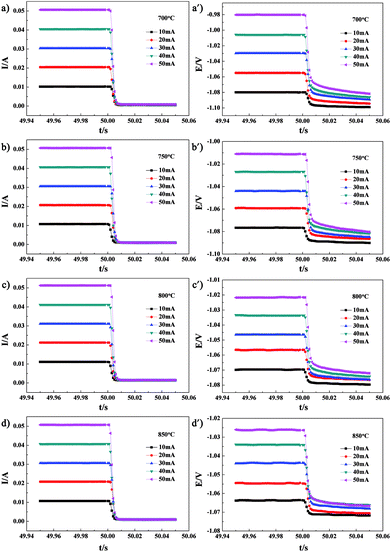 | ||
| Fig. 6 The voltage and current variations with time for Cell-1 measured at 700°, 750°, 800° and 850 °C. | ||
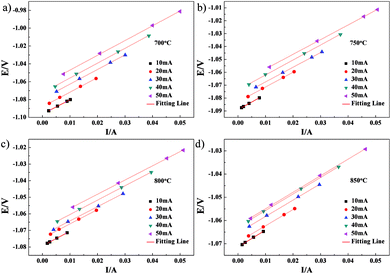 | ||
| Fig. 7 The variations of voltage and current with time for Cell-1 recorded at the times ranging from 50.001 s to 50.006 s shortly after current interruption. | ||
| Temperature | Ro (Ω cm2) | |||||
|---|---|---|---|---|---|---|
| 10 mA | 20 mA | 30 mA | 40 mA | 50 mA | Average | |
| 700 °C | 1.251 | 1.286 | 1.286 | 1.304 | 1.300 | 1.285 |
| 750 °C | 0.929 | 0.902 | 0.894 | 0.913 | 0.893 | 0.906 |
| 800 °C | 0.690 | 0.678 | 0.671 | 0.680 | 0.673 | 0.678 |
| 850 °C | 0.572 | 0.549 | 0.554 | 0.560 | 0.560 | 0.559 |
| Temperature | Ro (Ω cm2) | |||||
|---|---|---|---|---|---|---|
| 10 mA | 20 mA | 30 mA | 40 mA | 50 mA | Average | |
| 700 °C | 2.753 | 2.651 | 2.852 | 2.863 | 2.959 | 2.816 |
| 750 °C | 1.957 | 1.760 | 1.808 | 1.960 | 1.879 | 1.952 |
| 800 °C | 1.147 | 1.213 | 1.213 | 1.187 | 1.176 | 1.187 |
| 850 °C | 0.939 | 0.909 | 0.928 | 0.895 | 0.871 | 0.909 |
The relationships between voltage and current for Cell-1 and Cell-2 at different temperatures were determined by using the abovementioned three-electrode systems. The voltage–current (V–I) characteristics of Cell-1 and Cell-2 at 700°, 750°, 800° and 850 °C are shown in Fig. 8. Over the range of temperatures considered, the current density of Cell-1 was greater than Cell-2. For example, under the voltage of −0.6 V at 850 °C, the current density of Cell-1 was 0.65 A cm−2 while the one of Cell-2 was 0.35 A cm−2, which further demonstrated that the kinetics of Cell-1 was greater than Cell-2.
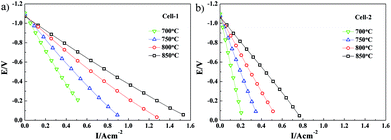 | ||
| Fig. 8 Voltage–current (V–I) characteristics of (a) Cell-1 and (b) Cell-2 at 700°, 750°, 800° and 850 °C. | ||
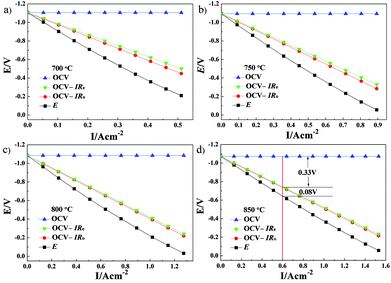
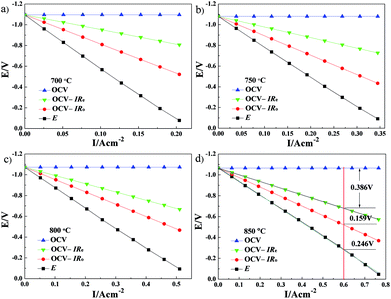
The cell ohmic voltage drop and the voltage drop caused by electrode electrochemical reaction increase with increasing current density under operating conditions, which results in a decrease in cell voltage. At a certain temperature, Re and electrode ohmic resistance (the sum of both resistances is Ro) are constant and have not varied with the cell operating condition (i.e., the magnitude of current density). The cell voltage (OCV) minus the total ohmic voltage drop is equal to the voltage drop caused by the electrode electrochemical reaction. Combined with the results of V–I characteristics, the potential drops caused by electrolyte ohmic resistance, electrode ohmic resistance and electrode electrochemical reaction, each potential drop on the kinetics of Cell-1 and Cell-2 are clearly illustrated in Fig. 9 and Fig. 10. For example, under the current density of 0.6 A cm−2 at 850 °C (see Fig. 9d), the electrolyte ohmic potential drop for Cell-1 was 0.330 V (around 79.14% of the total potential drop). The electrode ohmic potential drop and the potential drop caused by electrode electrochemical reaction of NF-LST–GDC were respectively 0.007 V (1.67%, too small and not shown in Fig. 9d) and 0.080 V (19.19%). Thus it can be seen that NF-LST–GDC has good electrochemical performance. Compared to Rp, Re is the major factor in degrading the electrochemical performance of Cell-1. Cell-1 kinetics can be highly improved when reducing the thickness of the electrolyte. While for Cell-2 under the same condition, the corresponding potential drops were respectively 0.386 V (48.80%), 0.159 V (20.10%) and 0.246 V (31.10%), as shown in Fig. 10d. Besides electrolyte ohmic resistance, the anode resistance of NP-LST–GDC was another main factor in degrading the Cell-2 kinetics and the effect increased with the increasing temperature. These results reveal that the main reason why the kinetics of Cell-1 is greater than Cell-2 is due to the greater kinetics of NF-LST–GDC than NP-LST–GDC.
4 Conclusions
The factors influencing the cell kinetics include electrolyte ohmic resistance, electrode ohmic resistance and electrode electrochemical reaction resistance. The conclusions can be drawn from the analysis results of EIS, CI and so on in the current study:The Re values of Cell-1 were lower than Cell-2, relative to the thicker LSGMC electrolyte for Cell-2. The lower Re was expected by lowering the thickness of the electrolyte, which facilitated lowering the potential drop of the electrolyte ohmic resistance and increasing the cell current density, i.e. enhancing the cell kinetics. The Rp values of Cell-1 were lower than Cell-2. The electrolyte ohmic potential drop, the electrode ohmic potential drop and the potential drop caused by electrode electrochemical reaction for Cell-1 were all lower than the corresponding potential drops for Cell-2. It can be concluded that the electrochemical performance of Cell-1 was greater than Cell-2. The Rp values of NF-LST–GDC were smaller than Re in Cell-1. The electrolyte ohmic resistance dominates the potential drop for Cell-1, comparing with Rp. While the Rp values of NP-LST–GDC were larger than Re in Cell-2. By contrast, the anode resistance was the main factor of the potential drop for Cell-2, and the influence increased with the reducing temperature. The main reason why the kinetics property of Cell-1 was greater than Cell-2 was due to the greater kinetics property of NF-LST–GDC than NP-LST–GDC.
Conflicts of interest
There are no conflicts.Acknowledgements
This work was supported by the National Natural Science Foundation of China (51502148 and 51502318).References
- R. J. Gorte and J. M. Vohs, Curr. Opin. Colloid Interface Sci., 2009, 14, 236–244 CrossRef CAS.
- C. D. Savaniu and J. T. S. Irvine, Solid State Ionics, 2011, 192, 491–493 CrossRef CAS.
- K. B. Yoo, B. H. Park and G. M. Choi, Solid State Ionics, 2012, 225, 104–107 CrossRef CAS.
- O. A. Marina, N. L. Canfield and J. W. Stevenson, Solid State Ionics, 2002, 149, 21–28 CrossRef CAS.
- X. W. Zhou, N. Yan, K. T. Chuang and J. L. Luo, RSC Adv., 2014, 4, 118–131 RSC.
- P. R. Slater, D. P. Fagg and J. T. S. Irvine, J. Mater. Chem., 1997, 7, 2495–2498 RSC.
- K. B. Yoo and G. M. Choi, Solid State Ionics, 2011, 192, 515–518 CrossRef CAS.
- C. D. Savaniu, D. N. Miller and J. T. S. Irvine, J. Am. Ceram. Soc., 2013, 96, 1718–1723 CrossRef CAS.
- X. Sun, S. Wang, Z. Wang, X. Ye, T. Wen and F. Huang, J. Power Sources, 2008, 183, 114–117 CrossRef CAS.
- K. B. Yoo and G. M. Choi, Solid State Ionics, 2009, 180, 867–871 CrossRef CAS.
- M. Roushanafshar, J. L. Luo, A. L. Vincent, K. T. Chuang and A. R. Sanger, Int. J. Hydrogen Energy, 2012, 37, 7762–7770 CrossRef CAS.
- L. Fan, Y. Xiong, L. Liu, Y. Wang, H. Kishimoto, K. Yamaji and T. Horita, J. Power Sources, 2014, 265, 125–131 CrossRef CAS.
- L. Fan, Y. Xiong, Y. Wang, H. Kishimoto, K. Yamaji and T. Horita, J. Power Sources, 2015, 294, 452–459 CrossRef CAS.
- K. Sugiura, H. Matsuoka and K. Tanimoto, J. Power Sources, 2005, 145, 515–525 CrossRef CAS.
- K. R. Cooper and M. Smith, J. Power Sources, 2006, 160, 1088–1095 CrossRef CAS.
- M. A. Rubio, A. Urquia and S. Dormido, J. Power Sources, 2007, 171, 670–677 CrossRef CAS.
- M. U. Iftikhar, D. Riu, F. Druart, S. Rosini, Y. Bultel and N. Retière, J. Power Sources, 2006, 160, 1170–1182 CrossRef CAS.
- L. Q. Fan, Y. P. Xiong, L. B. Liu, Y. W. Wang and M. E. Brito, Int. J. Electrochem. Sci., 2013, 8, 8603–8613 CAS.
- L. Q. Fan, Y. W. Wang, H. Huo and Y. P. Xiong, ECS Trans., 2013, 57, 1193–1199 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |