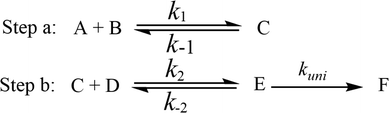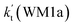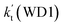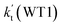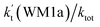Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Catalytic effect of (H2O)n (n = 1–3) on the HO2 + NH2 → NH3 + 3O2 reaction under tropospheric conditions†
Tianlei Zhang *,
Kai Wang‡
,
Zhangyu Qiao‡,
Yongqi Zhang‡,
Lin Geng‡,
Rui Wang,
Zhiyin Wang,
Caibin Zhao
*,
Kai Wang‡
,
Zhangyu Qiao‡,
Yongqi Zhang‡,
Lin Geng‡,
Rui Wang,
Zhiyin Wang,
Caibin Zhao and
Linxia Jin*
and
Linxia Jin*
Institute of Theoretical and Computational Chemistry, Shaanxi Key Laboratory of Catalysis, School of Chemical & Environment Science, Shaanxi University of Technology, Hanzhong, Shaanxi 723001, China. E-mail: ztianlei88@l63.com; jinlx@snut.edu.cn; Fax: +86-0916-2641083; Tel: +86-0916-2641083
First published on 5th November 2018
Abstract
The effects of (H2O)n (n = 1–3) clusters on the HO2 + NH2 → NH3 + 3O2 reaction have been investigated by employing high-level quantum chemical calculations with M06-2X and CCSD(T) theoretical methods, and canonical variational transition (CVT) state theory with small curvature tunneling (SCT) correction. The calculated results show that two kinds of reaction, HO2⋯(H2O)n (n = 1–3) + NH2 and H2N⋯(H2O)n (n = 1–3) + HO2, are involved in the (H2O)n (n = 1–3) catalyzed HO2 + NH2 → NH3 + 3O2 reaction. Due to the fact that HO2⋯(H2O)n (n = 1–3) complexes have much larger stabilization energies and much higher concentrations than the corresponding complexes of H2N⋯(H2O)n (n = 1–3), the atmospheric relevance of the former reaction is more obvious with its effective rate constant of about 1–11 orders of magnitude faster than the corresponding latter reaction at 298 K. Meanwhile, due to the effective rate constant of the H2O⋯HO2 + NH2 reaction being respectively larger by 5–6 and 6–7 orders of magnitude than the corresponding reactions of HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2, the catalytic effect of (H2O)n (n = 1–3) is mainly taken from the contribution of the water monomer. In addition, the enhancement factor 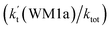 of the water monomer is 10.06–13.30% within the temperature range of 275–320 K, which shows that at whole calculated temperatures, a positive water effect is obvious under atmospheric conditions.
of the water monomer is 10.06–13.30% within the temperature range of 275–320 K, which shows that at whole calculated temperatures, a positive water effect is obvious under atmospheric conditions.
1. Introduction
The hydroperoxyl radical (HO2) and amidogen radical (NH2) are two important reactive radicals in atmospheric processes and combustion chemistry. As one of the most abundant free radicals in the atmosphere, HO2 is a very important and reactive intermediate in atmospheric pollutant degradation,1,2 photocatalysis,3 and molecular oxygen activation on metal surfaces4,5 or in enzymes.6 Produced from the gas phase oxidation of ammonia (NH3) by the hydroxyl radical (eqn (1)), NH2 is not only interesting in the combustion of fossil fuels, but is also considered to play an important role in the atmospheric formation and elimination of NOx (ref. 7) and in the oxygen isotopic exchange of N2O. Meanwhile, NH2 reacts with nitric acid can regenerate ammonia (eqn (2)). This reaction and the reaction shown in eqn (1) have been proposed as a potential new catalytic-like cycle which couples the oxidation of ammonia by hydroxyl radicals and the reaction of nitric acid with amidogen radicals in the Earth's atmosphere.8 Based on these facts, the kinetics and mechanism of the NH2 + HO2 reaction (eqn (3)) have been studied experimentally and theoretically.9–15| NH3 + HO → NH2 + H2O | (1) |
| NH2 + HNO3 → NH3 + NO3 | (2) |
| NH2 + HO2 → NH3 + O2 | (3) |
On experimental aspect, Sarkisov et al.10 have measured the gas-phase reaction between NH2 and HO2 by the analytical technique of the VIS-UV absorption at a total pressure of 133–9.33 × 104 Pa and the rate constant of the reaction (3) has been found to be 7.51 × 10−11 cm3 per molecule per s at 300 K. Meanwhile, the rate constant of NH2 + HO2 reaction has been estimated indirectly by flash-photolysis, which is 2.5 × 10−11 cm3 per molecule per s at 300 K.9 Theoretically, Sumathi et al.14 obtained the singlet potential energy surface of reaction (3) at QCISD(T)/6–311++ G(2df,2pd)//6–311++G**/MP2 level. In their work, to obtain the ratio of their product formation and to estimate the contribution of different channels over a wide range of temperature, the primary concern is to analyze the competition among the various reaction channels. However, the triplet potential energy surface of reaction (3), especially, the triplet hydrogen abstraction (HA) is not involved, which is not neglected for the HA in many previous reports reaction between radical and HO2 radical.16–30 Even in some HA reaction, triplet HA is favorable kinetically.16,18,20,23,26,29,30 So, both the singlet and triplet HA have been investigated at the CCSD(T)//B3LYP/6–311++G(3df,3pd) level by Xiang et al.31 In their work, for the favorable HA, the reaction mechanism on the triplet potential surface to be mainly a barrierless addition of HO2 to NH2 leading to an intermediate OOH⋯NH2 (3im1), and then the adduct 3im1 goes through an H transfer forming the product of NH3 and 3O2.
These investigations provide meaningful information about the HA of NH2 + HO2 reaction under atmospheric conditions. Nevertheless, these studies did not take into consideration the influence of water vapors on the reaction. In fact, firstly, water is ubiquitous in the Earth's atmosphere and its monomer can form hydrogen bonded complexes with other abundant radicals changing their photochemical features.32 Such as previous investigations showed that in the process of HO2 self-reaction, hydrogen bonded complexes HO2⋯H2O are formed with approximately 30% of the HO2 in the atmosphere bonding with water under typical atmospheric conditions.33 Another example is that water monomer can bind with NH2 radical, forming H2O⋯H2N, and H2N⋯H2O complexes.34 Secondly, it is also known that water was found to actively participate in the atmospheric reactions of HO2 + HO2,25,35 HO2 + HS,28 HO2 + HO,26,36 HO2 + SO2,37 HO2 + NO2 (ref. 24) and HO2 + O3 (ref. 38 and 39) reactions. Meanwhile, in these processes, water vapor had a catalytic effect by increasing the stability of pre-reactive complexes and reducing the activation energy of transition states. The above facts forecast that it cannot ignore water in modeling the different atmospheric HA reactions. These situations stimulated our interest in modeling the gas-phase reaction of H2O⋯HO2⋯NH2 ternary system, in which the single water molecule serves as a catalyst.
Although atmospheric water molecule implies a significant catalytic effect by monomers, the catalytic effect of water dimers and also water trimers can't be ignored, because their concentrations are up to 9 × 1014 and 2.6 × 1012 molecules per cm3 at 298 K.40,41 Moreover, the experimental and theoretical studies have been reported in the literature on the electronic structure of the clusters HO2⋯(H2O)n (n = 2–3).28,39 Thus, the catalytic effects of (H2O)n (n = 2–3) are worth being investigated further on the HO2 + NH2 → NH3 + 3O2 reaction.
In the present study, based on the HO2 + NH2 → NH3 + 3O2 reaction without water molecule, a detailed effects of (H2O)n (n = 1–3) on the HA reaction of HO2 + NH2 → NH3 + 3O2 have been studied at the CCSD(T)/CBS//M06-2X/6-311+G(3df,2pd) level of theory, which is organized as follows: firstly, the triplet HA reaction of HO2 + NH2 → NH3 + 3O2 was investigated to compare with (H2O)n (n = 1–3)-assisted processes. Secondly, the reactions of H2O⋯HO2 + NH2, HO2⋯H2O + NH2, H2O⋯H2N + HO2 and H2N⋯H2O + HO2 with water monomer were evaluated by investigating direct HA process and double hydrogen transfer mechanism. In what follows, direct HA processes of HO2⋯(H2O)2 (water dimer and the whole HO2 radical formed a ring by hydrogen bonds) + NH2, HO2⋯(H2O)2–I (water dimer and the HO moiety of HO2 radical formed a ring by hydrogen bonds) + NH2 and H2N⋯(H2O)2 + HO2 reactions with (H2O)2 were also calculated. Then, based on the discussed results of water dimer, the reactions of HO2⋯(H2O)3 + NH2 and H2N⋯(H2O)3 + HO2 were mainly investigated for the channel of NH3 + 3O2 formations with water trimer. Finally, the effective rate constants of the HA reaction of HO2 + NH2 → NH3 + 3O2 with (H2O)n (n = 1–3) were calculated to investigate the atmospheric relevance of the effect of (H2O)n (n = 1–3). Overall, this work may lead to a better understanding of the effects of (H2O)n (n = 1–3) on the gas-phase reactions under tropospheric conditions.
2. Computational methods
2.1 Electronic structure calculation
The electronic structure calculations were performed using Gaussian 09 program package42 software. The geometries of all the reactants, intermediates, transition states and products have been optimized using the M06-2X43–46 method using the 6-311+G(3df,2pd) basis set. The corresponding frequencies of the optimized geometries were computed at the same level to confirm the characteristics of the transition states with one imaginary frequency and the stationary points without imaginary frequency. Moreover, the minimum energy path (MEP) was obtained by the intrinsic reaction coordinate (IRC)47–49 theory with a gradient step size of 0.01 − 0.05 (amu)1/2 bohr to prove that the TS connects to minima along the reaction path. In order to obtain more accurate relative energies, single-point energy calculations for the stationary points were performed at the CCSD(T) method50 in conjunction with CBS basis set based on the M06-2X/6-311+G(3df,2pd)-optimized geometries. The single point energy calculations of CCSD(T)/CBS have been carried out for all the species at CCSD(T) level of theory using aug-cc-pVDZ and aug-cc-pVTZ basis sets. The energy values obtained at DZ and TZ levels have been used to extrapolate the results to a complete basis set (CBS) limit.512.2 Rate constant calculations
To estimate the effect of (H2O)n (n = 1–3) added, the theoretical rate constants of canonical variational transition (CVT) state theory52–54 with small curvature tunneling (SCT) correction55,56 for every H-abstraction channels were calculated by employing VKLab program57 coupled with the steady state approximation.In the presence of (H2O)n (n = 1–3), all the processes for the formations of NH3 and 3O2 from the reaction of HO2 and NH2 involve two major steps as follows.
Here, A and B are any two among HO2, NH2 and (H2O)n (n = 1–3) clusters (water monomer, WM; water dimer, WD; and water trimer, WT), C is the binary complex formed by A and B. D is the remaining third species other than A and B. E is the ternary complex formed by HO2, NH2 and (H2O)n (n = 1–3). In the step a, A combines with B to from an adduct C, whereas the step b consists of two elementary processes: in the first one, C reacts with D to form E and subsequently E undergoes uni-molecular transformation to produce the formation F via the corresponding TS.
Assuming that the intermediate E was in equilibrium with the corresponding reactants (C and D) and was at steady state,58 the rate constant for step b can be written as
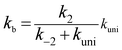 | (4) |
If kuni ≪ k−2, the rate constant of kb was rewritten as
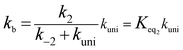 | (5) |
The rate constant kuni in eqn (5) has been evaluated by VKLab program57 in the framework of the canonical variational transition state theory (CVT).54 To include the tunneling effects for motion along the reaction coordinate for the title reactions at the CCSD(T)/CBS//M06-2X/6-311+G(3df,2pd) level, the small curvature tunneling (SCT)55 approximation has been adopted in this study. Besides, Keq2 in eqn (5) was given by eqn (6).
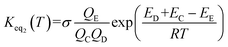 | (6) |
In eqn (6), the various Q values denote the partition functions of the intermediate E, reactants C and D, respectively. All partition functions were obtained using the M06-2X/6-311+G(3df,2pd) method. ED, EC and EE stand for the energies of the species of D, C and E, respectively; σ is the symmetry factor. In the present work, kb has been used to compare the rates between bare reaction and catalyzed reactions.
2.3 Effective rate constant calculations
If one incorporates the effect of step a, the resultant rate constant (kt) can be written as:| kt = Keq1Keq2kuni | (7) |
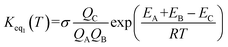 | (8) |
In eqn (8), the various Q values denote the partition functions of the complex C, reactants A and B, respectively. EA, EB and EC stand for the energies of the species of A, B and C, respectively. From the above, the rate of the reaction (v) in the presence of catalysts can be written as:
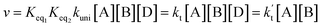 | (9) |
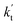 is the effective rate constant, which could be considered as a measure of the relative efficiencies of the different catalysts under atmospheric conditions, as it includes the concentration as well as rate constant of a particular catalyst.
is the effective rate constant, which could be considered as a measure of the relative efficiencies of the different catalysts under atmospheric conditions, as it includes the concentration as well as rate constant of a particular catalyst.
3. Results and discussion
The transition states in each reaction channel were signed by “TS” followed by a number, and intermediates were denoted by “IM” followed by a number. The letters “a”, “b”, and “c” were used to distinguish the transition states and intermediates that were conformers of each other and therefore had the same features; a species in the presence of water monomer, water dimer and water trimer was respectively denoted by a “WM”, “WD”, and “WT” suffix.3.1 Potential energy surfaces and the rate constants for the hydrogen abstraction of HO2 + NH2 → NH3 + 3O2 reaction
The HO2 + NH2 → NH3 + 3O2 reaction was investigated theoretically by Xiang et al.31 at the CCSD(T)/6–311++G(3df,3pd)//B3LYP/6–311++G(3df,3pd) level. In this study, we have reinvestigated that work at the CCSD(T)/CBS//M06-2X/6-311+G(3df,2pd) level to determine the outcome of this reaction when (H2O)n (n = 1–3) was present. As seen in Fig. 1, regarding the HA reaction of HO2 + NH2 to produce NH3 + 3O2, only one elementary reaction path was identified (Channel R1). Starting from HO2 + NH2 reactants, Channel R1 began with the intermediate IM. The binding energy of IM was 6.9 kcal mol−1, agree with that (3im1, 7.4 kcal mol−1) in the literature reported by Xiang et al.31 For IM, from geometrical point of view, a hydrogen bond shown in Fig. 1 was formed between the H atom of HO2 and the N atom of NH2 radical (with a computed H⋯N bond distance of 1.81 Å at the M06-2X/6-311+G(3df,2pd) level of theory). With the N atom of NH2 radical attacks the H atom of HO2, the intermediate IM in Channel R1 proceeded through a transition state TS with the energy predicted to be at 4.5 kcal mol−1 below the initial reactants. The energy of TS is quite different from 3ts3 (6.8 kcal mol−1 below HO2 + NH2 reactants) in the literature reported by Xiang et al.31 This difference is possible due to the fact that the different levels of theory used for the ZPE and single-point energy calculation. Besides, the ΔH (298) of HO2 + NH2 → NH3 + 3O2 reaction was predicted to be −57.0 kcal mol−1, compared with the experimental59 estimation of −58.5 ± 0.4 kcal mol−1. For reaction (1) without water, Table S1† lists its CVT/SCT rate constant. As seen in Table S1,† tunneling slightly increases the rate constant, while the recrossing effects decrease the rate constant. For example, the rate constant is increased by 62% due to tunneling, while the rate constant is decreased to 52% because of recrossing effects at the M06-2X/6-311+G(3df,2pd) level and at 298 K (Table S1†). It is noted that tunneling and recrossing effects slightly depend on temperature. Tunneling slightly increases with the decrease of temperature, while recrossing effects slightly increase with the increase of temperature as listed in Table S1.† Specifically, the calculated results using M06-2X/aug-cc-pVTZ indicate that the rate constant is increased by 32% and 20% due to tunneling, while the rate constant is decreased to 44% and 60% at 275 and 320 K, respectively. So, similar with previous investigations,60,61 the tunneling transmission coefficients are very large for the hydrogen atom transfer process. Thus, herein the computed CVT/SCT rate constants have been used to estimate the catalytic effect of (H2O)n (n = 1–3). CVT/SCT rate constant calculations were carried out for Channel R1 at various temperatures. The values are listed in Table S1.† At 300 K, the calculated value of kR1 was 2.68 × 10−11 cm3 per molecule per s. The calculated values compare closely with 7.51 × 10−11 cm3 per molecule per s and 2.5 × 10−11 cm3 per molecule per s, at 300 K respectively predicted by Sarkisov et al.10 and Cheskis et al.9 indicating that the calculations for the HO2 + NH2 → NH3 + 3O2 reaction without and with (H2O)n (n = 1–3) at the CCSD(T)/CBS//M06-2X/6-311+G(3df,2pd) level of theory are acceptable.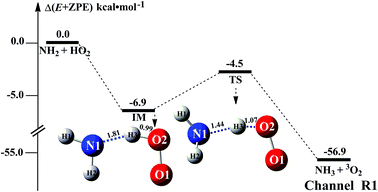 | ||
| Fig. 1 Schematic energy diagram for the HO2 + NH2 reaction; energies (kcal mol−1) at the CCSD(T)/CBS//M06-2X/6-311+G(3df,2pd)) level of theory. | ||
3.2 Geometrical analysis and the concentration calculation for HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3) complexes
In the presence of (H2O)n (n = 1–3), both bodies of HO2 and NH2 can respectively interact with the second body of (H2O)n (n = 1–3) via hydrogen bond to form two-body complexes of HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3) first in the entrance channels before interacting with the third body of NH2 or HO2. So, it is very necessary to find the stable configurations of the complexes HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3) firstly. In order to find all possible stable configurations of the complexes HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3), the global minimum searching of geometric structures were carried out using Tsinghua Global Minimum (TGMin).62,63 Then the initial structures for HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3) were selected for geometry optimization using the M06-2X/6-31G(d) method. The isomer structures within 6.0 kcal mol−1 of the global minimum were re-optimized by M06-2X/6-311+G(3df,2pd) method. The Fig. 2 and S1† show the optimized geometrical reactants of HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3), which are in good agreement with available previous results.64,65 As seen in Fig. 2 and S1,† as the number of water molecules increases in a given cluster of HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3), the number of possible configurations for the cluster increases quickly, and each of the configurations becomes increasingly complicated. Regarding to each type equilibrium structure of HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3), herein we only focus on the stable configuration shown in Fig. 2, which has the larger stabilization energy and the higher concentration than its isomers.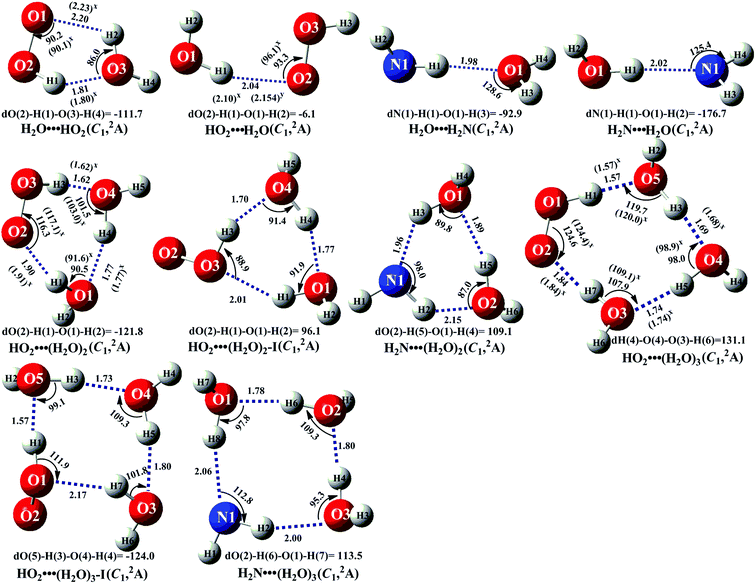 | ||
| Fig. 2 The geometrical structures of the optimized complexes at the M06-2X/6-311+G(3df,2pd) level of theory (bond length Å, bond angle °). | ||
As seen in Fig. 2 and Table S2,† consistent with previous reports,24,25,28,37,66 five-membered ring complex H2O⋯HO2 was much more stable than the single hydrogen bond complexes HO2⋯H2O, H2N⋯H2O and H2O⋯H2N with its binding energy larger by 3.6–5.9 kcal mol−1 than those of latter ones. The equilibrium constants of these complexes at 298 K are 1.83 × 10−19, 3.05 × 10−22, 1.34 × 10−22 and 8.40 × 10−21 cm3 per molecule, respectively (Table S3†). Considering typical tropospheric concentrations of 7.73 × 1017 molecules per cm3 of H2O, 3 × 108 molecules per cm3 of HO2,67 and our estimated concentrations of NH2 (6.0 × 10−11 molecules per cm3 seen in ESI†), it is estimated that the atmospheric concentration of the H2O⋯HO2 complex to be 4.24 × 107 molecules per cm3, which is larger by 6.00 × 102 times than that of HO2⋯H2O. However, in our previous works,25,26 the reaction channels of HO2⋯H2O + HO2 and HO2⋯H2O + HO were not neglected in water-catalyzed HO2 + HO2 and HO2 + HO. So, for water catalyzed HO2 + NH2 → NH3 + 3O2 reaction, both H2O⋯HO2 + NH2 and HO2⋯H2O + NH2 reactions have been investigated in the following section. Besides these, at 298 K, the concentrations of H2N⋯H2O (3.90 × 10−13 cm3 per molecule) and H2O⋯H2N (6.21 × 10−15 cm3 per molecule) shown in Table S3† were much lower than those of H2O⋯HO2 (4.24 × 107 cm3 per molecule) and HO2⋯H2O (7.07 × 104 cm3 per molecule). Thus, in water catalyzed HO2 + NH2 → NH3 + 3O2 reaction, we predict that the atmospheric relevance of H2O⋯HO2 + NH2 and HO2⋯H2O + NH2 reactions will be much more obvious than those of H2N⋯H2O + HO2 and H2O⋯H2N + HO2 reactions. Thus, only H2O⋯HO2 + NH2 and HO2⋯H2O + NH2 reactions have been taken into account in the following section, whereas, for comparison, the potential energy surfaces (PESs) for H2N⋯H2O + HO2 and H2O⋯H2N + HO2 reactions has been displayed in Fig. S5,† and their corresponding rate constants were shown in Table S7.†
For the clusters constituted by HO2 (or NH2) radical and water dimer, in geometrical point of view, HO2⋯(H2O)2 (water dimer and the whole HO2 radical formed a ring by hydrogen bonds) shows seven-membered ring structure, whereas both HO2⋯(H2O)2–I (water dimer and the HO moiety of HO2 radical formed a ring by hydrogen bonds) and H2N⋯(H2O)2 involves a six-membered ring. So, the binding energy of HO2⋯(H2O)2 (shown in Table S2†) was 12.6 kcal mol−1, which was larger by 3.9–6.4 kcal mol−1 than those of HO2⋯(H2O)2–I and H2N⋯(H2O)2 due to smaller ring tension. Similarity, nine-membered ring HO2⋯(H2O)3 (water trimer and the whole HO2 radical formed a ring by hydrogen bonds) was larger by 2.0–7.3 kcal mol−1 than those of eight-membered ring HO2⋯(H2O)3–I (water trimer and the HO moiety of HO2 radical formed a ring by hydrogen bonds) and H2N⋯(H2O)3. From another point of view shown in Table S3,† the concentrations of H2N⋯(H2O)2 (5.13 × 10−17 cm3 per molecule) and H2N⋯(H2O)3 (1.02 × 10−19 cm3 per molecule) are also much lower than those of HO2⋯(H2O)2 (5.14 × 105 cm3 per molecule) and HO2⋯(H2O)3 (8.02 × 103 cm3 per molecule) at 298 K, thus we predict that the atmospheric relevance of H2N⋯(H2O)2 + HO2 and H2N⋯(H2O)3 + HO2 reactions can be neglected. However, for comparison, the PESs for H2N⋯(H2O)2 + HO2 and H2N⋯(H2O)3 + HO2 reactions have been displayed in Fig. S6 and S7,† and their corresponding rate constants were shown in Table S7.† Besides these, the concentrations of HO2⋯(H2O)2 and HO2⋯(H2O)3 are respectively larger by 140 and 9 times than the corresponding complexes of HO2⋯(H2O)2–I and HO2⋯(H2O)3–I at 298 K. So, we predict that the catalytic effect of HO2⋯(H2O)2–I + NH2 and HO2⋯(H2O)3–I + NH2 reactions are less obvious than the corresponding reactions of HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2.
3.3 Potential energy surfaces and the rate constants for HO2 + NH2 → NH3 + 3O2 reaction with H2O
It has been pointed out in Section 3.2 that water-catalyzed the reaction (3) is mainly occurring through H2O⋯HO2 + NH2 and HO2⋯H2O + NH2 reactions. So, Fig. 3 presents the PESs for H2O⋯HO2 + NH2 (Channel WM1) and HO2⋯H2O + NH2 (Channel WM2) reactions along with the local minimum geometries on the corresponding reaction pathways.Regarding to Channel WM1, by different collisions between H2O⋯HO2 and NH2, two kinds of reaction types have been found, which were labeled as Channel WM1a and Channel WM1b. For Channel WM1a, starting from H2O⋯HO2 + NH2 reactants, hydrogen-bonded complex IM_WM1 was formed by the interaction between N atom of NH2 radical and one H atom of the H2O moiety in H2O⋯HO2 complex with a bonding energy of 5.5 kcal mol−1. After a flat potential energy surface through TS_WM1, with an energy barrier of 4.3 kcal mol−1, the formation of seven-member cyclic complex IM_WM2 was formed with a binding energy of 7.3 kcal mol−1 relative to H2O⋯HO2 + NH2 reactants. Following complex IM_WM2, Channel WM1a proceeded through transition state TS_WM2 to produce the product of NH3⋯H2O and 3O2 after climbing the barrier height of 3.4 kcal mol−1. In the transition state TS_WM2, the seven-membered ring structure was still conserved with the N atom of NH2 radical abstracting the H atom of HO2 moiety in H2O⋯HO2 complex.
Similar with Channel WM1a, Channel WM1b also followed stepwise process. In the first step, similar with the ring enlargement from IM_WM1 to IM_WM2 in Channel WM1a, the five-membered ring complex IM_WM3 is rearranged into seven-membered ring complex IM_WM4 through TS_WM3. In geometrical point of view, complex IM_WM4 has similar seven-membered cyclic structure as IM_WM2 with the NH2 radical and the water molecule exchanging their positions. The binding energy of IM_WM4 is 6.4 kcal mol−1, lowered by 0.9 kcal mol−1 than that of IM_WM2. In the second step, differently from transition state TS_WM2 in Channel WM1a that involves a direct HA, transition state TS_WM4 in Channel WM1b contains a double hydrogen transfer mechanism. Consistent with our previous reports,28 such mechanism discrepancy between Channels WM1a and WM1b may lead that the energy barrier of the second step in Channel WM1a is 3.4 kcal mol−1, which is lower by 4.6 kcal mol−1 than that of the second step in Channel WM1b. The reason can be possibly explained in three following aspects: (1) transition state TS_WM2 in the former reaction shows seven-member ring structure, whereas the transition state TS_WM4 in the latter reaction shows six-member ring structure. That is, TS_WM4 has larger ring tension than that of TS_WM2; (2) different from the structures in the process of IM_WM4 → TS_WM4 where the three hydrogen atoms (H2, H4 and H5) are out of plane, the structure in the process of IM_WM2 → TS_WM2 is close to the coplanar structure, which makes the conjugated hydrogen bonding system (H3⋯N1, H4⋯O1 and H1⋯O2) more stable; (3) NBO charge analysis shows that (Fig. S8†), the distance between the negatively NBO charged O3 and N1 atoms was decreases from IM-WM4 (2.70 Å) → TS-WM4 (2.33 Å), resulting in enhanced repulsive interactions, and hence the energy of the system is increased.
As shown in Table 1, it is worth noting that the rate constants both of Channel WM1a (kb(WM1a)) and Channel WM1b (kb(WM1b)) are increased with the decrease of temperature. This is because the calculated bimolecular rate constant contains two different components, (see Table S7†)); (1) Keq from the first step (bimolecular addition between H2O⋯HO2 and NH2) and (2) k2 from the second step (IM_WM1 (or IM_WM3) → NH3⋯H2O + 3O2). The second step always contributes to the positive activation energy due to the finite positive barrier, while the first step corresponds to negative activation energy as it involves barrierless addition of isolated reactants to form the complex IM_WM1 (or IM_WM3). Consequently, Keq always decreases with increase in temperature, whereas k2 behaves in opposite manner (Table S7†). Whenever k2 dominates over Keq the overall activation energy of the reaction is found to be positive and when Keq dominates over k2 then the overall activation energy of the reaction become negative. For example, for Channel RW1a, Keq decreases by ∼6.69 times and k2 value increases ∼1.26 times with increasing temperature from 275 to 320 K. The rate constant of Channel WM1a (kb(WM1a)) within the temperature range of 275–320 K is much larger than the corresponding value of kb(WM1b) in Channel WM1b, given that the ratio of kb(WM1a)/kb(WM1b) is 3.67 × 103 to 1.03 × 104. As a result, in the following section, the reaction type where water dimer and water trimer act as a “bridge” will not be considered in the reactions between HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2.
| T(K) | kb(WM1a) | kb(WM1b) | kb(WM2) | kb(WD1) | kb(WD2) | kb(WT1) |
|---|---|---|---|---|---|---|
| a kb(WM1a), kb(WM1b), kb(WM2) and kb(WD1), kb(WD2), kb(WT1) is the rate constants of (H2O)n (n = 1–3)-assisted HO2 + NH2 → NH3 + 3O2 reaction occurring through Channels WM1a, WM1b, WM2 WD1, WD2, and WT1, respectively.b 1/kuni(WM1a) = 1/k(TS_WM1) + 1/k(TS_WM2); 1/kuni(WM1b) = 1/k(TS_WM3) + 1/k(TS_WM4); 1/kuni(WD1) = 1/k(TS_WD1) + 1/k(TS_WD2); 1/kuni(WT1) = 1/k(TS_WT1) + 1/k(TS_WT2). | ||||||
| 275 | 6.53 × 10−11 | 6.36 × 10−15 | 2.21 × 10−11 | 1.35 × 10−15 | 1.84 × 10−17 | 1.47 × 10−14 |
| 280 | 5.23 × 10−11 | 5.85 × 10−15 | 1.70 × 10−11 | 1.39 × 10−15 | 1.92 × 10−17 | 1.45 × 10−14 |
| 290 | 3.46 × 10−11 | 5.00 × 10−15 | 1.04 × 10−11 | 1.48 × 10−15 | 2.07 × 10−17 | 1.42 × 10−14 |
| 298 | 2.54 × 10−11 | 4.44 × 10−15 | 7.19 × 10−12 | 1.56 × 10−15 | 2.20 × 10−17 | 1.41 × 10−14 |
| 300 | 2.38 × 10−11 | 4.32 × 10−15 | 6.62 × 10−12 | 1.58 × 10−15 | 2.23 × 10−17 | 1.40 × 10−14 |
| 310 | 1.68 × 10−11 | 3.79 × 10−15 | 4.34 × 10−12 | 1.68 × 10−15 | 2.39 × 10−17 | 1.39 × 10−14 |
| 320 | 1.23 × 10−11 | 3.35 × 10−15 | 2.92 × 10−12 | 1.78 × 10−15 | 2.55 × 10−17 | 1.38 × 10−14 |
Differently from Channel WM1a and Channel WM1b above which involve a stepwise process, HO2⋯H2O + NH2 reaction (Channel WM2) contains a one-step mechanism. As for Channel WM2, the reaction started with the formation of a pre-reactive hydrogen bond complex IM_WM5. Compared with the naked complex IM (Fig. 1), in view of geometry, complex IM_WM5 was stabilized by an additional weak hydrogen bond (O3⋯H1, 2.02 Å) and thus, the binding energy of IM_WM5 was enhanced by 1.6 kcal mol−1 than that of IM. Starting from IM_WM5, Channel WM2 proceeded through transition state TS_WM5, which is similar in structure to the naked transition state TS, where the N atom of NH2 radical directly abstracted the hydrogen of HO2. The rate constant of Channel WM2 (kb(WM2)) listed in Table 1 is only lower by 3–4 times than the corresponding value of kb(WM1a) in Channel WM1a. However, for H2O⋯HO2 complex, both the concentration and equilibrium constant at 298 K is larger by 2 orders of magnitude than that of HO2⋯H2O. As a result, atmospheric relevance of H2O⋯HO2 + NH2 reaction occurring through directing HA will be obvious than that of HO2⋯H2O + NH2 reaction. Besides these, compared with the rate constant of H2N⋯H2O + HO2 reaction (kb(WM3)) listed in Table S7,† though the value of kb(WM1a) is smaller by 2 orders of magnitude, atmospheric relevance of H2N⋯H2O + HO2 reaction will be neglected with respect to H2O⋯HO2 + NH2 reaction, due to the fact that the concentration of H2N⋯H2O complex is much lower than that of H2O⋯HO2. This result can be further proved by the effective rate constant in the following section. So, atmospheric relevance of H2O⋯HO2 + NH2 reaction occurring through directing HA will be most obvious in water monomer catalyzed HO2 + NH2 → NH3 + 3O2 reaction.
3.4 Potential energy surfaces and the rate constants for HO2 + NH2 → NH3 + 3O2 reaction with (H2O)2
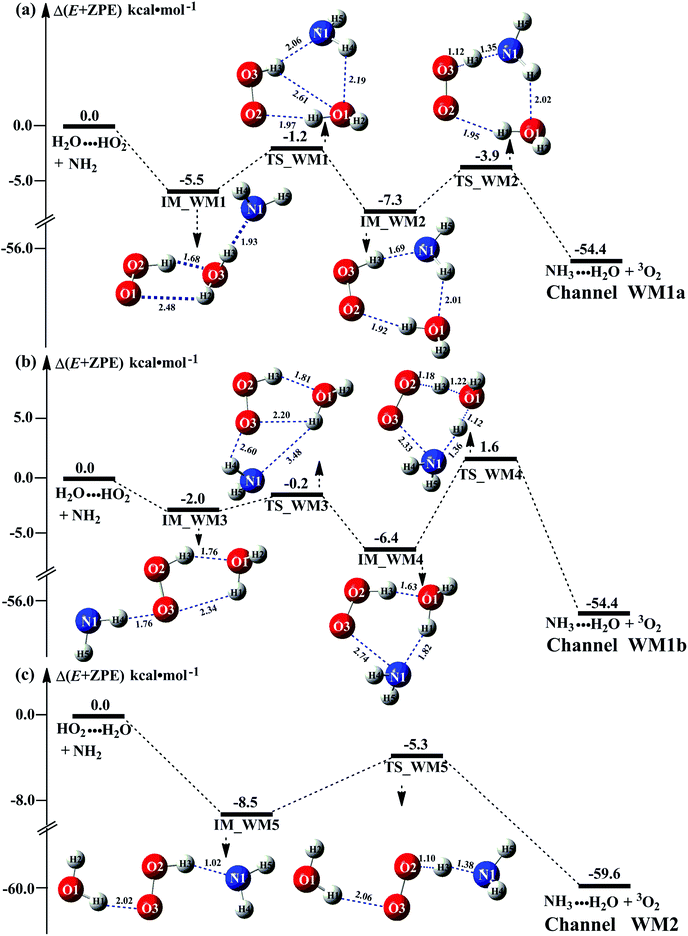
As the discussion in Section 3.2 that the atmospheric relevance of HO2⋯(H2O)2 + NH2 reaction is most obvious in water dimer-catalyzed the reaction (3). So, Fig. 4 shows the PESs of HO2⋯(H2O)2 + NH2 reaction (Channel WD1) with its rate constant listed in Table 1. For comparison, PESs for HO2⋯(H2O)2–I + NH2 reaction (Channel WD2) was displayed in Fig. 4, and its corresponding rate constant was shown in Table 1.For Channels WD1 and WD2 shown in Fig. 4, both reactions proceeded through a stepwise mechanism, where the reaction firstly occurred via a ring enlargement, and then proceed through a direct HA. However, the rate constant of Channel WD2 (kb(WD2)) listed in Table 1 is much smaller than the corresponding value of kb(WD1) in Channel WD1, given that the ratio of kb(WD1)/kb(WD2) is 69.8–73.4. Meanwhile, the value of kb(WD1) is larger by 6 orders of magnitude than that of kb(WD3) (H2N⋯(H2O)2 + HO2 reaction). Thus, for the reaction (3) with water dimer, HO2⋯(H2O)2 + NH2 reaction (Channel WD1) is of great atmospheric relevance due to its larger rate constant, and only this channel has been mainly taken into account here.
Consistent with the favorable channel of H2O⋯HO2 + NH2 reaction (Channel WM1a) above, as for Channel WD1, with the collision between NH2 and HO2⋯(H2O)2, the reaction occurred via a stepwise mechanism. In the first step, Channel WD1 went through a ring enlargement from seven-membered ring complex IM_WD1 to nine-membered ring complex IM_WD2 via transition state TS_WD1 with an energy barrier of 4.7 kcal mol−1. In geometrical point of view, complexes IM_WD1 and IM_WD2 have similar structures as the corresponding complexes of IM_WM1 and IM_WM2, expecting that water monomer was substituted by water dimer. So, in energetic point of view, similar with the fact that the complex IM_WM2 in Channel WM1a (Fig. 3) is more stable than IM_WM1, complex IM_WD2 in Channel WD1 is stable than IM_WD1. However, the stabilization energy of IM_WD2 has been reduced by 2.8 kcal mol−1 than that of IM_WM2. In the second step, following IM_WD2 complex, with the N atom of NH2 abstracting the H atom of HO2 moiety in HO2⋯(H2O)2, Channel WD1 can proceed via an elementary reaction of direct HA (TS_WD2) to form the products of NH3⋯(H2O)2 + 3O2. Similar with complex IM_WD2, TS_WD2 also shows a nine-membered ring structure with water dimer, NH2 radical and HO2 radical involved. The relative energy of TS_WD2 to HO2⋯(H2O)2 + NH2 is −1.7 kcal mol−1, which is higher by 2.2 kcal mol−1 than that of the water-assisted transition state TS_WM2 to H2O⋯HO2 + NH2 reactants. Meanwhile, the rate constant of Channel WD1, as shown in Table 1, is smaller by 3–4 orders of magnitude than that of kb(WM1a) with single water. Due to the fact that H2O⋯HO2 has higher concentration than that of HO2⋯(H2O)2, we predict that Channel WD1 has less obvious positive influence on enhancing the rate of the reaction (eqn (3)) than Channels WM1a.
3.5 Potential energy surfaces and the rate constants for HO2 + NH2 → NH3 + 3O2 reaction with (H2O)3
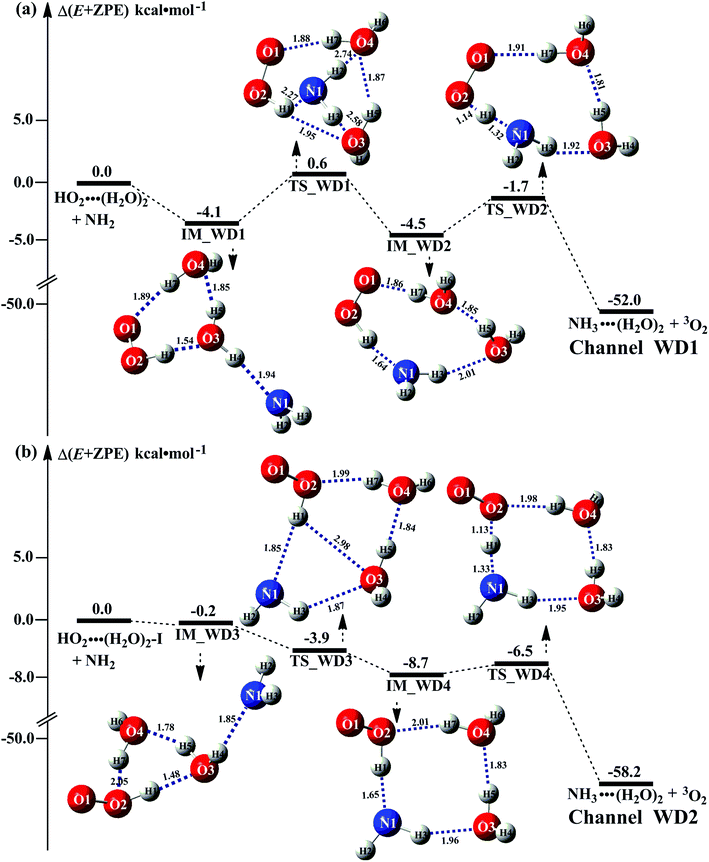
It is of interest to known whether (H2O)3 will affect the HO2 + NH2 → NH3 + 3O2 reaction. Thus, based on the discussed results above that the reaction of NH2 radical with HO2⋯(H2O)2 is more favorable than the reactions of NH2 radical with HO2⋯(H2O)2–I in the presence of water dimer, only the reaction of NH2 radical with HO2⋯(H2O)3 was mainly investigated for the channel of NH3 + 3O2 formations with water trimer due to that the binding energy (Table S2†) and the concentration (Table S3†) of HO2⋯(H2O)3 are much larger than those of H2N⋯(H2O)3, HO2⋯(H2O)3–I. The schematic potential energy surfaces for HO2⋯(H2O)3 + NH2 reaction was shown in Fig. 5, meanwhile its rate constant is also listed in Table 1, which is larger by 6 orders of magnitude than that of kb(WT2) (H2N⋯(H2O)3 + HO2 reaction) involved in Table S7.†Regarding the reaction of HO2⋯(H2O)3 + NH2, the pre-reactive complex IM_WT1 was formed with the energy of 1.1 kcal mol−1 with respect to the HO2⋯(H2O)3 + NH2 reactants. Starting from complex IM_WT1, the reaction occurs via transition state TS_WT1 and to form a complex IM_WT2 with a barrier of 0.1 kcal mol−1 relative to the pre-reactive complex IM_WT1. This step involves a geometric rearrangement that plays a crucial role in HO2⋯(H2O)3 + NH2 reaction. IM_WT2 is more stabilized than IM_WT1 by 3.2 kcal mol−1. From the geometric point of view, complex IM_WT2 has similar quasi-planar structure as that of IM_WD2 with the additional water molecule inserted between HO2 and NH2. The relative energy of IM_WT2 is −4.3 kcal mol−1 with respect to HO2⋯(H2O)3 + NH2.
Transition state TS_WT2 was found between IM_WT2 and the products (H3N⋯(H2O)3 and 3O2). For the TS_WT2, a HA reaction occurs by the N atom of NH2 abstracted the H atom of HO2 radical as that in TS_WD2 with the additional water molecule inserted between HO2 and NH2. TS_WT2 lies 1.4 kcal mol−1 below the HO2⋯(H2O)3 + NH2 reactants, which is 0.3 kcal mol−1 higher in energy than the relative energy of TS_WD2 to HO2⋯(H2O)2 + NH2 reactants. Meanwhile, the rate constant of Channel WT1 (shown in Table 1) is larger by 8–11 times than that of kb(WD1) with water dimer. Due to the fact that HO2⋯(H2O)2 has higher concentration than that of HO2⋯(H2O)3, thus, whether the atmospheric relevance of HO2⋯(H2O)3 + NH2 reaction is obvious than that of HO2⋯(H2O)3 + NH2 reaction or not, needs further discussion in the next section.
3.6 Application in atmospheric chemistry
Beyond above mechanisms and rate constant without and with (H2O)n (n = 1–3), another aim of our work was to study the influence of (H2O)n (n = 1–3) on the HO2 + NH2 reaction under atmospheric conditions. Thus, it is necessary to compare the title rate in the absence of (H2O)n (n = 1–3) with the effective rates of the favorable reactions in the presence of (H2O)n (n = 1–3). Table 2 lists the calculated effective rate constants for the favorable channels of HO2 + NH2 → NH3 + 3O2 reaction without and with (H2O)n (n = 1–3). For comparisons, the effective rate constants of other channels have been displayed in Table S7.†| T(K) | kR1 | ||||
|---|---|---|---|---|---|
a Effective rate constants (cm3 per molecule per s) of 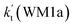 and and 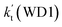 , and , and 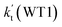 have been calculated using 100% relative humidity.b have been calculated using 100% relative humidity.b 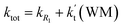 , , 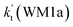 , , 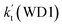 and and 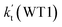 is respectively the effective rate constants of H2O⋯HO2 + NH2(a), HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2 reaction.c is respectively the effective rate constants of H2O⋯HO2 + NH2(a), HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2 reaction.c 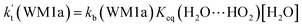 ; ; 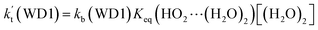 ; and ; and 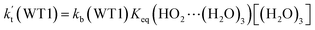 . Keq(H2O⋯HO2), Keq(HO2⋯(H2O)2) and Keq(HO2⋯(H2O)3) is respectively the equilibrium constants for the formation of the H2O⋯HO2, HO2⋯(H2O)2 and HO2⋯(H2O)3 complexes, whereas [H2O], [(H2O)2], and [(H2O)3] are the concentrations of water vapor, water dimer and water trimer.65 . Keq(H2O⋯HO2), Keq(HO2⋯(H2O)2) and Keq(HO2⋯(H2O)3) is respectively the equilibrium constants for the formation of the H2O⋯HO2, HO2⋯(H2O)2 and HO2⋯(H2O)3 complexes, whereas [H2O], [(H2O)2], and [(H2O)3] are the concentrations of water vapor, water dimer and water trimer.65 |
|||||
| 275 | 5.50 × 10−11 | 6.02 × 10−12 | 1.33 × 10−18 | 1.40 × 10−19 | 10.06% |
| 280 | 4.72 × 10−11 | 5.25 × 10−12 | 1.51 × 10−18 | 1.69 × 10−19 | 10.24% |
| 290 | 3.52 × 10−11 | 4.20 × 10−12 | 2.05 × 10−18 | 2.60 × 10−19 | 10.94% |
| 298 | 2.82 × 10−11 | 3.59 × 10−12 | 2.64 × 10−18 | 3.76 × 10−19 | 11.64% |
| 300 | 2.68 × 10−11 | 3.36 × 10−12 | 2.77 × 10−18 | 4.05 × 10−19 | 11.47% |
| 310 | 2.08 × 10−11 | 2.90 × 10−12 | 3.59 × 10−18 | 5.90 × 10−19 | 12.64% |
| 320 | 1.64 × 10−11 | 2.42 × 10−12 | 4.43 × 10−18 | 7.99 × 10−19 | 13.30% |
As shown in Table 2, within the temperature range of 275–320 K, the effective rate constant of H2O⋯HO2 + NH2 reaction 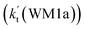 is 2.42 × 10−12 to 6.02 × 10−12 cm3 per molecule per s, which is larger by 3 orders of magnitude than the corresponding value of HO2⋯H2O + NH2 reaction
is 2.42 × 10−12 to 6.02 × 10−12 cm3 per molecule per s, which is larger by 3 orders of magnitude than the corresponding value of HO2⋯H2O + NH2 reaction 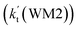 , as shown in Table S7.† Meanwhile, the value of
, as shown in Table S7.† Meanwhile, the value of 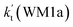 is respectively larger by 23.5–46.0 and 1.17 × 1010 to 4.10 × 1011 times than the value of
is respectively larger by 23.5–46.0 and 1.17 × 1010 to 4.10 × 1011 times than the value of 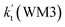 (H2O⋯H2N + HO2 reaction) and
(H2O⋯H2N + HO2 reaction) and 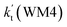 (H2N⋯H2O + HO2 reaction) listed in Table S7.† This indicates that the catalytic effect of water monomer is mainly taken from H2O⋯HO2 + NH2 reaction.
(H2N⋯H2O + HO2 reaction) listed in Table S7.† This indicates that the catalytic effect of water monomer is mainly taken from H2O⋯HO2 + NH2 reaction.
For the catalytic effect of water dimer, the effective rate constant of 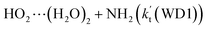 is 1.33 × 10−18 to 4.43 × 10−18 cm3 per molecule per s, which is larger by 3–4 and 9–10 orders of magnitude than the corresponding value of HO2⋯(H2O)2–I + NH2 reaction
is 1.33 × 10−18 to 4.43 × 10−18 cm3 per molecule per s, which is larger by 3–4 and 9–10 orders of magnitude than the corresponding value of HO2⋯(H2O)2–I + NH2 reaction 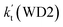 and
and 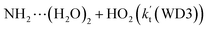 listed in Table S7,† showing that the catalytic effect of water dimer is mainly taken from HO2⋯(H2O)2 + NH2 reaction. Similarity, the catalytic effect of water trimer is mainly taken from HO2⋯(H2O)3 + NH2 reaction
listed in Table S7,† showing that the catalytic effect of water dimer is mainly taken from HO2⋯(H2O)2 + NH2 reaction. Similarity, the catalytic effect of water trimer is mainly taken from HO2⋯(H2O)3 + NH2 reaction 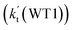 , with the rate constant of
, with the rate constant of 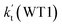 is larger by 10–11 orders of magnitude than the corresponding value of
is larger by 10–11 orders of magnitude than the corresponding value of 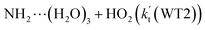 listed in Table S7.† Besides, the effective rate constant of
listed in Table S7.† Besides, the effective rate constant of 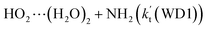 is larger by 6–10 times than the corresponding value of
is larger by 6–10 times than the corresponding value of 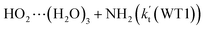 . This shows that compared with water trimer, the catalytic effect of water dimer is not neglected. However, the value of
. This shows that compared with water trimer, the catalytic effect of water dimer is not neglected. However, the value of 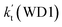 is smaller by 5–6 orders of magnitude than the effective rate constant of H2O⋯HO2 + NH2 reaction
is smaller by 5–6 orders of magnitude than the effective rate constant of H2O⋯HO2 + NH2 reaction 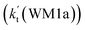 . So, the catalytic effect of single water is the largest among the effect of water, water dimer and water trimer, and the catalytic effect taken from water dimer and water trimer is neglected.
. So, the catalytic effect of single water is the largest among the effect of water, water dimer and water trimer, and the catalytic effect taken from water dimer and water trimer is neglected.
To obtain a more complete understanding of the influence of a water vapor on the title reaction, it is also necessary to compare the title rate constant (kR1) in the absence of a water vapor with the effective rate constant of the most favorable channel of H2O⋯HO2 + NH2 reaction 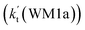 . The result in Table 2 is also estimated that within the temperature range of 275–320 K, the enhancement factor of water vapor
. The result in Table 2 is also estimated that within the temperature range of 275–320 K, the enhancement factor of water vapor 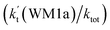 is 10.06–13.30%, showing, in the whole calculated range, the positive water effect is obvious under atmospheric conditions.
is 10.06–13.30%, showing, in the whole calculated range, the positive water effect is obvious under atmospheric conditions.
4. Summary and conclusions
The HO2 + NH2 → NH3 + 3O2 reaction catalyzed by (H2O)n (n = 1–3) has been studied theoretically using quantum chemical methods and the canonical variational transition state theory, which results in the following conclusions:(a) Regarding to each type equilibrium structure of HO2⋯(H2O)n (n = 1–3) and H2N⋯(H2O)n (n = 1–3), complexes of H2O⋯HO2, HO2⋯H2O, HO2⋯(H2O)2, and HO2⋯(H2O)3 are the most stable configurations, which have larger stabilization energies and higher concentrations than their isomers, and thus (H2O)n (n = 1–3) catalyzed HO2 + NH2 → NH3 + 3O2 reactions are mainly occurring through four kinds of reactions of H2O⋯HO2 + NH2, HO2⋯H2O + NH2, HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2.
(b) For water-assisted HO2 + NH2 → NH3 + 3O2 reaction, the channel occurring through the H2O⋯HO2 + NH2 reactants may be of great atmospheric relevance due to its larger effective rate constant and the larger concentration of H2O⋯HO2. Besides, though HO2⋯H2O + NH2 reaction has lower activation energy, its effective rate constant is smaller by 3 orders of magnitude than the corresponding value of H2O⋯HO2 + NH2 reaction. So, the catalytic effect of water monomer is mainly taken from H2O⋯HO2 + NH2 reaction.
(c) For HO2⋯(H2O)2 + NH2 and HO2⋯(H2O)3 + NH2 reactions, both the reactions followed through a stepwise mechanism, where the reaction firstly occurred via a ring enlargement, and then proceed through a direct HA. However, the effective rate constant of 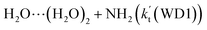 is larger by 6–10 times than the corresponding value of
is larger by 6–10 times than the corresponding value of 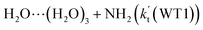 , showing that compared with water trimer, the catalytic effect of water dimer is not neglected. However, the effective rate constant of HO2⋯(H2O)2 + NH2 is smaller by 5–6 orders of magnitude than that of H2O⋯HO2 + NH2 reaction, showing that the catalytic effect of single water is the largest among the effect of water, water dimer and water trimer, and the catalytic effect taken from water dimer and water trimer is neglected.
, showing that compared with water trimer, the catalytic effect of water dimer is not neglected. However, the effective rate constant of HO2⋯(H2O)2 + NH2 is smaller by 5–6 orders of magnitude than that of H2O⋯HO2 + NH2 reaction, showing that the catalytic effect of single water is the largest among the effect of water, water dimer and water trimer, and the catalytic effect taken from water dimer and water trimer is neglected.
(d) The enhancement factor of water vapor 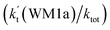 is 10.06–13.30% within the temperature range of 275–320 K, showing that, in the whole calculated range, the positive water effect is obvious under atmospheric conditions.
is 10.06–13.30% within the temperature range of 275–320 K, showing that, in the whole calculated range, the positive water effect is obvious under atmospheric conditions.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No: (21603132), the Funds of Research Programs of Shaanxi University of Technology (No: SLGQD13(2)-3, SLGQD13(2)-4).References
- M. Kumar and J. S. Francisco, Angew. Chem., Int. Ed., 2015, 54, 15711–15714 CrossRef CAS PubMed.
- J. M. Anglada, M. Martins-costa, J. S. Francisco and M. F. Ruiz-lópez, Acc. Chem. Res., 2015, 48, 575–583 CrossRef CAS PubMed.
- J. C. Colmenares and R. Luque, Chem. Soc. Rev., 2014, 43, 765–778 RSC.
- Y. Zheng, Y. Jiao, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2015, 54, 52–65 CrossRef CAS PubMed.
- C. R. Chang, X. F. Yang, B. Long and J. A. Li, ACS Catal., 2013, 3, 1693–1699 CrossRef CAS.
- P. Campomanes, U. Rothlisberger, M. Alfonsoprieto and C. Rovira, J. Am. Chem. Soc., 2015, 137, 11170–11178 CrossRef CAS PubMed.
- B. J. Finlayson-Pitts and J. N. Pitts Jr, Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications, Academic Press, 1999, pp. 633–637 Search PubMed.
- J. M. Anglada, S. Olivella and A. Solé, J. Am. Chem. Soc., 2014, 136, 6834–6837 CrossRef CAS PubMed.
- S. G. Cheskis and O. M. Sarkisov, Chem. Phys. Lett., 1979, 62, 72–76 CrossRef CAS.
- O. M. Sarkisov, S. G. Cheskis, V. A. Nadtochenko, E. A. Sviridenkov and V. I. Vedeneev, Arch. Combust., 1984, 4, 111–120 CAS.
- J. W. Bozzelli and A. M. Dean, J. Phys. Chem., 1989, 93, 1058–1065 CrossRef CAS.
- D. L. Baulch, C. J. Cobos, R. A. Cox, C. Esser, P. Frank, Th. Just, J. A. Kerr, M. J. Pilling, J. Troe, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 1992, 21, 411–734 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, R. F. Hampson Jr, J. A. Kerr and J. Troe, J. Phys. Chem. Ref. Data, 1989, 18, 881–1097 CrossRef CAS.
- R. Sumathi and S. D. Peyerimhoff, Chem. Phys. Lett., 1996, 263, 742–748 CrossRef CAS.
- W. B. Demore, S. P. Sander, D. M. Golden, R. F. Hampson, M. J. Kurylo, C. J. Howard, A. R. Ravishankara, C. E. Kolb and M. J. Molina, JPL Publ., 1985, 90, 1135–1151 Search PubMed.
- J. M. Anglada, S. Olivella and A. Solé, J. Phys. Chem. A, 2006, 110, 6073–6082 CrossRef CAS PubMed.
- E. Assaf, C. Schoemaecker, L. Vereecken and C. Fittschen, Phys. Chem. Chem. Phys., 2018, 20, 10660–10670 RSC.
- R. Chow, D. K. W. Mok, E. P. F. Lee and J. M. Dyke, Phys. Chem. Chem. Phys., 2016, 18, 30554–30569 RSC.
- E. Drougas, Comput. Theor. Chem., 2016, 1093, 98–103 CrossRef CAS.
- J. M. Anglada, S. Olivella and A. Solé, J. Phys. Chem. A, 2007, 111, 1695–1704 CrossRef CAS PubMed.
- J. Li, N. T. Tsona and L. Du, Phys. Chem. Chem. Phys., 2018, 20, 10650–10659 RSC.
- L. Vereecken and J. S. Francisco, Chem. Soc. Rev., 2012, 41, 6259–6293 RSC.
- T. Zhang, G. Li, W. Wang, Y. Du, C. Li and J. Lü, Comput. Theor. Chem., 2012, 991, 13–21 CrossRef CAS.
- T. Zhang, R. Wang, H. Chen, S. Min, Z. Wang, C. Zhao, Q. Xu, L. Jin, W. Wang and Z. Wang, Phys. Chem. Chem. Phys., 2015, 17, 15046–15055 RSC.
- T. Zhang, R. Wang, W. Wang, S. Min, Q. Xu, Z. Wang, C. Zhao and Z. Wang, Comput. Theor. Chem., 2014, 1045, 135–144 CrossRef CAS.
- T. Zhang, W. Wang, C. Li, Y. Du and J. Lü, RSC Adv., 2013, 3, 7381–7391 RSC.
- T. Zhang, W. Wang, P. Zhang, J. Lü and Y. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 20794–20805 RSC.
- T. Zhang, C. Yang, X. Feng, J. Kang, L. Song, Y. Lu, Z. Wang, Q. Xu, W. Wang and Z. Wang, Phys. Chem. Chem. Phys., 2016, 18, 17414–17427 RSC.
- Y. Zhang, T. Zhang and W. Wang, Int. J. Quantum Chem., 2011, 111, 3029–3039 CrossRef CAS.
- Y. Zhang, W. Zhang, T. Zhang, W. Tian and W. Wang, Comput. Theor. Chem., 2012, 994, 65–72 CrossRef CAS.
- T. Xiang, H. Si, P. Han and R. Yang, Comput. Theor. Chem., 2012, 985, 67–71 CrossRef CAS.
- R. J. Buszek, J. S. Francisco and J. M. Anglada, Int. Rev. Phys. Chem., 2011, 30, 335–369 Search PubMed.
- S. Aloisio, J. S. Francisco and R. R. Friedl, J. Phys. Chem. A, 2000, 104, 6597–6601 CrossRef CAS.
- C. P. Ennis, J. R. Lane, H. G. Kjaergaard and A. J. McKinley, J. Am. Chem. Soc., 2009, 131, 1358–1359 CrossRef CAS PubMed.
- D. Stone and D. M. Rowley, Phys. Chem. Chem. Phys., 2005, 7, 2156–2163 RSC.
- D. Stone, L. K. Whalley and D. E. Heard, Chem. Soc. Rev., 2012, 41, 6348–6404 RSC.
- X. Chen, C. Tao, L. Zhong, Y. Gao, W. Yao, S. Li and S. Chem, Phys. Lett., 2014, 608, 272–276 CAS.
- L. P. Viegas and A. J. C. Varandas, Chem. Phys., 2012, 399, 17–22 CrossRef CAS.
- L. P. Viegas and A. J. C. Varandas, Eur. Phys. J. D, 2016, 70, 48 CrossRef.
- N. Goldman, R. S. Fellers, C. Leforestier and R. J. Saykally, J. Phys. Chem. A, 2001, 105, 515–519 CrossRef CAS.
- M. E. Dunn, E. K. Pokon and G. C. Shields, J. Am. Chem. Soc., 2004, 126, 2647–2653l CrossRef CAS PubMed.
- M. J. Frisch, G. Trucks and J. A. Pople, et al., Gaussian 09, Revision A.01, Gaussian Inc, Pittsburgh, PA, 2009 Search PubMed.
- M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- N. Bork, L. Du, H. Reiman, T. Kurten and H. G. Kjaergaard, J. Chem. Phys. A, 2014, 118, 5316–5322 CrossRef CAS PubMed.
- F. Y. Liu, X. F. Tan, Z. W. Long, B. Long and W. J. Zhang, RSC Adv., 2015, 5, 32941–32949 RSC.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- M. Page and J. W. McIver Jr, J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- Y. S. Lee, S. A. Kucharski and R. J. Bartlett, J. Chem. Phys., 1984, 81, 5906–5912 CrossRef.
- A. J. C. Varandas and F. N. N. Pansini, J. Chem. Phys., 2014, 141, 224113 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Am. Chem. Soc., 1979, 101, 4534–4548 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730–1748 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- D. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y. P. Liu, B. C. Garrett, R. Steckler, A. D. Isaacson, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- S. W. Zhang and N. T. Truong, VKLab version 1.0, University of Utah, Salt Lake City, 2001 Search PubMed.
- D. L. Singleton and R. J. Cvetanovic, J. Am. Chem. Soc., 1976, 98, 6812–6819 CrossRef CAS.
- From the NIST chemistry webbook, http://webbook.nist.gov/chemistry.
- T. L. Zhang, W. L. Wang, P. Zhang, J. Lü and Y. Zhang, Phys. Chem. Chem. Phys., 2011, 13, 20794–20805 RSC.
- J. L. Bao, P. Seal and D. G. Truhlar, Phys. Chem. Chem. Phys., 2015, 17, 15928–15935 RSC.
- X. Chen, Y. F. Zhao, L. S. Wang and J. Li, Comput. Theor. Chem., 2017, 1107, 57–65 CrossRef CAS.
- Y. Zhao, X. Chen and J. Li, Nano Res., 2017, 10, 3407–3420 CrossRef CAS.
- T. L. Zhang, X. G. Lan, Z. Y. Qiao, R. Wang, X. H. Yu, Q. Xu, Z. Y. Wang, L. X. Jin and Z. Q. Wang, Phys. Chem. Chem. Phys., 2018, 20, 8152–8165 RSC.
- K. S. Alongi, T. S. Dibble, G. C. Shields and K. N. Kirschner, J. Phys. Chem. A, 2006, 110, 3686–3691 CrossRef CAS PubMed.
- B. Long, X. Tan, Z. Long, Y. Wang, D. Ren and W. Zhang, J. Phys. Chem. A, 2011, 115, 6559–6567 CrossRef CAS PubMed.
- J. Gonzalez, M. Torrent-Sucarrat and J. M. Anglada, Phys. Chem. Chem. Phys., 2010, 12, 2116–2125 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra06549g |
| ‡ Kai Wang, Zhangyu Qiao, Yongqi Zhang and Lin Geng contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |