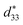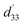Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Temperature independence of piezoelectric properties for high-performance BiFeO3–BaTiO3 lead-free piezoelectric ceramics up to 300 °C†
Li-Feng Zhu‡
 a,
Qing Liu‡b,
Bo-Ping Zhang
a,
Qing Liu‡b,
Bo-Ping Zhang *a,
Zhen-Yong Cenb,
Ke Wang
*a,
Zhen-Yong Cenb,
Ke Wang *b,
Jun-jie Lic,
Yang Baic,
Xiao-Hui Wangb and
Jing-Feng Li
*b,
Jun-jie Lic,
Yang Baic,
Xiao-Hui Wangb and
Jing-Feng Li b
b
aSchool of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China. E-mail: bpzhang@ustb.edu.cn
bState Key Laboratory of New Ceramics and Fine Processing, School of Materials Science and Engineering, Tsinghua University, Beijing 100084, China. E-mail: wang-ke@tsinghua.edu.cn
cKey Laboratory of Environmental Fracture (Ministry of Education), University of Science and Technology Beijing, Beijing 100083, China
First published on 19th October 2018
Abstract
The temperature-dependence behaviors of ferroelectric, piezoelectric, kp and electrical-field-induced strain were carefully evaluated for high-performance BiFeO3–0.3BaTiO3 (BF–0.3BT) ceramics. There results indicate, combined with Rayleigh analysis and temperature-dependence XRD and PFM, that the increase of strain and large signal 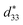 with increasing the temperature from room temperature to 180 °C is related to the joint effect of intrinsic contribution (lattice expansion) and extrinsic contribution (domain switching). With further increasing the temperature to 300 °C, the large signal d33 and electrical-field-induced strain mildly decrease because of the increase of conductivity for BF–0.3BT ceramics. However, different from strain and large signal
with increasing the temperature from room temperature to 180 °C is related to the joint effect of intrinsic contribution (lattice expansion) and extrinsic contribution (domain switching). With further increasing the temperature to 300 °C, the large signal d33 and electrical-field-induced strain mildly decrease because of the increase of conductivity for BF–0.3BT ceramics. However, different from strain and large signal 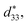 the small signal d33(E0) and kp exhibit excellent temperature stability behavior as the temperature increases from room temperature to 300 °C.
the small signal d33(E0) and kp exhibit excellent temperature stability behavior as the temperature increases from room temperature to 300 °C.
1. Introduction
Piezoelectric materials can realize the interconversion of mechanical energy and electrical energy and have been widely used in actuators, transducers and sensors, and so on.1 With the enhancement of the awareness of environmental protection, the Pb(Zr,Ti)O3 (PZT) family, being the most dominant piezoelectric materials, is faced with global restrictions because of the considerable portion of hazardous lead it contains. Therefore, it is urgent to seek lead-free alternative materials which have comparable electromechanical properties to these lead-based counterparts.2–20 A series of typical lead-free piezoelectric ceramics, such as: BaTiO3,5–7, (1 − x)Bi0.5(Na,K)0.5TiO3–xBaTiO3,8,9, (K1−xNax)NbO3 (ref. 10–14) and BiFeO3–BaTiO3 (BF–BT),15–20 have been extensively investigated in recent years. Some of them exhibit excellent piezoelectric properties, such as: d33 = 620 pC N−1 in the Ba0.7Ca0.3TiO3–50BaZr0.2Ti0.8O3 system6 and d33 = 570 pC N−1 in the K1−wNawNb1−zSbzO3–yBaZrO3–xBi0.5K0.5HfO3 system,12 in which the d33 is comparable to that of the PZT system. However, these lead-free ceramics do not meet the industrial application requirements because of their inferior temperature-insensitive behavior and low Curie temperature, such as: TC = 93 °C in the Ba0.7Ca0.3TiO3–50BaZr0.2Ti0.8O3 system6 and ∼250 °C in the K1−wNawNb1−zSbzO3–yBaZrO3–xBi0.5K0.5HfO3 system.12 Thus, the task of substituting for PZT ceramics fell on the BF–BT lead-free piezoelectric system because it has a high TC, over 580 °C,16 and a morphotropic phase boundary (MPB), which is similar to PZT system. Nevertheless, comparing with the PZT system, the electrical properties of BF–BT ceramics, especially the piezoelectric property, resistance and dielectric loss, need to be improved.Recently, considerable efforts have been carried out to address this problem mentioned above ,16–31 such as: (1) adding oxide additives, e.g., MnO2,16,20,21 Bi2O3,18,22 CuO,23 La2O3,24 and so on, have been added to improve the resistivity as well as the piezoelectric properties. (2) Building ternary system, e.g., BF–BT–Bi(Mg1/2Ti1/2)O3,19 BF–BT–Bi(Zn1/2Ti1/2)O3,17,25,26 BF–BT–Bi0.5K0.5TiO3,27 and so on. (3) Ion substitutions. Ion substitutions for Bi3+ (e.g., La3+, Er3+)28 or Fe3+ (e.g., Ga3+, Al3+, Sc3+, Co3+)20,29 in BF–BT system were carried out to improve the electrical properties. It is worth mentioning that the BF33BT–3BG ceramics, prepared by the water-quenched process, reported by Lee20 exhibit excellent piezoelectric properties (d33 = 402 pC N−1) and high Curie temperature (TC = 454 °C), indicating that the BF–BT system is the most promising candidate to replace Pb-based piezoelectric ceramics.
It is well known that industrial implementation not only demands good piezoelectric performance at room temperature but also hopes an excellent stability for piezoelectric properties in response to temperature changes. Despite the d33 of BF–BT system has achieved major breakthroughs20 and even it can meet the industrial application, how about the temperature stability of piezoelectric properties for the BF–BT ceramics is, and whether it is similar with the PZT system? Very few articles31 point out that the ferroelectric property for BF–BT ceramics was enhanced with increasing the temperature from room temperature to 150 °C. Nevertheless, there have been few investigations of the temperature dependence of piezoelectric properties for BF–BT ceramics. In addition, the reasons which cause the improvement of ferroelectric and kp properties are still vague for BF–BT ceramics so far.
In this work, 0.7BiFeO3–0.3BaTiO3 (abbreviated as BF–0.3BT) ceramics were prepared to reveal the temperature-dependence behavior of its ferroelectric, piezoelectric, kp and electrical-field-induced strain properties in the wide temperature range between room temperature and 300 °C. Because of the joint effect of intrinsic contribution (lattice expansion tested by temperature-dependence XRD) and extrinsic contribution (domain switching proved by temperature-dependence PFM), the remanent polarization (Pr), strain and large signal 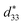 increase with increasing the temperature from room temperature to 180 °C. This result is also verified by Rayleigh analysis models, which indicates that the extrinsic contribution and intrinsic contribution (dint × 10−12) increase from 18.70% and 161.84 m V−1 at 24 °C to 34.45% and 207.06 m V−1 at 100 °C. With further increasing the temperature from 180 °C to 300 °C, the large signal d33 and electrical-field-induced strain mildly decrease. However, different the strain and large signal
increase with increasing the temperature from room temperature to 180 °C. This result is also verified by Rayleigh analysis models, which indicates that the extrinsic contribution and intrinsic contribution (dint × 10−12) increase from 18.70% and 161.84 m V−1 at 24 °C to 34.45% and 207.06 m V−1 at 100 °C. With further increasing the temperature from 180 °C to 300 °C, the large signal d33 and electrical-field-induced strain mildly decrease. However, different the strain and large signal 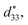 the small signal d33(E0) and kp for BF–0.3BT lead-free piezoelectric ceramics exhibit an excellent temperature-insensitive behavior at measured temperature range between the room temperature and 300 °C because it has high TC ∼475 °C and stability phase structure below TC, which is even superior to PZT system. This result offers an evidence for industrial application of BF–BT ceramics to replace Pb-based piezoelectric ceramics in high-temperature piezoelectric devices.
the small signal d33(E0) and kp for BF–0.3BT lead-free piezoelectric ceramics exhibit an excellent temperature-insensitive behavior at measured temperature range between the room temperature and 300 °C because it has high TC ∼475 °C and stability phase structure below TC, which is even superior to PZT system. This result offers an evidence for industrial application of BF–BT ceramics to replace Pb-based piezoelectric ceramics in high-temperature piezoelectric devices.
2. Experimental procedure
Nano-BaTiO3 (about 100 nm, 99%), Fe2O3 (99%) and Bi2O3 (99%) powders were used as raw materials, which were weighed on the basis of a composition of 0.7BiFeO3–0.3BaTiO3 (abbreviated as BF–0.3BT), and mixed in nylon tank. After dried and calcined at 800 °C for 12 h, the resultant powders were milled again and pressed into disks of 10 mm in diameter and 1.5 mm in thickness under 80 MPa using 3 wt% polyvinyl alcohol (PVA) as the binder, followed by burning the binder at 650 °C by 5 °C min−1 and for 2 h. After removing the PVA, the samples were sintered at 1000 °C with holding for 6 h, and then furnace cooled to room temperature. The sintered specimens were coated with silver for the electrical measurement. The coated samples were poled under a DC field of 4 kV mm−1 at 130 °C for 30 min in a silicone oil bath.The crystallographic structures were investigated by using X-ray diffraction (XRD: D/max-RB, Rigaku Inc., Japan) with a Cu Kα radiation (λ = 0.15406 nm) filtered through a Ni foil. Bulk densities of samples were measured using the Archimedes method. The temperature dependence of dielectric properties was examined using a programmable furnace with an LCR analyzer (TH2828S) at 1 kHz in temperature range of 20 °C to 650 °C. Microstructure of the sintered samples was observed by field emission scanning electron microscopy (FESEM, SUPRATM 55, Japan). Piezoelectric properties were measured using a quasi-static piezoelectric coefficient testing meter (ZJ-3A, Institute of Acoustics, Chinese Academy of Sciences, Beijing, China). Field-dependent and temperature-dependent parameters including d33(E) hysteresis loops, ferroelectric hysteresis (P–E) loops and unipolar strain S(E) were measured with ferroelectric measuring equipment (aixACCT TF Analyzer 2000, Germany). The temperature-dependent planar electromechanical coupling coefficient kp was determined by resonance-antiresonance method using an Agilent 4294A precision impedance analyzer (Hewlett-Packard, Palo Alto, CA). The temperature-dependent of leakage currents (J) were measured by precision 10 kV HVI-SC precision materials analyzer (Radiant technologies INC, USA). In addition, the PFM experiments were carried out by a commercial atomic force microscope (MFP-3D, Asylum Research, USA)
3. Results and discussion
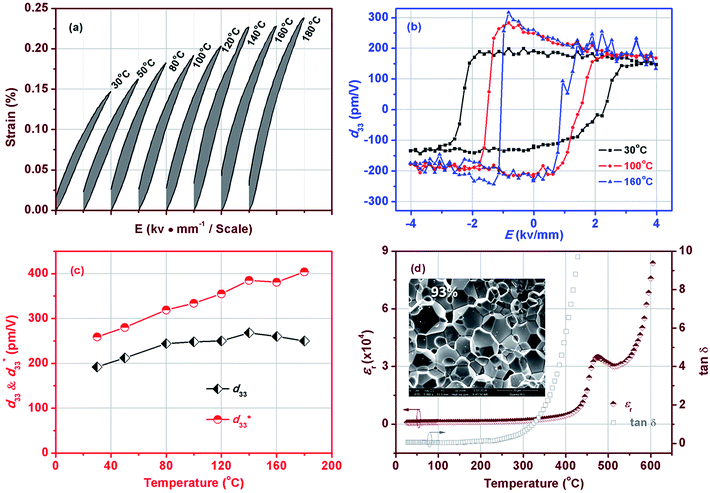
Temperature-dependent P–E loops of BF–0.3BT ceramics under a field of 4.0 kV mm−1 at the frequency of 1 Hz are shown in Fig. 1(a–e). The samples exhibit a relative saturation P–E hysteresis loops measured at room temperature as shown in Fig. 1(a) and only a single polarization current peak located in E1 corresponding to the normal domain switching is observed during electric loading. However, the E1 is larger than coercive field (EC). This indicates that the domain switching is suppressed by the defect dipole under a low electric field. With increasing the temperature to 100 °C, a typical ferroelectric polarization hysteresis loop is detected, along with E1 = EC, indicating that increase of temperature is benefit for reducing the pinning of defect dipole and promoting the domain switching. As the temperature reaches to 180 °C, the E1 is lower than EC as shown in Fig. 1(e), suggesting that the conductivity of samples increases, caused by the increase of migration of defect ions. The detailed variations of Pr, Pmax and EC with different temperature are shown in Fig. 1(f). As the temperature increases, the EC monotonously decreases. Instead, the Pr and Pmax from 13.57 μC cm−2 and 17.03 μC cm−2 increase to 54.23 μC cm−2 and 46.44 μC cm−2 with increasing the temperature from 25 °C to 180 °C, respectively. In addition, it also can find that the Pr is larger than Pmax when the temperature is over 160 °C. This may be because the fact that the leakage abruptly increases as the temperature is over 160 °C as shown in Fig. S1.†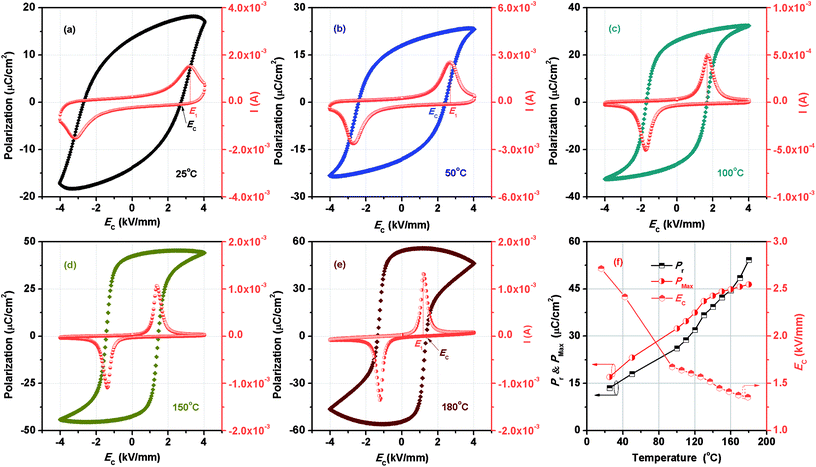 | ||
| Fig. 1 Temperature dependence of P–E loops of BF–0.3BT ceramics (a–e), and the variation of Pr, Pmax and EC with the different temperature (f). | ||
Temperature-dependent electrical-field-induced strain (S–E loop) under a field of 5.5 kV mm−1 is shown in Fig. 2(a). The strain of samples measured at room temperature is 0.15%, which is comparable to that of soft PZT ceramics (typical strain values 0.15% at 2 kV mm−1)32 and 0.95(Na0.49K0.49Li0.02) (Nb0.8Ta0.2)O3–0.05CaZrO3 (CZ5) ceramics (0.16% at 6 kV mm−1).13 With increasing the temperature, the strain increases. This phenomenon is consistent with the PZT system, such as PZT-5H32 and PZT4,10 indicating that the BF–0.3BT ceramics exhibit slight temperature-dependent behaviors. As the temperature increases from 30 °C to 180 °C, the strain increases from 0.15% to 0.237%. Different from strain, the small signal d33(E) exhibits few changes with increasing the temperature as shown in Fig. 2(b) and (c). Fig. 2(b) shows the field-dependent piezoelectric coefficient d33(E) loops, which were measured by applying a triangular signal of 4.0 kV mm−1 at the frequency of 1 Hz with an superimposed AC voltage of 25 V at 250 Hz, and were used to characterize the quasi-static d33. The equivalence between the piezoelectric constant value achieved by the d33(E) measurement and that acquired from quasi-static d33 meter has also been confirmed by Fialka et al.33 and Yao.34 Generally, the positive value at zero field in d33(E) loops is considered as piezoelectric constant d33. The small signal d33(E0) of BF–0.3BT ceramics is about 195 pm V−1 at room temperature that is comparable to the piezoelectric coefficient d33(205 pC N−1) measured by a quasi-static piezoelectric constant apparatus. Therefore, the temperature-dependence electric-field-dependent piezoelectric coefficient d33(E) loops were used to represent the temperature-dependence d33. From the Fig. 2(b), it can find that the small signal d33(E0) has little change as the temperature increases from 30 °C to 160 °C. The detailed variations for small signal d33(E0) and larger signal 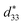 with different temperature are shown in Fig. 2(c). With increasing the temperature from 30 °C to 180 °C, the
with different temperature are shown in Fig. 2(c). With increasing the temperature from 30 °C to 180 °C, the 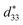 increases from 260 pm V−1 to 404 pm V−1. It is well known that the piezoelectric coefficient is comprised of both an intrinsic
increases from 260 pm V−1 to 404 pm V−1. It is well known that the piezoelectric coefficient is comprised of both an intrinsic 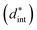 and extrinsic
and extrinsic 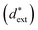 components as shown in eqn (1). The intrinsic piezoelectric contribution is related to the lattice variation. However, the extrinsic contribution is associated with domain switching and phase boundary motions. Here the increases of
components as shown in eqn (1). The intrinsic piezoelectric contribution is related to the lattice variation. However, the extrinsic contribution is associated with domain switching and phase boundary motions. Here the increases of 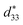 with increasing temperature may also be ascribed to crystal lattice variation and domain switching. Different from large signal
with increasing temperature may also be ascribed to crystal lattice variation and domain switching. Different from large signal 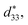 small signal d33(E0) exhibits an evident temperature-stability behavior. This indicates that BF–0.3BT ceramics have a good promising in high temperature sensors areas. Fig. 2(d) shows the temperature dependence of dielectric permittivity εr and dielectric loss factor tan
small signal d33(E0) exhibits an evident temperature-stability behavior. This indicates that BF–0.3BT ceramics have a good promising in high temperature sensors areas. Fig. 2(d) shows the temperature dependence of dielectric permittivity εr and dielectric loss factor tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for BF–0.3BT ceramics measured at 1 kHz between 20 °C and 650 °C. Only one εr peak is detected, corresponding to Curie temperature TC = 475 °C, which is superior to other lead-free piezoelectric systems, such as: KNN, BNT–BT, BT, and most Pb-based systems, further indicating that BF–BT ceramics have a good promising in high temperature sensors and actuators. In addition, the fracture surface SEM of samples is shown in inset of Fig. 2(d), in which few pores, caused by Bi2O3's volatilization at sintering process, are detected. The relative density of the BF–0.3BT ceramics is about 93%.
δ for BF–0.3BT ceramics measured at 1 kHz between 20 °C and 650 °C. Only one εr peak is detected, corresponding to Curie temperature TC = 475 °C, which is superior to other lead-free piezoelectric systems, such as: KNN, BNT–BT, BT, and most Pb-based systems, further indicating that BF–BT ceramics have a good promising in high temperature sensors and actuators. In addition, the fracture surface SEM of samples is shown in inset of Fig. 2(d), in which few pores, caused by Bi2O3's volatilization at sintering process, are detected. The relative density of the BF–0.3BT ceramics is about 93%.
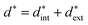 | (1) |
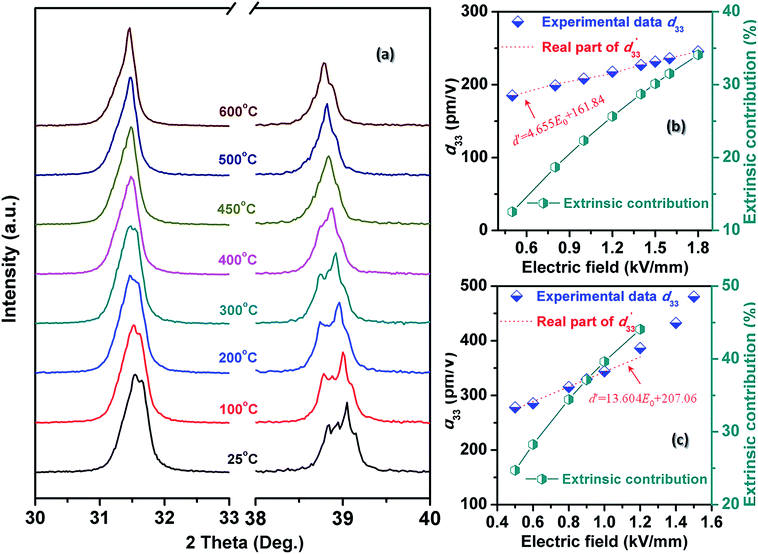
In order to clarify the effect of intrinsic and extrinsic contribution on the Pr, d33(E0) and 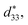 the temperature dependence of XRD for BF–0.3BT ceramics was measured and shown in Fig. 3(a) and S2.† The crystal structure is R and T two-phase coexistence at room temperature as shown in Fig. S3† and does not change until the temperature over 450 °C as shown in Fig. 3(a) and S2.† Moreover, with increasing the temperature, the diffraction peaks shift to the low angle, indicating that the lattice expands as shown in Fig. 3(a). From XRD results, it is still difficult to exclude the effect of extrinsic contribution on the piezoelectric properties. The Rayleigh model, which was originally used for analyzing the nonlinear response of ferromagnetic materials35,36 and also successfully applied to ferroelectric materials to describe the linear dependence of piezoelectric constant on the electric field amplitude recently, is one of the simplest approaches to obtaining details on nonlinear phenomena due to the domain motion. Thus, the intrinsic and extrinsic contribution on strain and piezoelectric coefficient can be evaluated by using the Rayleigh model analysis as shown in Fig. S4.† The BF–0.3BT ceramics exhibit linear Rayleigh behavior over the range of 0.5 ≤ E0 ≤ 1.8 kV mm−1 measured at room temperature as shown in Fig. 3(b) and 0.5 ≤ E0 ≤ 1.0 kV mm−1 measured at 100 °C as shown in Fig. 3(c), respectively. With increasing the electric field, the extrinsic contribution linearly increases, resulting in the increase of d33. Comparing with the samples measured at room temperature, with increasing the temperature both of intrinsic and extrinsic contribution increase as shown in Table 1. The intrinsic contribution value is 161.84 pm/V at room temperature, and increases to 207.06 pm V−1 at 100 °C. This may be related to the lattice expansion. The ratio of extrinsic contribution using E0 = 0.8 kV mm−1 increases from 18.7% at 24 °C to 34.45% at 100 °C as shown in Table 1, indicating that the increase of temperature is propitious to domain switching.
the temperature dependence of XRD for BF–0.3BT ceramics was measured and shown in Fig. 3(a) and S2.† The crystal structure is R and T two-phase coexistence at room temperature as shown in Fig. S3† and does not change until the temperature over 450 °C as shown in Fig. 3(a) and S2.† Moreover, with increasing the temperature, the diffraction peaks shift to the low angle, indicating that the lattice expands as shown in Fig. 3(a). From XRD results, it is still difficult to exclude the effect of extrinsic contribution on the piezoelectric properties. The Rayleigh model, which was originally used for analyzing the nonlinear response of ferromagnetic materials35,36 and also successfully applied to ferroelectric materials to describe the linear dependence of piezoelectric constant on the electric field amplitude recently, is one of the simplest approaches to obtaining details on nonlinear phenomena due to the domain motion. Thus, the intrinsic and extrinsic contribution on strain and piezoelectric coefficient can be evaluated by using the Rayleigh model analysis as shown in Fig. S4.† The BF–0.3BT ceramics exhibit linear Rayleigh behavior over the range of 0.5 ≤ E0 ≤ 1.8 kV mm−1 measured at room temperature as shown in Fig. 3(b) and 0.5 ≤ E0 ≤ 1.0 kV mm−1 measured at 100 °C as shown in Fig. 3(c), respectively. With increasing the electric field, the extrinsic contribution linearly increases, resulting in the increase of d33. Comparing with the samples measured at room temperature, with increasing the temperature both of intrinsic and extrinsic contribution increase as shown in Table 1. The intrinsic contribution value is 161.84 pm/V at room temperature, and increases to 207.06 pm V−1 at 100 °C. This may be related to the lattice expansion. The ratio of extrinsic contribution using E0 = 0.8 kV mm−1 increases from 18.7% at 24 °C to 34.45% at 100 °C as shown in Table 1, indicating that the increase of temperature is propitious to domain switching.
| a The extrinsic contribution is estimated by eqn (S5 see ESI) using E0 = 0.8 kV mm−1. | ||||
|---|---|---|---|---|
| Temperature (°C) | 24 | 50 | 80 | 100 |
| ad × 10−17 (m2 V−2) | 4.655 | 8.624 | 11.282 | 13.604 |
| dint × 10−12 (m V−1) | 161.84 | 177.93 | 193.84 | 207.06 |
| Extrinsic contribution (%) | 18.70% | 27.94% | 31.77% | 34.45% |
| R2 | 0.9952 | 0.9945 | 0.9967 | 0.9939 |
The apparatus PFM facilitates the observation of the components of spontaneous polarization vectors in domains, which consequently may shed light on the variation of the domain. In situ PFM phase and piezoresponse of BF–0.3BT ceramics were investigated at different temperatures 25 °C and 100 °C, as depicted in Fig. 4. Both micro and nano domain are observed in the samples at 25 °C. As the temperature increases to 100 °C, obvious domain switching (at 1 and 2 areas) was detected as shown in Fig. 4(b2), further verifying that the increase of temperature can release the pinning of ionic defect and facilitate the domain switching.
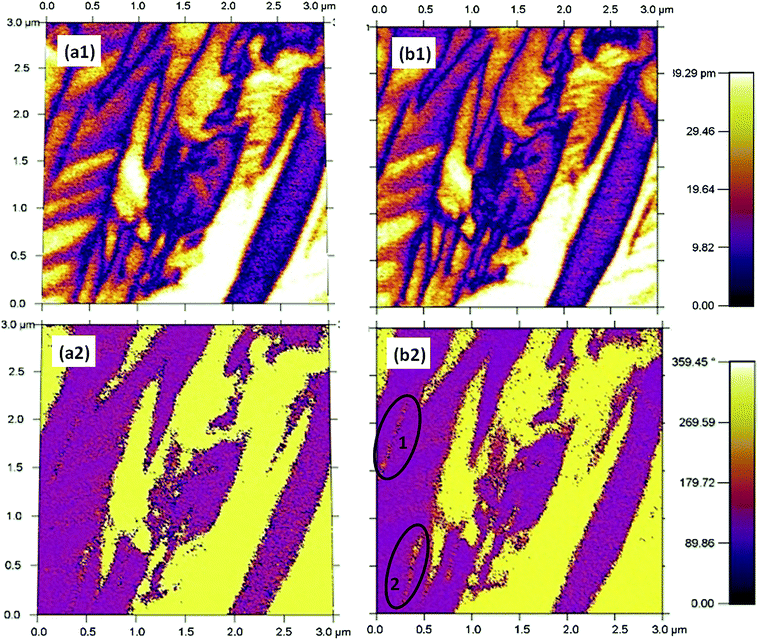 | ||
| Fig. 4 PFM scanning results of out-of-plane amplitude and phase for the sample measured at 25 °C (a1) and (a2), and 100 °C (b1) and (b2). | ||
In order to further measure the temperature stability of electrical-field-induced strain, 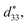 d33(E0) and kp for BF–0.3BT ceramics, the temperature-dependent strain curves, d33(E0) and kp from room temperature to 300 °C were tested as shown in Fig. 5. The strain under a field of 0.5 kV mm−1 slightly increases with increasing the temperature from 24 °C to 200 °C, and then it mildly decreases when the temperature increases from 200 °C to 300 °C as shown in Fig. 5(a). The slight increase of strain is consistent with previous results as shown in Fig. 2, which is due to the joint effect of intrinsic contribution (lattice expansion) and extrinsic contribution (domain switching). As the temperature further increases, the decrease of strain may be attributed to the increases of conductivity, which is adverse to the polarization of ceramics and dipole alignment.30 The temperature-dependent strain behavior (in terms of temperature-dependent
d33(E0) and kp for BF–0.3BT ceramics, the temperature-dependent strain curves, d33(E0) and kp from room temperature to 300 °C were tested as shown in Fig. 5. The strain under a field of 0.5 kV mm−1 slightly increases with increasing the temperature from 24 °C to 200 °C, and then it mildly decreases when the temperature increases from 200 °C to 300 °C as shown in Fig. 5(a). The slight increase of strain is consistent with previous results as shown in Fig. 2, which is due to the joint effect of intrinsic contribution (lattice expansion) and extrinsic contribution (domain switching). As the temperature further increases, the decrease of strain may be attributed to the increases of conductivity, which is adverse to the polarization of ceramics and dipole alignment.30 The temperature-dependent strain behavior (in terms of temperature-dependent  normalized to its room temperature value
normalized to its room temperature value 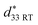 ) of several representative piezoceramics is also provided in Fig. 5(b) for comparison. It is noted that the strain variation of BF–0.3BT ceramics is superior to all these piezoelectric ceramics (including PZT-5H,32 PZT4,10 KNN-3T–0.5Mn,38 KNLN–BZ–BNT39 and BNT–BT–KNN37). BF–0.3BT ceramics can endure temperature as high as 300 °C and the large signal
) of several representative piezoceramics is also provided in Fig. 5(b) for comparison. It is noted that the strain variation of BF–0.3BT ceramics is superior to all these piezoelectric ceramics (including PZT-5H,32 PZT4,10 KNN-3T–0.5Mn,38 KNLN–BZ–BNT39 and BNT–BT–KNN37). BF–0.3BT ceramics can endure temperature as high as 300 °C and the large signal 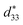 almost has a little change from room temperature up to 300 °C. In contrast, the range of applications of the PZT-5H, PZT4, KNN-3T–0.5Mn, KNLN–BZ–BNT and BNT–BT–KNN systems is restricted below 200 °C due to their low Curie temperature TC. The temperature-dependence piezoelectric properties d33(E0) are shown in Fig. 5(c). The small signal d33(E0) also exhibit excellent temperature-insensitive behavior. This phenomenon is different from that of CZ5, in which d33 drops fast with increasing temperature in the temperature range between room temperature and 175 °C, due to the existence of polycrystalline phase boundary (PPT) around room temperature.13 The excellent temperature stability behavior of d33(E0) for BF–0.3BT system indicates that BF–0.3BT ceramic have a good prospects for replacing the PZT systems in the high-temperature devices. The temperature-dependence planar electromechanical coupling factor (kp), which was determined by resonance-antiresonance method at different temperatures as shown in Fig. S5,† provides the further evidence for the temperature-insensitive behavior of BF–0.3BT ceramics as shown in Fig. 5(d). The variation of kp is less than 10% within the temperature range from room temperature up to 300 °C, which is better than textured KNN–3T ceramics.40 In addition, the BF–0.3BT ceramics also show excellent high-temperature anti-aging behavior, as shown in Fig. S6.† After experiencing a heat treatment at 300 °C or 400 °C for 500 h, the variation of the piezoelectric coefficient (d33) is less than 5%.
almost has a little change from room temperature up to 300 °C. In contrast, the range of applications of the PZT-5H, PZT4, KNN-3T–0.5Mn, KNLN–BZ–BNT and BNT–BT–KNN systems is restricted below 200 °C due to their low Curie temperature TC. The temperature-dependence piezoelectric properties d33(E0) are shown in Fig. 5(c). The small signal d33(E0) also exhibit excellent temperature-insensitive behavior. This phenomenon is different from that of CZ5, in which d33 drops fast with increasing temperature in the temperature range between room temperature and 175 °C, due to the existence of polycrystalline phase boundary (PPT) around room temperature.13 The excellent temperature stability behavior of d33(E0) for BF–0.3BT system indicates that BF–0.3BT ceramic have a good prospects for replacing the PZT systems in the high-temperature devices. The temperature-dependence planar electromechanical coupling factor (kp), which was determined by resonance-antiresonance method at different temperatures as shown in Fig. S5,† provides the further evidence for the temperature-insensitive behavior of BF–0.3BT ceramics as shown in Fig. 5(d). The variation of kp is less than 10% within the temperature range from room temperature up to 300 °C, which is better than textured KNN–3T ceramics.40 In addition, the BF–0.3BT ceramics also show excellent high-temperature anti-aging behavior, as shown in Fig. S6.† After experiencing a heat treatment at 300 °C or 400 °C for 500 h, the variation of the piezoelectric coefficient (d33) is less than 5%.
 | ||
Fig. 5 Temperature dependence of unipolar strain of BF–0.3BT ceramics at 0.5 kV mm−1 field excursion (a), comparison of temperature dependence of normalized strain 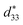 for various piezoceramics as normalized to its room temperature value for various piezoceramics as normalized to its room temperature value 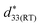 (b). The data for PZT5H,32 PZT4,10 BNT–BT–KNN37 KNN–3T–0.5Mn38 and KNLN–BZ–BNT39 ceramics are taken from figures in the respective references. Temperature dependence of static d33 (c), and the planar electromechanical coupling factor (kp) normalized to its room temperature value kp(RT) (d) for BF–0.3BT ceramics and KNN–3T ceramics.40 (b). The data for PZT5H,32 PZT4,10 BNT–BT–KNN37 KNN–3T–0.5Mn38 and KNLN–BZ–BNT39 ceramics are taken from figures in the respective references. Temperature dependence of static d33 (c), and the planar electromechanical coupling factor (kp) normalized to its room temperature value kp(RT) (d) for BF–0.3BT ceramics and KNN–3T ceramics.40 | ||
4. Conclusions
The temperature-dependent behaviors of ferroelectric, piezoelectric, kp and electrical-field-induced strain were investigated to uncover the temperature stability of high-performance BF–0.3BT piezoceramics. Because of the joint effect of intrinsic (lattice expansion) and extrinsic contribution (domain switching), both electrical-field-induced strain and large signal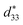 for BF–0.3BT ceramics increased with increasing the temperature from room temperature to 180 °C. As the temperature furthering increases, the large signal d33 and electrical-field-induced strain mildly decreased, which was due to the increase of conductivity for BF–0.3BT ceramics. No matter what, the strain and
for BF–0.3BT ceramics increased with increasing the temperature from room temperature to 180 °C. As the temperature furthering increases, the large signal d33 and electrical-field-induced strain mildly decreased, which was due to the increase of conductivity for BF–0.3BT ceramics. No matter what, the strain and 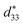 values at 300 °C are still higher than that at room temperature. In addition, the d33(E0) and kp exhibit excellent temperature-insensitive behavior in the wide temperature range between room temperature and 300 °C, which revealed the promising potential of using BF–0.3BT ceramics in high-temperature piezoelectric devices.
values at 300 °C are still higher than that at room temperature. In addition, the d33(E0) and kp exhibit excellent temperature-insensitive behavior in the wide temperature range between room temperature and 300 °C, which revealed the promising potential of using BF–0.3BT ceramics in high-temperature piezoelectric devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Beijing Natural Science Foundation (Grant No. 2174078), National Natural Science Foundation of China (Grant No. 51472026, 51572143), Fundamental Research Funds for the Central Universities (Grant No. FRF-TP-15-077A1)References
- K. Uchino, in Ferroelectric Devices, Marcel Dekker, New York, 2000 Search PubMed.
- J. Rödel, W. Jo, K. T. P. Seifert, E. M. Anton, T. Granzow and D. Damjanovic, Perspective on the Development of Lead-free Piezoceramics, J. Am. Ceram. Soc., 2009, 92, 1153–1177 CrossRef.
- T. R. Shrout and S. J. Zhang, Lead-free piezoelectric ceramics: alternatives for PZT, J. Electroceram., 2007, 19, 113–126 CrossRef.
- W. Jo, R. Dittmer, M. Acosta, J. Zang, C. Groh, E. Sapper, K. Wang and J. Rödel, Giant electric-field-induced strains in lead-free ceramics for actuator applications-status and perspective, J. Electroceram., 2012, 29, 71–93 CrossRef CAS.
- L. F. Zhu, B. P. Zhang, L. Zhao and J. F. Li, High piezoelectricity of BaTiO3-CaTiO3-BaSnO3 lead-free ceramics, J. Mater. Chem. C, 2014, 2, 4764–4771 RSC.
- W. Liu and X. Ren, Large Piezoelectric Effect in Pb-Free Ceramics, Phys. Rev. Lett., 2009, 103, 257602 CrossRef PubMed.
- L. F. Zhu, B. P. Zhang, L. Zhao, S. Li, Y. Zhou, X. C. Shi and N. Wang, Large piezoelectric effect of (Ba,Ca)TiO3-xBa(Sn,Ti)O3 lead-free ceramics, J. Eur. Ceram. Soc., 2016, 36, 1017–1024 CrossRef CAS.
- X. X. Wang, X. G. Tang and H. L. W. Chan, Electromechanical and ferroelectric properties of (Bi1/2Na1/2)TiO3-(Bi1/2K1/2)TiO3-BaTiO3 lead-free piezoelectric ceramics, Appl. Phys. Lett., 2004, 85, 91 CrossRef CAS.
- D. Maurya, Y. Zhou, Y. Yan and S. Priya, Synthesis mechanism of grain-oriented lead-free piezoelectric Na0.5Bi0.5TiO3-BaTiO3 ceramics with giant piezoelectric response, J. Mater. Chem. C, 2013, 1, 2102–2111 RSC.
- Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Lead-free piezoceramics, Nature, 2004, 432, 84–87 CrossRef CAS PubMed.
- J. F. Li, K. Wang, F. Y. Zhu, L. Q. Cheng and F. Z. Yao, (K,Na)NbO3-Based Lead-Free Piezoceramics: Fundamental Aspects, Processing Technologies, and Remaining Challenges, J. Am. Ceram. Soc., 2013, 96, 3677–3696 CrossRef CAS.
- K. Xu, J. Li, X. Lv, J. Wu, X. Zhang, D. Xiao and J. Zhu, Superior Piezoelectric Properties in Potassium–Sodium Niobate Lead-Free Ceramics, Adv. Mater., 2016, 28, 8519–8523 CrossRef CAS PubMed.
- K. Wang, F. Z. Yao, W. Jo, D. Gobeljic, V. V. Shvartsman, D. C. Lupascu, J. F. Li and J. Rödel, Temperature-Insensitive (K,Na)NbO3-Based Lead-Free Piezoactuator Ceramics, Adv. Funct. Mater., 2013, 23, 4079–4086 CrossRef CAS.
- M. H. Zhang, K. Wang, Y. J. Du, G. Dai, W. Sun, G. Li, D. Hu, H. C. Thong, C. Zhao, X. Q. Xi, Z. X. Yue and J. F. Li, High and Temperature-Insensitive Piezoelectric Strain in Alkali Niobate Lead-free Perovskite, J. Am. Chem. Soc., 2017, 139, 3889–3895 CrossRef CAS PubMed.
- L. F. Zhu, B. P. Zhang, Z. C. Zhang, S. Li, L. J. Wang and L. J. Zheng, Piezoelectric, ferroelectric and ferromagnetic properties of (1-x)BiFeO3-xBaTiO3 lead-free ceramics near morphotropic phase boundary, J. Mater. Sci.: Mater. Electron., 2018, 29(3), 2307–2315 CrossRef CAS.
- S. O. Leontsev and R. E. Eitel, Dielectric and Piezoelectric Properties in Mn-Modified (1-x)BiFeO3-xBaTiO3 Ceramics, J. Am. Ceram. Soc., 2009, 92(12), 2957–2961 CrossRef CAS.
- X. Shan, C. Zhou, Z. Cen, H. Yang, Q. Zhou and W. Li, Bi(Zn1/2Ti1/2)O3 modified BiFeO3-BaTiO3 lead-free piezoelectric ceramics with high temperature stability, Ceram. Int., 2013, 39, 6707–6712 CrossRef CAS.
- T. Zheng, Y. Ding and J. Wu, Bi nonstoichiometry and composition engineering in (1-x)Bi1+yFeO3+3y/2- xBaTiO3 ceramics, RSC Adv., 2016, 6, 90831–90839 RSC.
- L. F. Zhu, B. P. Zhang, S. Li and G. L. Zhao, Large piezoelectric responses of Bi(Fe,Mg,Ti)O3-BaTiO3 lead-free piezoceramics near the morphotropic phase boundary, J. Alloys Compd., 2017, 727, 382–389 CrossRef CAS.
- M. H. Lee, D. J. Kim, J. S. Park, S. W. Kim, T. K. Song, M. H. Kim, W. J. Kim, D. Do and I. K. Jeong, High-Performance Lead-Free Piezoceramics with High Curie Temperatures, Adv. Mater., 2015, 27, 6976–6982 CrossRef CAS PubMed.
- Q. Li, J. X. Wei, J. R. Cheng and J. G. Chen, High temperature dielectric, ferroelectric and piezoelectric properties of Mn-modified BiFeO3-BaTiO3 lead-free ceramics, J. Mater. Sci., 2017, 52, 229–237 CrossRef CAS.
- C. Zhou, H. Yang, Q. Zhou, G. Chen, W. Li and H. Wang, Effects of Bi excess on the structure and electrical properties of high-temperature BiFeO3–BaTiO3 piezoelectric ceramics, J. Mater. Sci.: Mater. Electron., 2013, 24, 1685–1689 CrossRef CAS.
- H. Yang, C. Zhou, X. Liu, Q. Zhou, G. Chen and W. Li, Piezoelectric properties and temperature stabilities of Mn- and Cu-modified BiFeO3-BaTiO3 high temperature ceramics, J. Eur. Ceram. Soc., 2013, 33, 1177–1183 CrossRef CAS.
- T. Zheng, Y. Ding and J. Wu, Effects of oxide additives on structure and properties of bismuth ferrite-based ceramics, J. Mater. Sci.: Mater. Electron., 2017, 28, 11534–11542 CrossRef CAS.
- Q. Zheng, Y. Guo, F. Lei, X. Wu and D. Lin, Microstructure, ferroelectric, piezoelectric and ferromagnetic properties of BiFeO3-BaTiO3-Bi(Zn0.5Ti0.5)O3 lead-free multiferroic ceramics, J. Mater. Sci.: Mater. Electron., 2014, 25, 2638–2648 CrossRef CAS.
- Y. Lin, L. Zhang, W. Zheng and J. Yu, Structural phase boundary of BiFeO3-Bi(Zn1/2Ti1/2)O3-BaTiO3 lead-free ceramics and their piezoelectric properties, J. Mater. Sci.: Mater. Electron., 2015, 26, 7351–7360 CrossRef CAS.
- D. Lin, Q. Zheng, Y. Li, Y. Wan, Q. Li and W. Zhou, Microstructure, ferroelectric and piezoelectric properties of Bi0.5K0.5TiO3-modified BiFeO3-BaTiO3 lead-free ceramics with high Curie temperature, J. Eur. Ceram. Soc., 2013, 33, 3023–3036 CrossRef CAS.
- Y. Guo, T. Wang, L. He, Q. Zheng, J. Liao, C. Xu and D. Lin, Enhanced ferroelectric and ferromagnetic properties of Er-modified BiFeO3-BaTiO3 lead-free multiferroic ceramics, J. Mater. Sci.: Mater. Electron., 2016, 27, 5741–5747 CrossRef CAS.
- T. Zheng, Z. Jiang and J. Wu, Enhanced piezoelectricity in (1-x)Bi1.05Fe1-yAyO3-xBaTiO3 lead-free ceramics: site engineering and wide phase boundary region, Dalton Trans., 2016, 45, 11277–11285 RSC.
- L. F. Zhu, B. P. Zhang, J. Q. Duan, B. W. Xun, N. Wang, Y. C. Tang and G. L. Zhao, Enhanced piezoelectric and ferroelectric properties of BiFeO3-BaTiO3 lead-free ceramics by optimizing the sintering temperature and dwell time, J. Eur. Ceram. Soc., 2018, 38, 3463–3471 CrossRef CAS.
- J. Wei, D. Fu, J. Cheng and J. Cheng, Temperature dependence of the dielectric and piezoelectric properties of xBiFeO3-(1-x)BaTiO3 ceramics near the morphotropic phase boundary, J. Mater. Sci., 2017, 52, 10726–10737 CrossRef CAS.
- D. Wang, Y. Fotinich and G. P. Carman, Influence of temperature on the electromechanical and fatigue behavior of piezoelectric ceramics, J. Appl. Phys., 1998, 83, 5342 CrossRef CAS.
- J. Fialka and P. Beneš, Comparison of Methods for the Measurement of Piezoelectric Coefficients, IEEE Trans. Instrum. Meas., 2013, 62, 1047–1057 Search PubMed.
- F. Z. Yao, Q. Yu, K. Wang, Q. Li and J. F. Li, Ferroelectric domain morphology and temperature- dependent piezoelectricity of (K,Na,Li)(Nb,Ta,Sb)O3 lead-free piezoceramics, RSC Adv., 2014, 4, 20062–20068 RSC.
- L. Rayleigh, XXV. Notes on electricity and magnetism.-III. On the behavior of iron and steel under the operation of feeble magnetic forces, Philos. Mag., 1887, 23, 225–245 Search PubMed.
- L. Neel, Theory of Rayleigh's law of magnetization, Cah. Phys., 1942, 12, 1 Search PubMed.
- S. T. Zhang, A. B. Kounga, E. Aulbach, T. Granzow, W. Jo, H. J. Kleebe and J. Rödel, Lead-free piezoceramics with giant strain in the system Bi0.5Na0.5TiO3-BaTiO3-K0.5Na0.5NbO3. I. Structure and room temperature properties, J. Appl. Phys., 2008, 103, 034107 CrossRef.
- P. Li, X. Chen, F. Wang, B. Shen, J. Zhai, S. Zhang and Z. Zhou, Microscopic insight into electric fatigue resistance and thermally stable piezoelectric properties of (K,Na)NbO3-based ceramics, ACS Appl. Mater. Interfaces, 2018, 10, 28772–28779 CrossRef CAS PubMed.
- Y. Quan, W. Ren, G. Niu, L. Wang, J. Zhao, N. Zhang, M. Liu, Z. G. Ye, L. Liu and T. Karaki, Large Piezoelectric strain with superior thermal stability and excellent fatigue resistance of lead-free potassium sodium niobate-based grain orientation-controlled ceramics, ACS Appl. Mater. Interfaces, 2018, 10, 10220–10226 CrossRef CAS PubMed.
- P. Li, J. Zhai, B. Shen, S. Zhang, X. Li, F. Zhu and X. Zhang, Ultrahigh piezoelectric properties in textured (K,Na)NbO3-based lead-free ceramics, Adv. Mater., 2018, 30, 1705171 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07553k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |