Open Access Article
Open Access ArticleStabilization of beryllium-containing planar pentacoordinate carbon species through attaching hydrogen atoms†
Xue-Feng Zhaoa,
Jian-Hong Biana,
Fang Huang c,
Caixia Yuana,
Qiang Wang
c,
Caixia Yuana,
Qiang Wang *b,
Ping Liub,
Debao Lib,
Xiaotai Wang
*b,
Ping Liub,
Debao Lib,
Xiaotai Wang d and
Yan-Bo Wu
d and
Yan-Bo Wu *ab
*ab
aKey Laboratory of Materials for Energy Conversion and Storage of Shanxi Province, Institute of Molecular Science, Shanxi University, Taiyuan, 030006, China. E-mail: wyb@sxu.edu.cn
bState Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, 27 South Taoyuan Road, Taiyuan, Shanxi 030001, China. E-mail: wqiang@sxicc.ac.cn
cCollege of Chemistry, Chemical Engineering and Materials Science, Shandong Normal University, 88 East Culture Road, Jinan, Shandong 250014, China
dDepartment of Chemistry, University of Colorado Denver, Campus Box 194, P.O. Box 173364, Denver, Colorado 80217-3364, USA
First published on 29th October 2018
Abstract
The diagonal relationship between beryllium and aluminum and the isoelectronic relationship between BeH unit and Al atom were utilized to design nine new planar and quasi-planar pentacoordinate carbon (ppC) species CAlnBemHxq (n + m = 5, q = 0, ±1, x = q + m − 1) (1a–9a) by attaching H atoms onto the Be atoms in CAl4Be, CAl3Be2−, CAl2Be32−, and CAlBe43−. These ppC species are σ and π double aromatic. In comparison with their parents, these H-attached molecules are more stable electronically, as can be reflected by the more favourable alternative negative–positive–negative charge-arranging pattern and the less dispersed peripheral orbitals. Remarkably, seven of these nine molecules are global energy minima, in which four of them are kinetically stable, including CAl3Be2H (2a), CAl2Be3H− (4a), CAl2Be3H2 (5a), and CAlBe4H4+ (9a). They are the promising target for the experimental realization of species with a ppC.
Planar hypercoordinate carbon chemistry can be dated back to 1968 when Monkhorst proposed the first planar tetracoordinate carbon (ptC) in a transition state structure.1 In 1970, Hoffmann and co-workers sponsored the project of stabilizing the ptC in equilibrium structure.2 After the proposal of first ptC energy minimum 1,1-dilithiocyclopropane (C3H4Li2) by Schleyer and Pople group in 1976,3 the most significant advance has been the conceptual extension of ptC to planar pentacoordinate or hexacoordinate carbon (ppC or phC),4 which promoted the extension of the number of planar coordination to values as high as ten and the central planar hypercoordinate atom from carbon to other main group elements or even transition metals.5 Nevertheless, the ppC are the most witnessed in all these extended type of structures,6 possibly due to the geometrically nice fit between the peripheral ligand atoms and center carbon and the electronically easy satisfaction of the 18 electron (18e) rule.
In 2001, Wang and Schleyer reported a family of ppC-containing molecules, i.e. the milestone “hyparenes”, which were designed by substituting the –(CH)n– moieties in aromatic or even anti-aromatic hydrocarbons with ppC building blocks –C3B3–, –C2B4–, and –CB5–.4b Subsequently, ppC species such as CCu5H5,7 CBe5 and CBe54−,8 wheel-like C2B8, C3B93+ and C5B11+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 were also proposed. However, it is still unknown to date whether these small ppC clusters are global minima on their potential energy surfaces. Hence, people cannot evaluate their experimental viability. Nonetheless, situation changed when Zeng and Schleyer group reported the first ppC global minimum D5h CAl5+ in 2008, which features not only the 18e structure, but also the σ and π double aromaticity.10 Taking CAl5+ as the seed structure and considering the periodicity as well as the diagonal relationship, etc., people had designed a series isoelectronic ppC structures, including CAlnBem1−m (m = 1–3),11 CAl4E+ (E = Al, Ga, In, Tl),12 CBe5E− (E = Al, Ga, In, Tl),13 CAl4TmX2 (Tm = Ti, Zr, Hf; X = F, Cl, Br, I, and cyclopentadienyl anion),14 and CGanBem1−m (n + m = 5, m = 1–4).15
9 were also proposed. However, it is still unknown to date whether these small ppC clusters are global minima on their potential energy surfaces. Hence, people cannot evaluate their experimental viability. Nonetheless, situation changed when Zeng and Schleyer group reported the first ppC global minimum D5h CAl5+ in 2008, which features not only the 18e structure, but also the σ and π double aromaticity.10 Taking CAl5+ as the seed structure and considering the periodicity as well as the diagonal relationship, etc., people had designed a series isoelectronic ppC structures, including CAlnBem1−m (m = 1–3),11 CAl4E+ (E = Al, Ga, In, Tl),12 CBe5E− (E = Al, Ga, In, Tl),13 CAl4TmX2 (Tm = Ti, Zr, Hf; X = F, Cl, Br, I, and cyclopentadienyl anion),14 and CGanBem1−m (n + m = 5, m = 1–4).15
During the design of these species, when each Al or its heavier congeners was replaced by a Be atom, a negative charge was added to maintain the isoelectronic relationship. However, it would be hard to experimentally realize such ppC structures due to the high molecular charges and the exposure of the electron deficient metal atoms. As a result, people had tried to stabilize the highly negatively charged ppC ions through attaching the certain number of auxiliary atoms. For example, H atoms had been attached to CAl4− and CAl42− in a joint experimental-theoretical study, leading to the new ptC species CAl4H and CAl4H−.16 For ppC species, the most studied seed structure should be CBe54−,8 which is even not an eligible minimum.17 Nevertheless, through attaching the auxiliary atoms, like alkali metals, hydrogen, halogens, and even transition metal gold, a family of ppC species can be designed, including CBe5Linn−4 (n = 1–5),17a CBe5Hnn−4 (n = 2, 3, 5),17b CBe5E5+ (E = F, Cl, Br, Li, Na, K),18 and CBe5Aunn−4 (n = 2–5).19 In these ppC species, the auxiliary atoms play the roles of both compensating the deficient electrons and reducing the high negatively charges. Remarkably, H atoms were also employed to stabilize the ppC-containing C–Be double chain nanoribbon, where its CBe5H2 ppC unit possesses the similar electronic structures to that of CAl5+.20
Very recently, using Li atoms to balance the high negative charge of Be-doped ppC structures results in neutral or mono-anionic species [(CAl2Be3)Li]−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11b and CGanBemLim−1 (n + m = 5, m = 1–4),15 where Li atoms generally show high affinity to Be atoms. In addition, our recent study revealed that Be and H can be bounded together through favourable covalent and ionic bonding,5c,21 thus H should be a better choice than Li as the auxiliary atoms around CBe5 ppC core.17b Herein, we wonder whether H atoms can be attached onto the Be-doped ppC structures to design the new ppC molecules possessing the molecular charges with ±1|e|, which facilitates the experimental generation and accurate calculation. The answer is positive and presented in this computational study, which designed nine new ppC molecules (see Fig. 1), in which four of them are kinetically stable global minima, thereby providing promising targets for experimental realization.
11b and CGanBemLim−1 (n + m = 5, m = 1–4),15 where Li atoms generally show high affinity to Be atoms. In addition, our recent study revealed that Be and H can be bounded together through favourable covalent and ionic bonding,5c,21 thus H should be a better choice than Li as the auxiliary atoms around CBe5 ppC core.17b Herein, we wonder whether H atoms can be attached onto the Be-doped ppC structures to design the new ppC molecules possessing the molecular charges with ±1|e|, which facilitates the experimental generation and accurate calculation. The answer is positive and presented in this computational study, which designed nine new ppC molecules (see Fig. 1), in which four of them are kinetically stable global minima, thereby providing promising targets for experimental realization.
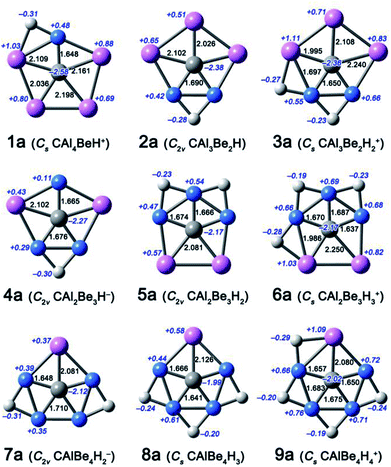 | ||
| Fig. 1 Optimized structures 1a–9a at the B3LYP/aug-cc-pVTZ level. Bond distances and NBO charges are given in black and italic blue fonts, respectively. | ||
Computational methods
The ppC species designed in this work were optimized and harmonic vibrational frequencies analyzed at the B3LYP/aug-cc-pVTZ level, which predicted these ppC structures to be true energy minima. The vibrations obtained using B3LYP functional was calibrated by the calculations using double hybrid functional B2PLYP22 with D3 empirical dispersion correction (B2PLYP-D3),23 which gave the similar results to those obtained at the B3LYP level. So B3LYP functional should be reliable for current ppC molecules. The thermodynamic stability of designed ppC species was studied using a stochastic search algorithm.24 Two sets of explorations were run for singlet potential energy surfaces until they converged. The triplet potential energy surfaces were examined by another two sets of explorations as well. The randomly generated initial structures were optimized at the B3LYP/6-31G(d) level and 20 lowest isomers were recalculated at the B3LYP/aug-cc-pVTZ level, then ten lowest isomers were refined at the B2PLYP-D3/aug-cc-pVTZ level. Finally, the energies of the five lowest isomers were improved at the CCSD(T)/aug-cc-pVTZ level. The relative energies were compared using CCSD(T)/aug-cc-pVTZ electronic energies plus B2PLYP-D3/aug-cc-pVTZ Gibbs free energy corrections. The wave function stability, natural bond orbital (NBO)25 analyses and the nucleus-independent chemical shifts (NICS)26 analyses were performed at B3LYP/aug-cc-pVTZ. Adaptive nature density partitioning (AdNDP)27 was carried out at B3LYP/6-31G(d) level. Born–Oppenheimer molecular dynamic (BOMD)28 simulations were run at the B3LYP/6-31g(d) level and 298 K. The stochastic search algorithm was realized using GXYZ 2.0 program,29 the AdNDP analysis was performed using AdNDP program, the CCSD(T) calculations were carried out using MolPro 2012.1,30 the NBO analyses were performed using NBO 3.1,31 and all other calculations were performed using the Gaussian 09 package.32Results and discussion
Design of CAlnBemHxq (n + m = 5, q = ±1, x = q + m − 1)
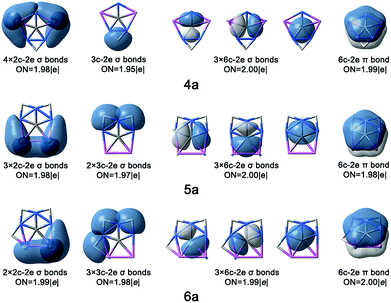
In this work, we focus on four components, including CAl4Be, CAl3Be2−, CAl2Be32−, and CAlBe43− (see Fig. S1†), in which the global energy minima of former three components had been proved to be ppC structure previously.11 We had studied CAlBe43− and found that it is a ppC local energy minimum at the B3LYP/aug-cc-pVTZ level. However, its wavefunction is unstable, possibly due to the high negative charge, so reducing such charge is necessary. Using the four ppC species and their ppC-containing isomers as the seed structures, we try to attach H atoms onto the Be–Be or Be–Al edges. Considering molecular charges within ±1|e|, there are nine possible components, including CAl4BeH+, CAl3Be2H, Cal3Be2H2+, CAl2Be3H−, CAl2Be3H2, CAl2Be3H3+, CAlBe4H2−, CAlBe4H3, CAlBe4H4+. Fig. 1 shows the most stable ppC structures (1a–9a) for each component. At the B3LYP/aug-cc-pVTZ level, 8a adopts the quasi-planar geometry, while other species adopt the perfectly planar structures. The C–Al distances in 1a–9a range from 1.995 to 2.250 Å and the C–Be distances range from 1.641 to 1.710 Å, which are close enough to consider each of corresponding Al or Be atom as a coordination to C atom, so 1a–9a can be regarded as ppC or quasi-ppC species.Electronic structure analyses
| υmin | Gap | VDE | VEA | WBI | ||||
|---|---|---|---|---|---|---|---|---|
| C–Be | C–Al | Be–H | Be–Al | |||||
| CAl4Be | 77 | 2.60 | 7.20 | −1.21 | 0.64 | 0.40/0.47 | ||
| CAl4BeH+ (1a) | 59 | 2.32 | 11.70 | −5.91 | 0.78 | 0.34–0.45 | 0.58 | 0.27 |
| CAl3Be2− | 98 | 2.04 | 2.39 | 2.35 | 0.51 | 0.46/0.54 | ||
| CAl3Be2H (2a) | 104 | 2.34 | 7.01 | −1.24 | 0.67 | 0.41/0.45 | 0.45 | |
| CAl3Be2H2+ (3a) | 81 | 2.70 | 12.21 | −5.90 | 0.69/0.75 | 0.30–0.45 | 0.43/0.49 | 0.28 |
| CAl2Be32− | 131 | 0.94 | −1.34 | 4.03 | 0.52/0.56 | 0.49 | ||
| CAl2Be3H− (4a) | 118 | 2.66 | 2.60 | 2.30 | 0.52/0.65 | 0.45 | 0.45 | |
| CAl2Be3H2 (5a) | 142 | 2.86 | 7.08 | −0.71 | 0.62/0.77 | 0.39 | 0.39/0.53 | |
| CAl2Be3H3+ (6a) | 96 | 2.96 | 12.35 | −5.56 | 0.66–0.69 | 0.30/0.41 | 0.42–0.54 | 0.32 |
| CAlBe43− | 173 | 0.33 | −3.71 | 5.13 | 0.59/0.61 | 0.42 | ||
| CAlBe4H2− (7a) | 144 | 2.40 | 2.26 | 2.28 | 0.57/0.63 | 0.45 | 0.41/0.48 | |
| CAlBe4H3 (8a) | 42 | 2.96 | 6.66 | 0.21 | 0.56/0.73 | 0.35 | 0.38–0.54 | |
| CAlBe4H4+ (9a) | 91 | 3.55 | 12.62 | −4.96 | 0.78–0.83 | 0.35 | 0.54–0.64 | 0.28 |
| CAl5+ | 69 | 2.82 | 11.67 | −5.48 | 0.43 | |||
Stability consideration
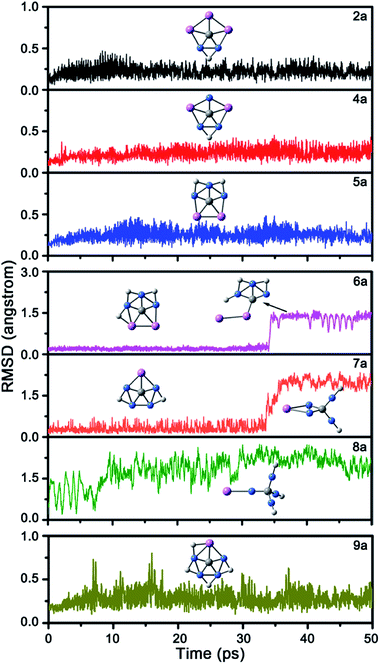
Next, we studied the kinetic stability of global energy minima 2a and 4a–9a by performing 50 pico-second (ps) Born–Oppenheimer molecular dynamic (BOMD)28 simulations at the B3LYP/6-31G(d) level and 298 K. The structural evolution during the simulation was described by the root-mean-square deviation (RMSD) relative to their B3LYP/6-31G(d)-optimized structures. As shown in Fig. 4, the RMSD plots of 6a–8a show irreversible upward jumps at about 34, 32, and 9 ps, respectively. Structural sampling suggested that the upward jumps of these RMSD plots correspond to the isomerization processes, so 6a–8a are kinetically unstable. As a comparison, the RMSD values of 2a, 4a, and 5a have no upward jump and the fluctuation also relatively small, ranging from 0.06, 0.08, and 0.09 to 0.47, 0.45 and 0.48 Å. The RMSD plot of 9a shows some reversible jumps. However, the highest RMSD value is only 0.80 Å, which corresponds to the flexibility of H atoms rather than the tendency to isomerize the structure. The average RMSD values for these four molecules are also small, being 0.22, 0.24, 0.25 and 0.29 Å, respectively. The dynamic simulations suggest their structures can be well-maintained during the simulations at 298 K. Being the kinetically stable global energy minima, 2a, 4a, 5a, and 9a would be promising targets for gas phase generation and followed spectroscopic characterization.
Conclusion
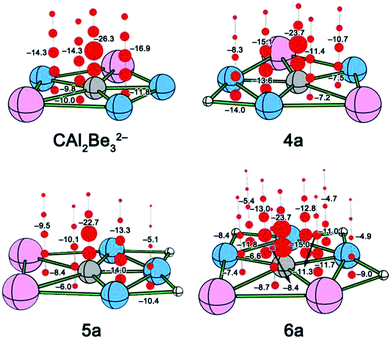
In summary, we have designed nine ppC species with molecular charges within ±1|e| through attaching the H atoms at the Be–Be or Be–Al edge of ppC species CAl4Be, CAl3Be2−, CAl2Be32−, and CAlBe43−. Similar to their parent molecules, these ppC species meet the octet rule and feature the σ and π double aromaticity. The introduction of H atoms on these ppC structures does not obviously influence the ppC core structure both geometrically and electronically, but can enlarge the HOMO–LUMO gaps, convert the dispersed Be–Be or Be–Al 2c-2e σ bonds to the less dispersed Be–H–Be or Be–H–Al 3c-2e π bonds, which further stabilize the ppC structures. In these nine H-attached ppC species, four of them were confirmed to be stable both thermodynamically and kinetically, including CAl3Be2H (2a), CAl2Be3H− (4a), CAl2Be3H2 (5a), and CAlBe4H4+ (9a). They are the promising targets for generation and characterization in the gas phase experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support for this work from the NSFC (Grant No. 21720102006, 21273140, and 21471092), the Special Program for Applied Research on Supercomputation of the NSFC-Guangdong Joint Fund (the second phase) (Grant No. U1501501), the One Hundred-Talent Program of Shanxi Province, the Program for Outstanding Innovative Teams of Higher Learning Institutions of Shanxi, the Shanxi 1331KIRT, the Foundation of the State Key Laboratory of Coal Conversion (Grant No. J17-018-610), and the Shanxi University supercomputing platform.Notes and references
- H. J. Monkhorst, Chem. Commun., 1968, 1111 RSC.
- R. Hoffmann, R. W. Alder and C. F. Wilcox Jr, J. Am. Chem. Soc., 1970, 92, 4992 CrossRef CAS.
- J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419 CrossRef CAS.
- (a) K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937 CrossRef CAS PubMed; (b) Z. X. Wang and P. v. R. Schleyer, Science, 2001, 292, 2465 CrossRef CAS PubMed.
- (a) L. M. Yang, E. Ganz, Z.-F. Chen, Z. X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468 CrossRef CAS PubMedand the references therein. (b) H. Li, X. Tian, X. M. Luo, M. Yan, Y. Mu, H. G. Lu and S.-D. Li, Sci. Rep., 2017, 7, 5701 CrossRef PubMed; (c) X.-F. Zhao, J.-J. Li, H. Li, C. Yuan, X. Tian, S.-D. Li, Y.-B. Wu, J.-C. Guo and Z.-X. Wang, Phys. Chem. Chem. Phys., 2018, 20, 7217 RSC.
- (a) V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114 CrossRef CASand the references therein. (b) P. Liu, J.-H. Bian, Q. Wang, F. Huang, D. Li and Y.-B. Wu, Phys. Chem. Chem. Phys., 2018, 20, 12642 RSC; (c) S. Pan, J. L. Cabellos, M. Orozco-lc, P. K. Chattaraj, L. L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350 RSC.
- S. D. Li, C. Q. Miao and G. M. Ren, Eur. J. Inorg. Chem., 2004, 2232 CrossRef.
- Q. Luo, Sci. China, Ser. B: Chem., 2008, 51, 1030 CrossRef CAS.
- S. Erhardt, G. Frenking, Z. Chen and R. S. P. Schleyer, Angew. Chem., Int. Ed., 2005, 44, 1078 CrossRef CAS PubMed.
- Y. Pei, W. An, K. Ito, P. v. R. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394 CrossRef CAS PubMed.
- (a) J. O. C. Jimenez-Halla, Y.-B. Wu, Z.-X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776 RSC; (b) Y.-B. Wu, Y. Duan, H. G. Lu and S.-D. Li, J. Phys. Chem. A, 2012, 116, 3290 CrossRef CAS PubMed.
- X. Y. Zhang and Y. H. Ding, Comput. Theor. Chem., 2014, 1048, 18 CrossRef CAS.
- A. C. Castro, G. Martinez-Guajardo, T. Johnson, J. M. Ugalde, Y.-B. Wu, J. M. Mercero, T. Heine, K. J. Donald and G. Merino, Phys. Chem. Chem. Phys., 2012, 14, 14764 RSC.
- Z. H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y. H. Ding and G. Merino, Chem. Commun., 2017, 53, 138 RSC.
- S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350 RSC.
- J. Xu, X. Zhang, S. Yu, Y.-h. Ding and K. H. Bowen, J. Phys. Chem. Lett., 2017, 8, 2263 CrossRef CAS PubMed.
- (a) R. Grande-Aztatzi, J. L. Cabellos, R. Islas, I. Infante, J. M. Mercero, A. Restrepo and G. Merino, Phys. Chem. Chem. Phys., 2015, 17, 4620 RSC; (b) J. C. Guo, G. M. Ren, C. Q. Miao, W. J. Tian, Y. B. Wu and X. T. Wang, J. Phys. Chem. A, 2015, 119, 13101 CrossRef CAS PubMed.
- J.-C. Guo, W.-J. Tian, Y.-J. Wang, X.-F. Zhao, Y.-B. Wu, H.-J. Zhai and S.-D. Li, J. Chem. Phys., 2016, 144, 244303 CrossRef PubMed.
- J.-C. Guo, L. Y. Feng, X.-Y. Zhang and H. J. Zhai, J. Phys. Chem. A, 2018, 122, 1138 CrossRef CAS PubMed.
- J.-J. Li, Y. Mu, X. Tian, C. Yuan, Y.-B. Wu, Q. Wang, D. Li, Z.-X. Wang and S.-D. Li, J. Mater. Chem. C, 2017, 5, 408 RSC.
- (a) Y.-B. Wu, J. L. Jiang, R. W. Zhang and Z.-X. Wang, Chem.–Eur. J., 2010, 16, 1271 CrossRef CAS PubMed; (b) X.-F. Zhao, H. Li, C. Yuan, Y.-Q. Li, Y.-B. Wu and Z.-X. Wang, J. Comput. Chem., 2016, 37, 261 CrossRef CAS PubMed; (c) C. Yuan, X.-F. Zhao, Y.-B. Wu and X. Wang, Angew. Chem., Int. Ed., 2016, 55, 15651 CrossRef CAS PubMed; (d) Z.-Z. Qin, Q. Wang, C. Yuan, Y.-T. Yang, X.-F. Zhao, D. Li, P. Liu and Y.-B. Wu, Dalton Trans., 2018, 47, 4707 RSC.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- (a) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed; (b) L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291 CrossRef CAS PubMed.
- (a) M. Saunders, J. Comput. Chem., 2004, 25, 621 CrossRef CAS PubMed; (b) P. P. Bera, K. W. Sattelmeyer, M. Saunders, H. F. Schaefer and P. v. R. Schleyer, J. Phys. Chem. A, 2006, 110, 4287 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- (a) P. v. R. Schleyer, C. Maerker, A. Dransfeld, H.-J. Jiao and N. J. R. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317 CrossRef CAS PubMed; (b) Z. F. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207 RSC.
- J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, J. Chem. Phys., 1999, 111, 3800 CrossRef CAS.
- H. G. Lu and Y.-B. Wu, in GXYZ 2.0: A Random Search Program, Shanxi University, Taiyuan, China, 2015 Search PubMed.
- H.-J. Werner, et al., in MolPro 2012.1, University College Cardiff Consultants Limited, Cardiff, UK, 2012 Search PubMed.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1., 1990 Search PubMed.
- M. J. Frisch, et al., in Gaussian 09 Revision D.01, Gaussian Inc., Wallingford, CT, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The AdNDP and NICS results mentioned in the text, the structures and relative energies of isomers, as well as the necessary Cartesian coordinates. See DOI: 10.1039/c8ra07664b |
| This journal is © The Royal Society of Chemistry 2018 |