Open Access Article
Open Access ArticleIon transport through a nanoporous C2N membrane: the effect of electric field and layer number
You-sheng Yuab,
Lu-yi Huanga,
Xiang Lua and
Hong-ming Ding *b
*b
aNational Laboratory of Solid State Microstructures, Department of Physics, Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China
bCenter for Soft Condensed Matter Physics and Interdisciplinary Research, School of Physical Science and Technology, Soochow University, Suzhou 215006, China. E-mail: dinghm@suda.edu.cn
First published on 30th October 2018
Abstract
Ion transport through a two-dimensional membrane with nanopores plays an important role in many scientific and technical applications (e.g., water desalination, ion separation and nanofiltration). Although there have been many two-dimensional membranes for these applications, the problem of how to controllably fabricate nanopores with proper shape and size still remains challenging. In the present work, the transport of ions through a C2N membrane with intrinsically regular and uniformly distributed nanopores is investigated using all-atom molecular dynamic simulations. It was found that the monolayer C2N membrane possesses higher ion permeability compared to the graphene membrane because of its higher density of nanopores. In addition, it exhibits excellent ion selectivity under a low electric field due to the distinct dehydration capabilities and interaction behaviors (with the pore edges) of the different ions. Furthermore, we found that multilayer C2N membranes have weak ion selectivity, but show promising potential for desalination. The present study may provide some physical insights into the experimental design of C2N-based nanodevices in nanofluids.
1 Introduction
In recent years, ion transport through membranes with nanosized pores or channels has become a rapidly growing research field. For example, ion transport through cell membranes via ion channels is a key process in biology.1 Ion transport through semipermeable membranes is widely used in desalination,2–10 nanofiltration11–19 and nanofluids.20–25 In general, the transport behavior is mainly affected by electrostatic interactions, steric exclusion of the hydration shell and coordination with the solvent or functional group at the pore edges, where the size of the pore or channel in the membrane plays a key role. For example, K+ and Cl− (their hydrated diameters are about 0.66 nm) cannot be transported through a neutrally charged graphene nanopore with a diameter of 0.4 nm, but they can cross a graphene nanopore with a diameter of 0.8 nm.14 Nevertheless, if the pore is functionalized with a charged or partially charged functional group, the critical size of the pore can be changed (for ion transport). For example, Král et al.26 reported that a 0.5 nm-diameter graphene nanopore functionalized with F–N atoms allowed the transport of ions (Li+, Na+ and K+), due to the fact that the charged nanopore could reduce the transport energy barrier of ions carrying the opposite charge.As mentioned before, graphene is one of the most widely used 2D membranes for ion transport.27,28 In addition to graphene membranes, other materials (e.g., TiO2,29 silica30 and MoS2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31) can also be used as membranes for ion transport. However, these two-dimensional materials encounter the same limitations, namely, they must have some pre-treatment for real applications because they do not have inherent nanopores for mass transport. Despite the rapid development of nanotechnology, it is still difficult to fabricate nanopores with a proper shape and size for ion selectivity at present. Additionally, to resolve the trade-off between selectivity and permeability, the membrane generally needs a high density of nanopores.32
31) can also be used as membranes for ion transport. However, these two-dimensional materials encounter the same limitations, namely, they must have some pre-treatment for real applications because they do not have inherent nanopores for mass transport. Despite the rapid development of nanotechnology, it is still difficult to fabricate nanopores with a proper shape and size for ion selectivity at present. Additionally, to resolve the trade-off between selectivity and permeability, the membrane generally needs a high density of nanopores.32
As new 2D materials, C2N membranes have recently attracted great attention,33–38 and possess intrinsic regular and uniformly distributed nanopores with subnanometer diameters, and have an extremely high thermal stability and a tunable wide band gap.39,40 Thus, they may have inherent advantages for different molecules with different sizes. For example, a strained C2N membrane can serve as a filter for highly efficient water desalination. It has been found that only water from seawater can permeate the C2N membrane, their flux is strengthened by one to four orders of magnitude relative to that of other membranes and the transport behavior can be precisely controlled with tensile strain.34–36 Additionally, C2N membranes also possess excellent capability for gas separation. Liu et al.41 showed that C2N membranes exhibit remarkable selectivity for H2 from among other atmospheric gases. Xing et al.42 reported that C2N membranes exhibit an exceptional ability to separate He from natural gas with a high permeability (1 × 107 GPU) for He at room temperature. Although great progress has been made on water and gas separation using C2N membranes, to the best of our knowledge, there has still been no attempt to use a C2N membrane for ion transport and selectivity, which may hinder its wider application in nanotechnology.
In this work, we mainly focus on the transport of ions (i.e., Li+, Na+ and K+) through a C2N membrane using all-atom molecular dynamic (MD) simulations. As we will show below, the monolayer C2N membrane exhibits higher ion permeability (compared to that of graphene) and excellent ion selectivity under a low electric field. The underlying mechanism of the ion selectivity will be discussed in detail. Furthermore, the effect of the layer number of the C2N membrane on the ion transport and electroosmosis will also be investigated.
2 Methods
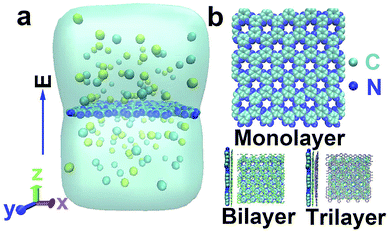
As shown in Fig. 1a, our simulation system contained one C2N membrane, water molecules and ions (Li+, Na+, K+ and Cl−). The modeling of the C2N membrane was taken from work by Zhou et al.37 It had multiple nanopores with diameters of ∼0.41 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 and was placed in the middle of the simulation box. The parallel edges of the C2N membrane were covalently bonded to each other to form an infinitely large membrane. In the present paper, three categories of C2N membranes with different numbers of layers (monolayer, bilayer and trilayer) were constructed. In the case of the multilayer membrane, the distance between the adjacent membranes was about 0.34 nm and the stacking was A–B–C40 (see Fig. 1b). The size of the simulation box was about 4.20 × 4.40 × 6.00 nm3. Periodic boundary conditions were adopted in all three directions. The system was solvated with water molecules and salts (NaCl, LiCl and KCl) with a concentration of 1.0 M unless otherwise stated.
35 and was placed in the middle of the simulation box. The parallel edges of the C2N membrane were covalently bonded to each other to form an infinitely large membrane. In the present paper, three categories of C2N membranes with different numbers of layers (monolayer, bilayer and trilayer) were constructed. In the case of the multilayer membrane, the distance between the adjacent membranes was about 0.34 nm and the stacking was A–B–C40 (see Fig. 1b). The size of the simulation box was about 4.20 × 4.40 × 6.00 nm3. Periodic boundary conditions were adopted in all three directions. The system was solvated with water molecules and salts (NaCl, LiCl and KCl) with a concentration of 1.0 M unless otherwise stated.
In this work, all-atom MD simulations were carried out with a Gromacs 5.0.4 package43 with an amber99sb force field. The TIP3P water model was chosen. The force field parameters for the C2N membrane were taken from the work of Zhou et al.37 LINCS constraints were used for all bonds involving hydrogen atoms. The particle mesh Ewald method was used when calculating the long-range electrostatic interactions, and the Lennard-Jones (LJ) interactions were cut off at a distance of 1.2 nm.
During the simulations, the systems were firstly energy-minimized for about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. Then 2 ns of NPT equilibration (the pressure coupling was isotropic in the x and y directions, but different in the z direction) was performed. Finally the translocation process of the ions through the membrane under an external electric field was simulated for 50 ns at the NVT ensemble. To save computing time, here we used a relatively strong electric field, which is a commonly used method (to speed up the translocation process) in simulations.44–48 In the case of the monolayer membrane, the N and C atoms of the C2N membrane were harmonically restrained with a spring constant of 1000 kJ mol−1 nm−2. In the case of the multilayer membrane, the membrane in the bottom layer was harmonically restrained and the remaining layers were free. The Nose–Hoover method with a time constant of 0.1 ps was used to keep the temperature at 300 K,49 and the pressure was kept at 1 bar using the Parrinello–Rahman method with a time constant of 0.1 ps.50 Each system was performed three times by changing the speed seed to obtain an error estimate. The integration time step was 2 fs. The ionic current was calculated using51,52
000 steps. Then 2 ns of NPT equilibration (the pressure coupling was isotropic in the x and y directions, but different in the z direction) was performed. Finally the translocation process of the ions through the membrane under an external electric field was simulated for 50 ns at the NVT ensemble. To save computing time, here we used a relatively strong electric field, which is a commonly used method (to speed up the translocation process) in simulations.44–48 In the case of the monolayer membrane, the N and C atoms of the C2N membrane were harmonically restrained with a spring constant of 1000 kJ mol−1 nm−2. In the case of the multilayer membrane, the membrane in the bottom layer was harmonically restrained and the remaining layers were free. The Nose–Hoover method with a time constant of 0.1 ps was used to keep the temperature at 300 K,49 and the pressure was kept at 1 bar using the Parrinello–Rahman method with a time constant of 0.1 ps.50 Each system was performed three times by changing the speed seed to obtain an error estimate. The integration time step was 2 fs. The ionic current was calculated using51,52
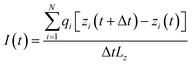 | (1) |
To calculate the free energy for ion transport through the C2N membrane (in the absence of an electric field), biased simulations were done using a harmonic potential with a force constant of 1000 kJ mol−1 nm−2 applied to restrain the position of the single ion. The reaction coordinate was defined as the distance in the z direction between the ion and the center of one certain pore of the C2N membrane. Since the potential of mean force (PMF) from the two sides of the membrane should be symmetric,46 we just calculated the PMF when z = −1.0 ∼ 0 nm (divided into 10 windows of 0.1 nm), and the PMF for 0 ∼ 1.0 nm was reproduced from that for −1.0 ∼ 0 nm. The weighted histogram analysis method (WHAM)53,54 was then applied to calculate the potential of mean force after 12 ns of simulation for each window (the first 4 ns were used to reach equilibrium and the last 8 ns were used for PMF calculation).
3 Results and discussion
3.1 Ion transport through the monolayer C2N membrane driven by an electric field
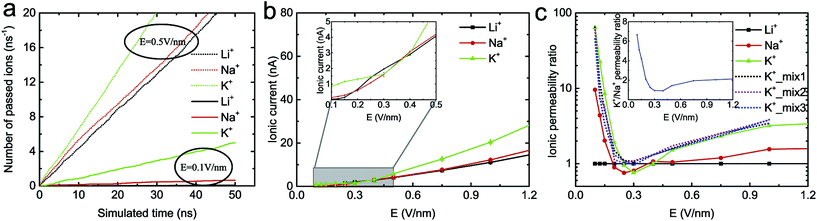
Fig. 2a shows the relationship between the number of passed ions and the simulated time under an electric field. It was found that the number of passed ions changes linearly with time, indicating that the ion transport is stable. Then, the ionic currents of three types of ion through the monolayer C2N membrane under different electric fields were calculated (see Fig. 2b). As expected, with an increase in electric field, the currents of each ion nonlinearly increase due to the accelerated dehydration of the cation shell under the higher electric field.27,55,56 Notably, the current of the K+ ion through a single nanopore in the C2N membrane is about 1.16/30 ≈ 0.039 nA under E = 0.15 V nm−1, where 30 is the number of nanopores in the C2N membrane. It is approximately the same as that from a single pore in a graphene membrane (0.032 nA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57) under the same conditions. However, the density of nanopores in the C2N membrane35 (∼1014 cm−2) is two orders greater in magnitude than that in the graphene membrane27 (∼1012 cm−2). As a result, the ion permeability of the monolayer C2N membrane is much larger than that of the graphene membrane. Moreover, Fig. 2b also shows that the ions with smaller hydrated diameters (the Li+ hydrated diameter is 0.76 nm, the Na+ hydrated diameter is 0.72 nm and the K+ hydrated diameter is 0.66 nm
57) under the same conditions. However, the density of nanopores in the C2N membrane35 (∼1014 cm−2) is two orders greater in magnitude than that in the graphene membrane27 (∼1012 cm−2). As a result, the ion permeability of the monolayer C2N membrane is much larger than that of the graphene membrane. Moreover, Fig. 2b also shows that the ions with smaller hydrated diameters (the Li+ hydrated diameter is 0.76 nm, the Na+ hydrated diameter is 0.72 nm and the K+ hydrated diameter is 0.66 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27) have larger ionic currents under the same electric field. However, this trend does not appear under an electric field of 0.25 V nm−1 to 0.4 V nm−1 (see the inset in Fig. 2b).
27) have larger ionic currents under the same electric field. However, this trend does not appear under an electric field of 0.25 V nm−1 to 0.4 V nm−1 (see the inset in Fig. 2b).
To better compare the performance of the membrane in applications such as ion separation, the ionic permeability ratio (defined as the ratio of the number of passed ions to the number of passed Li+ ions) under different electric fields was then calculated (Fig. 2c). It was found that the ratio of K+ and Na+ relative to Li+ was very high when the electric field was low. Then it rapidly decreased, before increasing gradually and then finally reaching equilibrium as the electric field went on increasing. A similar phenomenon was also observed in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary K+/Li+ mixed solution with the total concentrations 0.5 M, 1.0 M and 1.5 M (see the dashed line in Fig. 2c). In addition, very little difference existed between the three mixed solutions, which also indicates that the concentration of ions may have little influence on the ion selectivity. The ratio of K+ relative to Na+ (as a function of the electric field) was nearly identical to that of K+ relative to Li+ (see inset in Fig. 2c), which is consistent with that observed in the case of the graphene nanopore functionalized with carbonyl groups.58 Generally, the C2N membrane exhibits excellent ion selectivity, especially under a low electric field. The ions with smaller hydrated diameters generally have higher selectivity under the same electric field for the monolayer C2N membrane, in line with other membranes.32,59 In all the simulations, we found that the Cl− ion could not pass through the monolayer C2N membrane because the N atoms (carrying negative charges, −0.48e) were around the nanopores of the membrane. These negatively charged atoms can prevent the transport of Cl− ions, indicating that the monolayer C2N membrane exhibits cation selectivity.
1 binary K+/Li+ mixed solution with the total concentrations 0.5 M, 1.0 M and 1.5 M (see the dashed line in Fig. 2c). In addition, very little difference existed between the three mixed solutions, which also indicates that the concentration of ions may have little influence on the ion selectivity. The ratio of K+ relative to Na+ (as a function of the electric field) was nearly identical to that of K+ relative to Li+ (see inset in Fig. 2c), which is consistent with that observed in the case of the graphene nanopore functionalized with carbonyl groups.58 Generally, the C2N membrane exhibits excellent ion selectivity, especially under a low electric field. The ions with smaller hydrated diameters generally have higher selectivity under the same electric field for the monolayer C2N membrane, in line with other membranes.32,59 In all the simulations, we found that the Cl− ion could not pass through the monolayer C2N membrane because the N atoms (carrying negative charges, −0.48e) were around the nanopores of the membrane. These negatively charged atoms can prevent the transport of Cl− ions, indicating that the monolayer C2N membrane exhibits cation selectivity.
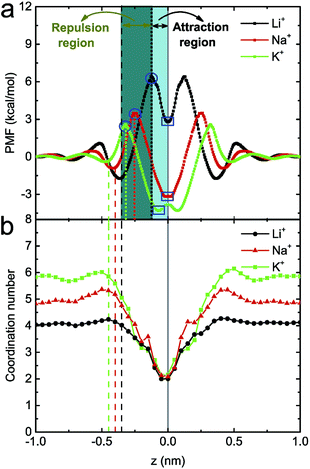
To study the underlying mechanism of the ion selectivity, the potential of mean force (PMF) of a single ion being transported through the monolayer C2N membrane (in the absence of an electric field) was calculated (see Fig. 3a). Taking the Li+ ion as an example, when it approaches the C2N membrane, due to the deformation of the hydration shell, the PMF firstly increases slowly. As it goes on approaching membrane, the PMF will then decrease a bit and reach a minimum at z = −0.36 nm, which is mainly attributed to the attraction interaction between the cation and the negatively charged nanopore (i.e., N atom). With the further decrease in z, due to the dehydration of the ion (the coordination number of ions with water molecules begins to decrease, see Fig. 3b), the PMF will again increase, and reach a maximum when z is about −0.12 nm (see the blue circles in Fig. 3a). Nevertheless, when the ion and the pore are very close, the electrostatic interaction becomes very large, and could be much larger than the dehydration-induced exclusion interaction. Hence, the PMF will again decrease and reach a minimum when z = 0 nm (see the blue rectangles in Fig. 3a). To better discuss the position distribution in the following sections, we define the region between the center of the C2N membrane (solid line) and the maximum (dotted line) in the PMF as the attraction region, and the region between the minimum (dashed line) and the maximum (dotted line) in the PMF as the repulsion region (see Fig. 3a). Similar phenomena were also observed in the case of Na+ and K+ ions although the values for the energy barrier/well and the corresponding z coordinates were different. In more detail, for the three types of ion, the heights of the energy barriers are about 2.9 kcal mol−1 (K+), 4.4 kcal mol−1 (Na+) and 8.0 kcal mol−1 (Li+), and the depths of energy wells are about −6.9 kcal mol−1 (K+), −6.6 kcal mol−1 (Na+) and −3.5 kcal mol−1 (Li+). The difference in the PMFs for the three types of ion at the pore position may originate from their different coordination abilities with N atoms. Since K+ has the lowest potential barrier and the deepest potential well, it is easiest for K+ to translocate through the membrane. In contrast, as Li+ has the highest potential barrier and the most shallow potential well, it is difficult for it to translocate through the membrane.
To further explain the distinct ion selection behaviors under high and low electric fields, the position probability distribution of ions along the z direction under E = 1.0 V nm−1, 0.1 V nm−1 and 0.3 V nm−1 were calculated (see Fig. 4). Under a high electric field (see Fig. 4a), the Li+ ions are mainly distributed at z = −0.37 nm (around the repulsion region), indicating that it is not easy for a Li+ ion to be transported through the C2N membrane, probably due to its higher hydration energy. The Na+ ions are mainly located at z = −0.48 nm and z = −0.22 nm, partly in the repulsion region and partly in the attraction region. As a result, there are more chances for a Na+ ion passing through the membrane (compared to those for a Li+ ion). Moreover, due to their lower hydration energy, the K+ ions are mainly located around the attraction region (z = −0.27 nm), where the ions can have their translocation facilitated. Under a low electric field, since the ions are mainly distributed far away from the pores (see Fig. 4b), the probability of ion transport should be much lower (when compared to that under a high electric field). In particular, as previously mentioned, the Li+ ion has the highest energy barrier and a low external field can hardly drive the Li+ ion through the pore (the position distribution of a Li+ ion inside the nanopore is nearly zero). Meanwhile, for a Na+ ion, a peak in the number density profile appears at z = 0 nm, indicating that the dwell time of a Na+ ion is elongated; for a K+ ion, a peak appears at the exit of the nanopore (z = 0.13 nm), meaning that the number of passed K+ ions has increased. These lead to a more obvious difference between the transport ability of the three ions at E = 0.1 V nm−1. In the case of E = 0.3 V nm−1, it was found that the three types of ion are mainly distributed in the repulsion region, and their distribution inside the nanopore is mostly the same (see Fig. 4c). Thus no obvious difference between the transport ability of the three ions occurs under this electric field.
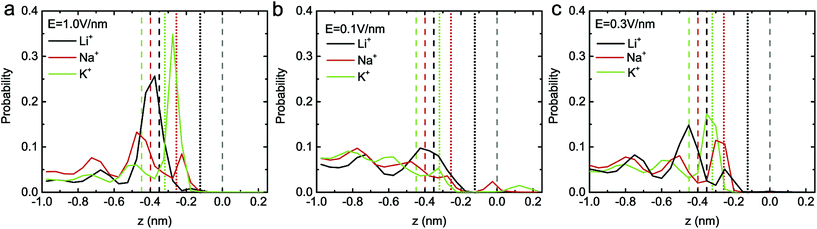 | ||
| Fig. 4 The position probability distribution of ions along the z direction under the electric fields E = 1.0 V nm−1 (a), E = 0.1 V nm−1 (b) and E = 0.3 V nm−1 (c). The meaning of the solid, dashed and dotted lines is the same as that in Fig. 3a. | ||
3.2 Ion transport through the multilayer C2N membrane driven by an electric field
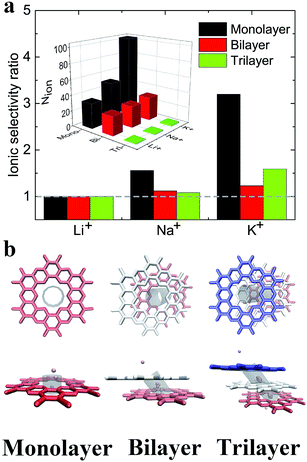
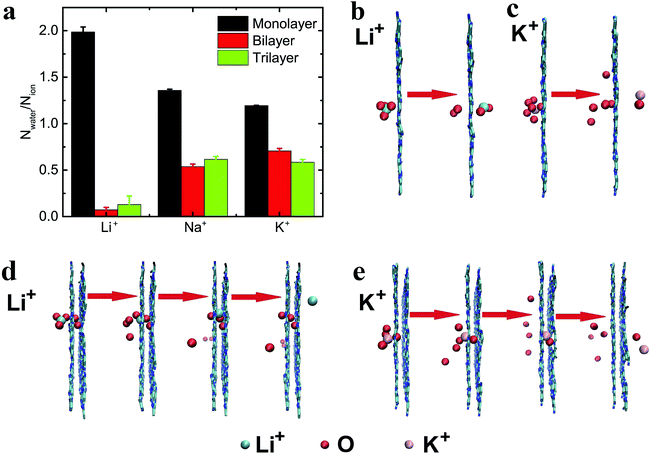
Previous reports have shown that multilayer membranes possess higher ion selectivity, attributed to the extension of the selection region.8,60 Here, the translocation of ions through the multilayer C2N membrane was also investigated under the electric field E = 1.0 V nm−1. As shown in the inset in Fig. 5a, it was found that ions with smaller hydrated diameters have larger passing rates regardless of the layer number. It also shows that the number of passed ions decreases with the increase in the number of layers. Additionally, the ionic selectivity for the monolayer C2N membrane is larger than that for the multilayer C2N membrane (see Fig. 5a). This means that increasing the number of layers cannot increase the ion selectivity for the C2N membrane, which seems to contradict the results from the graphene membrane.23To provide a possible explanation for the above results, typical snapshots of an ion passing through the C2N membranes are shown in Fig. 5b. Due to the electrostatic interactions and van der Waals interactions, the multilayer C2N membrane shows the A–B–C stacking mode,40 which is different from the aligned stacking mode in the graphene membrane. This unique stacking mode causes a decrease in the effective area of the pores (see Fig. 5b). Meanwhile, increasing the number of layers leads to an increase in channel length and roughness in the interior surface of the pores. As a result, the transport time of the ions through the membrane increases. As shown in Fig. 5b, K+ ions stay longer in the region between the adjacent C2N sheets when passing through the trilayer C2N membrane. This means that the ion passing rate in the case of the multilayer membrane is lower than that in that in the case of the monolayer membrane. Additionally, the K+ ion has a larger size compared to that of the Na+ ion and Li+ ion (the ionic radii of K+, Na+ and Li+ are 0.133 nm, 0.095 nm, 0.06 nm, respectively), resulting in a larger resistance. Thus, the K+ ion has a larger decrement. To summarize, the decreased ion passing rate in thick C2N membranes mainly originates from the increase in the length of the channels and the decrease in the effective area of the pores.
3.3 Electroosmosis induced by ion transport
The ion flow (through nanopores) driven by the electric field can lead to electroosmosis.60 To describe the electroosmotic flow, the mean number of passed water molecules (in the ionic hydration shell) induced by one passed ion (i.e., Nwater/Nion) was computed.60,61 As can be seen from Fig. 6a, the ratios of three types of ion for the monolayer C2N membrane are all larger than 1, while the ratios for the multilayer C2N membrane are all smaller than 1, indicating that the ion capability for dragging and pushing water is reduced with an increase in layer number. In addition, in the case of the monolayer C2N membrane, smaller ions (with larger hydrated diameters) have a stronger capability for electroosmosis, which is consistent with the results with graphene functionalized by F–N atoms.60 To further analyze the electroosmosis, typical snapshots of the transport process were taken. As shown in Fig. 6b, two water molecules distributed at both sides of the ions can be pushed and dragged by the Li+ ions, resulting in the permeation of both the ions and the water molecules through the monolayer membrane. In contrast, when the size of the ion increases, the partial water molecules around the K+ ion can be dragged (see Fig. 6c), leading to a smaller number of passed water molecules.In the case of the multilayer C2N membrane, ions of a smaller size drag fewer water molecules through the bilayer and trilayer C2N membranes. These results are the opposite to those with the monolayer C2N membrane. As a Li+ ion passes through the bilayer C2N membrane, due to its small size the relative position between the Li+ ion and the pushed water molecules can be adjusted inside the interlamination of the membrane (the line connecting the ion and the water molecule changes from perpendicular to parallel to the plane of the membrane, see Fig. 6d). As a result, the pushed water molecules will be stripped away from the ion when the Li+ ion further penetrates through the nanopore of the second layer. Thus, water molecules can hardly pass through the nanopore along with Li+ ions under these circumstances. On the other hand, with the increased ion size, the relative position of the water molecules and the K+ ion cannot be adjusted inside the interlamination of the membrane (see Fig. 6e). Consequently, the pushed water molecule will not be stripped away from the K+ ion when the ion goes on passing through the second layer, and can permeate the nanopore along with the ions. In general, the electroosmosis flow of the multilayer C2N membrane is smaller than that of the monolayer C2N membrane, but the multilayer C2N membrane may be well-suited as a cathode material for water desalination using an electroosmotic flow (the removal of ions from saline solution13).
4 Conclusion
In summary, three types of ion transport through C2N membranes under an electric field have been investigated using all-atom molecular dynamics simulations. When the ions pass through a monolayer C2N membrane, the ionic current nonlinearly increases with the electric field, and the current is larger than that in the case of a graphene membrane, which is mainly due to its higher density of nanopores. Moreover, it was found that the monolayer C2N membrane presents excellent ion selectivity (especially under a low electric field) due to the distinct dehydration ability of different ions and the interactions between the ions and the pore edges. In addition, the effect of the layer number of the C2N membrane on the ion transport was also studied. Interestingly, the multilayer C2N membrane showed the weaker ion selectivity, but has potential for desalination. Overall, this work can help us better understand the underlying mechanism of the transport of ions through a charged nanopore, and may shed light on the design of C2N membrane based nanodevices in real applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 21604060, 11474155, 11874045 and 11774147). We are grateful to the High Performance Computing Center (HPCC) of Nanjing University for doing the numerical calculations in this paper on its blade cluster system.References
- S. K. Bagal, A. D. Brown, P. J. Cox, K. Omoto, R. M. Owen, D. C. Pryde, B. Sidders, S. E. Skerratt, E. B. Stevens, R. I. Storer and N. A. Swain, J. Med. Chem., 2013, 56, 593–624 CrossRef CAS PubMed.
- D. Cohen-Tanugi and J. C. Grossman, Nano Lett., 2012, 12, 3602–3608 CrossRef CAS PubMed.
- J. W. Feng, H. M. Ding and Y. Q. Ma, Phys. Chem. Chem. Phys., 2016, 18, 28290–28296 RSC.
- L. Y. Wang, H. A. Wu and F. C. Wang, RSC Adv., 2017, 7, 20360–20368 RSC.
- E. Jordan, R. G. Bell, D. Wilmer and H. Koller, J. Am. Chem. Soc., 2006, 128, 558–567 CrossRef CAS PubMed.
- B. Corry, J. Phys. Chem. B, 2008, 112, 1427–1434 CrossRef CAS PubMed.
- B. Corry, Energy Environ. Sci., 2011, 4, 751–759 RSC.
- Z. Li, Y. Qiu, K. Li, J. Sha, T. Li and Y. Chen, J. Chem. Phys., 2018, 148, 014703 CrossRef PubMed.
- K. Li, Y. Tao, Z. Li, J. Sha and Y. Chen, Nanotechnology, 2017, 29, 035402 CrossRef PubMed.
- A. Kommu, S. Namsani and J. K. Singh, RSC Adv., 2016, 6, 63190–63199 RSC.
- J. W. Feng, H. M. Ding, C. L. Ren and Y. Q. Ma, Nanoscale, 2014, 6, 13606–13612 RSC.
- J. W. Feng, H. M. Ding and Y. Q. Ma, J. Chem. Phys., 2014, 141, 094901 CrossRef PubMed.
- J. Azamat, J. Phys. Chem. C, 2016, 120, 23883–23891 CrossRef CAS.
- S. Zhao, J. Xue and W. Kang, J. Chem. Phys., 2013, 139, 114702 CrossRef PubMed.
- Q. Yang, Y. Su, C. Chi, C. T. Cherian, K. Huang, V. G. Kravets, F. C. Wang, J. C. Zhang, A. Pratt and A. N. Grigorenko, Nat. Mater., 2017, 16, 1198–1203 CrossRef CAS PubMed.
- Q. L. Lei, R. Ni and Y. Q. Ma, ACS Nano, 2018, 12, 6860–6870 CrossRef CAS PubMed.
- A. Esfandiar, B. Radha, F. C. Wang, Q. Yang, S. Hu, S. Garaj, R. R. Nair, A. K. Geim and K. Gopinadhan, Science, 2017, 358, 511–513 CrossRef CAS PubMed.
- L. Chen, G. Shi, J. Shen, B. Peng, B. Zhang, Y. Wang, F. Bian, J. Wang, D. Li and Z. Qian, Nature, 2017, 550, 380–383 CrossRef CAS PubMed.
- J. Lyu, X. Wen, U. Kumar, Y. You, V. Chen and R. K. Joshi, RSC Adv., 2018, 8, 23130–23151 RSC.
- Y. Yu, X. Lu, H. Ding and Y. Ma, Phys. Chem. Chem. Phys., 2018, 20, 9063–9069 RSC.
- H. M. Ding, W. D. Tian and Y. Q. Ma, ACS Nano, 2012, 6, 1230–1238 CrossRef CAS PubMed.
- L. Liang, J. Li, L. Zhang, Z. Zhang, J. Shen, L. Li and J. Wu, Phys. Chem. Chem. Phys., 2017, 19, 30031–30038 RSC.
- S. Sahu and M. Zwolak, Nanoscale, 2017, 9, 11424–11428 RSC.
- Q. Zheng, Q. Xue, K. Yan, L. Hao, Q. Li and X. Gao, J. Phys. Chem. C, 2007, 111, 4628–4635 CrossRef CAS.
- K. Yang and Y. Q. Ma, Nat. Nanotechnol., 2010, 5, 579–583 CrossRef CAS PubMed.
- K. Sint, B. Wang and P. Král, J. Am. Chem. Soc., 2008, 130, 16448–16449 CrossRef CAS PubMed.
- L. Wang, B. Msh, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Nat. Nanotechnol., 2017, 12, 509–522 CrossRef CAS PubMed.
- R. C. Rollings, A. T. Kuan and J. A. Golovchenko, Nat. Commun., 2016, 7, 11408 CrossRef CAS PubMed.
- D. Li, W. Jing, S. Li, H. Shen and W. Xing, ACS Appl. Mater. Interfaces, 2015, 7, 11294–11300 CrossRef CAS PubMed.
- M. Duke, J. da Costa, D. Do, P. Gray and G. Lu, Adv. Funct. Mater., 2006, 16, 1215–1220 CrossRef CAS.
- J. Feng, K. Liu, M. Graf, D. Dumcenco, A. Kis, M. DiVentra and A. Radenovic, Nat. Mater., 2016, 15, 850 CrossRef CAS PubMed.
- P. Wang, M. Wang, F. Liu, S. Ding, X. Wang, G. Du, J. Liu, P. Apel, P. Kluth and C. Trautmann, Nat. Commun., 2018, 9, 569 CrossRef PubMed.
- L. Zhu, Y. Jin, Q. Xue, X. Li, H. Zheng, T. Wu and C. Ling, J. Mater. Chem. A, 2016, 4, 15015–15021 RSC.
- Z. Hu, B. Liu, M. Dahanayaka, A. W. Law, J. Wei and K. Zhou, Phys. Chem. Chem. Phys., 2017, 19, 15973–15979 RSC.
- Y. Yang, W. Li, H. Zhou, X. Zhang and M. Zhao, Sci. Rep., 2016, 6, 29218 CrossRef CAS PubMed.
- B. Liu, A. W. Law and K. Zhou, J. Membr. Sci., 2018, 550, 554–562 CrossRef CAS.
- B. Li, W. Li, J. M. Perez-Aguilar and R. Zhou, Small, 2017, 13, 1603685 CrossRef PubMed.
- Z. Gu, L. Zhao, S. Liu, G. Duan, J. M. Perez-Aguilar, J. Luo, W. Li and R. Zhou, ACS Nano, 2017, 11, 3198–3206 CrossRef CAS PubMed.
- H. Sahin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085421 CrossRef.
- R. Zhang, B. Li and J. Yang, Nanoscale, 2015, 7, 14062–14070 RSC.
- B. Xu, H. Xiang, Q. Wei, J. Q. Liu, Y. D. Xia, J. Yin and Z. G. Liu, Phys. Chem. Chem. Phys., 2015, 17, 15115–15118 RSC.
- L. Zhu, Q. Xue, X. Li, T. Wu, Y. Jin and W. Xing, J. Mater. Chem. A, 2015, 3, 21351–21356 RSC.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- H. Zhang, J. Hou, Y. Hu, P. Wang, R. Ou, L. Jiang, J. Z. Liu, B. D. Freeman, A. J. Hill and H. Wang, Sci. Adv., 2018, 4, eaaq0066 CrossRef PubMed.
- Y. Zhu, Y. Ruan, Y. Zhang, Y. Chen, X. Lu and L. Lu, Langmuir, 2017, 33, 9201–9210 CrossRef CAS PubMed.
- Y. Kang, Z. Zhang, H. Shi, J. Zhang, L. Liang, Q. Wang, H. Agren and Y. Tu, Nanoscale, 2014, 6, 10666–10672 RSC.
- G. Hu, M. Mao and S. Ghosal, Nanotechnology, 2012, 23, 395501 CrossRef PubMed.
- H. Zhang, B. Liu, M. S. Wu, K. Zhou and W. K. Law, Comput. Mater. Sci., 2017, 131, 100–107 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- W. Lv, M. Chen and R. Wu, Soft Matter, 2013, 9, 960–966 RSC.
- C. Sathe, X. Zou, J. P. Leburton and K. Schulten, ACS Nano, 2011, 5, 8842–8851 CrossRef CAS PubMed.
- S. Kumar, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- J. S. Hub, B. L. D. Groot and D. V. D. Spoel, J. Chem. Phys., 2015, 6, 3713–3720 Search PubMed.
- H. Qi, Z. Li, Y. Tao, W. Zhao, K. Lin, Z. Ni, C. Jin, Y. Zhang, K. Bi and Y. Chen, Nanoscale, 2018, 10, 5350–5357 RSC.
- T. Jain, B. C. Rasera, R. J. Guerrero, M. S. Boutilier, S. C. O’Hern, J. C. Idrobo and R. Karnik, Nat. Nanotechnol., 2015, 10, 1053 CrossRef CAS PubMed.
- S. Sahu, M. Di Ventra and M. Zwolak, Nano Lett., 2017, 17, 4719–4724 CrossRef CAS PubMed.
- Z. He, J. Zhou, X. Lu and B. Corry, ACS Nano, 2013, 7, 10148–10157 CrossRef CAS PubMed.
- Y. G. Yan, W. S. Wang, W. Li, K. P. Loh and J. Zhang, Nanoscale, 2017, 9, 18951–18958 RSC.
- Y. Yan, W. Li and P. Král, Nano Lett., 2017, 17, 6742–6746 CrossRef CAS PubMed.
- W. Li, W. Wang, Y. Zhang, Y. Yan, C. Dai and J. Zhang, J. Phys. Chem. C, 2017, 121, 17523–17529 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |